Abstract
The representation of land use (LU) in meteorological modeling strongly influences the simulation of fluxes of heat, moisture, and momentum; affecting the accuracy of 2-m temperature and precipitation. Here, the Weather Research and Forecasting (WRF) model is used with the Noah land surface model to compare a mosaic approach, which accounts for subgrid scale variability of LU types, to the default option which only considers the dominant category in each grid cell. Three-year historical dynamically downscaled WRF simulations are generated using a 12-km domain over the contiguous U.S. to assess the sensitivities to using mosaic LU and to changes to parameters associated with LU and soil categories. Compared to dominant LU, mosaic LU features decreased coverage of forest and agricultural types and increased low-density urban LU throughout much of the eastern and central U.S. However, highly urbanized areas show the opposite trend, as mosaic LU represents partial greenspace within areas that are exclusively urban within dominant LU. Mosaic LU results in widespread increases in sensible heat fluxes and 2-m temperatures, with reductions in latent heat flux, 2-m mixing ratio, and monthly precipitation across the central and eastern U.S. These changes exacerbate an existing warm bias found with dominant LU but reduce overestimations of precipitation. Highly urbanized areas in the eastern U.S. tend to have cooler, more realistic temperatures with mosaic LU relative to dominant LU. A pair of runs with updated surface parameters corroborates these results. Overall, differences between the simulations are largely attributable to their representations of urban LU.
1. Introduction
The representation of land use and land cover (hereinafter “LU”) plays a critical role in atmospheric modeling, as vegetation and surface properties influence fluxes of heat, moisture, and momentum between the land and atmosphere. These fluxes subsequently affect the simulation of temperature, winds, humidity, cloud cover, precipitation, and planetary boundary layer (PBL) height, among others. To ascertain threats to human health and ecosystems from pollutant concentrations or extreme weather events, these meteorological fields must be skillfully simulated using a realistic representation of the vegetative and radiative properties of the surface.
In the Weather Research and Forecasting (WRF) model, several vegetation and surface properties are defined according to LU type(s) within each grid cell. Various aspects of LU representation in WRF have previously been examined, including the use of different LU datasets (e.g., Sertel et al., 2009; Cheng et al., 2013; Yang & Duan et al., 2016; Mallard et al., 2018), methods of representing subgrid scale variability (e.g., Li et al., 2013a; Aas et al., 2017; Zhao & Wu, 2017), and the urban environment (e.g., Li et al., 2013b; Reames & Strensrud, 2017). These studies were all conducted at 3 km or finer grid spacings and across short temporal scales, except Mallard et al. (2018) and Zhao & Wu (2017) which used 36- and 30-km domains, respectively. While studies conducted at fine grid spacing can inform downscaling simulations for specific regions or locations, they are less applicable for continental-scale downscaling and regional climate applications that typically use coarser grid spacings.
In a dynamical downscaling approach, surface fluxes and radiative properties must be simulated realistically to quantify changes in temperature and precipitation, and related extreme events such as drought, flooding events, and heat waves. Yet, achieving a realistic representation of the air-surface interactions can be expected to become more difficult as resolution decreases. Continental- to regional-scale dynamical downscaling is often conducted over periods of multiple months to decades with grid spacings ranging from 50–12 km (e.g., Otte et al., 2012; Liang et al., 2012; Herwehe et al., 2014; Bullock et al., 2014; Walsh et al., 2014; Bieniek et al., 2016). The North American Regional Climate Change Assessment Program (NARCCAP; Mearns et al., 2012) and the Coordinated Regional Climate Downscaling Experiment (CORDEX; Giorgi et al., 2009) are collaborative efforts that produced ensembles of dynamical downscaling simulations over North America that have been leveraged to assess the impacts of climate change across the contiguous U.S. (CONUS).
The fluxes of heat, moisture, and momentum in WRF are controlled by the land surface model (LSM). Although the Noah LSM (Chen and Dudhia, 2001) was developed primarily for research and forecasting with observation-based drivers, it has become ubiquitous in WRF simulations of regional climate (e.g., Otte et al., 2012; Yang et al., 2012; Lim et al., 2014). However, the Noah LSM assumes that LU is homogeneous within each grid cell, and it uses the dominant, or most-prolific, LU category to define the properties of each grid cell. Consequently, small changes in LU percentage in each grid cell (e.g., due to changes in source LU dataset or interpolation method) can be amplified by changing the dominant category which alters the characteristics of the entire grid cell. The effects from using a single, dominant LU category to represent each grid cell could be more pronounced at the coarser grid spacings that are typical of downscaling simulations. Li et al. (2013a) developed a “mosaic” approach for the Noah LSM, wherein multiple LU types can coexist in the same grid cell. Contributions to the fluxes within each grid cell are proportional to the composition of LU categories in that cell. Li et al. (2013a) demonstrated that simulations with the mosaic LU were less sensitive to changes in grid spacing than those that used the dominant approach.
Li et al. (2013a), who focused on the Baltimore-Washington corridor, stated that urban environments are preferred for testing the implementation of a mosaic approach because of the heterogeneity of the landscape, as well as the contrast in surface and vegetation properties. Prior studies using mosaic LU were also focused on specific metropolitan areas [e.g., Las Vegas in Kamal et al. (2015), Chicago in Sharma et al. (2017), and Berlin in Li et al. (2017)]. However, accounting for subgrid variability in the landscape may have different effects in various regions, and subgrid heterogeneity of LU outside of high-density metropolitan centers should also be studied at regional and continental scales.
Here, 12-km simulations of the CONUS are utilized to examine the sensitivity to the effects of including of subgrid-scale variability in LU type within a dynamical downscaling application. In this paper, 3-year historical dynamical downscaling simulations over the CONUS are conducted with WRF using the Noah model with either the dominant LU or the mosaic option following Li et al. (2013a). To our knowledge, similar studies across these spatial and temporal scales have not been published. The analysis here focuses on precipitation and 2-m temperature because these fields are typically used to assess changes to air quality, human health, and ecosystems services under various scenarios. Surface fluxes and 2-m mixing ratio values are examined to further understand the effects of LU representation on precipitation and 2-m temperature. To explore the implications of mosaic LU on near-surface temperature and moisture, indices that illustrate the frequency of precipitation, as well as the intensity and frequency of heat waves, are presented. Lastly, recommendations are made regarding the use of mosaic LU within a continental-scale dynamical downscaling framework. The present work is designed to support decision-makers at continental and regional scales and inform representation of the land surface. While dynamical downscaling is the focus here, these results could apply to a variety of end-points with sensitivities to representing LU.
2. Methods
2.1. Simulations
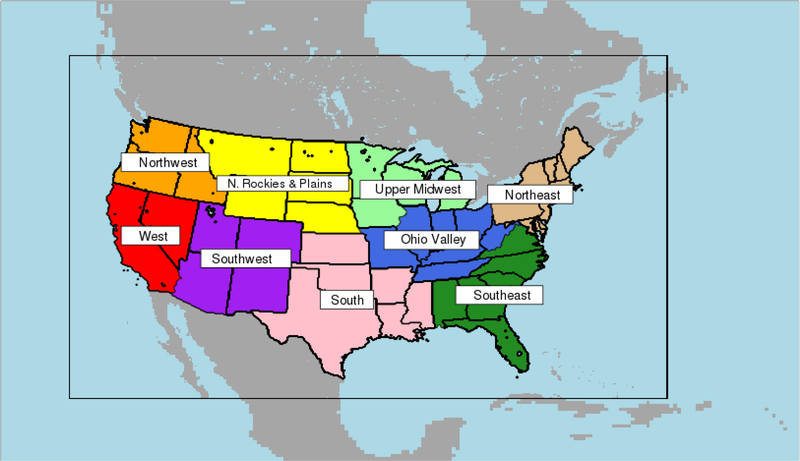
WRF version 3.9 (Skamarock and Klemp, 2008) is used to simulate 00 UTC 1 October 2004 to 00 UTC 1 January 2008, where the first 3 months are a spin-up period. Two two-way nested WRF domains over the CONUS (36- and 12-km grid spacing; Figure 1) are employed to downscale the ERA-Interim 0.75° reanalyses (Dee et al., 2011), which serves as a proxy for a similarly coarse global climate model (GCM). There are 35 vertical levels extending to a model top at 50 hPa. The analysis here focuses on the 12-km domain.
FIG. 1.
The WRF 36-km and 12-km domains, with the 12-km domain outlined in black. The nine NCEI U.S. climate regions are also shown.
Physics options include the WRF single-moment six-class microphysics scheme (Hong and Lim, 2006), the Rapid Radiative Transfer Model for global climate models (Iacono et al., 2008), and the Kain–Fritsch (KF) convective parameterization scheme including radiative feedbacks with subgrid clouds (Kain, 2004; Alapaty et al., 2012; Herwehe et al., 2014). Processes in the PBL are simulated using the Yonsei University scheme (YSU; Hong et al., 2006). The Noah LSM (Chen and Dudhia, 2001) and Revised MM5 Monin-Obukhov surface scheme (Jimenez et al., 2012) are used to simulate air-surface interactions and land processes. Although imperfect, this suite of physics options in WRF has been used for several regional climate studies of the CONUS (e.g., Bowden et al., 2012; Bullock et al., 2014; Herwehe et al., 2014; Spero et al., 2016). Some similarities in the biases associated with the physics options are discussed below. Bullock et al. (2014) simulated 2006 on a 12-km domain using an older version of WRF and similar physics options as in the present work, which resulted in overestimated precipitation. Other studies within the CONUS have also experienced overestimated precipitation when using the KF scheme (e.g., Pei et al., 2014; Li et al., 2014; Bullock et al., 2015, Zheng et al., 2016). A sensitivity study of PBL schemes in WRF conducted by Shin and Hong (2011) over the central U.S. found that simulations with YSU reproduced the observed diurnal profile of 2-m temperature better than those with other schemes but was prone to a warm bias. Similarly, Hu et al. (2010) found that YSU reduced the cool bias in the diurnal temperature profiles over Texas compared to other parameterizations. Regional climate simulations conducted over the CONUS (Otte et al., 2012; Spero et al., 2014; Bullock et al., 2014; Spero et al., 2018) with the Noah LSM have found mixed results in terms of 2-m temperature bias. However, a sensitivity study conducted by Chen et al. (2014) over the western CONUS found that use of Noah resulted in negative biases in mean 2-m temperature, while other LSMs in WRF produced slight positive biases.
Here, spectral nudging (Miguez-Macho et al., 2004) of horizontal wind components, potential temperature, and geopotential is applied above the PBL on both domains. A maximum wavenumber of 11 (6) in the X- (Y-) directions is used with a nudging strength of 3 × 10−4 s−1 on the 36-km domain. On the 12-km domain, nudging is applied at wavenumbers 8 (4) in the X- (Y-) directions with nudging coefficients reduced to 1 × 10−4 s−1 following Bullock et al. (2014). Spectral nudging of moisture (Spero et al., 2014) is used above the PBL with a coefficient of 1 × 10−5 s−1 in both domains. The results here are expected to be sensitive to the nudging strategy. Bullock et al. (2014) tested various nudging strengths while using spectral nudging with a 12-km downscaling application similar to the one used in the present study, finding that the coefficients used here resulted in the most skillful simulation. Spero et al. (2018) evaluated 2-m temperature and precipitation from 45 nudging strategies within a dynamical downscaling application using a suite of three-year WRF simulations run at 36 km over the CONUS, and they showed that a strategy that used spectral nudging toward temperature, wind components, geopotential, and moisture was the most skillful. The nudging coefficient used for moisture is reduced here, relative to the strengths used for other variables, as was recommended by Spero et al. (2018). The nudging strategy used here is consistent with one of the most skillful configurations shown in Spero et al. (2018), but we use weaker nudging for consistency with the 12-km simulations of Bullock et al. (2014). Nudging is used only above the PBL in order to follow best practices from Spero et al. (2018) and to allow the influence of LU changes on fields at the surface and low levels to remain unconstrained. Prior WRF studies focused on sensitivity to LU representation have also employed nudging (e.g., Cheng et al., 2013; Yang & Duan et al., 2016; Mallard et al., 2018).
All simulations use the 30 m 2011 National Land Cover Database (Homer et al., 2015), which is blended with the 1000 m Moderate Resolution Imaging Spectroradiometer (MODIS) data (with the product herein referred to as “NLCD” for consistency with WRF documentation (Ran et al., 2010). NLCD is applied within the CONUS, and MODIS data are used elsewhere. The LU data are interpolated to the model grid using the default method (a grid cell averaging approach); however, results here can be expected to be sensitive to the interpolation scheme used (Mallard et al., 2018).
Four simulations are conducted. Dominant (“domLU”) and mosaic (“mosLU”) representations are used for the two simulations that are the focus of the analysis. The Noah LSM within WRF sets several land and vegetation properties, including leaf area index (LAI), roughness length, and albedo, using lookup tables that assign values corresponding to the LU in each grid cell. A second pair of simulations (“domLUnewTBL” and “mosLUnewTBL”) demonstrates sensitivities to updating the soil and vegetation properties, following Campbell et al. (2018) and Kishné et al. (2017). In those studies, revising the tables to leverage current observational datasets improved simulations. As noted by Kishné et al. (2017), the soil table has not been revised in over 25 years. The updated values are from Tables 3 and 4 in Campbell et al. (2018). Campbell et al. (2018) showed that changes to the vegetation table tended to increase 2-m temperatures and decrease near-surface moisture because LAI is reduced in most LU categories. Conversely, the updated soil table reduced temperatures and increased mixing ratio due to changes in several properties that moderate soil moisture and evapotranspiration. The sensitivity to changes to the soil and vegetation properties are fully examined in Campbell et al. (2018), so this study examines the sensitivity to table updates to assess their impact on LU representation.
TABLE 3.
Pearson correlation coefficients (r) for the CONUS and each region between the LU change and the change in summer-averaged Tmean (with each taken as mosLU minus domLU), organized by ranking the NLCD categories in the CONUS according to the strongest correlation or anticorrelation. Urban categories appear in italics.
| NLCD Categories | r | NLCD Categories | r | ||
|---|---|---|---|---|---|
| CONUS |
Developed Open Space (23) Developed Low Intensity (24) Shrub/Scrub (32) Developed High Intensity (26) Cultivated Crops (38) |
0.51 0.34 0.31 −0.27 −0.25 |
South | Shrub/Scrub (32) Developed Low Intensity (24) Developed Open Space (23) Developed High Intensity (26) Evergreen Forest (29) |
0.47 0.41 0.33 −0.30 −0.27 |
| Northeast |
Developed Open Space (23) Deciduous Forest (28) Developed High Intensity (26) Developed Low Intensity (24) Grassland/Herbaceous (33) |
0.72 −0.28 −0.22 0.19 0.07 |
Southeast |
Developed Open Space (23) Developed Medium Intensity (25) Developed High Intensity (26) Shrub/Scrub (32) Developed Low Intensity (24) |
0.70 −0.41 −0.40 0.27 0.22 |
| N. Rockies & Plains |
Developed Open Space (23) Cultivated Crops (38) Developed Low Intensity (24) Evergreen Forest (29) Shrub/Scrub (32) |
0.39 −0.35 0.29 −0.25 0.23 |
Southwest | Shrub/Scrub (32) Evergreen Forest (29) Developed Low Intensity (24) Mixed Forest (30) Developed High Intensity (26) |
0.48 −0.45 0.39 0.28 −0.27 |
| Northwest | Evergreen Forest (29) Shrub/Scrub (32) Developed Low Intensity (34) Developed High Intensity (26) Cultivated Crops (38) |
−0.52 0.52 0.41 −0.22 −0.18 |
Upper Midwest |
Developed Low Intensity (24) Developed Open Space (23) Cultivated Crops (38) Developed High Intensity (26) Deciduous Forest (28) |
0.48 0.45 −0.42 −0.41 0.22 |
| Ohio Valley |
Developed Low Intensity (24) Developed Open Space (23) Developed High Intensity (26) Cultivated Crops (38) Developed Medium Intensity (25) |
0.56 0.48 −0.39 −0.24 −0.22 |
West |
Developed Medium Intensity (25) Cultivated Crops (38) Developed Open Space (23) Evergreen Forest (29) Developed High Intensity (26) |
0.40 −0.38 0.36 −0.36 −0.31 |
2.2. Dominant and Mosaic LU Representations
In its default configuration, the Noah LSM sets land and vegetative properties based solely on the dominant LU category in each grid cell. This practice of representing only a single, most prolific LU category in each grid cell was the only option available for Noah until Li et al. (2013a) introduced an alternative which was made available as of WRF version 3.6 (NCAR, 2015). In this framework, the user can specify the number of mosaic tiles (i.e., maximum number of LU categories to allow within each grid cell); the default in WRF version 3.9 allows up to 3 categories in each cell. When the mosaic LU is used, surface state variables and fluxes are computed for each tile within the grid cell. All surface prognostic fields are calculated within each tile and then weighted averaging is used to aggregate those fields up to a grid cell value. Here, mosaic LU was configured to allow up to 6 LU categories in each grid cell, so that ≥90% of the grid cells across the domain could have at least 90% of their original LU across all 40 categories explicitly represented. For portions of this analysis, related NLCD categories are clustered into “consolidated categories” (Table 1) following Mallard et al. (2018) to summarize LU changes in a consistent but concise manner. However, individual NLCD categories are discussed where appropriate.
TABLE 1.
Assignment of NLCD LU categories to consolidated LU categories. The category index used within WRF is provided in parentheses. Note that categories that comprise “Unclassified” are not present in the model domain (Figure 2).
| Consolidated LU | NLCD Category |
|---|---|
| Urban | Urban and Built Up (13) Developed Open Space (23) Developed Low Intensity (24) Developed Medium Intensity (25) Developed High Intensity (26) |
| Agricultural | Croplands (12) Cropland/Natural Vegetation Mosaic (14) Pasture/Hay (37) Cultivated Crops (38) |
| Grass/Shrub Land | Closed Shrublands (6) Open Shrublands (7) Woody Savannas (8) Savannas (9) Grasslands (10) Shrub/Scrub (32) Grassland/Herbaceous (33) |
| Forest | Evergreen Needleleaf Forest (1) Evergreen Broadleaf Forest (2) Deciduous Needleleaf Forest (3) Deciduous Broadleaf Forest (4) Mixed Forest (5) Deciduous Forest (28) Evergreen Forest (29) Mixed Forest (30) |
| Wetlands | Permanent Wetlands (11) Woody Wetlands (39) Emergent Herbaceous Wetlands (40) |
| Barren/Tundra | Barren or Sparsely Vegetated (16) Barren Land (Rock/Sand/Clay) (27) |
| Ice/Snow | Permanent Snow and Ice (15) Perennial Ice/Snow (22) |
| Ocean | International Geosphere–Biosphere Programme (IGBP) water (17) |
| Unclassified | Unclassified (18) Fill Value (19) Unclassified (20) Open Water (21) Dwarf Scrub (31) Sedge/Herbaceous (34) Lichens (35) Moss (36) |
2.3. Datasets Used for Model Validation
The Parameter elevation Regression on Independent Slopes Model (PRISM) dataset is used to validate simulated 2-m temperature and precipitation. PRISM is developed using regressions of station data, where each station in a grid cell is weighted based on its physiographic similarity to the grid cell features using characteristics such as elevation and topographic orientation, among others (Daly et al., 2008). Daily precipitation totals, as well as minimum, maximum, and daily mean temperatures, are available at 4 km in PRISM. Here, the PRISM data are aggregated to the 12-km WRF grid to facilitate direct comparisons on the modeling domain. Daly et al. (2008) discusses potential error in the PRISM dataset and contains an analysis of PRISM values compared with two other observational datasets. Daly et al. conclude that PRISM provided a more accurate representation of temperature and precipitation relative to these alternative datasets, while noting that disparities are generally largest in the western U.S. in areas of complex terrain or coastal proximity.
Model-simulated LAI is compared to the 8-day averaged LAI from the combined MODIS/Terra+Aqua product archived at 500-m resolution (MCD15A2H; Myneni et al., 2015). Additionally, monthly-average sensible heat (SH) and latent heat (LH) fluxes from FLUXNET2015 (Tier 1) are utilized from 20 stations that have data covering the period being simulated here (Pastorello et al., 2017); see Appendix A. Regional analysis is conducted using the nine National Centers for Environmental Information (NCEI) U.S. climate regions (Karl and Koss, 1984) (Figure 1).
3. Results
3.1. Effects of Mosaic on LU Composition
Figure 2 summarizes the LU composition and compares the dominant and mosaic distributions across the 12-km grid. As expected, the dominant LU shows various forest NLCD types to be prolific across the eastern U.S., with some agricultural LU and wetland types visible in the Southeast. Cultivated Crops dominate the Upper Midwest and Ohio Valley, while grass and shrubland occupy most of the western U.S. in the dominant run, with deciduous forest in the Pacific Northwest. When LU categories are binned into the consolidated LU types, the difference in the percentage of LU within each category is maximized in the urban LU category, which increases by over 3% when mosaic LU is used. Increasing urban LU is compensated by decreasing forest and cultivated LU. There is less than 1% change in the remaining consolidated categories.
FIG. 2.
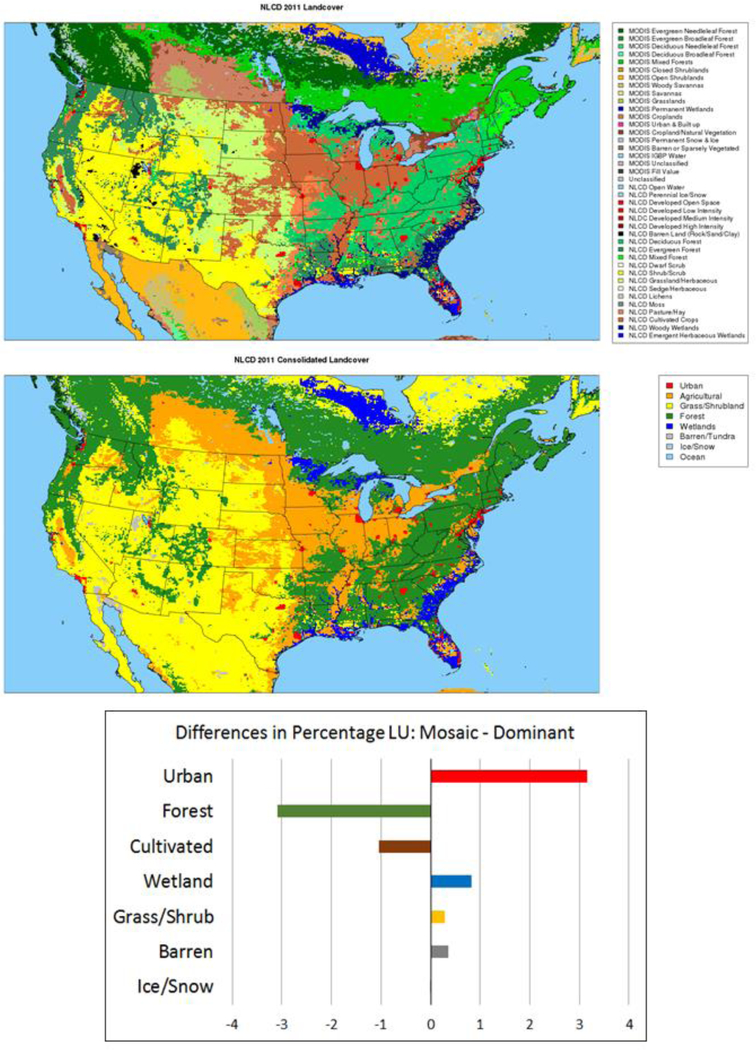
NLCD dominant LU on the 12-km WRF domain (top), with the same LU field plotted according to the consolidated categories listed in Table 1 (middle). The differences in percentage of LU (aggregated under the consolidated LU) taken as the mosLU minus domLU runs (bottom).
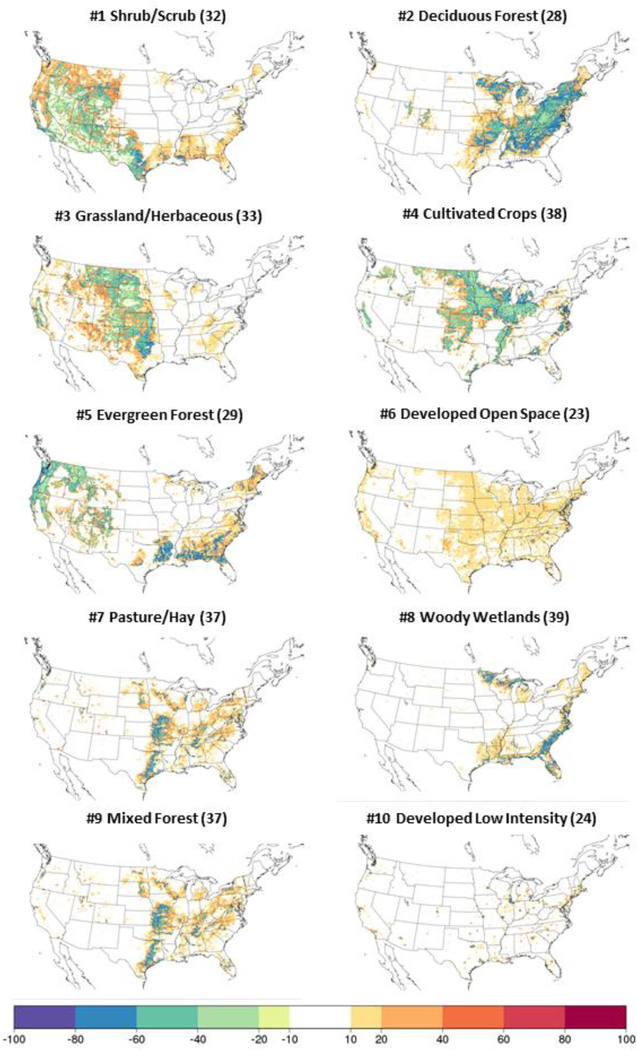
Differences of LU percentage of each of the NLCD categories are computed to illustrate the spatial changes in LU resulting from using mosaic instead of dominant LU. The spatially averaged absolute value of the change between the two runs in each category is computed and then used to rank the changes in all NLCD categories (excluding MODIS categories, which are used outside the CONUS). The top 10 are shown in Figure 3. Here, 2 of the top 3 LU categories with the largest changes are shrub/grassland categories, with both increases and decreases found across much of the western U.S. The highest ranking urban category is 6th, NLCD’s Developed Open Space. This category is the least dense of the urban types, defined as having less than 20% impervious surface and including single-family homes with large lots, as well as developed recreational areas, such as parks or golf courses, among other examples (Homer et al., 2004). Small (10–20%) but widespread increases in this type occur across most of the eastern half of the U.S. and portions of the CONUS on the west coast. This contributes most to the urban consolidated categories showing the large increase in spatially aggregated LU when using mosaic LU (Figure 2). Urban centers show sharp, localized decreases in Developed Open Space (#6) and Developed Low Intensity (#10), as the mosaic treatment allows greenspaces and other LU types to coexist within metropolitan areas that are represented as only urban in the dominant LU representation. Other categories show widespread reductions in regions of the CONUS when using the mosaic, most notably Deciduous Forest, Cultivated Crop, and Evergreen Forest (ranked #2, 4, and 5, respectively). In several areas, these reductions are at least partially offset by the increase in Developed Open Space. Overall, urban, forest, and agricultural LU types experience unidirectional changes (primarily increased urban LU and decreased forest and cultivated LU). Meanwhile, changes in shrub/grassland categories feature widespread increases and decreases within the same category.
FIG. 3.
The differences in percentage of LU (mosLU minus domLU) in NLCD categories. This subset of categories represents the top 10 NLCD categories (by rank) with the largest absolute value of the difference field averaged over the domain. Panels are titled with their rank, description, and the index used within WRF.
3.2. 2-m Temperature
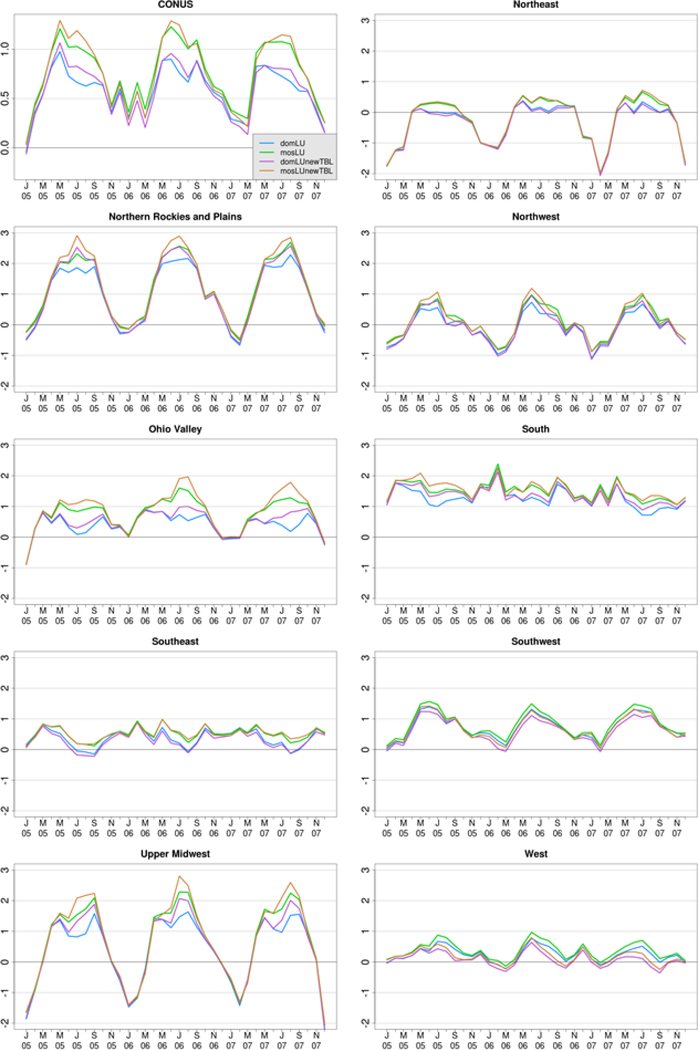
Mean absolute error (MAE) and timeseries of bias in monthly-averaged 2-m temperature are shown for the CONUS- and regionally-averaged fields (Table 2 and Figure 4). All four simulations have a high bias in temperatures across the CONUS, which is exacerbated by using the mosaic LU (Figure 4). A paired Student’s t-test indicates that differences between domLU and mosLU in Figure 4 are significant in the CONUS and all regions using a p=0.05 criterion (not shown). Consistent with the bias shown in Figure 4, both mosaic runs have higher MAE than the dominant runs over the CONUS (Table 2). Over the CONUS and in each region, the largest divergence between the runs occurs during the summer months (June, July, and August), with the mosaic simulations consistently warmer than the dominant LU runs. Summer is also the season when the warm bias is most enhanced in the Northern Rockies and Plains, Ohio Valley, and the Upper Midwest. Overall, the domLU run has the lowest MAE in monthly temperatures across the CONUS and in 5 of the 9 regions (Table 2). However, the differences in MAE between the runs are smaller than the MAE of any individual simulation within the CONUS and in all regions; therefore, other sources of model error (originating from the physics parameterizations or driving data, among others) are bigger contributors than LU representation to the errors in simulated temperature.
TABLE 2.
MAE in monthly averaged 2-m temperature (K) and monthly accumulated precipitation (mm month−1) for each run compared to PRISM. Statistics are calculated using only land grid cells within each region. Bold type indicates the run with the lowest MAE, with none used in rows where no single run has the lowest.
| Monthly Averaged 2-m Temperature | Monthly Accumulated Precipitation | |||||||
|---|---|---|---|---|---|---|---|---|
| domLU | mosLU | domLU newTBL | mosLU newTBL | domLU | mosLU | domLU newTBL | mosLU newTBL | |
| CONUS | 1.31 | 1.41 | 1.35 | 1.43 | 23.88 | 23.66 | 23.86 | 23.78 |
| Northeast | 0.93 | 0.91 | 0.93 | 0.91 | 27.90 | 26.73 | 27.46 | 26.27 |
| N. Rockies & Plains | 1.89 | 1.98 | 1.97 | 2.02 | 17.17 | 17.17 | 17.37 | 17.58 |
| Northwest | 1.52 | 1.46 | 1.49 | 1.43 | 23.55 | 23.83 | 23.23 | 23.59 |
| Ohio Valley | 0.75 | 1.00 | 0.85 | 1.09 | 27.86 | 27.04 | 28.15 | 27.82 |
| South | 1.36 | 1.58 | 1.43 | 1.61 | 28.80 | 28.94 | 29.08 | 29.35 |
| Southeast | 0.70 | 0.74 | 0.71 | 0.78 | 38.58 | 36.83 | 37.85 | 35.99 |
| Southwest | 1.56 | 1.58 | 1.54 | 1.53 | 16.98 | 17.05 | 16.59 | 16.65 |
| Upper Midwest | 1.15 | 1.37 | 1.25 | 1.44 | 23.17 | 23.68 | 23.88 | 24.74 |
| West | 1.34 | 1.32 | 1.30 | 1.26 | 14.16 | 14.17 | 14.02 | 14.03 |
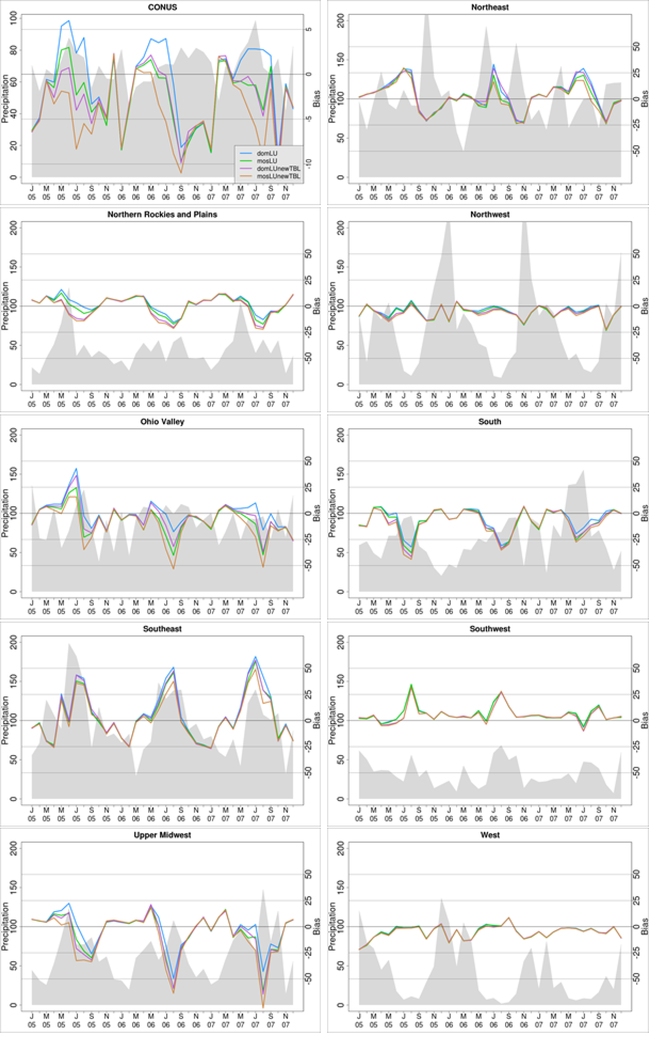
FIG. 4.
Bias relative to PRISM in regionally- and monthly-averaged 2-m temperature (K) for the domLU (blue), mosLU (green), domLUnewTBL (purple), and mosLUnewTBL (orange) runs, shown over the CONUS and in each of the nine NCEI U.S. climate regions ordered alphabetically. Note that all regional plots share common axes to ease comparison.
Figure 4 shows that the largest difference in simulated mean 2-m temperature occurs during the summer; therefore, this analysis focuses on the average summer conditions. Daily maximum, mean, and minimum temperatures (Tmax, Tmean, and Tmin, respectively) averaged over the summer are warmer with mosLU than domLU (Figure 5). Tmax in mosLU is 0.5–1.0 K higher than in domLU throughout the eastern U.S., and as much as 1–3 K warmer in the Upper Midwest and Ohio Valley. Additionally, using mosaic LU similarly increases temperatures in the coastal Northwest. Average consolidated LU changes within each temperature bin show that increases in Tmax of >1 K occur where urban LU shows an increase of 15–18% and forest and cultivated LU decreases from 9–19% (Figure 5).
FIG. 5.
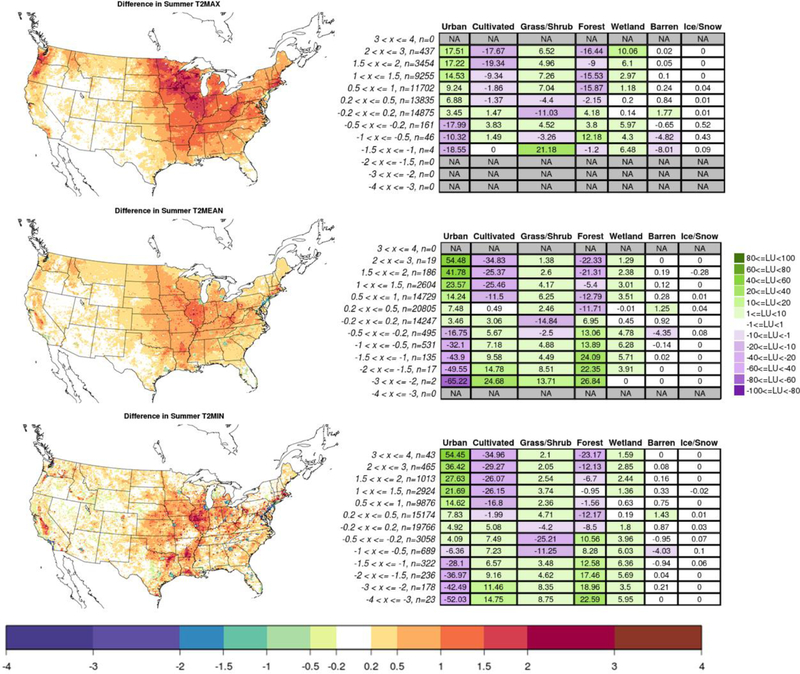
Differences (mosLU minus domLU) in daily maximum, mean, and minimum 2-m temperature plotted within the CONUS and averaged over the summer months for the simulated 3-year period (left: top, middle, and bottom, respectively). Corresponding tables (right) show the LU change (mosLU minus domLU) in each of the consolidated categories, as spatially-averaged over areas that lie within each of the temperature intervals as plotted on the left. Boxes are filled with darker colors as the absolute value of the LU change increases; see legend on the right. Temperature bins are listed on the left of each table, along with the number of grid cells averaged.
The mosLU simulation has higher Tmean and Tmin than domLU. Those higher values of Tmin with mosLU are mainly in the eastern U.S., but they are more localized than Tmax changes. However, several areas in the Upper Midwest, Ohio Valley, and southern U.S. show increases of 0.5–3.0 K in Tmin. Although the greatest contrast between the runs is concentrated in the central and eastern U.S., warming of a similar magnitude also occurs in California within the San Joaquin Valley where changes in mean temperatures appear to be driven more by increases in Tmin than in Tmax. Both Tmean and Tmin have localized cooler temperatures near large cities (e.g., Los Angeles, Atlanta, Chicago, Detroit, Houston, Baltimore-Washington-New York corridor) in mosLU compared to domLU. Increases in urban LU in mosLU result in warmer Tmin (of 22–54% when considering warming >1 K), while lower Tmin occurs in areas of decreased urban LU (reductions of 28–52% when considering cooling >1 K). Where Tmin is reduced, decreases in urban LU are offset by increases in forest LU (of 13–23% in areas of cooling >1 K). Similar temperature and LU changes as in Tmin occur in Tmean, which reflect the influence of the nighttime temperatures on the daily mean.
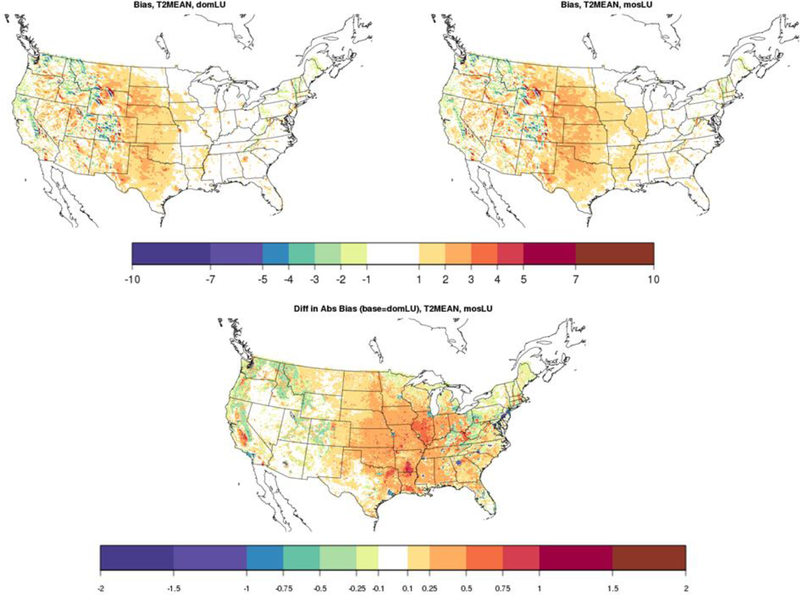
The largest widespread bias in Tmean occurs in the central U.S. (Figure 6). Using mosLU generally increases the magnitude of the bias in the eastern and central U.S. However, several cities where Tmean was reduced with mosLU compared to domLU have reduced error. The bias was also reduced along the Pacific coast, where the coverage of Evergreen Forest in domLU was replaced with Developed Open Space and Shrub/Scrub types in mosLU (Figure 3).
FIG. 6.
Bias in simulation-averaged 2-m temperature (K) for domLU (top left) and mosLU (top right), and the difference (mosLU minus domLU) between the absolute value of the biases (bottom).
Overall, these results indicate that using mosaic LU better represents widespread low-intensity urbanization in the eastern U.S., but that the associated increases in near-surface temperatures exacerbate the existing warm bias. However, this trend is reversed in large cities, where mosaic LU allows more heterogeneous LU (such as the existence of green spaces within urban areas) where there would otherwise be uniformly urban areas by using dominant LU. Accordingly, the model’s warm bias is reduced in highly populated areas.
3.3. Precipitation
There is a large spread in the bias in precipitation across the CONUS and between the runs, especially during the summer months (Figure 7). Runs with the dominant LU tend to generate higher precipitation, with domLU showing a high bias during the warm season. Conversely, the mosLUnewTBL run has the lowest precipitation and maintains a low bias during most of the 3-year period. Unlike the temperature comparison against PRISM, the summer sensitivity of the simulated precipitation to LU treatment is comparable to the magnitude of the bias within the CONUS-wide results. The runs are more consistent in winter months but they often underpredict precipitation. MAE is lowest in mosLU for the CONUS, but regional results vary (Table 2). Simulated precipitation is the most divergent between runs in the Upper Midwest, Ohio Valley, and Southeast where MAE is minimized for the domLU, mosLU, and mosLUnewTBL runs, respectively. However, the West and Southwest, which are dominated by the Shrub/Scrub LU type (Figure 2), show little discernable differences between the runs. Using the same criteria as for temperature, the timeseries of precipitation (Figure 7) contains statistically significant differences between domLU and mosLU in the CONUS and over all regions except the Southwest.
FIG. 7.
Monthly total observed precipitation (mm month−1, shown on the left axis with gray shading) and model bias (shown on right axis with colored lines), spatially averaged over the CONUS and in each of the nine NCEI U.S. climate regions. Colored lines are as in Figure 4. The y-axis is consistent across the regions.
To understand the influences of LU treatment on daily precipitation intensities, the annual occurrences of daily precipitation ≥0.1 in (2.54 mm), ≥0.5 in (12.7 mm), and ≥1.0 in (25.4 mm) (hereinafter “DP01,” “DP05,” and “DP10,” respectively) are examined from domLU and mosLU and compared with PRISM observations. Figure 8 shows the bias in the domLU run for each of the three of thresholds daily precipitation, as well as the difference in exceedances of each threshold when mosaic LU is used. DP01 is overpredicted over much of the central and eastern U.S. within domLU, with areas east of the Mississippi River showing positive biases from 5–60 days. However, bias in the moderate and large events (DP05 and DP10) is negative, ranging from 5–20 days, and concentrated in the Southeast and South. All metrics show isolated maxima and minima in model bias in portions of the Northwest over areas of complex terrain.
FIG. 8.
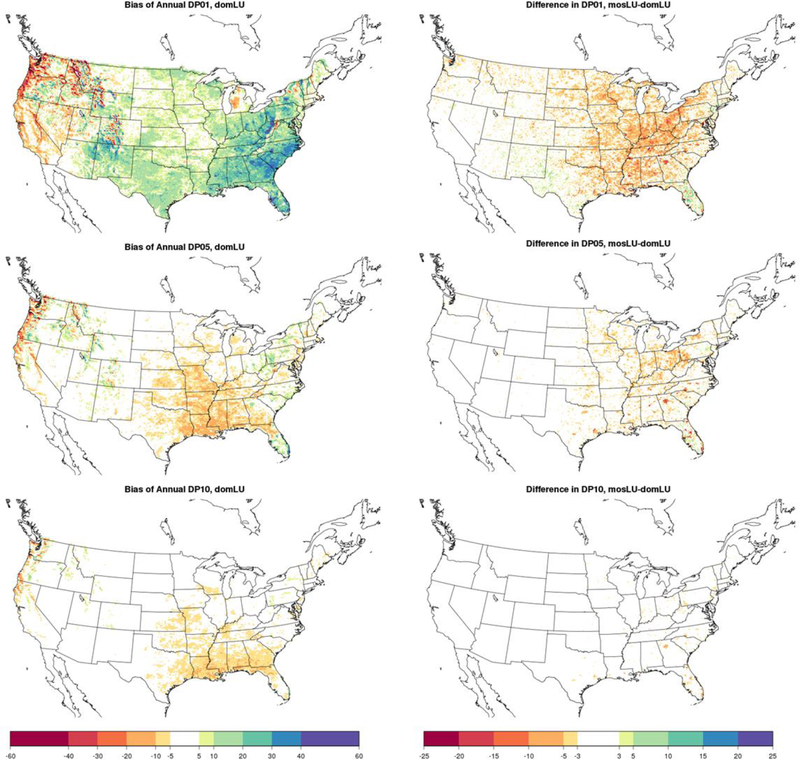
Bias in DP01, DP05, and DP10 (days year−1, shown in the left column: top, middle, and bottom, respectively) in the domLU run relative to PRISM. Model changes, taken as mosLU minus domLU, for the corresponding fields are shown on the right.
The incidences of mild (DP01), moderate (DP05), and heavy precipitation (DP10) events all generally decrease by using mosLU instead of domLU. This somewhat alleviates the high bias in DP01, as reductions of 3–25 days occur across much of the eastern U.S. when mosaic LU is utilized. However, DP05 and DP10 are generally underpredicted in all runs. DP05 has a high bias in domLU in some metropolitan areas (e.g., Atlanta and Charlotte), which is reduced with mosLU. DP10 is also somewhat underpredicted (by 5–20 days in the South and Southeast for domLU), with little change in the mosLU run except for limited reductions around urban areas including Atlanta, Orlando, and Charlotte. Overall, the propensity for WRF to produce light precipitation too frequently is improved when the subgrid variability of LU is considered, with some additional improvement to the accuracy of moderate events around large cities in the eastern U.S.
Precipitation differences between the simulations appear to occur primarily due to reductions in the frequency of rainfall events. Simulation-averaged daily rainfall rates, when normalized by the number of days with non-zero precipitation, are similar between the runs, with a mean difference of less than 0.05 mm and a maximum change of only 2.3 mm throughout the domain. These results are further discussed below in context with the influence of LU on surface fluxes.
3.4. Moisture and Surface Fluxes
LU representation is used by WRF to set upper and lower limits on LAI, stomatal resistance, and other values in the Noah LSM that influence surface heat and moisture fluxes, thereby affecting precipitation and near-surface temperatures [e.g., look-up table parameters in Table 4 of Campbell et al. (2018)]. Using mosLU decreases 2-m mixing ratio and LH from the surface relative to domLU (Figure 9). The analysis is focused on summer when there is the most divergence in monthly mean temperature and accumulated precipitation between the runs (Figures 4 & 7). Decreases in mixing ratio of 0.25–1.25 g kg−1 occur throughout much of the eastern U.S. by using mosLU, with the largest reductions concentrated in the Ohio Valley and Upper Midwest. Smaller (0.25–0.75 g kg−1) reductions occur in the Northwest. Consistently, precipitable water vapor is also decreased over a similar area, with summertime reductions of 0.25–1.5 kg m−2 in mosLU as compared to domLU (not shown).
FIG. 9.
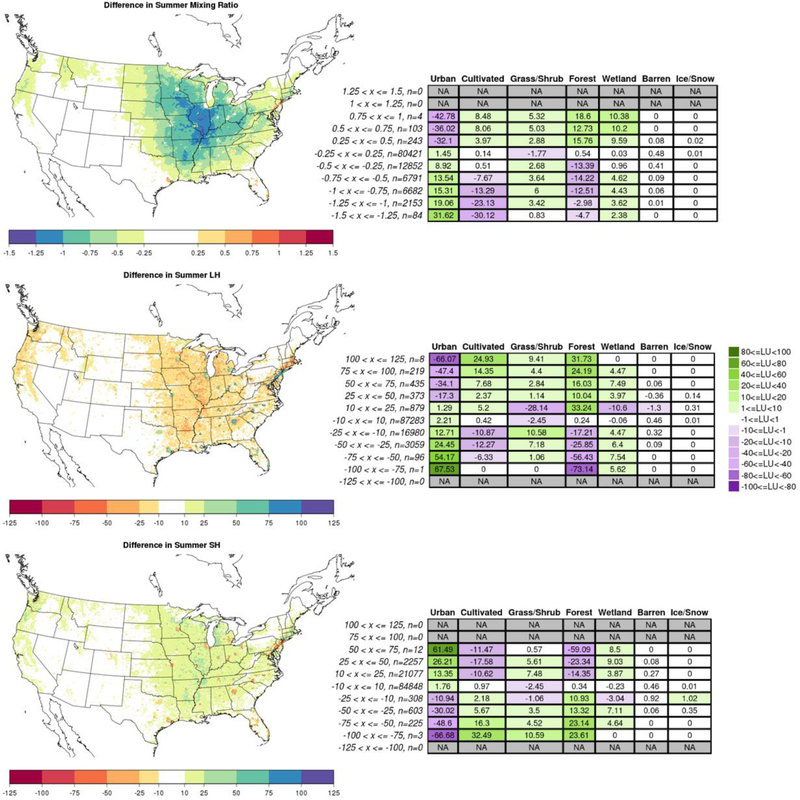
Difference in 2-m mixing ratio [g kg−1], and latent and sensible heat fluxes [W m−2] (left column: top, middle, and bottom, respectively) in mosLU relative to domLU, averaged over summer months and shown over the CONUS. Corresponding tables (right) show the LU change.
The surface evaporation and evapotranspiration decrease when using mosaic LU. In mosLU relative to domLU, LH reductions of 10–50 W m−2 occur across much of the central and eastern CONUS (Figure 9), an area where average LH values in domLU generally range from ~ 100 to 150 W m−2 in summer (not shown). Corresponding LU changes are largest among the urban categories (with a 13–25% increase in areas where LH decreases by 10–50 W m−2 in mosLU), while the largest decreases occur in forest LU (17–26%) and with some reduction in cultivated land (11–12%). Average SH flux increases of comparable magnitude occur in the eastern and central U.S., an area where summertime average SH in domLU ranges between 20 to 90 W m-2. An overall increase in SH and decrease in LH in mosLU, relative to domLU, is consistent with the LU changes shown between the simulations, as the increased low-density urban land and decreased forest and agricultural types in mosLU increases the proportion of impervious surface and reduces the amount of vegetation represented by the model. While changes in net radiation are also examined, differences in LH and SH are found to be the largest terms when considering changes in the energy budget at the surface between the mosLU and domLU runs, as changes in net radiation and upwelling longwave and shortwave radiation from the surface are generally 15 W m−2 or less (not shown).
Comparison of monthly-averaged LH and SH from 20 FLUXNET stations (Table A1) in the CONUS results in positive biases for LH that are reduced in mosLU (which has a mean bias of 12.17 W m−2 when averaged over all stations) compared to domLU (which has a mean bias of 15.72 W m−2). This is consistent with the overall reduction in LH when LAI is reduced. The high bias in LH in domLU may also contribute towards its tendency to overproduce precipitation events, regardless of the choice of other physics options. In contrast, SH biases of 11.42 and 15.26 W m−2, respectively, for domLU and mosLU, suggest that including subgrid-scale LU information increases model error in SH, which is consistent with the increased warm bias found in the mosLU simulation. Comparisons of RMSE give the same conclusion regarding the simulations’ error (not shown). Since both fluxes are positively biased, the model’s deficiency is not in the partitioning of fluxes but elsewhere in the representation of the energy balance at the surface; a more rigorous analysis of the Noah LSM would be needed to explore this hypothesis. The comparison shown here is conducted using only a small number of stations compared against the nearest model grid point, and the representativeness of 12-km grid cells may have only limited compatible with point observations. Also, the 20 stations included represent a limited range of LU types: 10 in forests, 5 in grasslands or savannas, 4 in croplands, and 1 in wetlands; there are no stations in this analysis that are in urbanized areas.
When comparing domLU and mosLU in major metropolitan areas, an opposite trend is found between the runs. Heavily urbanized areas (such as Atlanta, the Baltimore-Washington-New York corridor, and Detroit) show LH increases of 25–100 W m−2 with corresponding LU changes that include a decrease of 17–47% in urban categories with compensating increases in forest LU of 10–24%. As these cities contain more greenspace in the mosLU simulation, SH decreases by a similar magnitude in these areas with mosLU compared to domLU.
Ultimately, accounting for subgrid variability in LU changes several land-surface characteristics, with reductions in LAI values among the most widespread changes (Figure 10). Compared with MODIS observations for January and July, the overprediction of LAI in domLU is most pronounced in the winter over most of the CONUS and in the western U.S. in summer. Both the mosLU and mosLUnewTBL runs improve estimates of LAI, most notably in the central U.S. in winter. Summertime LAI values are overestimated in the Upper Midwest and Ohio Valley regions most dramatically in the domLU run, while using either the mosaic LU or the revised tables produces LAI values that better resemble MODIS. However, the mosaic LU runs underpredict LAI in some areas of the eastern CONUS.
FIG. 10.

Observed LAI [m2 m−2] from MODIS (top) shown along with monthly-averaged LAI in the domLU, domLUnewTBL, mosLU, and mosLUnewTBL runs (ordered from top to bottom) for January (left) and July (right) 2005. Observed values are taken from representative times using the 8-day averages ending on 17 January 2005 and 20 July 2005, respectively.
Reducing LAI with mosLU (relative to domLU) decreases evapotranspiration and LH while increasing SH, resulting in warmer temperatures and reducing atmospheric moisture available for precipitation. This reduction in low-level moisture and precipitable water reduces the precipitation frequency. Precipitation results here are consistent with Findell et al. (2011), an observational study that found that high evaporation in the eastern U.S. increased the probability of summertime afternoon rainfall by 10–25%, whereas precipitation intensity was largely insensitive to changes in surface fluxes. Comparison of the runs with updated look-up tables also corroborates that using mosaic LU generally reduces precipitation and increases temperatures (Figures 4 and 7), increases SH and decreases LH (not shown), and reduces LAI (Figure 10) across the central and eastern U.S.
3.5. Heat Waves
Dynamical downscaling is often used to generate high-resolution simulations of extreme events that affect human health and ecosystem services. Increases in the frequency, duration, and intensity of heat waves are very likely in the 21st century (IPCC, 2013). Figures 4, 5, and 6 showed that summer 2-m temperatures are influenced by using mosaic LU, which would impact simulation of heat waves.
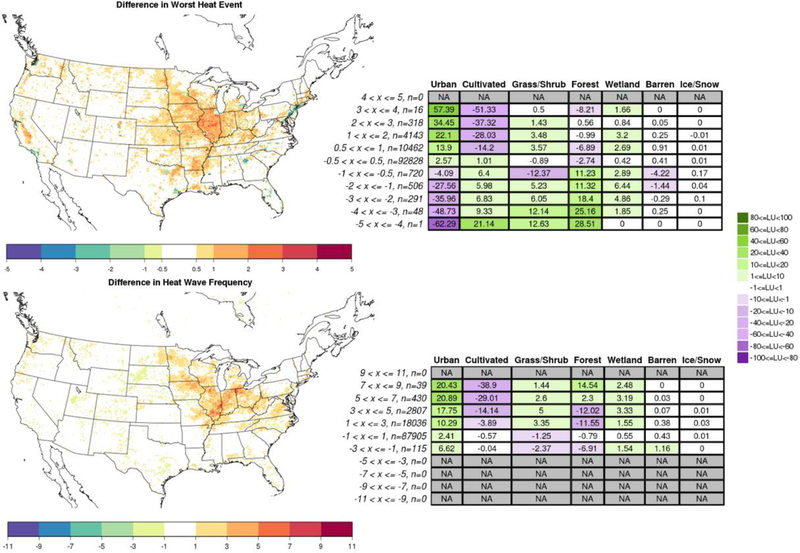
The intensity and frequency of heat events during the 3-year simulation period is determined using the criteria implemented by Meehl and Tebaldi (2004), following Karl and Knight (1997) and Huth et al. (2000). The severity of the “annual worst heat event” is determined from the warmest 3-day average Tmin. These events are then averaged over all 3 years to create the simulation-averaged field, and the difference between mosLU and domLU is shown in Figure 11. The difference in the frequency of heat waves is also shown in Figure 11. This frequency is defined by accumulating events that meet the following criteria: 1) Tmax must remain above T1 (which is defined at each grid cell as the 97.5th percentile in the distribution of Tmax over May–September of each year) for at least 3 days, 2) the event-average Tmax must be greater than T1, and 3) Tmax must remain above T2 (which is defined as in T1 but for the 81st percentile) for each day of the event. Following Meehl and Tebaldi, T1 and T2 are derived from the distribution of observed (PRISM) and simulated (domLU) temperatures. The domLU run is used because the goal of this study is to understand how downscaled results change when mosaic LU is included, relative to the default treatment. The intensity metric used here is intended to be calculated on an annual basis. However, note that both Meehl and Tebaldi (2004) and Huth (2000) use multi-decadal periods to define the T1 and T2 thresholds, and those thresholds could be expected to be sensitive to the shorter period used in the present work. Therefore, model-to-model differences are emphasized here. As this definition of heat wave frequency relies exclusively on Tmax and not Tmin, these model-to-model differences can be expected to reflect differences in maximum temperatures regardless of the effect of nighttime minimum temperatures on frequency.
FIG. 11.
Differences (mosLU minus domLU) in the average annual “worst” heat wave (top, in K) and total number of heat wave events over the study period (bottom), shown over the CONUS. Corresponding tables (right) show the LU change.
Using mosLU increases the intensity of heat events by 0.5–3.0 K in the central U.S., concentrated in the Ohio Valley region, especially in Illinois. The corresponding LU shows decreases in cultivated land of 14–37% with increases in urban LU of 14–34% in mosLU relative to domLU. Because heat events are defined here from minimum daily temperatures, these results follow the increased Tmin values (Figure 5), which were also collocated with areas of decreased agricultural LU and increased urban land. The trend is reversed for cities in the U.S., where decreases in heat severity of 1–4 K correspond to decreases in urban LU and compensating increases in forest LU and other categories. Using mosLU increases the number of heat waves in parts of the eastern and central U.S. by 1–9 events over the course of the simulation, with compensating LU changes in the urban (+10 to 21%) and cultivated (−4 to −39%) consolidated LU types. The increase in mosLU of heat wave frequency exacerbates the bias by 1–5 events in the Upper Midwest and Ohio Valley (relative to domLU), with an increase of 1–2 K in the bias in the average worst heat event within areas of the Upper Midwest, Ohio Valley and South (not shown).
3.6. Impacts from Changes in the Representation of Urban LU
Comparison of the runs indicates that using mosaic LU results in different representation of urban areas and the urban heat island (UHI; e.g., Manley, 1958 & Oke, 1982). The mosLU run includes more of the lowest-intensity urban category (Developed Open Space) within grid cells throughout the eastern U.S. that are dominated by forest and cultivated areas in domLU, increasing temperatures and SH and decreasing rainfall, near-surface moisture, and LH (Figs. 4, 5, 7, and 9). These changes generally result in widespread warming and drying, with the largest changes in Tmean, Tmax, and mixing ratios concentrated in the Ohio Valley and Upper Midwest, as well as portions of the South and Southeast. The largest changes frequently occur in Illinois, where increasing Developed Open Space coincides with a reduction in Cultivated Crops when using mosaic LU (Figure 3). For the portion of each grid cell that transitions from Cultivated Crops to Developed Open Space, evapotranspiration should be reduced as minimum and maximum LAI values from WRF’s default look-up tables would be decreased by ~36 and 82%, respectively, along with an increase in stomatal resistance of 400%, among other changes. The loss of Deciduous Forest also plays a role in portions of these regions, where a transition from this category to Developed Open Space would cause a reduction in maximum LAI of ~81% and an increase of 60% in stomatal resistance. While other grid cell properties would change as well, these are some examples of surface characteristics which would coincide with a reduction in evapotranspiration and LH, as well as an increase in SH and near-surface temperatures within the mosLU run where this urban category is more prolific.
Table 3 shows the association between temperature and LU changes, which is also analyzed by computing correlation coefficients between LU change in each of the NLCD categories and differences in summer-averaged Tmean (based on Figure 5). Over the CONUS, the largest correlations are found with the Developed Open Space type (0.51), Developed Low Intensity (0.34), and Shrub/Scrub (0.31) when comparing mosLU and domLU. Over the regions, urban categories had the strongest correlation to mean temperature changes in 6 of the 9 regions (ranging from 0.39 to 0.72). Of the remaining regions, the South and Southwest favored the largest correlation coefficients for the Shrub/Scrub category (~0.47), while warming in the Northwest correlated best with reductions in Evergreen Forest (−0.52). In the CONUS and some regions, high intensity urban LU shows weak anticorrelations with temperature; however, when using mosaic LU, this category only shows small increases confined to large cities (not shown), where there are cooler temperatures accompanied by an overall decrease in urban land due to large reductions in low intensity urban categories (Figures 3 & 5). Overall, tying temperature change to a difference in a single LU category is confounded by the expectation that temperature changes in a grid cell would result not only from a reduction in one category and but also a compensating change in others (which is also why correlation coefficients here are not expected to be very large). However, the largest coefficients are associated with urban categories, which further supports the conclusion that the representation of urban types is an important distinction when comparing mosaic LU to the default representation, even at continental to regional scales.
Although the amount of warming due to UHI can be highly variable, it is generally between 1 and 3 K (Grimmond, 2007), with UHI-enhancement of precipitation found in several cities (e.g., Huff and Changnon, 1973; Bornstein and Lin, 2000). The effects of UHI are often more pronounced at night, as heat absorbed during the day reduces nighttime cooling (Oke, 1982). In the present work, within heavily urbanized areas, the use of the mosaic results in cooler Tmean values in Figure 5 of 0.5–1.5 K (e.g., Atlanta, Houston, Chicago) and up to 2 K (Philadelphia-New York corridor); therefore, the differences in representing heavily urbanized areas in the dominant and mosaic runs produce temperature contrasts that are comparable in magnitude to the UHI effect in some areas. Additionally, the increase in greenspace within mosLU tends to reduce the frequency of moderate and heavy precipitation in several eastern U.S. cities (e.g., Atlanta, GA; Houston, TX; Jacksonville, FL; Charlotte, NC), as shown in Figure 8. While this work addresses the effects of the mosaic at continental and regional scales, regional climate modeling efforts should also include realistic representations of complex topography and other mesoscale features so that the downscaled simulations can add value relative to the GCM (Feser et al., 2011). Representation of UHI could also add value for many applications, especially those focused on human health, as these urban areas represent major population centers.
Our findings for urban areas corroborate Li et al. (2013a) and Sharma et al. (2017), who also compared the dominant and mosaic approaches in WRF using the Noah LSM. However, those studies used nested 1-km domains focused on specific metropolitan areas, which differs from the CONUS-wide domain used here. Similar to Figures 5 & 9 here, Sharma et al. found that mosaic LU reduced Tmin and SH, but increased LH, inside the urban center of Chicago, with the opposite trends found in the surrounding suburban area. Also, Li et al. concluded that using the mosaic LU increased LH and reduced SH at a tower site within the Baltimore-Washington area, as the dominant approach represented an area of mixed LU solely as low-intensity urban land.
4. Summary
In the present work, 3-year dynamically downscaled WRF simulations over the CONUS are used to assess the sensitivity of simulated 2-m temperature and precipitation to using mosaic LU within each grid cell in the Noah LSM instead of using a single dominant category to set surface and vegetative properties for the entire grid cell. Physics options commonly used for continental- and regional-scale downscaling experiments are implemented, and the potential biases inherited from these schemes are discussed in Section 2. This includes the use of spectral nudging only above the PBL to allow surface and low-level fields to more freely evolve and respond to changes in LU using WRF’s scale-appropriate physics. Using mosaic LU increases temperatures and SH throughout much of the eastern and central U.S., and decreases LH, 2-m mixing ratio, LAI, and precipitation, relative to using dominant LU (Figures 4, 5, 7, 9, & 10). These results corroborate Zhao and Wu (2017), who used mosaic LU in Noah and had reductions in precipitation and LH and warmer 850-hPa temperatures in 30-km simulations over east Asia. In the current work, using the mosaic LU improved precipitation results by alleviating an overestimation of precipitation frequency; however, it exacerbated an existing warm bias in 2-m temperature in several regions of the CONUS (Figures 4, 6, 7, & 8). When considering fluxes, error in the simulation of LH was reduced by the use of the mosaic but a high bias in SH was increased.
These changes are attributable to including subgrid low-density urban LU in this area of the U.S. with the mosaic option, which results in a compensating decrease in forest and agricultural LU types within NLCD 2011. The largest LU changes in these categories are the widespread increase in Developed Open Space throughout the central and eastern U.S., as well as decreased Deciduous Forest in the eastern CONUS and reduced Cultivated Crops in the central U.S. (Figure 3). Reductions in both agricultural and forest types, as well as increased urban land, are the largest LU changes found in areas where LH and 2-m mixing ratio are reduced and where larger SH and warmer 2-m temperatures occur in the mosaic run, relative to the dominant simulation. Changes in forest LU are larger than agricultural LU changes when considering areas where LH is decreased and SH is increased. Meanwhile, increased nighttime temperatures often occur in areas where low-intensity urban areas are increased with an offsetting decrease in agricultural land. Nevertheless, exchanging both agricultural and forest land for partial urban space generally reduces LAI, evapotranspiration, and LH and increases SH and near-surface temperatures.
In contrast, large cities have a decrease in SH and in mean and daily minimum 2-m temperatures, as the use of the mosaic LU enables a partial coverage of forest types inside of large urban centers, as opposed to the monolithic urban areas portrayed when the default is used. These cooler temperatures reduce the intensity of heat events as well as alleviate a high bias in annual mean temperature within those cities. Including greenspaces within urban areas also increases LH via evapotranspiration from the increased vegetation coverage. These results corroborate previous studies comparing dominant and mosaic LU within fine-resolution domains focused on specific cities (Li et al., 2013a; Sharma et al., 2017).
The updated vegetation and soil tables from Campbell et al. (2018) are also tested to assess how the sensitivity to LU treatment compares to the sensitivity to these table changes. Throughout the CONUS and in most regions, 2-m temperature is more sensitive to using the mosaic option than to including updated LU and soil parameters. However, monthly precipitation throughout the CONUS is occasionally more sensitive to the table changes than to using the mosaic. Consequently, the accuracy of soil and vegetation tables used with WRF’s Noah LSM should continue to be refined. Generally, when comparing domLUnewTBL to mosLUnewTBL, the differences in precipitation, mixing ratios, Tmax, Tmin, and Tmean are analogous to the comparison of domLU with mosLU. Again, warmer temperatures, as well as reduced precipitation and low-level moisture are widespread across the eastern U.S., with the largest changes generally in the Ohio Valley region (not shown).
Prior studies using the mosaic option within the Noah LSM in WRF used high-resolution simulations of large urban centers (e.g., Li et al., 2013a; Sharma et al., 2017). When examining LU at 12-km grid spacing over the entire CONUS, the prominence of forest, agricultural, and shrub and grasslands over much of the U.S. could suggest that changes to these categories when using mosaic LU rather than dominant LU would have the most notable effects on the LU and, therefore, the resulting meteorological fields in these simulations. However, the representation of mixed-urban landscapes results in the largest distinction between the mosaic and dominant runs. Over the CONUS, these low-intensity urban LU categories featured the highest correlation coefficients when mean temperature changes are correlated with differences in individual NLCD categories. Nevertheless, throughout the central and eastern U.S., widespread areas of low-density urban LU are underrepresented with the dominant approach, which favors forest and agricultural land over much of this area. By contrast, the mosaic approach reflects the heterogeneity of the low-density urban areas by simultaneously capturing influences of multiple LU types within the same grid cell. Furthermore, the LU classification system could contribute to this underrepresentation, as the assumptions inherent in the dominant approach cannot be expected to affect all LU types or LU classification systems equally. For example, urban LU is split across 4 categories in NLCD, while cropland is only represented by a single category. If related LU types are split across multiple categories, it is more difficult for any of these individual categories to represent a majority of the grid cell and become the dominant LU.
Within the current experiment, use of the mosaic LU treatment improved precipitation and LH but generally increased existing high biases in 2-m temperature and SH relative to the run with dominant LU. This is an unexpected result, given that the mosaic run provides a more realistic representation of the land surface. However, we speculate that the better performance of the dominant LU run may be a consequence of compensating errors within this model configuration from interactions between physics options. Furthermore, the magnitude of the model’s sensitivity to LU treatment is generally smaller than the model error, indicating that other aspects of the model configuration more strongly contribute to this temperature bias.
This analysis supports using the mosaic capability within the Noah LSM for dynamical downscaling applications because it captures subgrid variability of LU to better represent the land-surface exchange processes. By contrast, an LSM based on dominant LU may underrepresent or exclude urban influences in the transitional landscapes between urban and rural areas, which could adversely affect the heat fluxes and near-surface temperature and moisture profiles. This deficiency could adversely affect dynamical downscaling applications that span years or decades. Additionally, continental- or regional-scale WRF modeling is often performed to support ecological, hydrological, and air quality simulations (e.g., Cooter et al., 2012; Bash et al., 2013; Tang and Dennis, 2014; Schwede and Lear, 2014). LU treatment can strongly influence the simulation of emissions, atmospheric deposition, and changes in ecosystem services (e.g., Cooter et al., 2013), so including subgrid LU variability within WRF could improve fields that are important within downstream modeling efforts.
Key Points.
WRF’s Noah LSM is used in a dynamical downscaling application to compare the effects of mosaic land use against using the dominant category.
Within the U.S., mosaic increases urban area and reduces forest and cultivated land, leading to warmer temperatures and less precipitation.
Within large cities, the opposite trend occurs, as greenspace within cities increases and 2-m temperatures are reduced.
Acknowledgements
The views expressed in this article are those of the authors and do not necessarily represent the views or policies of the U.S. EPA. The authors appreciate the technical reviews and comments on the manuscript from Donna Schwede and Brian Eder (EPA), as well as the constructive comments of three anonymous reviewers. The PRISM data were obtained from the PRISM Climate Group, Oregon State University, http://prism.oregonstate.edu. MODIS data were downloaded from the Application for Extracting and Exploring Analysis Ready Samples (AρρEEARS) interface, available at https://lpdaacsvc.cr.usgs.gov/appeears/ and hosted by the U.S. Geological Survey. The FLUXNET2015 dataset was obtained from http://fluxnet.fluxdata.org/data/fluxnet2015-dataset/.
Appendix A
Table A1.
List of FLUXNET stations used to evaluate surface fluxes, listed by the site ID, site name, location, latitude, longitude, and International Geosphere–Biosphere Programme (IGBP) land cover type.
| Site ID | Site Name | Location | Latitude | Longitude | IGBP |
|---|---|---|---|---|---|
| US-ARM | ARM Southern Great Plains site- Lamont | Billings, OK | 36.6058 | −97.4888 | Croplands |
| US-Blo | Blodgett Forest | Pino Grande, CA | 38.8953 | −120.6328 | Evergreen Needleleaf Forests |
| US-Cop | Corral Pocket | San Juan County, UT | 38.0900 | −109.3900 | Grasslands |
| US-GLE | GLEES | Centennial, WY | 41.3665 | −106.2399 | Evergreen Needleleaf Forests |
| US-Ha1 | Harvard Forest EMS Tower (HFR1) | Petersham, MA | 42.5378 | −72.1715 | Deciduous Broadleaf Forests |
| US-Los | Lost Creek | Sherman, WI | 46.0827 | −89.9792 | Permanent Wetlands |
| US-Me2 | Metolius mature ponderosa pine | Camp Sherman, OR | 44.4523 | −121.5574 | Evergreen Needleleaf Forests |
| US-MMS | Morgan Monroe State Forest | Benton Township, IN | 39.3232 | −86.4131 | Deciduous Broadleaf Forests |
| US-Ne1 | Mead - irrigated continuous maize site | Wahoo, NE | 41.1651 | −96.4766 | Croplands |
| US-Ne2 | Mead - irrigated maize-soybean rotation site | Wahoo, NE | 41.1649 | −96.4701 | Croplands |
| US-Ne3 | Mead - rainfed maize-soybean rotation site | Marble, NE | 41.1797 | −96.4397 | Croplands |
| US-NR1 | Niwot Ridge Forest (LTER NWT1) | Ward, CO | 40.0329 | −105.5464 | Evergreen Needleleaf Forests |
| US-PFa | Park Falls/WLEF | Eisenstein, WI | 45.9459 | −90.2723 | Mixed Forests |
| US-SRM | Santa Rita Mesquite | Sahuarita, AZ | 31.8214 | −110.8661 | Woody Savannas |
| US-Syv | Sylvania Wilderness Area | Watersmeet Township, MI | 46.2420 | −89.3477 | Mixed Forests |
| US-Ton | Tonzi Ranch | Ione, CA | 38.4316 | −120.9660 | Woody Savannas |
| US-UMB | Univ. of Mich. Biological Station | Pellston, MI | 45.5598 | −84.7138 | Deciduous Broadleaf Forests |
| US-Var | Vaira Ranch- Ione | Ione, CA | 38.4133 | −120.9507 | Grasslands |
| US-WCr | Willow Creek | Emery, WI | 45.8059 | −90.0799 | Deciduous Broadleaf Forests |
| US-Wkg | Walnut Gulch Kendall Grasslands | Cochise County, AZ | 31.7365 | −109.9419 | Grasslands |
References
- Aas KS, Gisnås K, Westermann S, & Berntsen TK (2017) A tiling approach to represent subgrid snow variability in coupled land surface-atmosphere models, Journal of Hydrometeorology, 18, 49–63. 10.1175/JHM-D-16-0026.1, 2017. [DOI] [Google Scholar]
- Alapaty K, Herwehe JA, Otte TL, Nolte CG, Bullock OR, Mallard MS, Kain JS, & Dudhia J. (2012) Introducing subgrid-scale cloud feedbacks to radiation for regional meteorological and climate modeling, Geophysical Research Letters, 39, L24808. 10.1029/2012GL054031. [DOI] [Google Scholar]
- Bash JO, Cooter EJ, Dennis RL, Walker JT, & Pleim JE (2013) Evaluation of a regional air-quality model with bidirectional NH3 exchange coupled to an agroecosystem model. Biogeosciences, 10, 1635–1645. 10.5194/bg-10-1635-2013 [DOI] [Google Scholar]
- Bieniek PA, Bhatt US, Walsh JE, Rupp TS, Zhang J, Krieger JR, & Lader R. (2016) Dynamical downscaling of ERA-Interim temperature and precipitation for Alaska. Journal of Applied Meteorology and Climatology, 55, 635–654. 10.1175/JAMC-D-15-0153.1 [DOI] [Google Scholar]
- Bornstein R, & Lin Q. (2000) Urban heat islands and summertime convective thunderstorms in Atlanta: Three case studies. Atmospheric Environment, 34, 507–516. 10.1016/S1352-2310(99)00374-X [DOI] [Google Scholar]
- Bowden JH, Otte TL, Nolte CG, & Otte MJ (2012) Examining interior grid nudging techniques using two-way nesting in the WRF model for regional climate modeling. Journal of Climate, 25, 2805–2823. 10.1175/JCLI-D-11-00167.1 [DOI] [Google Scholar]
- Bullock OR, Alapaty K, Herwehe JA, Mallard M, Otte TL, Gilliam RC, & Nolte CG (2014) An observation-based investigation of nudging in WRF for downscaling surface climate information to 12-km grid spacing. Journal of Applied Meteorology and Climatology, 53, 20–33. 10.1175/JAMC-D-13-030.1 [DOI] [Google Scholar]
- Bullock OR Jr., Alapaty K, Herwehe JA, & Kain JS (2015) A dynamically computed convective time scale for the Kain–Fritsch convective parameterization scheme. Monthly Weather Review, 143, 2105–2120. 10.1175/MWR-D-14-00251.1. [DOI] [Google Scholar]
- Campbell PC, Bash JO, & Spero TL (2018) Updates to the Noah land surface model in WRF-CMAQ to improve simulated meteorology, air quality, and deposition. Journal of Advances in Modeling Earth Systems, 11 10.1029/2018MS001422 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen F, & Dudhia J (2001) Coupling an advanced land surface–hydrology model with the Penn State–NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Monthly Weather Review, 129, 569–585. [DOI] [Google Scholar]
- Chen F, Liu C, Dudhia J, & Chen M. (2014) A sensitivity study of high‐resolution regional climate simulations to three land surface models over the western United States. Journal of Geophysical Research: Atmospheres, 119, 7271–7291. 10.1002/2014JD021827 [DOI] [Google Scholar]
- Cheng FY, Hsu YC, Lin PL, & Lin TH (2013) Investigation of the effects of different land use and land cover patterns on mesoscale meteorological simulations in the Taiwan area, Journal of Applied Meteorology and Climatology, 52, 570–587. 10.1175/JAMC-D-12-0109.1 [DOI] [Google Scholar]
- Cooter EJ, Bash JO, Benson V, & Ran L. (2012) Linking agricultural crop management and air quality models for regional to national-scale nitrogen assessments, Biogeosciences, 9, 4023–4035. 10.5194/bg-9-4023-2012 [DOI] [Google Scholar]
- Cooter EJ, Rea A, Bruins R, Schwede D, & Dennis R. (2013) The role of the atmosphere in the provision of ecosystem services, Science of the Total Environment, 448, 197–208. 10.1016/j.scitotenv.2012.07.077 [DOI] [PubMed] [Google Scholar]
- Daly C, Halbleib M, Smith JI, Gibson WP, Doggett MK, Taylor GH, Curtis J, & Pasteris P. (2008), Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States, International Journal of Climatology, 28, 2031–2064. 10.1002/joc.1688 [DOI] [Google Scholar]
- Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, et al. (2011). The ERA‐Interim reanalysis: Configuration and performance of the data assimilation system. Quarterly Journal of the Royal Meteorological Society, 137(656), 553–597. 10.1002/qj.828 [DOI] [Google Scholar]
- Feser F, Rockel B, von Storch H, Winterfeldt J, & Zahn M. (2011) Regional climate models add value to global model data: A review and selected examples, Bulletin of the American Meteorological Society, 92, 1181–1192. 10.1175/2011BAMS3061.1 [DOI] [Google Scholar]
- Findell K, Gentine P, Lintner BR, & Kerr C. (2011) Probability of afternoon precipitation in eastern United States and Mexico enhanced by high evaporation. Nature Geoscience, 4, 434–439. 10.1038/NGEO1174 [DOI] [Google Scholar]
- Giorgi F, Jones C, & Asrar C. (2009) Addressing climate information needs at the regional level: the CORDEX framework. WMO Bulletin, 58, 175–183. [Google Scholar]
- Grimmond S. (2007), Urbanization and global environmental change: Local effects of urban warming, Geographic Journal, 173, 83–88. 10.1111/j.1475-4959.2007.232_3.x [DOI] [Google Scholar]
- Herwehe JA, Alapaty K, Spero TL, & Nolte CG (2014) Increasing the credibility of regional climate simulations by introducing subgrid-scale cloud–radiation interactions. Journal of Geophysical Research: Atmospheres, 119, 5317–5330. 10.1002/2014JD021504 [DOI] [Google Scholar]
- Homer CG, Huang C, Yang L, Wylie B, & Coan M. (2004) Development of a 2001 National Landcover Database for the United States. Photogrammetric Engineering and Remote Sensing, 70 (7), 829–840. 10.14358/PERS.70.7.829 [DOI] [Google Scholar]
- Homer CG, Dewitz JA, Yang L, Jin S, Danielson P, Xian G, Coulston J, Herold ND, Wickham JD, & Megown K. (2015) Completion of the 2011 National Land Cover Database for the conterminous United States-Representing a decade of land cover change information. Photogrammetric Engineering and Remote Sensing, 81 (5), 345–354 [Google Scholar]
- Hong S-Y, Noh Y, & Dudhia J. (2006) A new vertical diffusion package with an explicit treatment of entrainment processes. Monthly Weather Review, 134, 2318–2341. 10.1175/MWR3199.1 [DOI] [Google Scholar]
- Hong S-Y, & Lim J-OJ (2006) The WRF single-moment 6-class microphysics scheme (WSM6). Journal of the Korean Meteorological Society, 42 (2), 129–151. [Google Scholar]
- Hu XM, Nielsen‐Gammon JW, & Zhang FQ (2010). Evaluation of three planetary boundary layer schemes in the WRF model. Journal of Applied Meteorology and Climatology, 49(9), 1831–1844. 10.1175/2010JAMC2432.1 [DOI] [Google Scholar]
- Huff FA, & Changnon SA (1973) Precipitation modification of major urban areas. Bulletin of the American Meteorological Society, 54, 1220–1232. [DOI] [Google Scholar]
- Huth R, Kysely J, & Pokorna L. (2000) A GCM simulation of heat waves, dry spells, and their relationships to circulation. Climatic Change, 46, 26–60. 10.1023/A:1005633925903 [DOI] [Google Scholar]
- Iacono MJ, Delamere JS, Mlawer EJ, Shephard MW, Clough SA, & Collins WD (2008) Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. Journal of Geophysical Research, 113, D13103 10.1029/2008JD009944. [DOI] [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC) (2013) Climate Change 2013: The Physical Science Basis. Cambridge, United Kingdom and New York, NY: Cambridge University Press. [Google Scholar]
- Jimenez PA, Dudhia J, Gonzalez-Rouco JF, Navarro J, Montávez JP, & Garcia-Bustamante E. (2012) A revised scheme for the WRF surface layer formulation. Monthly Weather Review, 140, 898–918. 10.1175/MWR-D-11-00056.1. [DOI] [Google Scholar]
- Kain JS, 2004: The Kain–Fritsch convective parameterization: An update. Journal of Applied Meteorology and Climatology., 43, 170–181. [DOI] [Google Scholar]
- Karl TR, & Knight RW (1997) The 1995 Chicago heat wave: How likely is a recurrence? Bulletin of the American Meteorological Society, 78, 1107–1119. [DOI] [Google Scholar]
- Karl TR, & Koss WJ (1984) Regional and National Monthly, Seasonal, and Annual Temperature Weighted by Area, 1895–1983. Historical Climatology Series 4–3, National Climatic Data Center, Asheville, NC, 38 pp. [Google Scholar]
- Kishné AS, Yimam YT, Morgan CLS, & Dornblaser BC (2017), Evaluation and improvement of the default soil hydraulic parameters for the Noah Land Surface Model, Geoderma, 285, 247–259. 10.1016/j.geoderma.2016.09.022 [DOI] [Google Scholar]
- Li D, Bou‐Zeid E, Barlage M, Chen F, & Smith JA (2013. a). Development and evaluation of a mosaic approach in the WRF‐Noah framework. Journal of Geophysical Research: Atmospheres, 118, 11,918–11,935. 10.1002/2013JD020657 [DOI] [Google Scholar]
- Li D, Bou-Zeid E, Baeck M, Jessup S, & Smith J. (2013. b) Modeling land surface processes and heavy rainfall in urban environments: Sensitivity to urban surface representations. Journal of Hydrometeorology, 14, 1098–1118. 10.1175/JHM-D-12-0154.1. [DOI] [Google Scholar]
- Li L, Li W, & Jin J. (2014), Improvements in WRF simulation skills of southeastern United States summer rainfall: Physical parameterization and horizontal resolution, Climate Dynamics, 43, 2077 10.1007/s00382-013-2031-2. [DOI] [Google Scholar]
- Li H, Wolter M, Wang X, & Sodoudi S. (2017) Impact of land cover data on the simulation of urban heat island for Berlin using WRF coupled with bulk approach of Noah-LSM. Theoretical and Applied Climatology, 1–15. 10.1007/s00704-017-2253-z [DOI] [Google Scholar]
- Liang X-Z, & Coauthors (2012) Regional Climate-Weather Research and Forecasting Model (CWRF). Bulletin of the American Meteorological Society, 93, 1363–1387. 10.1175/BAMS-D-11-00180.1 [DOI] [Google Scholar]
- Lim K-SS, Fan J, Leung LR, Ma P-L, Singh B, Zhao C, Zhang Y, Zhang G,& Song X. (2014), Investigation of aerosol indirect effects using a cumulus microphysics parameterization in a regional climate model, Journal of Geophysical Research: Atmospheres, 119, 906–926. 10.1002/2013JD020958. [DOI] [Google Scholar]
- Ma Y, Yang Y, Mai X, Qiu C, Long X, & Wang C. (2016) Comparison of analysis and spectral nudging techniques for dynamical downscaling with the WRF model over China. Advances in Meteorology, 2016, 4761513 10.1155/2016/4761513 [DOI] [Google Scholar]
- Mallard MS, Spero TL, & Taylor SM (2018) Examining WRF’s sensitivity to contemporary land use datasets across the contiguous U.S. using dynamical downscaling. Journal of Meteorology and Climatology, 57, 2561–2583. 10.1175/JAMC-D-17-0328.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manley G. (1958) On the frequency of snowfall in metropolitan England. Quarterly Journal of the Royal Meteorological Society, 84, 70–72. 10.1002/qj.49708435910 [DOI] [Google Scholar]
- Mearns LO, et al. (2012) The North American Regional Climate Change Assessment Program: Overview of phase I results. Bulletin of the American Meteorological Society, 93, 1337–1362. 10.1175/BAMS-D-11-00223.1 [DOI] [Google Scholar]
- Meehl GA, & Tebaldi C. (2004) More intense, more frequent, and longer lasting heat waves in the 21st century. Science, 305, 994–997. 10.1126/science.1098704 [DOI] [PubMed] [Google Scholar]
- Miguez-Macho G, Stenchikov GL, & Robock A. (2004) Spectral nudging to eliminate the effects of domain position and geometry in regional climate model simulations. Journal of Geophysical Research, 109, D13104. 10.1029/2003JD004495. [DOI] [Google Scholar]
- Myneni R, Knyazikhin Y, & Park T. (2015) MCD15A2H MODIS/Terra+Aqua Leaf Area Index/FPAR 8-day L4 Global 500m SIN Grid V006. NASA EOSDIS Land Processes DAAC. 10.5067/MODIS/MCD15A2H.006 [DOI] [Google Scholar]
- National Center for Atmospheric Research (NCAR), (2015) WRF User’s Guide Version 3.6: User’s Guide for the Advanced Research WRF (ARW) Modeling System Version 3.6. Accessed 1 May 2018 [Available online at: http://www2.mmm.ucar.edu/wrf/users/docs/user_guide_V3.6/ARWUsersGuideV3.6.1.pdf]
- Oke TR (1982) The energetic basis of the urban heat island. Quarterly Journal of the Royal Meteorological Society, 108, 1–24. 10.1002/qj.49710845502 [DOI] [Google Scholar]
- Otte TL, Nolte CG, Otte MJ, & Bowden JH (2012) Does nudging squelch the extremes in regional climate modeling? Journal of Climate, 25, 7046–7066. 10.1175/JCLI-D-12-00048.1 [DOI] [Google Scholar]
- Pastorello GZ, Papale D, Chu H, Trotta C, Agarwal DA, Canfora E, Baldocchi DD, & Torn MS (2017), A new data set to keep a sharper eye on land-air exchanges, Eos, 98 10.1029/2017EO071597 [DOI] [Google Scholar]
- Pei L, Moore N, Zhong S, Luo L, Hyndman DW, Heilman WE, et al. (2014). WRF model sensitivity to land surface model and cumulus parameterization under short‐term climate extremes over the southern Great Plains of the United States. Journal of Climate, 27(20), 7703–7724. 10.1175/JCLI-D-14-00015.1 [DOI] [Google Scholar]
- Ran L, Pleim J, & Gilliam R. (2010) Impact of high resolution land-use data in meteorology and air quality modeling systems, in Air Pollution Modeling and its Applications XX, edited by Steyn DG and Rao ST, chap. 1, C(section 1.1):3–7, Springer, Netherlands. [Google Scholar]
- Reames LJ & Stensrud DJ (2017) Sensitivity of simulated urban–atmosphere interactions in Oklahoma City to urban parameterization. Journal of Applied Meteorology and Climatology, 56, 1405–1430. 10.1175/JAMC-D-16-0223.1 [DOI] [Google Scholar]
- Schicker I, Arias DA, & Seibert P. (2016) Influences of updated land-use datasets on WRF simulations for two Austrian regions. Meteorology and Atmospheric Physics, 128, 279–301. 10.1007/s00703-015-0416-y [DOI] [Google Scholar]
- Schwede DB, & Lear GG (2014) A novel hybrid approach for estimating total deposition in the United States, Atmospheric Environment, 92, 207–220. 10.1016/j.atmosenv.2014.04.008 [DOI] [Google Scholar]
- Sertel E, Robock A, & Ormeci C. (2009) Impacts of land cover data quality on regional climate simulations. International Journal of Climatology, 30, 1942–1953. 10.1002/joc.2036 [DOI] [Google Scholar]
- Sharma A, Fernando HJS, Hamlet AF, Hellmann JJ, Barlage M, & Chen F. (2017) Urban meteorological modeling using WRF: A sensitivity study. International Journal of Climatology. 37, 1885–1900. 10.1002/joc.4819 [DOI] [Google Scholar]
- Shin HH, & Hong SY (2011), Intercomparison of planetary boundary layer parameterizations in the WRF model for a single day from CASES‐99, Boundary Layer Meteorology, 139, 261–281. 10.1007/s10546-010-9583-z [DOI] [Google Scholar]
- Skamarock WC, & Klemp JB (2008) A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. Journal of Computational Physics, 227, 3465–3485. 10.1016/j.jcp.2007.01.037 [DOI] [Google Scholar]
- Spero TL, Otte MJ, Bowden JH, & Nolte CG (2014) Improving the representation of clouds, radiation, and precipitation using spectral nudging in the weather research and forecasting model. Journal of Geophysical Research: Atmospheres, 119, 11,682–11,694. 10.1002/2014JD022173 [DOI] [Google Scholar]
- Spero TL, Nolte CG, Bowden JH, Mallard MS, & Herwehe JH (2016) The impact of incongruous lake temperatures on regional climate extremes downscaled from the CMIP5 archive using the WRF model. Journal of Climate, 29, 839–853. 10.1175/JCLI-D-15-0233.1 [DOI] [Google Scholar]
- Spero TL, Nolte CG, Mallard MS, & Bowden JH (2018) A maieutic exploration of nudging strategies for regional climate applications using the WRF model. Journal of Applied Meteorology and Climatology, 57, 1883–1906. 10.1175/JAMC-D-17-0360.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang C, & Dennis RL (2014) How reliable is the offline linkage of Weather Research & Forecasting Model (WRF) and Variable Infiltration Capacity (VIC) model? Global and Planetary Change, 116, 1 10.1016/j.gloplacha.2014.01.014 [DOI] [Google Scholar]
- Walsh J, and Coauthors (2014) Ch. 2.: Our Changing Climate. Climate Change Impacts in the United States: The Third National Climate Assessment, Melillo JM, Richmond TC, and Yohe GW, Eds., U.S: Global Change Research Program, 19–67. 10.7930/J0KW5CXT. [DOI] [Google Scholar]
- Yang B, Qian Y, Lin G, Leung R, & Zhang Y. (2012) Some issues in uncertainty quantification and parameter tuning: A case study of convective parameterization scheme in the WRF regional climate model. Atmospheric Chemistry and Physics, 12, 2409–2427. [Google Scholar]; doi: 10.5194/acp-12-2409-2012. [DOI] [Google Scholar]
- Yang J, & Duan K(2016) Effects of Initial Drivers and Land Use on WRF Modeling for Near-Surface Fields and Atmospheric Boundary Layer over the Northeastern Tibetan Plateau, Advances in Meteorology, 7849249. 10.1155/2016/7849249. [DOI] [Google Scholar]
- Zhao D, & Wu J. (2017) The impact of land use and land cover changes on East Asian summer monsoon precipitation using the WRF‐mosaic approach. Atmospheric Science Letters, 18, 450–457. 10.1002/asl.788 [DOI] [Google Scholar]
- Zheng Y, Alapaty K, Herwehe JA, Del Genio AD, & Niyogi D. (2016) Improving high-resolution weather forecasts using the Weather Research and Forecasting (WRF) Model with an updated Kain–Fritsch scheme. Monthly Weather Review, 144, 833–860. 10.1175/MWR-D-15-0005.1. [DOI] [Google Scholar]