Controlling infectious disease outbreaks: Lessons from mathematical modelling

Abstract

Epidemiological analysis and mathematical models are now essential tools in understanding the dynamics of infectious diseases and in designing public health strategies to contain them. They have provided fundamental concepts, such as the basic and effective reproduction number, generation times, epidemic growth rates, and the role of pre-symptomatic infectiousness, which are crucial in characterising infectious diseases. These concepts are outlined and their relevance in designing control policies for outbreaks is discussed. They are illustrated using examples from the 2003 severe acute respiratory syndrome outbreak, which was brought under control within a year, and from pandemic influenza planning, where mathematical models have been used extensively.

Introduction

The study of infectious diseases has been transformed by the use of mathematical models to gain insight into the dynamics of epidemics, to identify potential public health interventions, and to assess their impact.¹ Mathematical models were useful in informing policy during the foot and mouth disease outbreak in the United Kingdom in 2001, during the severe acute respiratory syndrome (SARS) outbreak in 2003 and in recent planning of responses to potential smallpox or pandemic influenza outbreaks. These analyses and subsequent ongoing research have led to insights into epidemic dynamics and control, which have informed public health policy in this field. These results can often be presented in a technically complex or intimidating fashion, making the field inaccessible to non-specialists. This paper is designed to provide a non-technical summary of the core results and concepts for the non-specialist.

Mathematical models of epidemics rigorously represent our knowledge and assumptions about disease transmission. Models can range from simple systems of ordinary differential equations to complex individual-based stochastic simulations of millions of people.² Depending on the quality and detail of data available, the models can represent variability in the disease course of individuals, as well as variability in spatial structure, demographic structure, population density, travel patterns, or treatment protocols.³ Model complexity is not, in itself, a virtue and indeed may not be necessary. The more intricate a model becomes, the more realism it can aspire to, but estimating parameters and interpretation of results is also increasingly difficult.

Models must be designed to make effective use of the available (and reliable) data and they must be tailored to answer clearly defined scientific or policy questions in a timely fashion. Epidemiological analyses allow quantification of characteristics such as mortality rates, incubation periods, and transmission rates; identification of disease transmission route(s), heterogeneities, and risk factors for disease spread; and the effectiveness of disease-control/risk-reduction policies. Analysis of well-constructed models can provide insight into the course of an epidemic and can be used to test ‘what if’ scenarios to inform the development of policy. In this paper, I outline important concepts of and insights on outbreaks of directly transmissible infections provided by quantitative approaches and epidemiological models, using examples from the 2003 SARS outbreak and recent analyses of a potential pandemic influenza outbreak.

Severe acute respiratory syndrome

The World Health Organisation (WHO) issued a global alert for SARS on 12 March 2003, at which point there were 150 suspected cases in seven countries (Figure 1).⁵ Although the disease had already spread to several countries across the globe, the epidemic was brought under control within a few months, with most of the 27 affected countries reporting fewer than 10 suspected cases. Epidemiological analysis and mathematical models played a crucial role in informing public health policy and contributing to the control of the outbreak.^{6, 7, 8} Effective international collaboration and data sharing facilitated rapid completion of most of the essential tasks, including identification of the aetiological agent.⁹

Figure 1.

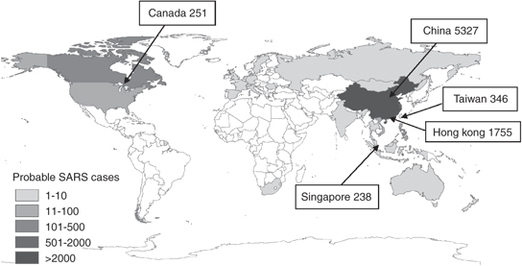
Probable SARS cases with onset between 1 November 2002 and 31 July 2003 by country, as reported by the WHO on 26 September 2003.⁵ The five countries with the largest number of probable cases are labelled.

Influenza

The global spread of a highly pathogenic H5N1 influenza virus among wild fowl and domestic poultry flocks and the continuing occurrences of human cases⁴ poses the threat of a global influenza pandemic, should a strain emerge which is transmissible between humans. The 1918 influenza epidemic spread extremely rapidly and killed 20–40 million people worldwide. The world population has more than tripled since 1918, so high population densities, as well as increasing domestic and international travel, may facilitate such a pandemic. Improved surveillance, technological advances, and an increased understanding of epidemiology together enable societies to prepare for a range of possible pandemic scenarios. National governments and the WHO are monitoring human and avian cases of H5N1 and other novel strains,⁴ antiviral treatments are being produced in large quantities for stockpiling by governments¹⁰ and novel vaccines are being developed to protect against the avian form of the virus and being stockpiled by governments.¹⁰ Despite these precautions, the exact characteristics of a potentially pandemic strain which may emerge cannot be predicted exactly, although ranges can be estimated from previous pandemics.^{11, 12, 13} Therefore, it is essential to understand how the effects of such an outbreak might be contained, or at least mitigated, for a range of scenarios. Complex, often individual-based, models of influenza outbreaks, informed by re-analysis of previous pandemics, are being used to inform the design of public health strategies should a strain emerge which is capable of human-to-human transmission.²

Key Epidemiological Quantities

When faced with an emerging or re-emerging outbreak of an infectious disease, it is important to quantify the characteristics of the disease in order to evaluate the level of threat and the timescales over which the threat is likely to develop, and to consider possible methods of control. Accurate estimation of these characteristics depends on real time centralised collation of epidemiological information.

Basic reproduction number, R₀

The basic reproduction number, R₀, is typically defined as the mean number of new infections caused by a single infectious individual in a wholly susceptible population¹ (the definition is slightly different for heterogeneous populations¹⁴). If each infected individual on average infects more than one other individual, that is, if R₀ is greater than one, then a small number of cases in a population will usually lead to an epidemic. When there are small numbers of cases and R₀ is large, there is a small probability that the epidemic will ‘fade-out’ after only a few infections because the early cases recover before infecting enough other individuals (Figure 2a). This probability of fading out before the epidemic takes off becomes smaller as R₀ gets larger. If R₀ is less than one the outbreak will surely die out. Infections with reproduction numbers close to, but exceeding, one are potentially easier to control than infections with reproduction numbers much larger than one.

Figure 2.

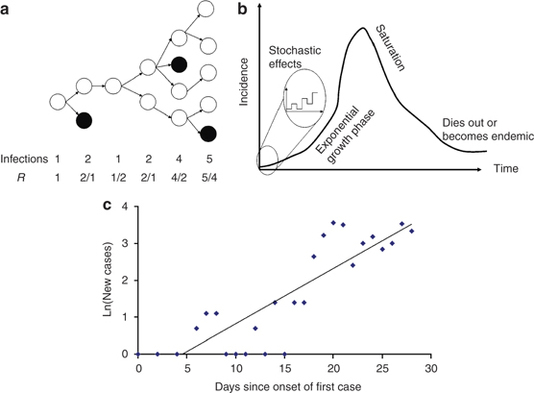
The basic reproduction number and the characteristics of epidemics. (a) Illustration of an epidemic with discrete generations. If the basic reproduction number, R₀ is greater than 1 (here R₀=1.75) then the epidemic expands exponentially. The effective reproduction number, R, is calculated as the number of new infections divided by the number of infected individuals in the previous generation.¹⁵ (b) The characteristic shape of an uncontrolled outbreak where R₀>1. Initially the epidemic may die out because of stochastic factors, but once it is established it grows exponentially until susceptibles are exhausted at which point the epidemic slows until the disease either becomes endemic or extinct.¹⁶ (c) Estimating R₀ from the first month of cases in Hong Kong, shown by date of onset, as published by the WHO⁵ R₀ may be estimated from the exponential growth rate, here the slope of the log-linear fitted line, r=0.15. See text for estimation of R₀.

The basic reproduction number for a particular infection is dependent on the biological characteristics of the disease and on the behavioural patterns of a population. The higher the transmission rate of the disease per unit time and the longer the duration of the infectious period, the larger the R₀. A disease which is highly infectious for a short period of time may have the same basic reproduction number as a disease that is not as infectious but has a much longer infectious period. For diseases with similar characteristics the basic reproduction number is different for each population, as the opportunities for onward infection are affected by the contact patterns of a population. In a city where most people commute to work by public transport, for example, the opportunities for onward transmission of an airborne pathogen may be much greater than in less densely populated areas. For many directly transmitted diseases, such as measles¹ and pandemic influenza,¹¹ R₀ is usually assumed to be similar in unvaccinated populations. For sexually transmitted diseases, large differences in sexual behaviour within populations can lead to estimates of R₀ for heterosexual populations from 2 for low risk populations¹⁷ to over 10 for high activity groups and sex workers.¹⁸

Generation time, serial interval, T_g

Alongside the basic reproduction number, it is important to have some estimate of how quickly the number of cases of a novel infection will grow and how long an outbreak will last. The generation time, T_g, is defined as average time from an individual being infected to that individual infecting others.^{1, 14, 19, 20} This includes any latent period when the infected individual may not show symptoms or may not be infectious, and excludes any period when infected individuals may still be showing symptoms but are no longer infectious. It is sometimes assumed to be equivalent to the serial interval, which is the average time from when one person shows symptoms until the person they infect shows symptoms.²⁰ For SARS this was initially estimated as 8–12 days.^{7, 21}

Estimating R₀ from the epidemic growth rate, r

When a novel infection is introduced to a population, there is a finite probability that it may not take hold in this population and die out, even if R₀>1, because of the chance events when there are small numbers of infected individuals (Figure 2b). If, however, the infection takes hold, the number of new cases grows exponentially.¹ The rate at which the number of cases will grow during this early stage, r, is dependent on both the reproduction number and the generation time of the infection, and can therefore be used to estimate the basic reproduction number. For a homogeneous population with onward infection occurring throughout the infectious period as R₀=rT_g+1, but there are other formulations for different model assumptions.^{1, 19, 22, 23} As for the basic reproduction number, the relationship between the epidemic growth rate, the serial interval, and the basic reproduction number is more complex for heterogeneous populations.^{14, 19} In Figure 2c I have used this equation to estimate R₀ from first month of the SARS outbreak in Hong Kong in 2003 (Figure 2c). The best fitting straight line to the log incidence data gives a growth rate, r, of 0.15 per day (equivalent to a doubling time 4.6 days). The generation time of SARS, T_g, has been estimated to be 10 days from data on the number of days between the start of symptoms for individuals who infected each other.^{7, 24} We can now use the equation above to get an estimate of the basic reproduction number for SARS as R₀=1+0.15 × 10=2.5. This relatively simple calculation gives a similar estimate to those made by more sophisticated methods.^{7, 21, 25}

The basic reproduction number for influenza has been estimated to be as high as 21,²⁶ but recent reanalysis of pandemic outbreaks estimate R₀ for pandemic influenza to be in the range of 1.4–3.0,^{11, 12, 27} which is similar to that for SARS. The generation time for influenza is, however, much shorter than that for SARS, approximately 4–6 days,^{11, 27} which gives a doubling time of the epidemic of 1–4 days, much faster than was observed for SARS. This means that control of an outbreak of pandemic influenza will require very swift implementation of public health measures.

Effective reproduction number, R

During the course of an epidemic the effective reproduction number, R, is the average number of secondary cases per primary case at that point in the epidemic (Figure 2a). Estimation of this number during an epidemic facilitates quantitative assessment of the effectiveness of intervention strategies, with reduction below one meaning the outbreak being brought under control.^{25, 28} During the course of the SARS epidemic in 2003, mathematical modelling was an essential tool in showing that intervention methods gradually brought the epidemic under control in Hong Kong, Special Administrative Region of China and Singapore,^{7, 8, 25, 28} and that controls appear to have been lifted too early in Toronto, Canada.²⁹ Reanalysis of the 1918–1919 influenza pandemic shows that public health measures were effective in mitigating this outbreak.^{30, 31, 32}

Although R is an estimate of average transmission at a population level, individuals vary both in how they respond to an outbreak of a novel infection (such SARS) or an outbreak of a known infection (such as pandemic influenza), and in their behaviour in terms of the number of contacts that they make.¹⁴ Some individuals, termed ‘superspreaders’, may transmit to many others either because of some characteristic of their infection, because of their contacts or purely by chance – being in the wrong place at the right stage of their infection.^{7, 8, 33, 34}, Care should be taken when gathering and interpreting data on possible exposures because they may be subject to bias towards previously identified sources and away from transmission from casual contacts; and may neglect asymptomatic transmissions.

Case fatality rate and age-distribution of cases

In assessing the potential consequences of an infectious disease outbreak, one of the most important concerns of policy makers is the number of fatalities. The case fatality rate (CFR) for a particular aetiological agent is the proportion of those who acquire the disease who will eventually die from it. In the early stages of an outbreak there will be many new cases of the disease for whom the outcome is not yet known and therefore estimates of the CFR must be carefully calculated.^{6, 35} In 2003 the WHO initially reported a CFR of 5 per cent,⁴ in fact the CFR for SARS was a much higher 15 per cent overall.^{6, 35}

The overall CFR often hides large variations, with the young and the elderly often at highest risk. In the 2003 SARS outbreak in Hong Kong, the CFR was very low among the young (<1 per cent for ages <30 years) and increased to 55 per cent for patients over 60 years of age.¹⁵ Very few cases were admitted to hospital among the very young,⁶ which is unusual because children are often considered to be the group with the highest rate of transmission of directly transmitted pathogens, while also serving as a source of infection for their parents and other adults (sometimes called a ‘core group’).¹ Serological surveys showed little evidence to support asymptomatic cases among this age group.

In the influenza pandemic of 1918, the CFR was much higher (∼3 per cent) in young adults aged 20–40 years than in non-pandemic years (<0.5 per cent).³⁶ Also, those aged 5–14 years contributed disproportionately to the numbers of cases (∼25 per cent), but not to the numbers of deaths.³⁶ There could be many possible explanations for these distributions, such as previous exposure to the pandemic strain, environmental factors, patterns of mixing and transmission because of the world war,³⁶ or because of biological factors which could have made the virus so pathogenic overall (such as those discussed by Loo et al³⁷). High numbers of cases and fatalities among the 20–40 age group are likely to have huge economic impact because they form an important part of the workforce, and are primary carers for children.

Public Health Interventions

Isolation and contact tracing

Isolation of symptomatic individuals together with tracing and quarantine of their contacts constitute major weapons in the armoury of public health outbreak control measures. The success of these strategies has been shown to be crucially dependent on the proportion of transmissions which occur before infected individuals show symptoms.²⁶ Isolation of a proportion of symptomatic individuals can control an outbreak provided this proportion is large enough for that infection.²⁶ Normally circulating influenza is believed to be infectious before the infected individual is showing symptoms,³⁸ which makes control extremely difficult. If, however, the disease is mainly transmitted to close contacts, for example family members, then contact tracing may be manageable and effective. If transmission is likely for more casual contacts, contact tracing is much more difficult. Contact tracing has also been shown to depend on the degree of variability in the timing of infectiousness between different infected people in the population.^{39, 40} Before large amounts of resources are allocated, it may be important to assess the effectiveness of such a policy early in an epidemic through analysis of transmission chains and the impact of the intervention on the effective reproduction number.

Vaccination and prophylactic treatment

Both vaccination and prophylactic treatment with antiviral drugs or antibiotics restrict the spread of an infectious disease by limiting the number of individuals to whom the infection can be transmitted. Such strategies do not have to eliminate susceptibility from the population, but merely need to reduce the number of susceptible individuals so that the epidemic cannot be sustained. The minimum proportion of the population that must be vaccinated to prevent a large outbreak is 1−1/R₀ for homogeneous populations.¹ (There are also expressions for heterogeneous populations.⁴¹) This proportion is higher for diseases with large R₀. The whole population need not be vaccinated, as those who are not vaccinated are protected by ‘herd immunity’, that is, the fact that the epidemic cannot be sustained in the population because there are so few susceptible individuals.

Limited vaccine and antivirals stockpiles available to governments may be employed in a number of ways, to those most at risk, to key workers, or to contain an outbreak. If antivirals are to be distributed prophylactically to prevent the spread of disease, rather than to treat cases, then containment may be possible, provided (i) there are enough doses or courses of treatment, (ii) the programme is implemented extremely rapidly, and (iii) cases are situated in a limited geographic region.^{11, 13, 40} The evolution of drug resistance would, of course, be a concern if large scale prophylaxis were implemented. Because of the short doubling time of influenza epidemics, these strategies would have to be implemented when there are very few cases. One such responsive strategy – implementing travel restrictions and prophylactic treatment of everyone within 10 km ring of each case – would require a stockpile of approximately 3 million courses of antiviral drugs to contain an outbreak of pandemic influenza.¹¹ Following the publication of this analysis by Ferguson et al, Roche donated 3 million doses of their antiviral drug to the WHO for this very purpose and the WHO has set up project to develop protocols for practical implementation of containment.

Travel advisories and screening of passengers

International air travel greatly facilitates global spread of infectious diseases such as SARS and influenza.^{42, 43, 44, 45} The SARS epidemic of 2003 spread across the globe within a matter of days, eventually affecting 27 countries, with suspected cases reported in every populated continent (Figure 1). Public health measures, including screening and travel restrictions, can be put in place to slow this spread. The effectiveness of such methods, however, is dependent on the characteristics of the disease. If an infection has an incubation period which is longer than the duration of a flight then infected people are unlikely to develop symptoms during a flight. Thus even 100 per cent effective entry screening is unlikely to be useful in identifying cases.⁴⁵ Imported SARS cases caused new outbreaks only in the early stages of the global outbreak, because of effective exchanges of information about the disease, the lack of pre-symptomatic infectiousness, and local outbreak control. If an outbreak is uncontrolled, then the number of new cases continues to grow exponentially and sheer weight of numbers means that cases will be exported. Travel reductions of greater than 99 per cent will be required to slow the spread of influenza.^{43, 44, 46, 47} Strategies aimed at protecting the public from pandemic influenza should focus resources on surveillance and rapid control of outbreaks wherever potentially pandemic strains arise.⁴⁸

Summary

Epidemiological analyses and mathematical models are essential tools in understanding and controlling outbreaks of directly transmissible pathogens. There are many clinical and biological tasks to be completed, such as formulating a case definition and treatment strategies, identifying the aetiological agent and developing diagnostic tests. Alongside these tasks the estimation of key parameters, such as the basic and effective reproduction numbers, the generation time, and the proportion of transmissions occurring before symptoms, are essential to characterise an outbreak and its potential scope. Estimation of the effective reproduction number during an ongoing outbreak also provides an early indication of whether an infectious disease outbreak is under control or not. CFRs are an important consideration in public policy and must also be estimated accurately.

Epidemiological parameters cannot be estimated for outbreaks with new influenza strains until they actually emerge, but mathematical models can be used to investigate the likely consequences of a future influenza pandemic, based on analysis of previous epidemics and of current population structures and behaviours. Integration of epidemiological and statistical approaches increases the power of such analysis and the usefulness of models. Both statistical analyses and models require high quality epidemiological data, collected and collated centrally while the outbreak is ongoing and made available for analysis. Prediction of the exact progress of an epidemic will never be possible because of the variability of human behaviour. Nonetheless, mathematical models, which precisely represent knowledge and assumptions about disease transmission add significant insight into the dynamics of infectious diseases and are increasingly recognised as a vital part of any public health policy development.

About the Author

Déirdre Hollingsworth is an epidemiological modeller at Imperial College London. She develops models for the design of effective interventions to control epidemic outbreaks of directly transmitted pathogens. Her research has included studies on the impact of international travel restrictions on the spread of pandemic influenza with Roy Anderson and Neil Ferguson. She studied mathematics and mathematical epidemiology at Oxford and Cambridge Universities, UK.