Comparative quantification of primary mitral regurgitation by computer modeling and simulated echocardiography

Abstract

Clinical investigations have demonstrated that mitral regurgitation (MR) quantification using echocardiography (echo) may significantly underestimate or overestimate the regurgitant volume, especially for two-dimensional (2D) echo. Computer modeling and simulated echo were conducted to evaluate the fundamental assumptions in the echo quantification of primary MR that is due to posterior mitral leaflet prolapse. The theoretical flaw of the proximal isovelocity surface area (PISA) method originates from the assumption that the MR flow rate is the product of the isovelocity surface area and aliasing velocity, which is only valid when the velocity vectors are perpendicular to the isovelocity surface. Other factors such as the Doppler angle effect, the view planes of 2D echo, and the single time instant of PISA were also analyzed. We find that the hemielliptic PISA method gives the smallest error for moderate and severe MR cases compared with other PISA methods. Compared with the PISA method, the volumetric technique (VT) is theoretically more robust. By considering correction factors that are caused by nonflat velocity profiles and the closing volume of the aortic valve, the accuracy of the VT method can be significantly improved. The corrected volumetric technique provides more accurate results compared with the PISA methods, especially for mild MR.

NEW & NOTEWORTHY We evaluate the accuracy of common echocardiography techniques for the quantification of primary mitral regurgitations using computer modeling. The hemielliptic proximal isovelocity surface area (PISA) method gives the smallest error (within 15%) for moderate and severe mitral regurgitation cases compared with other PISA methods. The volumetric method is theoretically more robust than the PISA method. The accuracy of the volumetric method can be improved by a correction factor around 0.7 because of the nonflat velocity profiles and the closing volume of the aortic valve.

INTRODUCTION

Mitral regurgitation (MR) is the most common valvular heart disease, with a prevalence of 9.3% in the United States population aged 75 and above (4). Although Doppler echocardiography (echo) is the primary clinical tool to assess the severity of MR, quantitative assessment of MR remains challenging, and a true gold standard technique is still lacking (27). Two commonly used quantitative methods were recommended by American Society of Echocardiography guidelines (53): the proximal isovelocity surface area (PISA) method (35, 49) and the volumetric technique (VT; the quantitative pulsed Doppler method).

Clinical and in vitro studies have demonstrated that the two-dimensional (2D) PISA method may significantly underestimate or overestimate the regurgitant volume (RVol) (5, 27, 33, 44). The geometric assumption of a hemispheric isovelocity surface is often not correct, as it is only valid for a small and roughly circular orifice in a flat plate. The three-dimensional (3D) PISA method, which is based on 3D color Doppler, may be a better choice to directly measure the isovelocity surface area irrespective of its shape (28). However, the effect of Doppler angulation (34) and the “urchinoid” true iso-Doppler velocity shape (13, 31) need to be accounted for.

The VT method requires the measurement of the diastolic stroke volume (SV) through the regurgitant mitral valve (MV) and the measurement of the forward SV through a nonregurgitant valve, usually the aortic valve (AV). Because of the law of mass conservation, the flow going into the left ventricle during diastole equals the systolic forward flow across the AV plus the systolic regurgitant flow into the left atrium. This method is simple in principle; however, it has not achieved a widespread usage in the clinical community (46).

Therefore, the objectives of this study were to evaluate the fundamental assumptions in the clinical echo quantification of primary MR based on computer modeling, identify the pitfalls in the assessment of MR severity, and provide suggestions that could improve its assessment in the clinical setting.

METHODS

Computer Models of Primary MR

Four left heart acute MR computer models with posterior mitral leaflet (PML) prolapse following chordae rupture were used in this study (7). These models were developed from a previously validated subject-specific left heart fluid-structure interaction (FSI) computer model (72-yr-old, female patient), which served as the control model (29). Institutional Review Board approval to review deidentified clinical data was obtained. PML prolapse was modeled by removing chordae elements from different chordae groups, starting from marginal and intermediate chordae and then progressing toward partial and total chordal origins, representing a pathological process in which minimal chordae rupture precedes more extensive chordae rupture. Chordal rupture models were named based on the ruptured chordae insertions on the PML: marginal and intermediate P1 (M&I P1), marginal and intermediate P2 (M&I P2), P2 & P1, and P2 & P3, in which the lateral PML scallop is P1, the central scallop is P2, and the medial scallop is P3.

Clinically, chordae rupture is recognized as one of the main causes of mitral valve prolapse (14). PML prolapse is more common than the anterior mitral leaflet prolapse, usually involving ruptured chordae in the central P2 scallop, which may extend to the lateral P1 and P3 scallops (17, 51). Thus, four PML prolapse models that represent common clinical scenarios of acute chordae rupture were analyzed in this study.

The patient’s heart rate was 75 beats/min. For the control model, a constant left atrial pressure of 20 mmHg was prescribed, and a physiological aortic pressure waveform was applied at the outlet. For the chordae rupture models, we employed a pathological left atrial pressure waveform with an elevated peak systolic pressure of 55 mmHg. More details on the left heart FSI model setup can be found in our previous studies (7, 29).

Simulated Echo MR Quantification Using the PISA Method

Theoretical basis.

The flow approaching a regurgitant orifice will form a series of concentric isovelocity shells with decreasing surface area and increasing velocity. Assuming an inviscid flow, if the orifice is a small circle on a flat plate, these isovelocity shells will be hemispheric in shape with an area of 2πr², in which r is the shell radius. Multiplying this area by the velocity of the isovelocity shell (v_a) will yield the flow rate Q = 2r²v_a. The radius r and aliasing velocity v_a can be obtained by shifting the baseline color in the direction of the MR or by lowering the Nyquist limit to optimize the visualization of the isovelocity shell in the color Doppler display (45). In the PISA method, once the flow rate is known, the effective regurgitant orifice area (EROA) and RVol can be calculated as EROA = Q/v_MR = 2πr²v_a/v_MR and RVol = EROA VTI_MR, respectively, in which v_MR is the temporal peak regurgitant jet velocity measured by continuous wave Doppler (CWD) ultrasound, which is normally measured by steering the ultrasound beam to ensure that the beam is aligned with the MR jet, and VTI_MR is the velocity time integral (VTI) of the regurgitant jet waveform, which is the enclosed area under the MR jet velocity signal from the CWD in systole.

Simulated echo MR quantification.

In this study, the flow data from the FSI models were extracted at four discrete time instances in systole (including the instance of peak MR). To emulate the measurement of PISA in clinical practice, velocity magnitudes (i.e., v_a) were chosen to obtain a closed and nearly hemispherical shell proximal to the orifice. It is suggested that this aliasing velocity should be <10% of the peak regurgitant jet velocity, and often ranges from 30–50 cm/s (33, 53). The CWD velocity waveform was obtained by extracting the flow velocity along a beam aligned with the regurgitant jet. By doing so, we assumed that the ultrasound beam was optimally aligned with the jet, indicating no underestimation of the velocity because of misalignment in the simulated echo measurements.

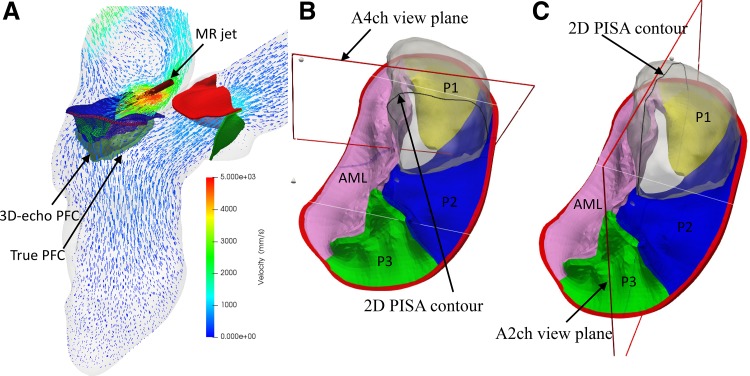
It is known that Doppler angle affects the color Doppler imaging in the PISA measurement. This effect is caused by a limitation of Doppler ultrasound, as it is a one-component velocity measuring technique that only detects the velocity component aligned with the ultrasound beam. When there are angles between the ultrasound beam and flow directions, velocities are underestimated; thus, the isovelocity surface areas are underestimated (13). As seen in Fig. 1, even when the proximal flow convergence (PFC) is hemispherical, the visualized isovelocity contour is not a hemisphere. Instead, a flattened sphere shape, which has a surface shape resembling an urchinoid, is displayed in the echo image (31).

Fig. 1.

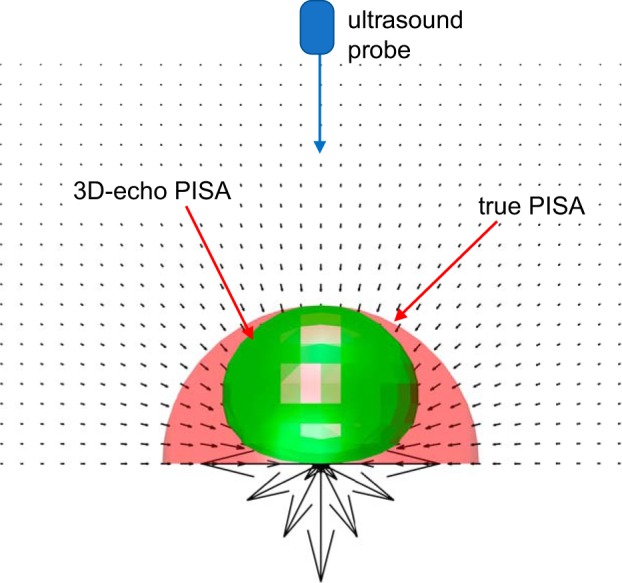
Schematic of the Doppler angle effect in the proximal isovelocity surface area (PISA) measurement. The black arrows represent velocity vectors inversely proportional to the square of the radius, which mimic an upstream flow passing through a small hole on a flat plate. The true proximal flow convergence (PFC) in red has a hemispherical shape, whereas the three-dimensional echocardiography (3D-echo) PFC in green is a flattened sphere like an “urchinoid”. This is due to the angle between the vertical ultrasound beam and the flow direction. Note that the no-slip boundary condition on the plate was not considered in this representation.

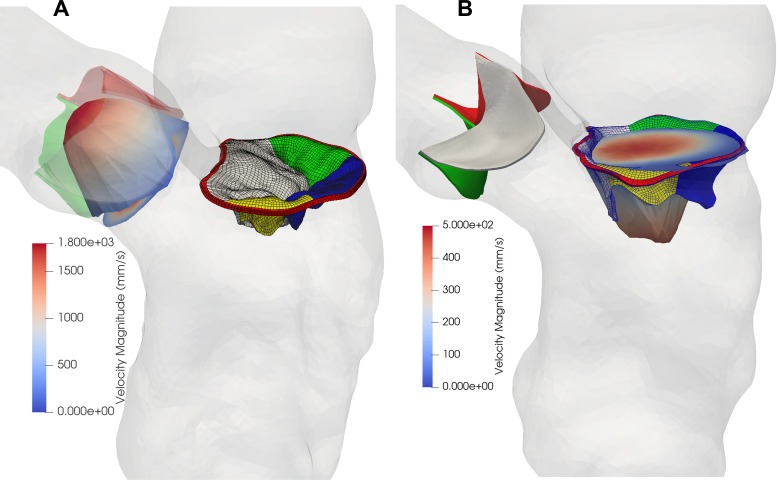
In the simulated echo measurements, to account for the effect of Doppler angulation, the artificial ultrasound probe was located 13 cm away from the mitral annulus (MA) in the apical direction, representing a scan depth of 12–16 cm in transthoracic echocardiogram (TTE) examination in clinical practice (43). By projecting the velocity vectors along the direction of the probe, the altered velocity field, which is smaller than the original velocity, was used to extract PFC (i.e., the 3D-echo PISA). Theoretically, the 3D-echo PISA should be smaller than the true PISA (without Doppler angulation effect) (Fig. 2A). The surface areas of the true PFC and 3D-echo PFC can be readily extracted by triangulation. The 3D hemielliptic (HE) PISA was calculated using the Knud Thomsen approximation (25), S = 2π[(a^pb^p + a^pc^p + b^pc^p)/3]^1/p, through the measurements of three orthogonal radii (i.e., a, b, c) of PFC and a constant p ≈ 1.6075. This method was demonstrated to better represent the flow field proximal to a noncircular orifice (19, 50, 52). Furthermore, the 2D-echo PFC was obtained by slicing the 3D isovelocity contours in an apical four-chamber (A4ch) view (Fig. 2B) or an apical two-chamber (A2ch) view (Fig. 2C). Because of the uncertainty in the angulation of view planes, two different slices for each view were extracted. The shell radius could be easily estimated by delineating the border of the isovelocity contour (Fig. 2, B and C), and the averaged radius was used to calculate the surface area of hemispheres.

Fig. 2.

A representative model (A) of severe mitral regurgitation (MR) that is due to P2 and P1 leaflet prolapse at peak MR from the fluid-structure interaction simulation. The velocity field is shown in a cross-sectional plane with a maximum MR jet velocity of ~5 m/s. The red cylinder denotes the ultrasound beam direction of the continuous wave Doppler in the measurement of MR jet velocity. The translucent green shell shows the true proximal flow convergence (PFC) contour, whereas the interior white shell denotes the three-dimensional (3D) echocardiography (echo) PFC contour. Representative two-dimensional (2D)-echo PFC contours were measured in an apical four-chamber (A4ch) view (B) and in an apical two-chamber (A2ch) view (C) from transthoracic echocardiogram. AML, anterior mitral leaflet.

Simulated Echo MR Quantification Using the VT Method

Theoretical basis.

For the VT method, the flow going into the left ventricle during diastole equals the forward flow across the AV plus the regurgitant flow into the left atrium. Therefore, we can obtain SV_MV + RVol_AV = SV_AV + RVol_MV, in which SV_MV and SV_AV are the forward stroke volumes across the MV in diastole and AV in systole, respectively, and RVol_MV and RVol_AV are the regurgitant volumes through the MV and AV, respectively. If the regurgitant volume from the AV is negligible, then RVol_MV = SV_MV − SV_AV. Clinically, SV_AV is calculated by multiplying the area of the aortic annulus (AA) in systole by the VTI of the pulsed wave Doppler (PWD) velocity waveform measured at the same location. Similarly, SV_MW is obtained by measuring the MA area in diastole and multiplying it by the diastolic VTI at that location.

Simulated echo MR quantification.

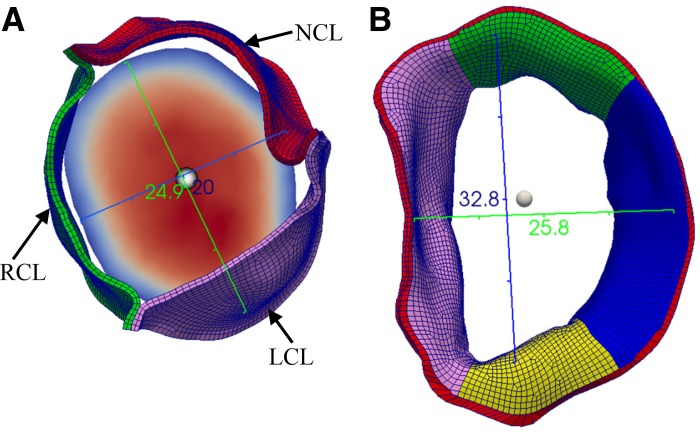
As in clinical practice, the cross-sectional area (CSA) of the mitral annulus (MA), CSA_MA, was measured at the MA in mid-diastole (first frame after maximal leaflet excursion), and the CSA_AA was measured at the AA in midsystole to ensure the least variation of anatomic areas (53). As in the TTE, the diameter of the AA was usually measured in the sagittal plane [the parasternal long axis (PLAX) view], as shown by the blue ruler (20.6 mm) in Fig. 3A. Assuming a circular orifice as in clinical practice, the CSA_AA can be calculated with a single diameter measurement. For the MA, we can measure two mitral orifice diameters (usually the anterior-posterior diameter in the PLAX view and the intercommissural diameter) at the annulus level in mid-diastole because of its “D-type” shape (Fig. 3B) (21). The white sphere in Fig. 3B represents the detection location of PWD velocity at the center of the mitral orifice at the level of the annulus. The corresponding area was calculated as CSA = πD₁D₂/4, in which D₁ and D₂ are the two measured mitral diameters. For each calculation, three independent measurements were conducted, and the averaged value was adopted.

Fig. 3.

Diameter measurements and location of the pulsed wave Doppler detection points (white spheres) in the simulated echo at the aortic annulus in midsystole (A) and mitral annulus in mid-diastole (B). LCL, left coronary leaflet; NCL, noncoronary leaflet; RCL, right coronary leaflet.

RESULTS

Ground Truth MR Quantification from the FSI Models

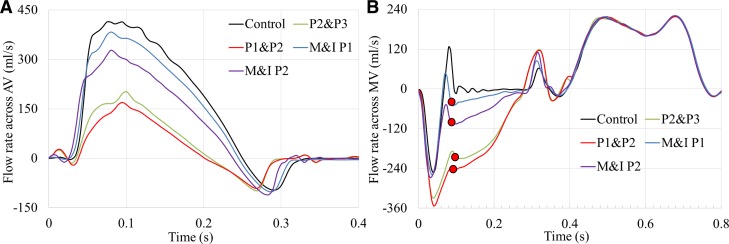
The flows from the FSI simulations are treated as the ground truth values in this study. A total of five simulations were analyzed, including one control model and four acute MR models with increasing MR severities. Figure 4 shows the flow rate waveforms across the AV and MV during the entire cardiac cycle. The negative flow at the end of systole in Fig. 4A indicates the retrograde flow into the left ventricle during AV closing, whereas the negative systolic mitral flow in Fig. 4B indicates the backflow into the left atrium because of the MV closing and MR. During systole, the control model had the largest forward SV. In the MR models, the forward SV decreased as the severity of MR increased, which is consistent with the increasing negative flow volume across the MV. Because the left ventricular size and wall motion were assumed to remain unchanged in all models, mimicking acute MR, it can be seen that the diastolic inflow rates across the MV were approximately the same for all models.

Fig. 4.

Flow rates across the aortic valve (AV) (A) and mitral valve (MV) (B) throughout the cardiac cycle from fluid-structure interaction simulations. M&I, marginal and intermediate.

The ground truth RVol_MV was obtained from the FSI models by integrating the negative MV flow rate curve over time. Similarly, the RVol_AV, SV_AV, and SV_MV were calculated and listed in the top section of Table 1. The combination of the SV_AV and RVol_MV is known as the total SV of the left ventricle (LVSV), which was used to calculate the regurgitant fraction, RF_MV = RVol_MV/LVSV. Using RF_MV as a quantitative parameter in the grading of MR severity (53), Table 1 shows that two MR models (P2 & P3 and P2 & P1) can be classified as severe MR, one can be classified as moderate MR (M&I P2), and one can be classified as mild MR (M&I P1). As expected, RVol_AV was largely the same for all models, with the lowest value obtained from the control model. Note that because of the coupled effect between the AV and MV, Fig. 4A shows that the onset time of AV closing is different, showing distinct early closure of AV in the severe MR models.

Table 1.

Summary of hemodynamic parameters obtained from the FSI simulations (ground truth) and calculated from the simulated echo measurements using the PISA method at peak M

	Control	M&I P1	M&I P2	P2&P3	P2&P1
FSI-RVolAV, mL	4.27*	4.63	4.61	4.62	4.72
FSI-SVAV, mL	58.22	51.55	41.94	20.46	16.16
FSI-SVMV, mL	63.22	61.67	61.65	63.03	62.97
FSI-RVolMV, mL	9.27*	14.75	24.32	47.19	51.53
FSI-RFMV, %	13.7	22.2	36.7	69.8	76.1
MR severity	Normal	Mild	Moderate	Severe	Severe
True PISA EROA, cm2		0.195	0.43	0.99	0.97
3D-echo PISA EROA, cm2		0.17	0.36	0.87	0.83
3D-HE PISA EROA, cm2		0.128	0.26	0.64	0.636
2D-A2ch PISA EROA, cm2		0.15	0.61	1.11	1.25
2D-A4ch PISA EROA, cm2		0.11	0.34	0.85	0.54
True PISA RVolMV, mL (%)		14.1 (−5)	36.4 (50)	82.9 (76)	88.5 (72)
3D-echo PISA RVolMV, mL (%)		12.3 (−17)	29.8 (23)	72.7 (54)	76.3 (48)
3D-HE PISA RVolMV, mL (%)		9.2 (−38)	21.8 (−10)	53.1 (13)	58.2 (13)
2D-A2ch PISA RVolMV, mL (%)		11.1 (−25)	50.7 (108)	92.9 (97)	114.3 (122)
2D-A4ch PISA RVolMV, mL (%)		8.1 (−45)	28.5 (17)	71.0 (50)	49.1 (−5)

Values in parenthesis denote the relative percentage error with respect to the ground truth values (i.e., FSI-RVol_MV). 2D, two-dimensional; 3D, three-dimensional; A2ch, apical two-chamber; A4ch, apical four-chamber; AV, aortic valve; echo, echocardiography; EROA, effective regurgitant orifice area; FSI, fluid-structure interaction; M&I, marginal and intermediate; MR, mitral regurgitation; MV, mitral valve; PISA, proximal isovelocity surface area; RVol, regurgitant volume; SV, stroke volume; RF, regurgitant fraction; HE, hemielliptic.

^*Since in the control model both aortic and mitral valves are healthy and have no leakage volume, 4.27 mL and 9.27 mL are the closing volumes of the aortic and mitral valves, respectively.

Simulated Echo MR Quantification by the PISA Method

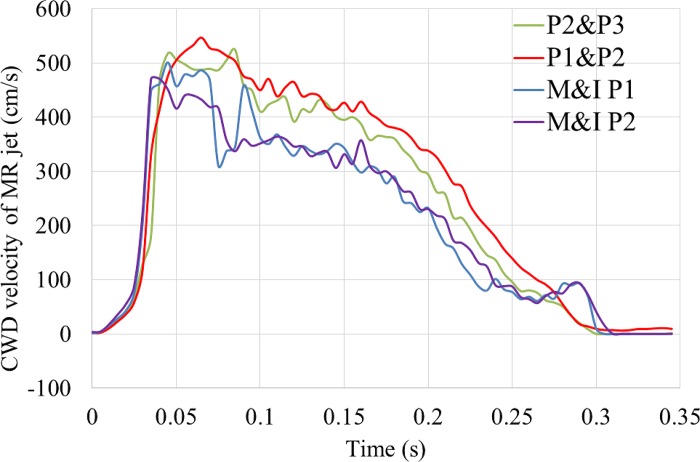
Figure 5 shows the CWD measurements of MR jet velocity during systole. The peak jet velocity was around 5 m/s for all models because the same atrial pressure waveforms were used. Note that the timing of peak MR jet may not coincide with the timing of peak systole, defined as the peak flow rate across the AV. For example, the peak flow rate for the M&I P1 model occurred at 0.08 s, but the peak MR jet was detected at ~0.05 s. Therefore, the echo frame for the PISA measurement should be carefully chosen to match the instant of the peak MR.

Fig. 5.

Mitral regurgitation (MR) jet velocity waveforms measured by the simulated continuous wave Doppler (CWD). M&I, marginal and intermediate.

True PISA, 3D-echo PISA, 3D-HE PISA, 2D-A2ch PISA, and 2D-A4ch PISA were measured for all MR models (Table 1). As expected, the true PISA EROA was 13%–19% larger than the 3D-echo PISA EROA. We found that the PISA methods underestimated RVol for mild MR but overestimated RVol for moderate and severe MR. In general, the 3D-HE PISA gave the smallest error (within 15% for moderate and severe MR), followed by the 3D-echo PISA, 2D-A4ch PISA, true PISA, and 2D-A2ch PISA. If the EROA is used to grade MR severity, true PISA and 2D-A2ch PISA misclassified the MR severity from moderate to severe for the M&I P2 model.

To examine the error from a single PFC (Table 1), we calculated the EROA and RVol by averaging four instances of PISA results during systole. The results are summarized in Table 2. It can be seen that the averaged EROA was only slightly smaller than the calculation from the single PFC at peak MR. This implies that the MR is holosystolic in our study. Indeed, to quantify the variance of the regurgitant orifice size, we calculated the anatomic MV orifice areas using an in-house MATLAB script. As shown in Supplemental Fig. S1 (at https://www.doi.org/10.6084/m9.figshare.11845566.v1), the anatomic orifice areas are almost constant throughout the systole for all models except for the P1 & P2 model. Even for the P1 & P2 model, the averaged orifice area in systole is approximately the same as the orifice area at peak MR, which explains why the results from a single PFC at peak MR are similar to the results from the averaged PISA results.

Table 2.

Summary of hemodynamic parameters calculated from the simulated echo measurements using the PISA method based on the average of four instances in systole

	M&I P1	M&I P2	P2&P3	P2&P1
True PISA EROA, cm2	0.17	0.37	1.10	0.97
3D-echo PISA EROA, cm2	0.14	0.32	0.92	0.84
3D-HE PISA EROA, cm2	0.11	0.25	0.66	0.60
2D-A2ch PISA EROA, cm2	0.13	0.61	0.93	1.39
2D-A4ch PISA EROA, cm2	0.10	0.31	0.82	0.58
True PISA RVolMV, mL (%)	12.0 (−19)	30.6 (26)	91.4 (94)	88.4 (72)
3D-echo PISA RVolMV, mL (%)	10.3 (−30)	26.4 (95)	76.8 (63)	76.5 (48)
3D-HE PISA RVolMV, mL (%)	7.8 (−47)	21.1 (−13)	54.7 (16)	54.9 (7)
2D-A2ch PISA RVolMV, mL (%)	9.6 (−35)	51.3 (111)	77.3 (64)	127.5 (147)
2D-A4ch PISA RVolMV, mL (%)	7.2 (−52)	26.3 (8)	68.6 (45)	53.4 (4)

Values in parenthesis denote the relative percentage error with respect to the ground truth values (i.e., FSI-RVol_MV). 2D, two-dimensional; 3D, three-dimensional; A2ch, apical two-chamber; A4ch, apical four-chamber; echo, echocardiography; EROA, effective regurgitant orifice area; FSI, fluid-structure interaction; M&I, marginal and intermediate; MV, mitral valve; PISA, proximal isovelocity surface area; RVol, regurgitant volume; HE, hemielliptic.

Simulated Echo MR Quantification by the VT Method

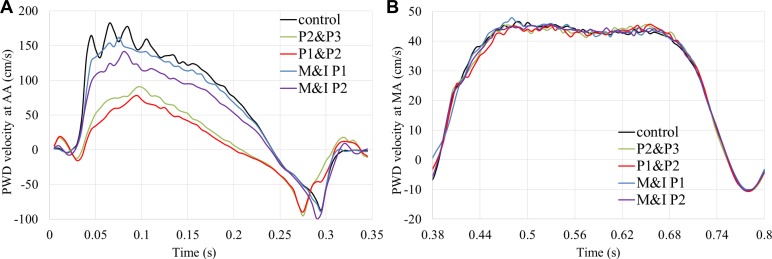
Figure 6 shows the velocity waveforms measured at the center of AA and MA using the simulated PWD. The peak velocity at the AA was 1.82 m/s for the control model and decreased with the increasing MR severity. The velocity waveforms are very similar at the MA because of the unchanged diastolic function. Knowing the CSA of the AA and MA, the forward SVs across the AV and MV, and the RVol_VM, based on the mass conservation, were calculated (Table 3). The VT method introduced large underestimations for the mild MR and control models but provided reasonable estimations for the moderate and severe MR models (<25% errors). Comparing the SV through the AV and MV between the ground truth values and the simulated echo measurements, we found that the VT method systematically overestimated these values and that correction factors of 0.72 and 0.7 can be applied for the VT-SV_AV and VT-SV_MV, respectively, to minimize these errors.

Fig. 6.

Velocity waveforms at the center of aortic annulus (AA) (A) during the systole and mitral annulus (MA) (B) measured by the simulated pulsed wave Doppler (PWD) during the diastole. M&I, marginal and intermediate.

Table 3.

Summary of hemodynamic parameters calculated from the simulated echo measurements using the VT

	Control	M&I P1	M&I P2	P2&P3	P2&P1
VT-SVAV, mL	79.63	72.13	59.47	31.17	23.77
VT-SVMV, mL	89.13	89.47	88.91	88.89	88.04
VT-RVolMV, mL (%)	9.50 (2)	17.35 (18)	29.44 (21)	58.72 (24)	64.27 (25)
0.72 × VT-SVAV, mL (%)	57.34 (−2)	51.93 (1)	42.82 (2.1)	21.72 (6)	17.12 (6)
0.7 × VT-SVMV, mL (%)	62.39 (−1)	62.63 (−1.6)	62.24 (1)	62.22 (−1)	61.63 (−2)
Corrected VT-RVolMV, mL (%)	5.06 (−45)	10.70 (−27)	19.42 (−20)	40.50 (−14)	44.51 (−14)
CVAV + corrected VT-RVolMV, mL (%)	9.66 (4)	15.30 (4)	24.02 (−1)	45.10 (−4)	49.11 (−5)

Values in parenthesis denote the relative percentage error with respect to the ground truth values (i.e., FSI-RVol_MV). The forward stroke volumes (SVs) calculated by the volumetric technique (VT) method from the aortic valve (AV) and the mitral valve (MV) are represented by VT-SV_AV and VT-SV_MV, respectively. The multipliers of 0.72 and 0.7 are correction factors used to compensate the error caused by nonflat velocity profiles at the orifices. Therefore, the calculated regurgitant volume (RVol) of MV based on the corrected stroke volumes from the AV and MV is represented by VT-RVol_MV. CV_AV + corrected VT-RVol_MV represents an additional correction of regurgitant volume because of the closing volume of AV. Echo, echocardiography; CV, closing volume.

DISCUSSION

Evaluation of the PISA Method

There are multiple sources of error in the PISA method. 1) Theoretically, the PISA method is only valid for inviscid flow through an infinitesimal orifice on a flat plane (38). This restriction could be loosened to include the viscous flow and finite circular flat orifices if the isovelocity contours are more than two orifice diameters away from the orifice (38). For a nonflat surface, many corrections have been proposed to correct the inaccuracy of the PISA method, such as a convergence angle correction for the funnel-shaped surface in the case of flail leaflets (33) or for conical-shaped leaflets in the case of tethered leaflets (37). 2) The shape of the flow convergence is often nonhemispheric. Multiple corrections for the elliptical or crescent-shaped orifice were proposed, including the use of the hemiellipsoid PISA (23, 36). 3) The EROA is determined at a single time point (normally at peak MR), ignoring the dynamic size changing mitral orifice (2, 6). This could cause significant errors under many MR conditions, including when MR jets are not holosystolic, such as in the case of late systolic primary MR (9) or in functional MR, which is biphasic (20, 26). The effect of Doppler angulation may be remedied by choosing the urchinoid distance (the distance from the valve orifice to the aliasing point of the Doppler signal) as the radius to calculate the hemispheric surface area (31). Although the convergence angle correction can largely mitigate the overestimation of EROA in patients with mitral leaflet prolapse, it was found that the overestimation was still quite large (ΔRVol = 15.5 ± 19.3 mL) in clinical practice (33).

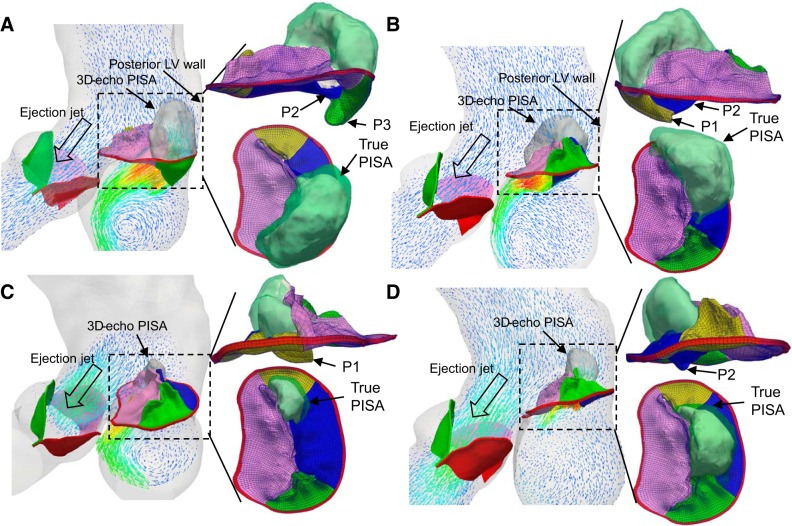
Figure 7 shows the shapes of the true PFC and 3D-echo PFC for four MR models. It is worth noting that mitral valve prolapse could produce both eccentric and noneccentric MR jets depending on the prolapsed scallops (7). It can be seen that the PFC is confined in the anteroposterior direction because of the constraints from both the posterior ventricular wall and the ejection flow through AA, displaying a cashew shape. From a fluid mechanics perspective, the isovelocity surface cannot guarantee that velocity vectors at the PFC are perpendicular to the surface, which is also pointed out by Jamil et al. (22). If there is an angle θ between the surface normal and the velocity vector, the PISA overestimates the true cross-sectional area by 1/cos θ. Therefore, the calculated regurgitant flow rate will be overestimated. It is clear that the proximal velocity field, confined by the ventricular wall and aortic ejection, is far from an ideal field that is inversely proportional to the square of the distance in Fig. 1. As shown in Table 1, this impact was also reflected by the gross overestimation of the EROA and RVol for the severe MR models from both the true PISA and the 3D-echo PISA methods. Furthermore, the lower aliasing velocity thresholds cannot be chosen since an expanded PFC would collide with the ventricular wall and overlap with the aortic ejection jet, thus distorting its shape (36). It is worth noting that because the 3D-echo PFC is smaller than the true PFC, it partially offsets the large overestimation of the projected area in the calculation of regurgitant flow rate and thus provides better results. The more the PFC deviates from the hemispheric or urchinoid shape, the larger the overestimation is. It may explain why the 3D-HE PISA gave good estimations when considering the hemielliptical shape of PFC.

Fig. 7.

Ejection and mitral regurgitation (MR) jets for the four MR models at peak MR. Shapes of true PISA (green) and three-dimensional echocardiography (3D-echo) proximal isovelocity surface area (PISA) (white) are shown on the side and top views. A: P2&P3. B: P2&P1. C: marginal and intermediate (M&I) P1. D: M&I P2. LV, left ventricle.

Compared with the 3D PISA method, the 2D PISA is even less reliable (54) because the measured radius of 2D PISA largely depends on the orientation of the 2D view plane and the choice of the orifice center. First, because of the irregular PFC shape, it is difficult to guarantee the 2D-echo view plane would cut through the apex of the PFC. As shown in Fig. 7, the PFC in the A2ch view, which usually cuts along the coaptation line, is visually wider than the PFC in the lateral A4ch view. Second, precisely locating the center of the regurgitant orifice is often challenging (36, 38), especially when the orifice is tilted against the annulus plane, as in prolapse conditions. Therefore, we obtained a larger radius in the A2ch view, explaining the larger EROA measured in the A2ch view than in the A4ch view, as listed in Table 1.

An additional possible error of the PISA method is that a single time point isovelocity contour at peak MR is usually used to calculate the EROA, which may be larger than the averaged EROA throughout systole. This is especially true for patients with only late systolic MR. Several methods have been proposed to remedy this issue (12). For example, Thomas et al. (6) investigated four different single-point and time-integral PISA methods in patients with MR and found that time-integral methods provided better consistency compared with MRI results. However, it is still challenging to obtain a unified quantification method for patients with different underlying etiologies. In our study, for patients with mitral prolapse, similar EROAs were obtained from the single time point at peak MR and averaged throughout the systole.

The closing volume, defined as the volume of blood flowing retrograde during valve closure, is often underestimated by the PISA method. Table 1 shows that the MV closing volume was around 9 mL/beat. The MV flow rate curve in Fig. 4B also shows that the regurgitant flow rate has a peak at early systole because of valve closure, followed by a second peak (denoted by the red dots in Fig. 4B) at midsystole, then gradually decreases throughout late systole. In clinical practice, the largest PISA in midsystole is commonly used for the calculation of EROA (6). Therefore, the RVol at early systole may be underestimated. This may explain the underestimation of the RVol in the M&I P1 model (mild MR).

It is known that the accuracy of regurgitant flow calculations by the PISA method critically depends on the chosen alias velocity (22, 40). Although guidelines suggest choosing the PFC resembling a hemisphere, it is often impossible in clinical practice because of the proximal flow confinement from the aortic outflow and lateral left ventricle walls (18). This effect is largely ignored in several in vitro experiments (22, 34, 41, 54) because of the small MR orifice compared with the chamber size and nonphysiological ejection flow through the AV. Moreover, because of the Doppler angle effect, when the surface is truly a hemisphere, it does not look like one in the echo and vice versa. Clinically, by fine-tuning the angle of the ultrasound beam, nearly semicircular PFC may be obtained in a 2D echo view. However, the 2D contour cannot reflect the 3D PFC shape and may lead to significant underestimation (11, 27, 36, 43, 54) or overestimation of the EROA (33, 34, 48) in clinical practice and in vitro experiments.

Evaluation of the VT Method

Theoretically, the VT method is more robust than the PISA method since it is solely based on the law of mass conservation with no other assumptions. However, it has not been widely used in the clinical community for multiple reasons. First, it is time consuming compared with the PISA method, requiring multiple measurements from two valve locations. Second, the calculation of MR relies heavily on the accuracy of echo measurements of valve annular diameter, the location of pulsed wave sampling, and SVs from the AV and MV. For example, if the valve annular diameter is not measured accurately, the error is doubled in the area calculation.

In our study, we found that the calculated RVol from VT method was within 25% error compared with the ground truth for the severe and moderate MR models (Table 3). The mean error was 6.5 mL for all models. However, there are a couple of pitfalls that may be encountered in clinical practice. First, the largest error comes from the calculation of the forward SV. By using SV = CSA × V_PWD, the underlying assumption is that the velocity is uniform at the measured cross section. In Fig. 8, however, it can be seen that the velocity profiles at the AA in peak systole and at the MA in mid-diastole are not flat but skewed and are somewhere between a flat shape and a parabolic shape. Note that for a fully developed laminar flow with a parabolic flow profile, the average velocity is half of the maximum velocity. Since the PWD velocity is often measured at the center of the orifice, where the velocity is maximal, a coefficient should be considered to correct this overestimation. We found that coefficients of 0.72 and 0.7 gave the best estimation for the aortic SV and mitral SV calculations, respectively. As shown in Table 3, when these coefficients are incorporated, the resulting SVs from the AV and MV are very close to the ground truth. The accuracy of the corrected RVol was improved, with a mean error of −5.4 mL for all models. The overestimation of maximum flow velocity compared with the mean velocity is also investigated by other studies (24, 39). Haugen et al. (15) found that the mean ratio of the maximum VTI to the spatial averaging VTI through the MV was 1.3 from 19 healthy volunteers. The reciprocal of this ratio is 0.77, which is similar to the coefficient of 0.7 obtained in our study. Similarly, the ratio of the maximum VTI to the spatial averaging VTI at the AA was found to be from 1.2 to 1.5 (16), which is also similar to the coefficient of 0.72 used in this study.

Fig. 8.

The velocity profiles at the aortic annulus in peak systole (A), and at the mitral annulus in mid-diastole (B).

Another source of error could be the omission of the closing volume of the AV. This is especially important in the mild MR. In a healthy AV, from our computer simulations, we found that the closing volume was ~4.6 mL/beat. By adding this value to the RVol, the final RVol is more consistent with the ground truth value, with <5% error for all models (Table 3). The mean difference is remarkably small (−0.8 mL).

Lastly, the calculation of the CSA at the AA and MA may introduce additional errors. Usually, the CSA of the AA is calculated based on a single diameter measurement in a PLAX view. As shown in Fig. 3A, however, the AA has an oval shape. This observation is supported by recent 3D echo and computed tomography data (3, 32). Therefore, the CSA of the AA was significantly underestimated compared with the planimetry (3.33 cm² vs. 3.96 cm²). Therefore, if the AA area can be measured accurately in 3D echo, the correction coefficient of the SV at the AA should be even smaller than 0.72. As for the area of the MA, it was calculated based on two diameters with biplane measurements. The CSA was almost identical to the planimetry measurement (6.64 cm² vs. 6.57 cm²). This observation is consistent with the clinical findings that biplane linear measurements of the MA area highly correlated with 3D planimetry measurements (21).

Caveat and clinical implication.

The accuracy of the SPH method has been criticized mainly because of its difficulties in handling boundary conditions. However, several researchers, including our group, have shown that it is a promising method in the field of cardiovascular biomechanics. It has been used to study the mitral valve mechanics (47), left ventricular flow (29), TAVR impact on MR (8), and wall shear stress of abdominal aortic aneurysm (1). Because of the limitations of the Abaqus SPH formulation, the small-scale flow features close to the wall boundary may not be accurately resolved. However, in the PISA method, the PFC is still relatively far away from the wall, with an aliasing velocity larger than 30 cm/s. In the appendix, we compared the PFC shapes obtained from the SPH method with those obtained from a traditional computational fluid dynamics method with equivalent instantaneous flow boundary conditions. The results show that they agree quite well. Therefore, we believe this limitation should not significantly affect the results from the PISA method.

The FSI method used in this study does not include any turbulence model. It has become a consensus that in the left ventricle, the turbulence could occur during the diastole when the vortex ring impinges on the lateral wall and during the E wave deceleration (10). In patients with MR, the impingement and deceleration of the regurgitant jet could cause additional turbulence in the atrium. The method used in this study cannot capture this high-frequency fluctuation of flow velocities. However, the accuracy of variables measured in this study is unlikely to deteriorate because of the lack of turbulence models. One reason for this is that the measurements are either not located in the turbulence region or taken during the period of turbulence. For instance, the PFC in the PISA method is located upstream the orifice, where the flow is fully laminar. Another reason is that the most measured variables are the characteristics of the bulk flow or integrated values. For example, the VTI is the integration of the velocity over time, which may mitigate the error caused by velocity fluctuations. Furthermore, whether turbulence analysis is effective at capturing blood flow behaviors in cardiovascular systems remains an open question. In a recent computational study of FDA benchmark nozzle (42), it has been shown that the laminar model better predicted the velocity, whereas the k-ε model provided the worst results. This is mainly because the flow is not fully turbulent in the whole domain. Therefore, simple turbulence models based on the fully developed turbulent flow may not work well. In the human heart, the flow regime is most transitional between laminar and turbulent, justifying the use of large eddy simulations (10). However, considering the computational cost and the complexity of the FSI, the laminar flow solver is a reasonable choice in this study.

The size of interrogation in a spectral Doppler exam is called sample volume size. The appropriate sample volume size changes depending on which structure is being interrogated. The typical sample volume size used at the AV and MV is between 1–5 mm (30). To be consistent with the clinical setting, the averaged velocity in a sphere of size 3 mm was used in our simulated echo to extract the velocity and VTI information. The time step used in our simulations is in the order of 1e-6 s; however, the time interval of the stored flow information is every 5 ms. This temporal resolution is still higher than what is normally used in the clinical practice, which usually has a frame rate <100 Hz (30). Therefore, the spatial and temporal resolutions in our simulated echo are in line with clinical echocardiography.

Limitations.

There are some limitations in this study. First, the MR models were numerically created by cutting mitral chordae from a healthy control model, and they employed the same baseline boundary conditions for all diseased cases. Therefore, the specific results from this patient, such as velocity profile correction factors and exact value of closing volumes, should not be assumed to represent the general patient population. Since the flow profile may vary under different patient conditions, the correction parameter values should be optimized and validated with a large patient cohort. However, since this is the first study of its kind, the general approach provided by this work for improving the accuracy of echo measurements is still valid. Second, the echo measurements were obtained in a simulated manner based on the flow results from the FSI models. Although these measurements were guided under an experienced sonographer, certain sources of errors from the real echo, such as reverberation artifacts and shadowing, were not incorporated. Thus, our simulated echo data should be treated as an ideal measurement with optimal positioning and angle of the echo probe under clinical situations. Finally, this study only focused on acute MR from PML prolapse following chordae rupture. Other types of MR, such as functional MR, have not been investigated, which warrants a future study.

Conclusions.

The findings of this study add in-depth insights into the identification of several pitfalls in current clinical MR quantification using 2D and 3D echo. First, we found that for the PISA method, the assumption that the isovelocity surface is perpendicular to the velocity vectors is incorrect for patients with mitral prolapse, which causes inherent errors of MR measurement (overestimation). Second, the angle dependence of color Doppler imaging on the PISA may cause a systematic underestimation of MR, although it is relatively small judging from our results (~15%). Third, the 3D-HE PISA method gave the best estimation for the moderate and severe MR models compared with other PISA methods. Fourth, the VT method, based on the mass conservation, is theoretically more robust. However, when calculating the SV, one should not treat the velocity measured from the PWD as the mean velocity of the cross section. Our study suggested that a coefficient around 0.7 should be used to compensate for this overestimation. The accuracy of the VT method can be further improved by considering the closing volume of the AV, with a mean difference of −0.8 mL compared with the ground truth.

GRANTS

This work was supported in part by the National Heart, Lung, and Blood Institute Grant HL-127570. W. Mao is in part supported by the American Heart Association Career Development Award 19CDA34660003. A. Caballero is in part supported by a Fulbright-Colciencias Scholarship.

DISCLOSURES

W. Sun is a cofounder and the Chief Scientific Advisor of Dura Biotech. He has received compensation and owns equity in the company. R. T. Hahn is a speaker for Abbott Vascular, Boston Scientific, Edwards Lifesciences, and Philips Healthcare and serves as an advisory board member/consultant for Edwards Lifesciences, Gore & Associates, Medtronic, and Navigate. None of the other authors has any conflicts of interest, financial or otherwise, to disclose.

AUTHOR CONTRIBUTIONS

W.M., A.C., and W.S. conceived and designed research; W.M. and A.C. performed experiments; W.M. and A.C. analyzed data; W.M., A.C., R.T.H., and W.S. interpreted results of experiments; W.M. prepared figures; W.M. drafted manuscript; W.M., A.C., R.T.H., and W.S. edited and revised manuscript; W.M., A.C., R.T.H., and W.S. approved final version of manuscript.

APPENDIX

To quantify the variance of the regurgitant orifice size from the MV, we calculated the anatomic MV orifice areas (AMVOA) using an in-house MATLAB script. First, the least square plane of the mitral annulus was calculated at each interrogated time point during the systole. Then, the AMVOA was measured as the projected 2D area of the free edge of the MV leaflets on the least square plane. The AMVOAs throughout the systole were plotted in Supplemental Fig. S1. The anatomic orifice areas are almost constant throughout the systole for all models except for the P1 & P2 model.

To verify the accuracy of our FSI results, a commercial computational fluid dynamics software, Star-CCM+, was used to simulate the regurgitant flow through the MV at the peak systole for the P2 & P3 model. In brief, we extracted the surfaces, including the MV and AV leaflets and LV wall, from the FSI simulation at the peak systole, imported them into the Star-CCM+, and then created a polyhedral volumetric mesh. The pressure boundary conditions used at the atrial and aortic sides are consistent with the FSI simulation. Meanwhile, we also extracted the flow velocity information at the LV wall from the FSI simulation and applied it as the velocity boundary condition in the Star-CCM+. We followed the same procedure as before to extract the PFC. The PFC shape is very similar to that obtained from the FSI simulation (Fig. 7A), as shown in Supplemental Fig. S2 (at https://www.doi.org/10.6084/m9.figshare.11845566.v1). The calculated 3D echo PISA is 7.7 cm², which is close to its counterpart from the FSI simulation (8.9 cm²). Although the steady flow assumption used in the Star-CCM+ cannot exactly replicate the transient flow in the FSI simulations, the small discrepancy in their results indicates that the inaccuracy of the SPH method at the wall boundary should not significantly affect the results of the PISA method.