Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2020 Jan 22;6(3):413–419. doi: 10.1021/acscentsci.9b01216

Bottlebrush Bridge between Soft Gels and Firm Tissues

Andrew N Keith †, Mohammad Vatankhah-Varnosfaderani †, Charles Clair ‡, Farahnaz Fahimipour †, Erfan Dashtimoghadam †, Abdelaziz Lallam ‡, Michael Sztucki §, Dimitri A Ivanov ∥,⊥,#,*, Heyi Liang ∇, Andrey V Dobrynin ∇,*, Sergei S Sheiko †,*
PMCID: PMC7099586  PMID: 32232141

Abstract

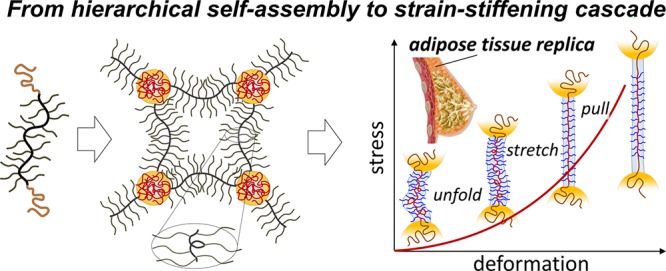
graphic file with name oc9b01216_0005.jpg

Softness and firmness are seemingly incompatible traits that synergize to create the unique soft-yet-firm tactility of living tissues pursued in soft robotics, wearable electronics, and plastic surgery. This dichotomy is particularly pronounced in tissues such as fat that are known to be both ultrasoft and ultrafirm. However, synthetically replicating this mechanical response remains elusive since ubiquitously employed soft gels are unable to concurrently reproduce tissue firmness. We have addressed the tissue challenge through the self-assembly of linear–bottlebrush–linear (LBL) block copolymers into thermoplastic elastomers. This hybrid molecular architecture delivers a hierarchical network organization with a cascade of deformation mechanisms responsible for initially low moduli followed by intense strain-stiffening. By bridging the firmness gap between gels and tissues, we have replicated the mechanics of fat, fetal membrane, spinal cord, and brain tissues. These solvent-free, nonleachable, and tissue-mimetic elastomers also show enhanced biocompatibility as demonstrated by cell proliferation studies, all of which are vital for the safety and longevity of future biomedical devices.

Short abstract

Bottlebrush elastomers bridge the elasticity of soft gels and firm tissue through a hierarchical structure that empowers a cascade of deformation mechanisms analogous to biological tissue.

Introduction

Soft tissues are distinct in possessing an oxymoronic mechanical property combination: they are compliant to the touch yet resistant to deformation, which imbues their characteristic feeling of firmness.1,2 While initially they are very soft with Young’s moduli ranging from E0 = 103–105 Pa, tissues rapidly stiffen by a factor of 102–103 within a short interval of strain (Figure 1a).3−6 This strain-adaptive stiffening represents one of nature’s key defense mechanisms that prevents accidental tissue rupture and serves as a benchmark for various industrial7,8 and biomedical applications.9−12 Tissue softness is routinely replicated with polymer gels,13 but gels are limited in their ability to copy nature’s strain-stiffening capabilities (Figure 1b) as accentuated by the sharply diverging deformation responses of adipose tissue and a silicone gel utilized in breast implants (Figure 1c). This mechanical mismatch is further exacerbated by both spontaneous14 and induced15 solvent migration leading to inadequate performance of engineered devices and unforeseen health risks.16

Figure 1.

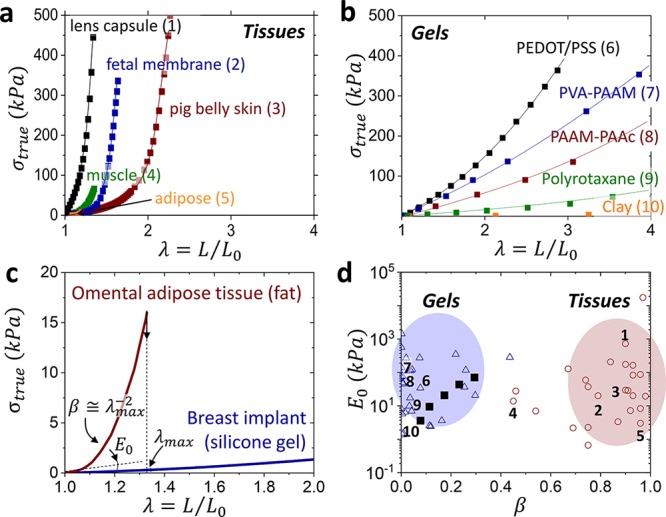
Figure 1

Open in a new tab

Mechanical mismatch. Stress–elongation curves of assorted (a) biological tissues and (b) polymeric gels, which demonstrate tissue’s much stronger stiffening (Tables S1 and S2). Lines guide the reader, while data points represent literature data. (c) Stress–elongation responses of omental adipose tissue and silicone gel extracted from a commercial breast implant display a significant difference in strain-stiffening (β) despite a similarity in the Young’s modulus (E0). (d) An E0 vs β map partitions polymeric gels (△) and biological tissues (○) as two distinct classes of materials. The β values are obtained by fitting stress–elongation curves with eq 1, whereas E0 corresponds to the curve slope at λ → 1 (eq 2). The model is successful in fitting the entirety of gel elasticity, but only the elastic portion of tissue response before yielding.17 Numbers at data points correspond to the stress–elongation curves in (a, b). Bottlebrush elastomers (■) mimic the stress–strain response of gels,18 but are unable to reach the tissue territory.

Results and Discussion

To guide the materials design toward soft tissue firmness, we introduce an equation of state relating true stress σtrue with sample uniaxial elongation ratio λ = L/L0 from its initial size L0 to deformed size L as

graphic file with name oc9b01216_m001.jpg 1

which describes the nonlinear elastic response of polymer networks (Figure 1a,b) as a function of two molecular parameters: structural modulus E and strain-stiffening parameter β.19 The modulus is controlled by the density (ρs) and conformation of stress-supporting strands as E ≅ kBTρs⟨Rin2⟩/(bKRmax), where bK, ⟨Rin2⟩, and Rmax are a strand’s Kuhn length, mean square end-to-end distance, and contour length. The strain-stiffening curvature (Figure 1c) is determined by potential extensibility of network strands from their initial mean-square end-to-end distance ⟨Rin2⟩ to the corresponding contour length of a fully extended strand as β = ⟨Rin2⟩/Rmax2 such that 0 < β < 1. For polymer networks with nonlinear responses, the Young’s modulus E0 depends not only on network strands density (E ∼ ρs), but also on their initial conformations (β ∼ ⟨Rin2⟩) as

graphic file with name oc9b01216_m002.jpg 2

Simply, this elastic model provides two parameters observable in stress–elongationplots (Figure 1c): the initial slope or softness (E0) followed by a curvature or firmness (β), which characterizes resistivity of material to deformation. Respectively, mapping [E0, β] allows partitioning gels and tissues into two distinct materials classes with similar E0 yet vastly different β (βgel ≪ βtissue) (Figure 1d). The limited firmness of linear-chain polymeric gels (βgel = βdry⟨Rin2⟩gel/⟨Rin2⟩dry = βdryα2/3 < 0.2) originates both from weak strand extension in as-prepared networks (βdry ≅ 0.01) and an upper bound on their swelling ratio (α < 100).20 For a deeper discussion on the origins and validity of this elastic model, we encourage the reader to pursue prior literature.19

Various molecular and macroscopic constructs have endeavored to bridge the strain-stiffening divide and replicate tissue firmness (0.7 < β < 1) in Figure 1b,17,18,21−26 but as of now, most attempts have fallen short of β > 0.4, including our earlier studies utilizing solvent-free bottlebrush elastomers (filled squares ■ in Figure 1d).18

In this regard, self-assembled networks of linear–bottlebrush–linear (LBL) block copolymers have proven to be a resourceful scaffold given the hierarchical integration of molecular and particulate motifs within each network strand (Figure 2a).17 On the molecular scale, B-block side chains simultaneously decrease cross-link density and extend network strands promoting both softness and firmness, respectively.27 Additional strain-stiffening results from strong microphase separation between both the chemically and architecturally distinct blocks forcing further strand extension (Rin increase).28 On a mesoscopic scale, bottlebrush strands behave as flexible filaments that exhibit low bending rigidity and unfold at lower forces followed by stretching of the bottlebrush backbone and concomitant withdrawal of L-blocks from microdomains at higher forces. Critically, L-block microdomains serve as hidden length reservoirs29 that offset the limited extensibility of the inherently strained brush-like strands while also mitigating uneven stress distributions. This hierarchical organization empowers telescoping activation of deformation mechanisms responsible for the soft-to-firm transition (Figure 2b), which qualitatively mimics the sequential unfolding, stretching, and yielding of microfibrils in collagen networks.30

Figure 2.

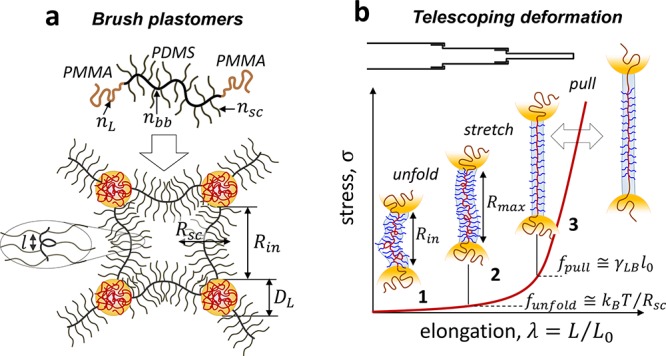
Figure 2

Open in a new tab

Hierarchical deformation. (a) LBL self-assembly is regulated by molecular (nbb, nsc, nL) and morphological (Rsc, DL, Rin, l) parameters, where Rsc - brush radius, DL - L-block domain diameter, and l - distance between neighboring side chains along the bottlebrush contour. (b) The cascade of deformation mechanisms during uniaxial extension of LBL networks: (1) unfolding of bottlebrush filaments limited by funfold < kBT/bK ≅ kBT/Rsc ≅ 0.5 pN (for nsc = 70), (2) stretching of backbones inside brush envelops ranging within kBT/Rsc < fstretch < kBT/l0 ≅ 20 pN, where l0 = 0.25 nm is the monomer projection length, and (3) pulling linear chains from microdomains creating a new interface between exposed linear block sections and the bottlebrush matrix. The two-head arrow indicates that chain pulling may overlap with backbone stretching. The pulling force is on the order of fpull ≅ γLBl0 ≅ 2.5 pN, where γLB ≅ 10 mN is the surface energy of the L–B interface. The actual fpull value may be higher due to kinetic barriers imparted by glassy L-domains.

To validate this concept, we synthesized two groups of LBL triblock copolymers with a polydimethylsiloxane (PDMS) bottlebrush block (B-block) and two poly(methyl methacrylate) (PMMA) linear end-blocks (L-blocks). These groups differ by the degree of polymerization (DP) of PDMS side chains, nsc = 14 (Group 1) and nsc = 70 (Group 2) and contain several series of LBL triblocks with different DP’s of bottlebrush backbone (nbb = 100–1100) and PMMA L-block (nL = 50–1300) (Table S3). Figure 3a compares representative stress–elongation curves from each group to demonstrate the effects of nL and nsc on the Young’s modulus and strain-stiffening (Figure S1 shows a complete set of deformation curves). An [E0, β] map reveals that all Group 1 plastomers coalesce (green, Figure 3b) to successfully cross the gel-tissue divide, yet skirt many essential tissues such as muscle (β = 0.7), skin (β = 0.8), and fat (β = 0.9) located in the bottom-right corner of the tissue territory. To reach this corner, LBL’s with longer side chains (Group 2) were employed. Elongating side chains simultaneously reduces cross-link density and extends network strands, thereby maintaining tissue-relevant softness with enhanced firmness that yields a shift in the observed coalescence (black symbols in Figure 3b).

Figure 3.

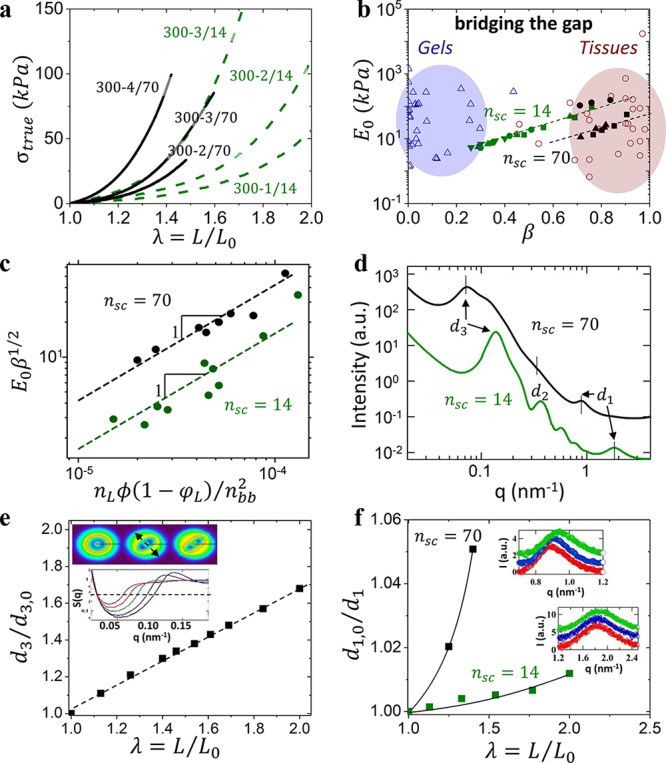
Figure 3

Open in a new tab

Bridging the gap. (a) Stress–elongation comparison of Group 1 (nsc = 14, dashed) versus Group 2 (nsc = 70, solid) plastomers with similar B-block backbone DP nbb = 300 and L-block volume fraction ϕL = 0.3–0.9 demonstrate Group 2’s enhanced strain-stiffening. (b) The E0 vs β plot from Figure 1d where Group 1 plastomers (green) enable gel-tissue bridging, while Group 2 plastomers (black) successfully penetrate into the tissue territory (Tables S1–S3). Dashed lines are used to guide the reader and not indicative of theoretical correlation. Group 2 plastomers with shorter backbones (nbb = 100) shift toward higher E0 (black ●), due to a star-like strand conformation as nbb ≈ nsc (Figure S1). (c) Correlation between mechanical properties (E0 and β) and molecular parameters (nL, nbb, ϕL) demonstrate good agreement with theoretical analysis summarized in eq S10, where ϕ=ng/(ng+nsc). (d) Selected USAXS/SAXS spectra of Group 1 and 2 plastomers with a similar nbb ≅ 300 (see Supporting Information for a complete set of X-ray curves for a complete set of X-ray curves). The observed increase of the interdomain spacing (d3) of Group 2 plastomers correlates with enhanced strain-stiffening from longer side chains. (e) Uniaxial extension of a Group 1 plastomer results in a d3 increase obtained from in situ variation of the structure factor S(q) in the stretching direction (arrow in inset). S(q) was computed by dividing the total scattering intensity by the fit of the form-factor of polydisperse solid spheres. The 2D USAXS patterns given in the inset correspond the to the values of λ of 1.0, 1.4, and 2.0 (from left to right). Azimuthal variations in the 2D USAXS pattern suggest network topology restructuring during deformation. (f) Relative decrease of the d1 spacing during elongation was deduced from the high-q shifts of the bottlebrush peak (insets) with Group 2 plastomers exhibiting stronger dependence consistent with enhanced strand firmness.

Theoretical analysis (eqs S1–S10 and Figure 3c) corroborates the observed nsc-specific coalescence in Figure 3b by correlating the attained mechanical properties with the corresponding architectural parameters (Figure 3c). For a fixed nsc, this universality serves as a theoretical foundation for independently tailoring plastomer firmness from its softness. The architectural firmness enhancement is probed by ultrasmall angle X-ray scattering (USAXS) at different length scales both before (Figure 3d) and during deformation (Figure 3e,f).31 Prior to deformation, B-block filaments are self-extended due to strong microphase segregation evidenced by the well-defined microdomain size (d2) and periodicity (d3) (Figure 3d and Table S3). For a given ϕL and nbb, an nsc increase results in a (2.2 ± 0.2)× increase in Rin ≈ d3 – DL consistent with the enhanced firmness (β70/β14 = 1.7 ± 0.1), where DL is the diameter of PMMA spherical domains determined from their form-factor (d2). During deformation, strand extension is a product of three mechanisms operating at different stresses (Figure 2b) evidenced by low-q shifts of the d3 spacing (Figure 3e) and high-q shift of the d1 spacing (Figure 3f). Even though the d1 spacing is nontrivially related to bottlebrush block diameter,32 the high-q shift is indicative of backbone extension given to the constant packing density constraint (condition). Because of a lower filament extension threshold of ∼(kBT)/Rsc, Group 2 plastomers undergo backbone extension prior to yielding of linear block domains at ∼γLBl0 (Figure 2b). This results in stronger dependence of d1 on deformation of ca. 5% compared to 1% shown by Group 1 (Figure 3f). Although both variations are marginal with respect to the total strain of 50–100%, they cause significant force augmentation due to nonlinear elasticity of the pre-extended backbone.8,9 In addition to unraveling of bottlebrush strands and backbone extension, a d3 shift includes withdrawal of linear blocks from the L-domains. Even though X-ray measurements did not give measurable evidence of linear block withdrawal due to its small effect on d2, microdomain yielding was corroborated by measuring loading–unloading hysteresis as a function of deformation (Figure S2) and by computer simulations of plastomer deformation.17 Despite microdomains yielding, deformation of plastomer samples was fully reversible up to rupture, whereas an onset of hysteresis was observed at λ ≈ 0.6λmax. At elongations λ < 0.6λmax, plastomers demonstrate elastic deformation without hysteresis ascribed to extension of network strands.

Regulating firmness (β) without compromising softness (E0) has significant implications in the design of biomedical devices and is particularly challenging for ultrasoft and ultrafirm tissues. Figure 4a exemplifies stress–elongation curves of assorted plastomers that reveal agreeable mechanical responses with brain, fetal membrane, and spinal cord tissues. These solvent-free materials also successfully replicate adipose tissues (Figure 4b) and serve as a superior solution to commercially available silicone gel-based products (Figure 1c) that leach into the body.15,16 Additionally, biological tissues exhibit significant variation in mechanical response depending on bodily location, age, strain rate, and deformation direction with respect to tissue texture. In the Supporting Information, we demonstrate additional tunability potential of the plastomer platform by mixing LBL plastomer networks with corresponding LB diblocks and free bottlebrushes (Figure S3). Although LBL plastomers precisely replicate most of the stress–strain response of biological tissue including the initial elasticity and subsequent yielding, they fall short of mimicking tissue strength at rupture and represent one of the challenges for future studies.

Figure 4.

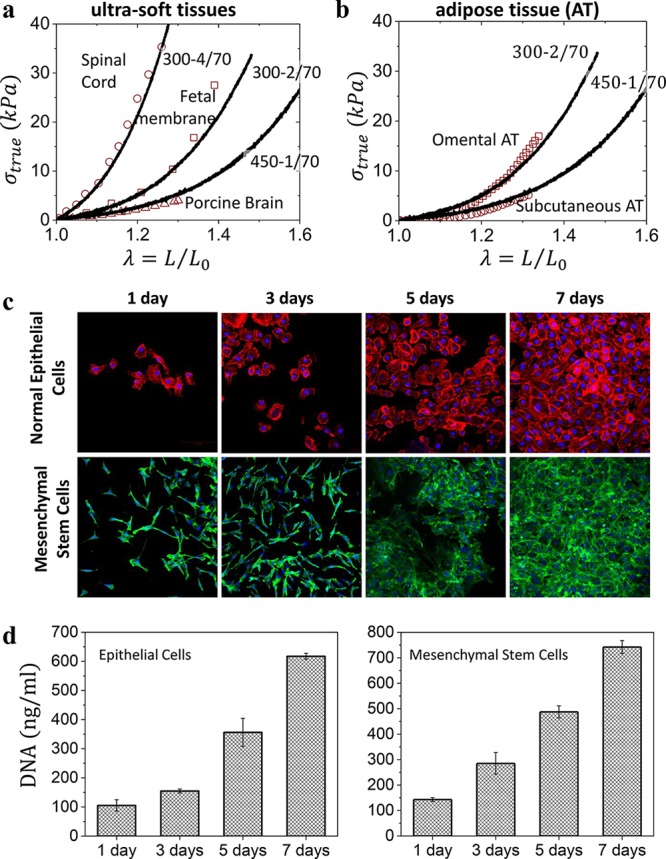
Figure 4

Open in a new tab

Plastomer tissue relevance and biocompatibility. (a) Selected true stress–elongation curves of Group 2 plastomers (lines) overlaid onto spinal cord, fetal membrane, and porcine brain tissues (symbols) found in the literature (Table S1) with similar mechanical properties. (b) Selected true stress–elongation curves of Group 2 plastomers (lines) match different types of adipose tissue (symbols). (c) The proliferation of human normal mammary epithelial and adipose-derived mesenchymal stem cells cultured onto a 300–1/70 plastomer surface and monitored by fluorescence microscopy after 1, 3, 5, and 7 days. Cells became confluent within 7 days. (d) Corresponding DNA quantification of the cultured human normal mammary epithelial and adipose-derived mesenchymal stem cells after 1, 3, 5, and 7 days.

The LBL platform also exhibits adequate biocompatibility as demonstrated by the adhesion and proliferation of human normal mammary epithelial and adipose-derived mesenchymal stem cells (MSCs) cultured onto a 300–1/70 surface (Figure 4c). Monitoring the cultured cells by fluorescence microscopy over the course of a week reveals plastomers as adequate substrates for both cell’s viability and proliferation (Figure 4c,d). In contrast, silicone gels used in commercial breast implants show a high cytotoxicity likely due to leaching of an ill-defined liquid fraction poisoning cells. We quantified the leachability via aqueous extraction of the sol fraction from both a commercial silicone gel and our plastomer over 1 month (Figure S4), which highlights the higher purity of plastomers as compared with current leading commercial products.

Conclusion

This study has significantly advanced our understanding of the materials design platform previously reported17 by (i) elucidating the material’s deformation mechanism encoded into a single network strand and (ii) demonstrating that our materials not only bridge the firmness divide between traditional soft gels and tissues, but have also successfully replicated the evolutionary soft-to-firm mechanical response found in particularly soft brain, fetal membrane, and fat tissues. Furthermore, these solvent-free materials exhibit superior biocompatibility compared with commercial products and show promise for further in vivo studies. We believe combining these unique characteristics will revolutionize future applications in the emerging biomedical and soft-robotics fields.

Experimental Section

Materials

Methyl methacrylate (MMA, 99%) was obtained from Thermo Fisher Scientific and purified using a basic alumina column to remove inhibitor. Tetrahydrofuran (THF), anisole, toluene, acetone, and isopropanol were purchased from Fisher Scientific and used as received. Monomethacryloxypropyl-terminated poly(dimethylsiloxane) (MCR-M17, Mn = 5000 g/mol, DP = 70, Đ = 1.15) was obtained from Gelest and purified using basic alumina columns to remove inhibitor. Copper(I) bromide (CuBr, 99.999%), tris[2-(dimethylamino)ethyl]amine (Me6TREN), and ethylene bis(2-bromoisobutyrate) (2-BiB, 97%) were purchased from Sigma-Aldrich and used as received.

No unexpected or unusually high safety hazards were encountered.

Synthesis of Poly(dimethylsiloxane) Bottlebrushes

Synthetic procedures are similar to previously reported linear–brush–linear plastomers.17 A 100 mL Schlenk flask equipped with a stir bar was charged with 2-BiB (9.6 mg, 26.6 μmol), MCR-M17 (50.0 g, 10 mmol), Me6TREN (12.2 mg, 14.2 μL, 53.3 μmol), and a solvent mixture of anisole (40 mL) and toluene (10 mL). The solution was bubbled with dry nitrogen for 1.5 h, and then Cu(I)Br (7.6 mg, 53.3 μmol) was quickly added to the reaction mixture under nitrogen atmosphere. The flask was sealed, purged for an additional 15 min, and then immersed in a 45 °C oil bath. The polymerization was stopped after 5 h to yield 79% monomer conversion as verified by 1H NMR (Figures S5 and S6), resulting in a bottlebrush PDMS polymer with DP of the backbone (nbb) ≈ 300. The polymer was precipitated two to three times from isopropanol to purify residual macromonomers. The resulting purified polymer was dried under a vacuum at room temperature until a constant mass was reached.

Linear–Bottlebrush–Linear ABA Plastomer Synthesis and Film Preparation

The resulting PDMS bottlebrushes were used as bifunctional ATRP macroinitiators to grow PMMA at both ends using a similar procedure. For example, PDMS marco-initiator (5 g, 3.37 μmol), excess MMA (1 g), and Me6TREN (1.5 g, 1.8 μL, 6.75 μmol) were dissolved in a mixture of anisole (5 mL) and toluene (10 mL), degassed and followed with the addition of Cu(I)Br (0.96 g, 6.75 μmol). Growth of linear MMA was monitored by 1H NMR, and samples were quenched to afford a series of ABA block copolymers with an increasing linear-to-bottlebrush ratio. The resulting products were swelled and washed two to three times with acetone to remove MMA homopolymer and then swelled and washed two to three times with hexanes to remove unreacted PDMS bottlebrush and dried overnight (Figure S5). A full synthetic inquiry into these impurities will be the subject of a later publication. Finally, the DP and volume fraction of linear end bocks were measured by 1H NMR (Figure S7) as summarized in Table S3. Samples were dissolved in 85 wt % THF and cast into Teflon Petri-dishes (Welch Fluorocarbon) and left to dry overnight.

Atomic Force Microscopy

The imaging was performed in PeakForce QNM mode using a multimode AFM (Brüker) with a NanoScope V controller and silicon probes (resonance frequency of 50–90 Hz and spring constant of ∼0.4 N/m). Bottlebrush B block dimensions are extracted from AFM images in Figure S8 and are consistent with expected dimensions described by 1H NMR.

Small- and Ultrasmall-Angle X-ray Scattering (SAXS and USAXS)

The USAXS and SAXS measurements (Figure S9 and Table S3) were carried out at the ID02 beamline of the European Synchrotron Radiation Facility (ESRF) in Grenoble, France. The experiments were conducted in transmission geometry using a photon energy of 12.46 keV. The recorded 2D data were centered, calibrated, regrouped, and reduced to 1D using the SAXS utilities platform described elsewhere.33 The analysis of the SAXS and USAXS data was performed using the SANS & USANS data reduction and analysis package provided by NIST34 for the Igor Pro environment (WaveMetrics Ltd.).

The monochromatic incident X-ray beam was collimated on the sample to a footprint of 100 × 200 μm2 (V × H). The total photon flux was estimated to be 9 × 1011 ph/s allowing for acquisition times of less than 100 ms. The accessed q values, with |q| = 4π sin(θ)/λ, where θ is the Bragg angle and λ is the wavelength, cover a range from 7.0 × 10–3 nm–1 to 5.0 nm–1. A Rayonix MX-170HS implemented in a 35 m long vacuum flight tube was applied for recording of SAXS and USAXS intensities at two different sample-to-detector distances of 1.5 and 10.0 m, respectively. For optimization of the scattering signal, a binning of 2 × 2 pixels was applied resulting in an effective pixel size of 89 μm in both directions.

The in situ mechanical and structural measurements were performed with the help of a custom-made stretching device compatible with the ID02 beamline environment. The stretching device allowed for computer controlled synchronized motion of the two symmetrical fixtures in which the dog bone-shaped sample was clamped. For each deformation, the position of the X-ray beam on the sample was refined by scanning it along two perpendicular directions. The structural irreversibility in the loading/unloading cycles in the linear regime was specifically checked and found negligible for all the samples studied.

For quantitative analysis of the USAXS–SAXS curves, we utilize the scattering intensity as I(q) ≈ Φ2(q)S(q) where S(q) is the structure factor and Φ(q) is the form-factor, which, for homogeneous monodisperse spheres, has the following form 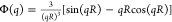Inline graphic. The polydispersity effect was incorporated by a convolution of the scattering intensity with the Gaussian size distribution functions. After extracting the PMMA sphere diameter (DL) and its polydispersity, the S(q) functions were analyzed.

Uniaxial Tensile Stress Strain Measurements

Dog bone-shaped samples with bridge dimensions of 12 mm × 2 mm × 1 mm were loaded into an RSA-G2 DMA (TA Instruments) and subjected to uniaxial extension at 20 °C and constant strain rate of 0.005 s–1. Samples were stretched until rupture, revealing the entire mechanical profile. In each case, tests were conducted in triplicate to ensure accuracy of the data. All stress–elongationcurves show dependence of the true stress σtrue on the elongation ratio λ in accordance with eq 1 at small and intermediate deformation range but switch to a linear scaling with λ at the later stages of deformation (Figure S1 and Table S3). The elongation ratio λ for uniaxial network deformation is defined as the ratio of the sample’s instantaneous size L to its initial size L0, λ = L/L0.

Biological Characterization of Tissue-like Substrates

To prepare substrates for cell culture study, tissue-like substrates were placed in a 24-well plate, and type-1 collagen was conjugated to their surface using the heterobifunctional linker N-sulfosuccinimidyl-6-(4′-azido-2′-nitrophenylamino) hexanoate (sulfo-SANPAH, Pierce). In brief, 500 μL of a 0.2 mg/mL solution of sulfo-SANPAH in milli-Q H2O was added to each well in a 24-well plate which was then placed under a 365 nm UV light, and irradiated for 5 min. Subsequently, the substrates were washed three times with 50 mM HEPES in PBS. Afterward, 500 μL of 50 μg/mL type-1 collagen was added to each well, and the plate was stored 3 h at 4 °C to prevent collagen polymerization but allow the collagen to react to the surface. The collagen coated tissue-like substrates were washed three times with PBS and then incubated with culture media, 10% fetal bovine serum with 1% pen-strep in Dulbecco’s modified Eagle medium warmed to 37 °C.

Two cell types of human normal mammary epithelial cells and adipose-derived mesenchymal stem cells were used for biological characterization of tissue-like substrates. Trypsinzed cells were seeded on the collagen functionalized substrates at an initial concentration of 20 000/cm2. Cell proliferation was analyzed over a week, while culture media was changed twice. To quantify the cellular proliferation on the substrate in the course of 1 week, the DNA content of the cells was measured using the Quanti-iT PicoGreen dsDNA kit (Invitrogen, USA) according to the manufacturer’s instructions. Fluorescence microscopy was also measured to monitor the cells over a week. Immunohistochemical staining was performed using Cytopainter Red Fluorescence F-actin Staining kit and Cytopainter Green Fluorescence F-actin Staining kit for epithelial and mesenchymal stem cells, respectively, following the manufacturer’s instructions. The 4′,6-diamidino-2-phenylindole (DAPI) was used to stain cell nuclei.

Acknowledgments

We acknowledge funding from the National Science Foundation (DMR 1407645, DMR 1921835, and DMR 1921923). S.S. acknowledges financial support from the Ministry of Education of the Russian Federation within State Contract No. 14.W03.31.0022. D.A.I. declares that this work was performed in accordance with the state task No. AAAA-A19-119101590029-0.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.9b01216.

  • Theoretical discussion of LBL plastomer structure and elastic properties, mechanical parameters of literature tissues and gels, structural and mechanical properties of LBL plastomers from 1H NMR, AFM, X-ray and stress–elongation curves, and leachability tests of samples (PDF)

Author Contributions

A.N.K. and M.V.V. designed, synthesized, and characterized the monomers, block copolymers, and polymer networks; A.N.K. performed mechanical tests and AFM experiments. H.L. and A.V.D. provided theoretical analysis of mechanical properties, developed theoretical foundation for materials design and LBL networks; C.C., A.L., M.S., and D.A.I. conducted X-ray studies and data analysis; F.F. and E.D. contributed to methodology, biological assays, and mechanical tests; S.S.S. was the principal investigator, A.N.K. and S.S.S were primary writers of the manuscript. All authors discussed the results and provided feedback on the manuscript.

The authors declare no competing financial interest.

Supplementary Material

oc9b01216_si_001.pdf (1.5MB, pdf)

References

  1. Blair G. W. S. A new criterion for expressing the ‘intensity of firmness’ of soft bodies. Nature 1943, 152, 412. 10.1038/152412a0. [DOI] [Google Scholar]
  2. Faber T. J.; Jaishankar A.; McKinley G. H. Describing the firmness, springiness and rubberiness of food gels using fractional calculus. Part I: Theoretical framework. Food Hydrocolloids 2017, 62, 311–324. 10.1016/j.foodhyd.2016.05.041. [DOI] [Google Scholar]
  3. Fung Y. C.Biomechanics: Mechanical Properties of Living Tissues, 2nd ed.; Springer, 1993. [Google Scholar]
  4. Holzapfel G. A.Biomechanics of soft tissue. In Handbook of Material Behavior Models, 1st ed.; LeMaitre J., Eds.; Academic Press, 2001; pp 1057–1071. [Google Scholar]
  5. Storm C.; Pastore J. J.; MacKintosh F. C.; Lubensky T. C.; Janmey P. A. Nonlinear elasticity in biological gels. Nature 2005, 435, 191–194. 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
  6. Carrillo J.-M. Y.; MacKintosh F. C.; Dobrynin A. V. Nonlinear elasticity: from single chain to networks and gels. Macromolecules 2013, 46, 3679–3692. 10.1021/ma400478f. [DOI] [Google Scholar]
  7. Whitesides G. M. Soft robotics. Angew. Chem., Int. Ed. 2018, 57, 4258–4273. 10.1002/anie.201800907. [DOI] [PubMed] [Google Scholar]
  8. Xu K.; Lu Y.; Takei K. Multifunctional skin-inspired flexible sensor systems for wearable electronics. Adv. Mater. Technol. 2019, 4, 1800628. 10.1002/admt.201800628. [DOI] [Google Scholar]
  9. Peters W.; Brandon H.; Jerina K. L.; Wolf C.; Young V. L. In Biomaterials in Plastic Surgery. Breast Implants; Woodhead Publishing, 2012. [Google Scholar]
  10. Jeong J.-W.; Shin G.; Park S. I.; Yu K. J.; Xu L.; Rogers J. A. Soft materials in neuroengineering for hard problems in neuroscience. Neuron 2015, 86, 175–186. 10.1016/j.neuron.2014.12.035. [DOI] [PubMed] [Google Scholar]
  11. Scholten K.; Meng E. Materials for microfabricated implantable devices: A review. Lab Chip 2015, 15, 4256–4272. 10.1039/C5LC00809C. [DOI] [PubMed] [Google Scholar]
  12. Teo A. J. T.; Mishra A.; Park I.; Kim Y.-J.; Park W.-T.; Yoon Y.-J. Polymeric biomaterials for medical implants and devices. ACS Biomater. Sci. Eng. 2016, 2, 454–472. 10.1021/acsbiomaterials.5b00429. [DOI] [PubMed] [Google Scholar]
  13. Feig V. R.; Tran H.; Lee M.; Bao Z. Mechanically tunable conductive interpenetrating network hydrogels that mimic the elastic moduli of biological tissue. Nat. Commun. 2018, 9, 2740. 10.1038/s41467-018-05222-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Li Y.; Sariyer O. S.; Ramachandran A.; Panyukov S.; Rubinstein M.; Kumacheva E. Universal behavior of hydrogels confined to narrow capillaries. Sci. Rep. 2015, 5, 17017. 10.1038/srep17017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Yu L. T.; Latorre G.; Marotta J.; Batich C.; Hardt N. S. In vitro measurement of silicone bleed from breast implants. Plast. Reconstr. Surg. 1996, 97, 756–764. 10.1097/00006534-199604000-00011. [DOI] [PubMed] [Google Scholar]
  16. Coroneos C. J.; Selber J. C.; Offodile A. C.; Butler C. E.; Clemens M. W. US FDA breast implant postapproval studies: long-term outcomes in 99,993 patients. Ann. Surg. 2019, 269, 30–36. 10.1097/SLA.0000000000002990. [DOI] [PubMed] [Google Scholar]
  17. Vatankhah-Varnosfaderani M.; Keith A. N.; Cong Y.; Liang H.; Rosenthal M.; Sztucki M.; Clair C.; Magonov S.; Ivanov D. A.; Dobrynin A. V.; Sheiko S. S. Chameleon-like elastomers with molecularly encoded strain-adaptive stiffening and coloration. Science 2018, 359, 1509–1513. 10.1126/science.aar5308. [DOI] [PubMed] [Google Scholar]
  18. Vatankhah-Varnosfaderani M.; Daniel W. F. M.; Everhart M. H.; Pandya A. A.; Liang H.; Matyjaszewski K.; Dobrynin A. V.; Sheiko S. S. Mimicking biological stress-strain behavior with synthetic elastomers. Nature 2017, 549, 497–501. 10.1038/nature23673. [DOI] [PubMed] [Google Scholar]
  19. Dobrynin A. V.; Carrillo J. Y. Universality in nonlinear elasticity of biological and polymeric networks and gels. Macromolecules 2011, 44, 140–146. 10.1021/ma102154u. [DOI] [Google Scholar]
  20. Jacobs M.; Liang H.; Dashtimoghadam E.; Morgan B. J.; Sheiko S. S.; Dobrynin A. V. Nonlinear Elasticity and Swelling of Comb and Bottlebrush Networks. Macromolecules 2019, 52, 5095–5101. 10.1021/acs.macromol.9b00956. [DOI] [Google Scholar]
  21. Gong J. P.; Katsuyama Y.; Kurokawa T.; Osada Y. Double-network hydrogels with extremely high mechanical strength. Adv. Mater. 2003, 15, 1155–1158. 10.1002/adma.200304907. [DOI] [Google Scholar]
  22. Chen Q.; Liang S.; Thouas G. A. Elastomeric biomaterials for tissue engineering. Prog. Polym. Sci. 2013, 38, 584–671. 10.1016/j.progpolymsci.2012.05.003. [DOI] [Google Scholar]
  23. Ducrot E.; Chen Y.; Bulters M.; Sijbesma R. P.; Creton C. Toughening elastomers with sacrificial bonds and watching them break. Science 2014, 344, 186–189. 10.1126/science.1248494. [DOI] [PubMed] [Google Scholar]
  24. Wang Z.; Jiang F.; Zhang Y.; You Y.; Wang Z.; Guan Z. Bioinspired design of nanostructured elastomers with cross-linked soft matrix grafting on the oriented rigid nanofibers to mimic mechanical properties of human skin. ACS Nano 2015, 9, 271–278. 10.1021/nn506960f. [DOI] [PubMed] [Google Scholar]
  25. Jaspers M.; Vaessen S. L.; van Schayik P.; Voerman D.; Rowan A. E.; Kouwer P. H. J. Nonlinear mechanics of hybrid polymer networks that mimic the complex mechanical environment of cells. Nat. Commun. 2017, 8, 15478. 10.1038/ncomms15478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. So J.-H.; Tayi A. S.; Güder F.; Whitesides G. M. Stepped moduli in layered composites. Adv. Funct. Mater. 2014, 24, 7197–7204. 10.1002/adfm.201401548. [DOI] [Google Scholar]
  27. Sheiko S. S.; Dobrynin A. V. Architectural code for rubber elasticity: from Super-soft to super-firm materials. Macromolecules 2019, 52, 7531–7546. 10.1021/acs.macromol.9b01127. [DOI] [Google Scholar]
  28. Ohta T.; Kawasaki K. Equilibrium morphology of block copolymer melts. Macromolecules 1986, 19, 2621–2632. 10.1021/ma00164a028. [DOI] [Google Scholar]
  29. Fantner G. E.; Oroudjev E.; Schitter G.; Golde L. S.; Thurner P.; Finch M. M.; Turner P.; Gutsmann T.; Morse D. E.; Hansma H.; Hansma P. K. Sacrificial bonds and hidden length: unraveling molecular mesostructures in tough materials. Biophys. J. 2006, 90, 1411–1418. 10.1529/biophysj.105.069344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Depalle B.; Qin Z.; Shefelbine S. J.; Buehler M. J. Influence of cross-link structure, density and mechanical properties in the mesoscale deformation mechanisms of collagen fibrils. J. Mech. Behav. Biomed Mater. 2015, 52, 1–13. 10.1016/j.jmbbm.2014.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Clair C.; Lallam A.; Rosenthal M.; Sztucki M.; Vatankhah-Varnosfaderani M.; Keith A. N.; Cong Y.; Liang H.; Dobrynin A. V.; Sheiko S. S.; Ivanov D. A. Strained bottlebrushes in super-soft physical networks. ACS Macro Lett. 2019, 8, 530–534. 10.1021/acsmacrolett.9b00106. [DOI] [PubMed] [Google Scholar]
  32. Liang H.; Wang Z.; Dobrynin A. V. Scattering from melts of combs and bottlebrushes: molecular dynamics simulations and theoretical study. Macromolecules 2019, 52, 5555–5562. 10.1021/acs.macromol.9b01034. [DOI] [Google Scholar]
  33. Sztucki M.; Narayanan T. Development of an ultra-small-angle x-ray scattering instrument for probing the microstructure and the dynamics of soft matter. J. Appl. Crystallogr. 2007, 40, 459–462. 10.1107/S0021889806045833. [DOI] [Google Scholar]
  34. Kline S. R. Reduction and analysis of SANS and USANS data using IGOR Pro. J. Appl. Crystallogr. 2006, 39, 895–900. 10.1107/S0021889806035059. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc9b01216_si_001.pdf (1.5MB, pdf)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES