Improving musculoskeletal model scaling using an anatomical atlas: the importance of gender and anthropometric similarity to quantify joint reaction forces

Abstract

Objective

The accuracy of a musculoskeletal model relies heavily on the implementation of the underlying anatomical dataset. Linear scaling of a generic model, despite being time and cost-efficient, produces substantial errors as it does not account for gender differences and inter-individual anatomical variations. The hypothesis of this study is that linear scaling to a musculoskeletal model with gender and anthropometric similarity to the individual subject produces similar results to the ones that can be obtained from a subject-specific model.

Methods

A lower limb musculoskeletal anatomical atlas was developed consisting of ten datasets derived from magnetic resonance imaging of healthy subjects and an additional generic dataset from the literature. Predicted muscle activation and joint reaction force were compared with electromyography and literature data. Regressions based on gender and anthropometry were used to identify the use of atlas.

Results

Primary predictors of differences for the joint reaction force predictions were mass difference for the ankle (p<0.001) and length difference for the knee and hip (p≤0.017). Gender difference accounted for an additional 3% of the variance (p≤0.039). Joint reaction force differences at the ankle, knee and hip were reduced by between 50% and 67% (p=0.005) when using a musculoskeletal model with the same gender and similar anthropometry in comparison with a generic model.

Conclusion

Linear scaling with gender and anthropometric similarity can improve joint reaction force predictions in comparison with a scaled generic model.

Significance

The scaling approach and atlas presented can improve the fidelity and utility of musculoskeletal models for subject-specific applications.

I. Introduction

Computational modelling and simulation of the musculoskeletal system can be used to address biomechanical questions, including those that require information that is not amenable to direct measurement, such as muscle forces and articular, or joint, loading. This type of information is essential for clinical applications, including: designing assistive devices [1], planning rehabilitative treatments [2], [3], analysing pathology such as osteoarthritis [4], designing implants [5], and the prevention of injuries [6].

The quantification of muscle forces and articular loading requires a detailed description of musculoskeletal geometry in the musculoskeletal model that is used to mathematically model the skeletal bones, joint articulations and musculotendon actuators. The lower limb model created by Delp et al. has been used extensively, and its underlying dataset is an amalgamation of two classic studies using measurements of five cadaver subjects [7] that has since been altered and refined [8], [9]. This generic model is used to investigate the general features of musculoskeletal design [8] and has been extended to include large numbers of additional subject measurements, such as incorporating variations in muscle volume and length [10], [11]. Klein Horsman et al. [12] published the first complete dataset that was based on the geometrical measurement of a single cadaveric specimen (male, age 77 years, mass 105 kg, height 1.74 m), and others have followed this approach (Carbone et al. [13]; male cadaver, age 85 years, mass 45 kg).

Linear scaling of generic models is the most time and cost efficient way in the clinical setting of representing an individual’s musculoskeletal geometry [14] – [16]. In this approach simple measurements of anthropometry such as body mass and limb lengths are used to scale the documented generic dataset to the individual subject [16], [17]. However, the generic models currently available (presented in TABLE I) do not enable gender and inter-individual anatomical variations to be accounted for [18], [19]. Such variations in human anatomy cannot be extrapolated comfortably from a single model and substantial errors have been reported when generic models are used, through scaling, to represent individual subjects [20] – [23].

Table I. Single Complete Subject Lower Limb Musculoskeletal Generic Models Used in the Literature.

Model	Gender	Height (m)	Body mass (kg)	Lower limb length (mm)	Age (years)
Rajagopal et al.[9]	Male	1.70	75	not provided	not provided
Carbone et al.[13]	Male	not provided	45	813	85
Klein Horsman et al.[12]	Male	1.74	105	904a	77

^aLimb length is calculated as the sum of femur and tibia lengths of the right leg: femur length is measured as the distance from the trochanter major to the mid point of the femoral epicondyles; tibia length is measured as the distance from the mid point of the femoral epicondyles to the medial malleolus.

Three-dimensional reconstructions of high-resolution magnetic resonance imaging (MRI) can accurately reproduce bone and muscle geometry [24] and accurately quantifies moment arm and muscle length [25]. Thus, MRI can be used to generate an anatomical dataset of in vivo subjects; such subject-specific models improve musculoskeletal modelling accuracy when compared to generic scaling [26], [27]. However, creating such a dataset for every subject for which musculoskeletal modelling is used is time and technology intensive, and thus is not in widely clinical use. The hypothesis of this study is that linear scaling to a musculoskeletal model with gender and anthropometric similarity to the individual subject produce similar results to the ones that can be obtained from a subject-specific model. This hypothesis is tested through: first, developing a lower limb musculoskeletal anatomical database, or atlas, consisting of datasets derived from MRI and a generic dataset from the literature; secondly, quantifying the discrepancies from scaled models where the outputs from the personalised, subject-specific musculoskeletal model are considered as a reference [28] – [30]; and finally, establishing any relationship between discrepancies of scaled models and the discrepancies from the underlying datasets to the modelled subject to define the use of the atlas in situations where it is impractical to create a subject-specific model to quantify joint reaction forces.

II. Methods

This study was approved by the NHS Research Ethics Committee and the Imperial College Research Ethics Committee. Written informed consent was obtained from all ten healthy subjects, covering a wide range of body heights, all with no lower limb musculoskeletal conditions (TABLE II).

Table II. Participant Characteristics.

Subject	Age (years)	Height (m)	Height percentile (%ile)a	Body mass (kg)	Limb length (mm)b
Male 1	27	1.92	99th	85.0	910
Male 2	42	1.83	90th	96.0	836
Male 3	25	1.80	80th	70.0	876
Male 4	28	1.72	39th	70.0	787
Male 5	21	1.68	20th	64.0	727
Female 1	43	1.84	99th	78.0	873
Female 2	45	1.68	87th	70.0	796
Female 3	39	1.64	68th	61.6	757
Female 4	24	1.58	31th	55.6	714
Female 5	27	1.55	17th	45.0	690
Mean (SD)	32 (9)	1.72 (0.12)		69.5 (14.5)	797 (76)

^aHeight percentile is calculated based on British adults [31].

^bLimb length is calculated as the sum of femur and tibia lengths of the right leg: femur length is measured as the distance from the major trochanter to the mid point of the femoral epicondyles; tibia length is measured as the distance from the mid point of the femoral epicondyles to the medial malleolus.

A. MRI-based musculoskeletal atlas

MRIs of each subject were acquired. T1 weighted axial spin echo scans were performed with the subjects lying supine with extended knees using a 3.0 T MRI scanner (MAGNETROM Verio, Siemens, Germany). Six axial image series were taken contiguously from the fifth lumbar vertebra to the distal end of the limb with the following settings: field of view 450 × 450 mm², acquisition matrix = 320 × 320, axial plane resolution 1.406 mm ×1.406 mm, slice thickness 1 mm. The total acquisition time per subject was approximately 40 minutes.

Each series of axial images was automatically registered, providing a field of view of the entire lower limbs. 3D bone surfaces of the pelvis and the right femur, tibia/fibula, patella and foot (calcaneus, talus and navicular bones for all subjects, and metatarsal bones for six subjects) were reconstructed based on manual segmentation of bone contours in the axial images.

Twenty-one anatomical landmarks were manually digitised on the bone surface. The landmarks were used to construct the local coordinate systems of the lower limb, as described by the Standardisation and Terminology committee of the International Society of Biomechanics [32]. Tibiofemoral contact points were digitised as the most distal ends of the medial and/lateral femoral condyles.

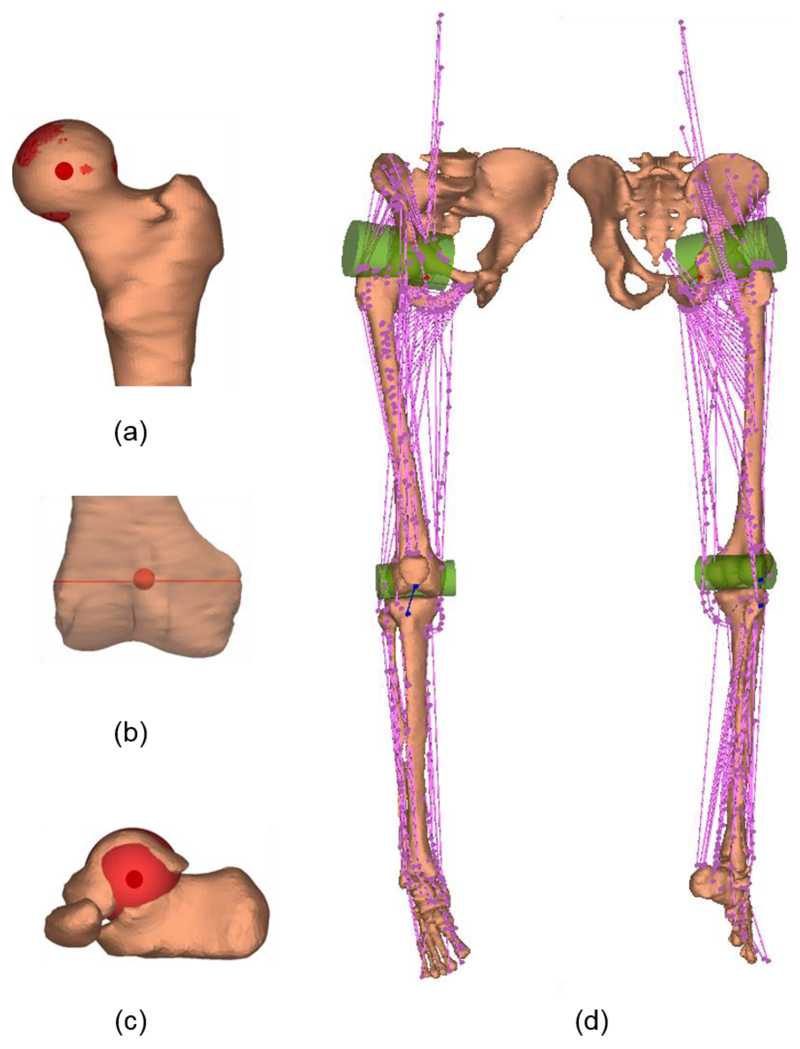
The joint parameters were identified by manually fitting geometrical objects to the articular surfaces. The following joint parameters were identified: hip joint centre (centre of a sphere fitted to the femoral head, Fig. 1a); knee joint centre (midpoint of the central axis of a cylinder fitted to the boundaries of both femoral condyles, Fig. 1b); and ankle joint centre (centre of a sphere fitted to the talar dome, Fig. 1c). The fitting error, the root mean squared distance between a set of 50 digitised points on the articular surface to the surface of the fitted object, was 0.7 (± standard deviation 0.3) mm, 1.7 (± 0.6) mm, and 1.8 (± 1.0) mm for the hip, knee and ankle joints, respectively. The fitting error in each dataset is reported in the supplementary datasets.

Fig. 1.

Lower limb anatomy geometry for a representative subject. (a) Hip centre (b) Knee centre and knee axis (c) Ankle centre; (d) Muscle element lines-of-action (in pink) and patella ligament (in blue). Wrapping objects (in green) were defined for iliopsoas and gastrocnemius.

Muscle and ligament lines-of-action were described by the origin, via and insertion points. Following the topology of the generic dataset of Klein Horsman et al. [12], which has been implemented in this atlas, lines-of-action of 163 muscle elements and the patella ligament were measured in the MR images (Fig. 1d), where the origins of psoas were estimated based on the measured length of the fifth lumbar vertebra and the intervertebral disc. For gastrocnemius and iliopsoas that are free to glide over the underlying bone of the femoral condyles and pubis of the pelvis, two wrapping cylinders were defined in the generic dataset. These cylinders were manually identified in MR images based on the curved muscle lines-of-action of gastrocnemius and iliopsoas and the segmented bone surface. The fitting error, the root mean squared distance between a set of 50 points digitised on the posterior surface of the femoral condyles and the superior surface of the pubic ramus to the cylindrical surface, was 1.5 (± 0.2) mm and 1.3 (± 0.2) mm, respectively. The fitting error in each dataset is reported in the supplementary datasets.

Segmentation and digitisation of MR images were performed using Mimics (Mimics 17.0, Materialise, Belgium) by two experienced operators. On completion, one operator reviewed and refined all segmentation and digitisation to ensure consistency across the atlas. The intra- and inter-operator reliability in digitisation of the anatomical landmarks and tibiofemoral contact points was tested for a subset of six subjects (three male, three female). The intraclass correlation coefficient (ICC, two-way mixed effects, absolute agreement) was higher than 0.99 and the intra- and inter-operator differences are reported in supplementary Fig. A.1.

As shown in the literature, the whole lower limb muscle volume is correlated with the subject’s height-mass product and the distribution of each individual muscle volume is well preserved across a group of healthy young subjects [11]. According to the equation in [11] the whole lower limb muscle volume (V_lm) of each subject was calculated:

$$V_{lm}=47\times m\times h+1285$$ (1)

where m is subject mass in kg and h is subject height in metres.

The muscle volume (V_m) was proportional to the whole lower limb muscle volume and the muscle length (L_m) was proportional to the lower limb length, according to the mean value from the literature [11]. Muscle physiological cross-sectional area (PCSA) was calculated as:

$$\text{PCSA}=\frac{V_{m}cos\theta }{L_m\times \frac{L_f}{L_m}\times \frac{2.7}{L_s}}$$ (2)

where θ is the pennation angle; $\frac{L_f}{L_m}$ is fibre length to muscle length ratio [10]; and $\frac{2.7}{L_s}$ is the ratio of optimal sarcomere length to the sarcomere length in μm [33].

Muscle parameters of a representative subject are presented in TABLE III. Ten MR-based anatomical datasets (including coordinates of bony landmarks, joint centres/axes, contact points, lines-of-action of muscles and ligament, wrapping object parameters and muscle parameters) are available in the supplementary datasets.

Table III. Muscle Parameters of a Representative Subject (F1).

Muscle	PCSA (cm2)	Muscle volume (Vm, cm3)	Muscle length (Lm, cm)	Fibre length to muscle length ratio $(\frac{L_f}{L_m})$	Pennation angle (θ, °)	sarcomere length (Ls, μm)
Adductor brevis	11.26	118.05	14.23	0.68	6.10	2.91
Adductor longus	14.79	181.49	21.91	0.50	7.10	3.00
Adductor magnus	58.58	631.19	32.82	0.39	15.50	2.19
Biceps femoris long head	31.75	234.49	29.68	0.28	11.60	2.35
Biceps femoris short head	6.80	112.43	26.89	0.49	12.30	3.31
Extensor digitorum longusa	7.28	77.90	37.89	0.24	10.80	3.12
Extensor hallucis longusa	2.64	37.74	37.89	0.31	9.40	3.24
Flexor digitorum longus	8.50	34.53	26.02	0.16	13.60	2.56
Flexor hallucis longus	19.87	87.53	24.01	0.20	16.90	2.37
Gastrocnemius lateral	24.32	169.44	25.14	0.27	12.00	2.71
Gastrocnemius medial	55.89	290.70	28.11	0.19	9.90	2.59
Gemellus inferiorb	1.01	7.29	7.20	1.00	0.00	2.70
Gemellus superiorb	1.01	7.29	7.20	1.00	0.00	2.70
Gluteus maximus	49.01	958.03	30.38	0.62	21.90	2.60
Gluteus medius	51.94	364.58	19.99	0.37	20.50	2.40
Gluteus minimus	8.78	118.05	13.44	1.00	0.00	2.70
Gracilis	3.63	117.24	33.70	0.79	8.20	3.24
Iliacus	11.76	199.15	26.19	0.56	14.30	3.02
Obturator externus	5.92	61.03	10.30	1.00	0.00	2.70
Obturator internus	3.68	30.52	8.29	1.00	0.00	2.70
Pectineus	5.53	73.88	13.36	1.00	0.00	2.70
Peroneus brevisc	6.47	47.38	37.10	0.19	11.50	2.76
Peroneus longusc	13.54	99.58	37.10	0.19	14.10	2.72
Peroneus tertiusd	6.20			1.00	0.00	2.70
Piriformis	4.88	48.99	10.04	1.00	0.00	2.70
Plantarisd	2.40			1.00	0.00	2.70
Popliteus	2.64	26.50	10.04	1.00	0.00	2.70
Psoas minord	1.10			1.00	0.00	2.70
Psoas	15.30	305.16	34.05	0.50	10.60	3.11
Quadratus femoris	4.76	36.14	7.60	1.00	0.00	2.70
Rectus femoris	46.82	304.35	33.52	0.21	13.90	2.42
Sartorius	3.22	183.90	55.00	0.90	1.30	3.11
Semimembranosus	40.63	277.85	28.46	0.24	15.10	2.61
Semitendinosus	9.06	208.79	32.30	0.65	12.90	2.89
Soleus	151.65	498.69	33.52	0.11	28.30	2.12
Tensor fasciae latae	4.31	71.47	16.59	1.00	0.00	2.70
Tibialis anterior	14.01	153.38	33.09	0.27	9.60	3.14
Tibialis posterior	31.23	119.65	31.95	0.12	13.70	2.56
Vastus intermedius	45.99	308.37	34.66	0.24	4.50	2.17
Vastus lateralis	76.97	936.35	38.32	0.38	18.40	2.14
Vastus medialis	67.23	486.64	34.48	0.22	29.60	2.24

Fibre length to muscle length ratio $(\frac{L_f}{L_m})$, pennation angle (θ), and sarcomere length (L_s) were taken from [10]. For muscles which were not measured in [10] their fibre length to muscle length ratio was set as 1, pennation angle was set as 0° and sarcomere length was set as 2.7μm.

^aMuscle volume was only available for the combined extensor digitorum longus and extensor hallucis longus in [11]. Volume proportion in [12] was used to divide the two muscles.

^bMuscle volume was only available for the combined gemellus inferior and gemellus superior in [11]. Volume proportion in [12] was used to divide the two muscles.

^cMuscle volume was only available for the combined peroneus longus and peroneus brevis in [11]. Volume proportion in [12] was used to divide the two muscle.

^dMuscle was not included in [11]. Its PCSA was obtained from [12].

B. Gait data collection

Within six months (mean ± standard deviation [range]: 3.1 ± 2.3 [0.1 - 6.0] months) from MR imaging acquisition, gait data from the same subjects were acquired using a 10-camera VICON motion analysis system (Oxford Metrics Group, UK) with two force plates (Kistler Type 9286B, Kistler Instrumente AG, Winterthur, Switzerland). The marker set comprised anatomical landmarks of the whole lower limbs (markers on the anterior/posterior superior iliac spine, medial/lateral femoral epicondyles, medial/lateral malleolus, the second/fifth metatarsal and the heel) as well as clusters of three markers each for the thighs and shanks [34]. Subjects were instructed to perform six level walking trials at a self-selected comfortable speed (1.25 ± 0.15 [1.03 - 1.41] m/s). The final three trials were selected for analysis. Surface electromyography (EMG; Myon 320, Myon AG., Switzerland) during gait was recorded at 1000 Hz from eight muscles: gluteus medius, rectus femoris, vastus lateralis, vastus medialis, biceps femoris long head (LH), semitendinosus, soleus and tibialis anterior. The electrodes were aligned parallel to the muscle fibres over the muscle belly, as described in the literature [35], [36]. Prior to electrode placement, the skin was shaved and cleaned with alcohol wipes. Recorded EMG signals were corrected for offset, high-pass filtered at 30 Hz using a zero phase-lag, four order Butterworth filter and rectified. The rectified signals were then low-pass filtered at 10 Hz [37].

C. Lower limb musculoskeletal model

A lower limb musculoskeletal model FreeBody V2.1 was used to quantify forces during gait [38], [39]. It consists of four rigid segments (foot, shank, thigh and pelvis), articulated by ankle, knee and hip joints, actuated by 163 lower limb muscle elements and the patellar ligament. The ankle and knee joints each possess six degrees of freedom (DOFs, a combination of 3DOFs planar joint and 3DOFs spherical joint), and, in this use of the model, the hip joint possesses three rotational DOFs (a spherical joint). The position and orientation of each rigid segment was constructed based on the measured kinematics using the method in [40], with a constraint to the hip joint [39]. The net joint force and moment was calculated using wrench notation in the inverse dynamic method [41]. Afterwards, muscle forces and resultant articulated contact forces across the ankle, knee and hip joints were calculated using a one-step static optimisation [42] by minimising the sum of cubed muscle activations [43]. The optimisation model is formulated, as below (3):

$$min{{\displaystyle \sum _{m=1}^{163}\left(\frac{f_m}{f_{{max}_m}}\right)}}^3\text{subject}\text{to}\left[\begin{array}{c}{\displaystyle \sum _{l=1}^L{f}_l.{\mathit{\text{n}}}_{\mathit{\text{li}}}-{\displaystyle \sum _{k=1}^K{f}_k.{\mathit{\text{n}}}_{\mathit{k}(\mathit{i}-\mathbf{1})}+{\mathit{\text{J}}}_{\mathit{i}}-{\mathit{\text{J}}}_{\mathit{i}-\mathbf{1}}}}\\ {\displaystyle \sum _{l=1}^L{f}_l.{\mathit{\text{n}}}_{\mathit{l}\mathit{i}}\times r_{\mathit{l}\mathit{i}}-{\displaystyle \sum _{k=1}^K{f}_k.{\mathit{\text{n}}}_{\mathit{k}(\mathit{i}-\mathbf{1})}\times r_{\mathit{k}(\mathit{i}-\mathbf{1})}-{\widetilde{\mathit{\text{d}}}}_{\mathit{i}}\times {\mathit{\text{J}}}_{\mathit{i}-\mathbf{1}}}}\end{array}\right]=\left[\begin{array}{cc}{M}_i{\mathit{\text{E}}}_{\mathbf{3}\times \mathbf{3}}& {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}\\ M_i{\tilde{\mathit{c}}}_i& {\mathit{I}}_i\end{array}\right]\left[\begin{array}{c}{\mathit{a}}_{\mathit{i}}-\mathit{\text{g}}\\ {\ddot{\mathit{\theta }}}_{\mathit{i}}\end{array}\right]+\left[\begin{array}{c}{\mathbf{0}}_{\mathbf{3}\times \mathbf{1}}\\ {\dot{\mathit{\theta }}}_i\times I_i{\dot{\mathit{\theta }}}_i\end{array}\right]0\le f_m\le f_{{\mathit{\text{max}}}_m},m=1,\dots ,163$$ (3)

where f_m is the muscle force of muscle element m (m=1,…,163) and f_maxm is the maximum muscle force of muscle element m, i is the segment number (numbering from distal to proximal), L is the number of the proximal muscle element at the segment i, K is the number of the distal muscle element at the segment i, n_i the line of action of the proximal muscle element, n_i-1 the line of action of the distal muscle element, r_i the moment arm of the proximal muscle element, r_i-1 the moment arm of the distal muscle element, J_i the proximal joint reaction force, J_i-1 the distal joint reaction force, I_i the inertia tensor, ${\ddot{\mathit{\theta }}}_i$ the angular acceleration about COM, ${\dot{\mathit{\theta }}}_i$ the angular velocity about the COM, a_i the linear acceleration of COM, g the gravitational acceleration, M_i the segment mass, E_3×3 the identity matrix, c_i the vector from the proximal joint to the segment COM and d_i is the vector from the proximal to the distal joint, ${\widetilde{\mathit{\text{c}}}}_{\mathit{\text{i}}}\text{and}{\widetilde{\mathit{\text{d}}}}_{\mathit{\text{i}}}$ are the skew sysmetirc matrix of c_i and d_i, respectively.

For each individual subject, eleven lower limb musculoskeletal models were created: one using the subject-specific MR-based dataset and the others through linear scaling of the generic and the remaining nine MR-based datasets. In the scaled models, scaling factors were the ratios of the intersegmental length and width measured of the subject to intersegmental length and width in the underlying dataset. The following anatomical parameters scaled using this methodology were: lines-of-action of muscles/ligament, muscle wrapping parameters, joint centres and contact points [39]. Segment inertia parameters were determined based on the subject’s height, mass and gender, using the regression equations in De Leva [44], which were identical in the eleven models. Maximum muscle force of each muscle element was calculated as the maximum muscle stress (60 N/cm²) [9] multiplied by the PCSA of each muscle element. In total, 330 simulations (10 subjects × 11 anatomical datasets × 3 gait trials) were analysed in the study.

D. Data analysis and statistics

Predicted muscle force, muscle activation and joint reaction force from models were expressed at a gait cycle percentage from 0% (right heel strike) to 100% (the consecutive right heel strike) at 1% intervals and averaged over three trials. The subject-specific (reference) model was evaluated: first, as a verification of the model the predicted muscle activation was compared to the experimental EMG of this subject. The magnitude (M), phase (P) and combined (C) errors were quantified using the Sprague and Geers metric [45], where a combined error of less than 0.40 is the best validation for similar work in the literature [28]; secondly, the predicted knee and hip joint reaction force was compared to the measured data in the literature [46], [47]. The measured knee joint reaction force was from eight subjects with instrumented knee implants [46]; the measured hip joint reaction force was from ten subjects with instrumented hip implants [47].

Differences between the scaled and subject-specific model outputs were quantified using the root mean square difference (RMSD) and normalised by the mean force from the subject-specific model (3):

$${\text{RMSD}}_d=\sqrt{\frac{{\sum }_{i=0}^{100}{({\mathit{\text{F}}}_s^i-{\mathit{\text{F}}}_d^i)}^2}{100}}/\overline{{\mathit{\text{F}}}_s}\times 100(\%)$$ (4)

where F_s is the predicted force from the subject-specific model; F_d is the predicted force using the dth scaled model; and ${\overline{F}}_s$ is the mean force during gait from the subject-specific model.

Pearson correlation and multiple linear regression analyses were used to identify the model in the atlas that produced the closest joint reaction forces to the ones from a subject-specific model. The following anthropometric measurements were investigated: height, mass, body mass index (BMI), limb length, pelvis width, femur length, tibia length, and the limb length to pelvis width ratio. Multiple regressions to the discrepancies in joint reaction forces were identified based on stepwise forward regression (p_in = 0.05, p_out = 0.1). The appropriateness of the final regression was checked by inspecting the normal probability plot of the regression standardised residual and the scatterplot of the standardised residual.

A Wilcoxon Signed Rank test was performed to test the hypothesis that scaling of the model (the ten remaining underlying datasets in the atlas) with gender and anthropometric similarity as identified by the regression, produced minor discrepancies of joint reaction force predictions from the subject-specific model, than scaling of a single generic model. The appropriate use of the atlas was tested through the gait data in the “6th Grand Challenge Competition to Predict In Vivo Knee Loads” from one subject (DM, male, height: 172 cm, mass: 70 kg) [48]. The subject-specific model of DM from Ding et al. [39] was implemented in Freebody V2.1 and is freely available at http://www.msksoftware.org.uk/software/freebody. All statistical procedures were performed using IBM SPSS with an alpha level of 0.05 (Version 24.0, IBM Corp., USA).

III. Results

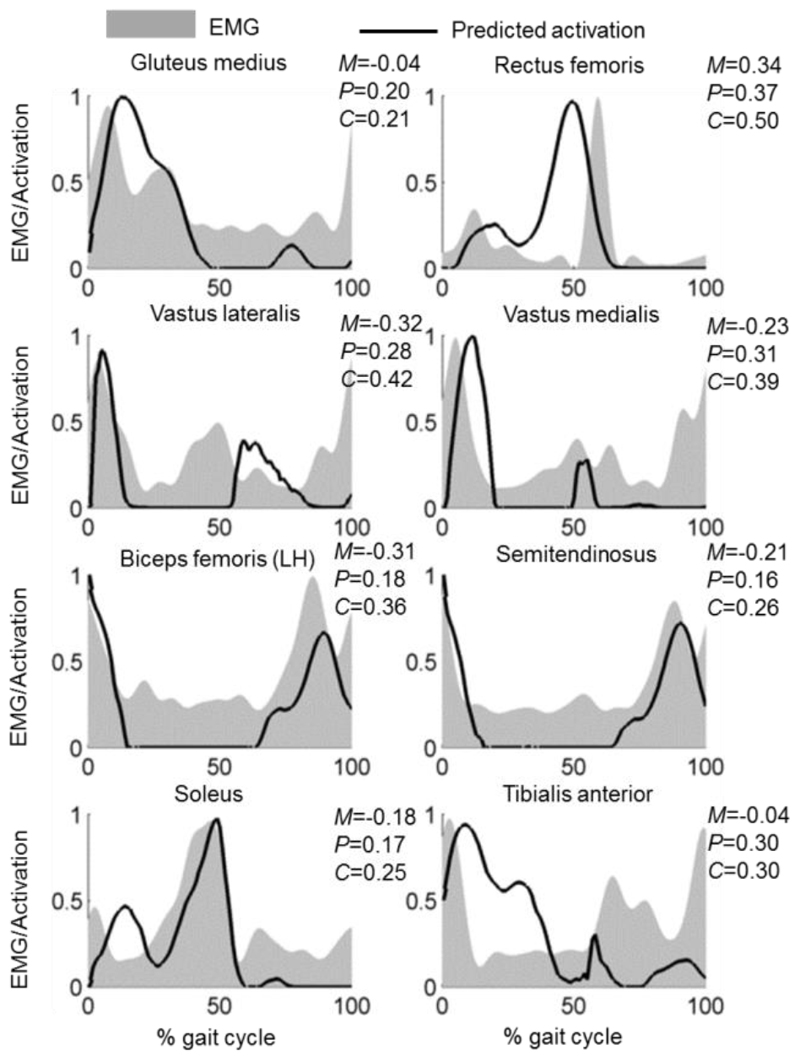
Subject-specific modelling of muscle activation showed consistency with the EMG signals (Fig. 2 for a representative subject and see supplementary Fig. A.2 for the other nine subjects). Across all subjects, the quantitative evaluation of predicted muscle activations to EMG data using Sprague and Geers metric is shown in TABLE IV, with phase errors ranging from 0.17 (soleus, standard deviation, SD = 0.06) to 0.32 (rectus femoris, SD = 0.03) and combined errors ranging from 0.26 (soleus, SD = 0.09) to 0.44 (rectus femoris, SD = 0.12) from the subject-specific models. The predicted muscle activations from ten scaled models to each subject are shown in Supplementary Fig. A.3 with quantitative magnitude (M), phase (P) and combined (C) errors expressed as mean ± standard deviation [range]. When compared to the errors from the subject-specific model, the mean phase errors from the scaled models were greater (p ≤ 0.013) for gluteus medius, vastus lateralis, vastus medialis, semitendinosus, soleus and tibialis anterior.

Fig. 2.

Predicted muscle activations (solid line) from the subject-specific model compared to the experimental EMG data (grey area) in a representative subject (F1). EMG data were individually normalised to the maximum recorded signal of each muscle during gait and predicted muscle activations were defined to be between 0 (fully deactivated) and 1 (fully activated) in terms of the peak value predicted during gait. Magnitude (M), phase (P) and combined (C) errors from predicted muscle activations are quantified using Sprague and Geers metric. See supplementary Fig. A.2 for the results of the other nine subjects.

Table IV. Absolute Values of Magnitude (M), Phase (P) and Combined (C) Errors Between Predicted Muscle Activations From Models (Subject-Specific and Scaled Models) to Measured EMG Data, Reported as Mean (Standard Deviation) for All Ten Subjects.

	M			P			C
	Subject-specific model	Scaled model	p valuea	Subject-specific model	Scaled model	p valuea	Subject-specific model	Scaled model	p valuea
Gluteus medius	0.22 (0.13)	0.34 (0.20)	0.028	0.20 (0.03)	0.24 (0.02)	0.013	0.31 (0.10)	0.44 (0.17)	0.017
Rectus femoris	0.26 (0.20)	0.38 (0.24)	0.013	0.32 (0.03)	0.34 (0.04)	0.799	0.44 (0.12)	0.53 (0.18)	0.047
Vastus lateralis	0.20 (0.09)	0.37 (0.09)	0.005	0.27 (0.08)	0.40 (0.04)	0.005	0.35 (0.09)	0.55 (0.07)	0.005
Vastus medialis	0.20 (0.15)	0.21 (0.10)	0.799	0.28 (0.06)	0.31 (0.05)	0.007	0.37 (0.07)	0.39 (0.06)	0.169
Biceps femoris (LH)	0.19 (0.11)	0.23 (0.16)	0.575	0.21 (0.03)	0.22 (0.03)	0.575	0.30 (0.07)	0.32 (0.14)	0.575
Semitendinosus	0.15 (0.14)	0.21 (0.10)	0.093	0.22 (0.06)	0.28 (0.06)	0.005	0.29 (0.11)	0.36 (0.08)	0.009
Soleus	0.18 (0.11)	0.18 (0.09)	0.959	0.17 (0.06)	0.26 (0.08)	0.007	0.26 (0.09)	0.36 (0.10)	0.059
Tibialis anterior	0.17 (0.13)	0.23 (0.15)	0.721	0.26 (0.05)	0.31 (0.04)	0.005	0.32 (0.11)	0.41 (0.12)	0.114

^ap value is from the Wilcoxon Signed Rank test by comparing the error from the subject-specific model with the mean error from ten scaled models (α = 0.05).

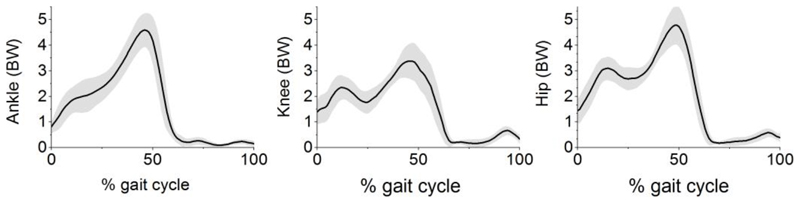
Joint reaction forces predicted from the subject-specific models are shown in Fig. 3 while mean and maximum values from each subject-specific model are summarised in Supplementary TABLE A.I. When compared to the measured forces in the literature, differences in mean and maximum joint reaction forces are 23% and 26% at the knee, 33% and 47% at the hip.

Fig. 3.

Mean joint reaction force (solid line) and standard deviation (shaded area), expressed in bodyweight (BW), from ten subject-specific models at the ankle, knee and hip joint. Mean and maximum joint reaction force for each subject-specific model is reported in Supplementary TABLE A.I.

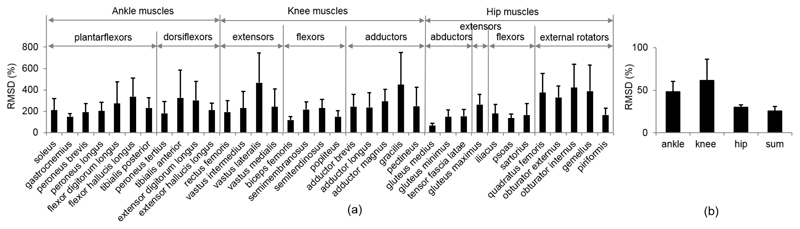
The maximum RMSDs, expressed as the percentage of mean force from the subject-specific model, are shown in Fig. 4. Differences are greater for the muscle forces than the joint forces: in the ankle planar flexors, maximum RMSDs were found to be 336% at flexor hallucis longus and 271% at flexor digitorum longus; in the ankle dorsiflexors, 325% and 301% at tibialis anterior and extensor digitorum longus, respectively; in the knee extensors 465% at vastus lateralis; and in the hip adductors, 448% at gracilis. The differences in joint reaction forces were greatest at the knee joint with a maximum RMSD of 61%, followed by the ankle joint with 48% and hip joint with 30%. The maximum RMSD of the sum of joint reaction forces (ankle, knee and hip) was 26% from the scaled model, in comparison with the sum of these from the subject-specific model.

Fig. 4.

RMSDs in muscle and joint reaction forces: (a) maximum RMSDs and standard deviations in muscle forces crossing the ankle, knee and hip joints, (b) maximum RMSDs and standard deviations in ankle, knee and hip joints, and the sum of these. RMSDs are expressed as a percentage of mean force from the subject-specific model.

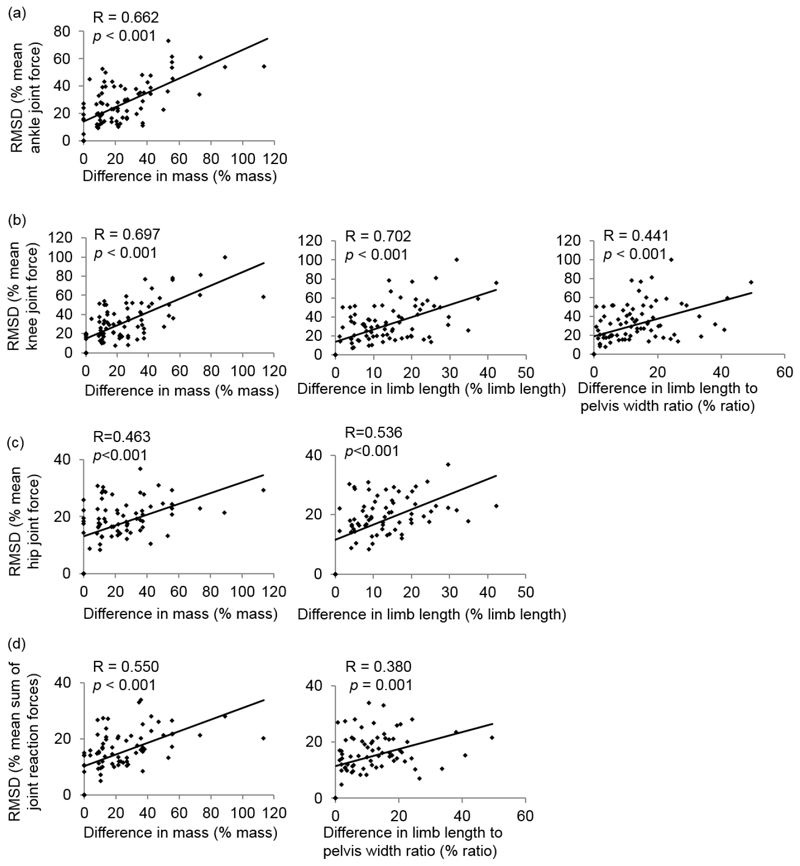
A significant moderate to strong correlation (R > 0.30, p < 0.05) was found between the discrepancies in the joint reaction force predictions and the discrepancies in gender and anthropometric measurements of the underlying anatomical datasets (apart from the pelvis width, see TABLE V).

Table V. Correlation Between Root Mean Square Difference (RMSD) in Joint Reaction Forces From Scaled Models and the Discrepancies from the Underlying Datasets to the Modelled Subject.

	RMSDa
	Ankle		Knee		Hip		Sum
	R	p value	R	p value	R	p value	R	p value
∆genderb	0.354	0.001	0.373	<0.001	0.355	0.023	0.341	0.002
∆heightc	0.612	<0.001	0.585	<0.001	0.475	<0.001	0.528	<0.001
∆massc	0.662	<0.001	0.697	<0.001	0.463	<0.001	0.550	<0.001
∆limb lengthc	0.426	<0.001	0.702	<0.001	0.536	<0.001	0.435	<0.001
∆femur lengthc	0.426	<0.001	0.585	<0.001	0.520	<0.001	0.435	<0.001
∆tibia lengthc	0.490	<0.001	0.658	<0.001	0.536	<0.001	0.485	<0.001
∆pelvis widthc	0.103	0.335	0.101	0.354	0.256	0.001	0.142	0.212
∆BMIc	0.459	<0.001	0.360	0.001	0.401	<0.001	0.404	<0.001
∆limb length to pelvis width ratioc	0.324	0.002	0.441	<0.001	0.516	<0.001	0.380	0.001

The values in italics are statistically significant.

^aRMSDs in ankle, knee and hip joints, and the sum of these, are expressed as the percentage of mean force from the subject-specific model.

^bDifference in gender is defined as 1 or 0.

^cDifference in anthropometry measurements is expressed as a percentage difference from the underlying dataset to the subject; pelvis width is defined as the distance between right and left anterior superior iliac spine; the limb length to pelvis width ratio (ratio) is defined as limb length divided by pelvis width.

The final multiple regression found the significant predictors to the difference in the joint reaction force predictions, which are, for the different predictions of the ankle joint forces: the differences in gender (regression coefficient, B = 7.66, p = 0.005) and mass (B = 0.49, p < 0.001); for the different predictions of knee joint forces: differences in gender (B = 7.75, p = 0.013), mass (B = 0.38, p = 0.001), limb length (B = 1.00, p = 0.017), and the limb length to pelvis width ratio (B = 37.22, p = 0.011); for the different predictions of hip joint forces: differences in gender (B = 2.64, p = 0.039), mass (B = 0.10, p = 0.033) and limb length (B = 0.38, p < 0.001); and for the different predictions of the sum of these: differences in gender (B = 25.24, p = 0.003), mass (B = 0.99, p = 0.001) and limb length (B = 2.23, p = 0.046) (Fig. 5 and TABLE VI). The regression models accounted for 49%, 61%, 36% and 40% of the variances of the differences at the ankle, knee, hip joint force predictions, and the sum of these, respectively (TABLE VI).

Fig. 5.

Significant anthropometric predictors of root mean square difference (RMSD) in joint forces at (a) the ankle, (b) the knee, (c) the hip and (d) the sum of all joints. Difference in anthropometric measurements is expressed as a percentage difference from the underlying dataset to the subject. R and p values are from the Pearson correlation analysis.

Table VI. Identified Multiple Regression Models to Quantify Root Mean Square Difference (RMSD) in Joint Reaction Forces.

Ankle	Predictor	R	R2	Adjusted R2	Change in R2	p value
	constant + ∆mass	0.662	0.439	0.432	0.439	<0.001
	constant + ∆mass+∆ gender	0.698	0.488	0.476	0.049	<0.001
	Multiple Regression Model	RMSDa = 11.06+0.49×∆mass+7.66×∆gender
		Bb	Standard error	p value	95% CIb
	constant	11.061	2.156	<0.001	6.775	15.346
	∆mass	0.490	0.063	<0.001	0.365	0.615
	∆genderc	7.663	2.672	0.005	2.350	12.975
Knee	Predictor	R	R2	Adjusted R2	Change in R2	p value
	constant+∆LL	0.702	0.493	0.487	0.493	<0.001
	constant+∆LL+∆mass	0.744	0.553	0.542	0.060	<0.001
	constant+∆LL+∆mass+∆ratio	0.764	0.583	0.568	0.030	<0.001
	constant+∆LL+∆mass+∆ratio+∆gender	0.783	0.613	0.595	0.030	<0.001
	Multiple Regression Model	RMSD = 5.32+1.00×∆LL+0.38×∆mass+37.22×∆ratio+7.75×∆gender
		B	Standard error	p value	95% CI
	Constant	5.321	2.780	0.059	-0.210	10.851
	∆LLd	1.001	0.411	0.017	0.184	1.819
	∆massd	0.379	0.108	0.001	0.165	0.594
	∆ratiod	37.221	14.257	0.011	8.860	65.582
	∆gender	7.751	3.062	0.013	1.660	13.842
Hip	Predictor	R	R2	Adjusted R2	Change in R2	p value
	constant+∆LL	0.536	0.287	0.278	0.287	<0.001
	constant+∆LL+∆mass	0.580	0.337	0.319	0.050	<0.001
	constant+∆LL+∆mass+∆gender	0.599	0.359	0.333	0.022	<0.001
	Multiple Regression Model	RMSD = 9.60+0.38×∆LL+0.10×∆mass+2.64×∆gender
		B	Standard error	p value	95% CI
	Constant	9.595	1.436	<0.001	6.642	12.549
	∆LL	0.377	8.337	<0.001	0.172	0.582
	∆mass	0.096	0.041	0.033	0.008	0.183
	∆gender	2.641	1.626	0.039	-0.634	5.917
Overall		R	R2	Adjusted R2	Change in R2	p value
	constant+∆mass	0.550	0.302	0.293	0.302	<0.001
	constant+∆mass+∆gender	0.602	0.363	0.346	0.061	0.009
	constant+∆mass+∆gender+∆LL	0.629	0.396	0.372	0.033	0.046
	Multiple Regression Model	RMSD = 7.40+0.16×∆mass+4.03×∆gender+0.16×∆ratio
		B	Standard error	p value	95% CI
	Constant	7.399	1.326	<0.001	4.758	10.040
	∆mass	0.163	0.037	<0.001	0.089	0.237
	∆gender	4.031	1.484	0.008	1.074	6.987
	∆ratio	0.158	0.078	0.046	0.003	0.313

^aRMSDs from the scaled modes in joint reaction forces at the ankle, knee, hip and their sum are expressed as the percentage of mean force from the subject-specific model.

^bB indicates regression coefficient; CI indicates confidence interval.

^cDifference in gender is defined as 1 or 0.

^dDifference in mass (∆mass), limb length (∆LL) and limb length to pelvis width ratio (∆ratio) is expressed as percentage difference from the underlying dataset to the modelled subject.

In comparison with the RMSDs produced by scaling of the generic model, scaling of the musculoskeletal model with gender and anthropometric similarity as identified by the regression significantly reduced the RMSDs in joint reaction forces of ankle, knee, hip and their sum (p = 0.005, TABLE VII).

Table VII. A Comparison of Root Mean Square Difference (RMSD) and Coefficient of Determination (R²) in Joint Reaction Forces Produced by the Scaled Generic Model and the Scaled Closest Model.

	Ankle				Knee				Hip				Sumc
	Scaled-generic		Scaled-closesta		Scaled-generic		Scaled-closest		Scaled-generic		Scaled-closest		Scaled-generic		Scaled-closest
	RMSD (%)	R2	RMSD (%)	R2	RMSD (%)	R2	RMSD (%)	R2	RMSD (%)	R2	RMSD (%)	R2	RMSD (%)	R2	RMSD (%)	R2
M1	20	0.99	14	0.98	55	0.64	18	0.92	32	0.86	16	0.97	25	0.83	11	0.96
M2	43	0.76	13	0.98	37	0.82	15	0.97	32	0.81	11	0.98	38	0.80	13	0.98
M3	31	0.90	15	0.99	40	0.79	20	0.97	36	0.91	21	0.94	49	0.87	10	0.97
M4	43	0.79	5	0.99	55	0.76	13	0.93	19	0.97	16	0.97	54	0.84	11	0.96
M5	87	0.81	9	0.99	56	0.75	20	0.99	39	0.92	9	0.99	31	0.82	11	0.99
F1	13	0.99	10	0.99	37	0.89	10	0.99	43	0.86	17	0.98	47	0.91	5	0.99
F2	47	0.70	35	0.96	35	0.96	14	0.90	26	0.88	22	0.94	52	0.85	10	0.94
F3	51	0.17	28	0.94	57	0.55	12	0.99	48	0.94	30	0.99	34	0.56	17	0.97
F4	40	0.76	17	0.95	44	0.75	11	0.93	37	0.83	13	0.95	52	0.78	10	0.94
F5	64	0.57	18	0.89	69	0.54	30	0.89	24	0.94	10	0.93	79	0.68	27	0.91
Mean	44	0.72	16	0.97	48	0.76	16	0.95	34	0.90	17	0.96	46	0.79	13	0.96
SD	21	0.23	9	0.03	11	0.14	6	0.04	9	0.05	7	0.02	15	0.10	6	0.02
p valueb			0.005				0.005				0.005				0.005

M and F designate male and female.

^aThe closest musculoskeletal model for scaling (scaled-closest) is derived from the multiple regression model with the minimum RMSD (min f(RMSD_d)) in joint reaction forces: for the ankle, min f(RMSD_d) = min (11.06 + 0.49 × Δmass_d + 7.66 × Δgender_d) ; for the knee, min f(RMSD_d) = min (5.32 + 1.00 × ΔLL_d + 0.38 × Δmass_d + 37.22 × Δratio_d + 7.75 × Δgender_d) ; for the hip, min f(RMSD_d) = min (9.60 + 0.38 × ΔLL_d + 0.10 × Δmass_d + 2.64 × Δgender_d); and for their sum, min f(RMSD_d) = min (7.40 + 0.16 × Δmass_d + 4.03 × Δgender_d + 0.16 × Δratio_d), where: Δgender_d indicates the difference in gender between the subject and the model (d), which is 1 when gender is different else is 0; Δmass_d, ΔLL_d and Δratio_d indicate the percentage difference in mass, limb length (LL) and the limb length to pelvis width ratio from the underlying dataset (d) to the modelled subject.

^bp value is from the Wilcoxon Signed Rank test between RMSDs from scaled-generic and scaled-closest models (α = 0.05).

^cRMSDs of the sum of joint reaction forces of ankle, knee and hip; R² is the mean R² in joint reaction forces of ankle, knee and hip.

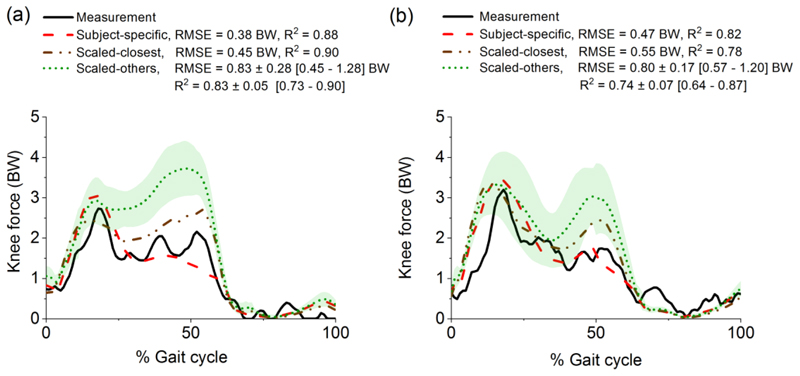
Based on the regression to the knee joint force prediction, the closest scaled model in the atlas was identified for subject DM in the “6th Grand Challenge Competition to Predict In Vivo Knee Loads”. It produced similar values as the subject-specific model for RMSE and R² when compared to the measured knee joint reaction force, as shown in Fig. 6 for two representative gait cycles. The RMSE from the closest model was lower than the RMSEs from all other ten models in the atlas.

Fig. 6.

Predicted knee joint reaction force, expressed in body weight (BW), using eleven models in the atlas compared to the experimental measurement (solid line) and the subject-specific prediction (dashed line) in two representative gait cycles: (a) DM_ngait1 and (b) DM_bouncy5. The subject-specific model of DM from Ding et al. [39] is freely available at http://www.msksoftware.org.uk/software/freebody. The scaled-closest model is identified based on the regression; the scaled-others are presented as mean (dotted line) and standard deviations (shaded area). The root mean square error (RMSE) and coefficient of determination (R²) are calculated by comparing the difference between the model prediction with the experimental measurement. The RMSE and R² from the scaled-others models are expressed as mean ± standard deviation [range].

IV. Discussion

Use of a single, scaled generic musculoskeletal model is unable to account for wide inter-individual variability in lower limb anatomy [27] – [29]. This study for the first time has demonstrated that the discrepancies from the scaled models are significantly correlated with the discrepancies in gender and anthropometric measurements of the underlying anatomical datasets when compared to a subject-specific model. The discrepancy in mass was the primary anthropometric predictor of the discrepancy in the ankle joint force prediction and the discrepancy of limb length was the primary anthropometric predictor of the discrepancies in knee and hip joint force predictions. After mass and limb length, the limb length to pelvis width ratio was found to be the third significant predictor: it accounted for an additional 3% of the variance of discrepancies at the knee. Therefore, these anthropometric measures should be taken into account and varied when creating a comprehensive lower limb anatomical atlas.

The differences in predicting the knee and hip joint forces are expected as there are known gender differences in pelvic shape [18], [49] and there is some evidence of gender differences at the distal femur [50]. Such differences are not accounted for by scaling of one unique gender model. These differences may promulgate throughout the whole lower limb force predictions through the action of biarticular muscles [51]. Our study has shown that these gender differences do not dominate differences in joint reaction force predictions, when compared to anthropometry, but do improve the fit of the regression of RMSDs by 5% at the ankle (p = 0.005), 3% at the knee (p = 0.013), 2% at the hip (p = 0.039) and 6% for their sum (p = 0.009).

Linear scaling of a dataset with same gender and similar anthropometry to the subject reduced discrepancies when compared to scaling of a generic dataset: discrepancies were reduced at the ankle joint from 44% to 16%, a 64% reduction (p = 0.005); at the knee joint from 48% to 16%, a 67% reduction (p = 0.005); and at the hip joint from 34% to 17%, a 50% reduction (p = 0.005). The reduction was most evident for subjects with lower body mass, for example, subject M5 showed a reduction of 89% at the ankle joint and 77% at the hip joint. As a demonstration of the use of the atlas, scaling of the closest model to one subject in the literature with an instrumented knee implant produced knee joint forces consistent with the measured knee joint forces (R² ≥ 0.78). The RMSE from the scaled closest model was comparable to the best ones that can be obtained from the subject-specific model. The results support our hypothesis. It is worth noting that the subject-specific model of DM predicted lower later-stance knee forces than the scaled closest model. This may be attributed the geometry differences between the artificial knee and the natural knee [52], [53]. Previous studies have found that muscle architecture scales with subject morphology, such as body mass and limb length [11]. The results of our study, however, suggest that the muscle attachments may not scale with these morphological parameters, highlighting the importance of having an anatomical atlas that far closer represents the subjects.

There are methodological differences between the generic and MR-based datasets which may affect the consistency of the atlas. First, joint centres and axes were measured using the functional method in [12] and measured based on joint geometry from the MR images. Additionally, the foot was maintained in plantar flexion position during the cadaveric measurement [12] and was in a more neutral position in the MR scanners. The MRI-based anatomical datasets showed a good consistency as indicated by the high coefficient of determination value of over 0.96 in joint reaction forces (TABLE VII).

Scaling using the closest anatomical model still produced a discrepancy of 16% in joint reaction force predictions, when compared to the subject-specific model. This discrepancy corresponds to a 0.37 BW difference for hip joint force during gait. In addition, the final regression model for the hip joint only accounted for approximately 33% of variance (adjusted R² = 0.333) of the discrepancy. This indicates that the linear scaling based on the gender and anthropometric similarity may not be adequate, especially for the hip joint force prediction. Recent studies have demonstrated a better estimation of muscle attachment sites by applying a morphing technique to the bone surface when compared to linear scaling [54], [55]. This technique could in future be applied to generate a larger, population-based dataset of subject-specific musculoskeletal models.

To facilitate the development of subject-specific musculoskeletal models, the entire anatomical atlas is accessible at http://www.msksoftware.org.uk, including segmented bone surfaces (STL files), bony landmark coordinates, joint centres, contact points, lines-of-action of muscles and ligaments, wrapping object parameters and muscle parameters. Subject-specific musculoskeletal models from the atlas implemented in FreeBody are available in the same repository. The fidelity of subject-specific musculoskeletal models was evaluated by comparing the predicted muscle activation against the experimental EMG of the same subject, and secondly, by comparing the calculated joint reaction forces against the instrumented implant measurements from other subjects in the literature. EMG patterns from eight muscles were comparable with the literature [56], [57] and the errors between muscle activations and EMG were comparable with other validation studies [28], [39]. Considerable differences were found between the higher calculated joint reaction forces with the measured joint reaction forces in the literature. This can be partially explained by the discrepancy between the artificial joint and the natural joint and subsequently, the discrepancy introduced in gait: a slightly higher walking speed and greater ground reaction force were found from our young healthy subjects and so a higher joint reaction force is expected. We acknowledge that improvements to the musculoskeletal geometry alone may not be sufficient to minimise the disagreement between model outcomes and true physiological loading in the musculoskeletal system. Other improvements in the literature focusing on taking greater account of realistic neuromuscular strategies have enabled better estimation of muscle activation and joint reaction force. These improvements include EMG-driven musculoskeletal models [58] – [60] and subject-specific synergy controls [61], [62].

There are some limitations to this study. First the muscle parameters including fibre length to muscle length ratio $(\frac{L_f}{L_m}),$ pennation angle (θ), and sarcomere length (L_s) were obtained from studies of elderly cadavers [10], [12]. Until now, there is no complete and comprehensive dataset measuring these parameters in vivo and it is known that uncertainty in these parameters can affect muscle force predictions significantly [63], [64]; they cannot be obtained from MRI. Second, MR images were acquired in the standardised position of subjects lying in the MR scanner, resulting in a muscle moment arm definition for that position only; the variation in muscle moment arm during dynamic and loaded conditions was not taken into account. Some studies have recently demonstrated the feasibility for physiological measurements of muscle moment arms over a range of joint motion [65], [66] and using this approach will provide a better representation of the musculoskeletal geometry during functional activities. Third, in our optimisation model, each muscle element was modelled with a constant strength and it was independent of any contraction dynamics associated with muscle length and velocity. For muscles that covered a large muscle attachment site, their strength was evenly distributed across the separate elements and the effect of this muscle decomposition was not corrected in the cost function in either the subject-specific model or the scaled model. Decomposition and muscle dynamics have been shown to affect the prediction of muscle forces [28], [67]. Finally, the errors quantified in the study were from healthy subjects during gait only and thus the effect of extrapolating these results to other activities and pathological subject should be investigated.

V. Conclusion

This study tested the hypothesis that linear scaling to a musculoskeletal model with gender and anthropometric similarity to the individual subject can produce similar results to the ones that can be obtained from a subject-specific model. A lower limb musculoskeletal anatomical atlas, consisting of datasets derived from MRI and a generic dataset from the literature, was developed; the discrepancies from scaled models were quantified where joint reaction forces from the personalised, subject-specific musculoskeletal models are considered as references; and finally, the use of the atlas was identified based on gender and anthropometric similarity. This method produced the lowest discrepancies when compared to the other linearly scaled models, thus supporting our hypothesis. Discrepancies of 16% in joint reaction force calculations remain, indicating that there is potential for further improvements. We have provided a new anatomical atlas that is publically available to accelerate the development and adoption of subject-specific musculoskeletal models.

Supplementary Material

This paper has supplementary downloadable material available at http://ieeexplore.ieee.org.