Quantitative Measurement of Cerebral Physiology Using Respiratory-Calibrated MRI

Abstract

Functional magnetic resonance imaging typically measures signal increases arising from changes in the transverse relaxation rate over small regions of the brain and associates these with local changes in cerebral blood flow, blood volume and oxygen metabolism. Recent developments in pulse sequences and image analysis methods have improved the specificity of the measurements by focussing on changes in blood flow or changes in blood volume alone. However, FMRI is still unable to match the physiological information obtainable from positron emission tomography (PET), which is capable of quantitative measurements of blood flow and volume, and can indirectly measure resting metabolism. The disadvantages of PET are its cost, its availability, its poor spatial resolution and its use of ionising radiation. The MRI techniques introduced here address some of these limitations and provide physiological data comparable with PET measurements. We present an 18-minute MRI protocol that produces multi-slice whole-brain coverage and yields quantitative images of resting cerebral blood flow, cerebral blood volume, oxygen extraction fraction, CMRO₂, arterial arrival time and cerebrovascular reactivity of the human brain in the absence of any specific functional task. The technique uses a combined hyperoxia and hypercapnia paradigm with a modified arterial spin labelling sequence.

Introduction

Functional magnetic resonance imaging (FMRI) is typically used to produce images and data showing relative signal changes in brain regions activated while performing a task or in response to a stimulus. These signal changes are typically based on the blood oxygenation level dependent (BOLD) approach, in which contrast arises from an amalgam of regional physiological phenomena that include changes in cerebral blood flow (CBF), changes in cerebral blood volume (CBV), and changes in oxygen extraction by the tissue. The non-quantitative and complex nature of the BOLD FMRI signal is one reason why the technique has rarely made the transition from research tool to clinical application. Conversely, positron emission tomography (PET) is capable of quantitative measurements of both glucose (using ¹⁸FDG) and oxygen (using ¹⁵O) metabolism, but due to its high cost and use of ionising radiation is rarely used clinically, particularly in the case of ¹⁵O. The gold standard for oxygen metabolism measurement in humans is provided by triple oxygen PET imaging (Ito et al., 2005). This method employs inhalation of ¹⁵O-labelled O₂ and CO as well as an injection of a bolus of ¹⁵O-labelled water. It enables the calculation of CBF, CBV, oxygen extraction fraction (OEF) from the arterial versus venous blood, and hence cerebral metabolic rate of oxygen consumption (CMRO₂). Due to the short half-life of ¹⁵O, a cyclotron is required on site to perform these measurements, thus increasing the cost and limiting the availability of ¹⁵O PET. As it involves a sequence of three scans, it also results in a significant dose of radiation being administered to the patient. A typical triple oxygen PET scan might consist of the sequential administration of C¹⁵O (5 minute acquisition 1 minute after an inhalation of 300 MBq), ¹⁵O₂ (20 minute inhalation of 7200 MBq, with data acquired after a 10 minute build up period) and H₂¹⁵O (20 minute infusion of 800 MBq with data acquired after a 10 minute build up period) (Smielewski et al., 2002). Thus this sequence takes at least 46 minutes and exposes the patient to a radiation dose of 8300 MBq.

It would be of considerable benefit to diagnostic imaging to develop MRI-based methodologies that offer comparable information to triple oxygen PET in similar or less time, at significantly lower cost, with greater availability and with no exposure to ionising radiation. In this study we propose a short paradigm for obtaining whole brain images of resting CBF₀, CBV₀, cerebrovascular reactivity (CVR) (both BOLD and CBF reactivity), arterial arrival time (AAT), OEF₀ (from which CMRO_2|0 may be calculated) and the theoretical maximum BOLD signal change (denoted by M). The subscript ‘0’ above refers to measurement of the relevant parameter during a baseline resting condition that does not correspond to any particular functional task.

The calibration of FMRI techniques has been previously demonstrated through a variety of methods. These have usually focused on the estimation of relative changes in blood flow, blood volume or oxygen metabolism at the site of activation in response to a stimulus or during a functional task. However, some methods have attempted to measure flow, volume or metabolism during a resting or non-active state. Approaches combining near-infrared spectroscopy (NIRS) with MRI have shown promise in measuring CMRO₂ (Tak et al., 2010), as have MRI techniques using ¹⁷O (Mellon et al., 2010; Zhu et al., 2009). While each of these methods has its own strengths, they all also have weaknesses, such as being limited to one slice, having a long scan duration, being only able to obtain global values rather than spatially resolved images, requiring specialised or expensive hardware or consumables that can limit availability, or requiring substantial prior information about baseline physiological parameters. A significant limitation of these methods is that each of them is only capable of obtaining one, or at most two, of the measurements listed above.

In the absence of pathology or abnormal physiology, the OEF tends to be very similar across all brain regions; this implies that variations in oxygen demand are generally accounted for by concurrent variations in blood supply. MRI techniques have been developed that measure a “whole brain” or global value for the OEF (Huppert et al., 2009; Lu and Ge, 2008; Qin et al., 2011; Van Zijl et al., 1998; Xu et al., 2009), which is valuable in healthy subjects and for developing or validating FMRI methods. However, in the presence of compromised vasculature, brain injury or tumours, these methods do not provide the regional information required for detailed diagnoses. Other methods that produce OEF images have been developed, but these require the venous CBV to be estimated and provide limited brain coverage (Bolar et al., 2011; He and Yablonskiy, 2007). In summary, there is a demonstrated need for a clinically viable MRI alternative to triple oxygen PET. To be suitable for diagnostic use with patients the method must be capable of producing quantitative images providing whole brain coverage, be performed quickly and non-invasively, and be cost effective.

Theory

BOLD FMRI (Ogawa et al., 1990) is the most commonly used FMRI technique, and thus it has been the focus of most of the efforts to achieve quantitation of physiological parameters. Methods involving alterations to the inspired gas content have proved to be quite effective in calibrating the BOLD signal. These approaches tend to be either based on CBF changes induced by altering the arterial partial pressure of carbon dioxide (PaCO₂) (Bulte et al., 2009; Davis et al., 1998; Hoge et al., 1999; Kastrup et al., 1999), or based on changes in venous saturation due to altering the arterial partial pressure of oxygen (PaO₂) (Chiarelli et al., 2007b). All of these techniques rely on estimating the size of the BOLD signal change that would be induced by the complete removal of deoxyhaemoglobin from the voxel of interest, yielding a map of the maximum theoretical BOLD signal change, denoted by the symbol M. This calibration constant was initially introduced in terms of BOLD signal and flow changes induced by hypercapnia (Davis et al., 1998), and was subsequently defined directly in terms of the total deoxyhaemoglobin (dHb) content of the voxel (Hoge et al., 1999). In this model the BOLD signal change is given by

$$\frac{\Delta \text{BOLD}}{{\text{BOLD}}_0}=\text{TE}\cdot A\cdot {\text{CBV}}_0\cdot {[\text{dHb}]}_{{\text{v}}_0}^{\beta }\left(1-\left(\frac{\text{CBV}}{{\text{CBV}}_0}\right){\left(\frac{{[\text{dHb}]}_{\text{v}}}{{[\text{dHb}]}_{{\text{v}}_0}}\right)}^{\beta }\right)$$ (1)

where A and β are constants that depend on the field strength and vessel sizes in the tissue. CBV is the non-arterial cerebral blood volume (approximately 70% of the total cerebral blood volume), and [dHb] is the concentration of deoxyhaemoglobin in the veins. Considering the maximum signal that can be achieved by the removal of all dHb from the tissue sample, the maximum possible BOLD signal change is given by

$$M=\text{TE}\cdot A\cdot {\text{CBV}}_0\cdot {[\text{dHb}]}_{{\text{v}}_{0.}}^{\beta }$$ (2)

This theoretical framework was initially developed under the assumption that only extravascular BOLD effects contribute to the signal changes; however, the model provides a reasonable approximation to more complex ones that account for other compartments (Buxton et al., 2004; Griffeth and Buxton, 2011) (see Discussion below).

The value of M may be measured by means of a mild hypercapnia stimulus such as performed by Davis et al (Davis et al., 1998) or Hoge et al (Hoge et al., 1999). The model is developed from Eq. 1 by replacing the relative CBV term with a relative CBF term via the Grubb power law relationship (Grubb Jr et al., 1974) and thereby introducing the Grubb coefficient α. The relative [dHb] term can also be substituted by a relative CBF term through Fick's mass conservation principle between oxygen delivery and consumption thereby introducing a CMRO₂ term. The full form of the hypercapnia calibration model, including a term for metabolic changes, is thus given by

$$\frac{\Delta \text{BOLD}}{{\text{BOLD}}_0}=M\left(1-{\left({\frac{{\text{CMR}}_{{\text{O}}_2}}{\text{CM}{\text{R}}_{{\text{O}}_2}|}}_0\right)}^{\beta }{\left(\frac{\text{CBF}}{{\text{CBF}}_0}\right)}^{\alpha -\beta }\right)$$ (3)

An alternative means of determining the value of M by means of a hyperoxia stimulus has also been developed (Chiarelli et al., 2007b). The equivalent form of the hyperoxia calibration model is

$$\frac{\Delta \text{BOLD}}{{\text{BOLD}}_0}=M\left(1-{\left(\frac{\text{CBF}}{{\text{CBF}}_0}\right)}^{\alpha }{\left(\frac{{[\text{dHb}]}_V}{{[\text{dHb}]}_{V0}}+\frac{{\text{CBF}}_0}{\text{CBF}}-1\right)}^{\beta }\right)$$ (4)

This is the full model, which includes terms to account for flow changes induced by the (modest) vasoconstrictive effect of hyperoxia.

In its original formulation the hyperoxia method of determining M was severely limited by the need to assume an OEF value in order to calculate [dHb] from the end-tidal oxygen measurement. This restricted its use to healthy subjects at best, and introduced significant errors at worst. It is, however, this very feature that is exploited here. An experiment that measures M independently, and includes a hyperoxia stimulus, may use the hyperoxia calibration model to instead calculate the OEF. The deoxyhaemoglobin terms in the hyperoxia model were originally estimated from measurement of the end-tidal partial pressure of oxygen (P_ETO₂), which is closely correlated with the arterial partial pressure (PaO₂) from which the arterial saturation (SaO₂) and arterial content (CaO₂) may be calculated.

The relative change in deoxyhaemoglobin concentration [dHb] in Eq. 4 is equivalent to the relative change in venous saturation if haematocrit (Hct) and venous CBV remain constant. The OEF is defined as the difference between the arterial and venous oxygen saturations (SaO₂ – SvO₂). It has been shown that the net extraction of oxygen remains constant between normoxic and hyperoxic conditions as long as there is no significant change in CBF (Mark et al., 2011; Xu et al., 2011a), thus (CaO₂ – CvO₂) is constant. As we can calculate CaO₂ under both normoxic and hyperoxic conditions, the constant (CaO₂ – CvO₂) is the only unknown quantity. Eq. 4 can be rearranged to calculate (CaO₂ – CvO₂), and this can then be subtracted from the normoxic CaO₂ to produce a value for CvO₂, and therefore the SvO₂ and OEF (see Appendix A).

Thus, an imaging paradigm that combines periods of hypercapnia and periods of hyperoxia while measuring both BOLD signal changes, CBF changes and end-tidal oxygen values would enable the production of voxel-by-voxel values for M, and produce images of the resting, normoxic OEF.

Although single-TI arterial spin labelling methods can in theory be used to estimate CBF (Wong et al., 1998), the use of multiple inversion times (multi-TI) provides a more robust calculation of resting CBF, as well as yielding an estimate of arterial arrival times (AAT) in each voxel (MacIntosh et al., 2010; Wong et al., 1997). As the calculation of OEF would not be affected by the use of a multi-TI sequence, we elected to use such a sequence with sufficient BOLD weighting preserved by the removal of background signal suppression pulses and a lengthening of the usual TE. The generated maps of resting CBF₀ and OEF₀ are sufficient to estimate the CMRO₂|₀ from the equation used by Xu et al. (Xu et al., 2009)

$${\text{CMRO}}_2=\text{CBF}\cdot (\text{OEF})\cdot {\text{C}}_{\text{a}}$$ (5)

where CBF is in mL/100 g/min, and C_a is a constant representing the amount of oxygen molecules that a unit volume of blood can carry. CVR may be calculated from either the CBF or BOLD response to the hypercapnia stimulus with measurement of the end-tidal CO₂ values.

As mentioned above, the Davis model (Davis et al., 1998) is based directly on the original Ogawa model (Ogawa et al., 1993), which assumed that the BOLD signal was entirely extravascular. This has subsequently been shown not to be true. At 3 Tesla the proportion of extra- to intravascular signal is approximately 2:1 in grey matter (Lu and Van Zijl, 2005). The exact nature of the signal source is effectively absorbed by the A and β terms in Eq. 1. As such, provided all signals involved in the measurement and calibration models are all weighted equally, the physiological terms should be interpretable as intended.

Data from an R₂*-weighted imaging sequence incorporating a mild hyperoxia stimulus can also be used to produce a cerebral blood volume (CBV) weighted image (Bulte et al., 2007a). As with all R₂*-weighted CBV techniques, this method suffers from the problem of contamination from extravascular signal sources (Newman et al., 2006), and so the resulting image is not truly quantitative at 3 Tesla, however the data will show relative regional variations in CBV.

Methods

Ethical approval for this study was obtained from the UK Central Office of Research Ethics Committees (COREC). 10 healthy volunteers were recruited (4 female, mean age 31±4 years); however only 8 completed the study as 2 subjects (1 male, 1 female) experienced anxiety when breathing through the mask in the magnet bore. The subjects were scanned at the FMRIB Centre on a 3 Tesla Siemens Verio MRI scanner (Siemens, Erlangen, Germany) equipped with a transmit body coil and a 32-channel receive head coil, using foam inserts to minimise head motion. A pseudo-continuous arterial spin labelling (PCASL) sequence was utilized (Dai et al., 2008) with a gradient-echo echo-planar imaging (EPI) readout (TR = 3.75 s, TE = 22 ms, 6/8 k-space, PCASL module flip angle 20°, EPI readout flip angle 90°). Twenty-three axial slices in ascending order (3.2×3.2×5 mm³ voxels, with a 10% inter-slice gap of 0.5 mm) were prescribed. A labelling duration of 1.4 seconds was used, and five different post labelling delay (PLD) times (0.64, 0.792, 0.896, 1.0 and 1.152 seconds) were adopted according to an optimised sampling schedule (OSS) (Xie et al., 2008). A field map with the same resolution as the PCASL sequence was obtained in order to correct for EPI distortion. A high-resolution structural image was acquired to enable registration of functional data and generation of anatomically derived masks (MPRAGE (Mugler and Brookeman, 1990): repetition time/inversion time/echo time = 1,778/900/4.4 ms, 1.7×1.7×2.0 mm³).

The location of the labelling plane for the PCASL sequence was determined by performing a time-of-flight scan at the base of the brain. The labelling plane was prescribed approximately halfway between the upper and lower contortions of the vertebral arteries, so that the plane was perpendicular to both the vertebral and carotid arteries.

The images were pre-processed using FSL software tools for motion correction, slice timing correction, and brain extraction (http://www.fmrib.ox.ac.uk/fsl) (Smith et al., 2004) before being high-pass filtered (510 s) and spatially smoothed using a Gaussian kernel (full-width half-maximum = 5 mm). The functional data acquired from each scan were registered to the subject’s own structural image and then transformed into MNI152 space (Montreal Neurological Institute) (Mazziotta et al., 2001) using FLIRT (Jenkinson and Smith, 2001).

The ~18 minute (288 volumes) paradigm consisted of delivering medical air via a sealed facemask (8920 Series, Hans Rudolph Inc., Kansas City, MO, USA), alternating with 2×2 minute blocks of 4% CO₂ in air and 2×3 minute blocks of 50% oxygen, balance nitrogen. This was accomplished by altering the proportion of input gases delivered to the mixing chamber (medical air, 100% oxygen and 5% CO₂ in air). The paradigm started with 30 seconds of medical air. Each of the hypercapnia blocks was followed by 1 minute of medical air, whereas the two hyperoxia blocks were followed by 2.5 minutes and 3 minutes of medical air, respectively (Fig. 1). The end-tidal levels of oxygen take approximately 2 minutes to reach a plateau with a FiO₂ of 0.5. In order to use the hyperoxia method of CBV calculation, sufficient data must be obtained from this steady-state period. This was not required from the hypercapnia stimulus. Thus the periods of hyperoxia were longer than the periods of hypercapnia.

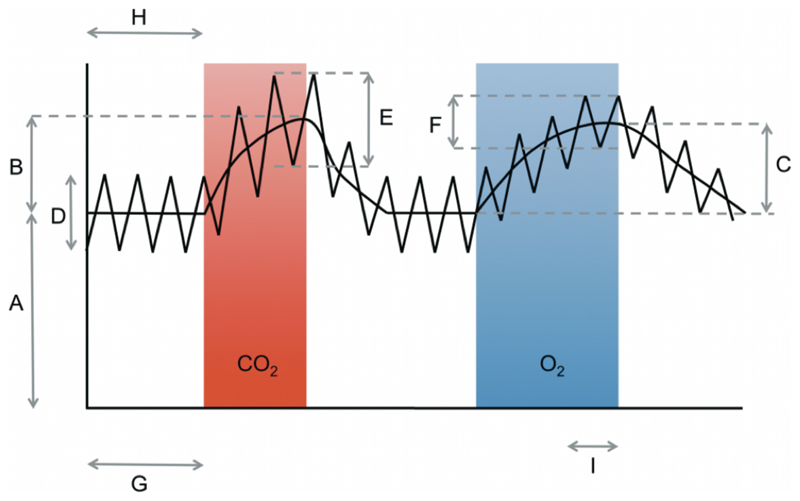
Fig. 1.

Schematic of the stimulus paradigm

Inspired gases were delivered via a multi-tube system that mixed the gases in a small chamber 30 cm from the subject’s mouth. The total delivery rate was 30 L/min, with excess gases passing into a flood chamber (a 2 m long, 10 cm diameter, open-ended tube), into which the expired gases were also exhaled. Owing to the high delivery rate, this chamber allowed an accumulation of the supplied gases to build up for inhalation, and yet provided an exhaust path that did not produce significant re-breathing of exhaled gases. Monitoring of the inspired and expired gases was performed through a port in a disposable filter directly connected to the facemask. This simple method of altering the inspired gas content was selected over more sophisticated techniques (Mark et al., 2011; Slessarev et al., 2007) due to the simplicity and availability of the equipment, thus being more appropriate for use in clinical environments with patients.

The inspired CO₂ level was selected in order to provide a robust stimulus and CBF response with minimal discomfort for the subject. For hyperoxia an inspired fraction of oxygen (FiO₂) of 0.5 was selected in order to minimise any blood flow reduction induced by the hyperoxia (Bulte et al., 2007b), and to minimise magnetic susceptibility artefacts in the frontal regions due to the mildly paramagnetic nature of molecular oxygen. The reduction in CBF induced by the hyperoxic stimulus is obtained from the PCASL data and incorporated into the model. Gases were monitored at 20 Hz using Biopac CO₂100C and O₂100C modules connected to a BIOPAC MP150 base unit (Biopac, Goleta, CA, USA). End-tidal (ET) values were extracted using code developed in Matlab (MathWorks, Natick, MA, USA).

The MR signal responses to the respiratory stimuli in the PCASL data were analysed by fitting a standard general linear model to the data (FEAT, http://www.fmrib.ox.ac.uk/fsl/). The BOLD time course was modelled by convolving the paradigms for the hypercapnia and hyperoxia blocks with a gamma-variate function with a mean lag of 30 s and a standard deviation of 30 s to account for the slow response of the arterial partial pressures to the changes in inspired fractions (Poulin et al., 1996). The PCASL tag/control variations were modelled explicitly by a series of alternating 0’s and 1’s with a frequency of 3.75 s. The ratio of the parameter estimate (PE) of the baseline PCASL tag/control time course and the PE of the interaction between the PCASL tag/control and the BOLD time courses corresponds to the fractional change in CBF (Fig. 2). The BOLD and CBF signal changes associated with the hypercapnia stimulus were then used to calculate a value for M using the method detailed by Hoge et al (Hoge et al., 1999). The value of the Grubb coefficient α used in the calculation of M was 0.2 to represent the non-arterial blood volume (Chen and Pike, 2010). The value of the parameter β used was 1.3, as has previously been used at 3 T (Bulte et al., 2009).

Fig. 2.

Schematic of the data and the sections from which each relevant aspect is extracted (not to scale)

As there is growing evidence that inspired CO₂ causes a modest reduction in CMRO₂, the possibility that hypercapnia is not a purely isometabolic stimulus was incorporated into the model. Xu et al (Xu et al., 2011b) found an average decrease of 13.4% with a 5% CO₂ stimulus, and so a decrease in CMRO₂ of 10% during the 4% CO₂ stimulus was assumed in our calculations. This correction has rarely been considered and may not be critical, however it was thought prudent to allow for the possibility that hypercapnia may affect the metabolism. The effect of this correction on the final values calculated is considered in Appendix B.

During the 2 minute blocks of 4% CO₂, an increase in arterial flow velocity and a resultant decrease in the inversion efficiency of the PCASL labelling scheme may arise due to the vasodilatory effects of CO₂. The method proposed by Aslan et al. (Aslan et al., 2010) was employed to measure the PCASL inversion efficiency at rest (before beginning the main experiment) and during a 4% CO₂ stimulus (after the main experiment). In this method, whole brain average blood flow (mL/100g/min) is measured separately using both phase contrast (PC) velocity MRI (integrated over the main feeding vessels to the brain and divided by brain volume) and single-TI PCASL. The inversion efficiency is calculated from the ratio of PCASL whole brain average blood flow to PC whole brain average blood flow. PC velocity MRI was performed at the position of the PCASL labelling plane with the following parameters: single slice, voxel size = 0.5×0.5×1.5 mm³, TR/TE = 22/3.6 ms, flip angle = 18°, maximum velocity encoding = 80 cm/s. The single-TI PCASL acquisition was set up identically to the multi-PCASL sequence described above and had a single PLD of 1.525 seconds. Estimating both the resting block (0.92 ± 0.05%) and CO₂ block (0.83 ± 0.07%) inversion efficiencies in this manner meant that the PCASL time series could be normalised for this stimulus-dependent change in inversion efficiency before being analysed.

BOLD-weighted images were produced by averaging adjacent PCASL tag and control images. Each image was averaged with both its predecessor and the subsequent image to maintain the same effective temporal resolution. The BOLD signal change during the plateau of the hyperoxia stimulus (the final 1 minute of the 3-minute stimulus) and the BOLD signal during the normoxic, normocapnic periods in both tissue and venous voxels were used to calculate the resting CBV (Bulte et al., 2007a). A number of venous reference voxels were extracted automatically to reduce both operator bias and the influence of noise that is inherent when using only one calibration voxel. Initially, a large volume of interest (VOI) (8×8 pixel in-plane) was defined in the descending portion of the posterior sagittal sinus. All voxels within the VOI (with greater than zero baseline signal) were used to create an average reference time-course, from which an initial estimate of CBV₀ was calculated. In order to focus the reference VOI on the macrovascular voxels (generally those contained within the sagittal sinus) the CBV map was masked to select the initial reference VOI, and then any voxels that lay outside of the brain (noting that the sagittal sinus itself is defined as being part of the brain) were also removed. The top 1% of the remaining CBV values were assigned as the new reference voxels. An average reference time-course was again created, from which the final CBV₀ map was calculated.

Fig. 2 is a schematic of the data obtained and illustrates how each portion of the data was used for the calculations. The curved line shows the BOLD data, and the zigzag line shows the original PCASL tag/control data. From this diagram the BOLD response is B/A for the CO₂ epoch and C/A for the O₂ epoch. The CBF response is E/D for the CO₂ epoch and F/D for the O₂ epoch. The sections of BOLD data used for the normoxic period and the hyperoxic period for the CBV calculation were H and I, respectively, and G was the period of the PCASL data used for the multi-TI calculation of the resting CBF.

These data are sufficient by themselves to create an OEF image. However, by using a multi-TI PCASL sequence, one can also produce maps of resting CBF and AAT. The nonlinear model for continuous ASL time series proposed by Buxton (Buxton et al., 1998) was fitted to the multi-TI PCASL data from the resting blocks (Fig. 2) using a variational Bayesian inference approach. This method has been shown to provide estimates of CBF and AAT with increased sensitivity when compared to nonlinear least squares fitting approaches (Chappell et al., 2009). Fixed T1 values for arterial blood and tissue at 3 T of 1.6 s and 1.3 s respectively, and a bolus duration, τ, equal to the PCASL tagging duration (1.4 s) were used. Two calibration EPI readout scans were acquired in order to calculate the blood equilibrium magnetization, M_0,blood, for the subsequent quantification of CBF in absolute units (mL/100g/min). Firstly, a calibration image with the same TR/TE/TI as the PCASL acquisition but with no spin labelling preparation was acquired. The equilibrium magnetization of cerebrospinal fluid (CSF) was measured from this image and the relative proton density ratio of CSF to blood (Herscovitch and Raichle, 1985) was used to infer M_0,blood (note that this parameter is unrelated to the maximum BOLD signal change). A second calibration image was acquired using the body transmit/receive coil to correct for the uneven sensitivity profile of the 32-channel head receive coil. The CBF₀ maps were also corrected for subject-specific inversion efficiency as described above. CMRO₂ images were created using Eq. 5 from the OEF₀ and CBF₀ images and a value for C_a of 833.7 μmol O₂/100 mL blood (purely for consistency with Xu et al (Xu et al., 2009)). Grey matter masks were created from each subject’s structural image using FAST (Zhang et al., 2001), and all voxels in these masks were averaged for each parameter.

Results

The data for one subject were excluded from the analysis as the individual’s BOLD and CBF response to the hypercapnia stimulus was negligible, resulting in an implausibly low estimate for M. It is assumed that the subject’s mask was not sealed to their face properly; resulting in significantly lowered inspired CO₂ levels.

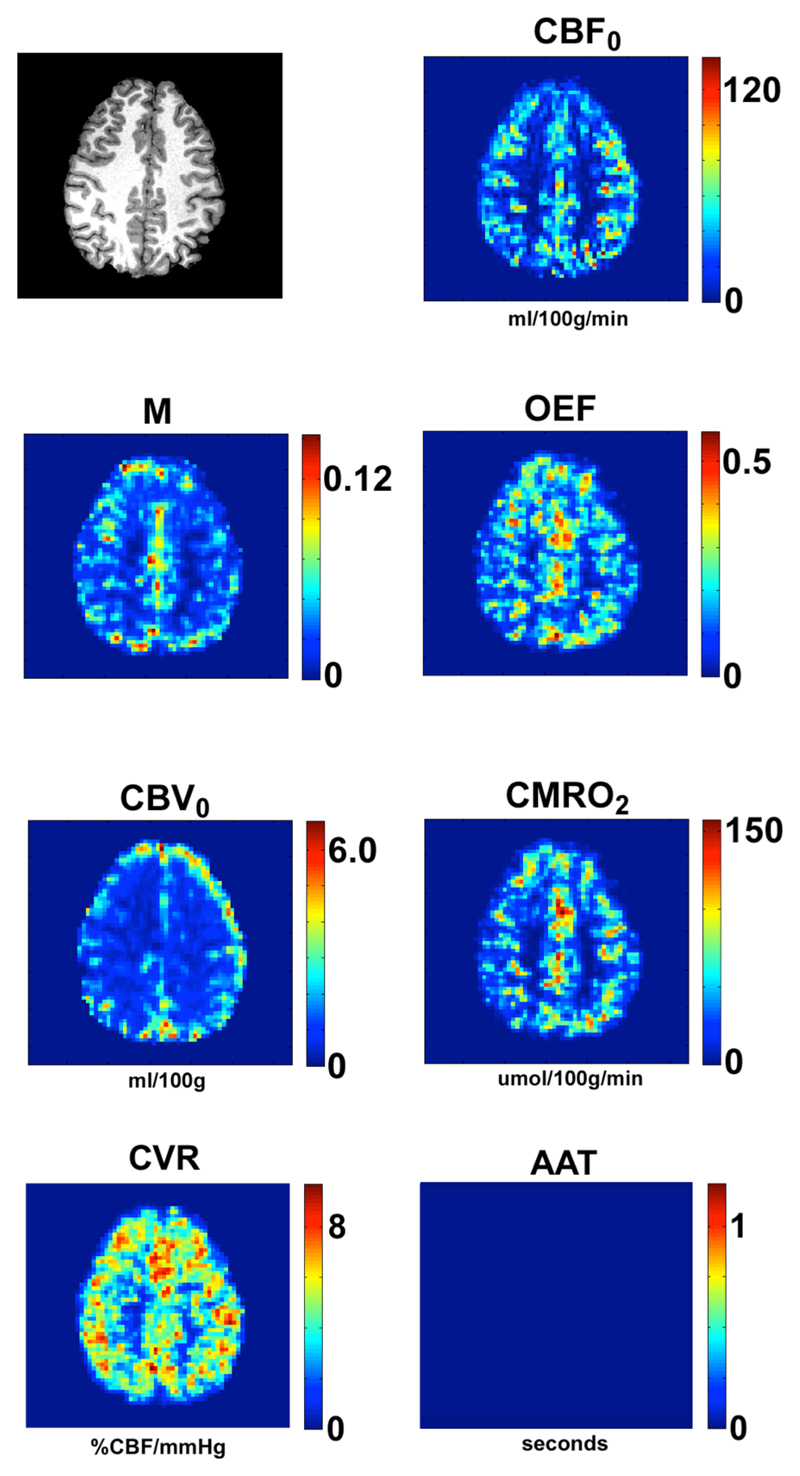
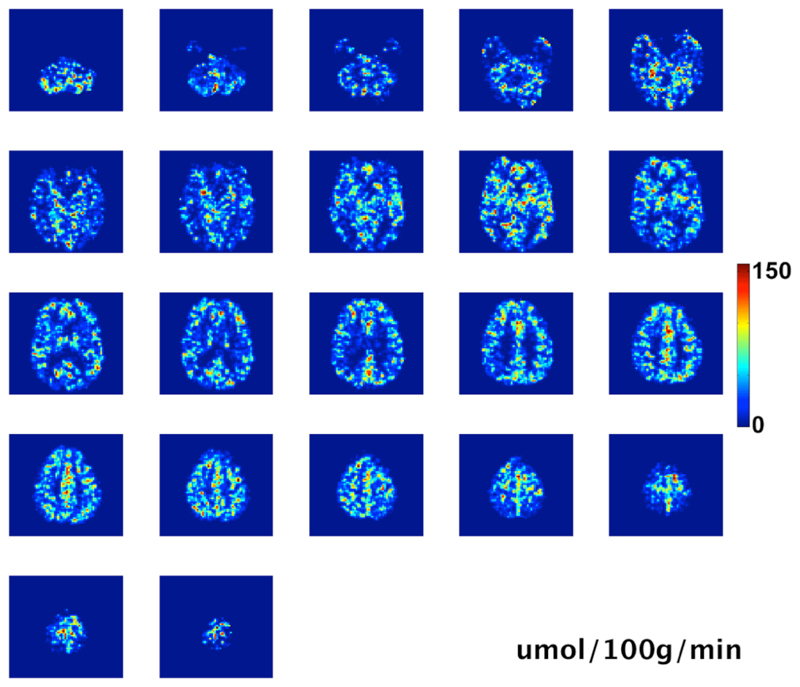
Fig. 3 shows the results from a single slice from a representative subject. The colour scales are independent and are in units of mL of blood/100 g of tissue/min for the CBF, mL of blood/100 g of tissue for the CBV, and μmol of oxygen/100 g of tissue/min for the CMRO₂. The scale for the OEF image is a fraction (range 0 to 1), and for the maximum BOLD value is in fractional change in signal from baseline. Thus both these latter measures are unitless. The CVR image shown was produced from the ASL CBF response to the CO₂ stimulus, however it would also be possible to produce a BOLD CVR map from the tag and control averaged data. The CVR map is in units of %ΔCBF/mmHg (ΔPET-CO₂). A blank square is shown in place of an AAT map to indicate that such a map can be produced from the technique if the correct post-labelling delay times are employed. Fig. 4 shows all slices of the CMRO₂ image for the same subject as shown in Fig. 3. Table 1 shows the mean values in grey matter for the 8 subjects that completed the study and the group means and group standard deviations, however the group values in the last row are only from Subjects 2 through 7. The data from Subjects 1 and 8 were considered outliers due to issues with the respiratory stimuli that became apparent during the analysis (see Discussion below).

Fig. 3.

Results from a single slice, from a representative subject. Units are in mL/100g/min for CBF, mL/100g for CBV, μmol/100g/min for CMRO₂, %ΔCBF/mmHg ΔPETCO₂ for CVR, and seconds for AAT. The AAT results are not shown, please see the main text.

Fig. 4.

All slices of the CMRO₂ data for the same subject as shown in Figure 3. Units are μmol/100g/min (empty top slice omitted)

Table 1.

Mean grey matter values ± the standard deviation across the ROI for all subjects, and group means ± standard deviation of the means for all subjects, and for subjects 2 to 6 (The subjects marked with a * were excluded from the mean group values in the bottom row)

Subject	CBF (mL/100g/min)	M	OEF	CMRO2 (μmol/100g/min)	CVR %ΔCBF/mmHg	CBVν (mL/100g)
1*	43.4±26.1	0.057±0.086	0.66±0.41	223±206	3.62±4.24	3.01±2.59
2	44.0±31.1	0.084±0.122	0.41±0.25	190±180	5.61±5.29	3.27±2.80
3	38.3±28.3	0.056±0.079	0.31±0.22	122±124	4.07±4.77	3.27±2.81
4	54.1±35.1	0.064±0.084	0.33±0.22	161±150	4.44±4.67	3.44±2.64
5	32.7±31.3	0.066±0.095	0.32±0.23	115±156	4.81±4.75	2.01±2.16
6	37.1±26.5	0.065±0.101	0.38±0.24	144±144	6.83±5.31	2.30±2.22
7*	55.8±43.9	0.042±0.065	0.25±0.22	132±165	9.36±3.25	2.46±2.52
Mean ± s.d. (inc. *)	43.6±8.7	0.062±0.01	0.38±0.14	155±39	5.53±2.0	2.82±0.56
Mean ± s.d. (exc. *)	41.3±8.3	0.067±0.01	0.35±0.05	146±30	5.15±1.1	2.86±0.65

Discussion

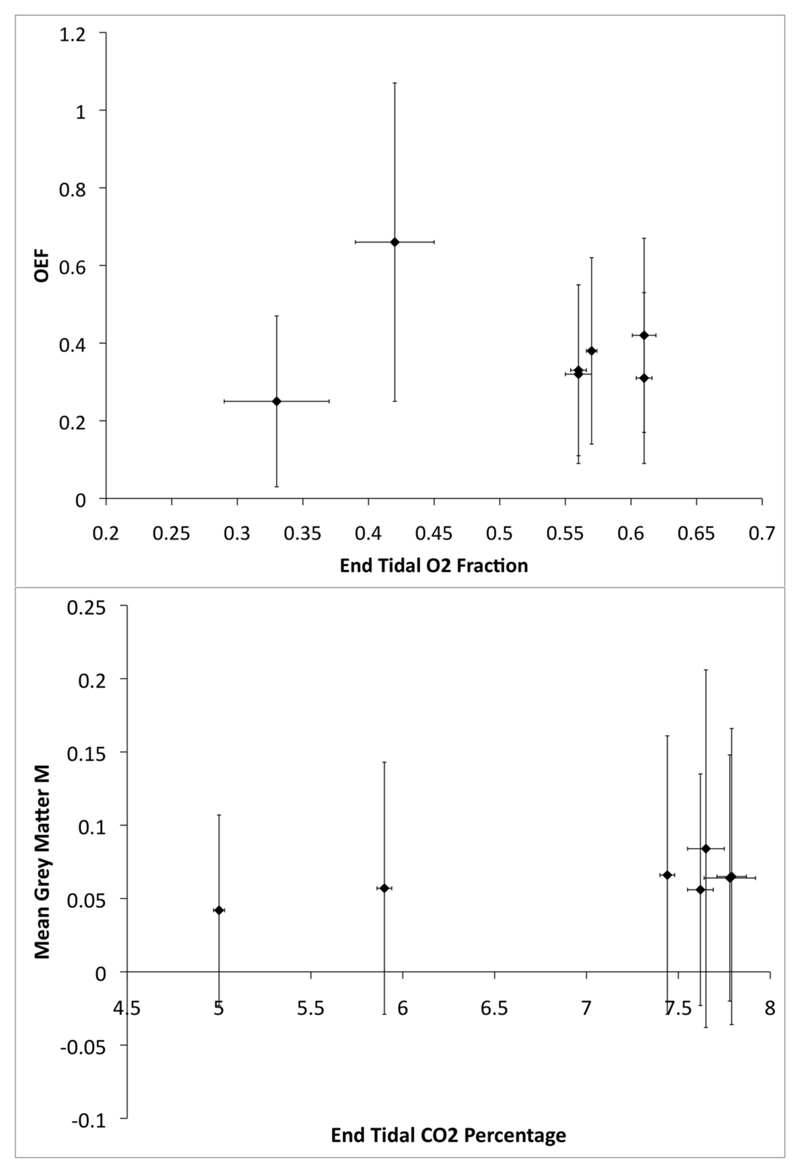
The images produced show values for each of the parameters within expected normal ranges, and are comparable to values determined by both PET and other MRI methods as shown in Table 2 (Ito et al., 2004; Jain et al., 2010; Knutsson et al., 2010; Van Zijl et al., 1998; Xu et al., 2009) and Table 3 (Gauthier et al., 2011; Kastrup et al., 2001; Mandell et al., 2008; Mark et al., 2010). They also depict structures resembling the grey/white matter distributions expected. The results from two of the subjects appeared to be outliers, as OEF values of 0.66 and 0.25 seem unlikely. The MR parameters seem to be similar, however an analysis of the measured peak end-tidal oxygen levels during the hyperoxia stimuli showed that these two subjects achieved only very low levels of hyperoxia with much higher variability than the other subjects (see Fig. 5.), and thus the BOLD signal change induced would be much lower, resulting in a poorer signal-to-noise ratio for these subjects. It may be significant that the two outliers and the subject with the unreliable M measurement were all female and quite petite, this might have caused problems with the mask fitting tightly over their faces, or because the dead-space in the gas delivery system was relatively larger compared to their tidal volume. This highlights the need to ensure adequate delivery of oxygen and carbon dioxide to the subjects. We are trialling the use of nasal cannula to effectively remove the incidence of subject stress, mask leakage and dead-space issues.

Table 2.

PET and MRI measurements of physiological parameters for comparison with the current study.

Study	CBF (mL/100g/min)	OEF	CMRO2 (μmol/100g/min)	CBV (mL/100g)
Ito 2004	44.4±6.5	0.44±0.06	129.6±19.6	3.8±0.7
Jain 2010	44.4±1.2	0.35±0.01	123±4
Knutsson 2010	44±10
Xu 2009	43±7.1		132.1±20.0
Van Zijl 1998	46	0.359	137
Lu 2008		0.352± 0.063
Bolar 2011	56±8	0.26±0.02	125±15

Table 3.

Values of M from (Gauthier et al., 2011), adjusted to a TE of 22ms and expressed as fractions. Values of CVR measured with ASL and hypercapnia from 3 studies and the mean of these.

	M		CVR %ΔCBF/mmHg
Bulte 2009	0.039	Mandell 2008	5.70
Ances 2008	0.042	Kastrup 2001	6.8±3
Ances 2009	0.048	Mark 2010	3.35±1.63
Chen and Parrish 2009	0.049
Chiarelli 2007	0.051
Ances 2009	0.054
Gauthier 2011	0.070
Lin 2008	0.077
Leontiev and Buxton 2007	0.081
Perthen 2008	0.085
Mean±s.d.	0.060±0.017		5.3±1.8

Fig. 5.

(Top) Plot of calculated OEF values against the measured mean end-tidal oxygen levels (fraction) during the 2-minute plateaus of the hyperoxia stimuli. (Bottom) Plot of calculated M values against the measured end-tidal carbon dioxide levels (percentage) during the peak of the hypercapnia stimuli. Error bars are ± 1 standard deviation

It is worth noting that within white matter, M relates to the signal change expected with the reduction of dHb to zero, and is not related to the potential signal associated with any conventional FMRI task. The M values reported here are at a shorter echo time than is normally used for BOLD FMRI at 3T, and so would be expected to be slightly lower than those reported with longer echo times. The expected range of M values is itself a contentious area (Chiarelli et al., 2007a) and careful consideration is needed when interpreting these data. As well as regional variability, it has been suggested that there may be inter-session variability within subjects, and the possible effects of the respiratory challenges themselves may be sources of error. The standard deviations in the M value calculated across the grey matter for each of the subjects is quite large (Fig. 5). This is most likely a result of regional variations, the inclusion of non-grey matter voxels in the masks, and partial volume effects. The use of smaller ROIs based on functional areas would likely reduce the level of variance. As each calculation in the models was performed voxel by voxel, and the values for the grey matter shown in the tables are calculated using a mask from each data set, these effects will not propagate.

There is mounting evidence that high levels of hypercapnia suppresses CMRO₂ (Xu et al., 2011b; Zappe et al., 2008) and so we have tried to minimise the levels of hypercapnia and have also incorporated an assumed modest reduction in CMRO₂ during hypercapnia into the models. However, as only an estimate of this effect was used, this may cause some error. Similarly, high levels of hyperoxia are known to reduce blood flow (Bulte et al., 2007b), and estimates of this effect were included in the calculation of the OEF. There may also be an effect on the CMRO₂ due to hyperoxia that may need to be taken into account (Xu et al., 2011a), if this is indeed shown to be a significant effect, the assumptions made in Eq. 4 and the equations in Appendix A are no longer valid and an appropriately altered model would be needed. Models can be produced which explicitly account for changes in the physiology beyond those desired (Gauthier et al., 2011). As the magnetic properties of oxygen differ from nitrogen, an increase in the inspired oxygen fraction can cause a change in magnetic susceptibility artefacts in the images (particularly in the frontal sinuses), and thus using minimal oxygen levels is beneficial (Pilkinton et al., 2011).

Limitations

The Davis model (Davis et al., 1998) is not the only model of BOLD signal contrast, and is known to have limitations. It is based on a much-simplified model of physiology and primarily considers the extra-vascular BOLD signal. The adaptation of the analysis for use with more sophisticated models (Gauthier et al., 2011; Lu et al., 2004; Obata et al., 2004; Stephan et al., 2007) could potentially improve the technique. However, the Davis model, despite its limitations, has been shown to be remarkably robust, and produces results that are quantitatively comparable to the other models (Buxton et al., 2004).

A potential limitation of this technique is the assumption that the (CaO₂ – CvO₂ difference) remains constant under hyperoxic conditions. Although this is a reasonable assumption in healthy individuals, there is a high likelihood that in ischaemic regions the net oxygen extraction would be greater during hyperoxia. The exact effect of this on the calculation of the OEF would need to be carefully modelled and patient data would ultimately need to be collected to investigate the degree of error this will introduce.

The OEF image shows an apparent difference between grey and white matter regions. It is suspected that this is due mainly to the SNR difference between grey and white matter for the PCASL sequence. Since the ASL signal from white matter at 3T is significantly lower than from grey matter the values of OEF have a lower SNR and greater variability. In spite of this, the OEF images appear quite similar to PET images (Ito et al., 2004).

The multi-TI PCASL method has the advantage of quantifying both CBF and AAT. However, the five post-labelling delay times used in the multi-TI ASL sequence, ranging from 0.64 to 1.152 seconds, were selected using an optimised sampling schedule (Xie et al., 2008) that was focused solely on accurate CBF quantification. The PLDs used appear not to be optimal for AAT quantification, particularly since the combination of labelling time and PLDs used primarily sample the outflow portion of the ASL kinetic curve. As a result, the AAT images produced showed neither the regional variability nor structure that might be expected. It would be expected that a protocol that better sampled the arrival of the PCASL bolus would yield more robust AAT maps. Data from resting healthy volunteers were used for the PLD optimisation, which, whilst appropriate for the cohort considered here, might be sub-optimal in a patient population. In future experiments, it is hoped that a real-time feedback optimisation method that would be sensitive to subject-specific and physiology-specific changes in the ASL kinetic curve can be implemented.

The current method of venous voxel selection for the CBV calculation is susceptible to partial volume effects as there is no guarantee that the selected voxels are completely enclosed within a vein. This could lead to an over-estimation of CBV₀, as the reference values will be artificially low (containing both blood and tissue/CSF signal).

Measurements of CBV using an intravascular contrast agent and an R₂*-weighted sequence suffer from contamination of the signal by extravascular effects. This is true of the hyperoxia method just as it is for gadolinium-based techniques (Newman et al., 2006). At 3T this will be more of a problem than at lower fields, and will be even worse at 7T. As the hyperoxia method of CBV measurement is only obtaining contrast in non-arterial vessels, the CBV measured should be approximately 70% of the total CBV.

Conclusions

In summary, we have presented a method for measuring fundamental cerebral physiological parameters using MRI with a combined hyperoxia and hypercapnia stimulus. The values measured are absolute rather than relative changes or responses to specific cognitive or sensory stimuli. These types of measurements are comparable to those obtained with PET imaging, but are obtained at a considerably lower cost, using more widely available scanner technology and without the need for exposure to ionising radiation. This is the first MRI method that produces total brain coverage, moderate resolution, quantitative images in a short enough time to be clinically viable and using a passive stimulus that will be tolerated by the majority of subjects.