Modelling the Epidemiology of Infectious Diseases for Decision Analysis

Abstract

The number of economic evaluations related to infectious disease topics has increased over the last 2 decades. However, many such evaluations rely on models that do not take into account unique features of infectious diseases that can affect the estimated value of interventions against them. These include their transmissibility from infected to susceptible individuals, the possibility of acquiring natural immunity following recovery from infection and the uncertainties that arise as a result of their complex natural history and epidemiology. Modellers conducting economic evaluations of infectious disease interventions need to know the main features of different types of infectious disease models, the situations in which they should be applied and the effects of model choices on the cost effectiveness of interventions.

1. The Importance of Infectious Disease Models in Pharmacoeconomics

The number of economic evaluations related to infectious disease topics has gradually increased over the last 2 decades, with a database search suggesting that they may now account for around 13% of the literature on model-based economic evaluations (see figure 1 and Appendix 1), which are themselves an area rapidly growing in importance.[1]

Fig. 1.

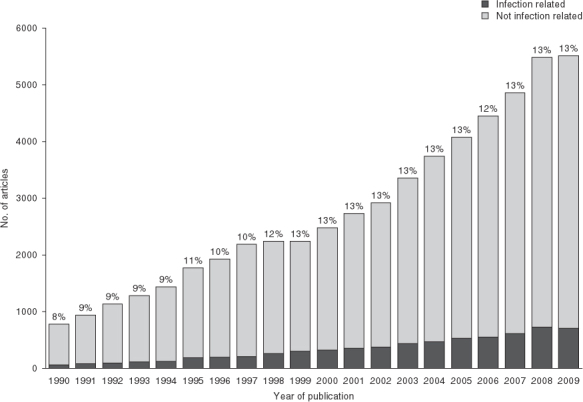
Number of articles found on model-based economic evaluations that are infection and non-infection related, according to year of publication. Percentages on top of each bar show the proportion of articles that are infection related. See Appendix 1 for search terms used.

Several concurrent trends have contributed to this expansion. Despite large reductions in the incidence of infectious diseases over the last 50 years, they are still the second most common cause of death worldwide, accounting each year for about 18 million deaths and 600 million lost disability-adjusted life-years.[2] This burden, combined with the risk of high-profile and economically damaging outbreaks, have ensured their continual importance from a public health perspective. Infectious diseases have been kept in the public consciousness as a result of emerging diseases such as the West Nile virus and HIV, pandemics such as severe acute respiratory syndrome (SARS) and influenza A/H1N1, the threat of bioterrorism and the emergence of antimicrobial-resistant strains of existing pathogens. The human and economic impact of an emerging pathogen is difficult to estimate but potentially devastating. Additionally, infectious aetiology has been discovered for a number of diseases such as hepatitis C and E, peptic ulcers and cervical cancer, originally thought to be non-communicable.

At the same time, advances in molecular medicine have facilitated the development of new tools to prevent and control infectious diseases. The last 2 decades have been called a new ‘golden age’ in the development of vaccines, the most effective intervention we have against infectious diseases.[3] The main purchasers of these vaccines have been governments and large non-governmental organizations, since they are most effective when used as part of a population-level public health programme. Although vaccines are traditionally one of the most cost-effective interventions available,[4] the high price of the new vaccines has resulted in them being subject to greater scrutiny, including pharmacoeconomic evaluation, by decision makers. For instance, there is an increasing role for economic evaluation to inform the priorities of global initiatives such as the Global Alliance for Vaccines and Immunisation (GAVI Alliance).[5,6]

Mathematical modelling offers public health planners the ability to make predictions about the impact of emerging diseases as well as the effects of possible response and control measures. Such models are needed to bridge the gap between clinical trials (which measure individual-level efficacy over a short period of time, and for highly selected subpopulations), and population-level use. This is particularly crucial for infectious diseases, where mass interventions such as vaccination and screening can result in effects at a population level not seen on an individual level, including herd immunity, changes in the epidemiology of infection and changes to pathogen ecology as a consequence of selective pressure.

Infectious disease models are in common use in epidemiology, and a well developed set of techniques has been developed over the past few decades to model the epidemiological impact of interventions such as vaccination.[7] Since these interventions consume scarce healthcare resources, decision makers are increasingly interested in combining such models with pharmacoeconomic techniques in order to investigate whether or not interventions provide good value for resources invested. However, despite the expansion in the applied literature on economic evaluations of infectious disease interventions, the models underpinning such evaluations have not always been used appropriately. Many economic evaluations of infectious disease interventions apply models that do not take into account the unique complexities of infectious diseases, such as their transmissibility from infected to susceptible individuals, the possibility of acquiring natural immunity to infection and the uncertainties that arise as a result of their complex natural history and epidemiology.

Recently, a number of health economists have commented on these shortcomings and urged modellers to adopt techniques that are well established in the infectious disease epidemiology literature. A recent systematic review of economic models of Chlamydia trachomatis screening found that almost all inappropriately used static models that failed to take into account onward transmission of Chlamydia infection, and hence were likely to incorrectly estimate the cost effectiveness of screening.[8] Similar conclusions were drawn in reviews of models of hepatitis A,[9] hepatitis B,[10] varicella,[11] meningococcal[12] and human papillomavirus (HPV) vaccination.[13,14]

This article is an introduction to the basic types and underlying principles of epidemiological modelling of infectious disease interventions, and the way these affect economic evaluations built around such models. The review focuses on the issues around modelling the epidemiology of infectious diseases, as the normative economic issues around economic evaluations of infectious disease interventions have been discussed extensively elsewhere.[15–18]

A comprehensive taxonomy of decision analytic models has been published.[19] More recently, the taxonomy was adapted to economic evaluations of vaccination.[20] The taxonomy categorizes models based on whether (i) states in the model change over time (dynamic) or not (static); (ii) changes to the model occur at random (stochastic) or are fixed (deterministic); (iii) the model averages the behaviour of populations (aggregate) or tracks individuals (individual based); (iv) events occur in discrete or continuous time; (v) individuals can enter or leave the population (open) or not (closed); and (vi) the model’s equations are linear or non-linear functions of parameters. This article highlights some of the key distinctions between types of infectious disease models that are not discussed in detail in previous reviews, as well as the way these model features affect their estimates of the cost effectiveness of interventions. Key terms used in this review are defined in Appendix 2 and are indicated by italics when first used in the text.

2. Interventions that Can be Modelled

Infectious disease models that are of interest to economists are usually those that estimate the effects of an intervention (and hence can be used to evaluate its costs and outcomes), rather than simply make predictions about the unfolding of an epidemic or the long-term trends in the incidence of an endemic disease. The type of intervention to be evaluated determines the type of epidemiological model used to capture key elements of the disease. Some of the most common interventions related to infectious disease that have been analysed using economic models include the following:

• Vaccination. Vaccination has been one of the main areas of application for pharmacoeconomic models that incorporate models of infectious disease transmission. Such transmission models are needed in order to capture the inherent nonlinear effects of vaccination, as a result of the potential of vaccines to protect not only directly vaccinated individuals but also their contacts. The infectious disease models used to predict the effects of vaccination have been reviewed elsewhere.[20]

• Screening. Screening for infected individuals allows them to be treated before they progress to more severe disease and/or infect other individuals. Models need to incorporate transmission if early detection affects transmissibility. This has been shown to be important for many infectious diseases such as Chlamydia[8] and HIV.[21] Such models may allow for the possibility that a screened and treated individual may be re-infected, which would decrease the cost effectiveness of screening.

• Social distancing. Planned responses to large outbreaks of infectious diseases such as an influenza pandemic often involve social distancing measures such as isolation of suspected cases, school closures, travel restrictions and cancellation of mass gatherings such as football matches.[22,23] While these may affect the progress of the epidemic, they come with a cost in terms of both individual liberty and economic activity within the population. Their benefit depends crucially on the frequency and type of interactions that occur between individuals in different age groups and settings (such as families, work places and schools). Such information can be obtained from population-based surveys that are available in Europe[24] and the US.[25] On a smaller level, models can estimate the impact of isolating infectious individuals during outbreaks in closed institutional settings such as hospitals, nursing homes and schools.[26,27]

• Post-exposure treatment. Chemotreatment options such as antimicrobials can be dealt with using static models, unless they alter the transmissibility of an individual, or a transmittable characteristic of the infection. Models falling into the latter categories include the use of antiretrovirals for HIV (which increases the life expectancy of infected individuals but decreases their infectiousness),[28] antimicrobial use against pathogens that can develop resistance[29] and antiviral prophylaxis to delay the spread of pandemic influenza.[30]

• Culling. For animal and plant diseases, one option to interrupt transmission is to deplete the host population by culling both infected livestock and even healthy livestock at risk of being infected. Models examine the trade-off between reduced infection transmission and the detrimental death of animals or plants as a result of culling. Such models have been applied to epidemics of diseases such as foot-and-mouth disease[31] and avian influenza.[32]

3. Modelling Infection Transmission

3.1 Types of Models

Most infectious diseases are communicable, that is, they are caused by agents that can be directly transmitted from host to host. Their communicable nature has important effects on the effectiveness of a preventative intervention. This is because the risk of acquiring an infection is dependent not only on the individual characteristics of a potential host (such as age and whether or not a prophylactic intervention has been received), but also on the prevalence of the infection among other people in the population with whom a potential host may come into contact. Hence, protecting a proportion of people in the population from becoming infected can have nonlinear effects on the remainder of the population.[33]

If the proportion of a population that is susceptible to an infection is sufficiently low (because other individuals are either infected, naturally immune to infection or vaccine protected), then each infected individual will transmit the disease to fewer than one susceptible person before recovering. Consequently, the prevalence of the infection will decrease over time. Herd immunity is a decrease in the rate of infection in a population in which a large proportion of its members are immune, hence reducing the probability that an infected individual will have contact with a susceptible individual.[33] The proportion of the population that needs to be resistant in order to ensure that an epidemic will not spread (because each infected individual transmits the infection to less than one susceptible person) is called the herd immunity threshold. Such a concept is vital in models of vaccination programmes, since the aim of vaccination is to protect a large enough proportion of the population to eliminate the infection.

This has important implications on the way infectious diseases should be modelled. When evaluating interventions involving non-communicable diseases, the most common types of decision analytic models used by health economists are cohort models, such as decision trees and Markov models.[34] These have two main characteristics. First, they usually model a closed population (with no individuals allowed to enter the population over time), consisting of a single birth cohort. Second, the probability of an individual moving between states represented by different branches of a decision tree or different transition states of a Markov model is dependent only on characteristics of each individual, and not on the number of other people who are infectious. For this reason, they have been variously called static models[20] or models without interaction.[19]

For infectious diseases, it is usually more appropriate to use transmission dynamic models. These represent an entire population with multiple birth cohorts. The population modelled is usually open (with new individuals being created by births), although models over a very short time scale may have a single closed population without births. Furthermore, an intervention on one individual can have effects on others. This is because the probability of a susceptible individual moving to an infectious state depends not only on the proportion of people in the susceptible state, but also on the proportion of people in the infected state. The instantaneous rate at which susceptible people become infected is called the force of infection. In a static model, the force of infection is constant in time, while in a dynamic model it is a function of the proportion of the population that is infected (and hence changes over time).

3.2 When to Use Transmission Dynamic Models

Compared with static cohort models, transmission dynamic models are usually more analytically complex, require more epidemiological information to parameterize and demand more computing resources to implement. Hence, it is advantageous to use them only when necessary, that is, when an intervention can potentially produce significant changes in the force of infection. This can occur in several ways. An intervention may decrease the proportion of the population that is susceptible, decrease the proportion of the population that is infected or decrease the rate at which the infection is transmitted between infected and susceptible people. Examples of each of these interventions are vaccinating infants against measles,[35] screening for and treating tuberculosis carriers in a population[36] and closing schools during an influenza pandemic.[37] An intervention may also cause changes to the characteristics of an infectious agent through selective pressure. Examples of this include the emergence of antibacterial-resistant strains of bacteria as a result of antibacterial use,[29] and the increase in prevalence of certain strains of bacteria as a result of vaccination against other strains.[38,39]

In an economic model where a preventative intervention such as vaccination, screening or social distancing is compared with no intervention, a dynamic model will usually indicate that the intervention is more cost effective than an equivalent static model. This occurs for two reasons. First, a dynamic model will predict that a greater number of infections are prevented by the intervention (both those directly protected by the intervention predicted by the static model, as well as those indirectly protected through herd immunity). Second, a dynamic model will predict a faster reduction in the number of infections than a static model, which is more beneficial in an economic model with positive time preference. This has been discussed for the case of meningococcal[40] and varicella vaccination,[41] and is illustrated using a hypothetical infant vaccination programme in figure 2. Hence, a dynamic model will usually predict a more cost-effective outcome, both in the short term (due to a more rapid effect) and also in the long term (as the effect of herd immunity accumulates over time).

Fig. 2.

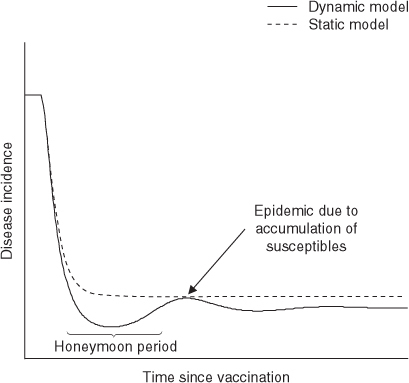
Dynamic and static model predictions about changes to varicella incidence following the introduction of an infant immunization programme. Initially, following vaccination, there is a honeymoon period where incidence drops rapidly, but accumulation of susceptible individuals eventually causes a sharp temporary increase in incidence (post-honeymoon epidemic) before infection reaches a new equilibrium (post-vaccination equilibrium). Assumptions: infant vaccination with 80% coverage and a perfect vaccine (100% protection for life).

Consequently, if a static model indicates that the intervention is cost effective, a dynamic model will usually show the same. Hence, a static model may be sufficient to obtain a conservative estimate of cost effectiveness. However, there are several reasons why a dynamic model may still be necessary.

• Even when both static and dynamic models agree on a qualitative prediction (such as the favourable cost effectiveness of an intervention), the dynamic model might predict a more complex (and realistic) time course in disease incidence than would a static model. One example is the dynamics of a population following vaccination to a level of coverage insufficient to reduce the number of susceptibles below the herd immunity threshold. Figure 2 shows how a dynamic model predicts that such a vaccination programme can cause the incidence of infection to initially drop to a very low level (during a time period called the honeymoon period), but then later show a sharp temporary increase due to the accumulation of susceptible individuals during the period when the force of infection was low. A real-life example is an outbreak of rubella in Greece in 1993 following years of low disease incidence after partial rubella vaccination.[42] None of this behaviour can be shown by a static model. This sharp increase can be economically important, because it can indicate the need to retain spare healthcare capacity to accommodate future spikes in demand.

• A dynamic model may show that interventions cause changes in the profile of infected individuals not seen in a static model. For instance, vaccination reduces the force of infection, which causes the average age at infection to increase and the period between any cycles in infection incidence to lengthen. This can be economically important. For instance, vaccination against rubella with a low level of coverage can cause the average age at the time of rubella infection to increase from childhood to child-bearing age, increasing the risk of congenital rubella syndrome, which is a condition caused by being born to a mother who had rubella during pregnancy.[35]

• A dynamic model may reveal relationships between variables that are not apparent using the static model alone. This is seen in a comparison between static and dynamic models of therapeutic antiviral use in the Netherlands during an influenza pandemic.[43] Both models predicted that the intervention would be cost effective; however, the dynamic model suggested that the cost-effectiveness ratio would be sensitive to the size of the pandemic, whereas the static model did not show this relationship.

• When one preventative intervention is compared with another, a dynamic model does not necessarily give a more cost-effective result than a static model, since it will predict that both options have a greater effect than predicted by a static model. An example of this is using economic modelling to determine the appropriate age for a catch-up vaccination campaign, which requires comparing several catch-up vaccination strategies covering different age ranges.[44]

• Some diseases are caused by several types or subtypes of organisms, and interventions can induce selective pressures that cause a subset of these types to gain a fitness advantage over others. Examples are replacement of one type of bacteria by another following vaccination[38,39] and emergence of antimicrobial-resistant respiratory tract infections following antibacterial use.[29] A dynamic model incorporating multiple bacteria types can predict long-term emergent behaviour that will not be seen in static models. Such a model usually incorporates a competition parameter that measures the ability of one strain to infect a host who is already infected by another strain.

On the other hand, dynamic models are unnecessary when interventions have no effect on the force of infection on people not receiving the intervention. One such case is that of infections such as rabies and West Nile virus, which have environmental reservoirs largely unaffected by the proportion of infected people in the population. An intervention targeting human hosts rather than animal or insect reservoirs will have little effect on the force of infection. The same is true for interventions affecting the severity of disease in infected people but not their transmissibility, such as end-of-life therapy for cervical cancer, which does not significantly affect the transmission of the causative infective agent (HPV), since this occurs decades before the development of cancer. Another example is that of a vaccine that prevents individuals from getting disease from an infection but does not prevent them from acquiring the infection asymptomatically. For instance, early economic models of pneumococcal[45] and rotavirus[46] vaccination were largely static because it was not known whether vaccination would prevent transmission, or simply reduce the risk of disease. More recently, however, evidence has emerged that the vaccines may also prevent transmission,[47,48] so, more recently, dynamic models of vaccination incorporating herd immunity have been developed.[39,49]

3.3 Approximating Herd Immunity in Static Models

One method that has been used to avoid the complexity of dynamic models is to retain a static cohort model structure, but then to approximate the population effect of an intervention from the experience of another similar population that has undergone the intervention, or from the results of a dynamic model used in a different situation. There are several examples of this from economic evaluations of vaccination. Static cohort models used to estimate the cost effectiveness of pneumococcal vaccination in England,[50] and of meningococcal C vaccination in Quebec,[51] were extended using information from post-vaccination surveillance in the US to estimate the population-level impact. Similarly, the indirect benefit of pertussis vaccination was estimated in a cohort model of pertussis vaccination[52] by using equilibrium values of a separate dynamic model. Besides evaluations of vaccination, some cost-effectiveness evaluations of HIV screening have assumed a fixed reduction in secondary cases from detecting and treating a primary HIV case.[53]

There are a number of dangers with this approach. First, it requires the use of estimates from either a dynamic model or surveillance conducted in a different population or situation, since it would be unnecessary to use a model at all if there was already good information on the long-term effect of an intervention in the same population. However, differences between populations (such as in age profile, likely uptake of the intervention, size of age and risk groups or mixing frequency between individuals in the population) may alter an intervention’s effect in unpredictable ways. For instance, post-marketing surveillance following the introduction of pneumococcal vaccination in England and Wales revealed a level of serotype replacement not seen in US surveillance data.[54] Second, estimating herd immunity benefit from the equilibrium state of a dynamic model ignores the period of change between the start of an intervention and reaching the equilibrium, when disease prevalence may fluctuate. This can be extremely important in an economic evaluation with positive time preference, since the initial period is closer in time to the intervention and hence the costs and benefits accrued during this period are more influential. Because of these reasons, this technique should ideally be used only when construction of a population-specific transmission dynamic model is restricted by data limitations, and even then, a wide range of possible scenarios for key parameters governing the differences in the populations being modelled should be considered. Also, more sophisticated approximations could be used than simply applying the equilibrium state of a dynamic model from the start of an intervention. For example, one method of approximating herd immunity has been proposed that retains a cohort structure but takes into account a gradual reduction in the force of infection until a post-vaccination equilibrium is reached.[55]

Figure 3 is a flow diagram with an algorithm with key questions that need to be asked when choosing between different types of models to investigate an infectious disease intervention.

Fig. 3.

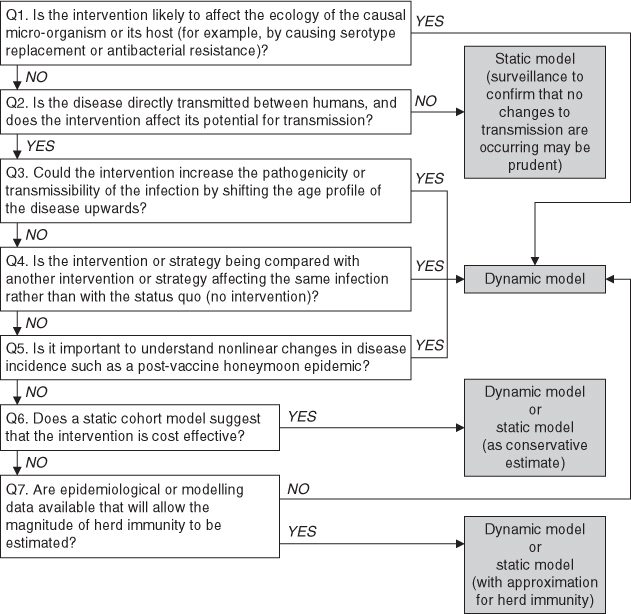
Flow diagram showing how the choice of a static model, static model with approximation for herd immunity or dynamic model could be made based on answers to seven key questions.

4. Modelling the Natural History of Infection and Disease

This section provides a brief description of the features of infectious disease natural history most relevant to modelling; further details are available elsewhere.[56]

There are many stages of infection and disease (see figure 4a and b). Both infection and disease begin with the exposure of a susceptible host to the infectious agent. If the host is infected, then the latent period begins, followed by the infectious period when the individual is infectious to others. The length of the latent period can vary from several days (influenza) to decades (tuberculosis). The final stage is the one where the host is removed from the infected population, through recovery or death.

Fig. 4.

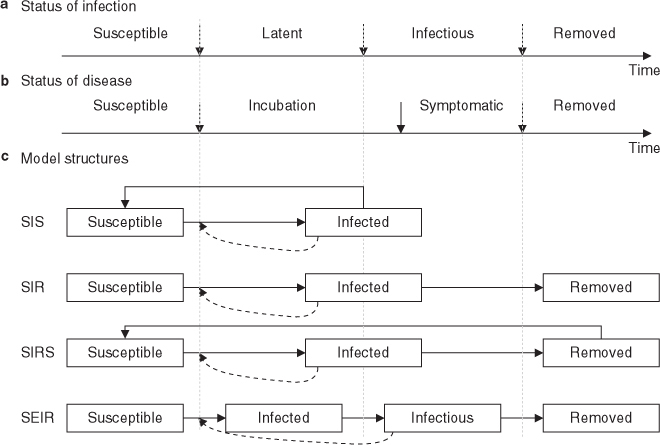
Timeline for the natural history of (a) infection and (b) disease, together with (c) corresponding model structures. In (c), direct lines indicate movement between health states, while dotted lines indicate that the rate at which susceptible individuals are infected is influenced by the proportion of the population that is infectious. SEIR = susceptible-exposed-infectious-recovered; SIR = susceptible-infectious-recovered; SIRS = susceptible-infectious-recovered-susceptible; SIS = susceptible-infectious-susceptible.

Different stages of disease also commence at the time of infection. This first stage of disease, the incubation period, usually lasts until partway through the infectious period, and is followed by the symptomatic period. However, some infections may simply result in asymptomatic infection rather than disease. Although the purpose of an intervention is ultimately to reduce the burden of disease rather than infection, transmission models need to take into account unreported cases (both asymptomatic and symptomatic), as these contribute to infection transmission and hence affect the consequences of interventions. One example is the 2009 influenza pandemic, where the number of cases of symptomatic disease were reduced by widespread asymptomatic infection leading to natural immunity in the population.[57]

An individual who recovers from infection may develop natural immunity. Most epidemiological models do not attempt to capture the detailed biological mechanisms of immune response, but instead make one of several assumptions about natural immunity, illustrated in figure 4c.

• Susceptible-infectious-susceptible (SIS) models assume that no natural immunity occurs, so individuals who recover from infection are immediately susceptible to further infections of the same kind. This is the simplest option and may be appropriate to represent diseases such as gonorrhoea that do not confer immunity, usually because they are caused by pathogens that are highly diverse or evolve rapidly to avoid immune defences.

• Susceptible-infectious-recovered (SIR) models assume that a host can only be infected once in an individual’s lifetime (or the time horizon of the model). This is appropriate for representing diseases such as measles for which natural immunity is close to lifelong.

• Susceptible-infectious-recovered-susceptible (SIRS) models assume that a host is protected from re-infection for some time after recovering, but that this natural immunity to infection wanes over time. This is appropriate for modelling infection by a virus such as influenza, which continuously changes over time so that natural immunity to a particular season’s strain is lost after a few years.

• Susceptible-exposed-infectious-recovered (SEIR) models are SIR models modified to include a latent period during which an individual is infected but does not transmit infection. This is important in infectious disease dynamics since it introduces a delay that reduces the speed at which an epidemic spreads through a population. This can also represent a phase when the host is infectious but without symptoms, which may be important if individuals are expected to change their contacts patterns after the onset of symptoms. Note that SEIS and SEIRS models are also possible by incorporating a latent period into SIS and SIRS models.

The way natural immunity is modelled has an influence on the cost effectiveness of an intervention. An intervention such as vaccination against an infection will have the largest effect (and hence be most cost effective) in a model where natural immunity to the infection is modelled using an SIS model, and the least effect when using an SIR model.[58] This is because natural immunity creates a pool of individuals already resistant to the infection and, hence, anyone who has been infected before can no longer benefit from vaccination. Often, the choice of model to represent natural immunity is not straightforward because of lack of data on the existence and persistence of natural immunity.

5. Incorporating Uncertainty into Models

In order to evaluate the effects of an intervention, infectious disease models first need to be calibrated to pre-intervention epidemiology by choosing suitable parameters representing infectivity and immunity. Next, the intervention is introduced, either by altering these parameters or by introducing new model states to represent directly affected individuals.

These steps rely on assumptions that are often inherently uncertain. The most common way of accounting for this uncertainty is to vary key parameters in a model across their plausible distributions, either in a univariable fashion or together,[59] and to see the effect this has on the predictions of the model. Several authors discussing both infectious disease models[17,60] and economic models in general[61,62] have pointed out that this only takes into account parametric uncertainty. Other forms of uncertainty that have been proposed include model uncertainty, structural uncertainty and methodological uncertainty. Here we discuss the relevance of different sources of uncertainty in pharmacoeconomic models of infectious diseases, as well as appropriate ways to account for them.

5.1 Parametric Uncertainty

Parametric uncertainty refers to variation in the numerical input values of a decision analytic model. These parameters may include transition rates between health states, values governing the efficacy of interventions, as well as cost and utility weights associated with health states.

Parametric uncertainty occurs when parameters are estimated from the results of epidemiological and economic studies that are subject both to sampling error and to lack of validity (bias) due to differences in modelled and actual study populations. Probabilistic sensitivity analysis is often considered the best method of accounting for uncertainty in the joint distribution of the parameters; for example, it is required in economic evaluations commissioned by the UK National Institute for Health and Clinical Excellence.[63] However, probabilistic sensitivity analysis can be particularly challenging to conduct for infectious disease models. Key parameters in these models include the contact rates between different individuals (e.g. individuals in different age or risk groups) and the probability that an infected individual will transmit an infection to a susceptible individual during a contact. Until recently, contact rates were difficult to quantify and were estimated by imposing a simple age structure on the model, and fitting the contact rates to data about the current infection status of a population.[64] Recent population-based contact surveys have measured contact rates relevant to airborne or close contact infections directly.[65] However, they are subject to sampling and measurement error, and still require the probabilities of transmission for different types of contacts (such as close-contact or airborne) to be known. Hence, the uncertainty in both contact rates and transmission probabilities needs to be captured in a way that incorporates their relatedness to each other. One method is to take every contact between two individuals recorded in a survey as a sample space, and draw random (bootstrap) samples from this space, while at the same time sampling from matching individuals in current infection status surveys, thus obtaining a joint distribution representing the uncertainty in both. Next, the probability of transmission is chosen that enables the model to fit data about the current infection status of a population.[66]

5.2 Structural Uncertainty

Structural uncertainty refers to different choices of health states in a model and relationships between them. For instance, natural immunity following recovery from infection can be modelled using different possible structures such as SIS, SIR and SIRS (figure 4c). All three structures can be successfully fitted to outcome data by appropriately adjusting the force of infection. However, an SIS structure will predict that a preventative measure such as vaccination with long-term duration of protection has the greatest impact (and is most cost effective), while an SIR structure will predict the least impact.[58] One way of dealing with structural uncertainty is by parameterizing the range of choices and then averaging outcomes as these structural parameters are varied.[62] In the case of natural immunity, the duration of natural immunity could be considered a parameter that is varied over a plausible range. This range could potentially take values between zero and the lifetime of the individual, so that an SIS model corresponded to a value of zero, SIR to a value of infinity and SIRS to intermediate values. Hence, many forms of structural uncertainty can be reduced to parametric uncertainty. However, in practice, many models are constructed that do not parameterize all plausible model choices that fit the understanding of the disease being modelled. Consequently, the usual techniques for accounting for parametric uncertainty may underestimate uncertainty.

5.3 Model Uncertainty

Model uncertainty refers to variations that arise as a result of different categorical choices that cannot be readily parameterized. For instance, Brisson and Edmunds[60] discuss a series of models of varicella vaccination involving several model choices: (i) a choice between static and dynamic models; and (ii) a choice between a model where exposure to a person infected with varicella reduced an individual’s risk of zoster (another disease caused by reactivation of the same virus in previously infected individuals) and one without such an effect. Neither choice can be reliably parameterized. The first is a decision to use either a simplified model or a more complex but potentially more realistic one, based on considerations such as those discussed in this article. The second depends on the modeller’s belief in a hypothesis for which there is some epidemiological evidence[67] but is by no means completely accepted. In this case, it may be appropriate to weight different model choices and use model averaging over the range of choices.[62]

5.4 Methodological Uncertainty

Methodological uncertainty refers to variations that arise as a result of different choices for model values due to normative issues rather than as a result of the difficulty in reflecting objective reality. Such considerations include the appropriate discount rates to apply, the type of economic analysis (such as cost effectiveness or cost benefit), the time horizon and the analytical perspective to use. These choices are often made based on a ‘reference case’ that decision-making bodies adopt[68] to reflect societal preferences on issues such as time preference and equity trade-offs between different sectors of society. However, these guidelines are usually written with non-infectious diseases in mind. Indeed, most country-specific guidelines for economic evaluations do not specifically discuss infectious diseases, although Australian guidelines have a vaccine-specific appendix that discusses the need to consider herd immunity,[69] and the WHO has a guide for standardizing evaluations of vaccination programmes.[70] Because of their unique characteristics, these methodological choices can have large effects on the results of economic evaluations of infectious disease interventions that are not always predictable from their effects on other interventions.[71]

One example is the issue of the time horizon over which costs and outcomes are assessed. A lifetime time horizon is usually appropriate for evaluating interventions for chronic non-infectious diseases in which no further costs or health benefits are incurred after the death of the recipient of the intervention. However, for an intervention such as vaccination against an infectious disease, wider costs and benefits can continue to accrue long after the lifetime of the person receiving it. Indeed, infectious disease interventions can cause permanent changes to pathogen ecology (such as eradication or evolution). Hence, the choice of time horizon is crucial and difficult to establish. This is illustrated by the case of varicella vaccination,[60,72] where a short time horizon causes vaccination to appear less cost effective because of the increase in cases of zoster in older unvaccinated adults as a result of reduced immune boosting from contact with people infected with varicella. However, for a longer time horizon, the intervention becomes increasingly cost effective because zoster incidence decreases as the vaccinated cohorts are protected from zoster in later life. Apart from the time horizon, interventions with outcomes that occur many years after the intervention (such as vaccination against HPV or hepatitis B) are also highly sensitive to choice of discount rates.[14,73]

Another example is the strong externalities associated with communicable diseases because of the possibility that an infected individual will spread the infection to others. Hence, interventions such as vaccination and social distancing may have benefits to people other than the individual receiving the intervention (and possibly net disbenefits to the direct recipient). Furthermore, the impact of preventing or mitigating pandemics such as SARS, influenza and HIV on the wider economy may be considered by decision makers to be more important than the actual health impact.[74,75] Hence, perspectives that are limited to health sector costs and outcomes may ignore what are considered as the most important benefits of certain infectious disease interventions.

6. Conclusions

Economic evaluations of infectious disease interventions are likely to continue to play an important role in decision making. However, modellers conducting such evaluations need to understand the unique features of the disease and intervention they are modelling, as well as the appropriate choices of models to use.

Appendix 1

Database Search Strategy

Database searched: Ovid MEDLINE

Date of searching: 17 April 2010

Search terms used:

All economic evaluations

1. Economics/

2. exp Economics, Dental/

3. exp Economics, Hospital/

4. exp Economics, Medical/

5. exp Economics, Nursing/

6. exp Economics, Pharmaceutical/

7. cost$.mp.

8. economic$.mp.

9. pharmacoeconomic$.mp.

10. or/1–9

11. model$.mp.

12. Models, Economic/

13. Models, Theoretical/

14. Decision Support Techniques/

15. Markov Chains/

16. Computer Simulation/

17. simulation$.mp.

18. Decision Trees/

19. decision tree$.mp.

20. or/10–19

21. 10 and 20

Infection-related economic evaluations

• 22.Communicable Diseases/
• 23.infection/
• 24.infect$.mp.
• 25.bacter$.mp.
• 26.viral.mp.
• 27.virus.mp.
• 28.helminth$.mp.
• 29.or/22–28
• 30.21 and 29

Titles of articles returned were examined briefly to ensure that the search terms appeared valid, but no attempt at systematic screening was made. Hence, the reported number of articles returned should be regarded as indicative of the literature rather than exact.

Appendix 2

Glossary of Key Terms Used in Infectious Disease Modelling

Aggregate (compartmental) model. Model that is divided into various compartments representing the average state of individuals assigned to that compartment. Within a single compartment, all individuals are considered to be identical (homogeneous).

Catch-up vaccination campaign. Programme in which vaccination is offered initially to age cohorts above the age of routine vaccination in order to rapidly increase the proportion of the population that is vaccine protected.

Closed population. Model population that is fixed in size, and that no new individuals can enter or leave.

(Single) cohort model. Model of a closed population consisting of a single birth cohort, usually with a fixed force of infection (and hence static).

Communicable disease. A disease caused by an infection that can be transmitted directly from host to host.

Competition parameter. Parameter in a transmission dynamic model measuring the ability of one type or subtype of pathogen to infect a host that is already infected by another type or subtype.

Deterministic model. Model in which each iteration with the same input parameters and initial conditions will generate exactly the same output, because there is no source of randomness (stochasticity) within the model.

(Transmission) dynamic model. Model of an entire population with multiple birth cohorts, and a force of infection varying depending on the proportion of the population who are infected. The population may be stratified into different subgroups (by age, risk factors or other demographic attributes) based on each group’s susceptibility to infection and probability of contact with other subgroups.

Force of infection. The instantaneous rate at which susceptible people become infected.

Herd immunity. The resistance to infection of a population in which a large proportion of its members are immune, hence reducing the probability that an infected individual will have contact with a susceptible individual.

Herd immunity threshold. The proportion of the population that needs to be resistant in order to ensure that an epidemic will not spread.

Honeymoon period. Initial time period following vaccination when infection incidence drops to a very low level before subsequently rising.

Incubation period. Time from an initial infection to the start of symptomatic disease, during which the host has no symptoms.

Individual-based model. Model in which each individual has its own characteristics rather than being assigned to homogeneous compartments based on average states of groups of individuals.

Infection. Acquisition by a host of the agent (such as a bacterium or virus) that can potentially cause the disease.

Infectious period. Time during which an infected individual can transmit the infectious agent to others.

Latent period. Time period from an initial infection to the start of the infectious period, during which an infected individual does not transmit the infectious agent to others.

Natural immunity. The potential of a host’s acquired immune system to develop mechanisms after a first infection that reduce the risk of the same type of pathogen infecting the host again.

Open population. Model population in which new individuals can enter or leave the model (for instance, through births, deaths, immigration and emigration).

Static model (or model without interaction). Model with a force of infection that is independent of the proportion of the population that is infected. These are usually single cohort models.

Stochastic model. Model in which two iterations with the same input parameters and initial conditions may generate different outputs, because there is a source of randomness (stochasticity) within the model itself that determines whether or not events occur.

Symptomatic period. Time during which an infected individual has symptoms.