Soft crystal martensites: An in situ resonant soft x-ray scattering study of a liquid crystal martensitic transformation

The martensitic nature of soft crystals is captured by soft x-ray scattering, broadening the analogy with atomic crystal systems.

Abstract

Liquid crystal blue phases (BPs) are three-dimensional soft crystals with unit cell sizes orders of magnitude larger than those of classic, atomic crystals. The directed self-assembly of BPs on chemically patterned surfaces uniquely enables detailed in situ resonant soft x-ray scattering measurements of martensitic phase transformations in these systems. The formation of twin lamellae is explicitly identified during the BPII-to-BPI transformation, further corroborating the martensitic nature of this transformation and broadening the analogy between soft and atomic crystal diffusionless phase transformations to include their strain-release mechanisms.

INTRODUCTION

Martensitic transformations are diffusionless phase transformations characterized by the homogeneous and cooperative movement of large numbers of atoms over distances smaller than their nearest-neighbor spacing (i.e., without long-range diffusion). As an example of a displacive crystalline structural phase transition, martensitic transformations have long generated substantial interest. Structural transitions at the atomic level translate to superlative changes in mechanical (1), magnetic (2), and electronic material properties (3, 4), and the study of martensitic transformations increases our fundamental understanding of crystal nucleation, transformation, and growth processes observed in many technologically relevant metals and alloys. As well as atomic crystals, martensitic transformations have been observed in a range of “soft” material systems, e.g., in the microscopic structure of some virus species during the process of bacterial cell infection (5).

Recently, we demonstrated that martensitic transformations can also be found in three-dimensional liquid crystalline mesostructures (6). Specifically, the process by which liquid crystal (LC) blue phases (BPs)—soft crystals of chiral liquid crystalline mesogens with either a body-centered cubic (BCC; BPI) or a simple cubic (BPII) unit cell—transform from BPII to BPI was shown to proceed in a diffusionless manner analogous to a classic martensitic transformation of an atomic crystal (6). During the martensitic transformation, the “double-twist” cylinders rearrange between simple (BPII) and body-centric (BPI) cubic structures, through a cooperative motion of the constituent mesogens within only a few seconds. This observation was possible only through the use of LC-directed self-assembly techniques to create large single domains of BPII, with fixed in-plane and out-of-plane orientation, which transformed upon cooling into polycrystals of BPI.

Because of the commensurability of BP unit cell sizes (c. 150 to 250 nm) and the wavelength of visible light, photonic bandgap effects (i.e., selective reflections) can be used to observe the morphology and orientation of BP mesostructures during phase transformations. This is not the case for metal or alloy systems, for which direct study of the displacive collective movement of atoms remains challenging owing to the increased speed of the transformation and the reduced length scale of the system. Difficult and cumbersome techniques such as in situ high-resolution transmission electron microscopy are required (7–9). Soft crystals, such as LC BPs, therefore readily allow detailed study of crystal reconfiguration processes using nothing more than a benchtop optical microscope.

However, the use of soft mesoscopic crystals as a “scale model” for atomic crystals, particularly with respect to martensitic transformations, relies on the robustness of the analogy between soft and hard matter at vastly different length scales. The mesoscopic nature of the BPI martensite—beyond its morphology and out-of-plane orientation—could only previously be speculated upon based on optical observations alone. One means by which to further probe this analogy is, therefore, to study the distortion—and thus, the strain release mechanism—of the BP unit cell during the martensitic transformation.

Here, we use resonant soft x-ray scattering (RSoXS) to probe in situ the morphology of BP LC unit cells during a martensitic transformation from BPII to BPI and use the results to further broaden the analogy between diffusionless phase transformations in soft and hard matter. Conventional x-ray scattering using hard x-rays can be challenging to perform on soft matter systems (10, 11), which normally consist of light atomic elements and thus exhibit low electron density contrast. RSoXS, however, is ideally suited to the study of such systems, operating at the absorption edge of light elements including carbon, nitrogen, and oxygen, and therefore resonantly enhancing the contrast in the system. In particular, RSoXS near the carbon K-edge has successfully been exploited to study various soft matter systems including LCs, block copolymers (10, 12, 13), and bulk heterojunction solar cells (14–18). Although RSoXS has been used before to study BP LCs (19), it has not previously been coupled with directed self-assembly techniques (20, 21) to allow measurement upon single domain BPs (22). Previously inaccessible observations of unit cell transformations during a martensitic transformation are thus reported. We therefore are able to confirm that the cross-hatched structures previously observed in monodomain BPI, transformed from single-crystal BPII, are the result of strain release via twinning (as anticipated for a true martensite) rather than some other physical mechanism unique to soft crystals.

RESULTS

LC phases in LC sandwich cells

LC “sandwich” cells, necessary to probe the material by RSoXS, are fabricated as shown in Fig. 1A. Briefly, a chemical pattern consisting of alternating regions of a poly(6-(4-methoxyazobenzene-4′-oxy) hexyl-methacrylate) (PMMAZO) polymer brush and bare silicon nitride (SiN) substrate (23) is transferred to the front side of one membrane window by electron beam lithography and subsequent reactive ion etching. The front side of the complementary membrane is functionalized with octadecyltrichlorosilane (OTS). Whereas the PMMAZO brush supports weak homeotropic anchoring of the LC mesogens, and the OTS strong homeotropic anchoring, the bare SiN substrate instead supports planar degenerate anchoring. As a result, when confined between the two membrane windows, the LC mesogens of the sandwich cell may exhibit large single crystals of both BPI and BPII, depending on the size and morphology of the underlying chemical pattern, and the ambient temperature (Fig. 1B). The structure of the BPI BCC unit cell (i.e., the constituent double-twist cylinders and disclination network) is shown in Fig. 1C, and its orientation with respect to the incident x-ray beam—and therefore, the experimental coordinate system—is shown in Fig. 1D; the same for the BPII simple cubic unit cell is shown in Fig. 1 (F and G). The chemical pattern used in this work induces an arrangement of the BPI and BPII lattices whereby the (110) and (100) axes are oriented out-of-plane, respectively. Projections of the BPI and BPII lattices along these crystallographic axes are shown in Fig. 1 (E and H), along with the corresponding simulated scattering patterns. Single crystals are anticipated to result in scattering patterns consisting of distinct peaks (solid points), whereas small polycrystals randomly oriented in-plane are anticipated to result in scattering patterns consisting instead of isotropic rings (dotted lines).

Fig. 1. RSoXS of BP LCs.

(A) Fabrication scheme for BP LC sandwich cells. (B) Optical micrographs of single crystals of BPI₍₁₁₀₎ (top) and BPII₍₁₀₀₎ (bottom) under crossed polarizers, and the corresponding Kossel diagrams (insets). Structures of the (C) body-centered cubic (BCC) BPI and (F) simple cubic BPII. RSoXS geometry for (D) the BPI, with the (110) orientation out-of-plane, and (G) the BPII, with the (100) orientation out-of-plane. Lattice projections and simulated scattering patterns for (E) BPI₍₁₁₀₎ and (H) BPII₍₁₀₀₎, where scattering patterns for single crystals correspond to solid peaks and scattering patterns for small, randomly oriented polycrystals correspond to dotted rings. The first Brillouin zone is shown in yellow.

Upon heating and cooling, the texture of the LC within the chemically patterned sandwich cell, observed by optical microscopy under crossed polarizers, changes considerably (Fig. 2). Upon heating from room temperature, the texture changes from that associated with a cholesteric (Chol.) LC phase to that associated with the BPI (green domains; 40.1°C), BPII (blue domains; 41.1°C), and, lastly, the isotropic (Iso.) (black; 43.1°C) LC phase. Based on the color of the textures observed, the out-of-plane orientation may be identified as (110) for the BPI [i.e., BPI₍₁₁₀₎] and (100) for the BPII [i.e., BPII₍₁₀₀₎]. In all cases, polycrystals with random in-plane orientations are observed. Of course, this behavior is sensitive to the kinetics and thermal history of the experiment: The relatively fast heating rate, ≈0.5°C/min, and previous thermal cycling here result in polycrystals of BPII₍₁₀₀₎, but a slower rate, e.g., 0.2°C/min or less, would have resulted in a single domain (6). During the transition from BPI₍₁₁₀₎ to BPII₍₁₀₀₎, a coexistent mixture of green BPI₍₁₁₀₎ and blue BPII₍₁₀₀₎ domains is observed (e.g., at 41.0°C). Upon cooling, the same sequence of LC phases is observed, i.e., Iso. → BPII → BPI → Chol. (Fig. 2B). However, in this case, a single domain (crystal) of BPII₍₁₀₀₎ is observed (uniform blue; 41.6°C), which transitions to a heavily cross-hatched polycrystalline BPI₍₁₁₀₎ at 41.0°C. The textures—and, therefore, LC phase and domain size—vary strongly depending on the thermal history of the sample, and the transition from single-crystal BPII to BPI polycrystals happens only upon cooling.

Fig. 2. LC phases during heating and cooling of BP LC sandwich cells.

Optical micrographs (top) of sandwich cell LC textures, under crossed polarizers and corresponding RSoXS scattering pattern (bottom) during (A) heating [LC phase sequence, cholesteric (Chol.) → BPI → BPII → isotropic (Iso.)] and (B) cooling (Iso. → BPII → BPI → Chol.). The periodic horizontal peaks visible in the RSoXS pattern of Iso. phase are due to the underlying chemical pattern.

RSoXS on LC phase transition from BPI to BPII during heating

Two distinct RSoXS patterns may be observed during heating of the LC sandwich cells (Fig. 3; see details in fig. S1). When the LC is at 41.0°C, rings are observed at q values corresponding to the {110}, {200}, {211}, and {220} planes of a 244.6-nm unit cell size BPI with the (110) orientation out-of-plane (Fig. 3A; see details in fig. S1A). Note that the temperatures reported here, corresponding to those of the in situ RSoXS heating stage, are slightly offset from those of the optical microscope heating stage due to a thermal differential between the sample cell and the thermocouple in the stage. The intensity of the rings varies from the polarization-dependent contrast due to the local molecular orientation. At 42.8°C, the RSoXS pattern again consists of rings but at q values corresponding to the {100}, {110}, {200}, and {210} planes of a 142.2-nm unit cell size BPII with the (100) orientation out-of-plane (Fig. 3B and fig. S1B). The observation of rings, rather than distinct peaks, confirms that the samples consist of small polycrystals with random in-plane orientation, as observed optically (cf. Fig. 2A).

Fig. 3. RSoXS scattering patterns of BP LCs during heating.

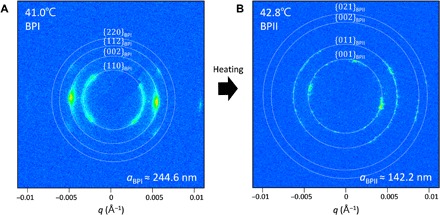
RSoXS scattering pattern of (A) BPI at 41.0°C and (B) BPII at 42.8°C during heating.

RSoXS on LC phase transition from BPII to BPI during cooling

The RSoXS patterns observed upon cooling are much more structured (Fig. 4). Upon cooling from the isotropic into the BPII₍₁₀₀₎ phase (cooling rate ≈ 0.1°C/min), a scattering pattern may be observed consisting of numerous distinct peaks (Fig. 4A). All but two of these peaks are consistent with those anticipated for a single-crystal BPII lattice with the (100) orientation out-of-plane (cf. Fig. 2B) and a unit cell size of 146.5 nm (see below) (see Supplementary Notes and fig. S2 for more details about the two peaks). The in-plane orientation of the BPII₍₁₀₀₎ coincides with that of the underlying chemical pattern. The in-plane orientation of the chemical pattern can be determined based on the weak scattering peaks still observed when the LC is in the isotropic state, highlighting the azimuthal orientation of the chemical pattern with respect to the experimental coordinate frame (Fig. 2). Upon cooling further, the number of observed peaks increases dramatically (Fig. 4B). Although peaks corresponding to BPII₍₁₀₀₎ may still be identified (white) (fig. S3A), four additional sets of peaks consistent with those anticipated for a single-crystal BPI lattice with the (110) orientation out-of-plane and a unit cell size of ≈231.7 ± 1.2 nm (Table 1) are also observed (red, orange, blue, and magenta) (Fig. 4B; see details in fig. S3, B to E). Each of the four additional sets arise, however, not from four single crystals but from four similarly oriented sets of BPI₍₁₁₀₎ polycrystals, each with a different in-plane (azimuthal) orientation relative to the underlying chemical pattern. Defining θ as the (clockwise positive) angle between the [001] orientation of the BPI₍₁₁₀₎ lattice and the lattice vector of the underlying chemically patterned stripes, then these four sets of BPI₍₁₁₀₎ domains are found to be oriented at θ = −9.52°, −80.77°, 10.55°, and 81.3° (Table 2). These four orientations will be referred to using the modeled θ values, −9.75°, −80.25°, 9.75°, and 80.25°, for reasons explained below. As the lattice vector of the chemical pattern coincides with the (010) in-plane orientation of the single-crystal BPII₍₁₀₀₎ domain, the angle θ also describes the relative orientation of the four sets of BPI₍₁₁₀₎ domains with respect to the single-crystal BPII₍₁₀₀₎ domain from which it transitioned (Fig. 4D). The spatial overlap of the (011)_BPII peak and the ($1\overline{1}2$)_{BPI,−9.75°} and ($\overline{1}12$)_{BPI,−80.25°} peaks in Fig. 4C indicates that the {011}_BPII and {112}_BPI planes are parallel and similarly spaced during this transition from BPII to BPI. In other words, the {112}_BPI planes arise from {011}_BPII planes and the four sets of BPI₍₁₁₀₎ polycrystals are oriented relative to the fixed orientation of these planes (Fig. 4D). In addition, since {112} planes are commonly associated with twinning in BCC lattices, it is anticipated that the four sets of BPI polycrystals form two subsets (i.e., BPI_−80.25° and BPI_−9.75°, and BPI_80.25° and BPI_9.75°), which exhibit twinning along the {112}_BPI plane, parallel to the {011}_BPII plane.

Fig. 4. RSoXS of BP soft crystals during cooling.

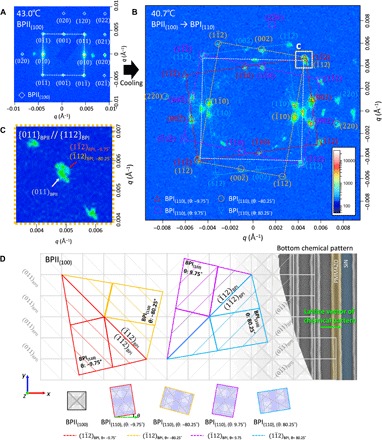
RSoXS pattern of (A) single-crystal BPII₍₁₀₀₎ at 43.0°C and (B) polycrystalline BPI₍₁₁₀₎, which has a distinct set of polycrystals with four different in-plane orientations, θ, of −9.75°, −80.25°, 9.75°, and 80.25° at 40.7°C during cooling, where θ is an angle difference between [001] of BPI₍₁₁₀₎ lattice and lattice vector of the underlying chemically patterned stripes. (C) Scattering peaks of the {112}_BPI plane appear near the scattering peaks of the {011}_BPII plane and merge with one another during the transformation. (D) Schematic of the BPI₍₁₁₀₎ lattice after martensitic transformation from single-crystalline BPI₍₁₀₀₎.

Table 1. Lattice constants of BPI during various phase transformation conditions, including with (w MT) and without a martensitic transformation (w/o MT).

All the measured values are the average of the lattice constants acquired between 41° and 42°C.

Lattice	aBPI (nm)	cBPI (nm)	c/a
BPITheoretical	250	250	1
BPIheating, w/o MT	242.2 ± 1.2	242.2 ± 2.0	1.00
BPIcooling, w MT	231.7 ± 2.2	236.4 ± 0.7	1.02

Table 2. Modeled and measured strain components of the BPI₍₁₁₀₎ lattices after the martensitic transformation from BPII₍₁₀₀₎.

ϵ_b and ϵ_c are the normal strain components in their lattice coordination, and ϵ_x, ϵ_y, and γ_xy are the strain components in the xy global coordination.

Lattice		θ (°)	ϵb	ϵc	ϵx	ϵy	γxy
Modeled	BPI(110), −9.75°	−9.75	−0.172	0.172	−0.162	0.162	−0.115
	BPI(110), −80.25°	−80.25	−0.172	0.172	0.162	−0.162	−0.115
	BPI(110), 9.75°	9.75	−0.172	0.172	−0.162	0.162	0.115
	BPI(110), 80.25°	80.25	−0.172	0.172	0.162	−0.162	0.115
Measured	BPI(110), −9.75°	−9.52	−0.171	0.163	−0.162	0.154	−0.109
	BPI(110), −80.25°	−80.77	−0.170	0.157	0.149	−0.162	−0.104
	BPI(110), 9.75°	10.55	−0.166	0.179	−0.154	0.168	0.124
	BPI(110), 80.25°	81.3	−0.161	0.166	0.159	−0.153	0.098

DISCUSSION

When making a direct analogy between martensitic transformations in BP LCs and atomic crystals, the transformation from BPII to BPI should induce equal and opposite strains that are released through the creation of two sets of twinned polycrystals, which, in turn, form a cross-hatched lamellae structure. Together, these twinned polycrystals will eliminate both the normal and shear strain components on a macroscopic length scale. Figure 5A depicts the anticipated lattice deformation process during the BPII → BPI phase transformation based on this model (fig. S4). Eight unit cells of BPII₍₁₀₀₎ are shown (2 × 2 × 2) in three-dimensional space; orange lines indicate the disclination lines. The hexahedral supercell depicted within the BPII lattice (blue) transforms into the cubic BPI₍₁₁₀₎ supercell due to the action of lattice strain and internal reconstruction. For simplicity, a two-dimensional lattice, projected onto the xy plane (i.e., perpendicular to direction of the incident x-rays), is considered. Initially, all strain components of the BPII₍₁₀₀₎ lattice are zero, i.e.

$$S_0=\left\{\begin{array}{c}{\mathrm{ϵ}}_b\\ {\mathrm{ϵ}}_c\\ {\mathrm{\gamma }}_{\mathit{bc}}\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\\ 0\end{array}\right\} \text{and} {S\prime }_0=\left\{\begin{array}{c}{\mathrm{ϵ}}_x\\ {\mathrm{ϵ}}_y\\ {\mathrm{\gamma }}_{\mathit{xy}}\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\\ 0\end{array}\right\}$$ (1)

where S₀ is the strain vector in the frame of reference of the unit cell (i.e., the local coordinate frame, b and c), $S_0^{\prime }$ is the strain vector in the frame of reference of the experiment (i.e., the global xy-coordinate frame), ϵ is normal strain, and γ is shear strain. Relative to its eventual configuration in the BPI₍₁₁₀₎ lattice, the hexahedral supercell in the BPII₍₁₀₀₎ lattice is distorted, contracted along the b axis and elongated along the c axis. Therefore, for the BPII₍₁₀₀₎ hexahedral supercell to transform to a cubic BPI₍₁₁₀₎ supercell, it must be strained along those axes (fig. S4). Furthermore, to ensure that the {011}_BPII and {112}_BPI planes, before and after the transformation, remain parallel and maintain a similar d-spacing, an in-plane rotation (−9.75°) of the lattice is required. The anticipated two-dimensional strain accompanying the martensitic transformation is therefore

$$S=\left\{\begin{array}{c}{\mathrm{ϵ}}_b\\ {\mathrm{ϵ}}_c\\ {\mathrm{\gamma }}_{\mathit{bc}}\end{array}\right\}=\left\{\begin{array}{c}-0.172\\ 0.172\\ 0\end{array}\right\}$$ (2)

in the frame of reference of the unit cell, and

$$S\prime =\left\{\begin{array}{c}{\mathrm{ϵ}}_x\\ {\mathrm{ϵ}}_y\\ {\mathrm{\gamma }}_{\mathit{xy}}\end{array}\right\}=\left\{\begin{array}{c}-0.162\\ 0.162\\ -0.115\end{array}\right\}$$ (3)

in the frame of reference of the experiment (i.e., taking into account the −9.75° rotation of the lattice) (see the Supplementary Materials for more details). Last, within the (pseudo) cubic lattice obtained after the above lattice transformation, the double-twist cylinders and disclination lines of the BPII₍₁₀₀₎ lattice are rearranged to form the BPI₍₁₁₀₎ lattice. The predicted normal strains in the frame of reference of the unit cell, i.e., ϵ_b = − ϵ_c = − 0.172, are close to those observed experimentally (ϵ_b = − 0.172 → − 0.167 and ϵ_c = 0.172 → 0.167; Table 2), corroborating the validity of the model with respect to the local strain of the unit cell. Alternatively, the transformation path could also be explained with reference to the crystallographic shear (see Supplementary Notes and fig. S5 for more details).

Fig. 5. Proposed mechanism of cross-hatched structure formation during the martensitic transformation.

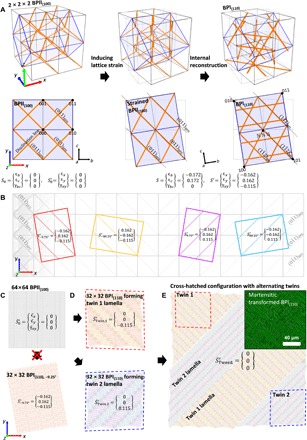
(A) Model highlighting the transformation of eight unit cells of BPII₍₁₀₀₎ (2 × 2 × 2) to BPI_{(110),−9.75°}. All the strain components are idealized values. (B) Four BPI₍₁₁₀₎ lattices, which can be transformed from single-crystalline BPII₍₁₀₀₎, and their strain values in global coordination after the transformation. (C) 64 × 64 single-crystalline BPII₍₁₀₀₎ and transformed 32 × 32 BPII_{(110),−9.75°}. (D) Representative twin 1 and twin 2 lamellae formation. (E) Idealized cross-hatched structure formation, which consists of twin 1 and twin 2 and actual cross-hatched structure of BPI₍₁₁₀₎ after the martensitic transformation (inset).

In reality, lattice deformation and internal rearrangement of the disclination lines occur simultaneously, rather than sequentially. In addition, the BPI lattice, which arises as the result of a martensitic transformation from the BPII (i.e., during cooling), has a smaller unit cell size than the BPI lattice, which arises as the result of a transformation from the cholesteric phase (i.e., during heating) (figs. S6 and S7). This is due to the unit cell size of the BPII parent lattice upon cooling (Table 1). Similarly, the BPI lattice resulting from a martensitic transformation exhibits a c axis elongated relative to the a and b axes, i.e., c/a ≈ 1.02. The lattice is thus tetragonal rather than cubic. It is likely that this c-axis elongation is the result of additional tension in the c-axis direction necessary to reduce the small mismatch in d-spacing between the {011}_BPII and {112}_BPI planes. Note that although Fig. 5A only depicts the anticipated lattice transformation process for BPI_{(110),−9.75°}, the four modeled sets of BPI₍₁₁₀₎ lattices with different in-plane orientations, i.e. −9.75°, −80.25°, 9.75°, and 80.25° (Fig. 5B), will all transform similarly (Table 2).

Continuum simulations based on the mean field Landau-de Gennes approach were also performed to analyze the BPII₍₁₀₀₎-BPI₍₁₁₀₎ lattice transformation (see the Supplementary Materials for more details). The corresponding results show good agreement with the experimental results. From the simulations, we observe that the BPII₍₁₀₀₎ transforms into a nonequilibrated BPI₍₁₁₀₎ with an in-plane rotation of ±9.75° and a unit cell with lattice constant a_BPI≈$\sqrt{2}$a_BPII = 212.13 nm. At this stage, the just-formed BPI₍₁₁₀₎ continues to relax while its unit cells expand (a_BPI≈1.65a_BPII = 248 nm) and rotate until the in-plane rotation is reduced, ending in ±8.25° (fig. S8 and movie S1). Therefore, in concordance with the experimental observation, the BPI that results from the martensitic transformation has a smaller, and slightly tetragonal (c/a ≈ 1.01), unit cell with respect to the reference BPI formed from the cholesteric phase (fig. S9).

Compared to the average strain of a single-crystal BPI₍₁₁₀₎ lattice consisting of only one orientation of BPI₍₁₁₀₎, ϵ_x = − 0.174 and ϵ_y = 0.145 (Fig. 5C), twinning results in a more energetically favorable macroscopic arrangement of unit cells. Figure 5D depicts how BPI₍₁₁₀₎ lattices transformed via a martensitic transformation prevent bulk motion of unit cells and, therefore, supercell deformation through the formation of twin lamellae. There are two possible configurations for twinning in this system (cf. Fig. 4D): “twin 1,” which consists of BPI_{(110),−9.75°} and BPI_{(110),−80.25°} lattices, twin plane parallel to the (110) plane of BPII₍₁₀₀₎ (Fig. 5D, top); and “twin 2,” which consists of BPI_(110),9.75° and BPI_{(110),80.25°} lattices, twin plane parallel to the $(\overline{1}10)$ plane of BPII₍₁₀₀₎ (Fig. 5D, bottom). The alternating lamellar of the two BPI₍₁₁₀₎ lattice types with equal proportions additionally reduces the average macroscopic strain values of the supercell, for which only a residual, macroscopic shear remains for each twin (red and blue dotted lines). The bulk motion of unit cells required for the adoption of the transformed lattice type (including rotation) is therefore minimized. The average strain of twin 1 and twin 2, respectively, is

$$\begin{array}{c}{\overline{S}\prime }_{\text{Twin}1}=\frac{{S\prime }_{-9.75°}+{S\prime }_{-80.25°}}{2}=\left\{\begin{array}{c}0\\ 0\\ -0.115\end{array}\right\}\text{and}\\ {\overline{S}\prime }_{\text{Twin}2}=\frac{{S\prime }_{9.75°}+{S\prime }_{-80.25°}}{2}=\left\{\begin{array}{c}0\\ 0\\ 0.115\end{array}\right\}\end{array}$$ (4)

Each twin results in a macroscopic supercell with an average normal strain of ϵ_x = ϵ_y = 0. However, shear strain cannot be resolved through the formation of a single twin, and each twin exhibits a shear strain of similar magnitude but opposite direction, ∣γ_xy∣ = 0.115. The average macroscopic shear strain can only be eliminated if both twins exist in equal proportions within the sample. In such a case, the average shear strain of the whole system is

$$\overline{S}\prime =\frac{{S\prime }_{-9.75°}+{S\prime }_{-80.25°}+{S\prime }_{-9.75°}+{S\prime }_{-80.25°}}{4}=\left\{\begin{array}{c}0\\ 0\\ 0\end{array}\right\}$$ (5)

It is for this reason that the cross-hatched structure is observed in BPI₍₁₁₀₎ lattices, resulting from a martensitic transformation from the BPII₍₁₀₀₎ (Fig. 5E, inset). As shown in the idealized arrangement of the two twin types in Fig. 5E, the cross-hatched structure appears due to the presence and orthogonality of the twin planes of the two different twin types. The measured normal and shear strain values for the four sets of polycrystals, at the measured orientations, similarly demonstrate the near cancellation of strain for the soft-matter martensite (i.e., $\overline{S}=\{-0.002,0.002,0.002\}$), corroborating yet further the model presented here with respect to the existence and orientations of the four BPI₍₁₁₀₎ polycrystals (table S1).

The use of in situ RSoXS offers a clear means by which to reconstruct the lattice structure—and its morphological changes—during the BPII to BPI crystal-crystal phase transformation. In addition, the use of directed self-assembly techniques ensures that the transformation is observed from a single-crystal BPII parent, thereby excluding the possible influence of grain boundaries and other defects. The results presented here further corroborate the conclusion that the phase transformation between BP LCs takes place in a diffusionless manner, whereby only small lattice deformations and rotations of the parent lattice are required. However, in addition, it has been demonstrated that, to minimize bulk motion and to reduce strain on a macroscopic scale, the transformed BPI polycrystals form twin lamellae, exactly as would be anticipated for a classic atomic martensitic transformation. It is therefore clear that BP LCs, despite their liquid crystalline nature and mesoscopic length scales, still undergo crystal-crystal transformations in a way that is directly analogous to martensitic transformations in classical, solid atomic crystals. This improved understanding of soft crystal phase transformations will provide important insight when designing and envisioning various future applications for BP soft crystals, including novel optical switching and sensing devices.

MATERIALS AND METHODS

Materials

1-Methyl-2-pyrrolidinone (NMP), OTS, dichloromethane (DCM), heptane, anisole, isopropyl alcohol (IPA), chlorobenzene, toluene, and n-amyl acetate were purchased from Sigma-Aldrich and used without further purification. MLC 2142 and 4-(1-methylheptyloxycarbonyl) phenyl-4-hexyloxybenzoate (S-811) were purchased from Merck (Darmstadt, Germany). Five-minute epoxy glue was obtained from Henkel (Germany). Glass microscope slides were purchased from Fisher Scientific in the finest premium grade. The silicon wafers used here is 4″, N-type with 〈100〉 orientation, coated with silicon nitride from WRS Materials. Both sides of the wafers were polished and deposited with nitride by low-pressure chemical vapor deposition process. The thickness of the wafer is 535 μm with 100-nm-thick nitride on both sides.

Preparation of BP materials

The mixture of 36.32 weight % (wt %) S-811 and 63.68 wt % MLC 2142 was prepared in toluene. Vortex mixer was used to fully mix the solution. The mixture solution was put into vacuum oven at 50°C overnight to evaporate the co-solvent toluene.

Preparation of LC cell with SiN windows

Patterning of back side nitride

Hexamethyldisilazane solution was spin-coated at 4000 rpm, and then the S1813 photoresist was spin-coated at the same rate and baked at 150°C for 1 min. The resist was then patterned with Heidelberg MLA150 to define windows and alignment marks on the backside. The patterned wafer was developed in a 1:3 mixture of 351 developer and deionized (DI) for 60 s and rinsed with water. The exposed nitride was then etched and removed with CHF₃/O₂ plasma [50-sccm (standard cubic centimeters per minute) CHF₃, 2-sccm O₂, 20°C, 10 mT, 3-min conditioning, 100-W forward radio frequency (RF) power, and 200-W forward inductively coupled plasma (ICP) power]. The remaining resist was removed with acetone, rinsed in IPA, and dried with nitrogen.

Patterning of front-side alignment marks

The same photolithography process was processed on the front side. The exposed nitride and beneath Si were etched and removed with HBr/Cl/O₂ (20-sccm Cl, 20°C, 10 mT, 300-W forward RF power, and 1000-W forward ICP power for 5 s; Si etch, 2-sccm O₂, 50-sccm HBr, 12 mT, 20°C, 100-W forward RF power, and 250-W forward ICP power for 6 min). The remaining resist was removed with acetone, rinsed in IPA, and dried with nitrogen.

Preparing chemical pattern on the front side

A 4- to 5-nm-thick PMMAZO film was deposited on the piranha solution [7:3 (v/v) of 98% H₂SO₄/30% H₂O₂]–cleaned SiN substrate by spin coating a 0.05 wt % toluene solution and annealed at 250°C for 5 min in a glove box. Nongrafted PMMAZO brush was removed by sonication in toluene and the remaining PMMAZO brush was about 4.5 nm. A 60-nm-thick GL2000 photoresist was deposited on top of the PMMAZO brush and baked at 150°C for 3 min. The designed stripe patterns were obtained on the resist’s layer by using electron beam lithography (JEOL 9300FS electron-beam writer at the Center for Nanoscale Materials, Argonne National Laboratory). N-amyl acetate was used to develop the exposed substrates for 15 s, followed by rinsing with IPA. Then, the stripe pattern was transformed into the PMMAZO brush layer by oxygen plasma etching and stripping the GL2000 photoresist in NMP and chlorobenzene.

Preparing OTS-modified surface

Another nonpatterned SiN wafer was boiled in a piranha solution for 30 min and then washed by DI water and dried with nitrogen. The cleaned wafer was immersed in an OTS solution (13.8 μl of OTS and 120 ml of heptane). After 1 hour, it was removed from the OTS solution, washed by DCM for two times, and dried with nitrogen.

Back etch in KOH

The wafers, after the chemical pattern and OTS modification process, were set in a wet etch holder, O-rings were used to seal off the front side to protect the chemical pattern or OTS layer, and the window pattern at the back side was exposed. The wet etch holder was immersed in 30 wt % KOH solution at 85°C. The etching of silicon proceeded until reaching the silicon nitride on the front side. When the etching was done, the holder was removed from the KOH solution and rinsed with DI water in a cascade with the wafer inside. Last, the wafer was removed from the holder and dried.

Preparation of LC cells

The OTS SiN window and the window with the PMMAZO chemical patterns were heated above the isotropic temperature (~65°C). A 5-μl mixture of 2142/S-811 was dropped on the PMMAZO-coated SiN window. The OTS SiN window was placed face to face on top of the PMMAZO-coated window without spacer. The system was then slowly cooled down to room temperature. Five-minute cured epoxy glue was used to seal the sample, and the thickness of the final samples was less than 500 nm.

Characterization

Optical characterization was performed using cross-polarized and reflection mode with an Olympus BX60 microscope. Samples were heated up to the isotropic phase using a Bioscience Tools TC-1-100s temperature controller controlling hot stage at a rate of 0.2°C/1 min.

RSoXS was measured with transmission geometry at beamline 11.0.1.2 at the Advanced Light Source at Lawrence Berkeley National Laboratory (24). The BP LC was measured in the SiN sandwich membrane cell as described in the previous sample preparation section. All the measurements were conducted at 284.5 eV. A post–carbon K-edge of 284.5 eV was selected to obtain an enhanced scattering intensity. The beam was circular with a diameter of approximately 300 μm, and collection time was varied from 0.1 to 10 s. The in situ RSoXS measurement of BP LC phase transformation during heating and cooling was measured using a temperature-controlled stage. The temperature readout for RSoXS measurements was the thermocouple mounted in the temperature stage. The SiN sandwich cells are mounted on the temperature stage using copper tape to give better thermal contact. Since the measurement takes place in vacuum and the temperatures are near room temperature, heat transfer primarily takes place through the thermal contact between the sandwich cell and the stage, resulting in a small temperature differential between the thermocouple and the sample. Heating and cooling rates were 0.45°C/min and 0.10°C/min, respectively. A modified version of the NIKA software package was used for calibration and data reduction. The RSoXS data are calibrated using the peaks from the bottom chemical grating patterns (period, 150 nm).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/13/eaay5986/DC1

Note S1. Misaligned BP domains

Note S2. Continuum simulations

Note S3. Lattice strain calculation during the martensitic transformation

Note S4. Transformation pathway with shear strain

Fig. S1. RSoXS intensity profiles of BPI and BPII during heating.

Fig. S2. RSoXS peak indexing of misaligned domains.

Fig. S3. RSoXS peak indexing during the BPII to BPI martensitic transformation.

Fig. S4. Model system for the lattice transformation from BPII₍₁₀₀₎ to BPI₍₁₁₀₎.

Fig. S5. Transformation pathway with shear strain.

Fig. S6. Variation in half-pitch length (p/2) of chiral nematic during heating and cooling.

Fig. S7. The evolution of the scattering intensity and corresponding lattice constant during heating and cooling.

Fig. S8. Reconfiguration of disclination network during the martensitic transformation from BPII to BPI.

Fig. S9. Reconfiguration of disclination network on the yz and xz plane.

Table S1. Measured d-spacing and strain components of BPI₍₁₁₀₎ lattices at the beginning of the martensitic transformation from BPII₍₁₀₀₎.

Movie S1. Reconfiguration of disclination network during martensitic transformation.

References (25–27)