Abstract
We report on the synthesis and characterization of highly monodisperse amorphous silica nanoparticles (ASNs) and mesoporous silica nanoparticles (MSNs) with particle sizes of 15–60 nm. We demonstrate adsorption of Cr(VI) ions on amino-functionalized ASNs (NH2–ASNs) and MSNs (NH2–MSNs) and their removal from aqueous environments and show the specific surface area (SSA) of NH2–MSNs is four times as larger as that of NH2–ASNs and that more than 70% of the total SSA of NH2–MSNs is due to the presence of nanopores. Analyses of Cr(VI) adsorption kinetics on NH2–ASNs and NH2–MSNs exhibited relatively rapid adsorption behavior following pseudo-second order kinetics as determined by nonlinear fitting. NH2–ASNs and NH2–MSNs exhibited significantly higher Cr(VI) adsorption capacities of 34.0 and 42.2 mg·g−1 and removal efficiencies of 61.9 and 76.8% than those of unfunctionalized ASNs and MSNs, respectively. The Langmuir model resulted in best fits to the adsorption isotherms of NH2–ASNs and NH2–MSNs. The adsorption of Cr(VI) on NH2–ASNs and NH2–MSNs was an endothermic and spontaneous process according to the thermodynamic analyses of temperature-dependent adsorption isotherms. The removal efficiencies of NH2–ASNs and NH2–MSNs exhibited a moderate reduction of less than 25% of the maximum values after five regeneration cycles. Furthermore, NH2–MSNs were also found to reduce adsorbed Cr(VI) into less harmful Cr(III).
Subject terms: Nanoparticles, Characterization and analytical techniques, Pollution remediation, Nanoparticle synthesis, Synthesis and processing, Nanoparticles
Introduction
Chromium is used for many purposes in modern industries. For example, it is used to harden steel and make stainless steel, which are essential raw materials in the construction, heavy machinery, automotive, transportation, energy, and medical industries. Chromium is also used extensively in chrome electroplating processes, in paint pigments, and to produce dyes, leather, plastics, and photographs. These industrial activities generate substantial amounts of hazardous wastes containing relatively high concentrations of chromium, which is recognized as one of the most toxic inorganic pollutants due to its mutagenic and carcinogenic effects on biological species1,2.
In aqueous environments, chromium generally exists in the trivalent (Cr(III)) or hexavalent (Cr(VI)) oxidation states. Ionic species containing Cr(VI) such as CrO42− or HCrO4− are highly soluble and mobile in nature than Cr(III), and thus, Cr(VI) containing species pass through cell membranes readily, whereas Cr(III) species are poorly cell-permeable3. In fact, it has been estimated Cr(VI) is almost ~100 times more toxic than Cr(III) in aqueous environments4,5. Sequestration strategies targeting the adsorption and reduction of Cr(VI) to less harmful Cr(III) attracted considerable research attention because of their obvious advantages over strategies aimed at the separation of Cr(VI)6.
Methods such as adsorption7–9, ion-exchange10,11, membrane separation12,13, coagulation14, chemical precipitation15,16, extraction17, dialysis18, and electrochemical separation19 have been shown to be capable of removing heavy metal ions, including hexavalent chromium from wastewater. Of these different methods, adsorption is probably the most effective, economically feasible, environmentally sustainable, and technologically promising processes20. Recently, a variety of adsorbents such as activated carbons7,21, iron-based metal oxides22, metal-organic frameworks23, polymeric and biomass-based materials9,24,25 have been used for Cr(VI) removal. In particular, polymeric materials have been shown to be highly efficient at adsorbing Cr(VI) and their highly branched structures can be readily functionalized to selectively adsorb and remove different heavy metal ions26,27.
Silica and silica-based composite materials are an essential class of adsorbents that have been widely employed due to their unique and adjustable physicochemical characteristics, which include large surface areas and excellent chemical, thermal, and mechanical stabilities27. Stöber silica is often used as an adsorbent and generally described as a nonporous, monodisperse, and amorphous silica composed of spherical particles28. A variety of methods such as sol-gel, microemulsion, hydrothermal, and flame-based methods have been devised to synthesize silica particles with diameters in the colloidal range29. Over the past years, a collection of mesoporous silica, such as SBA-130, SBA-1531, MCM-4132, and MCM-4833 have been synthesized and also used as adsorbents that have highly ordered nanoscale pores with a wide range of pore geometries including hexagonal and cubic arrangements with relatively narrow size distributions. Mesoporous silica with uniform and tailorable pore dimensions exhibits unique material properties such as high specific surface areas and excellent thermal and mechanical stabilities, and hence, has been employed in potential applications34. These include their use in heavy metal removal from wastewater6, indoor air purification35, CO2 capture36, pervaporation membranes for the separation of water from ethanol37.
Both Stöber and mesoporous silica materials have been chemically functionalized to enhance Cr(VI) adsorption38,39. For example, nitrogen-containing functional groups like aliphatic and aromatic amines have demonstrated to be extremely effective at enhancing Cr(VI) adsorption27. It has been suggested that the adsorption behavior of Cr(VI) on functionalized silica surfaces depends on parameters such as the number densities and the binding strengths of the donor groups grafted onto adsorbent surfaces40,41. However, little is known of the processes involved, such as of the effect of specific functional groups, or of relationships between adsorption efficiencies and adsorbent sizes, shapes, morphologies, pore densities, and specific surface areas and many aspects of the processes have yet to be explored systematically.
Herein, we present the results of work aimed at preparing two types of bare and two types of NH2-functionalized silica nanoparticles of similar sizes, that is, amorphous silica nanoparticles (ASNs) with an amorphous solid core and mesoporous silica nanoparticles (MSNs) with a nanoporous core. Also, we investigated their Cr(VI) adsorption and removal performances using aqueous batch systems. N2 sorption measurements showed the specific surface areas (SSAs) of unfunctionalized MSNs were twice as large as those of ASNs, and that the SSAs of 3-aminopropyl triethoxysilane (APTES) functionalized MSNs (NH2–MSNs) were four times as large as those of APTES functionalized ASNs (NH2–ASNs). In addition, we confirmed that> 70% of the total SSAs of bare and NH2-functionalized MSNs were ascribable to nanopores using a simplified geometric scaling approach. We examined the effect of temperature and pH on adsorption and removal of Cr(VI) using bare and NH2-functionalized ASNs and MSNs. We discovered that unfunctionalized ASNs and MSNs had considerably lower adsorption capacities that were less than ~4% of those of NH2–ASNs and NH2–MSNs. Furthermore, we confirmed that the optimal pH for reaching maximum Cr(VI) uptake and removal efficiency were 2.0. Systematic analyses of Cr(VI) adsorption kinetics using non-linear fitting of a pseudo-second order kinetic model at pH 2.0 and 25 °C revealed rapid adsorption of Cr(VI) on NH2–ASNs and NH2–MSNs whereby ~90% of Cr(VI) was adsorbed within one minute. In-depth analyses of the equilibrium adsorption isotherms of NH2–ASNs and NH2–MSNs revealed that Langmuir model resulted in the best fit to the experimental data. NH2–ASNs and NH2–MSNs exhibited significantly higher Cr(VI) adsorption capacities (qe) of 34.0 and 42.2 mg·g−1 and removal efficiencies (R) of 61.9 and 76.8% than those of unfunctionalized ASNs and MSNs (0.4 and 1.3 mg·g−1 and 0.7 and 2.4%), respectively. Furthermore, we found that NH2-functionalized ASNs and MSNs could also reduce adsorbed Cr(VI) to Cr(III) and that the amount of Cr(VI) reduction adsorbed on NH2–MSNs was three times as large as those on NH2–ASNs.
Materials and Methods
Materials
Tetraethyl orthosilicate (TEOS, ≥ 99%, Aldrich), cetyltrimethyl ammonium chloride (CTAC, 95%, Wako), triethanolamine (TEA, ≥ 99%, Aldrich), 3-aminopropyl triethoxysilane (APTES, 99%, Aldrich), potassium dichromate (K2Cr2O7, ≥99.5%, KANTO), and 1,5-diphenylcarbazide (DPC, special GR grade, SAMCHUN) were purchased and used as supplied. All other chemicals including the solvents used such as toluene, acetone, absolute ethanol, 1 N sulfuric acid, hydrochloric acid solution (10 wt%), and ammonium hydroxide (NH4OH) solution (25 wt%) were of analytical ACS regent grade and once purchased, they were used as supplied.
Preparation of monodisperse ASNs
Stöber et al. originally reported the synthesis of ASNs via a base-catalyzed hydrolysis and condensation of TEOS42. This method and its modifications have been widely used to synthesize monodisperse ASNs43,44. We synthesized ASNs using a modified version of the original method. Typically, 4.43 mL TEOS was added dropwise to a pre-mixed solution of 1.35 mL doubly distilled deionized water (18.2 MΩ·cm), 200 mL absolute ethanol, and 2.25 mL 25 wt% NH4OH solution with stirring at 400 rpm. The resulting suspension was immediately stirred for 24 h at 25 °C and then dialyzed against 5 L of doubly distilled deionized water using a dialysis cellulose membrane tubing (pore size of 2.5–5 nm, Sigma Aldrich) to remove ethanol and ammonia from the suspension. The dialysate was refreshed 4 times at 2 h intervals. Finally, ASNs were precipitated by rotaevaporation for 30 min, filtered through a 0.2 μm nylon membrane, washed with an excess of absolute ethanol, and dried in a vacuum oven at 25 °C.
Preparation of monodisperse MSNs
Bein et al. reported the synthesis of MSNs using TEA as a complexing agent for silicic precursors and CTAC as a templating agent for inner pores within ASNs45. We synthesized highly monodisperse MSNs with sizes that closely matched those of as-prepared ASNs prepared in a similar manner46. Briefly, 0.5 g CTAC and 0.06 g TEA were dissolved in 20 mL doubly distilled deionized water at 80 °C with stirring at 700 rpm for 1 h. 1.5 mL of TEOS was then added dropwise at a rate of 1 mL/min. The resulting suspension was then immediately stirred for 1 h at 80 °C and as-synthesized MSNs were precipitated by centrifugation at 12,000 rpm for 15 min, washed with an excess of absolute ethanol to remove residual reactants, and dried in a vacuum oven at 25 °C. Finally, MSNs were calcined at temperatures up to 550 °C for 4 h using a heating rate of 10 °C·min−1 to remove CTAC from inner pores.
Surface functionalization of ASNs and MSNs with APTES
ASNs and MSNs were functionalized with APTES using a modification of a previously described method6,47. Approximately ~1 g of as-synthesized ASNs or calcined MSNs were reacted with 1 mL of APTES separately in 100 mL of toluene at 80 °C with vigorous stirring overnight. Products were removed by filtration, washed with an excess of absolute ethanol, and doubly distilled deionized water to remove most of the unreacted APTES, and dried in air at 25 °C. Because this washing step was not enough to remove all the unreacted and physisorbed APTES, products were re-immersed in doubly distilled deionized water (at sample/water ratio 1 g/L) with stirring for at least 24 h at 30 °C48. Finally, products were filtered, washed with an excess of absolute ethanol and doubly distilled deionized water, and dried in a vacuum oven at 25 °C.
Scanning electron microscopy (SEM), transmission electron microscopy (TEM), X-ray powder diffraction (XRD)
Sizes and morphologies of ASNs and MSNs were investigated by field emission scanning electron microscopy (FESEM) using a Zeiss Supra 40 FESEM unit at an accelerating voltage of 5 to 10 kV and by transmission electron microscopy (TEM) using a Hitachi H-7600 TEM operating at an accelerating voltage of 80 kV. High-resolution TEM (HRTEM) and scanning TEM (STEM) analyses were performed on an FEI TALOS F200X TEM operating at an accelerating voltage of 200 kV. The chemical compositions of ASNs and MSNs were analyzed simultaneously using an energy dispersive X-ray spectroscopy (EDS) detector attached to Zeiss Supra 40 FESEM. X-ray powder diffraction (XRD) patterns were produced using a Philips X’Pert-MPD Diffractometer equipped with a monochromatic X-ray of Cu Kα1 radiation (λ = 0.15405 nm) at 1.6 kW (40 kV, 30 mA).
Fourier transform infrared spectroscopy (FT-IR) and thermogravimetric analysis/differential thermal analysis (TGA/DTA)
ASNs, MSNs, NH2–ASNs, and NH2–MSNs were subjected to Fourier transformation infrared spectroscopy (FT-IR) using a Spectrum GX FT-IR spectrometer and KBr pellet and attenuated total reflection (ATR) techniques. Thermal analyses of NH2–ASNs and NH2–MSNs were carried out using a TA SDT Q600 thermal gravimetric analysis/differential thermal analysis (TGA/DTA) instrument. Typically, ~5 mg of sample was heated in an Al2O3 crucible at a heating rate of 5 °C/min under N2 flow of 100 mL/min for up to 750 °C.
X-ray photoelectron spectroscopy (XPS)
XPS data of ASNs, MSNs, NH2–ASNs, and NH2–MSNs were acquired using an ESCALAB 250 spectrometer equipped with a monochromatic X-ray source of Al anode Kα radiation (1486.6 eV) used as an excitation source. Binding energy was calibrated with respect to the C 1 s line of carbon at 284.6 eV before actual measurements.
Nitrogen (N2) physisorption experiments for Brunauer-Emmett-Teller (BET) and Barrett-Joyner-Halenda (BJH) analysis
N2 adsorption-desorption measurements were performed on a Quantachrome Autosorb-iQ surface area and pore size analyzer. Samples of ASNs, MSNs, NH2–ASNs, and NH2–MSNs were degassed at 300 °C for ~3 hours before actual measurements. BET analysis was used to calculate specific surface areas. Pore size distributions were calculated by BJH analysis of the isotherms’ desorption branches.
Reagents and standard preparations for UV-Visible spectrophotometric analysis (a.k.a. the DPC method)
A standard stock solution of Cr(VI) was prepared by dissolving 2.829 g of dried K2Cr2O7 in doubly distilled deionized water (18.2 MΩ cm) and then diluting further to 1000 mL and a 100 mg/L solution of Cr(VI) was prepared by diluting the standard stock solution. Separately, a 1,5-diphenylcarbazide (DPC) stock solution was prepared by dissolving 50 mg of DPC in 25 mL of acetone containing 250 μL of 1 N sulfuric acid49,50. Working standard Cr(VI) concentrations of 1, 10, 20, 50, and 100 mg/L were prepared from the standard stock solution and their pH values were adjusted to ~2.0 with a hydrochloric acid solution (10 wt%). Then, 3 mL aliquots from working standard solutions were mixed with 100 μL DPC stock solution to form Cr(VI)-DPC complexes, which were quantified by spectrophotometry (λmax = 540 nm) at equilibrium. The standard absorbance vs. concentration calibration plot was determined by linear regression to have a correlation coefficient (R2) of 0.9969 and used to determine Cr(VI) concentrations together with the results from inductive coupled plasma optical emission spectroscopy (ICP OES) before batch and kinetic batch experiments.
Batch and kinetic batch experiments on Cr(VI) adsorption and removal
Cr(VI) adsorption and removal experiments were conducted under equilibrium batch conditions. A series of solutions containing predetermined concentrations of Cr(VI) was prepared by diluting a 100 mg/L standard stock solution. All experiments were performed in duplicates under ambient conditions at a controlled temperature of 25 °C. Briefly, 4 mL of 100 mg/L Cr(VI) solution (pH = 2.0) was added to individual 10 mL volumetric flasks containing 8 mg of ASNs, MSNs, NH2–ASNs, and NH2–MSNs. Samples were mixed using a magnetic stirrer at 200 rpm for ~120 min, which was enough to establish adsorption equilibrium. Then, the liquid phase of each solution obtained by filtration through a polytetrafluoroethylene (PTFE-H) membrane of a pore diameter of 0.45 μm. Cr(VI) concentrations in solutions before and after the batch experiments were measured using the DPC method, and the results were used to calculate the amount of adsorption per used sorbents (qt) at equilibrium.
The effect of different initial pH values was investigated in the range of 2.0–7.0 with initial Cr(VI) concentration of 100 mg/L at 25 °C. The optimum pH value for yielding the maximum adsorption capacity was adopted for the remaining experiments. The effect of initial Cr(VI) concentration was explored in the range of 1–100 mg/L. The adsorption isotherms were measured by varying initial Cr(VI) concentration from 1–100 mg/L at four different temperatures of 25, 35, 45, and 55 °C within 2 h, respectively.
Time-dependent adsorption experiments were also conducted under a kinetic batch condition. NH2–ASNs or NH2–MSNs (4 mg of each) were added to a 10 mL volumetric flask containing a 100 mg/L Cr(VI) solution. Samples were then mixed using a magnetic stirrer at 200 rpm, and filtrates were obtained after incubation for 1, 3, 5, 10, 15, 30, 60, or 120 min. The Cr(VI) concentrations in solutions before and after the kinetic batch experiments were measured using the DPC method, and the results were used to calculate qt values.
Adsorption efficiency, (i.e., defined as the amount of Cr(VI) adsorbed by ASNs, MSNs, NH2–ASNs, and NH2–MSNs) and removal efficiency, (i.e., defined as the ability of non-functionalized and NH2–functionalized ASNs and MSNs to reduce Cr(VI) concentrations) at equilibrium, were calculated in each case using the following mathematical Eqs. 1 and 2
| 1 |
| 2 |
where qe (mg g−1) is the adsorption capacity, R (%) is the maximum Cr(VI) removal capacity, C0 (mg L−1) is the initial concentration of Cr(VI), Ce (mg L−1) is the equilibrium concentration of Cr(VI) remained in the solution after the batch experiment, V (L) is the volume of the solution used in the batch experiment, and W (g) is the weight of the nanoparticles such as ASNs, MSNs, NH2–ASNs, and NH2–MSNs used as adsorbents in the batch experiments.
Regeneration experiments
Desorption-regeneration experiment was performed 4 times for initial Cr(VI) concentration of 100 mg/L at 25 °C after Cr(VI) desorption by 0.1 M HCl solution at temperature and pH of 25 °C and 2.0. After desorption, NH2–ASNs and NH2–MSNs were filtered, dried, and re-dispersed in a 100 mL Cr(V) standard solution for 2 h incubation. The Cr(VI) concentrations in solutions before and after the incubation were determined using the DPC method. All the experiments were duplicated, and the average values of the measurements were selected for analysis and plotting while the errors of the measurements were kept within 5%.
Data analysis of adsorption kinetics
If an adsorption rate follows pseudo-second order kinetics with respect to the adsorption sites of sorbents, the appropriate kinetic equation may be expressed as Eq. 3
| 3 |
where qt is the amount adsorbed per sorbents used (mg·g−1) at time t (min), qe is the equilibrium adsorption capacity (mg·g−1), and k is the adsorption rate constant (g·mg−1·min−1). In general, pseudo-second order kinetics describes the kinetics of a system in which the concentration of one reactant is essentially constant, because it is present in excess, and thus, its concentration does not affect reaction rate. The reason why Eq. 3 used the term pseudo in our system was that the amount adsorbed on ASNs, MSNs, NH2–ASNs, and NH2–MSNs governed Eq. 3 instead of the concentration of Cr(VI) in solutions51. The adsorption reaction with forward (k1) and reverse (k−1) rates corresponding to Eq. 3 may be written as follows
| 4 |
where AS is a vacant adsorption site on a nanoparticle surface and Cr·AS2 represents a Cr(VI) ion adsorbed at two sites. Given the assumption that the adsorption process is not limited by diffusion and Eq. 4 is an elementary step, the corresponding rate of the above reaction is expressed as;
| 5 |
where Ci represents to the concentration of species i at time t, k1 is the forward reaction rate, and k−1 is the reverse reaction rate. Two additional assumptions are made to simplify Eq. 5 to 3. First, as adsorption is an irreversible process, the rate of desorption, (), is relatively insignificant and can be neglected. Second, the concentration of Cr(VI) in solutions (CCr) remains almost constant during the adsorption process52. Based on these assumptions, the concentrations of adsorbed species () and vacant sites to the amounts adsorbed () at time t and at equilibrium are proportional to qt and qe − qt, respectively.
| 6 |
| 7 |
Applying Eqs. 6 and 7 to Eq. 5 and subsequent integration of Eq. 5 and applying the initial condition of qt = 0 at t = 0 resulted in a non-linear equation for qt as a function of t.
| 8 |
where k2 is the pseudo-second order adsorption rate constant (g·mg−1·min−1), qt is the adsorption capacity (mg·g−1), i.e., the amount of Cr(VI) adsorbed per mass of nanoparticles used at time t, and qe is adsorption capacity (mg·g−1) at equilibrium.
A linearized form of Eq. 8 has often been used to obtain adsorption kinetics parameters using linear regression, which has been most widely used to analyze pseudo-order adsorption kinetics51,53–55.
| 9 |
Best fits to the adsorption data shown in Fig. 8A were obtained using both linear and non-linear regression using Eqs. 8 and 9, respectively. Plots of standardized residuals of the above best fits were obtained in order to assess the quality of the good fit (Fig. S5). Standardized residuals were calculated using the following expression
| 10 |
where (mg·g−1) is the amount of Cr(VI) adsorbed per mass of nanoparticles used at time t as predicted by best fit, and sd is the standard deviation of residuals (mg·g−1)51.
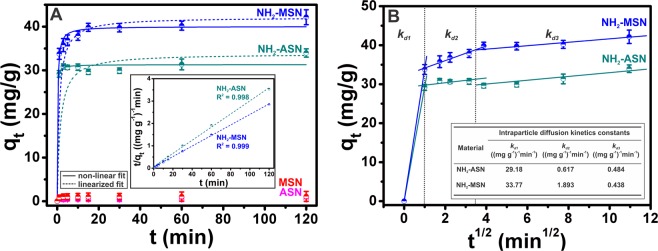
Figure 8.
(A) Cr(VI) adsorption kinetics of ASNs (magenta), MSNs (red), NH2–ASNs (dark cyan), and NH2–MSNs (blue) as determined by assuming pseudo-second order adsorption kinetics. Best fits to data were successfully obtained using linearized and non-linear fits. (B) Cr(VI) adsorption kinetics of NH2–ASNs and NH2–MSNs as determined using the intraparticle diffusion kinetics model. Best fits to data were successfully obtained in time regions, which indicated Cr(VI) adsorption was a multi-step process.
The intraparticle diffusion kinetics, as described by the Weber-Morris model, may be expressed with the following expression
| 11 |
where Kdi (g·mg−1·min1/2) is the rate parameter during stage i, which is calculated from the slope of the plot of qt versus t1/2, and Ci is the intercept during stage i, which provides information about the thickness of the boundary layer56,57. Best fits to the adsorption data shown in Fig. 8B were obtained by linear regression using Eq. 11.
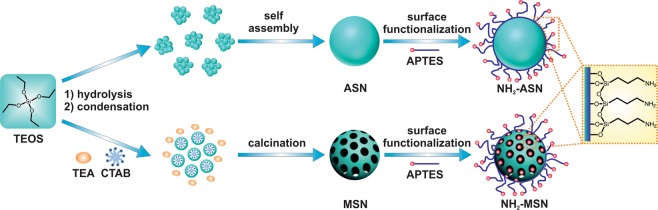
Figure 1.
Schematic diagram of the preparation of amorphous silica nanoparticle (ASN), mesoporous silica nanoparticle (MSN), and aminopropyl-functionalized ASN and MSN.
Results and Discussion
Structural analysis of ASNs and MSNs
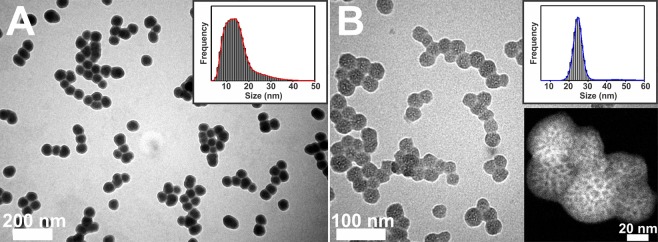
We used a method reported by Stöber and others42–44 to prepare amorphous silica nanoparticles (ASNs) of various sizes ranging from ~15 and ~60 nm. By using triethanolamine (TEA) and cetyltrimethylammonium chloride (CTAC) as surfactants to form sacrificial micelles, which templated pores within ASNs, we were able to produce mesoporous silica nanoparticles (MSNs) with nanoscale mesopores (a.k.a. nanopores) using a modified Stöber method46. Figure 1 illustrates a schematic diagram of their preparation. Figure 2 shows TEM micrographs of as-synthesized ASNs and MSNs with a relatively narrow size distribution (< ~10%). Annular dark-field scanning TEM (ADF-STEM) measurements of MSNs revealed a substantial contrast differentiation within the MSNs, which we attributed the difference of electron densities caused by the presence of nanopores (inset in Fig. 2B). These results suggest that nanopores of approximately sub-8nm diameter were present within MSNs but did not provide detailed information about the precise sizes, shapes, nor connectivities of the pores.
Figure 2.
TEM micrographs of (A) ASNs and (B) MSNs. Inset images (upper right) showing histograms of measured particle sizes. The inset in (B) (lower right) shows an annular dark-field scanning transmission microscopy (ADF-STEM) image of MSNs, which show contrast differences due to the existence of intraparticle nanopores.
FT-IR analysis of NH2–ASNs and NH2–MSNs
The ASNs and MSNs prepared were reacted with 3-aminopropyl triethoxysilane (APTES) to introduce surface amino (NH2–) groups immediately after their syntheses. Figure 3 shows FT-IR spectra of ASNs (magenta curve) and MSNs (red curve) before APTES functionalization exhibiting the following IR bands of silica moiety at ~3480 cm−1 (Si–OH), ~1100–1000 cm−1 (Si–O–Si), and ~920 cm−1 (Si–OH), which were consistent with values previously reported for silica nanoparticles synthesized by the Stöber method58,59. FT-IR spectra of NH2-functionalized ASNs (NH2–ASNs) and MSNs (NH2–MSNs) contained IR bands at ~2846–2932 cm−1 and ~1459 cm−1 (dark cyan and blue curve) that were assigned to the ν(C-H) stretching and δ(C-H) bending modes of the alkyl chain of bound APTES. The weak IR bands at ~1459 cm−1 of NH2–ASNs and of NH2–MSNs were assigned to the δ(N-H) bending mode of the amino group of bound APTES, respectively. These IR bands of the NH2–ASNs and NH2–MSNs were also consistent with previously reported values60,61.
Figure 3.
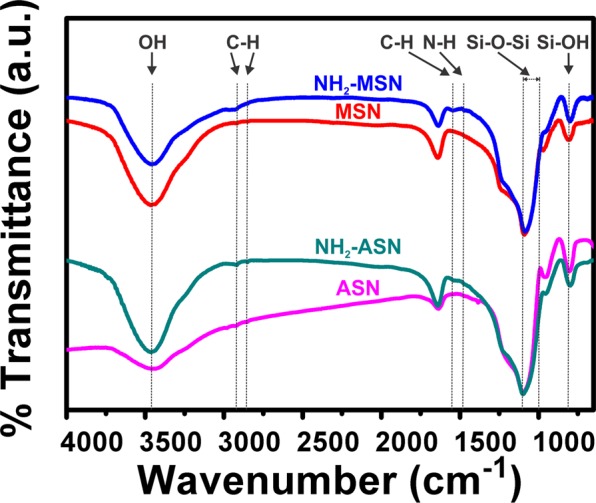
FT-IR spectra of ASNs (magenta), NH2–ASNs (dark cyan), MSNs (red), and NH2–MSNs (blue). The dotted lines indicate the characteristic IR bands of particular vibrational modes.
Specific surface area of non-functionalized and NH2–functionalized ASNs and MSNs
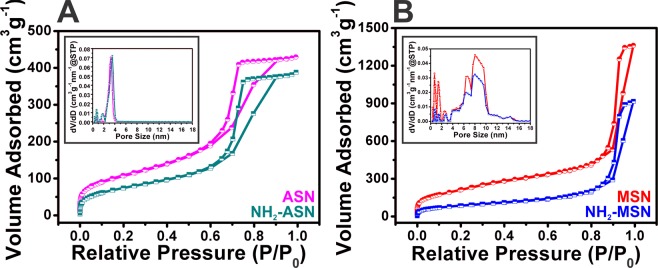
Low temperature N2 adsorption-desorption isotherms of ASNs, MSNs, and NH2–ASNs and NH2–MSNs were obtained to determine their specific surface areas and porosities. Figure 4 shows N2 sorption isotherms and pore size distributions of ASNs, NH2–ASNs, MSNs, and NH2–MSNs. The shapes of all four isotherms were similar to that of the characteristic type IV isotherm described in the IUPAC classification62,63. In particular, the isotherms of the ASNs and NH2–ASNs exhibited distinctive type H2 hysteresis (IUPAC classification) with an extended loop indicating the existence of disordered pores in the pressure (P/P0) range between 0.6 and 1. However, the hysteresis loop of isotherms of MSNs and NH2–MSNs was similar to type H1 hysteresis (IUPAC classification), which is commonly observed for mesoporous silica materials with well-defined cylindrical pores64,65 within the same pressure (P/P0) range. The pore size distributions of ASNs and NH2–ASNs (inset plots in Fig. 4A), as determined by the Brunauer-Emmett-Teller (BET)66 and Barrett-Joyner-Halenda (BJH)67 analysis, showed a major peak corresponding to their most probable size at ~3 nm. On the other hand, the pore size distributions of MSNs and NH2–MSNs (inset in Fig. 4B) revealed additional peaks, which suggested the presence of pores of different types slightly larger than ~3 nm. These results suggest that the major peaks observed in the pore size distributions of MSNs and NH2–MSNs were probably caused by void interstices formed by the external surfaces of the aggregated nanoparticles and that the additional peaks observed in those of MSNs and NH2–MSNs were caused by disordered nanopores within the nanoparticles.
Figure 4.
N2 sorption isotherms and pore size distributions of (A) ASNs (magenta) and NH2–ASNs (dark cyan) and of (B) MSNs (red) and NH2–MSNs (blue). The inset plots show the pore size distribution of (A) ASNs (magenta) and NH2–ASNs (dark cyan) and of (B) MSNs (red) and NH2–MSNs (blue).
The specific surface areas (SBET) and pore sizes of ASNs, MSNs, NH2–ASNs, and NH2–MSNs were determined from their low temperature N2 adsorption-desorption isotherms using the BET and BJH models. Table 1 summarizes the results. Measured specific surface areas of ASNs, NH2–ASNs, MSNs, and NH2–MSNs were 387.0, 272.9, 792.1, and 517.4 m2·g−1, respectively. Notably, the specific surface areas of MSNs and NH2–MSNs were nearly twice those of ASNs and NH2–ASNs, which suggested the presence of nanopores.
Table 1.
Sizes, specific surface areas (SBET), pore volumes, pore sizes, and functional group loadings of ASNs, NH2–ASNs, MSNs, and NH2–MSNs as determined by TEMa measurements, N2 sorption isotherms (BETb and BJHc models), and TGA/DTAd measurements.
| Material | Particle diameter (nm)a | Specific surface area (m2 g−1)b | Specific surface area (m2 g−1)c | Pore volume (cm3 g−1)c | Pore diameter (nm)c | Functional group loading (mmol g−1)d |
|---|---|---|---|---|---|---|
| ASN | 15 ± 1 | 387.0 | 281.9 | 0.66 | 3.43 | − |
| NH2-ASN | 15 ± 1 | 272.9 | 189.9 | 0.60 | 4.40 | 0.25 |
| MSN | 26 ± 2 | 792.1 | 517.4 | 2.11 | 5.32 | − |
| NH2-MSN | 26 ± 2 | 517.4 | 213.5 | 1.42 | 8.94 | 0.81 |
It has been reported that the hysteresis exhibited by the sorption isotherms of ASNs and NH2–ASNs is associated with capillary condensation in porous structures62,68. Because ASNs and NH2–ASNs can be modeled as hard spheres comprised of bulk SiO2, the arrangements of aggregated ASNs and NH2–ASNs and the interfacial gaps between particles also suggest that the hysteresis loop in their isotherms reflects porosity. Therefore, the SBET values of ASNs and NH2–ASNs are likely to be the result of contributions, by the geometric surface areas of ASNs and NH2–ASNs that are presumed to behave like hard nanospheres, and the surface areas of the porous architecture formed by the aggregations of these nanoparticles. On the other hand, the SBET values of mesoporous materials are equal to the sum of geometric surface, and micro- and meso-pore surface28,69.
The geometric specific surface areas (Sext) of nonporous spherical silica particles are inversely proportional to their diameter ‘d’ as described by the following mathematical expression 1228,70, where ρ is the density of bulk silica (SiO2).
| 12 |
Thus, Sext can be calculated from the d values of the silica nanoparticles as determined by TEM measurements. Based on assumptions made for the case of ASNs and NH2–ASNs, the SBET values of ASNs and NH2–ASNs were considered to be approximately equal to the sum of Sext and the surface area contributions of inner pores and resulting porous structures formed by the external surfaces of the aggregated nanoparticles (St) according to the following expression 13.
| 13 |
This approach has proven to be useful for understanding the nature of the specific surface areas of solid powders comprised of aggregated nanoparticles because the walls of their interstices are presumably formed by the external surface of the nanoparticles48. In the case of MSNs and NH2–MSNs, it is reasonable to assume that nanopore specific surface area (Snp) contributes to SBET, as described by the following expression 14.
| 14 |
In the case of 26 nm diameter MSNs and NH2–MSNs, interstitial environments are probably similar to those of comparably sized ASNs and NH2–ASNs. Therefore, it is reasonable to assume that the St values of 26 nm diameter MSNs and NH2–MSNs are similar to those of 26 nm diameter ASNs and NH2–ASNs, respectively. Size-corrected specific surface areas (S’BET) of 26 nm diameter ASNs and NH2–ASNs were extrapolated from a plot of SBET versus ASN size (see Fig. S1) and consequently, the corresponding St of 26 nm diameter MSNs and NH2–MSNs were estimated by the Sext of 26 nm diameter MSNs and NH2–MSNs from extrapolated S’BET values using the expression 13. In addition, the Snp of 26 nm diameter MSNs and NH2–MSNs were obtained from the expression 14 using the calculated S’BET and Sext values.
Table S1 summarizes various specific surface area types of ASNs, NH2–ASNs, MSNs, and NH2–MSNs. The Snp values of MSNs and NH2–MSNs were 519.0 and 358.4 m2·g−1, respectively. Comparison of the Snp and SBET values of MSNs and NH2–MSNs showed that the surface area contributions due to the presence of the nanopores were>65% of the total specific surface area (SBET). Accordingly, the geometric scaling approach enabled the different types of specific surface area of MSNs and NH2–MSNs to be evaluated, and the results obtained demonstrated the important roles of nanopores play in the adsorption of Cr(VI).
TGA analysis of ASNs, MSNs, NH2–ASNs, and NH2–MSNs
Amounts of amino groups on the surface of NH2–ASNs and NH2–MSNs were estimated by thermogravimetric analysis/differential thermal analysis (TGA/DTA). Figure S2 shows TGA/DTA curves of ASNs (magenta curve), NH2–ASNs (dark cyan curve), MSNs (red curve), and NH2–MSNs (blue curve) showing weight losses as a function of temperature. Based on TGA/DTA measurements, the functional group loading values of NH2–ASNs and NH2–MSNs were determined to be ~0.25 and ~0.81 mmol·g−1, respectively. Table S2 summarizes weight losses and functional group loadings of ASNs, NH2–ASNs, MSNs, and NH2–MSNs. Note that the functional group loading on NH2–MSNs was more than three times greater than on NH2–ASNs, which we attribute the presence of nanopores.
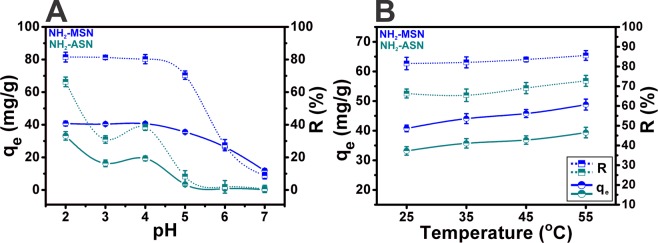
Effects of pH and temperature on Cr(VI) adsorption and removal from aqueous solutions using ASNs, MSNs, NH2–ASNs, and NH2–MSNs
ASNs and MSNs exhibited an extremely lower Cr(VI) adsorption (i.e., their adsorption capacity (qe) obtained using Eq. 1 less than ~4% of those of NH2–ASNs, and NH2–MSNs shown in Table 2 and Fig. 8A), which was considered to be relatively insignificant. Thus, only the Cr(VI) adsorption and removal of NH2–ASNs, and NH2–MSNs were investigated for most of the batch experiments. Figure 5 shows the effects of pH and temperature on Cr(VI) adsorption and removal from aqueous solutions in the pH and temperature range of 2.0–7.0 and 25–55 °C, respectively. A few aspects of the results are worth addressing. First, the adsorption capacity (qe), defined in Eq. 1, of NH2–ASNs and NH2–MSNs increased from 33.2 to 39.4 and 40.8 to 44.8 mg·g−1 while the removal efficiency (R), defined in Eq. 2, slightly increased from 66.3 to 72.7 and 81.5 to 85.6% with the increasing of temperature, respectively. Although the amounts of increase were not high, they were consistent with the hypothesis that raising the temperature from 25 to 55 °C marginally favors the adsorption of Cr(VI). Also, the increases in the adsorption capacity of NH2–ASNs and NH2–MSNs with the increasing temperature implied the endothermic nature of the adsorption process. Second, the qe of NH2–ASNs and NH2–MSNs improved from 0.2 to 33.2 and 11.8 and 40.8 mg·g−1, and the R from 0.6 to 66.3 and 8.8 to 82.2% significantly by decreasing the pH of the solution from 7.0 to 2.0, respectively. Hence, our results indicated that a higher adsorption capacity was obtained at a lower pH.
Table 2.
Adsorption and removal efficiency parameters of ASNs, NH2–ASNs, MSNs, and NH2–MSNs as determined by Cr(VI) adsorption batch experiments. Cr(VI) adsorption efficienciesa were obtained from spectrophotometric measurements using the DPC method. Cr(VI) removal efficienciesb were calculated using Eqs. 1 and 2. Total Cr removalc was estimated based on the amount of Cr(VI) and Cr(III) adsorbed on nanoparticle surfaces. Cr(VI) reductiond was estimated by considering the amount of Cr(III) in aqueous solutions and on the surfaces of nanoparticles.
| Material | Cr(VI) adsorption efficiencya (mg g−1) | Cr(VI) removal efficiencyb (%) | Total Cr removalc (mg g−1) | Cr(VI) reductiond (mg g−1) |
|---|---|---|---|---|
| ASN | 0.4 | 0.7 | — | — |
| MSN | 1.3 | 2.4 | — | — |
| NH2-ASN | 34.0 | 61.9 | 32.6 | 11.5 |
| NH2-MSN | 42.2 | 76.8 | 39.8 | 34.7 |
Figure 5.
Effect of pH and temperature on Cr(VI) adsorption and removal. The adsorption capacity (qe) and removal efficiency (R) of NH2–ASNs and NH2–MSNs as a function of solution pH and temperature.
The effect of pH can be rationalized by considering the surface charge of the nanoparticle adsorbents and the degree of ionization of Cr(VI) species. In general, Cr(VI) ions exist in several anionic forms such as HCrO4−, CrO42−, HCr2O7−, and Cr2O72− in aqueous solution depending on the solution pH and concentration3. H2CrO4 exists primarily at strong acidic pH (< ~2) and HCrO4− and Cr2O72− are usually detected at pH range of 2.0–6.0. When the pH increases to 7.0 and above, CrO42− is likely to be the primary ionic species. Considering that the pKa of the NH2–groups lies within the pH range 9–10, the surfaces of NH2–ASNs and NH2–MSNs are likely to be composed of ammonium (NH3+-) and silanol (-Si-O-H) moieties and confer nanoparticle surfaces a net positive charge under acidic conditions71. Figure S3 shows measurements of pH at the point of zero charge (pHpzc) on the surface of NH2-functionalized ASNs and MSNs. The values of pHpzc of NH2–ASNs and NH2–MSNs were determined to be 8.5 and 8.4, respectively. These results provide compelling evidence that the surface of NH2–ASNs and NH2–MSNs is positively charged for pH below the value of pHpzc. Since Cr(VI) species formed under these conditions are likely to be anionic HCrO4− and Cr2O72−, these results warrant electrostatic attraction of the anionic Cr(VI) species. However, with increasing pH, the amount of NH2–groups to be protonated is likely dropped. At the same time, the concentration of hydroxyl (OH−) ion increased and electrostatically competed against anionic Cr(VI) species, leading to a decline of Cr(VI) adsorption and removal efficiency. In summary, a very low solution pH was required to achieve high protonation of the surface NH2–groups and provide the necessary electrostatic attraction of anionic Cr(VI) species. Consequently, pH = 2.0 was selected as the optimal pH of Cr(VI) aqueous solution for the following batch experiments at 25 °C.
Cr(VI) adsorption and removal efficiency of ASNs, MSNs, NH2–ASNs, and NH2–MSNs
A series of batch experiments on Cr(VI) adsorption and removal was carried out at the optimal pH and temperature of 2.0 and 25 °C, respectively. Table 2 summarizes the adsorption and removal efficiency parameters of ASNs, MSNs, NH2–ASNs, and NH2–MSNs by the Cr(VI) adsorption batch experiments. Notably, the adsorption efficiencies (qe) of NH2–ASNs and NH2–MSNs were ~40 to 80 times greater than those of ASNs and MSNs, which confirmed the impact of NH2–functionalization on the Cr(VI) adsorption efficiency27,39. Maximum Cr(VI) removal capacity (R) represents the ability of an adsorbent to remove Cr(VI) from aqueous environments. The maximum Cr(VI) removal capacities of NH2–ASNs and NH2–MSNs were determined to be 61.9 and 76.8%, respectively. These values were comparable or marginally better than those reported for functionalized silica nanoparticles72,73, mesoporous silica6,39,48,74–76, and other hybrid multifunctional nanoparticles77,78 designed for Cr(VI) removal. Notably, the maximum Cr(VI) removal capacity of NH2–MSNs was 76.8%, which was 1.2 times higher than the 61.9% of NH2–ASNs. Thus, our results suggest that a combination of a high density of nanopores within silica nanoparticles and high surface coverage by functional amine groups enhance both adsorption and removal efficiencies of Cr(VI).
XPS analysis of Cr(VI) adsorption on ASNs, MSNs, NH2–ASNs, and NH2–MSNs
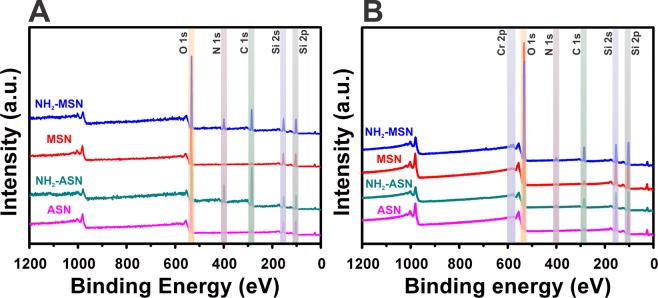
Figure 6 shows survey XPS spectra of ASNs, MSNs, NH2–ASNs, and NH2–MSNs before and after Cr(VI) adsorption. The survey XPS spectra in Fig. 6A, which were obtained over the full energy range confirm the existence of common elements such as O and Si before Cr(VI) adsorption. Note that the presence of C 1 s and N 1 s peaks in the spectra of NH2–ASNs and NH2–MSNs in Fig. 6A confirmed the presence of surface NH2 moieties. High resolution XPS scans of NH2–ASNs and NH2–MSNs in Fig. S4 revealed the following binding energies (BEs): a C 1 s peak at 284.7–284.9 eV, a N 1 s peak at 399.0–399.1 eV, a O 1 s peak at 532.2–532.3 eV, and a Si 2p peak at 101.9–102.3 eV. Comparison of O 1 s spectra of NH2–ASNs and NH2–MSNs in Fig. S4 shows that their oxygen BEs were similar to those of bound oxygen in bulk silicon di- and sub-oxides, which typically appear at 532.0–533.0 eV. It is worth mention that the Si 2p spectra of NH2–MSNs showed a single peak at 102.3 eV, which was marginally higher than that of NH2–ASNs at 101.9 eV. Considering the fact that the characteristic Si 2p BE peaks of elementary Si and SiO2 reported in the literature are at 99.5 and 103.5 eV79, respectively, our results imply that silicon in the surface layer of NH2–ASNs and NH2–MSNs may exist as intermediate sub-oxide phases (SiOx, 0 < x ≤ 1) rather than the fully oxidized SiO279,80 due to a greater presence of elementary non-oxidized Si in the surface layers of NH2–ASNs and NH2–MSNs. Furthermore, these values were consistent with those reported for functionalized silica nanoparticles39,81, and mesoporous silica6,46 systems.
Figure 6.
Survey XPS spectra of ASNs (magenta), NH2–ASNs (dark cyan), MSNs (red), and NH2–MSNs (blue) before (A) and after (B) Cr adsorption. Note the presence of C 1s and N 1s peaks in the survey spectra in (A and B), which confirmed NH2–functionalization of ASNs (NH2–ASNs) and MSNs (NH2–MSNs), and the Cr 2p peaks in B after Cr(VI) adsorption.
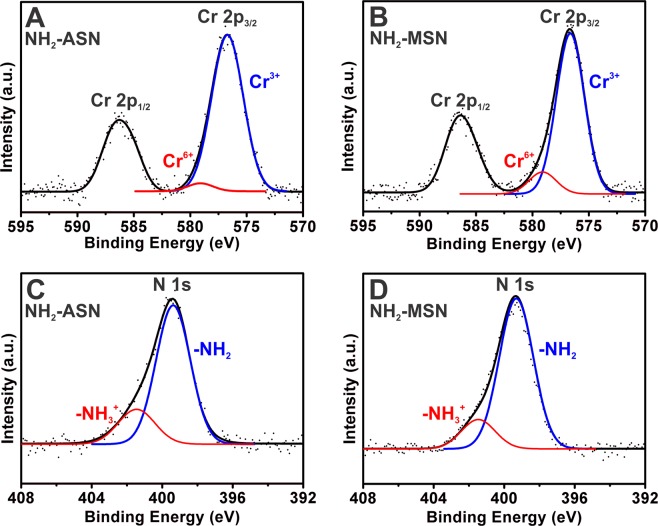
The presence of Cr 2p peaks in the survey XPS spectra of NH2–ASNs, and NH2–MSNs (Fig. 6B) confirmed the surface adsorption of chromium. Figure 7 shows high resolution Cr 2p and N 1 s XPS spectra of the Cr adsorbed NH2–ASNs and NH2–MSNs. The two asymmetric peaks shown in Fig. 7A,B were assigned to Cr 2p1/2 and Cr 2p3/2 orbitals. Deconvolution of the corresponding Cr 2p2/3 spectra in Fig. 7A,B showed two symmetric peaks that were best fitted by Lorentzian-Gaussian functions. The peak (blue) centered at ~576.7 eV was assigned to Cr(III) species, while peak (red) centered at ~579.1 eV was attributed to Cr(VI) based on previously reported values6,82. The relative ratios of Cr(III) to Cr(VI) on the surface of the NH2–ASNs and NH2–MSNs (Cr(III)/Cr(VI)) were ~24.7 and ~7.5, respectively, and were obtained from the areas of the Lorentzian-Gaussian curves (indicated by blue and red curves in Fig. 7). These values imply that most of the Cr adsorbed was in oxidation state III rather than VI. Therefore, the amount of Cr(VI) reduced to Cr(III) was estimated from the values in Table 2. The quantity of total Cr removal in Table 2 corresponds to the amount of chromium ions, including Cr(VI) and Cr(III), eliminated from the solutions after the batch adsorption experiments. They were quantitatively determined by inductively coupled plasma optical emission spectroscopy (ICP OES) in addition to the DPC method. Note that the values of total Cr removal were smaller than that of Cr(VI) adsorption capacity in Table 2. We hypothesize that this may be because a significant proportion of adsorbed Cr(VI) ions was reduced to Cr(III), and a fraction of adsorbed Cr(III) ions was released back to the aqueous solutions6. Based on the hypothesis, the values of Cr(VI) reduction in Table 2 were obtained by determining both the amount of Cr(III) ions in solution and the amount of Cr(III) adsorbed on the surface of NH2–ASNs and NH2–MSNs measured by high resolution XPS.
Figure 7.
High resolution XPS spectra of Cr 2p (A and B) and N 1s (C and D) of NH2–ASNs and NH2–MSNs after Cr(VI) adsorption. Dotted black curves were obtained from XPS measurements, and solid black curves are best fits obtained by Lorentzian-Gaussian deconvolution. Blue and red curves obtained by the deconvolution of (A and B) were assigned to Cr(III) and Cr(VI), respectively. Blue and red curves of (C and D) were assigned to neutral NH2- and cationic NH3+- moieties on the surfaces of NH2–ASNs and NH2–MSNs after Cr(VI) adsorption, respectively.
Our high resolution XPS results in Fig. 7, the pHpzc vaules, and the results summarized in Table 2 suggest that adsorption is initiated by electrostatic attraction between anionic Cr(VI) species and surface ammonium groups followed by the reduction of most Cr(VI) to Cr(III). Fellenz et al. reported that the Cr(III) to Cr(VI) ratio of chromium adsorbed on aminopropyl-functionalized MCM-41 sorbents as determined by XPS was close to 1 after Cr(VI) adsorption from aqueous environments at pH ~2.06. They also analyzed the XPS spectra of the same samples in the region of N 1 s and determined that N 1 s BEs of ~400.0 and ~402.0 eV corresponded to cationic ammonium (–NH3+) and neutral amino (–NH2) moieties, respectively, which concurred with previously reported values83. Figure 7C,D show deconvoluted N 1 s XPS spectra of Cr adsorbed NH2–ASNs and NH2–MSNs were composed of two peaks located at ~399.3 and ~401.5 eV, which were assigned to –NH3+ and –NH2 groups, respectively. In the present study, the relative ratios of –NH2 to –NH3+ groups on the Cr adsorbed NH2–ASNs and NH2–MSNs as determined from areas of the Lorentzian-Gaussian curves, were ~3.7 and ~5.2, respectively. These values suggest that –NH2 surface coverage was considerably higher than that of –NH3+ group coverage, which contradicts expectation because at a pH of ~2.0 –NH3+ groups should predominate71. We offer the following explanation for this observation. First, anionic HCrO4− and Cr2O72− species electrostatically interact and bind to surface cationic –NH3+ of NH2–ASNs and NH2–MSNs, and subsequently Cr(VI) is reduced to less toxic Cr(III), and either H+ from NH3+–groups is likely released to medium, or some of adsorbed Cr(III) are desorbed and released to the aqueous solution to maintain electrostatic charge balance. This explanation is reasonably consistent with the Cr(III) to Cr(VI) ratios shown in Fig. 7, although these ratios were slightly higher than previously reported values6,39.
Cr(VI) adsorption kinetics of ASNs, MSNs, NH2–ASNs, and NH2–MSNs
The Cr(VI) adsorption kinetics of ASNs, MSNs, NH2–ASNs, and NH2–MSNs are shown in Fig. 8. Figure 8A shows that >95% of Cr(VI) was rapidly adsorbed by NH2–ASNs and by NH2–MSNs during the first few minutes of experiments and that the remainder of the Cr(VI) was adsorbed slowly. The Cr(VI) adsorption on NH2–ASNs and NH2–MSNs exhibited a saturation behavior when the contact time reached 120 min, which suggests not enough adsorption sites for anionic Cr(VI) species were available. As more anionic Cr(VI) species were adsorbed on NH2–ASNs and NH2–MSNs, more electrostatic repulsion between negatively charged Cr(VI) species likely resulted in decreasing the removal efficiency. Although the Cr(VI) adsorption kinetics of ASNs and MSNs were similar to the trend of NH2–ASNs, and NH2–MSNs, they exhibited an extremely lower adsorption behavior with their qe values less than ~4% of those of NH2–ASNs, and NH2–MSNs. Because the adsorption capacities of ASNs and MSNs were considered to be relatively insignificant, only the results of NH2–ASNs, and NH2–MSNs were analyzed by obtaining best fit to data using a linearized form of the pseudo-first order model84,85, for which log(qe-qt) was plotted versus t, and a linearized form of the pseudo-second order model86,87, for which qt/t was plotted versus t/qe. These models are frequently used to describe various adsorption processes involving widely different adsorbents and adsorbates52,88. The validity of each model was confirmed using correlation coefficients (R2) and by checking agreement between experimental and fitted value of qe. The inset plot in Fig. 8A shows that applying the linearized form of the pseudo-second order model to our data resulted in much higher correlation coefficients (R2 > 0.99) than pseudo-first model (R2 < 0.86). Surprisingly, corresponding plots with correlation coefficients (R2 > 0.99) of the Cr(VI) adsorption kinetics of NH2–ASNs and NH2–MSNs (dashed curves in Fig. 8A) did not produce good fits using the linearized fitting process particularly for time between 0 and 20 min. Instead, using nonlinear regression and a pseudo-second order model resulted in much improved fit (solid curves in Fig. 8A) especially for time in the same window. As regards qe, reasonably good agreement was also obtained between calculated (qe,fit) and experimental (qe,exp) values for NH2–ASNs and NH2–MSNs using a pseudo-second order model. Table 3 summarizes the kinetic parameters of Cr(VI) adsorption kinetics on NH2–ASNs and NH2–MSNs as determined by best fits with the pseudo-second order model using nonlinear regression. It is worth mention that the qe,fit value of NH2–MSNs obtained under equilibrium condition was 40.01 mg·g−1 and this was ~1.3 times greater than that of NH2–ASNs. On the other hand, the pseudo-second order rate constant (k2) of NH2–MSNs was 0.111 (mg·g−1)−1·min−1, which was barely one-fourth of that of NH2–ASNs.
Table 3.
Kinetic parameters of Cr(VI) adsorption on NH2–ASNs and NH2–MSNs determined from best fits to the pseudo-second order model shown in Fig. 8A using linearizeda and nonlinearb fits.
| Material | qe,exp (mg g−1) | Pseudo-2nd order model (linearized fit)a | Pseudo-2nd order model (nonlinear fit)b | |||
|---|---|---|---|---|---|---|
| k2 ((mg g−1)−1 min−1) | qe,fit (mg g−1) | R2 | k2 ((mg g−1)−1 min−1) | qe,fit (mg g−1) | ||
| NH2-ASN | 33.97 | 0.020 | 33.78 | 0.998 | 0.430 | 31.28 |
| NH2-MSN | 42.16 | 0.023 | 41.13 | 0.999 | 0.111 | 40.01 |
The reason why the well-accepted linearized form of the pseudo-second order model did not lead to a good fit is unclear. This observation implies that the Cr(VI) adsorption process might violate one of the important assumptions of the pseudo-second order model, namely that, 1) the adsorption process is irreversible with no desorption, 2) the concentration of Cr(VI) in medium remains essentially constant, at least during the early adsorption period, and 3) the adsorption process is not limited by diffusion52. Xiao et al. investigated the reasons why they obtained spuriously high value of correlation coefficients (R2 ~ 1) even when a linearized form of the pseudo-second order model resulted in questionable fits51. They concluded that if the pseudo-second order model truly represents experimental data, the nonlinear form should be used instead and that the result be verified using a standardized residual (SR) plot to determine whether residuals are randomly determined and their standard deviations are close to zero51. Figure S5 shows that nonlinear fitting delivered the best overall fits with relatively low standardized residuals randomly distributed near zero (i.e., standardized deviations near zero), which was not the case for linearized fitting, and is consistent with a suggestion by Xiao et al.51. Therefore, our results show that pseudo-second order adsorption kinetics appropriately describe the adsorption of Cr(VI) by NH2–ASNs and NH2–MSNs. In addition, our results also suggest that Cr(VI) adsorption is the result of chemisorption by NH2–ASNs or NH2–MSNs via electrostatic interaction, which is also consistent with our XPS results.
The intraparticle diffusion kinetics based on the Weber-Morris model was used to investigate Cr adsorption process to obtain insight of the mechanism involved. Figure 8B shows the adsorption kinetics of Cr(VI) on NH2–ASNs and NH2–MSNs in three separate time windows and best fits to data resulted in three straight lines for plots of qt versus t1/2. These linearities imply adsorption probably involves three steps, and the slopes of these plots may determine adsorption rate during these steps. Inset table in Fig. 8B presented the values of the rate constant kd1, kd2, and kd3 involving three steps. Several aspects of processes based on the intraparticle diffusion kinetics are worth addressing. First, the kd1 value of NH2–MSNs was slightly larger than that of NH2–ASNs probably due to their higher specific surface area. However, the rate constant kd2 and kd3 of NH2–ASNs and NH2–MSNs were not significantly different. Second, a comparison of the rate constants (i.e., kd1≫ kd2 > kd3) revealed that the second and third steps of Cr(VI) adsorptions on NH2–ASNs and NH2–MSNs were slower than the first and that the rate constants kd2 and kd3 were similar to those obtained by nonlinear fitting using the pseudo-second order model. This analysis suggests the second and third steps were rate-limiting. Third, the results of our analysis based on the intraparticle diffusion kinetics is reasonably consistent with the idea that the concentration of Cr(VI) in solutions gradually decreased with time without significant desorption of Cr(VI) from the surface of NH2–ASNs and NH2–MSNs. Above all, our analyses show that the intraparticle diffusion kinetic model could interpret the mechanism of adsorption to a reasonable extent.
A few questions remain concerning our analysis of Cr(VI) adsorption kinetics. First, our results provide limited data of qt within the early time window (t ≪ 1 min) because measuring the amount of Cr(VI) adsorption after ≤ 1 min by the DPC methods was difficult and would probably result in unreliable measurements. Therefore, the lower bounds of kd1 rate constants were estimated using best fits with data. Based on these estimates, we concluded that the first step, which was completed within ≤ 1 min, is probably related to the instantaneous adsorption of Cr(VI) onto the external surfaces of NH2–ASNs and NH2–MSNs. Since Cr(VI) concentration in aqueous environments is relatively high during the initial step, a large concentration gradient may drive the diffusion of Cr(VI) species to the surfaces of NH2–ASNs and NH2–MSNs. It is worth recalling that the lower bound rate constant kd1 was ~6 times greater than those of Cr(VI) physisorption on Fe3O4 nanoparticles hybridized with carbonaceous materials88 and on unfunctionalized mesoporous silica38. Though we cannot say definitively that direct comparison between our system and these systems was valid, a sudden increment during the initial step is reminiscent of an enhancement effect by specific functional groups, such as –NH2 or –NH3+ groups, which likely accelerate the initial step of Cr(VI) chemisorption process by lowering the kinetic energy barrier. Second, it may be inadvisable to separate the second and third steps because kd2 and kd3 values were of the same order of magnitude as those obtained by nonlinear fitting using the pseudo-second order model. However, these rate-limiting steps may well be involved in an interplay between intraparticle diffusion and equilibration processes at extremely low Cr(VI) concentrations. We do not think it is likely that significant desorption of Cr(VI) occurred because most of the Cr(VI) adsorbed was reduced to Cr(III), as determined by XPS, and little Cr(VI) remained on NH2-ASNs and NH2-MSNs during the second and third steps.
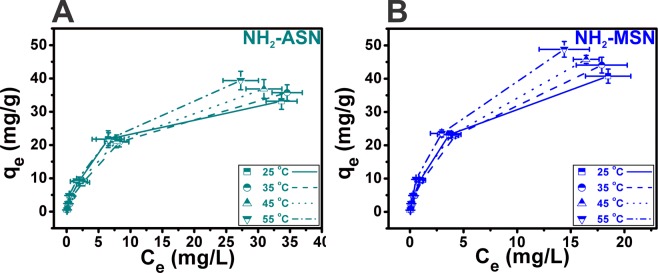
Effect of temperature and adsorption isotherm of NH2–ASNs and NH2–MSNs
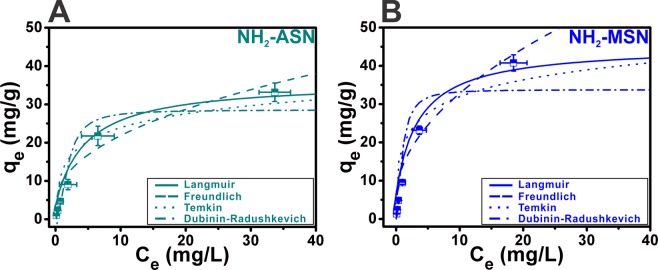
Figure 9 shows the correlation curves between the equilibrium adsorption capacity (qe) and equilibrium concentration (Ce) of Cr(VI) under four different temperatures at pH of 2.0. The equilibrium adsorption capacity of NH2–ASNs and NH2–MSNs increased with the increasing of temperature, which was consistent with the results shown in Fig. 5B. To understand the relationship between qe and Ce under equilibrium conditions, the adsorption isotherms of NH2–ASNs and NH2–MSNs were analyzed by obtaining best fits to data using the extensively used Langmuir, Freundlich, Temkin, and Dubinin-Radushkevich (D-R) models89.
Figure 9.
Cr(VI) adsorption isotherms of (A) NH2–ASNs and (B) NH2–MSNs as a function of temperature.
Langmuir model, which was primarily designed to describe gas-solid phase adsorption processes, has been often used to quantify the adsorption capacity of various adsorbents in solutions90. The Langmuir isotherm was expressed in the following nonlinear and linearized form
| 15 |
| 16 |
where KL (L·mg−1) and qm (mg·g−1) is the Langmuir isotherm constant and the corresponding saturation adsorption capacity, respectively.
Freundlich model has been used to characterize adsorption processes that occur on heterogeneous surfaces91. Its isotherm provides useful information on the surface heterogeneity, the exponential distribution of active sites, and their energetics. The Freundlich isotherm was expressed in the following nonlinear and linearized form
| 17 |
| 18 |
where KF (mg·g−1) is the Freundlich isotherm constant that is an approximate indicator of adsorption capacity, while 1/n is the measure of adsorption intensity.
Temkin model takes into account the effects of adsorbate-adsorbate interactions. It assumes that the heat of adsorption of all molecules in the layer decreases linearly rather than logarithmic with the increasing surface coverage92. The Temkin isotherm was expressed in the following nonlinear and linearized form
| 19 |
| 20 |
where R (8.314 J·mol−1·K−1) is the gas constant, T (K) is the absolute temperature, KT (L·g−1) is the Temkin isotherm equilibrium binding constant, and bT is the Temkin isotherm constant related to the heat of sorption (J·mol−1).
Dubinin-Radushkevich (D-R) model is a semi-empirical equation in which adsorption follows a pore filling mechanism with Gaussian energy distribution onto heterogeneous surfaces93. It has been successfully applied to describe the adsorption of gases on microporous adsorbents quantitatively94. The D-R isotherm was expressed in the following nonlinear and linearized form
| 21 |
| 22 |
where KDR (mol2·kJ−2) and qs (mg·g−1) is the D-R isotherm constant and the theoretical D-R isotherm saturation capacity, respectively.
Both the nonlinear and linearized form of the four models were used to obtain best fits to adsorption equilibrium data of NH2–ASNs and NH2–MSNs at 25–55 °C and pH of 2.0. Figure 10 illustrates the results of best fits to the adsorption equilibrium data of NH2–ASNs and NH2–MSNs using the nonlinear form of the four models. Figure S6 shows the results of best fits to the adsorption equilibrium data of NH2–ASNs and NH2–MSNs using the linearized form of the four models. Table S3 summarizes the isotherm parameters and correlation coefficients such as R2 and χ2 obtained from best fits to data using the linearized and nonlinear form of the four models, respectively. The value of sum-of-squares (i.e., a measure of scatter of data points around the fitted curve) is used to compute R2 and χ2 is similarly calculated by minimizing the sum-of-squares of the nonlinear regression. The validity of each model was confirmed using R2 and χ2. According to R2 (0.95 < R2 < 0.99), the Langmuir and Freundlich models could fit the adsorption process reasonably well. However, applying the Langmuir model to the data of NH2–ASNs and NH2–MSNs resulted in improved fits with much smaller χ2 values than the Freundlich model. Consequently, our results suggest that the adsorption process of NH2–ASNs and NH2–MSNs follows the Langmuir isotherm better than the Freundlich model. A dimensionless separation factor RL, one of the characteristic parameters of the Langmuir isotherm, was defined as
| 23 |
where the value of KL is the fitting parameters listed in Table S3 and the C0 is the initial Cr(VI) ion concentration (0 ≤ C0 ≤ 100). The value of RL indicates the shape of the Langmuir isotherm to be either unfavorable (RL > 1), linear (RL = 1), favorable (0 < RL < 1), or irreversible (RL = 0)95. Figure S7 shows the RL of NH2–ASNs and NH2–MSNs was less than 1. Note that the values of RL from the Langmuir model and 1/n from the Freundlich (Table S3) all lie between 0 and 1, which corroborates that the adsorption of Cr(VI) on both NH2–ASNs and NH2–MSNs is a favorable process with the maximum adsorption capacity of NH2–MSNs ~1.3 times greater than that of NH2–ASNs.
Figure 10.
Cr(VI) adsorption isotherms of (A) NH2–ASNs and (B) NH2–MSNs at 25 °C. Best fits to data were successfully obtained using non-linear fits of the Langmuir, Freundlich, Temkin, and Dubinin-Radushkevich (D-R) models.
Adsorption thermodynamics of NH2–ASNs and NH2–MSNs
Thermodynamic parameters of the adsorption process, such as change in standard free energy (ΔG°), enthalpy (ΔH°), and entropy (ΔS°) can be estimated from the data of the adsorption isotherm measured at various temperatures according to Eqs. 24, 25, and 26
| 24 |
| 25 |
| 26 |
where K0 is the adsorption distribution coefficient, which was obtained by plotting ln(qe/Ce) versus Ce at different temperatures and extrapolating to zero Ce96, ΔH° (kJ·mol−1) is the standard enthalpy change, ΔS° (J·mol−1·K−1) is the standard entropy change, ΔG° (kJ·mol−1) is the standard free energy change, R (8.314 J·mol−1·K−1) is the gas constant, and T (K) is the absolute temperature, respectively. ΔH° and ΔS° were obtained from the slope and intercept of the curve based on the well-known van’t Hoff equation (Eq. 27)
| 27 |
Figure 11 and Table 4 show the plot of lnK0 versus 1/T and the corresponding thermodynamic parameters of Cr(VI) adsorption on NH2–ASNs and NH2–MSNs, repectively. According to Karthik et al., the adsorption process is mainly governed by electrostatic interaction between adsorption sites and adsorbing ions if the magnitude of ΔH° lies between 2.1 and 20.9 kJ·mol−197. Note that ΔH° of NH2–ASNs and NH2–MSNs listed in Table 4 was 2.6 and 1.9 kJ·mol−1, respectively. These values were nearby the range (2.1 kJ·mol−1 ≤ ΔH° ≤ 20.9 kJ·mol−1), indicating the process was likely electrostatic physisorption. The positive values of ΔH° revealed the endothermic nature of the adsorption process, which was consistent with the results of temperature-dependent adsorption isotherms. In general, all ΔG° values of NH2–ASNs and NH2–MSNs were negative for the temperatures from 25 to 55 °C, exhibiting that the adsorption was a spontaneous process. The ΔG° of NH2–MSNs was approximately ~1.5 times greater than that of NH2–ASNs likely due to the presence of nanopores. The positive value of ΔS° suggests the increased randomness at the liquid-solid interface during Cr(VI) adsorption likely indicates the process is an entropy-driven process rather than enthalpy97.
Figure 11.
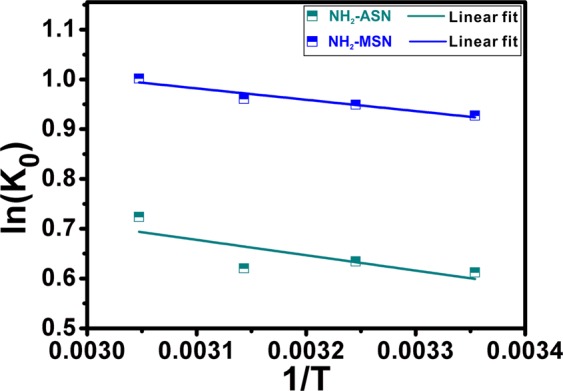
Plot of ln(K0) of NH2–ASNs (dark cyan) and NH2–MSNs (blue) versus inverse temperature (1/T). Best fits to data were successfully obtained using the linear regression of Eq. 26.
Table 4.
Thermodynamic parameters for Cr(VI) adsorption on NH2–ASNs and NH2–MSNs obtained from the linear regression shown in Fig. 11.
| Temperature (K) | NH2-ASN | NH2-MSN | ||||
|---|---|---|---|---|---|---|
| ΔG (kJ mol−1) | ΔH (kJ mol−1) | ΔS (J mol−1 K−1) | ΔG (kJ mol−1) | ΔH (kJ mol−1) | ΔS (J mol−1 K−1) | |
| 298.15 | −1.5792 | 2.5654 | 13.587 | −2.2985 | 1.8994 | 14.052 |
| 308.15 | −1.6251 | −2.4317 | ||||
| 318.15 | −1.6409 | −2.5412 | ||||
| 328.15 | −1.9742 | −2.7329 | ||||
Effect of foreign ions on Cr(VI) removal efficiency of NH2–ASNs and NH2–MSNs
Figure 12 shows the effect of foreign ions such as Na+, K+, Ca2+, Mg2+, Zn2+, and Fe2+ on the Cr(VI) removal efficiency (R) of NH2–ASNs and NH2–MSNs with Cr(VI) concentration of 100 mg/L at 25 °C. The results indicated that the adsorption capacity of NH2–ASNs and NH2–MSNs slightly declined with the presence of the foreign ions by no more than 28 and 22% of the control, respectively. Note that monovalent cations exerted a slightly more influence on the Cr(VI) removal performance of NH2–ASNs and NH2–MSNs than multivalent ions. The adverse effect of foreign cations on the uptake of Cr(VI) ions has been attributed to the presence of ion exchange during the adsorption process98,99. Under the circumstance of increased number of the foreign cations, the electrostatic attraction between the negatively charged Cr(VI) ions and the positively charged NH3+–groups becomes weaker, resulting in inhibiting the adsorption of Cr(VI) ions, and thus the decline of R. Nevertheless, our findings suggest that NH2–MSNs exhibit a robust and high enough Cr(VI) removal performance marginally better than NH2–ASNs under the influence of foreign ions.
Figure 12.
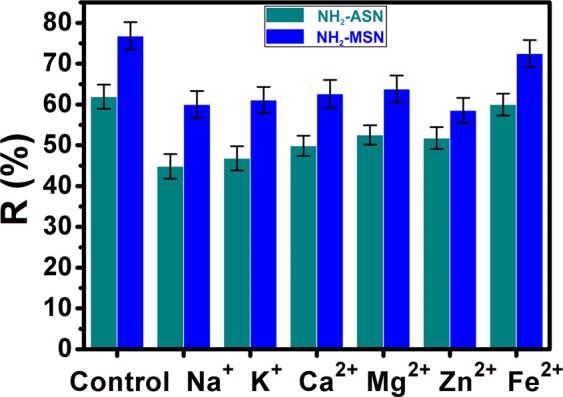
Effect of foreign ions on Cr(VI) removal by NH2–ASNs (dark cyan) and NH2–MSNs (blue).
Desorption-regeneration of NH2–ASNs and NH2–MSNs
Desorption-regeneration experiments of NH2–ASNs and NH2–MSNs were carried out to assess the feasibility of their recovery and future usage. Figure 13 shows the removal efficiencies (R) of NH2–ASNs and NH2–MSNs after five cycles of desorption-regeneration with 0.1 M HCl solution at temperature and pH of 25 °C and 2.0. The removal efficiency (R) of NH2–ASNs and NH2–MSNs after five regenerations had slightly decreased from 61.9 to 46.3 and 76.8 to 57.8%, respectively. The reduction of their removal efficiency after five cycles was only less than 25% of the starting value, which suggests that NH2–ASNs and NH2–MSNs may have a promising recycling property for Cr(VI) removal.
Figure 13.
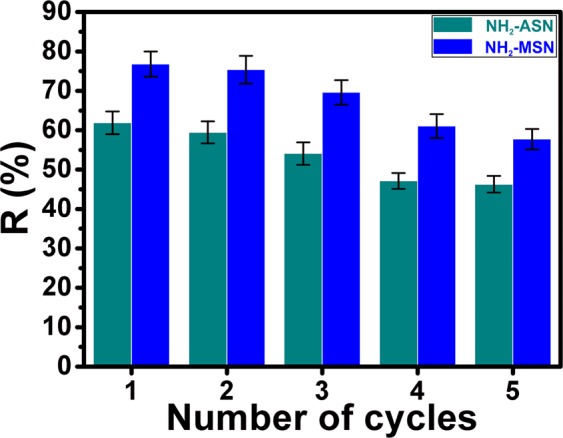
Desorption-regeneration of NH2–ASNs (dark cyan) and NH2–MSNs (blue) for Cr(VI) removal.
Conclusions
We present a comprehensive analysis of Cr(VI) adsorption and removal on both bare and NH2-functionalized ASNs and MSNs in aqueous environments. Highly monodisperse ASNs and MSNs of approximately equal sizes were successfully synthesized using modifications of the Stöber method and subsequently surface functionalized with amine groups. The specific surface area of MSNs (as obtained by N2 sorption measurements) was twice as large as that of ASNs, and the NH2–functional group loading value of APTES reacted MSNs was four times greater than that of APTES reacted ASNs. Further analyses of N2 sorption measurements using a simple geometric scaling approach revealed that more than 70% of the total specific surface area of MSNs and NH2–MSNs was attributable to nanopores within MSNs and NH2–MSNs, respectively. Furthermore, the specific surface areas of ASNs and MSNs decreased as APTES surface loading increased. Cr(VI) adsorption and removal efficiencies were determined using a series of kinetic adsorption batch experiments. The kinetics of the Cr(VI) adsorption processes exhibited a rapid adsorption whereby ~90% of Cr(VI) adsorption was achieved within a minute. Fits with experimental data of the pseudo-first and pseudo-second order kinetic models were investigated, and the intraparticle diffusion model was also applied in an attempt to understand the mechanism of the adsorption process. Best fits with experimental data were obtained by applying nonlinear fits to the pseudo-second order model. The outcomes of fitting processes were verified by evaluating standard residuals (SRs) rather than correlation coefficients (R2). Application of the intraparticle diffusion model also resulted in good fits with kinetic data and indicated adsorption might involve multiple steps. The adsorption isotherms were analyzed as a function of temperature by nonlinear and linearized regression, and the Langmuir model resulted in best fits to the isotherms. The thermodynamic parameters indicated that the adsorption of Cr(VI) on NH2–ASNs and NH2–MSNs was endothermic in nature and an entropy-driven spontaneous process. The results of desorption-regeneration experiments suggest that NH2–ASNs and NH2–MSNs may have a promising potential for recycling. Although the specific surface areas of NH2–ASNs and NH2–MSNs were lower than those of ASNs and MSNs, NH2–ASNs and NH2–MSNs had significantly higher Cr(VI) adsorption capacities (34.0 and 42.2 mg·g−1, respectively) and removal efficiencies (61.9 and 76.8%, respectively). These values compare reasonably well with those reported for powder-like mesoporous silica, Stöber silica, and hybrid silica nanoparticles27,39,76,100. Furthermore, these results suggest both the introduction of nanoporous architecture and appropriate chemical functionalization of nanoparticle surfaces are essential for enhancing Cr(VI) adsorption and removal process.
The findings of the current study are significant in two respects. First, they show silica nanoparticles possessing well-defined sizes and shapes with narrow distributions can be produced and chemically functionalized34. The spherical geometry of the nanoparticles provided admittedly simplified modeling interactions between them and Cr(VI) and facilitated the study of Cr(VI) adsorption processes. In the present study, we used model systems and material characterization tools to investigate Cr adsorption on silica nanoparticles and the results suggest a structural and chemical rationale for enhanced Cr(VI) adsorption and removal. Second, the NH2–ASNs and NH2–MSNs examined converted most of the adsorbed Cr(VI) to relatively non-toxic Cr(III) at levels comparable to or marginally better than those reported for similar mesoporous silica systems6,38,75,76,100. Our results suggest Cr(VI) reduction is caused by a mixed adsorption-partial reduction process that may be characteristic of functionalized nanoparticle-based systems6,73,101,102. Understanding the detailed mechanism of Cr(VI) to Cr(III) conversion represents a meaningful step toward the goal of removing toxic Cr(VI) from wastewater environments.
Acknowledgements
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education, Korea (NRF-2015R1D1A1A01059580 and NRF-2019R1F1A1060060), by the Nano-Material Technology Development Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (2009-0082580). This work was also supported by the Basic Core Technology Development Program for the Oceans and the Polar Regions of the National Research Foundation of Korea (NRF), funded by the Ministry of Science and ICT, Republic of Korea (NRF-2015M1A5A1037054).
Supporting Information
Author contributions
E.-H.J. and S.C. designed research. E.-H.J. performed all experiments. E.-H.J. and S.C. analyzed data. S.C. and E.-H.J. prepared all figures. E.-H.J., S.P.P., I.K., and S.C. wrote the paper. All authors revised, reviewed, and approved the manuscript.
Data availability
All data generated or analyzed during this study are included within the article and are available from the corresponding author upon request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
is available for this paper at 10.1038/s41598-020-61505-1.
References
- 1.US Department of Health and Human Services, Toxicological Profile for Chromium. Public Health Services Agency for Toxic Substances and Diseases Registry, Washington DC (2012). [PubMed]
- 2.Raghunathan VK, Tettey JN, Ellis EM, Grant MH. Comparative chronic in vitro toxicity of hexavalent chromium to osteoblasts and monocytes. J. Biomed. Mater. Res. A. 2009;88:543–550. doi: 10.1002/jbm.a.31893. [DOI] [PubMed] [Google Scholar]
- 3.Zhitkovich A. Chromium in drinking water: sources, metabolism, and cancer risks. Chem. Res. Toxicol. 2011;24:1617–1629. doi: 10.1021/tx200251t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Megharaj M, Avudainayagam S, Naidu R. Toxicity of hexavalent chromium and its reduction by bacteria isolated from soil contaminated with tannery waste. Curr. Microbiol. 2003;47:51–54. doi: 10.1007/s00284-002-3889-0. [DOI] [PubMed] [Google Scholar]
- 5.Katz, S. A. Salem, H. The biological and environmental chemistry of chromium. (VCH Publishers, New York, 1994).
- 6.Fellenz N, et al. Chromium (VI) removal from water by means of adsorption-reduction at the surface of amino-functionalized MCM-41 sorbents. Micropor. Mesopor. Mater. 2017;239:138–146. doi: 10.1016/j.micromeso.2016.10.012. [DOI] [Google Scholar]
- 7.Selvi K, Pattabhi S, Kadirvelu K. Removal of Cr(VI) from aqueous solution by adsorption onto activated carbon. Bioresour. Technol. 2001;80:87–89. doi: 10.1016/S0960-8524(01)00068-2. [DOI] [PubMed] [Google Scholar]
- 8.Yang T, et al. Synthesis of Na-X zeolite from low aluminum coal fly ash: Characterization and high efficient As(V) removal. Adv. Powder Technol. 2019;30:199–206. doi: 10.1016/j.apt.2018.10.023. [DOI] [Google Scholar]
- 9.Yang, T., Han, C., Tang, J. & Luo, Y. Removal performance and mechanisms of Cr(VI) by an in-situ self-improvement of mesoporous biochar derived from chicken bone. Environ. Sci. Pollut. Res., 10.1007/s11356-019-07116-4 (2019). [DOI] [PubMed]
- 10.Li L-L, Feng X-Q, Han R-P, Zang S-Q, Yang G. Cr(VI) removal via anion exchange on a silver-triazolate MOF. J. Hazard. Mater. 2017;321:622–628. doi: 10.1016/j.jhazmat.2016.09.029. [DOI] [PubMed] [Google Scholar]
- 11.Galan B, Castaneda D, Ortiz I. Removal and recovery of Cr(VI) from polluted ground waters: A comparative study of ion-exchange technologies. Water Res. 2005;39:4317–4324. doi: 10.1016/j.watres.2005.08.015. [DOI] [PubMed] [Google Scholar]
- 12.Kozlowski CA, Walkowiak W. Removal of chromium(VI) from aqueous solutions by polymer inclusion membranes. Water Res. 2002;36:4870–4876. doi: 10.1016/S0043-1354(02)00216-6. [DOI] [PubMed] [Google Scholar]
- 13.Riaz T, et al. Synthesis and characterization of polyurethane-cellulose acetate blend membrane for chromium (VI) removal. Carbohyd. Polym. 2016;153:582–591. doi: 10.1016/j.carbpol.2016.08.011. [DOI] [PubMed] [Google Scholar]
- 14.Adhoum N, Monser L, Bellakhal N, Belgaied J-E. Treatment of electroplating wastewater containing Cu2+, Zn2+ and Cr(VI) by electrocoagulation. J. Hazard. Mater. 2004;112:207–213. doi: 10.1016/j.jhazmat.2004.04.018. [DOI] [PubMed] [Google Scholar]
- 15.Gheju M, Balcu I. Removal of chromium from Cr(VI) polluted wastewaters by reduction with scrap iron and subsequent precipitation of resulted cations. J. Hazard. Mater. 2011;196:131–138. doi: 10.1016/j.jhazmat.2011.09.002. [DOI] [PubMed] [Google Scholar]
- 16.Golbaz S, Jafari AJ, Rafiee M, Kalantary RR. Separate and simultaneous removal of phenol, chromium, and cyanide from aqueous solution by coagulation/precipitation: Mechanisms and theory. Chem. Eng. J. 2014;253:251–257. doi: 10.1016/j.cej.2014.05.074. [DOI] [Google Scholar]
- 17.Dupont L, Guillon E. Removal of hexavalent chromium with a lignocellulosic substrate extracted from wheat bran. Environ. Sci. Technol. 2003;37:4235–4241. doi: 10.1021/es0342345. [DOI] [PubMed] [Google Scholar]
- 18.Peng C, Meng H, Song S, Lu S, Lopez-Valdivieso A. Elimination of Cr(VI) from electroplating wastewater by electrodialysis following chemical precipitation. Sep. Sci. Technol. 2004;39:1501–1517. doi: 10.1081/SS-120030788. [DOI] [Google Scholar]
- 19.Kongsricharoern N, Polprasert C. Chromium removal by a bipolar electro-chemical precipitation process. Water Sci. Technol. 1996;34:109–116. doi: 10.2166/wst.1996.0189. [DOI] [Google Scholar]
- 20.Chen T, Zhou Z, Xu S, Wang H, Lu W. Adsorption behavior comparison of trivalent and hexavalent chromium on biochar derived from municipal sludge. Bioresour. Technol. 2015;190:388–394. doi: 10.1016/j.biortech.2015.04.115. [DOI] [PubMed] [Google Scholar]
- 21.Hu Z, Lei L, Li Y, Ni Y. Chromium adsorption on high-performance activated carbons from aqueous solution. Sep. Purif. Technol. 2003;31:13–18. doi: 10.1016/S1383-5866(02)00149-1. [DOI] [Google Scholar]
- 22.Luo C, Tian Z, Yang B, Zhang L, Yan S. Manganese dioxide/iron oxide/acid Oxidized multi-walled carbon nanotube magnetic nanocomposite for enhanced hexavalent chromium removal. Chem. Eng. J. 2013;234:256–265. doi: 10.1016/j.cej.2013.08.084. [DOI] [Google Scholar]
- 23.Kobielska PA, Howarth AJ, Farha OK, Nayak S. Metal-organic frameworks for heavy metal removal from water. Coordin. Chem. Rev. 2018;358:92–107. doi: 10.1016/j.ccr.2017.12.010. [DOI] [Google Scholar]
- 24.Duranoglu D, Kaya IGB, Beker U, Senkal BF. Synthesis and adsorption properties of polymeric and polymer-based hybrid adsorbent for hexavalent chromium removal. Chem. Eng. J. 2012;181:103–112. doi: 10.1016/j.cej.2011.11.028. [DOI] [Google Scholar]
- 25.Bai RS, Abraham TE. Studies on chromium(VI) adsorption-desorption using. immobilized fungal biomass. Bioresour. Technol. 2003;87:17–26. doi: 10.1016/S0960-8524(02)00222-5. [DOI] [PubMed] [Google Scholar]
- 26.Abdel-Halim ES, Al-Deyab SS. Removal of heavy metals from their aqueous solutions through adsorption onto natural polymers. Carbohyd. Polym. 2011;84:454–458. doi: 10.1016/j.carbpol.2010.12.001. [DOI] [Google Scholar]
- 27.Dinker MK, Kulkarni PS. Recent Advances in Silica-Based Materials for the Removal of Hexavalent Chromium: A Review. J. Chem. Eng. Data. 2015;60:2521–2540. doi: 10.1021/acs.jced.5b00292. [DOI] [Google Scholar]
- 28.Plumeré N, Ruff A, Speiser B, Feldmann V, Mayer HA. Stöber silica particles as basis for redox modifications: Particle shape, size, polydispersity, and porosity. J. Colloid Interface Sci. 2012;368:208–219. doi: 10.1016/j.jcis.2011.10.070. [DOI] [PubMed] [Google Scholar]
- 29.Hyde EDER, Seyfaee A, Neville F, Moreno-Atanasio R. Colloidal Silica Particle Synthesis and Future Industrial Manufacturing Pathways: A Review. Ind. Eng. Chem. Res. 2016;55:8891–8913. doi: 10.1021/acs.iecr.6b01839. [DOI] [Google Scholar]
- 30.Kim MJ, Ryoo R. Synthesis and pore size control of cubic mesoporous silica SBA-1. Chem. Mater. 1999;11:487–491. doi: 10.1021/cm980691m. [DOI] [Google Scholar]
- 31.Zhao D, Sun J, Li Q, Stucky GD. Morphological control of highly ordered mesoporous silica SBA-15. Chem. Mater. 2000;12:275–279. doi: 10.1021/cm9911363. [DOI] [Google Scholar]
- 32.Lin HP, et al. The synthesis and application of the mesoporous molecular sieves MCM-41 - A review. J. Chin. Chem. Soc-Taip. 1999;46:495–507. doi: 10.1002/jccs.199900067. [DOI] [Google Scholar]
- 33.Kim TW, Chung PW, Lin VSY. Facile Synthesis of Monodisperse Spherical MCM-48 Mesoporous Silica Nanoparticles with Controlled Particle Size. Chem. Mater. 2010;22:5093–5104. doi: 10.1021/cm1017344. [DOI] [Google Scholar]
- 34.Slowing II, Vivero-Escoto JL, Trewyn BG, Lin VSY. Mesoporous silica nanoparticles: structural design and applications. J. Mater. Chem. 2010;20:7924–7937. doi: 10.1039/c0jm00554a. [DOI] [Google Scholar]
- 35.Delaney P, et al. Porous silica spheres as indoor air pollutant scavengers. J. Environ. Monitor. 2010;12:2244–2251. doi: 10.1039/c0em00226g. [DOI] [PubMed] [Google Scholar]
- 36.Kumar A, et al. Direct air capture of CO2 by physisorbent materials. Angew. Chem. Int. Ed. 2015;54:14372–14377. doi: 10.1002/anie.201506952. [DOI] [PubMed] [Google Scholar]
- 37.Flynn EJ, Keane DA, Tabari PM, Morris MA. Pervaporation performance enhancement through the incorporation of mesoporous silica spheres into PVA membranes. Sep. Purif. Technol. 2013;118:73–80. doi: 10.1016/j.seppur.2013.06.034. [DOI] [Google Scholar]
- 38.Li J, et al. Synthesis, amino-functionalization of mesoporous silica and its adsorption of Cr(VI) J. Colloid Interface Sci. 2008;318:309–314. doi: 10.1016/j.jcis.2007.09.093. [DOI] [PubMed] [Google Scholar]
- 39.Lee JH, et al. Investigation of the mechanism of chromium removal in (3-aminopropyl)trimethoxysilane functionalized mesoporous silica. Sci. Rep. 2018;8:12078. doi: 10.1038/s41598-018-29679-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Soliman EM. Synthesis and Metal Collecting Properties of Mono, Di, Tri and Tetramine Based on Silica Gel Matrix. Anal. Lett. 1997;30:1739–1751. doi: 10.1080/00032719708001690. [DOI] [Google Scholar]
- 41.Manu V, Mody HM, Bajaj HC, Jasra RV. Adsorption of Cu2+ on Amino Functionalized Silica Gel with Different Loading. Ind. Eng. Chem. Res. 2009;48:8954–8960. doi: 10.1021/ie900273v. [DOI] [Google Scholar]
- 42.Stöber W, Fink A, Bohn E. Controlled Growth of Monodisperse Silica Spheres in the Micron Size Range. J. Colloid Interface Sci. 1968;26:62–69. doi: 10.1016/0021-9797(68)90272-5. [DOI] [Google Scholar]
- 43.Thomassen LCJ, et al. Synthesis and characterization of stable monodisperse silica nanoparticle sols for in vitro cytotoxicity testing. Langmuir. 2010;26:328–335. doi: 10.1021/la902050k. [DOI] [PubMed] [Google Scholar]
- 44.Van Blaaderen A, Kentgens APM. Particle morphology and chemical microstructure of colloidal silica spheres made from alkoxysilanes. J. Non-Cryst. Solids. 1992;149:161–178. doi: 10.1016/0022-3093(92)90064-Q. [DOI] [Google Scholar]
- 45.Moller K, Kobler J, Bein T. Colloidal suspensions of nanometer-sized mesoporous silica. Adv. Funct. Mater. 2007;17:605–612. doi: 10.1002/adfm.200600578. [DOI] [Google Scholar]
- 46.Lv X, Zhang L, Xing F, Lin H. Controlled synthesis of monodispersed mesoporous silica nanoparticles: Particle size tuning and formation mechanism investigation. Micropor. Mesopor. Mater. 2016;225:238–244. doi: 10.1016/j.micromeso.2015.12.024. [DOI] [Google Scholar]
- 47.Park JW, Park YJ, Jun CH. Post-grafting of silica surfaces with pre-functionalized organosilanes: new synthetic equivalents of conventional trialkoxysilanes. Chem. Commun. 2011;47:4860–4871. doi: 10.1039/c1cc00038a. [DOI] [PubMed] [Google Scholar]
- 48.Fellenz N, Martin P, Marchetti S, Bengoa F. Aminopropyl-modified mesoporous silica nanospheres for the adsorption of Cr(VI) from water. J. Porous Mater. 2015;22:729–738. doi: 10.1007/s10934-015-9946-4. [DOI] [Google Scholar]
- 49.Ju J, et al. Accelerated redox reaction between chromate and phenolic pollutants during freezing. J. Hazard. Mater. 2017;329:330–338. doi: 10.1016/j.jhazmat.2017.01.031. [DOI] [PubMed] [Google Scholar]
- 50.APHA. Standard Method for the Examination of Water and Wastewater. 16th edn, (American Public Health Association, Washington DC, 1985).
- 51.Xiao Y, Azaiez J, Hill JM. Erroneous Application of Pseudo-Second-Order Adsorption Kinetics Model: Ignored Assumptions and Spurious Correlations. Ind. Eng. Chem. Res. 2018;57:2705–2709. doi: 10.1021/acs.iecr.7b04724. [DOI] [Google Scholar]
- 52.Blanchard G, Maunaye M, Martin G. Removal of heavy metals from waters by means of natural zeolites. Water Res. 1984;18:1501–1507. doi: 10.1016/0043-1354(84)90124-6. [DOI] [Google Scholar]
- 53.Ho YS, McKay G. A Comparison of Chemisorption Kinetic Models Applied to Pollutant Removal on Various Sorbents. Process Saf. Environ. Prot. 1998;76:332–340. doi: 10.1205/095758298529696. [DOI] [Google Scholar]
- 54.Azizian S. Kinetic models of sorption: a theoretical analysis. J. Colloid Interface Sci. 2004;276:47–52. doi: 10.1016/j.jcis.2004.03.048. [DOI] [PubMed] [Google Scholar]
- 55.Ho YS. Review of second-order models for adsorption systems. J. Hazard. Mater. 2006;136:681–689. doi: 10.1016/j.jhazmat.2005.12.043. [DOI] [PubMed] [Google Scholar]
- 56.Weber, W. J. & Morris, J. C. Advances in water pollution research. In Proceedings of the First International Conference on Water Pollution Research. 2, 231 (Pergamon Press Oxford, 1962).
- 57.Akram M, Bhatti HN, Iqbal M, Noreen S, Sadaf S. Biocomposite efficiency for Cr(VI) adsorption: Kinetic, equilibrium and thermodynamics studies. J. Environ. Chem. Eng. 2017;5:400–411. doi: 10.1016/j.jece.2016.12.002. [DOI] [Google Scholar]
- 58.Kirk CT. Quantitative-Analysis of the Effect of Disorder-Induced Mode-Coupling on Infrared-Absorption in Silica. Phys. Rev. B. 1988;38:1255–1273. doi: 10.1103/PhysRevB.38.1255. [DOI] [PubMed] [Google Scholar]
- 59.Kim BG, Kang SY, Kim JJ. FTIR study of fluorinated silicon oxide film. J. Phys. D Appl. Phys. 1997;30:1720–1724. doi: 10.1088/0022-3727/30/12/005. [DOI] [Google Scholar]
- 60.Chong ASM, Zhao XS. Functionalization of SBA-15 with APTES and characterization of functionalized materials. J. Phys. Chem. B. 2003;107:12650–12657. doi: 10.1021/jp035877+. [DOI] [Google Scholar]
- 61.Ebrahimi-Gatkash M, Younesi H, Shahbazi A, Heidari A. Amino-functionalized mesoporous MCM-41 silica as an efficient adsorbent for water treatment: batch and fixed-bed column adsorption of the nitrate anion. Appl. Water Sci. 2017;7:1887–1901. doi: 10.1007/s13201-015-0364-1. [DOI] [Google Scholar]
- 62.Sing KSW, et al. International Union of Pure and Applied Chemistry: reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity. Pure Appl. Chem. 1985;57:603–619. doi: 10.1351/pac198557040603. [DOI] [Google Scholar]
- 63.Balbuena PB, Gubbins KE. Theoretical interpretation of adsorption behavior of simple fluids in slit pores. Langmuir. 1993;9:1801–1814. doi: 10.1021/la00031a031. [DOI] [Google Scholar]
- 64.Thommes M, Cychosz KA. Physical adsorption characterization of nanoporous materials: progress and challenges. Adsorption. 2014;20:233–250. doi: 10.1007/s10450-014-9606-z. [DOI] [Google Scholar]
- 65.Thommes M, et al. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report) Pure Appl. Chem. 2015;87:1051–1069. doi: 10.1515/pac-2014-1117. [DOI] [Google Scholar]
- 66.Brunauer S, Emmett PH, Teller E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938;60:309–319. doi: 10.1021/ja01269a023. [DOI] [Google Scholar]
- 67.Barrett EP, Joyner LG, Halenda PP. The Determination of Pore Volume and Area Distributions in Porous Substances. I. Computations from Nitrogen Isotherms. J. Am. Chem. Soc. 1951;73:373–380. doi: 10.1021/ja01145a126. [DOI] [Google Scholar]
- 68.Giesche H, Unger KK, Muller U, Esser U. Hysteresis in Nitrogen Sorption and Mercury Porosimetry on Mesoporous Model Adsorbents Made of Aggregated Monodisperse Silica Spheres. Colloid Surf. 1989;37:93–113. doi: 10.1016/0166-6622(89)80109-X. [DOI] [Google Scholar]
- 69.Legrand, A. P. The surface properties of silicas. (Wiley, 1998).
- 70.Gregg, S. J. & Sing, K. S. W. The physical adsorption of gases by nonporous solids: The type II isotherm. Adsorption, surface area and porosity 41-110 (Academic Press, London, 1982).
- 71.Etienne M, Walcarius A. Analytical investigation of the chemical reactivity and stability of aminopropyl-grafted silica in aqueous medium. Talanta. 2003;59:1173–1188. doi: 10.1016/S0039-9140(03)00024-9. [DOI] [PubMed] [Google Scholar]
- 72.Oh YJ, Song H, Shin WS, Choi SJ, Kim YH. Effect of amorphous silica and silica sand on removal of chromium(VI) by zero-valent iron. Chemosphere. 2007;66:858–865. doi: 10.1016/j.chemosphere.2006.06.034. [DOI] [PubMed] [Google Scholar]
- 73.Zaitseva, N., Zaitsev, V. & Walcarius, A. Chromium(VI) removal via reduction-sorption on bi-functional silica adsorbents. J. Hazard. Mater.250–251, 454–461 (2013). [DOI] [PubMed]
- 74.Yoshitake H, Yokoi T, Tatsumi T. Adsorption of Chromate and Arsenate by Amino-Functionalized MCM-41 and SBA-1. Chem. Mater. 2002;14:4603–4610. doi: 10.1021/cm0202355. [DOI] [Google Scholar]
- 75.Lam KF, Yeung KL, Mckay G. Selective mesoporous adsorbents for Cr2O72− and Cu2+ separation. Micropor. Mesopor. Mat. 2007;100:191–201. doi: 10.1016/j.micromeso.2006.10.037. [DOI] [Google Scholar]
- 76.Li J, et al. Different N-containing functional groups modified mesoporous adsorbents for Cr(VI) sequestration: Synthesis, characterization and comparison. Micropor. Mesopor. Mat. 2008;110:442–450. doi: 10.1016/j.micromeso.2007.06.033. [DOI] [Google Scholar]
- 77.Thakur SS, Chauhan GS. Gelatin-Silica-Based Hybrid Materials as Efficient Candidates for Removal of Chromium(Vi) from Aqueous Solutions. Ind. Eng. Chem. Res. 2014;53:4838–4849. doi: 10.1021/ie401997g. [DOI] [Google Scholar]
- 78.Samiey B, Cheng C-H, Wu J. Organic-Inorganic Hybrid Polymers as Adsorbents for Removal of Heavy Metal Ions from Solutions: A Review. Materials. 2014;7:673–726. doi: 10.3390/ma7020673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Lenshin AS, Kashkarov VM, Domashevskaya EP, Bel’tyukov AN, Gil’mutdinov FZ. Investigations of the composition of macro-, micro- and nanoporous silicon surface by ultrasoft X-ray spectroscopy and X-ray photoelectron spectroscopy. Appl. Surf. Sci. 2015;359:550–559. doi: 10.1016/j.apsusc.2015.10.140. [DOI] [Google Scholar]
- 80.Swart HC, van Hattum ED, Arnoldbik WM, Habraken FHPM. Comparison of SiOx structure in RF sputtered samples. phys. status solidi c. 2004;1:2286–2291. doi: 10.1002/pssc.200404811. [DOI] [Google Scholar]
- 81.Bywalez R, Karacuban H, Nienhaus H, Schulz C, Wiggers H. Stabilization of mid-sized silicon nanoparticles by functionalization with acrylic acid. Nanoscale Res. Lett. 2012;7:76. doi: 10.1186/1556-276X-7-76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Moulder, J. F., Chastain, J. & King, R. C. Handbook of X-ray Photoelectron Spectroscopy: A Reference Book of Standard Spectra for Identification and Interpretation of XPS Data. (Physical Electronics, 1995).
- 83.Calvo A, et al. Mesoporous Aminopropyl-Functionalized Hybrid Thin Films with Modulable Surface and Environment-Responsive Behavior. Chem. Mater. 2008;20:4661–4668. doi: 10.1021/cm800597k. [DOI] [Google Scholar]
- 84.Lagergren SK. About the theory of so-called adsorption of soluble substances. Sven. Vetenskapsakad. Handingarl. 1898;24:1–39. [Google Scholar]
- 85.Santhy K, Selvapathy P. Removal of reactive dyes from wastewater by adsorption on coir pith activated carbon. Bioresour. Technol. 2006;97:1329–1336. doi: 10.1016/j.biortech.2005.05.016. [DOI] [PubMed] [Google Scholar]
- 86.Ho YS, Mckay G. The kinetics of sorption of basic dyes from aqueous solution by sphagnum moss peat. Can. J. Chem. 1998;76:822–827. doi: 10.1002/cjce.5450760419. [DOI] [Google Scholar]
- 87.Bulut E, Özacar M, Şengil İA. Adsorption of malachite green onto bentonite: Equilibrium and kinetic studies and process design. Micropor. Mesopor. Mat. 2008;115:234–246. doi: 10.1016/j.micromeso.2008.01.039. [DOI] [PubMed] [Google Scholar]
- 88.Zhao D, et al. Facile preparation of amino functionalized graphene oxide decorated with Fe3O4 nanoparticles for the adsorption of Cr(VI) Appl Surf Sci. 2016;384:1–9. doi: 10.1016/j.apsusc.2016.05.022. [DOI] [Google Scholar]
- 89.Foo KY, Hameed BH. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010;156:2–10. doi: 10.1016/j.cej.2009.09.013. [DOI] [Google Scholar]
- 90.Elmorsi TM, Elsayed MH, Bakr MF. Enhancing the removal of methylene blue by modified ZnO nanoparticles: kinetics and equilibrium studies. Can. J. Chem. 2017;95:590–600. doi: 10.1139/cjc-2016-0456. [DOI] [Google Scholar]
- 91.Reed BE, Matsumoto MR. Modeling Cadmium Adsorption by Activated Carbon Using the Langmuir and Freundlich Isotherm Expressions. Sep. Sci. Technol. 1993;28:2179–2195. doi: 10.1080/01496399308016742. [DOI] [Google Scholar]
- 92.Ayawei, N., Ebelegi, A. N. & Wankasi, D. Modelling and Interpretation of Adsorption Isotherms. J. Chem, 10.1155/2017/3039817 (2017).
- 93.Peric J, Trgo M, Medvidovic NV. Removal of zinc, copper and lead by natural zeolite - a comparison of adsorption isotherms. Water Res. 2004;38:1893–1899. doi: 10.1016/j.watres.2003.12.035. [DOI] [PubMed] [Google Scholar]
- 94.Aranovich GL, Donohue MD. Vapor adsorption on microporous adsorbents. Carbon. 2000;38:701–708. doi: 10.1016/S0008-6223(99)00157-8. [DOI] [Google Scholar]
- 95.Fan SS, et al. Facile synthesis of tea waste/Fe3O4 nanoparticle composite for hexavalent chromium removal from aqueous solution. RSC Adv. 2017;7:7576–7590. doi: 10.1039/C6RA27781K. [DOI] [Google Scholar]
- 96.Khan AA, Singh RP. Adsorption Thermodynamics of carbofuran on Sn(Iv) arsenosilicate in H+, Na+ and Ca2+-forms. Colloid Surf. 1987;24:33–42. doi: 10.1016/0166-6622(87)80259-7. [DOI] [Google Scholar]
- 97.Liu H, Zhang F, Peng ZY. Adsorption mechanism of Cr(VI) onto GO/PAMAMs composites. Sci. Rep. 2019;9:3663. doi: 10.1038/s41598-019-40344-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Pu SY, et al. An efficient photocatalyst for fast reduction of Cr(VI) by ultra-trace silver enhanced titania in aqueous solution. Catalysts. 2018;8:251. doi: 10.3390/catal8060251. [DOI] [Google Scholar]
- 99.Tan JS, Song YH, Huang XH, Zhou L. Facile functionalization of natural peach gum polysaccharide with multiple amine groups for highly efficient removal of toxic hexavalent chromium (Cr(VI)) ions from water. ACS Omega. 2018;3:17309–17318. doi: 10.1021/acsomega.8b02599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Choi K, et al. Chromium removal from aqueous solution by a PEI-silica nanocomposite. Sci. Rep. 2018;8:1438. doi: 10.1038/s41598-018-20017-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Park D, Yun YS, Park JM. Studies on hexavalent chromium biosorption by chemically-treated biomass of Ecklonia sp. Chemosphere. 2005;60:1356–1364. doi: 10.1016/j.chemosphere.2005.02.020. [DOI] [PubMed] [Google Scholar]
- 102.Mohan D, Pittman CU. Activated carbons and low cost adsorbents for remediation of tri- and hexavalent chromium from water. J. Hazard. Mater. 2006;137:762–811. doi: 10.1016/j.jhazmat.2006.06.060. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or analyzed during this study are included within the article and are available from the corresponding author upon request.