Abstract
Lymph node metastasis (LNM) is a significant prognostic factor in patients with head and neck cancer, and the ability to predict it accurately is essential to optimizing treatment. Positron emission tomography (PET) and computed tomography (CT) imaging are routinely used to identify LNM. Although large or highly active lymph nodes (LNs) have a high probability of being positive, identifying small or less reactive LNs is challenging. The accuracy of LNM identification strongly depends on the physician’s experience, so an automatic prediction model for LNM based on CT and PET images is warranted to assist LMN identification across care providers and facilities. Radiomics and deep learning are the two promising imaging-based strategies for node malignancy prediction. Radiomics models are built based on handcrafted features, while deep learning learns the features automatically. To build a more reliable model, we proposed a hybrid predictive model that takes advantages of both radiomics and deep learning based strategies. We designed a new many-objective radiomics (MaO-radiomics) model and a 3-dimensional convolutional neural network (3D-CNN) that fully utilizes spatial contextual information, and we fused their outputs through an evidential reasoning (ER) approach. We evaluated the performance of the hybrid method for classifying normal, suspicious and involved LNs. The hybrid method achieves an accuracy (ACC) of 0.88 while XmasNet and Radiomics methods achieve 0.81 and 0.75, respectively. The hybrid method provides a more accurate way for predicting LNM using PET and CT.
Keywords: Lymph node metastasis, Head & Neck Cancer, Radiomics, Convolutional neural network, evidential reasoning
1. INTRODUCTION
Lymph node metastasis (LNM) is a well-known prognostic factor for patients with head and neck cancer (HNC), which is the sixth most common malignancy worldwide (Cognetti et al., 2008). LNM negatively influences overall survival and increases the potential of distant metastasis (Pantel and Brakenhoff, 2004). Radiation therapy is commonly used to control regional disease in the presence of nodal metastasis (Moore et al., 2005), where nodes of different malignant probability can be prescribed with different dose levels. Hence, accurately identifying LNM status is critical for therapeutic control and management of HNC. Cervical LNM status are routinely evaluated on positron emission tomography (PET) and computed tomography (CT), where PET provides functional activity of the LNM and CT provides high-resolution anatomical localization (Yoon et al., 2009). Although large or highly active lymph nodes (LNs), as identified by PET-CT, have a high probability of being positive, identifying small or less reactive LNs is challenging. The accuracy of LNM identification strongly depends on the physician’s experience, so an automatic prediction model for LNM based on CT and PET images would help to assist LNM identification across care providers and facilities.
Imaging-based classification can be categorized into two major strategies: handcrafted feature-based and feature learning-based strategies. Among the handcrafted feature-based models, radiomics has shown great potentials for classification (Lambin et al., 2017). Through extracting and analyzing a large number of quantitative features, radiomics has been applied successfully to solve various prediction problems, such as tumor staging (Ganeshan et al., 2010), treatment outcome prediction (Coroller et al., 2016), and survival analysis (Huang et al., 2016b). Huang et al. (Huang et al., 2016a) developed a radiomics model to predict LNM in colorectal cancer. This model extracted features from CT images and used multivariable logistic regression to build the predictive model. This model aims to a two-class prediction and only uses the classification accuracy as the objective function. Garapati et al. implemented four different classifiers by using morphological features and texture features extracted from CT Urography scans to predict bladder cancer staging (Garapati et al., 2017). To build a more reliable model, our group developed a multi-objective radiomics model (Zhou et al., 2017) that considered both sensitivity and specificity simultaneously as the objective functions during model training. For feature learning-based models, deep learning is a powerful method that has been used to build predictive models for cancer diagnosis. Sung et al. (Sun et al., 2016) explored the use of deep learning methods, such as the convolutional neural network (CNN), deep belief network, and stacked de-noising auto-encoder to predict lung nodule malignancy. Zhu et al. designed a new CNN model to predict survival in lung cancer (Zhu et al., 2017). Yang et al. (Yang et al., 2017) built a model that combined the recurrent neural network and multinomial hierarchical regression decoder to predict breast cancer metastasis. Furthermore, Cha et al. investigated the radiomics and deep learning method for bladder cancer treatment response assessment (Cha et al., 2017).
As both handcrafted feature-based and feature learning-based models have yielded promising results, one practical challenge is to determine which model is best suited to predicting LNM status. Features extracted by the feature learning-based model might be sensitive to global translation, rotation and scaling (Gong et al., 2014) while handcrafted features such as intensity features are not. Manually extracted features and automatically learned features could be complementary (Wang et al., 2016; Antropova et al., 2017), so combining them may yield more stable predictive results. Hence, a strategy that combines both handcrafted and learning models is a desired choice to predict LNM.
In this work, we propose a hybrid model that combines many-objective radiomics (MaO-radiomics) and three-dimensional convolutional neural network (3D-CNN) through evidential reasoning (ER) (Yang and Singh, 1994; Yang and Xu, 2002b) to predict LNM in HNC. Since our previous multi-objective radiomics model (Zhou et al., 2017) can only handle binary problems, we proposed a new many-objective radiomics (MaO-radiomics) model to predict the three classes of lymph nodes: normal, suspicious, and involved. For this three-category classification problem, there are six objective functions (three pairs of producer’s accuracy (PA) and user’s accuracy (UA) for three categories of lymph nodes) to be optimized. Following the definition that multi-objective problem with more than three objective functions is many-objective problem (Li et al., 2015; He et al., 2014), we term the proposed method as many-objective radiomics model. ER algorithm was originally proposed for multi-criterion decision analysis, and it was developed based on Dempster-Shafer (D-S) theory (Dempster, 1968; Shafer, 1976) and decision theory. It is powerful for aggregating nonlinear information under uncertainty, which has achieved great success in clinical decision support (Zhou et al., 2013; Zhou et al., 2015). Moreover, in our previous work (Chen et al., 2018), the experimental results also demonstrated that ER can generate more reliable results which means obtaining higher similarity between output probability and label vector. Since one of our goals is obtaining more reliable results in this study, ER is adopted here. We also designed a 3D-CNN consisting of convolution, rectified linear units (ReLU), max-pooling, and fully connected layers to automatically learn both local and global features for LNM prediction. The final output was obtained by fusing the MaO-radiomics and 3D-CNN model outputs through the ER approach (Yang and Xu, 2002a).
2. Materials and methods
2.1. Patient dataset
The study included PET and CT images for 59 patients with HNC who had enrolled in the INFIELD trial (https://clinicaltrials.gov/ct2/show/NCT03067610) between 2016 and 2018 at UT Southwestern Medical Center. Pretreatment PET and CT images were exported from digital Picture Archiving Communication System (PACS). Nodal status for all trial patients was reviewed by a radiation oncologist and a nuclear medicine radiologist. Figure 1 shows one example of CT and overlapped CT&PET images of normal, suspicious, and involved nodes. These nodes were contoured on contrast-enhanced CT guided by PET. We trained the predictive model on the lymph nodes of the first 41 patients, which included 85 involved nodes, 55 suspicious nodes, and 30 normal nodes. Then, we validated the predictive model on the remaining 18 independent patients with 22 involved nodes, 27 suspicious nodes, and 17 normal nodes. We used a total of 170 nodes for training and 66 nodes for testing.
Figure 1:
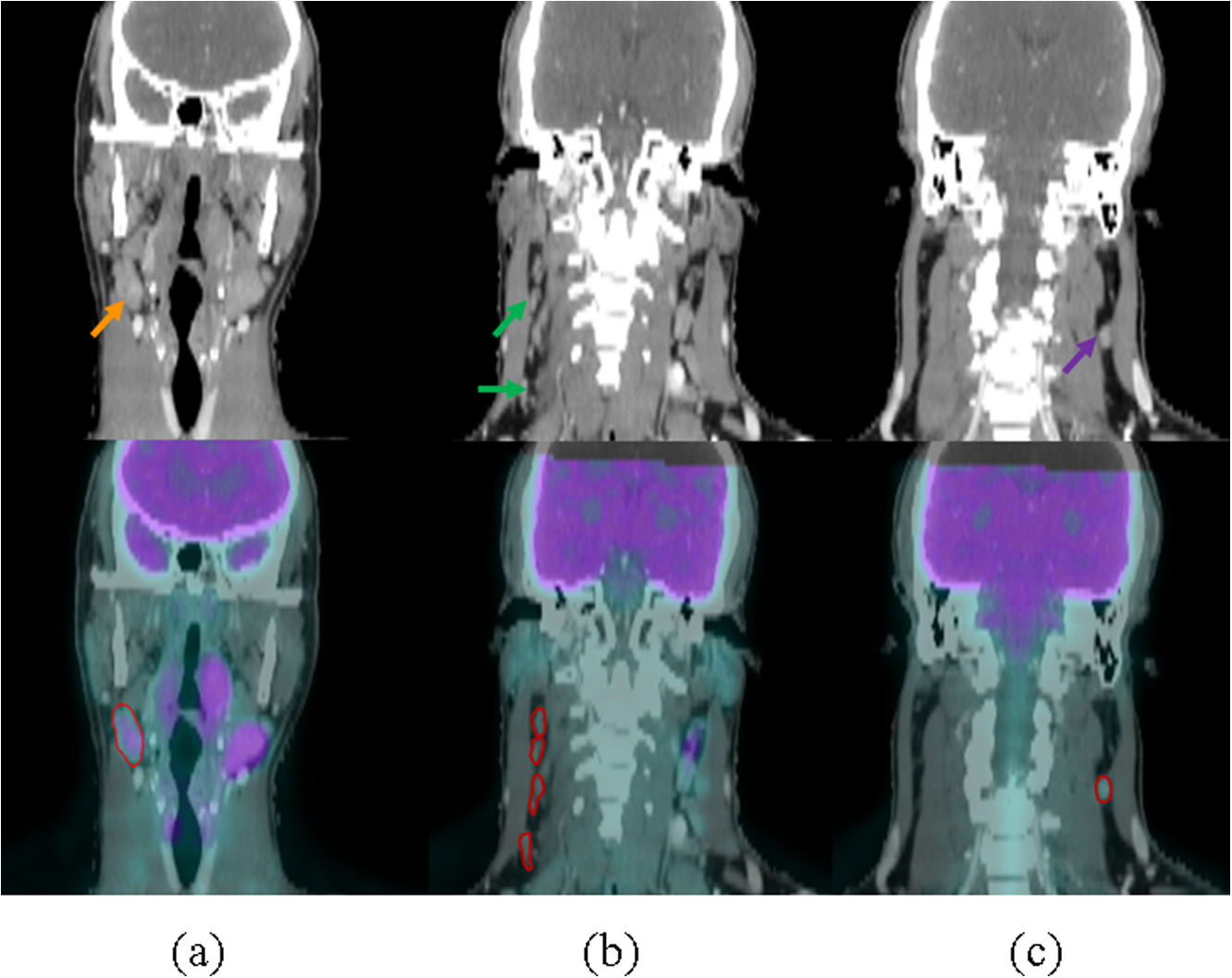
One example each of CT and overlapped CT & PET images of normal, suspicious, and involved nodes. Row 1: CT; Row 2: Overlapped CT & PET with contours of lymph nodes. (a)-(c) represent involved, suspicious and normal lymph nodes, respectively.
2.2. Model overview
The workflow of the hybrid model is illustrated in Figure 2. First, patches of size 48×48×32, which include nodes and their surrounding voxels, were extracted as inputs for the proposed 3D-CNN model, while the nodes themselves were extracted as inputs for the MaO-radiomics models. Then, the two model outputs were fused by ER to obtain the final output.
Figure 2:
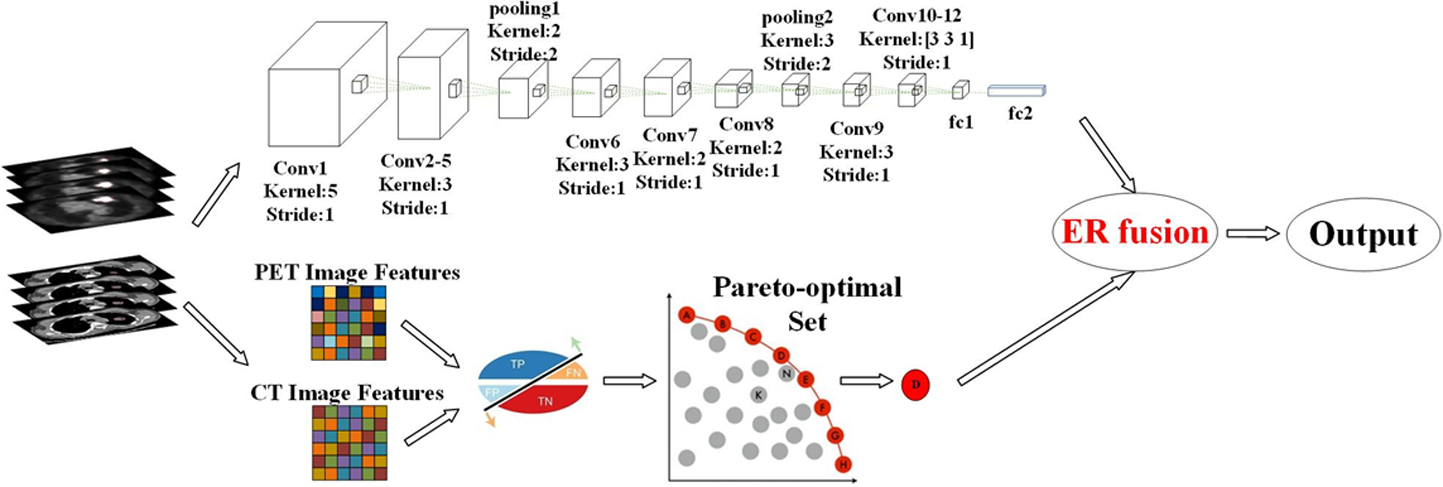
Workflow of the proposed hybrid model.
2.3. MaO-radiomics model
In the MaO-radiomics model, image features – including intensity, texture, and geometric features – are extracted from the contoured LNs (involved and suspicious) in PET and CT images. Additionally, at least one normal LN of similar size to the suspicious LNs was contoured to train the predictive model for each patient. Intensity features include minimum, maximum, mean, standard deviation, sum, median, skewness, kurtosis, and variance. Geometry features include volume, major diameter, minor diameter, eccentricity, elongation orientation, bounding box volume, and perimeter. Texture features based on 3D gray-level co-occurrence (GLCM) include energy, entropy, correlation, contrast, texture variance, sum-mean, inertia, cluster shade, cluster prominence, homogeneity, max-probability, and inverse variance. A total of 257 features were extracted for each PET and CT, respectively.
Then, we used the support vector machine (SVM) to build the predictive model. Since the feature selection can influence the model training, we perform feature selection as well as model parameter training simultaneously. Assume that the model parameters are denoted by α = {α1, ⋯, αM}, where M is the number of model parameters. All features, including PET and CT imaging features, are denoted by β = {β1, ⋯, βN}, where N is the number of features. During optimization, each feature has a binary label ‘0’ or ‘1’. In a solution obtained by the many-objective optimization algorithm, a feature is selected if it has a label ‘1’. If the label is ‘0’, then the corresponding feature is not selected. Procedure accuracy (PA) and user accuracy (UA) in confusion matrix were taken as objective functions because of the three classes of lymph nodes (Zhou et al., 2015) and they are denoted by and , respectively. We maximized and simultaneously to obtain the Pareto-optimal set:
| (1) |
Equation (1) shows that six objective functions are considered in our model. The final solution of the selected features and model parameters can be selected from the Pareto-optimal set according to different clinical needs. Then the test samples with the fixed selected features are fed into the trained model to get the final results.
To solve the optimization problem defined in equation (1), we developed a many-objective optimization algorithm based on our previous algorithm (Zhou et al., 2017). The proposed algorithm consists of two phases: (1) Pareto-optimal solution generation; and (2) best solution selection. The first phase is the same as in the multi-objective algorithm (Zhou et al., 2017) which includes initialization, clonal operation, mutation operation, deleting operation, population update, and termination detection. In the second phase, the final solution is selected according to accuracy and AUC. Assume that the thresholds for accuracy are denoted by Tacc. The Pareto-optimal solution is denoted by D = { D1, D2, ⋯, DP}. The corresponding accuracy and AUC for each individual Di, i = 1,,2, ⋯, P are denoted by , i = 1,2, ⋯, P, respectively. The procedure to select the best solution is as follows: Step 1) For each solution set Di, i = 1,2, ⋯, P, if , Di is selected. All selected candidates constitute the new candidate set denoted by , where Q is the number of selected individuals, i.e., feasible solutions. Step 2) Solution with highest AUC in DC is selected as the final solution P*.
2.4. 3D-CNN model
The architecture of the proposed 3D-CNN model consists of 12 convolutional layers, 2 max-pooling layers, and 2 fully connected layers (Figure 2). Each convolutional layer is equipped with ReLU activation (He et al., 2016) and batch normalization. The construction order of the different layers in the architecture is shown in Table 1.
Table 1:
3D-CNN architecture.
| Layer | Kernel Size | Stride | Output Size | Feature Volumes |
|---|---|---|---|---|
| Input | - | 48×48×32 | 1(or 2) | |
| C1 | 5×5×5 | [1 1 1] | 44×44×28 | 32 (or 64) |
| C2 | 3×3×3 | [1 1 1] | 42×42×26 | 64 |
| C3 | 3×3×3 | [1 1 1] | 40×40×24 | 64 |
| C4 | 3×3×3 | [1 1 1] | 38×38×22 | 64 |
| C5 | 3×3×3 | [1 1 1] | 36×36×20 | 64 |
| MP1 | 2×2×2 | [2 2 2] | 18×18×10 | 64 |
| C6 | 3×3×3 | [1 1 1] | 16×16×8 | 64 |
| C7 | 2×2×2 | [1 1 1] | 15×15×5 | 64 |
| C8 | 3×3×3 | [1 1 1] | 13×13×4 | 64 |
| MP2 | 3×3×3 | [2 2 2] | 6×6×2 | 64 |
| C9 | 3×3×3 | [1 1 1] | 6×6×2 | 64 |
| C10 | 3×3×1 | [1 1 1] | 6×6×2 | 64 |
| C11 | 3×3×1 | [1 1 1] | 6×6×2 | 64 |
| C12 | 3×3×1 | [1 1 1] | 6×6×2 | 32 |
| FC1 | 1×1×1 | 512 | ||
| FC2 | 1×1×1 | 256 | ||
| FC3 | 1×1×1 | 3 |
C indicates Convolution layer + ReLU layer +Batch Normalization layer; MP indicates Max-pooling layer; and FC indicates Fully connected layer.
Since the max-pooling layer provides basic translation invariance to the internal representation, the convolutional and max-pooling layers are arranged alternately in the proposed architecture. In addition, since the max-pooling layer down-samples the feature maps, the convolutional layers in the architecture can capture both local and global features. For the last four convolutional layers, we first pad zero around each feature map from previous layers and then perform the convolution to preserve the output size of each feature map, which guarantees deep extraction and analysis of the 3D image features. The second fully connected layer finally generates three predicted probabilities as output of the 3D-CNN model. Because we aim to extract information from both PET and CT simultaneously, the input consists of two volumetric images, each of which serves as a channel of the final 4D data input.
The key steps to train the proposed 3D-CNN model are as follows:
Normalization of the input:
Inputs with same scale can make converge faster during network training. The CT number range for our obtained CT images varies from −1000 to +3095. Hence, the specific normalization formula for CT image in this work is as follows:
| (2) |
which makes CT input into the range of [0, 1]. For PET, we first calculated the standardized uptake value (SUV) for each patient. Then the input of PET image is normalized as follows:
| (3) |
which also makes the PET input into the range of [0, 1]. Here, SUVmaximum,training indicates the maximum SUV value of the training dataset. We applied this normalization strategy for both training and testing images.
Data augmentation and balance:
Imbalanced data might affect the CNN model’s efficiency (Hensman and Masko, 2015). Our training dataset had 53 involved, 39 suspicious, and 30 normal nodes. Hence, we increased the number of samples for the suspicious and normal classes. We used the Synthetic Minority Over-sampling technique (SMOTE) to generate synthetic examples for these two minority classes. Synthetic examples were introduced along the line segments joining all of the k minority class nearest neighbors for each minority class sample until we had 53 nodes for each class for training. Data augmentation has been proven effective for network training (Wang and Perez, 2017). We rotated the 3D nodes along x, y, z three dimensions by 30°, 45°, 60°, 75° to generate more training samples.
Initialization of the 3D-CNN weights:
Initializing the network weights will affect the convergence of the network training. We use Xavier initialization in our network to guarantee that the variance of the input and output for each layer is the same to avoid back-propagated gradients vanishing or exploding, so that activation functions can work normally.
Loss function:
We use categorical cross entropy as the objective function that our network minimizes for LNM prediction. The categorical cross entropy formula for our network is as follows:
| (4) |
where q(x) is the target and p(x) represents the predicted probabilities.
2.5. Evidential reasoning fusion
After obtaining the outputs from the MaO-radiomics and 3D-CNN models, the final output is generated using analytic ER (Wang et al., 2006). Assume that represents the output of MaO-radiomics, and the 3D-CNN output is denoted by . They satisfy the following constraint:
| (5) |
Given the weight ω = {ω1, ω2}, which satisfies ω1 + ω2 = 1, 0 ≤ ωj ≤ 1, the final output Pi, i = 1,2,3 is obtained through the following equations (Wang et al., 2006):
| (6) |
| (7) |
where M = 3 and N = 2. Finally, the label L is obtained by:
| (8) |
To better understand the ER approach, the original ER recursive algorithm is described in Appendix.
2.6. Comparative methods
We compared the proposed hybrid model with a convolutional neural network-based method, XmasNet, which was recently proposed by Liu (Liu et al., 2017) and has been shown to be effective for prostate cancer diagnosis on Multi-parametric MRI. We also compared our hybrid model with the conventional radiomics method proposed by Vallières et al. (Vallières et al., 2015), which only considers accuracy as the objective function during the model training. Additionally, we evaluated the performance of the proposed MaO-radiomics and 3D-CNN methods separately to illustrate the effectiveness of the ER fusion technique in the hybrid model. In addition to combining PET and CT as input, we also used PET and CT alone to build the predictive models for each method.
2.7. Evaluation criteria
Since our hybrid model has to handle three categories of nodules (normal, suspicious and involved), we used five criteria – confusion matrix, accuracy (ACC), Macro-Average, mean-one-versus-all (OVA)-AUC, and multiclass AUC (Hand and Till, 2001) – to evaluate its performance. A confusion matrix is a commonly used specific table layout (Table 2) that visualizes the performance of a supervised learning algorithm. Each row of the matrix represents the instances in a predicted class, and each column represents the instances in an actual class. Accuracy is measured by the ratio of number of correctly labelled samples to total number of samples. Macro-Average is defined as the average of the correct classification rates. This measure has been used as a simple way to handle more appropriately unbalanced datasets (Ferri et al., 2003). Mean-OVA-AUC is defined as the average of the one-versus-all AUCs, which can be used as a measure of how well the classifier separates each class from all the other classes. Multi-class AUC, proposed by Hand et al. (Hand and Till, 2001), is an extended definition of two-class AUC that averages pairwise comparisons to evaluate multi-class classification problems.
Table 2:
An example of Confusion Matrix. (Here, Nab represents the instances of actual A class predicted in the B class.)
| Predicted | ||||
|---|---|---|---|---|
| A | B | C | ||
| Naa | Nab | Nac | ||
| Actual | B | Nba | Nbb | Nbc |
| C | Nca | Ncb | Ncc | |
The formulas for calculating ACC, Macro-average, Mean-OVA-AUC, and multi-class AUC values for measuring three-class prediction are listed in Table 3.
Table 3:
Formulas of the four evaluation criteria.
| Formula | |
|---|---|
| ACC | |
| Macro-average | |
| Mean-OVA-AUC | [AUCa vs.all + AUCb vs.all + AUCc vs.all]/3 |
| Multi-class AUC |
In Table 3, , i, j ∈ [a, b, c] with A(i, j) is the probability that a randomly drawn member of class j will have a lower estimated probability of belonging to class i than a randomly drawn member of class i. Based on the definitions of these four evaluation criteria, higher values indicate better prediction results.
2.8. Implementation Details
For the many-objective training algorithm, the population number was set to 100, while the maximal generation number was set to 200. The mutation probability was set to 0.9 in the mutation operation. For the 3D-CNN model training, the Adam optimization algorithm was used with learning rate as 1e-5. Based on our study, the weights in fusion stage for 3D-CNN and MaO-radiomics are set as [0.8, 0.2].
3. Results
We summarized the performance of the five methods (XmasNet, conventional radiomics, proposed 3D-CNN, MaO-radiomics and hybrid method) in predicting lymph node metastasis using CT and PET modality images by listing the ACC, Macro-average, Mean-OVA-AUC, and multi-class-AUC values obtained by each method (Table 4) and showing bar plots of the values of the four evaluation criteria in Fig. 3. The proposed CNN and MaO-radiomics models always show better prediction results than the popular XmasNet and conventional radiomics models, whether using only CT or PET images or a combination of PET and CT images. For example, the proposed CNN model using the CT images as input outperformed the XmasNet or Radiomics models in prediction accuracy by around 0.08 (around 11%). The hybrid method, which integrates the outputs of the proposed CNN and MaO-radiomics models, obtained even or higher evaluation criteria values compared to the CNN or MaO-radiomics model alone. Although the MaO-radiomics and 3D-CNN models had the classification accuracy values of 0.83 and 0.82 respectively using CT imaging, the hybrid model improved the accuracy to 0.85, indicating the effectiveness of the ER fusion strategy. The Macro-average value obtained by using CT imaging was improved by the hybrid model to 0.85 from 0.81 and 0.84 for MaO-Radiomics and CNN, respectively. The mean-OVA-AUC and multi-class-AUC values obtained by the hybrid model outperformed the two single models using PET imaging, suggesting that results are more reliable after combination. Since the proposed CNN model have already achieved a high accuracy of 0.88, mean-OVA-AUC of 0.95 and multi-class AUC of 0.95, the ER fusion strategy did not improve the classification further. We also investigated the statistical significance of the difference between the proposed hybrid method and the other methods including XmasNet and conventional radiomics model in Table 5. Bonferroni correction (Bonferroni, 1936; Dunn, 1958) was utilized. Based on the p-values shown in Table 5, the proposed hybrid method significantly outperforms the other methods in most cases at a significant level of 0.05.
Table 4:
Values of four evaluation criteria obtained by different methods.
| CT | PET | PET&CT | ||
|---|---|---|---|---|
| XmasNet | 0.76 | 0.68 | 0.81 | |
| Radiomics | 0.75 | 0.75 | 0.75 | |
| ACC | Proposed CNN | 0.83 | 0.79 | 0.88 |
| MaO-radiomics | 0.82 | 0.80 | 0.82 | |
| Hybrid | 0.85 | 0.80 | 0.88 | |
| XmasNet | 0.77 | 0.69 | 0.82 | |
| Radiomics | 0.76 | 0.76 | 0.76 | |
| Macro-average | Proposed CNN | 0.84 | 0.80 | 0.89 |
| MaO-radiomics | 0.81 | 0.80 | 0.81 | |
| Hybrid | 0.85 | 0.80 | 0.89 | |
| XmasNet | 0.90 | 0.85 | 0.91 | |
| Radiomics | 0.87 | 0.84 | 0.86 | |
| Mean-OVA-AUC | Proposed CNN | 0.94 | 0.88 | 0.95 |
| MaO-radiomics | 0.88 | 0.86 | 0.89 | |
| Hybrid | 0.94 | 0.90 | 0.95 | |
| XmasNet | 0.90 | 0.85 | 0.92 | |
| Radiomics | 0.89 | 0.86 | 0.88 | |
| Multi-class-AUC | Proposed CNN | 0.94 | 0.89 | 0.95 |
| MaO-radiomics | 0.89 | 0.86 | 0.89 | |
| Hybrid | 0.94 | 0.91 | 0.95 |
Figure 3:
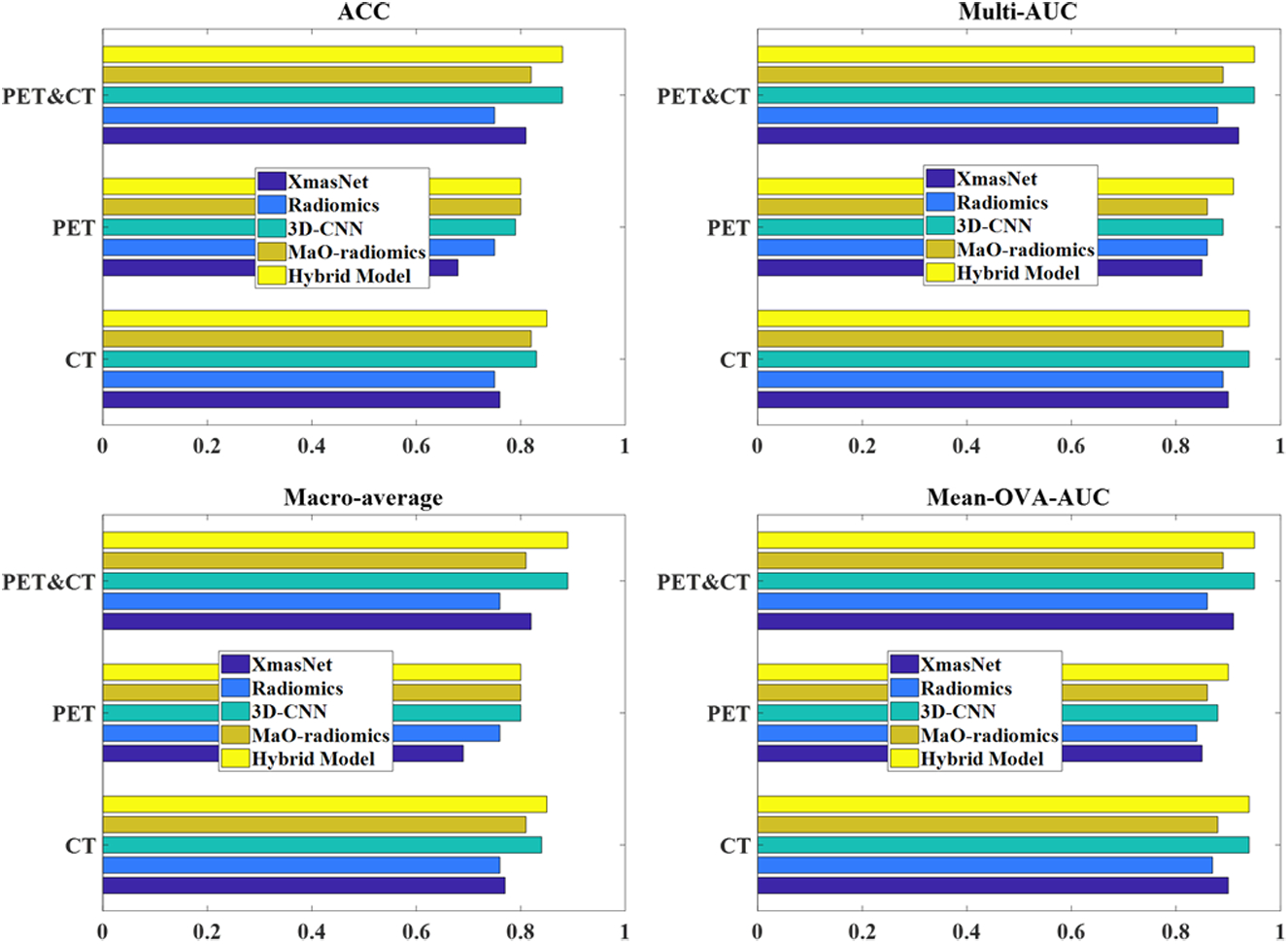
Bar plots of four evaluation criteria obtained by five methods. Longer bars indicate higher evaluation criteria values and better prediction results. The hybrid method that uses a combination of PET and CT images as input generated the best prediction results.
Table 5:
Results of p-values for two hypotheses after Bonferroni correction.
| Modality | XmasNet vs. Proposed Hybrid Model | Conventional Radiomics vs. Proposed Hybrid Method |
|---|---|---|
| CT | 0.0107 | 0.0158 |
| PET | 0.0007 | 0.1819 |
| PET&CT | < 0.0001 | p < 0.0001 |
Confusion matrix results for the MaO-radiomics model, the proposed 3D CNN model, and the hybrid model for the three categories of nodules are shown in Tables 6–8. The MaO-radiomics model was worse in predicting normal and involved nodes while better in predicting suspicious nodes than the CNN model by using CT imaging. After fusing the outputs of these two models by ER, the hybrid model improved the abilities of predicting normal, suspicious and involved nodes. In most cases, the proposed hybrid model was more effective than the two single models in predicting LNM. The same conclusion can be drawn from Figure 4. For the XmasNet and Radiomics models, it is difficult to find clear boundaries between each distribution of the prediction results for each type of node. However, the prediction results for the normal nodes obtained by the proposed CNN and MaO-radiomics models can form a separately clustered region, which indicates that these two models better differentiate the normal nodes among three types of nodes than the XmasNet and Radiomics models. There is still no clear boundary between distributions of the prediction results for the suspicious and involved nodes for the proposed CNN and MaO-radiomics models. The prediction results obtained by the hybrid method for three types of nodes construct three clustered regions, which imply that the hybrid method generates more reliable prediction results.
Table 6:
Confusion matrix for MaO-radiomics.
| Imaging | Node | Predicted Normal | Predicted Suspicious | Predicted Involved | UA |
|---|---|---|---|---|---|
| Normal | 13 | 4 | 0 | 0.76 | |
| CT | Suspicious | 0 | 23 | 4 | 0.85 |
| Involved | 1 | 3 | 18 | 0.82 | |
| PA | 0.93 | 0.77 | 0.82 | ||
| Normal | 14 | 3 | 0 | 0.82 | |
| PET | Suspicious | 0 | 23 | 4 | 0.85 |
| Involved | 1 | 5 | 16 | 0.73 | |
| PA | 0.93 | 0.74 | 0.80 | ||
| Normal | 13 | 4 | 0 | 0.76 | |
| PET & CT | Suspicious | 0 | 23 | 4 | 0.85 |
| Involved | 1 | 3 | 18 | 0.82 | |
| PA | 0.93 | 0.77 | 0.82 |
Table 8:
Confusion matrix for the hybrid model.
| Imaging | Node | Predicted Normal | Predicted Suspicious | Predicted Involved | UA |
|---|---|---|---|---|---|
| Normal | 14 | 3 | 0 | 0.82 | |
| CT | Suspicious | 0 | 23 | 4 | 0.85 |
| Involved | 1 | 2 | 19 | 0.86 | |
| PA | 0.93 | 0.82 | 0.83 | ||
| Normal | 14 | 3 | 0 | 0.82 | |
| PET | Suspicious | 0 | 24 | 3 | 0.89 |
| Involved | 1 | 6 | 15 | 0.68 | |
| PA | 0.93 | 0.73 | 0.83 | ||
| Normal | 16 | 1 | 0 | 0.94 | |
| PET & CT | Suspicious | 2 | 23 | 2 | 0.85 |
| Involved | 1 | 2 | 19 | 0.86 | |
| PA | 0.84 | 0.88 | 0.90 |
Figure 4:
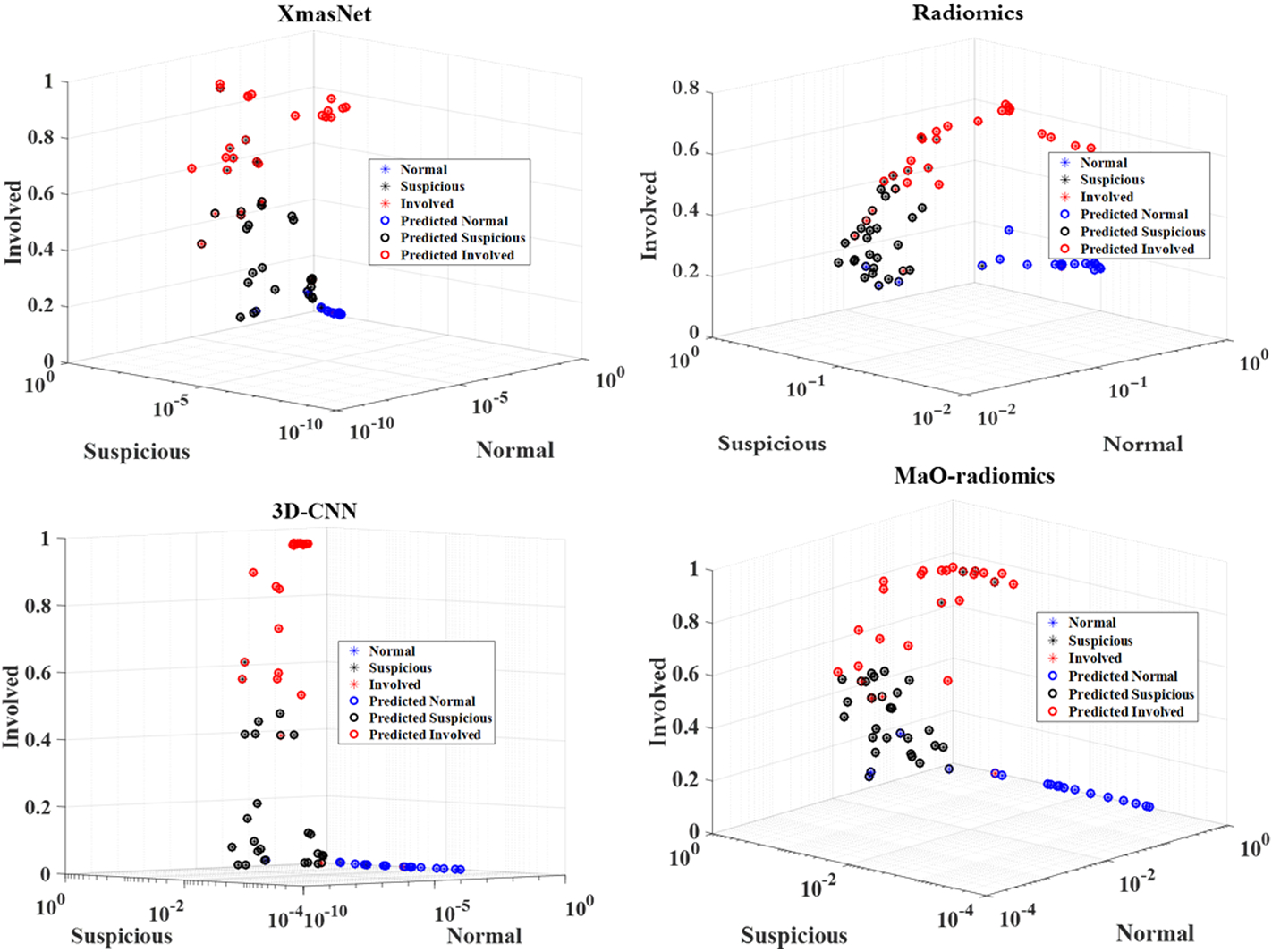
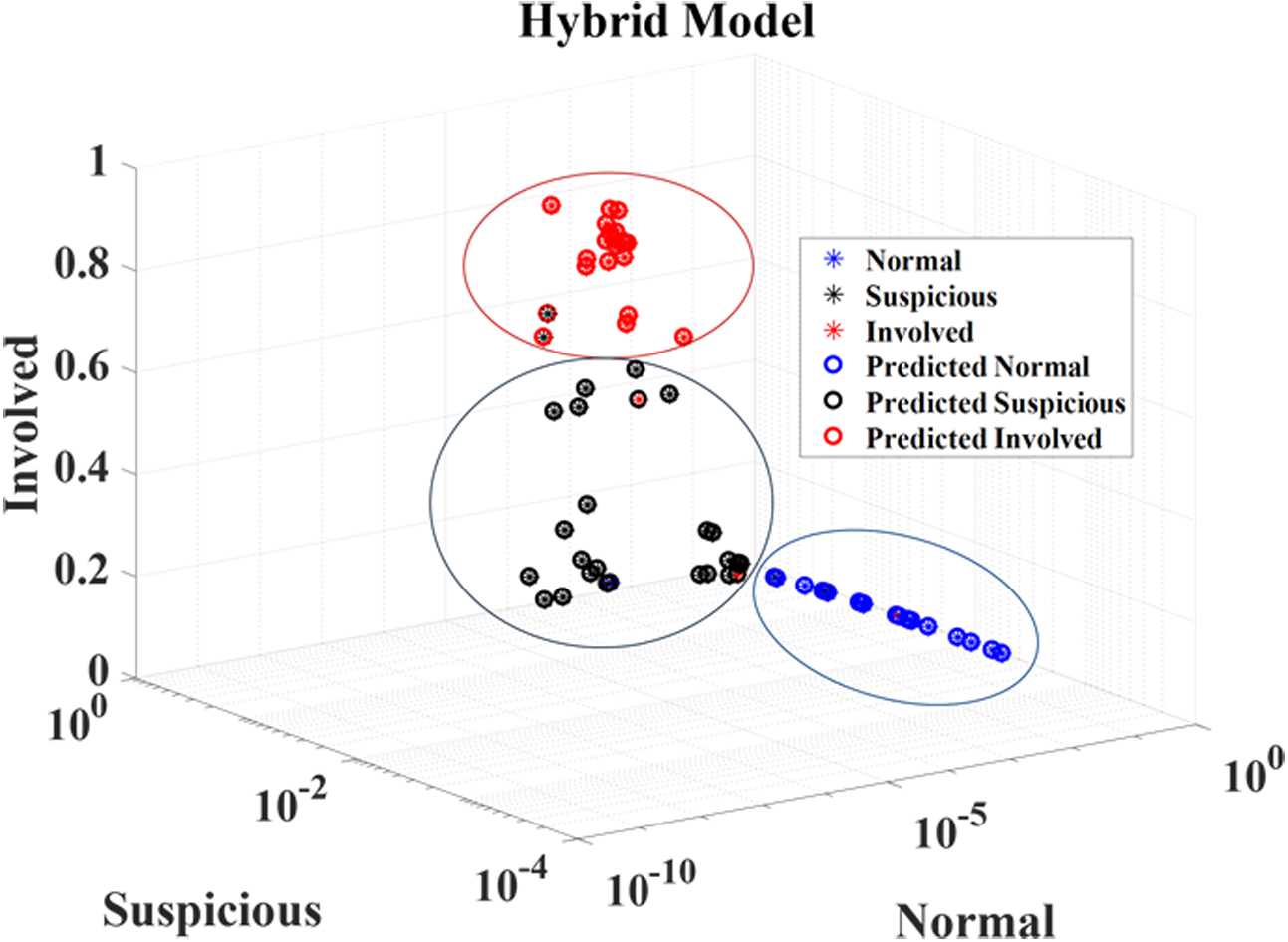
Prediction results obtained by five different models.
Finally, the four ROC curves in Fig. 5 illustrate the hybrid method’s performance in distinguishing different types of nodes by using combination of CT and PET imaging. The hybrid method achieved 0.97 AUC when differentiating normal nodes from the other two types of nodes (suspicious and involved). Additionally, the hybrid model achieved 0.96, 0.97, and 0.91 AUC values for distinguishing normal from suspicious, normal from involved, and suspicious from involved nodes, respectively. We also investigated the sensitivity of weight when using ER for fusion as shown in Figure 6. The results showed that when the weight of 3D-CNN is set from 0.6 to 0.8, the best performance can be obtained. Meanwhile, the performance reduces in other situation.
Figure 5:
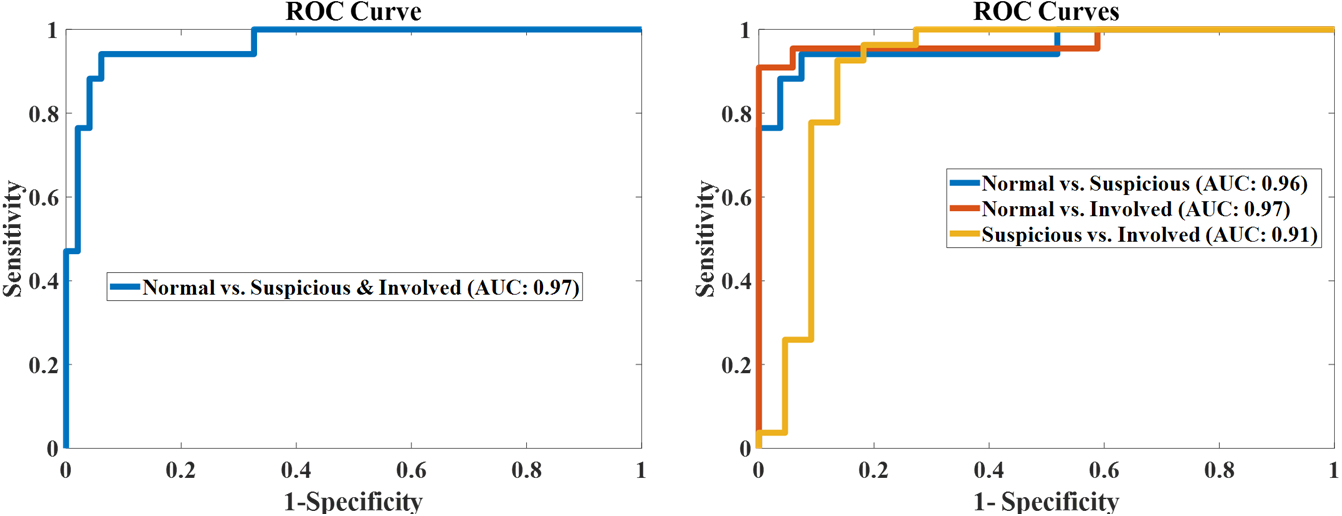
ROC curves for the Hybrid model.
Figure 6:
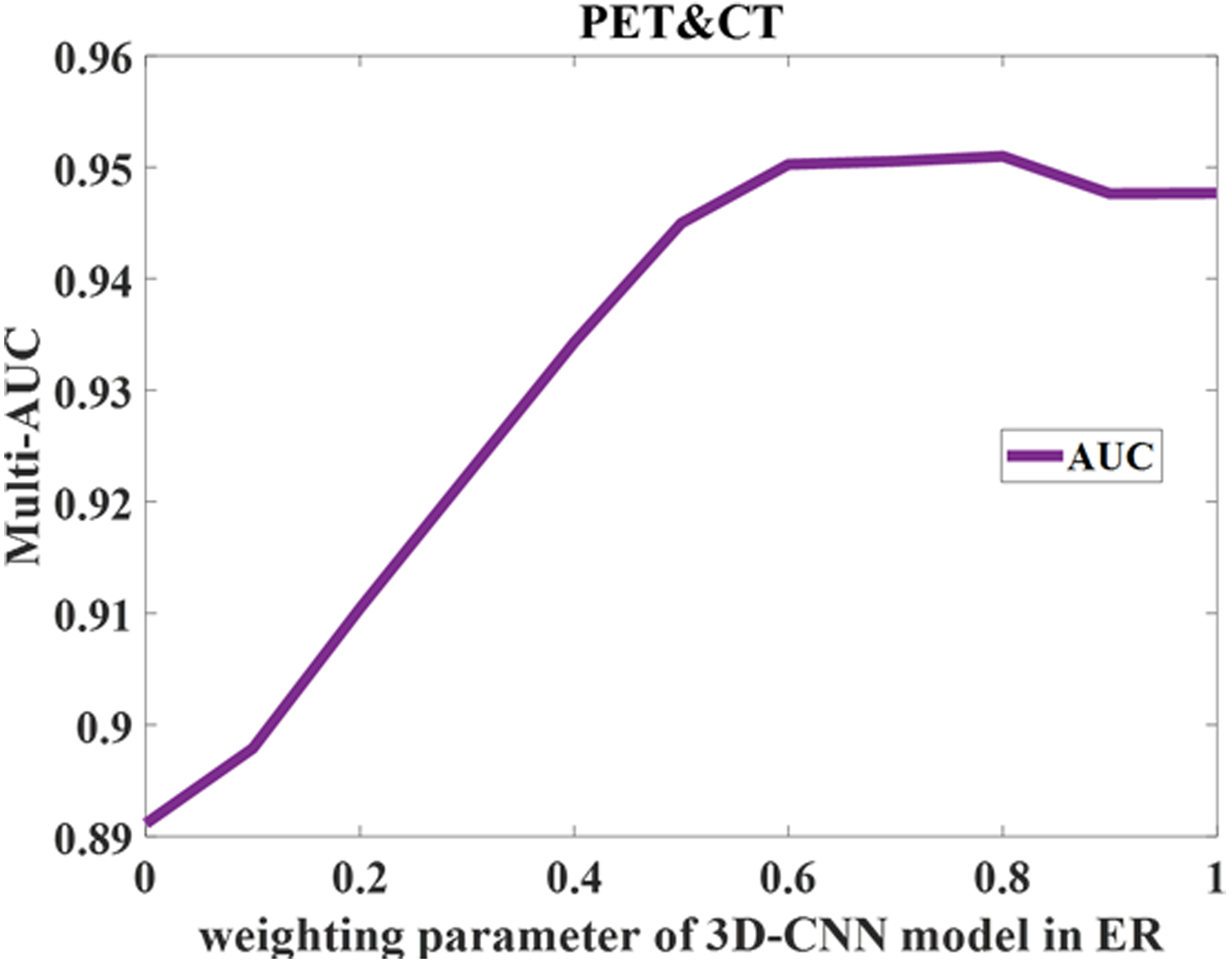
Sensitivity analysis of weight in ER fusion.
4. Discussion and conclusion
To obtain more reliable results, MaO-radiomics and 3D-CNN are fused through ER approach in the decision level in our work. Alternatively, information fusion could be performed in the feature level (Yan et al., 2018). The fusion performed on the feature level is desired when features are from different sources and complementary. The features used in our two individual models (MaO-radiomics or 3D-CNN) are essentially from the same imaging modalities (PET, CT and or combined PET and CT), there could be many redundancies in the feature space, which may have a negative effect on the model performance. On the other hand, if we fuse the information extracted by different models at the decision level, the redundancy in the feature space could be alleviated. Nevertheless, the fusion strategy at the feature level similar to HyRiskNet in (Yan et al., 2018) can be used to fused information extracted from PET and CT. The influence of fusing information at different levels is worthy of investigating in a future work.
In this study, we used a relatively simple architecture to learn and extract the features which are needed for the final prediction by implementing a convolutional neural network with 17 layers. The architecture of the proposed 3D-CNN is similar to the classical AlexNet (Krizhevsky et al., 2012) and VGG net (Simonyan and Zisserman, 2014) except that the proposed model is three-dimensional since the lymph nodes are 3D-objects. We also implemented CNNs with advanced architectures similar to ResNet (He et al., 2016) and DenseNet (Huang et al., 2017) and trained these models by using the current LN dataset. Similar predictive results were obtained with AUC values 0.93 and 0.92 by using PET&CT images for the ResNet and DenseNet models, respectively. Using the current LN dataset of lymph nodes, ResNet and DenseNet haven’t shown much improvement over the proposed 3D-CNN. Hence, we kept using the proposed 3D-CNN model which is simple and easy to implement in this study.
We proposed a hybrid model that predicts lymph node metastasis in head and neck cancer by combining outputs of MaO-radiomics and 3D-CNN models through an evidential reasoning fusion approach. Specifically, to obtain more reliable performance, we developed a new MaO-radiomics model based on our previous work. This new model considers PAs and UAs in confusion matrix as objective functions, in addition to sensitivity and specificity. Meanwhile, we developed a 3D-CNN model to make full use of contextual information in the images. The final output was obtained by combining the two models’ outputs using the ER approach. The experimental results show that the hybrid model improved the classification accuracy and reliability obtained by the two single models when using CT imaging alone. We also investigated the influence of input imaging. We obtained better results using both PET and CT imaging than using PET or CT imaging alone.
The current MaO-radiomics model optimized PAs and UAs simultaneously. These two types of objective function can be trained alternately, which could potentially improve the model’s performance. To obtain a more robust model, transfer learning can be introduced into the 3D-CNN model as a next step. We will also develop a new strategy for training the weights in fusion stage instead of manually setting. The dataset can also be expanded to include more patient data to build and validate the model, so it can be applied in the clinical settings. With better prediction of type of lymph nodes, we can make a better individualized treatment plan, potentially resulting in better control and lower toxicity in the HNC radiation treatment.
Table 7.
Confusion matrix for 3D-CNN.
| Imaging | Node | Predicted Normal | Predicted Suspicious | Predicted Involved | UA |
|---|---|---|---|---|---|
| Normal | 15 | 2 | 0 | 0.88 | |
| CT | Suspicious | 1 | 20 | 6 | 0.74 |
| Involved | 1 | 1 | 20 | 0.91 | |
| PA | 0.88 | 0.87 | 0.77 | ||
| Normal | 16 | 1 | 0 | 0.94 | |
| PET | Suspicious | 5 | 18 | 4 | 0.67 |
| Involved | 2 | 2 | 18 | 0.82 | |
| PA | 0.70 | 0.86 | 0.82 | ||
| Normal | 16 | 1 | 0 | 0.94 | |
| PET & CT | Suspicious | 2 | 23 | 2 | 0.85 |
| Involved | 1 | 2 | 19 | 0.86 | |
| PA | 0.84 | 0.88 | 0.90 |
5. Acknowledgment
This work was supported in part by the American Cancer Society (ACS-IRG-02-196) and the US National Institutes of Health (R01 EB020366). The authors would like to thank the following people for their contributions to this manuscript: Dr. Genggeng Qin from Southern Medical University, Guangzhou, China and Dr. Jonathan Feinberg from UT southwestern Medical Center.
Appendix
Assume that there are L evidence ei(i = 1, ⋯, L) for combination and N classes denoted by H = {θn, n = 1, ⋯, N}. If the output probability for a θn on ei is denoted by pn,i, the belief degree for each evidence can be defined as:
| (A.1) |
with 0 ≤ pn,i ≤ 1 (n = 1, ⋯, N), and being the degree of global ignorance. Assume that the weight of ith evidence is denoted by wi, and the constraint is:
| (A.2) |
Then the ER algorithm is implemented recursively. At first, the basic probability masses for ei are generated from weighted belief degrees, that is:
| (A.3) |
mH,i is divided into two parts, they are:
| (12) |
Let mn,I(i) (n = 1, ⋯, N), and .denote the combined probability masses which are generated by combining first i evidence. The ER algorithm is described as:
| (A.4) |
| (A.5) |
| (A.6) |
| (A.7) |
| (A.8) |
After all the evidences are combined, the final belief degree pn is generated using the following normalization process:
| (A.9) |
| (A.10) |
6. References
- Antropova N, Huynh BQ and Giger ML 2017. A Deep Feature Fusion Methodology for Breast Cancer Diagnosis Demonstrated on Three Imaging Modality Datasets Medical physics [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonferroni C 1936. Teoria statistica delle classi e calcolo delle probabilita Pubblicazioni del R Istituto Superiore di Scienze Economiche e Commericiali di Firenze 8 3–62 [Google Scholar]
- Cha KH, Hadjiiski L, Chan H-P, Weizer AZ, Alva A, Cohan RH, Caoili EM, Paramagul C and Samala RK 2017. Bladder cancer treatment response assessment in CT using radiomics with deep-learning Scientific reports 7 8738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Zhou Z, Hannan R, Thomas K, Pedrosa I, Kapur P, Brugarolas J, Mou X and Wang J 2018. Reliable gene mutation prediction in clear cell renal cell carcinoma through multi-classifier multi-objective radiogenomics model Physics in Medicine & Biology 63 215008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cognetti DM, Weber RS and Lai SY 2008. Head and neck cancer Cancer 113 1911–32 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coroller TP, Agrawal V, Narayan V, Hou Y, Grossmann P, Lee SW, Mak RH and Aerts HJ 2016. Radiomic phenotype features predict pathological response in non-small cell lung cancer Radiotherapy and Oncology 119 480–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster AP 1968. A generalization of Bayesian inference Journal of the Royal Statistical Society. Series B (Methodological) 205–47 [Google Scholar]
- Dunn OJ 1958. Estimation of the means of dependent variables The Annals of Mathematical Statistics 1095–111 [Google Scholar]
- Ferri C, Hernández-Orallo J and Salido MA European Conference on Machine Learning,2003), vol. Series): Springer; ) pp 108–20 [Google Scholar]
- Ganeshan B, Abaleke S, Young RC, Chatwin CR and Miles KA 2010. Texture analysis of non-small cell lung cancer on unenhanced computed tomography: initial evidence for a relationship with tumour glucose metabolism and stage Cancer imaging 10 137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garapati SS, Hadjiiski L, Cha KH, Chan HP, Caoili EM, Cohan RH, Weizer A, Alva A, Paramagul C and Wei J 2017. Urinary bladder cancer staging in CT urography using machine learning Medical physics 44 5814–23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong Y, Wang L, Guo R and Lazebnik S European conference on computer vision,2014), vol. Series): Springer; ) pp 392–407 [Google Scholar]
- Hand DJ and Till RJ 2001. A simple generalisation of the area under the ROC curve for multiple class classification problems Machine learning 45 171–86 [Google Scholar]
- He K, Zhang X, Ren S and Sun J Proceedings of the IEEE conference on computer vision and pattern recognition,2016), vol. Series) pp 770–8 [Google Scholar]
- He Z, Yen GG and Zhang J 2014. Fuzzy-based Pareto optimality for many-objective evolutionary algorithms IEEE Transactions on Evolutionary Computation 18 269–85 [Google Scholar]
- Hensman P and Masko D 2015. The Impact of Imbalanced Training Data for Convolutional Neural Networks
- Huang G, Liu Z, Van Der Maaten L and Weinberger KQ Proceedings of the IEEE conference on computer vision and pattern recognition,2017), vol. Series) pp 4700–8 [Google Scholar]
- Huang Y-q, Liang C-h, He L, Tian J, Liang C-s, Chen X, Ma Z-l and Liu Z-y 2016a. Development and validation of a radiomics nomogram for preoperative prediction of lymph node metastasis in colorectal cancer Journal of Clinical Oncology 34 2157–64 [DOI] [PubMed] [Google Scholar]
- Huang Y, Liu Z, He L, Chen X, Pan D, Ma Z, Liang C, Tian J and Liang C 2016b. Radiomics Signature: A Potential Biomarker for the Prediction of Disease-Free Survival in Early-Stage (I or II) Non—Small Cell Lung Cancer Radiology 281 947–57 [DOI] [PubMed] [Google Scholar]
- Krizhevsky A, Sutskever I and Hinton GE Advances in neural information processing systems,2012), vol. Series) pp 1097–105
- Lambin P, Leijenaar RT, Deist TM, Peerlings J, de Jong EE, van Timmeren J, Sanduleanu S, Larue RT, Even AJ and Jochems A 2017. Radiomics: the bridge between medical imaging and personalized medicine Nature Reviews Clinical Oncology [DOI] [PubMed] [Google Scholar]
- Li B, Li J, Tang K and Yao X 2015. Many-objective evolutionary algorithms: A survey ACM Computing Surveys (CSUR) 48 13 [Google Scholar]
- Liu S, Zheng H, Feng Y and Li W Medical Imaging 2017: Computer-Aided Diagnosis,2017), vol. Series 10134): International Society for Optics and Photonics; ) p 1013428 [Google Scholar]
- Moore BA, Weber RS, Prieto V, El‐Naggar A, Holsinger FC, Zhou X, Lee JJ, Lippman S and Clayman GL 2005. Lymph node metastases from cutaneous squamous cell carcinoma of the head and neck The Laryngoscope 115 1561–7 [DOI] [PubMed] [Google Scholar]
- Pantel K and Brakenhoff RH 2004. Dissecting the metastatic cascade Nature Reviews Cancer 4 448. [DOI] [PubMed] [Google Scholar]
- Shafer G 1976. A mathematical theory of evidence vol 1: Princeton university press Princeton; ) [Google Scholar]
- Simonyan K and Zisserman A 2014. Very deep convolutional networks for large-scale image recognition arXiv preprint arXiv:1409.1556
- Sun W, Zheng B and Qian W Medical Imaging 2016: Computer-Aided Diagnosis,2016), vol. Series 9785): International Society for Optics and Photonics; ) p 97850Z [Google Scholar]
- Vallières M, Freeman C, Skamene S and El Naqa I 2015. A radiomics model from joint FDG-PET and MRI texture features for the prediction of lung metastases in soft-tissue sarcomas of the extremities Physics in medicine and biology 60 5471. [DOI] [PubMed] [Google Scholar]
- Wang J and Perez L 2017. The effectiveness of data augmentation in image classification using deep learning. Technical report)
- Wang S, Hou Y, Li Z, Dong J and Tang C 2016. Combining convnets with hand-crafted features for action recognition based on an HMM-SVM classifier Multimedia Tools and Applications 1–16 [Google Scholar]
- Wang Y-M, Yang J-B and Xu D-L 2006. Environmental impact assessment using the evidential reasoning approach European Journal of Operational Research 174 1885–913 [Google Scholar]
- Yan P, Guo H, Wang G, De Man R and Kalra MK 2018. Hybrid deep neural networks for all-cause Mortality Prediction from LDCT Images arXiv preprint arXiv:1810.08503 [DOI] [PubMed]
- Yang J-B and Singh MG 1994. An evidential reasoning approach for multiple-attribute decision making with uncertainty Systems, Man and Cybernetics, IEEE Transactions on 24 1–18 [Google Scholar]
- Yang J-B and Xu D-L 2002a. On the evidential reasoning algorithm for multiple attribute decision analysis under uncertainty IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans 32 289–304 [Google Scholar]
- Yang J-B and Xu D-L 2002b. On the evidential reasoning algorithm for multiple attribute decision analysis under uncertainty Systems, Man and Cybernetics, Part A: Systems and Humans, IEEE Transactions on 32 289–304 [Google Scholar]
- Yang Y, Fasching PA and Tresp V Healthcare Informatics (ICHI), 2017 IEEE International Conference on,2017), vol. Series): IEEE; ) pp 46–55 [Google Scholar]
- Yoon DY, Hwang HS, Chang SK, Rho Y-S, Ahn HY, Kim JH and Lee IJ 2009. CT, MR, US, 18F-FDG PET/CT, and their combined use for the assessment of cervical lymph node metastases in squamous cell carcinoma of the head and neck European radiology 19 634–42 [DOI] [PubMed] [Google Scholar]
- Zhou Z-G, Liu F, Jiao L-C, Zhou Z-J, Yang J-B, Gong M-G and Zhang X-P 2013. A bi-level belief rule based decision support system for diagnosis of lymph node metastasis in gastric cancer Knowledge-Based Systems 54 128–36 [Google Scholar]
- Zhou Z-G, Liu F, Li L-L, Jiao L-C, Zhou Z-J, Yang J-B and Wang Z-L 2015. A cooperative belief rule based decision support system for lymph node metastasis diagnosis in gastric cancer Knowledge-Based Systems [Google Scholar]
- Zhou Z, Folkert M, Iyengar P, Westover K, Zhang Y, Choy H, Timmerman R, Jiang S and Wang J 2017. Multi-objective radiomics model for predicting distant failure in lung SBRT Physics in Medicine and Biology 62 4460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Yao J, Zhu F and Huang J IEEE Conference on Computer Vision and Pattern Recognition,2017), vol. Series) pp 7234–42 [Google Scholar]


