The Impact of Acoustic Clutter on Large Array Abdominal Imaging

Abstract

Abdominal imaging suffers from a particularly difficult acoustic environment – targets are located deep and overlying tissue layers with varying properties generate acoustic clutter. Increasing array size can overcome the penetration and lateral resolution problems in ideal conditions, but how the impact of clutter scales with increasing array extent is unknown and may limit the benefits in vivo. Previous ex vivo experimental work showed the promise of large arrays but was technically limited to a length of 6.4 cm and to only partial sampling of the array elements. We present an extension of those studies using the Fullwave simulation tool to create a 10 cm x 2 cm matrix array with full lateral element sampling. We used a numerical model of the abdomen based on maps of tissue acoustical properties and found that propagation through the modeled abdominal layers generated on average 25.4 ns of aberration and 0.74 cm of reverberation clutter across the array extent. Growing the full aperture from 2 cm to 10 cm improved contrast by 8.6 dB and contrast-to-noise ratio by 22.9% in addition to significantly improving target resolution. Alternative array strategies that may be useful for implementation – mismatched aperture sizes or a swept synthetic aperture – also produced improved quality with growing aperture size. These results motivate the development of larger diagnostic imaging arrays for the purpose of high-resolution imaging in challenging environments.

INTRODUCTION

In applications such as abdominal and fetal imaging, ultrasound often suffers from severely anisotropic resolution due to the depth of the target. While the axial resolution remains relatively constant through depth (degrading only slightly due to frequency-dependent attenuation), the width of the lateral point spread function increases linearly with f-number, the ratio of focal depth to aperture size. For example, at a depth of 10 cm with a 2 cm active array, the lateral resolution would be approximately five times worse than the axial resolution. Along with signal-to-noise ratio, such degraded resolution is one factor that compromises imaging in obese patients. Several studies in abdominal and fetal imaging have reported high diagnostic failure rates in this patient population due to poor image quality [1]–[4]. Acoustic clutter – aberration, reverberation, and off-axis scattering – adds to the difficulty of many exams [5], although technology such as harmonic imaging can reduce its impact [6]. Increasing the aperture size lowers the f-number and improves lateral resolution, but the impact of acoustic clutter on large arrays is still poorly understood and may compromise gains in image quality.

The experimental study of large aperture diagnostic imaging requires technical capabilities that are beyond the designs of the current generation of clinical and research scanners. Improvements in image quality have been observed up to the size limits of commercially available ultrasound arrays [7], [8]. Previous work experimentally demonstrated ex vivo large aperture imaging using a “swept synthetic aperture” approach by precisely mechanically translating a commercial matrix array transducer across an effective aperture space [9]. However, the study had technical limitations that limit the generalization of its results. The achievable transmit aperture size was only 6.4 cm, meaning that an f-number of 1 (isotropic resolution) could only be achieved at a depth of 6.4 cm, short of a clinically relevant depth for imaging obese patients. The lack of a precisely known target and the unknown impact of using a swept synthetic aperture rather than a fully populated large array in the presence of clutter make it difficult to put these results in a larger clinical context.

The Fullwave simulation tool [10] allows for accurate 3-D simulations of arbitrary transducer and acoustic media configurations. It is possible to change the tissue map, speckle realization, transducer configuration, or imaging target while holding all other factors fixed in order to isolate a single parameter. There is also no concern of electronic complexity, allowing for a fully sampled large array without restrictions on channel count or bandwidth. Additionally, it is possible to directly observe the time course of the transmit pressure field and study the changes induced in the propagating pulse that cause clutter. A limited study of large apertures in 2-D simulations has been previously presented [11].

The study presented here simulates the imaging of a deep anechoic lesion through the abdominal wall to examine the detectability of relatively small targets in the presence of clutter with varying array extents, up to 10 cm laterally. By acquiring all combinations of transmit and receive element pairs – a complete data set – an in-depth study of various transmit and receive combinations is performed to explore both variations across a clutter-generating tissue layer and the value of redundancy across a large array. Finally, a direct analysis of the aberration and reverberation clutter generated in the simulation is presented to provide context for the imaging results. These studies show that low f-number imaging at depth has the potential to greatly improve image quality in difficult imaging situations even in the presence of clutter-generating tissues.

MATERIALS AND METHODS

Simulation parameters

The Fullwave simulation tool [10] describes acoustic wave propagation in heterogeneous media with varying sound speed, density, attenuation and nonlinearity. The finite difference time domain solution to the full-wave equation allows for the simulation of effects such as aberration, reverberation, and harmonic generation. The simulation in this study was performed in the linear simulation regime. Perfectly matched layers (PMLs) of 80 points were placed around the border of the simulation to prevent echoes due to boundary conditions. The PMLs are shown in dark red in the maps of Figs. 1 and 2 and implemented effectively as a non-linear gradient, significantly impacting only a few pixels around the edge of the simulation.

Fig. 1.

Axial-lateral slice of 3-D tissue maps. The laterally concave transducer is shown in red, and the cylindrical anechoic lesion target is outlined in white in the sound speed map. Properties of the individual tissue types are noted on the colorbar of each map. The dark red outer border of the attenuation map represents a perfectly matched layer.

Fig. 2.

Axial-elevation slice of 3-D tissue maps. The laterally concave transducer is shown in red, and the cylindrical anechoic lesion target is outlined in white in the sound speed map. Properties of the individual tissue types are noted on the colorbar of each map. The dark red outer border of the attenuation map represents a perfectly matched layer.

The transducer was defined to be a laterally concave array with radius of curvature 10 cm, arc length 10 cm (1 radian) and elevation extent 2 cm. This shape removes the concern of angular sensitivity, ensuring that the deep target is in the field of view of all elements so that coherent summation can be performed. The transducer was made up of 270 elements in the lateral dimension and 54 elements in elevation, λ/2 pitch in each dimension. One simulation was performed for each lateral element in the center elevation row, 270 simulations total. Each simulation consisted of emitting a 2.0833 MHz sinusoidal pulse with approximately 2.5 cycles as a fixed pressure from grid points belonging to a single element (without phasing).

Run-time for the simulation is determined by the total extent and sampling of space and time, as opposed to the number of scattering targets. The simulation grid was defined to be 13 cm (axial) x 10.2 cm (lateral) x 2.2 cm (elevation) with 61.6 μm grid spacing in all dimensions (12 points per wavelength). The simulation was run with a time step of 16 ns and allowed to run for 185.8 μs. The signals at grid points belonging to each array element were recorded at 10.4 MHz and averaged without phasing to simulate larger physical elements. Additionally, the pressures at three orthogonal planes – the lateral and elevation mid-planes the axial-lateral plane at a depth of 6 cm (below the abdominal wall layers) – were recorded with a sampling of twice the grid spacing (6 points per wavelength).

Each simulation was run using 24 parallel CPUs with Open MPI and took between 63 and 95 hours to complete depending on the specific hardware configuration. Each running simulation required at least 80 GB of RAM. The total computational workload was estimated to be over 550000 CPU hours and the output files, stored in single-precision floating-point format, totaled 3.6 TB.

Visible Human Project maps

The Visible Human Project (US National Library of Medicine, Bethesda, MD) provides photographic, CT and MRI data for two complete human bodies for anatomical study [12]. Photographs from the 0.33 mm cryosections of the female body data set were converted into 3-D maps of acoustic properties – sound speed, density, and attenuation. Image processing was performed to segment several component tissues within the data, identifying fat, liver, muscle, connective tissue, blood, and ribs. For this study, the ribs were removed and replaced with the surrounding tissue types. The tissues were assigned the properties in Table I, derived from data in [13], [14].

TABLE I.

SIMULATION TISSUE PROPERTIES

Tissue	Speed m/s	Density kg/m3	Attenuation dB MHz−1 cm−1
Fat	1479	937	0.4
Liver	1570	1064	0.5
Muscle	1566	1070	0.15
Connective	1613	1120	0.5
Blood	1520	1000	0.005

The tissue maps were interpolated to fit the sampling grid of the simulation and were distorted such that the top skin layer matched the curvature of the transducer by rigidly shifting individual columns of the map appropriately, preserving the area of the underlying tissues. Sub-wavelength scatterers were created within the tissue by adding up to 5% variation in the sound speed. Scatterers were excluded from the 5 mm diameter cylindrical anechoic lesion target at a depth of 10 cm. This target was chosen to reduce the impact of the limited elevation focusing on the measured image quality. An axial-lateral slice of the tissue maps is shown in Fig. 1 and an axial-elevation slice is shown in Fig. 2.

Beamforming and image analysis

Beamforming was performed by synthetic aperture focusing for the single element diverging waves [15]. The data were arranged as s[t, i, j] as a function of time t, receive channel i ∈ I, and transmit element j ∈ J. The synthetic focused data set for a given reconstructed pixel ${\overrightarrow{r}}_0=\left[x_0,y_0,z_0\right]$ was performed using the transmit-receive time of flight t_ij :

$$s_{foc}\left[{\overrightarrow{r}}_0\right]=\sum _{i\in I}\sum _{j\in J}s\left[t_{ij},i,j\right]$$ (1)

For the point source emission located at ${\overrightarrow{r}}_i=\left[x_i,y_i,z_i\right]$ , an imaging point in the field to be reconstructed, and the receive element located at ${\overrightarrow{r}}_j=\left[x_j,y_j,z_j\right]$ , the time of flight is:

$$t_{ij}=\frac{\Vert {\overrightarrow{r}}_0-{\overrightarrow{r}}_i\Vert +\Vert {\overrightarrow{r}}_j-{\overrightarrow{r}}_0\Vert }{c}$$ (2)

This study took advantage of the complete data set (all transmit events and receive channels across the array were recorded individually) to synthetically create apertures of varying extent from the single set of simulations. By varying the transmit set I and the receive set J (as a function of I), four aperture configurations were created over a range of effective aperture sizes. In all cases for this study, all elevation channels were used over the selected lateral extent. The four aperture configurations created are described in Fig. 3 and are as follows:

Fig. 3.

Aperture configurations considered in this study with labeled parameters of interest. (a) Conventional aperture size (1.92 cm) positioned at different locations along the array extent. (b) Full synthetic aperture of varying size. (c) Variable transmit aperture size with a fixed 10 cm receive aperture. (d) Swept synthetic aperture formed by translating a small transmit aperture and 1.92 cm receive aperture and coherently summing across positions.

• 1)A 1.92 cm lateral aperture modeled after the Siemens 4Z1c matrix transducer (Siemens Healthineers, Issaquah, WA) was formed from the simulated data at varying positions across the field of view to provide a point of comparison for conventional imaging. The same lateral extent was used in transmit and receive, mimicking the full sampling of a conventional transducer.
• 2)The importance of aperture size was studied using complete apertures of varying lateral extent, centered laterally on the simulated arc. The same lateral extent was used in transmit and receive, both varying together, referred to as a “full synthetic aperture” (FSA). The synthesized point spread function from this configuration is that of a conventional aperture of the selected size focused in transmit and receive at the target.
• 3)Mismatched aperture sizes were formed to study the impact of off-axis scattering on target detectability. The receive aperture was held fixed at the full aperture size (10 cm) while the transmit aperture was grown from the center of the array. In this configuration, the main lobe resolution is not expected to vary drastically, but the side lobes are expected to decrease with improving transmit aperture resolution. The impact of this variation in the presence of clutter is unknown.
• 4)A swept synthetic aperture – a sparse array sampling achieved by translating a smaller active aperture across the array extent – was formed similarly to the small full synthetic aperture data set, using only a single emission from the center of each array rather than the full transmit aperture. The data were then coherently combined from the center of the sweep outwards to enlarge both the effective transmit and receive apertures. While the total spatial frequency extent of this data set is the same as in the second case, it lacks the redundant sampling of spatial frequencies provided by the complete data set. This data set potentially suffers from degraded image quality due to fewer independent observations of the abdominal wall clutter.

Image quality metrics were computed for the anechoic lesion target in each of the imaging configurations. Regions of interest (ROIs) were drawn based on the image formed with the full aperture size and are shown in Fig. 4. The interior ROI was positioned to tightly border the edge of the lesion to measure the impact of degraded edge resolution in some cases. The exterior ROI was positioned to sample the homogeneous background tissue surrounding the lesion.

Fig. 4.

Regions of interest for lesion image quality metrics overlaid on a sample image. The two circles are concentric about the estimated lesion center. The inner circle (dashed) denotes the lesion interior while the region outside the outer circle (dotted) represents the speckle background.

For each image, signal-to-noise ratio (SNR), contrast and contrast-to-noise ratio (CNR) were calculated:

$$SNR=\frac{{\mu }_o}{{\sigma }_o}$$

$$\text{Contrast}=20{\log }_{10}\frac{{\mu }_o}{{\mu }_i}$$

$$CNR=\frac{{\mu }_o-{\mu }_i}{\sqrt{{\sigma }_o^2+{\sigma }_i^2}}$$

with the mean value of the inside and outside ROIs, μ_i and μ_o respectively, and variance of the inside and outside ROIs, ${\sigma }_i^2$ and ${\sigma }_o^2$ respectively, for the uncompressed envelope image. Note that the ratio of means in the contrast metric is inverted from conventional usage so that contrast and CNR improvements are both represented by increasing numbers.

Clutter analysis

Clutter was studied directly in the transmit pressure wave field for the propagating pulse from each transmitting element. The pressure in the axial-lateral plane was recorded in the simulation with a spatial resolution of 123 μm and a temporal resolution of 96 ns. For each transmit event, the data was scan converted to polar coordinates r and θ relative to the transmitting element, modeled as a point source. A 2 cm x 20° field was reconstructed with 0° oriented from the source to the center of the lesion target and r ranging from 8.5 cm to 10.5 cm. This allowed for study of the propagating wave (a planar wavefront in polar space) as it approached the lesion target.

Ideally, a simulation would be performed without scattering media beyond the abdominal wall such that the propagating emitted pulse, its leading edge distortions caused by aberration, and the trailing clutter created by reverberation could be observed without the confounding effects of backscattered waves [16]. To remove the backscattered echoes in the present simulation, a directional filter was applied to each radial line in Fourier space [17], [18]. This technique isolated waves propagating away from the point source in time, including any multiply scattered trailing clutter. Any given temporal snapshot of the filtered 2-D wave field therefore represents the clutter-affected pulse that will impact the imaging target.

Aberration was characterized by finding the relative arrival time difference at the target depth of 10 cm from the source. The signal recorded at the target depth for each angle of the directional filtered data was temporally upsampled to a resolution of 1 ns using cubic spline interpolation. Peaks in each pressure waveform were detected using the derivative calculated with a 101 ns length 2nd order Savitzky-Golay filter [19]. The arrival time for the wave was determined by the time of the first peak in the sinusoidal pressure wave as identified by a threshold. The mean arrival time was subtracted from the measurements for each transmit event to give a relative shift in the wavefront caused by aberration that could not be corrected by a change in the bulk sound speed used in beamforming. The standard deviation of arrival times for each emission was reported to show the magnitude of the aberration effect.

Reverberation was characterized using the directional-filtered wave field after realignment using the aberration estimates for each radial line. Each line was advanced in time by the estimated delay value to approximate the wave impacting the target depth in phase across all angles. The intensity of the reverberation field was calculated as the square of the pressure magnitude and averaged across the recorded angles. The reverberation length was measured as the distance between the peak of the mean intensity waveform and the −30 dB point on the waveform.

Validation of simulation scope

The simulations described above use a single clutter realization with a lesion target at the geometric center of the curved array. In an effort to study the ability to generalize the results, two-way point spread functions (PSFs) were simulated to describe imaging performance over a wider field of view. The two-way PSF was simulated by focusing the array to the selected point in transmit and receiving the backscatter from a speed of sound scatterer. Beamforming was performed using the focused virtual source method of [20], approximating the region around the focus as a plane wave to enable visualization of a wide lateral field. The transmit pressure field was also recorded to produce a transmit intensity field, calculated as the time-integrated squared pressure at each field point.

To test the impact of target position relative to the array’s geometric focus (10 cm depth), the PSF was measured at the geometric focus as well as 3 cm above and to the side of the geometric focus. To test the impact of curving the tissue map to fit under the array, the PSF was measured for the control case (homogeneous tissue map) and a flat tissue map with a standoff matched to the skin.

RESULTS

Conventional aperture size

Images were produced from the full synthetic aperture data set to mimic the results from a conventional matrix array, in this case the 1.92 cm lateral extent Siemens 4Z1c matrix transducer, for positions across the 10 cm lateral arc. At each position the aperture experienced a slightly different realization of clutter in both transmit and receive depending on the tissue layers beneath it. The resolution, which would be constant in the absence of the clutter-generating layer, determines the width of speckle background that can overlap the anechoic region, blurring the lesion boundary. Imaging of the deep target was performed at an f-number of 5.2, giving an expected lateral resolution of 3.85 mm at the selected center frequency.

Images of the lesion target from selected representative aperture positions are shown in Fig. 5. The tilt of the speckle pattern reflects the position of the active transducer relative to the target and is not indicative of the clutter present. The speckle pattern varied with transducer position and is expected to decorrelate completely with a translation equal to the 1.92 cm aperture length [21], [22]. In each case the lesion border was different, only roughly showing the expected circular shape. Fig. 5(a,c,d,e) all show a non-circular lesion target, with large lateral speckles that crossed the true boundary. Fig. 5(b) was by chance more representative of the underlying scattering target shape. The low lateral resolution means that variability in the speckle pattern can randomly change which part of the pattern encroaches into the anechoic region. Clutter was also superimposed on the anechoic lesion region in all cases, reducing contrast and adding texture that obscures the target relative to the homogeneous speckle background. This clutter was created by a combination of reverberation trailing the main pulse and lateral off-axis scattering.

Fig. 5.

Sample synthesized D = 1.92 cm FSA images from positions across the large array. The lesion visibility varies with aperture position depending on the tissue properties. From this sample, (a) demonstrated the highest measured contrast and (b) demonstrated the highest measured CNR. Image metrics are shown in Fig. 6.

The measured SNR, contrast and CNR for the anechoic lesion target at each synthesized array location are shown in Fig. 6. The contrast varied by 6.18 dB and the CNR by 49.1% between the best and worst aperture positions for each metric. Differences of this magnitude were visually apparent in the B-mode images as shown in Fig. 5(a,c). Note that while speckle SNR is statistically expected to remain around 1.91 across apertures, the limited ROI causes measurement variance that is in turn reflected in the CNR. The image metrics indicate that there were fine changes in the sound path of through the abdominal wall, even over short aperture translation distances, that resulted in measurably different image quality. This spatial incoherence is particularly characteristic of reverberation clutter, which acts like additive random noise [23]. The choice of acoustic window in conventional imaging is therefore crucial to optimizing image quality and target detectability, which is consistent with clinical experience.

Fig. 6.

Lesion image quality metrics for synthesized 1.92 cm FSA images from positions across the large array. The red dots on the curves indicate the positions of the images from Fig. 5, from left to right.

Aperture growth study

The large array data set was used to study the effect of aperture size on image quality in the presence of the clutter-generating abdominal wall. Fundamentally, the array size corresponds to the lateral resolution. Under favorable imaging conditions, a larger array has better lateral resolution, reducing both the main lobe width and the lateral extent of the side lobes. At the maximum resolution of the array, using the full 10 cm aperture in transmit and receive, the expected lateral resolution would be 0.74 mm. A smaller main lobe width reduces the amount of the speckle pattern that extends into the interior region. An improvement in the side lobes reduces off-axis scattering extent, which improves the contrast in the anechoic lesion.

The images corresponding to varying aperture sizes from 1.92 cm to 10 cm are shown in Fig. 7. At the smallest aperture size, the imaging performance was equivalent to the average of those shown in Fig. 6. The lateral resolution of the images visibly improved with increasing aperture size, increasing the definition of the lesion boundary and reducing the speckle texture size. The inverse relationship between aperture length and main lobe lateral resolution means that the resolution of the largest aperture was roughly one-fifth that of the smallest. The largest aperture produced the best lesion border definition, contrast, and reduced texture within the lesion.

Fig. 7.

Sample synthesized FSA images with varying aperture size, growing from the center of the array. Image metrics are shown in Fig. 8.

The image quality measurements in Fig. 8 confirmed this observation. Contrast and CNR both steadily improved with increasing aperture size up to a certain extent, up to 9 cm for contrast and 6 cm for CNR. At full aperture, contrast improved by 8.62 dB and CNR improved by 22.9%. Despite the slight reduction in CNR and contrast at the full aperture, the improved border definition significantly aided the visual detection of the lesion compared to even the 7.33 cm aperture. Compared to the conventional-sized transducer at the best acoustic window, the contrast at the largest array size was 5.41 dB better. CNR was approximately the same for the two cases, within 2.4% difference for the largest aperture size and conventional array at the optimum position. Additionally, the lateral resolution of the large aperture image cannot be matched by the conventional array, limiting the overall achievable image quality for small targets with the current generation of ultrasound transducers.

Fig. 8.

Lesion image quality metrics for synthesized FSA images with varying aperture size, growing from the center of the array. The red dots on the curves indicate the positions of the images from Fig. 7, from left to right.

The impact of lateral resolution was also evaluated in the axial-elevation plane. While the elevation resolution does not vary with lateral aperture size, the target detectability still suffers when out-of-plane (lateral) clutter is present. Fig. 9 shows the images for the same set of apertures that was shown in Fig. 7. Even in the smallest case, the cylindrical target was clearly distinguished from the background as the elevation resolution does not affect border definition in this plane. However, the contrast of the target was reduced compared to the other three aperture sizes, 6.71 dB less than at the largest aperture size. Image metrics for the target over the range of aperture sizes are shown in Fig. 10. The variability in the measured metrics is indicative of the impact of the particular speckle and clutter realization due to the low elevation resolution.

Fig. 9.

Sample synthesized FSA images in the axial-elevation plane with varying lateral (out-of-plane) aperture size, growing from the center of the array. The aperture sizes correspond to those of Fig. 7. The image quality metrics are shown in Fig. 10

Fig. 10.

Lesion image quality metrics for synthesized FSA images in the axial-elevation plane with varying lateral (out-of-plane) aperture size, growing from the center of the array. The red dots on the curves indicate the positions of the images from Fig. 9, from left to right.

Variable transmit/fixed receive aperture size

Images were formed using the complete 10 cm receive aperture with varying extents of the transmit aperture. Unlike in previous sections where analysis started at an array size of 1.92 cm, the minimum array size considered for this case was a single pair of transmit elements. Fig. 11 shows the resulting images for the different configurations. The lateral speckle texture size at the smallest transmit aperture extent was fine and comparable to the texture size at the larger array lengths. This pattern is dictated by the main lobe resolution, in this case largely set by the large receive array irrespective of the transmit aperture. The lesion, however, was filled with off-axis clutter that severely reduced the contrast. The use of even a small transmit array in (b) significantly improved the contrast by lowering the magnitude of the side lobes, tightening the overall beam pattern. Small improvements such as tightening of clutter speckle texture within the lesion and improvement of contrast were observed up to the full extent of the transmit aperture.

Fig. 11.

Sample synthesized images with a 10 cm receive aperture and varying transmit aperture size, growing from the center of the array. Image quality metrics for the images steadily improved from left to right. Image metrics are shown in Fig. 12.

The image metrics measured for the range of transmit aperture extents are plotted in Fig. 12. Contrast and CNR both fairly steadily improved with growing transmit aperture, with contrast continuing to improve and CNR plateauing at large aperture sizes just as the full aperture growth had shown. As predicted, the contrast was a function of both the transmit and receive apertures while the main lobe resolution was dominated by the latter of the two, the full 10 cm array extent. Between the smallest and largest transmit apertures, contrast improved 14.64 dB and CNR improved by 88.8%. This result suggests that a reduced-complexity imaging setup could use one larger aperture and one smaller one. With a transmit aperture size of 1.92 cm, the lesion contrast was 15.40 dB and the CNR was 1.40. These contrast and CNR values equate to FSA extents of 3.4 cm and 2.7 cm respectively from Fig. 8, which, while not much larger than the 1.92 cm active transmit aperture, correspond to significantly worse lateral resolution without the influence of the 10 cm receive aperture. The reciprocal of this case should also hold true, using a small receive aperture to reduce hardware and processing complexity with a large transmit aperture.

Fig. 12.

Lesion image quality metrics for synthesized images with a 10 cm receive aperture and varying transmit aperture size, growing from the center of the array. The red dots on the curves indicate the positions of the images from Fig. 11, from left to right.

Swept synthetic aperture

The swept synthetic aperture imaging case differs from the FSA case in several ways. First, it removes redundant sampling of spatial frequencies, especially the low lateral spatial frequencies produced by element pairs spaced far from one another. Second, it suffers from reduced electronic signal-to-noise ratio due to the fewer transmit events and averaged receive channels that make up each image. Finally, fewer transmit/receive element pairs are sampled, reducing the number of acoustic clutter realizations observed. Just as image quality varied with aperture position in Fig. 6, the impact of clutter is expected to vary between every element pair. Averaging them together coherently would be expected to reinforce the target signal and suppress incoherent clutter.

The swept synthetic aperture is comprised of unequal transmit and receive aperture sizes because it translates the full lateral receive aperture with a single lateral transmit element. The analysis here is performed using the effective aperture size: the average of the transmit and receive aperture size (0.96 cm larger than the sweep length). Fig. 13 shows the results for varying swept aperture size. The lateral texture for a given effective aperture size is finer than for the corresponding FSA due to different weighting of the lateral spatial frequencies even though the total spatial frequency extent is the same. Clutter appeared to distort the lateral boundaries of the lesion more than in the FSA case. Additionally, lesion contrast was visibly reduced across all aperture sizes.

Fig. 13.

Sample synthesized images for the swept synthetic aperture configuration with varying effective aperture size, growing from the center of the array. Image metrics are shown in Fig. 14.

The measured image quality metrics are shown in Fig. 14. Contrast improved by 3.51 dB between the 1.92 cm array and the largest extent, while CNR improved by 16.9%. Both of these are smaller improvements than were observed for the FSA case. The curves were also more variable across aperture sizes, including a small decrease in CNR at the largest aperture extent. For approximately equal aperture sizes of 1.92 cm, the swept synthetic aperture case showed 1.81 dB less contrast and 8.7% lower CNR than the FSA case. At the largest aperture size, the difference grew to a 6.92 dB in contrast and a 13.2% lower CNR. The FSA has a clear advantage in clutter suppression, especially at the larger aperture sizes.

Fig. 14.

Lesion image quality metrics for synthesized images for the swept synthetic aperture configuration with varying effective aperture size, growing from the center of the array. The red dots on the curves indicate the positions of the images from Fig. 13, from left to right.

Clutter analysis

The transmit pressure field recorded in the axial-lateral plane was used to study the distortion of the propagating pulse that results in acoustic clutter. Fig. 15 shows sample pressure fields from across the array at the time when the propagating wavefront reached 10 cm depth. The ideal wavefront would be planar in the plotted polar space, indicating that the spherically diverging pulse remained coherent over all angles. The temporal waveform would only be the emitted Gaussian-weighted sinusoidal pulse, visible in the axial dimension. Instead, the images show waveforms with distorted magnitude and phase with trailing clutter behind the wavefront propagating radially outward. It should also be noted that these results are for one-way propagation through the abdominal wall only. The effects would be exacerbated by the return trip of the backscattered echoes through the abdominal wall.

Fig. 15.

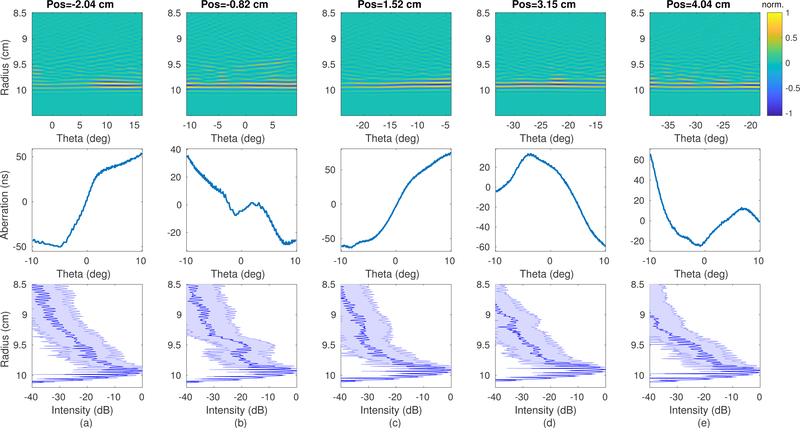
(top row) Forward-propagating transmit pressure field in polar coordinates relative to the emitting element at the time when the wave impacted the target at 10 cm depth. (middle row) Estimated aberration profile for the propagating wavefront. (bottom row) Average field intensity through depth. (a-e) Transmit events from elements laterally spaced across the aperture.

Aberration is the distortion of the propagating wavefront that reduces the coherence of the propagating pulse. Aberration was visible in the pressure field of Fig. 15 as a low-frequency oscillation of the planar wavefront in the angular dimension. The aberration profile for each case was estimated and is shown below the corresponding pressure field. Each case showed a different realization of aberration clutter, varying in both frequency and magnitude. The standard deviation of the aberration time for each transmit event across the array is shown in Fig. 16(a). As in the imaging results of Fig. 6, the clutter magnitude was observed to vary with position. The average aberration level was 25.4±14.3 ns, or 5.3% of the wavelength. A previous study of transmission through ex vivo human abdominal samples [24] showed an average aberration of 43.0±11.6 ns at 3.75 MHz, or 16.1±4.4% of the wavelength, although individual samples ranged from 25.6 ns to 63.9 ns. Another study of ex vivo animal abdomens [25] showed similar results with an average aberration of 41.9±20.3 ns at 3 MHz. The aberration observed in this study was of lower magnitude than the average but not out of the range of observed abdomens in those experiments.

Fig. 16.

(a) Standard deviation of arrival time differences across the field of view due to aberration for varying transmit element position. (b) Spatial extent of trailing reverberation clutter behind the leading pulse measured by the −30 dB intensity level for varying transmit element position.

Reverberation is the multiple scattering of the wavefront off of the abdominal wall layers, resulting in secondary pulses that trail the leading wavefront and effectively extend the axial pulse length. The spatially incoherent reverberation signal is visible in Fig. 15 behind the planar wavefront as segments of waves propagating from multiple directions with varying magnitude. These waves produce their own backscatter pattern from the target at a later time, overlapping the backscattered signals from the main pulse. For the anechoic lesion target, this results in an additive speckle pattern generated from the homogeneous tissue above the lesion. The average reverberation distance measured in the simulation was 0.74±0.21 cm, almost the entire extent of the 1 cm diameter lesion. As observed in the imaging results, this level of clutter severely reduced the observed target contrast. Unfortunately there does not appear to be a quantitative reference for aberration due to the abdominal wall in the literature to which these simulation results can be compared.

Validation of simulation scope

It may be expected that the array would perform best at its geometric center, where lesion imaging was performed. Fig. 17 shows the transmit intensity field and point spread function for three spatial locations. The PSF that matches the lesion target location in previous locations shows significant aberration, with a distorted main lobe and energy spread into the side lobes. This is reflective of the clutter and limited edge resolution observed in the lesion case. The PSFs representing targets 3 cm to the side and above the geometric array show sharper main lobes and similar side lobe distributions, indicating that imaging performance would be at least equivalent. Note that this simulation does not fully account for angular sensitivity, which limits the use of the full array at positions far off-axis or close to the transducer.

Fig. 17.

Simulated transmit intensity and B-mode image for (a) point at the geometric focus (0, 10) cm as in the lesion simulations, (b) point to the side of the geometric focus (−3, 10) cm, and (c) point above the geometric focus (0, 7) cm. The impact of clutter is revealed by the distortion of the transmit intensity field and the aberration of the point spread function. Reverberation from the tissue layer is visible in (c) and is not reflective of focusing performance.

Similarly, it may be expected that curving the tissue to match the array, placing tissue layers approximately parallel to the transducer face, would provide optimal imaging conditions. Fig. 18 shows that changing the tissue geometry has little if any effect on the PSF. The other possible imaging method with a curved array, compressing the tissue to fit under the array, would produce even smaller deviation than the flat tissue case. The PSF from the homogeneous case is provided for reference to show the high resolution and low side lobes expected in the ideal imaging case.

Fig. 18.

Sound speed map, transmit intensity and B-mode image for (a) homogeneous imaging case, (b) curved tissue case as in the lesion simulations, and (c) flat tissue case. No substantial differences were observed between the aberrated PSF of (b) and (c).

DISCUSSION

This study demonstrated the impact that a large aperture can have on the diagnostic quality of deep ultrasound imaging. The simulation approach allowed for the study of imaging with a larger extent without compromises in either lateral element size or sampling than has been achievable in past experiments and used a known imaging target. Even in the presence of clutter generated by the abdominal wall, image quality and target detectability were improved by the larger aperture size. Image quality improved with aperture size across all tested implementations of the large aperture, although by varying amounts depending on the configuration. The swept synthetic aperture configuration especially suffered from a loss of image quality relative to the full synthetic aperture case. Previous work that used the swept synthetic aperture configuration [9] demonstrated the expected resolution improvement with increasing aperture extent but negligible gains in contrast and CNR, in good agreement with this study.

Full synthetic aperture imaging as performed in this simulation, transmitting from individual elements and receiving on all elements, is impractical for real imaging scenarios. It suffers from low signal-to-noise ratio, requires high beamforming complexity (either full receive channel access or configurable sub-array beamforming), and requires an unacceptably long scan duration. However, these results represent the upper bound on image quality achievable with delay-and-sum beamforming with such an array. Either focused transmit beams or broad transmissions (e.g. plane waves), possibly combined with a walking active subaperture, could be used to cover the desired field of view with fewer total transmissions. Similarly, studies of element pitch could be performed by grouping the simulated subelements to optimize the beam pattern against total element count. Future work should optimize the trade-offs between frame rate, electronic complexity, and image quality.

The choice of curvature of the array, here an arc of a 10 cm circle, should be evaluated based on the desired lateral field of view and achievable element angular sensitivity. It is necessary to curve the array sufficiently to constructively interfere elements from the either end of the active array at the chosen imaging depth. More severe curvature restricts the lateral field of view, while reduced curvature may limit the maximum effective array size for a given imaging depth. The impact of the curvature is lessened closer to the array, where aperture growth would be used to maintain a fixed f-number and limit the array extent needed.

This work was limited by the computational cost of simulating propagation from individual transmit elements over a large field of view. It would be beneficial to fully populate the elevation dimension of the transmit array and perform imaging of a spherical target rather than a cylinder to fully assess the practical performance of the asymmetrical matrix array. Simulations using other abdominal wall realizations would be useful to evaluate the impact of varying clutter levels across the expected clinical population if such maps were available. It would also be desirable to produce a control case without the abdominal layer as well as cases with an isolated point target to directly study the generated clutter and point spread function. We hope the improvements in computing power and simulation efficiency will remove these barriers for future studies. Despite these limitations, the conclusions of this study indicate that large aperture abdominal imaging could significantly improve image quality compared to the current clinical standard.

CONCLUSIONS

We have demonstrated through numerical simulation the potential benefit of large aperture imaging in challenging acoustic environments. Low f-number imaging at depth for abdominal or fetal imaging would greatly improve image quality beyond the current standard at the expense of hardware and computational complexity. Even with increasing hardware capabilities, future work must carefully consider transducer complexity and pulse sequencing to take advantage of large channel count, large extent arrays.