Optimal control application to an Ebola model

Abstract

Ebola virus is a severe, frequently fatal illness, with a case fatality rate up to 90%. The outbreak of the disease has been acknowledged by World Health Organization as Public Health Emergency of International Concern. The threat of Ebola in West Africa is still a major setback to the socioeconomic development. Optimal control theory is applied to a system of ordinary differential equations which is modeling Ebola infection through three different routes including contact between humans and a dead body. In an attempt to reduce infection in susceptible population, a preventive control is put in the form of education and campaign and two treatment controls are applied to infected and late-stage infected (super) human population. The Pontryagins maximum principle is employed to characterize optimality control, which is then solved numerically. It is observed that time optimal control is existed in the model. The activation of each control showed a positive reduction of infection. The overall effect of activation of all the controls simultaneously reduced the effort required for the reduction of the infection quickly. The obtained results present a good framework for planning and designing cost-effective strategies for good interventions in dealing with Ebola disease. It is established that in order to reduce Ebola threat all the three controls must be taken into consideration concurrently.

1. Introduction

The principal aim of modeling infectious diseases is to be able to make judicious decisions in the application of control interventions of the infection to eliminate and ideally to eradicate it from the human population. Simulations and modeling can optimize control efforts such that limited resources are targeted to achieve the highest impact [1]. The aim of this paper is to review the epidemiology of the Ebola pandemic and discuss the optimal control model that governs the spread of the virus in human population and suggest the optimum control strategies to control and curb the spread in the future. The world witnessed an unprecedented Ebola outbreak in West Africa which in the end was reported in some parts of Europe and North America [2]. By December 13th 2015 there had been confirmed reported cases in excess of 28 600 in total with over 11 000 people losing their lives particularly in West Africa and to a lesser extent elsewhere in the world. Outside Africa; Italy, Spain, the United Kingdom and United States of America [2] were also affected albeit with no case fatalities except for one in the USA (Table 1 ).

Table 1.

Ebola situation report 13th December 2015 [2].

Country	Cases	Death	% Mortality
Guinea	3 807	2 536	67
Liberia	10 666	4 809	45
Sierra Leone	14 122	3 955	28
Italy	1	0	0
Mali	8	6	75
Nigeria	20	8	40
Senegal	1	0	0
Spain	1	0	0
UK	1	0	0
USA	4	1	25
Total	28 640	11 315	40

The outbreak has been acknowledged by the World Health Organization as a Public Health Emergency of International Concern. The three West African countries (Guinea, Sierra Leone and Liberia) by far been hardest hit now account for about 99.9% of all infections and deaths. These countries are known to have only recently emerged from long periods of conflict and instability and thus have weak health systems, human and infrastructural resources [3].

Ebola is known to be transmitted to humans via contact with bodily fluids and secretion of infected animals mainly fruit bats, monkeys, porcupines, forest antelope and the like. It is thereafter spread from person to person through direct contact with infected persons [2], [4], [5]. The incubation period beyond which infected people become symptomatic has been estimated to range between 2 and 21 days [6]. The Ebola virus is a unique virus having a filamentous, enveloped non-segmented negative-sense RNA. It belongs to the genus Ebolavirus, within the family of Filoviridae. Its envelope glycoprotein facilitates the entry of the virus to living cells [7], [8]. Till date five strains of the virus are known: Zaire, Sudan, Tai Forest, Bundibugyo, and Reston with Zaire stain being the most virulent with up to 90% fatalities [9]. The Pasteur Institute (Lyon, France) has sequenced the viral strain currently under circulation in West Africa and reports a strong homology of 98% with Zaire ebolavirus (the most virulent). The origin of the Ebola virus has been somewhat unclear [10], [11]. However, in 2005, Leroy and co-workers reported in the Nature, evidence of asymptomatic infection by Ebola virus in three species of fruit bat [12]. This indicated that fruit bats belonging to the family Pteropodidae are the natural host of the Ebola virus. Ebola viral disease has no effective treatment or vaccines, currently only supportive care can be given to patients.

Emerging tropical infectious diseases have been persistent in causing untold economic hardships to relatively poor countries with weak health systems. The overarching goal of public health is to reduce disease burden by curtailing transmission or mitigating its severity. There are at least two fundamental public health guiding principles that exist to manage the spread of an infectious disease like Ebola viral disease that has no effective vaccines or treatment. These are (i) effective isolation of persons with symptoms and (ii) tracing the contacts of symptomatic cases for clusters of exposed persons and quarantining them for monitoring [13].

Mathematical models have played a vital role in the dynamics and control of many epidemics including malaria, severe acute respiratory syndromes and Ebola [14].

Some previous models of Ebola virus, especially the predictive models endeavour to calculate a threshold called basic reproductive number R0. The dynamics of transmission of the disease has been analyzed in terms of the reduction of the basic reproductive number [15], [16], [17], [18].

However, all these models fail to take into account time dependent control strategies and all their discussions have been concentrated on prevalence of the disease at equilibra. Time dependent control has been employed in the study of dynamics of diseases. For example, Rachah and Torres, 2015 investigated the effect of vaccination on a proportion of susceptible population and observed that the rate of infection of Ebola reduced due to this intervention [19]. Chowell and Nishiura 2014 also applied time optimal control to study Ebola epidemic reduction [14]. Other studies on using time optimal control to provide appropriate interventions to minimize the spread of diseases have also been carried out successfully [20], [21], [22], [23]. This technique of studying control strategies present an enviable theoretical results that can assist in providing tools for designing epidemic control programmes.

In this work, time dependent optimal control is explored and considered which deals with both “case holding” and “case finding” on Ebola model proposed by Rivers et al. [24]. The model assumes that there is a difference between first-stage infections and late-stage infection called super infection. Their model further assumes individuals in the latent stage develop active Ebola infection at a given rate. It also assumes that a proportion of both first and late stage-infection (super infection) recover and others move to death compartment. We present three control mechanisms which comprise two “case finding” and a “case holding” in the model. The “case finding” is usually made up of activities that lead to preventive measures including screening, public education and others. The “case holding” also has to do with designed activities that ensure patients take their drugs within stipulated times so that they are cured. The first case finding is incorporated by adding a control term that characterizes the contact between susceptible and infectious individuals so that the rate of infection will be reduced. The second case finding is instituted in the model by adding a control term that identifies proportions of those individuals in the latent stage or exposed to the disease and cure them so that the rate of getting the disease will be reduced. The holding is incorporated in the model by adding a control term that may minimize the treatment failure rate of individuals with Ebola disease. We choose the reduction of infected individuals of Ebola to be our main objective having a lower cost of the controls.

The paper is arranged as follows: section 2 is devoted to describing an Ebola model with three control terms incorporated. In addition, the objective function is introduced in this section. In section 3, the analysis of optimal control is discussed. Section 4 contains some numerical studies of optimal controls. Finally, section 5 deals with the conclusions of the studies.

2. Ebola disease model

The model structure is presented in Figure 1 and the state system of the Ebola model is the following six nonlinear ordinary differential equations proposed by Pontryagin et al. [25] and slightly modified:

$$\begin{array}{l}\frac{dS}{dt}=\mu N-\left(1-u_1\right)\left({\beta }_1{I}_1+{\beta }_2{I}_2+{\beta }_{F}F\right)S-\mu S\\ \frac{dE}{dt}=\left(1-u_1\right)\left({\beta }_1{I}_1+{\beta }_2{I}_2+{\beta }_{F}F\right)S-\left(\alpha u_2+\mu \right)E\\ \frac{d{I}_1}{dt}=\alpha u_{2}E-\left(u_3{\delta }_1{\gamma }_1+\mu \right)I_1\\ \frac{d{I}_2}{dt}=u_3{\delta }_1{\gamma }_1{I}_1-\left(u_3{\delta }_2{\gamma }_2+\mu \right)I_2\\ \frac{dF}{dt}=u_3{\delta }_2{\gamma }_2{I}_2-{\gamma }_{F}F\\ \frac{dR}{dt}=u_3\left(1-{\delta }_1\right){\gamma }_1{I}_1+u_3\left(1-{\delta }_2\right){\gamma }_2{I}_2-\left(\mu +{\gamma }_R\right)R\end{array}$$ (1)

with S(0)≥0, E(0)≥0, I ₁(0)≥0, I ₂,F(0)≥0, R(0)≥0 given, where the model partitions the total population, denoted by into the following epidemiological sub-population of susceptible (S) those exposed to Ebola virus (E) those individuals with first stage of infection (I ₁), those individuals with second stage infection also known as super infection (I ₂), fraction of the population who are recovered is denoted by (R), fraction of the population who have died and being processed for burial (F). Coefficient β ₁ , β ₂ and β _F are the rates at which the susceptible become infected by an infectious individual in the first, second and burial stage per unit of time respectively. An exposed individual moves to the first stage of infectious class at a rate α. The average length of first stage of illness is denoted by ${{\gamma }_1}^{-1}$ and the average length of second stage of illness is ${{\gamma }_2}^{-1}$. The average time from death till one is buried is denoted by ${{\gamma }_{\text{F}}}^{-1}$. Average duration of Ebola treatment unit bed occupancy after recovery is ${{\gamma }_{\text{R}}}^{-1}$.

Figure 1.

Stage-structured compartmental model of Ebola virus disease, which splits the population into susceptible (S), exposed (E), first-stage infected (I₁), late-stage infected (I₂), recovered (R), and funeral transmissible (F).

Red compartments are transmissible, and recovery rates are greater from I₁ than from I₂[25].

δ ₁ Denotes the fraction of infected who progress to second stage of infectious and δ ₂ is the fraction who subsequently progress to death. The natural per capita mortality of Ebola disease rate is denoted by μ.

The control functions being employed, u ₁(t), u ₂(t) and u ₃(t) are bounded Lebesques integrable functions. The “case finding” control u ₁(t), deals with efforts that facilitate the keeping of a distance between susceptible and infectious individuals including education and public campaigns. The “case holding” control, u ₂(t) deals with effort needed to identify the proportion of typical Ebola exposed individuals that is known and will be put under treatment in order to reduce the number of individuals that may turn to be infectious. The term u ₃(t) deals with the effort that ensures those that are infectious both in the first and super infection stages are given treatment and monitored to take their drugs in order to minimize the number of individuals developing and dying of Ebola.

Our goal, therefore, is to minimize the number of infected individuals with the Ebola virus while at the same time keeping the cost of treatment very low. In mathematical perspective, for a fixed terminal time t _f, the problem is to minimize the objective functional

$$J\left(u_1,u_2,u_3\right)=\underset{0}{\overset{t_f}{\int }}\left[I_1\left(t\right)+I_2\left(t\right)+\frac{A_1}{2}{u}_1^2\left(t\right)+\frac{A_2}{2}{u}_2^2\left(t\right)+\frac{A_3}{2}{u}_2^2\left(t\right)\right]dt$$ (2)

It is assumed that cost of treatments is of nonlinear and takes a quadratic nature. The coefficients, A ₁, A ₂ and A ₃, are representing the balancing cost factors which have to do with the size and importance of the three segments of the objective functional. Thus, we seek to determine an optimal control, u ₁ ^*, u ₂ ^* and u ₃ ^*, such that

$$J\left(u_1^{\ast },u_2^{\ast },u_3^{\ast }\right)=\underset{\Omega }{\min }J\left(u_1,u_2,u_3\right)$$ (3)

where $\Omega =\left\{\left(u_1,u_2,u_3\right)\in L^1\left(0,t_f\right)|c_i\le u_i\le d_i,i=\mathrm{1,2,3}\right\}$ and c _i,d _i,i = 1,2,3, are denoted as fixed positive constants. In the entire work, we have assumed that the total population N to be constant. In order to achieve this, we choose $\Lambda =\mu N$.

3. Analysis of optimal controls

The indispensable conditions that an optimal pair must satisfy emanate from Pontryagin's maximum principle [25]. This principle actually does convert (1)–(3) into a problem of minimizing pointwise, H, with respect to u ₁, u ₂ and u ₃:

$$H=I_1+I_2\left(t\right)+\frac{A_1}{2}{u}_1^2+\frac{A_2}{2}{u}_2^2+\frac{A_3}{2}{u}_3^2+\sum _{i=0}^6{\lambda }_i{g}_i$$ (4)

g _i Denotes the right hand side of the ith differential equation of the state variable. By employing Pontryagin's maximum principle [25] and the existence results obtained for the optimal from [26], we arrive at Theorem 1. There exist an optimal control u ₁ ^∗, u ₂ ^∗, u ₃ ^∗ and associated solution, S ^*, E ^*, I ^* ₁, I ^* ₂, R ^* and F ^*, that minimizes J (u ₁, u ₂, u ₃) over Ω. Furthermore, there exist adjoint functions, λ ₁(t),…, λ ₆(t), such that

$$\begin{array}{l}{\stackrel{\ast }{\lambda }}_1=\left({\lambda }_1-{\lambda }_2\right)\left(1-u_1\right)\left({\beta }_1{I}_1^{\ast }+{\beta }_2{I}_2^{\ast }+{\beta }_F{F}^{\ast }\right)+{\lambda }_1\mu \\ {\stackrel{\ast }{\lambda }}_2=\left({\lambda }_2-{\lambda }_3\right)u_2\alpha +{\lambda }_2\mu \\ {\stackrel{\ast }{\lambda }}_3=\left({\lambda }_1-{\lambda }_2\right)\left(1-u_1\right){\beta }_1{S}^{\ast }+\left({\lambda }_3-{\lambda }_4\right)u_3{\gamma }_1{\delta }_1-u_3\left(1-{\delta }_1\right){\gamma }_1{\lambda }_6+{\lambda }_{3}u-1\\ {\stackrel{\ast }{\lambda }}_4=\left({\lambda }_1-{\lambda }_2\right)\left(1-u_1\right){\beta }_2{S}^{\ast }+\left({\lambda }_4-{\lambda }_5\right)u_3{\gamma }_2{\delta }_2-u_3\left(1-{\delta }_2\right){\gamma }_2{\lambda }_6+{\lambda }_{4}u-1\\ {\stackrel{\ast }{\lambda }}_5=\left({\lambda }_1-{\lambda }_2\right)\left(1-u_1\right){\beta }_F{S}^{\ast }+{\gamma }_F{\lambda }_5\\ {\stackrel{\ast }{\lambda }}_6={\lambda }_{6}u+{\gamma }_F{\lambda }_6\end{array}$$ (5)

With transversality conditions

$${\lambda }_i\left(t_f\right)=0,i=1,\mathrm{...},6$$ (6)

$$\begin{array}{l}{u}_1^{\ast }=\max \left\{0,\min \left\{1,\frac{\left({\lambda }_2-{\lambda }_1\right)\left({\beta }_1{I}_1^{\ast }+{\beta }_2{I}_2^{\ast }+{\beta }_F{F}^{\ast }\right)S^{\ast }}{A_1}\right\}\right\}\\ u_2^{\ast }=\max \left\{0,\min \left\{1,\frac{\left({\lambda }_2-{\lambda }_3\right)\alpha E^{\ast }}{A_2}\right\}\right\}\end{array}$$ (7)

$$u_3^{\ast }=\max \left\{0,\min \left\{1,\frac{\begin{array}{c}\left({\lambda }_3-{\lambda }_4\right){\gamma }_1{\delta }_1{I}_1^{\ast }+\left({\lambda }_4-{\lambda }_5\right){\gamma }_2{\delta }_2{I}_2^{\ast }\\ -\left(1-{\delta }_1\right){\gamma }_1{\lambda }_6{I}_1^{\ast }-\left(1-{\delta }_2\right){\gamma }_2{\lambda }_6{I}_2^{\ast }\end{array}}{A_3}\right\}\right\}$$

Proof. Corollary 4.1 Fleming and Rishel (1975) present the existence of an optimal control owing to the convexity of integrand of J with respect to (u ₁, u ₂, u ₃), a priori boundedness of the state solutions, and the Lipschitz property of the state system with respect to the state variables [26]. By employing Pontryagin's maximum principle, we have

$$\begin{array}{l}\frac{d{\lambda }_1}{dt}=-\frac{\partial H}{S},{\lambda }_1\left(t_f\right)=0,\\ \mathrm{.......}\\ \frac{d{\lambda }_6}{dt}=-\frac{\partial H}{F},{\lambda }_6\left(t_f\right)=0,\end{array}$$ (8)

evaluated at the optimal control and corresponding states, which result in the stated adjoin system (5) and (6) [27]. By considering the optimality condition,

$$\frac{\partial H}{\partial u_1}=\text{0,}\frac{\partial H}{\partial u_2}=\text{0,}\frac{\partial H}{\partial u_3}=\text{0}$$ (9)

and obtaining solution for u ₁ ^∗, u ₂ ^∗, u ₃ ^∗ gives

$$\begin{array}{l}\frac{dH}{d{u}_1}=A_1{u}_1+{\lambda }_1{\beta }_1{S}^{\ast }{I}_1^{\ast }+{\lambda }_1{\beta }_2{S}^{\ast }{I}_2^{\ast }+{\lambda }_1{\beta }_F{S}^{\ast }{F}^{\ast }-{\lambda }_2{\beta }_1{S}^{\ast }{I}_1^{\ast }-{\lambda }_2{\beta }_1{S}^{\ast }{I}_2^{\ast }-{\lambda }_2{\beta }_1{S}^{\ast }{F}^{\ast }=0,\\ \frac{dH}{d{u}_2}=A_2{u}_2+{\lambda }_3\alpha E^{\ast }-{\lambda }_2\alpha E^{\ast }=0,\end{array}$$ (10)

$$\frac{dH}{d{u}_3}=A_3{u}_3+{\lambda }_4{\gamma }_1{\delta }_1{I}_1^{\ast }-{\lambda }_3{\gamma }_1{\delta }_1{I}_1^{\ast }+{\lambda }_5{\gamma }_2{\delta }_2{I}_2^{\ast }-{\lambda }_4{\gamma }_2{\delta }_2{I}_2^{\ast }\left({\lambda }_3-{\lambda }_4\right){\gamma }_1{\delta }_1{I}_1^{\ast }+\left(1-{\delta }_1\right){\gamma }_1{\lambda }_6{I}_1^{\ast }+\left(1-{\delta }_2\right){\gamma }_2{\lambda }_{6}I=0,$$

subject to the constraints, the characterization (7) are determined at $u_1^{\ast }$ on the set $\left\{t|c<u_i^{\ast }\left(t\right)\text{for}i=\mathrm{1,2,3}\right\}$. On this set,

$$\begin{array}{l}{u}_1^{\ast }=\frac{\left({\lambda }_2-{\lambda }_1\right)\left({\beta }_1{I}_1^{\ast }+{\beta }_2{I}_2^{\ast }+{\beta }_F{F}^{\ast }\right)S^{\ast }}{A_1},\\ u_2^{\ast }=\frac{\left({\lambda }_2-{\lambda }_3\right)\alpha E^{\ast }}{A_2},\\ u_3^{\ast }=\frac{\left({\lambda }_3-{\lambda }_4\right){\gamma }_1{\delta }_1{I}_1^{\ast }+\left({\lambda }_4-{\lambda }_5\right){\gamma }_2{\delta }_2{I}_2^{\ast }-\left(1-{\delta }_1\right){\gamma }_1{\lambda }_6{I}_1^{\ast }-\left(1-{\delta }_2\right){\gamma }_2{\lambda }_6{I}_2^{\ast }}{A_3}.\end{array}$$ (11)

Owing to the priori boundedness of the state and adjoint functions and the resulting Lipschitz structure of the ordinary differential equations, we get the uniqueness of the optimal control for small. The uniqueness of the optimal control does move with the uniqueness of the optimality system, thus (1) and (5), (6) with characterizations (7). There is a restraint on the length of the time interval to ensure that uniqueness of the optimality system is obtained. This smallest restrictions on the length on the time interval has to do with the opposite time orientations of (1) and (5), (6). The state problem presents initial values and the adjoint problem also deals with final values. This restriction is frequently observed in control problem [28], [29].

4. Numerical simulation and discussion

In this section, we investigate the effect of optimal strategy on Ebola transmission applying some numerical techniques. The optimal strategy is achieved by obtaining a solution for the state system (1) and co-state system (4). An iterative scheme is explored and used to determine the solution for the optimality system.

The state equations are initially solved by guessing for the controls over the simulated time applying a forward fourth order Runge-Kutta scheme.

In addition, the co-state equations are at the same time computed by employing a backward fourth order Runge-Kutta scheme with the transversality conditions. This is then followed by the controls being updated by employing a convex combination of the preceding controls and the value obtained from the characterizations of u ₁ ^∗, u ₂ ^∗, u ₃ ^∗. This process is allowed to go on and iteration is ended if the values of unknowns at the previous iteration are almost the same as the value obtained at present iteration [30]. For numerical simulation, the state system solution is determined based on forward in time with initial conditions x(0) = (10 000, 300, 100, 40, 60, 70), whereas the co-state system is also dealt with backward in time. In the light of numerical simulation, we employed the following parameters: δ ₁ = 0.6/days; α = 8/days; β ₁ = 0.9/days; δ ₂ = 0.7/days; γ _F = 1.2/days; μ = 0.000 054 79/days; γ ₁ = 5.7/days; γ ₂ = 1.4/days; β ₂ = 0.67/days and the weighting control B ₁ = 20, B ₂ = 40, B ₃ = 50. The weight factor B ₁ associated with control u ₁ is less or equal to weight factor B ₂ associated with control, however, weight factor B ₃ associated with control u ₃ could be higher than all due to cost associated with it because of the cost implications.

4.1. Control with prevention

With this approach, only the control u ₁ which deals with prevention is applied to optimize the objective function J, whereas the control u ₂ and u ₃ on treatment are set to zero as shown in Figure 2 . In order to reduce infection control, u ₁ should be sustained intensively for the first seven days. Figure 2 shows the optimal solution for first stage infection I ₁ and super infection I ₂ which depict substantial difference with and without control in both figures. In Figure 2, Figure 3 , it is observed that effective preventive mechanisms such as proper education and campaign will help reduce the rate of infection of Ebola in communities.

Figure 2.

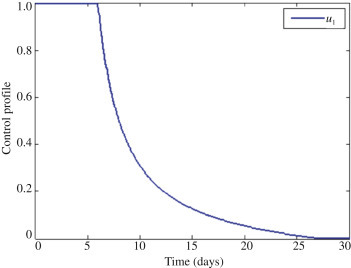
The profile of the optimal control.

Figure 3.

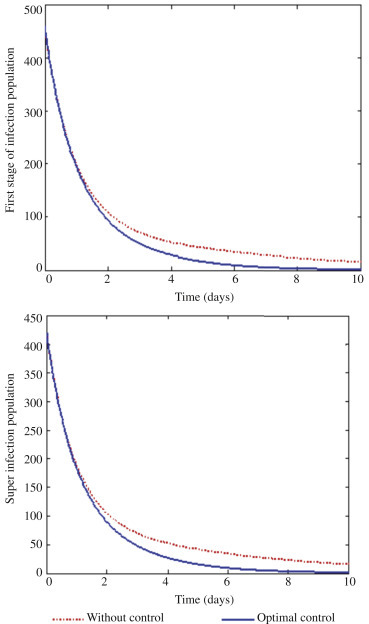
The optimal solutions for first stage of infection (I₁) and super infection (I₂) via prevention.

4.2. Control with treatment and prevention

With this scenario, we activate controls u ₁ and u ₂ on prevention and treatment to optimize the objective function J, whereas the control u ₃ which is the treatment of first stage of infection and super infection is set to zero as shown in Figure 4 . We can observe in Figure 4 that it will require about 12 days intensive intervention in the form of education and campaign and at the same time giving intensive treatment for those exposed to the disease through screening for about 5 days. Figure 5 shows the optimal solutions for both first stage infection and super infection. Clearly there is a vast difference between without treatment and treatment. Therefore, it can be deduced that giving the right education and campaign to susceptible individuals and providing good treatment to those exposed individuals will help reduce epidemic significantly.

Figure 4.

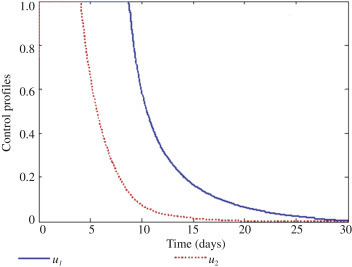
The profile of the optimal control u₁ and u₂.

Figure 5.

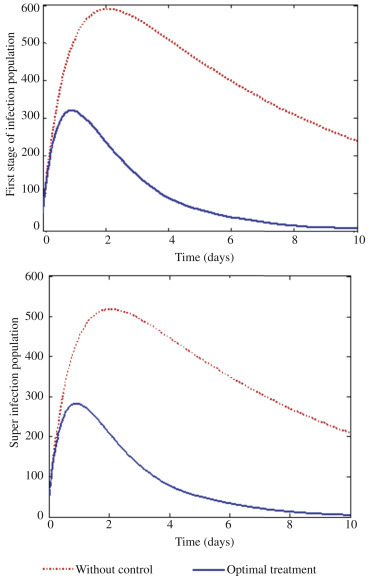
The optimal solutions for first stage of infection (I₁) and super infection (I₂) via treatment.

4.3. Control with prevention, treatment of exposed and treatment of infectious populations

With this approach, all the controls u ₁, u ₂ and u ₃ treatments and prevention are activated to optimize the objective function J, and none of the controls is set to zero as observed in Figure 6 . In Figure 6, it can be seen that with all the controls activated one requires less effort and time to reduce infection with respect to control u ₁ and u ₃. However, one needs about 17 days' intensive treatment for those exposed to Ebola. Figure 7 depicts optimal solutions for first stage I ₁ infection and super infection I ₂. It can be observed that there is a clear significant difference in Figure 7, both first stage infection I ₁ and super infection I ₂ in terms of with controls and without controls when all the three controls activated. It is therefore envisaged that in order to design a cost effective mechanism for effective interventions, the necessary attention should be given to all the three scenarios at the same time.

Figure 6.

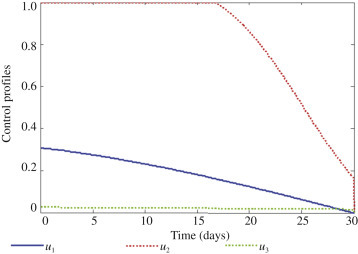
The profile of the optimal control u₁, u₂ and u₃.

Figure 7.

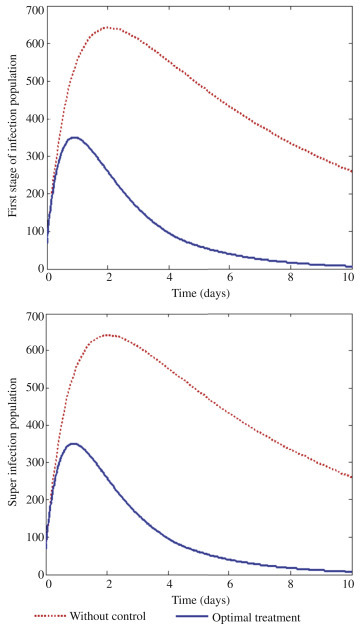
The optimal solutions for first stage of infection (I₁) and super infection (I₂) via treatment.

The optimal control strategy applied to this model for the “case holding” is similar to previous studies by Rachah and Torres [31], who used vaccination as a strategy to reduce the number of infection in the susceptible population in susceptible-infected-recovered (SIR) Ebola model. This “case holding” strategy again is further supported by Rachah and Torres in their extension of previous work by comparing optimal effect of vaccination on SIR and susceptible-exposed-infected-recovered Ebola models [31]. The numerical results from their comparison studies indicated that vaccination programme is more effective in susceptible-exposed-infected-recovered Ebola model than SIR Ebola model. In this study, the “case finding” activities include mass education and vigorous campaign which also reduced Ebola infections on “case finding” scenario. The numerical results obtained based on “case holding” strategy that is treatment is similar to the study of Jung et al. [23] on optimal treatment of tuberculosis. This therefore, shows that proper medication on right time bases will ensure that those affected with Ebola can be cured. The numerical result obtained in this study is new and is not contrary to any previous studies on Ebola models.

5. Conclusions

In this work, mathematical model of Ebola disease with three possible routes of transmission that include prevention and two treatment measures as optimal control has been examined. By exploring and applying Pontryagin maximum principle, condition for optimal control which addressed minimizing the disease in a finite time are derived and analyzed. It could therefore be concluded that the combination of education, screening and giving treatment for exposed as well as treatment for infectious population will be a more effective way of reducing Ebola disease in a community.

Conflict of interest statement

We declare that we have no conflict of interest.

17 Dec, 2nd revised form 23 Dec 2015