Why is it difficult to accurately predict the COVID-19 epidemic?

Abstract

Since the COVID-19 outbreak in Wuhan City in December of 2019, numerous model predictions on the COVID-19 epidemics in Wuhan and other parts of China have been reported. These model predictions have shown a wide range of variations. In our study, we demonstrate that nonidentifiability in model calibrations using the confirmed-case data is the main reason for such wide variations. Using the Akaike Information Criterion (AIC) for model selection, we show that an SIR model performs much better than an SEIR model in representing the information contained in the confirmed-case data. This indicates that predictions using more complex models may not be more reliable compared to using a simpler model. We present our model predictions for the COVID-19 epidemic in Wuhan after the lockdown and quarantine of the city on January 23, 2020. We also report our results of modeling the impacts of the strict quarantine measures undertaken in the city after February 7 on the time course of the epidemic, and modeling the potential of a second outbreak after the return-to-work in the city.

1. Introduction

In early December 2019, a novel coronavirus, later labelled as COVID-19, caused an outbreak in the city of Wuhan, Hubei Province, China, and it has further spread to other parts of China and many other countries in the world. By January 31, the global confirmed cases have reached 9,776 with a death toll of 213, and the WHO declared the outbreak as a public health emergency of international concern (WHO, 2020). By February 9, the global death toll has climbed to 811, surpassing the total death toll of the 2003 SARS epidemic, and the confirmed cases continued to climb globally. As governments and public agencies in China and other impacted countries respond to the outbreaks, it is crucial for modelers to estimate the severity of the epidemic in terms of the total number of infected, total number of confirmed cases, total deaths, and the basic reproduction number, and to predict the time course of the epidemic, the arrival of its peak time, and total duration. Such information can help the public health agencies make informed decisions.

Since the start of the outbreak in Wuhan, several modeling groups around the world have reported estimations and predictions for the COVID-19 (formerly called 2019-nCov) epidemic in journal publications or on websites, for an incomplete list see (Bai et al., 2020; Imai, Dorigatti, Cori, Riley, & Ferguson, 2020; Read, Bridgen, Cummings, Ho, & Jewell, 2020; Shen, Peng, Xiao, & Zhang, 2020; Tang et al., 2020b, a; Wu, Leung, & Leung, 2020; You et al., 2020; Yu, 2020; Zhao et al., 2020). The modeling results have shown a wide range of variations (Cyranoski, 2020): estimated basic reproduction number varies from 2 to 6, peak time estimated from mid-February to late March, and the total number of infected people ranges from 50,000 to millions. Why is there such a wide variation in model predictions, even among predictions made using transmission models based on either the SIR or SEIR framework? We attempt to address this variability issue in our study.

A simple answer for the wide range of model predictions might be that there was too little information at the beginning of the outbreak, especially before January 23 when Wuhan was quarantined and locked down, and that there was a lack of reliable data, except for the confirmed case data that could be used for model calibration. Rigorous model calibration methods, including maximum likelihood methods and the Bayesian inference based MCMC methods, already take into consideration uncertainties in data by allowing the data at each time point to follow a probability distribution with the mean given by the assumed model and the variance τ given by the assumed probability distribution, where the variance may depend on the mean. The lack of data, as we will demonstrate, is a more serious concern for modellers. A key issue that can explain the variability in model predictions is understanding how the available data (confirmed cases) compares with model predictions. Confirmed cases are people with symptoms who made contact with a hospital, got tested, and whose infection of COVID-19 was confirmed by DNA or imaging tests. The infected compartment in by transmission models represents all people who are infected. These include people who may or may not have symptoms and contacts with a hospital, as well as people with confirmed laboratory tests and those who are misdiagnosed. In this sense, confirmed cases (data) are only a fraction of the total infected population (model predictions). A metaphor of an iceberg best represents the difference between data and model predictions. The entire iceberg represents the total infected population, and the tip of the iceberg above the sea surface represents the case data. The part of the iceberg hidden under the water represents the infected people that are unknown to public health surveillance and testing; often called the hidden epidemic. The difference between cases and infections can be measured by the case-infection ratio ρ, between the newly confirmed cases and the number of infected people, or as a surrogate, the ratio between the cumulative confirm cases and the cumulative number of infected people.

The case-infection ratio ρ can vary widely for different viral infections that spread through air droplets and close contacts. For the SARS epidemic, the ratio ρ was in the range of $1/5-1/2$ (Chowell et al., 2004; Gumel et al., 2004; Lipsitch et al., 2003; Zhang et al., 2005). In contrast, for seasonal influenza in 2019–2020, the ratio ρ can be as small as $1/100$, based on estimates from the US CDC (US CDC, 2020). Why should this be a problem for the modellers? In model calibration, in order to estimate key model parameters such as the transmission rate β, by fitting the model output to the confirmed cases data, it is necessary to discount the total number of infectious people, $I\left(t\right)$, from the model prediction, by the case-infection ratio ρ to appropriately predict confirmed case data. For each value of the ratio ρ, a corresponding value for the transmission rate β can then be estimated by fitting the model to data, which in turn determines the basic reproduction number ${\mathcal{R}}_0$, the scale of the epidemic, as well as the peak time. Given the potential wide range for the case-infection ratio ρ of the COVID-19, the estimated transmission rate β has a wide range, and hence the wide range of reported model predictions.

In modeling terms, given the confirmed-case data, there is a linkage between the model parameter ρ and the transmission rate β, and potentially also with other model parameters. While many different combinations of ρ and β can show good fit to the data, they can produce very different model predictions of the epidemic. This is known as nonidentifiability in the modeling literature, see e.g. (Lintusaari, Gutmann, Kaski, & Corander, 2016; Raue et al., 2009; van der Vaart, 1998). It means that a group of model parameters can not be uniquely determined from the given data during model calibration. Different choices of parameter values with the same good fit to the data can lead to very different model predictions. The ways in which nonidentifiability is addressed in the model calibration process greatly influences the reliability of model predictions.

The standard nonlinear least squares method is known to be ill suited to detect or address the nonidentifiability issue, since it relies on a rudimentary optimization algorithm. These rudimentary optimization algorithms attempt to find a global minimum of the given objective function, but there are infinitely many global minima given nonidentifiability. Standard Markov chain Monte Carlo (MCMC) procedures based on Bayesian inference often fail to converge to the target posterior distribution in the presence of nonidentifiability, and can produce best-fit parameter values with unreliable credible intervals, since these often relies on elementary MCMC algorithms. Elementary MCMC algorithms converge very slowly given a very skewed posterior distribution. In our study, we used an improved model calibration method using Bayesian inference and affine invariant ensemble MCMC algorithm that can ensure fast convergence to the target posterior distribution when facing nonidentifiability, and provide more reliable credible intervals and model predictions.

Another important factor that can significantly influence model predictions is the choice of a suitable model to describe the epidemic under study: a more complex or simpler model. A complex model incorporates more biological and epidemiological information about the epidemic and is more biologically realistic. A drawback of a complex model is that it requires more model parameters to be estimated compared to a simpler model. Given the dataset, such as the confirmed case data of COVID-19, increased number of parameters in a complex model that are unknown and need to be estimated by model fitting can lead to a greater degree of uncertainty in model predictions. In choosing an appropriate model, it is important to draw a balance between biological realism and reducing uncertainty in model predictions, and this choice can significantly influence the reliability of model predictions. The modeling procedure to determine the right balance is model selection using various information criteria, for instance the Akaike Information Criteria (AIC) for nested models (Akaike, 1973; Sugiura, 1978).

In our study, we considered both SEIR and SIR models for model predictions and applied model-selection analysis. For the given dataset of confirmed cases, we determined that the SIR model is a better choice than the SEIR model, and more likely than models that are more complex than an SEIR model (Section 3). Our study focused on the development of the outbreak in Wuhan city after the quarantine and lockdown (January 23, 2020), given the reliability of confirmed case data and definition during this period and the simplicity in our predictions and analysis. We briefly outline in Section 2 the methodology for model calibration using an improved procedure based on Bayesian inference and model selection method using Akaike Information Criteria. In Section 4, using the SIR model, we illustrate the linkage between the transmission rate and case-infection ratio, and the presence of nonidentifiability when only the confirmed-case data is used for model calibration. In Section 5, we present detailed results of the SIR model calibration and our model predictions, including the distribution of peak time, prediction interval of future confirmed cases, as well as the total number of infected people. In Section 6, we estimate the impact of further control measures recommended in Wuhan after February 7 and predicted the changes in peak time under different assumptions on the reduction of transmission achieved by these measures. In Section 7, we estimated the impact of timing the return to work on the course of the epidemic, in terms of peak time, peak values, and the duration of the epidemics. Our results are summarized in Section 8.

2. Model calibration and model selection

In this section, we give a brief description of a model calibration method based on Bayesian inference and the method of model selection using Akaike Information Criterion (AIC). For more details the reader is referred to (Portet, 2020; Roda, 2020). Other model calibration procedures using nonlinear squares or more general maximum likelihood methods are not described here, and we refer the reader to (Rossi, 2018). Model selection methods using other information criteria can also be used, see e.g. (Burnham & Anderson, 2002).

2.1. Affine invariant ensemble Markov chain Monte Carlo algorithm for model calibration

Mathematical Model. Consider a mathematical model given by a system of differential equations:

$$x’=f\left(x\right),$$ (1)

where $x=\left(x_1,\cdots ,x_k\right)$ denotes the vector of state variables, $f\left(x\right)=\left(f_1\left(x\right),\cdots f_k\left(x\right)\right)$ the vector field. We let $u\in {\mathbb{R}}^{n_1}$ be the vector of all model parameters, which often include initial conditions $x_0=\left(x_{01},\cdots ,x_{0k}\right)$. We assume that there exists a unique solution $x=x\left(u,t\right)$ for each given u.

Data. Data is often given on the observable quantities, such as newly confirmed cases, which are linear or nonlinear combinations of the solutions $x\left(u,t\right)$ in the form:

$$y=y\left(w,t\right)=y\left(x\left(u,t\right),v\right),$$

where $v\in {\mathbb{R}}^{n_2}$ are parameters in the observables y and $w=\left(u,v\right)\in {\mathbb{R}}^n$, $n=n_1+n_2$, is the vector of all model parameters to be estimated. Furthermore, the dataset is collected at N time points $t_1,t_2,\cdots ,t_N$. We will fit the model outputs

$$y_i=y\left(w,t_i\right)=y\left(x\left(u,t_i\right),v\right),i=\mathrm{1,2},\cdots ,N,$$

to the time series dataset

$$D=\left\{D_1,D_2,\cdots ,D_N\right\}.$$

Likelihood functions. In order to account for noise in the data, we let the probability of observing $D_i$ at time $t_i$ be given by $f_i\left(D_i\right)$, with mean $y_i$ and variance $q_i={\sigma }_i^2=1/{\tau }_i$, $i=\mathrm{1,2},\cdots ,N$. Common probability distributions used for this purpose include the normal distribution, Poisson distribution, and negative binomial distribution. In our Bayesian inference, the variance $q_i=1/{\tau }_i$ in the noise distribution is also estimated from the data, giving us an accurate posterior distribution and accurate credible intervals for the estimated parameters. The entire set of parameters to be estimated includes model parameters u, parameters v in the observable function y, and the variances $q=\left(1/{\tau }_1,1/{\tau }_2,\cdots ,1/{\tau }_N\right)$, and is denoted by

$$\theta =\left(u,v,q\right).$$

We consider the likelihood function

$$L\left(\theta \right)=CP\left(D|\theta \right)=C{f}_1\left(D_1\right)f_2\left(D_2\right)\cdots f_N\left(D_N\right),$$

where C is a constant independent of θ used to simplify the likelihood function (Kalbfleisch, 1979).

Bayesian framework. The Bayesian framework assumes that a probability model for the observed data D given unknown parameters θ is $P\left(D|\theta \right)$, and that θ is randomly distributed from the prior distribution $P\left(\theta \right)$. Statistical inference for θ is based on the posterior distribution $P\left(\theta |D\right)$. Using Bayes Theorem we obtain

$$P\left(\theta |D\right)=\frac{P\left(D|\theta \right)P\left(\theta \right)}{P\left(D\right)}=\frac{P\left(D|\theta \right)P\left(\theta \right)}{{\int }_{\text{Ω}}P\left(D|\theta \right)P\left(\theta \right)d\theta }\propto L\left(\theta \right)P\left(\theta \right)=\pi \left(\theta |D\right),$$

where $\text{Ω}$ is the parameter space of θ and $L\left(\theta \right)$ is the likelihood function. Constant $P\left(D\right)={\int }_{\text{Ω}}P\left(D|\theta \right)P\left(\theta \right)d\theta$ is used to normalize the posterior distribution $P\left(\theta |D\right)$ (Chen, Shao, & Ibrahim, 2000). The unnormalized posterior distribution is given by $\pi \left(\theta |D\right)=L\left(\theta \right)P\left(\theta \right).$ The Bayesian framework is very useful for statistical inference that occurs in mathematical modeling since it allows utilization of the prior information about the unknown parameters in the literature. Epidemiological information about the infectious disease can often inform a general range for the parameters to be estimated, and the uniform distribution is typically chosen as the prior distribution in such a case.

Markov chain Monte Carlo algorithms. Markov chain Monte Carlo (MCMC) algorithms are used to approximate a posterior distribution of parameters by randomly sampling the parameter space (Lynch, 2007). In MCMC algorithms, a new vector of parameter values ${\theta }^{\left(t\right)}$ is sampled iteratively from the posterior distribution, based on the previous vector ${\theta }^{\left(t-1\right)}$, until a sample path (also called a chain or walker) has arrived at a stationary process and produces the target unnormalized posterior distribution. Commonly used MCMC algorithms include the Metropolis-Hastings algorithm and Random-Walk Metropolis-Hastings algorithms (Chen et al., 2000).

In our study, we used an improved MCMC algorithm, the affine invariant ensemble Markov chain Monte Carlo algorithm, which has been shown to perform better than Metropolis-Hastings and other MCMC algorithms, especially in the presence of nonidentifiability. The algorithm uses a number of walkers and the positions of the walkers are updated based on the present positions of all walkers. For details on this algorithm, we refer the reader to (Goodman and Weare, 2010, May, 2015) and recent lecture notes on this topic (Roda, 2020).

2.2. Method of model selection using Akaike information criterion

When using mathematical models to explain data that has been formed by an underlying disease process, the principle of parsimony should be used to select a suitable model. A parsimonious model is the simplest model with the least assumptions and variables but with the greatest explanatory power for the disease process represented by the data (Johnson & Omland, 2015). This principle is also reflected in a well known quotation: “Models should be as simple as possible but not simpler.” This quotation is often ascribed to A. Einstein. The model selection method using Akaike Information Criterion takes into account both how well the model fits the data and the principle of parsimony.

Akaike Information Criterion (AIC). Let $L\left({\hat{\theta }}_{MLE}\right)$ be the maximum likelihood value achieved at a best-fit parameter value ${\hat{\theta }}_{MLE}$. Let K be the number of parameters to be estimated in a model, and N be the number of time points where data are observed. The Akaike Information Criterion (AIC) is defined as (Akaike, 1973):

$$AIC=-2\text{ln}\left(L\left({\hat{\theta }}_{MLE}\right)\right)+2K.$$

This definition should be used when $K<N/40$, namely when the number of time points N is large in comparison to the number of parameters. When $K>N/40,$ namely when the number of parameters is large in comparison to the number of time points, the following corrected AIC should be used (Sugiura, 1978):

$$AI{C}_c=AIC+\frac{2K\left(K+1\right)}{N-K-1}.$$

We note that in the Bayesian inference based calibration, the unnormalized posterior distribution $\pi \left(\theta |D\right)$ is equal to the product of the likelihood function $L\left(\theta \right)$ and the prior distribution $P\left(\theta \right)$. The Akaike information criterion can be applied if uniform prior distributions are used for each parameter, since $\pi \left({\hat{\theta }}_{MLE}\right)=\gamma L\left({\hat{\theta }}_{MLE}\right)$, where γ is a constant.

Model selection using AIC. When several nested models, each having a different level of complexity, are considered as candidates for the most suitable model, AIC values can be computed for each model, and the model associated with the smallest AIC value is considered the best model. The difference of ${\text{AIC}}_i$ value of model i with the minimum ${\text{min}}_{i}AI{C}_i$:

$${\text{Δ}}_i=AI{C}_i-\underset{i}{\text{min}}AI{C}_i.$$

This measures the information lost when using model i instead of a model with the smallest AIC value. When ${\text{Δ}}_i$ is larger, model i is less plausible.

Useful guidelines for interpreting ${\text{Δ}}_i$ for nested models are as follows (Burnham & Anderson, 2002):

• •If $1\le {\text{Δ}}_i\le 2$, model i has substantial support and should be considered.
• •If $4\le {\text{Δ}}_i\le 7$, model i has less support.
• •If ${\text{Δ}}_i>10$, model i has no support and can be omitted.

When a large number of models are under consideration or the models are not nested, the model selection rules are different. We refer the reader to recent lecture notes (Portet, 2020) for an introduction to model selection.

3. Model selection analysis for an SEIR and an SIR model

We used both SEIR and SIR frameworks to model the COVID-19 epidemic in Wuhan, and we applied model selection analysis to decide which framework is more parsimonious.

3.1. The models

In our SIR and SEIR models, the compartment S denotes the susceptible population in Wuhan, compartment I denotes the infectious population, and R denotes the confirmed cases. In the SEIR model, a latent compartment E is added to denote the individuals who are infected but not infectious. The latency of COVID-19 infection is biologically realistic due to an incubation period as long as 14 days; newly infected individuals may not be infectious while the virus is incubating in the body. Here we note the difference between the latent period, which is the period from the time an individual is infected to the time the individual is infectious, and the incubation period, which is the period between the time an individual is infected to the time clinical symptoms appear, which include fever and coughing for COVID-19. For SARS, infected individuals become infectious on average two days after the onset of symptoms WHO (2003); so, the SARS latent period is on average longer than the incubation period. For COVID-19, evidence has shown that infected individuals can be infectious before the onset of symptoms (Bai et al., 2020), but the length of the latent period is largely unknown. In comparison to the SIR model, the SEIR model has the strength of being more biologically realistic, but the SEIR model has the drawback of having two additional unknown parameters: the latent period and the initial latent population.

The transfer diagrams for both models are shown in Fig. 1. The biological meaning of all model parameters are given in Table 1 and Table 2. A key assumption in both models is that deaths occurring in the S, E, and I compartments are negligible during the period of model predictions.

Fig. 1.

Transfer diagrams for an SIR and an SEIR model for COVID-19 in Wuhan.

Table 1.

Parameters in the SIR model (2) and their estimations from the confirmed case data.

	Epidemiological Meaning	Best-fit Value	95% Credible Interval	Prior
β	Transmission rate	$9.906e$−8	$(7.02e$−8, $2.09e$-$7)$	$U(1e$-$\mathrm{10,1}e$-$5)$
ρ	Diagnosis rate	0.24	$\left(0.064,0.901\right)$	$U\left(0.01,1\right)$
μ	Recovery rate	0.1	fixed value	source (You et al., 2020)
$I_0$	Size of I on 01/20/2020	245	$\left(\mathrm{65,890}\right)$	$U\left(\mathrm{1,8400}\right)$
τ	$1/\tau$ is the variance of data noise	$2.62e$−5	$(1.43e$-$\mathrm{5,4.33}e$-$5)$	$U(1e$-$\mathrm{8,100})$

Table 2.

Parameters in the SEIR models and their estimations from the confirmed case data.

	Epidemiological Meaning	Best-fit Value	95% Credible Interval	Prior
β	Transmission rate	$8.68e$−8	$(8.20e$−8, $1.26e$-$7)$	$U(1e$-$\mathrm{10,1}e$-$5)$
ρ	Diagnosis rate	0.018	$\left(0.016,0.024\right)$	$U\left(0.01,1\right)$
μ	Recovery rate	0.1	fixed value	source (You et al., 2020)
ε	Transfer rate from E to I	0.631	$\left(0.263,0.78\right)$	$U\left(0.07,1\right)$
$E_0$	Size of E on 01/20/2020	1523	$\left(\mathrm{3444,4682}\right)$	$U\left(\mathrm{1,1700}\right)$
$I_0$	Size of I on 01/20/2020	3746	$\left(\mathrm{3278,4171}\right)$	$U\left(\mathrm{3200,6700}\right)$
τ	$1/\tau$ is the variance of data noise	$2.61e$−5	$(1.43e$-$\mathrm{5,4.13}e$-$5)$	$U(1e$-$\mathrm{8,100})$

(4 months). Since we use the newly confirmed case data for model calibration, which is matched to the $\rho I$ term in both models, the death term in the R compartment has no effect on our model fitting. The systems of differential equations for each model is given below:

$$\begin{array}{l}S’=-\beta IS\\ I’=\beta IS-\left(\rho +\mu \right)I\\ R’=\rho I-dR\end{array}$$ (2)

$$\begin{array}{l}S’=-\beta IS\\ E’=\beta IS-\epsilon E\\ I’=\epsilon E-\left(\rho +\mu \right)I\\ R’=\rho I-dR\end{array}$$ (3)

3.2. Model calibration from the data

For data reliability, the data used for both models (2) and (3) is the newly confirmed cases in Wuhan city from the official reports from January 21 to February 4, 2020 (National Health Commission of the People’s Republic of China, 2020). It is common to use a Poisson or negative binomial probability model for observed count data. When the mean of a Poisson or negative binomial distribution is large, it approximates a normal distribution. Since the newly confirmed cases are approaching large values quickly, the distribution of the count data will be approximately normal and the probability model for the observed count data in our study was assumed to a normal distribution with mean given by $\rho I$ and variance given by $1/\tau$. There are four parameters to be estimated in the SIR model from data: transmission rate β, diagnosis rate ρ, the initial population size $I_0$ for the compartment I on January 21, 2019 ($t=0$), and the variance $q=1/\tau$ for the noise distribution in the data. There are six parameters to be estimated for the SEIR model: transfer rate ε from E to I, the initial population size $E_0$ for the latent compartment E on January 21, 2019, and β, ρ, $I_0$, and $q=1/\tau$. Since it was announced at a news conference by the mayor of Wuhan on January 23 that 5 million people have left the city by that date, we set the total population $N=S+I+R$ in Wuhan on January 21 to the conservative estimate of 6 million.

We used the same uniform distributions over the initial range of parameters as the priors for both models, as given in Table 1, Table 2. The affine invariant ensemble Markov chain Monte Carlo algorithm was used to produce posterior distributions for all estimated parameters. From these posterior distributions, we obtain the best-fit values and the 95% credible intervals, as given in Table 1 for the SIR model (2) and in Table 2 for the SEIR model (3).

3.3. Comparing SIR and SEIR models

Using the calibration results for both the SIR and SEIR models in Section 3.3, their corrected Akaike Information Criterion $AI{C}_c$ are calculated as 174 and 186, respectively. The difference $\text{Δ}=186-174=12$ is sufficiently large and this implies that using the SEIR model (3) will produce a significant loss of information in comparison to using the SIR model (2). Accordingly, our further investigation will be carried out using the SIR model (2).

4. Nonidentifiability: linkage between transmission rate β and diagnosis rate ρ

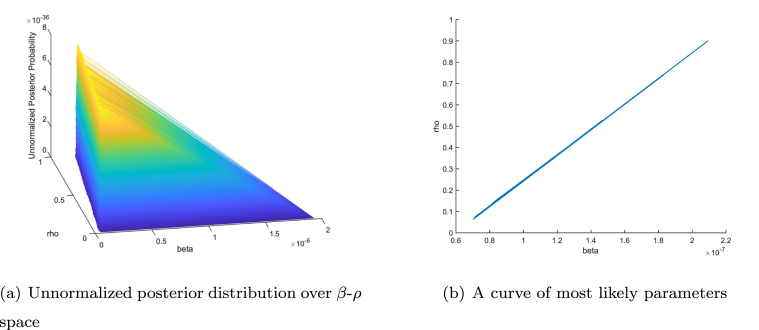
Based on our calibration results of the SIR model in Section 3.3, we detected a linkage between the transmission rate β and the diagnosis rate ρ. In Fig. 2 (a), we show the projection of the unnormalized posterior distribution in the β-ρ parameter space. It shows that the largest probability are concentrated along a flat strip rather than on a single point. Correspondingly, as shown in Fig. 2 (b), a curve in the β-ρ parameter space can be determined such that every point on the curve has approximately the same large probability. The linkage between two or more parameters implies the following: (1) the best-fit parameter values are effectively not unique; and (2) there is a continuum of parameter values that cause the model to fit the data approximately equally as well. This phenomenon is often referred to as nonidentifiability in the modeling literature.

Fig. 2.

Linkage between transmission rate β and diagnosis rate ρ.

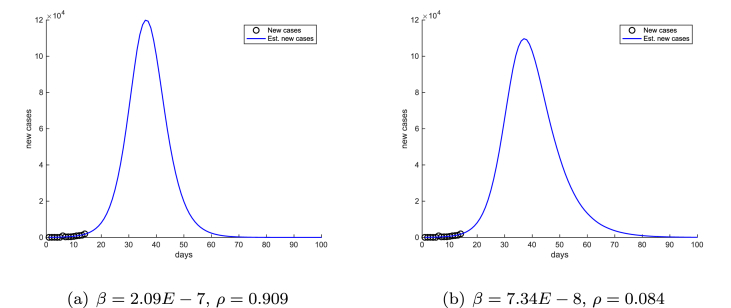
To further illustrate the significant impact of nonidentifiability on model predictions, we choose two endpoints on the curve in Fig. 2 (b), with respective values $(\beta ,\rho )=(2.09e$-$\mathrm{7,0.909})$ and $(\beta ,\rho )=(7.34e$-$\mathrm{8,0.084})$, and we plotted the corresponding projected new cases in Fig. 3(a) and (b), respectively. Fig. 3 shows that the peak height, as well as the duration and scale of the epidemic are different in the two projections, even though both choices of parameter values are effectively equally likely to produce the best fit between the model outcomes and the data.

Fig. 3.

Model projections using two likely β-ρ combinations, corresponding to two endpoints on the curve in Fig. 2 (b). Day 0 is January 21, 2020.

A striking feature in Fig. 3 is that the peak time of the two different projections are almost identical. This illustrates that, unlike the peak value, the peak time of the epidemic is insensitive to small parameter changes. This important property of the peak time will also be observed in later sections.

We further note that the diagnosis rate ρ is the case-infection ratio that is used to discount of the number of infected individuals $I\left(t\right)$ to properly predict the newly confirmed cases. The linkage between β and ρ reflects the dependency of the transmission rate and the case-infection ratio, and hence the scale of the epidemic. We believe that this nonidentifiability is the reason for the wide variability in published model predictions of COVID-19 epidemic.

To reduce the impact of nonidentifiability in model calibration from data, one approach is to search for more independent data, including clinical, surveillance, or administrative data, and from published literature, that can be used for model calibration. This approach is often difficult when facing an outbreak of unknown pathogens that occur in real time such as SARS in 2003 and the current COVID-19. Another approach is to adopt better inference methods and model fitting algorithms to narrow done the otherwise large confidence or credible intervals. Our fitting procedure using Bayesian inference and the affine invariant ensemble Markov chain Monte Carlo algorithm was able to achieve this objective.

5. Baseline predictions for Wuhan and three scenarios

Our baseline predictions for Wuhan are prediction intervals produced by randomly sampling the posterior distribution. The best-fit parameter values and credible intervals are shown in Table 1. The Bayesian inference used the newly confirmed cases for Wuhan contained in the official reports from January 21 to February 4, 2020. This is the period during the lockdown and travel restrictions in Wuhan, but before the further control measures that were undertaken in Wuhan after February 7, 2020, including the drastic increase in the available hospital beds and the door-to-door visits used to identify and quarantine suspected cases. These projections show our estimation for the hypothetical epidemic in Wuhan if further control measures after February 7 were not implemented.

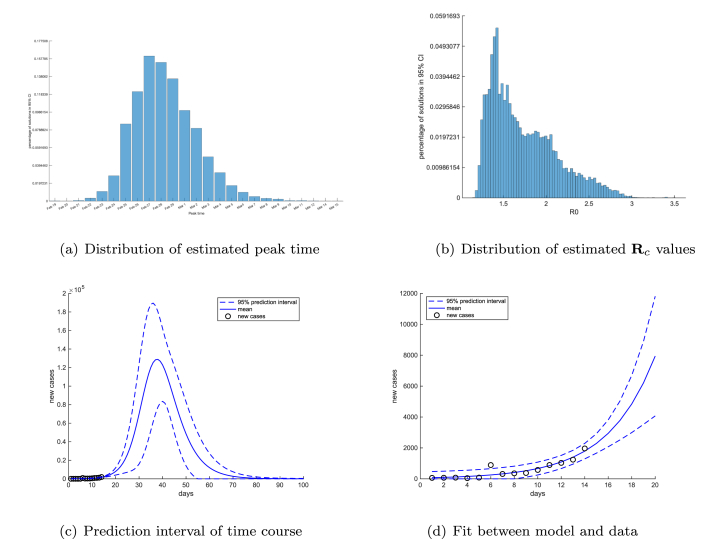
In Fig. 4(a) and (b), we show the distributions of the projected peak time and the estimated values of the control reproduction number ${\mathcal{R}}_c$. In Fig. 4 (c), we show the projected time course of newly confirmed cases in Wuhan together with its 95% prediction interval. The fit of our model predictions and the newly-confirmed case data is shown for the period between January 21 to February 4 in Fig. 4 (d). Based on these projections, if the more restrictive control measures after February 7 in the city were not implemented, the most likely peak time would have occurred on February 27, 2020, with the 95% credible interval from February 23 - March 6. The median value of ${\mathcal{R}}_c$ is 1.629 with the first quantile 1.414 and the third quantile 1.979. By our projection, without the strict quarantine measures after February 7, the peak case total would reach approximately $\mathrm{120,000}$, and the epidemic in Wuhan would not be over before mid-May of 2020.

Fig. 4.

Distributions of estimated peak time (a) and control reproduction number ${\mathcal{R}}_c$ (b) for COVID-19 epidemic in Wuhan after lockdown. The dashed lines represent the 95% prediction intervals for the time course of COVID-19 epidemic in Wuhan after lockdown (c) and (d). Day 0 in simulations is set at January 21, 2020.

At the time of this manuscript, the consensus among medical experts is that the basic reproduction number ${\mathcal{R}}_0$ near the beginning of the COVID-19 outbreak in Wuhan is around 2. Our result in Fig. 4 (b) is comparable with earlier estimates and the current consensus. It also shows that, even without the more restrictive control measures in Wuhan undertaken after February 7, the lockdown and travel restrictions in the city had slowed down the transmission and reduced the basic reproduction number to a control reproduction number ${\mathcal{R}}_c$ with a mean value 1.629. We will estimate the impact of the more restrictive control measures in Section 6.

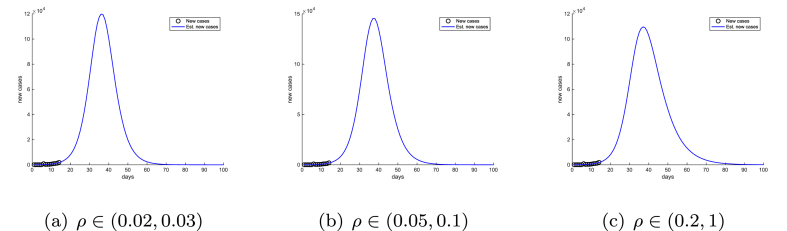
The baseline prediction intervals are computed over a large credible interval of the diagnosis rate ρ, $\left(0.0637,0.909\right)$, which represents a wide range of assumptions on the case-infection ratio and the scale of the epidemic in Wuhan. We further restricted the parameter ρ to three narrower ranges: $\left(0.02,0.03\right)$, $\left(0.05,0.1\right)$, and $\left(0.2,1\right)$, and recalibrated the SIR model (2) with each of the ρ ranges. The resulting predictions for newly confirmed cases are shown in Fig. 5.

Fig. 5.

Model predictions of time courses of COVID-19 epidemic in Wuhan with three different ranges of diagnosis rate ρ: $\left(0.02,0.03\right)$, $\left(0.05,0.1\right)$, and $\left(0.2,1\right)$. Day 0 in the simulations is set at January 21, 2020.

In Fig. 5, different ρ ranges have resulted in significant variations in the peak value of cases and the duration of the epidemic. In contrast, the projected peak times are very similar in all three cases, which further demonstrates that the peak time is insensitive to changes in parameters.

6. Impacts of more strict quarantine measures in Wuhan after February 7

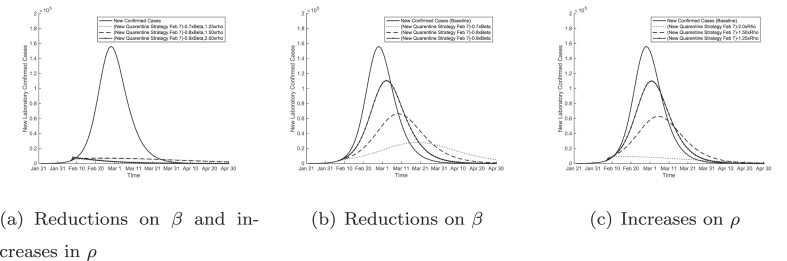
After February 7, 2020, Wuhan implemented more strict quarantine measures that included the following: locking down residential buildings and compounds, strict self quarantine for families, door-to-door inspection for suspected cases, quarantining suspected cases and close contacts in newly established hospitals and other quarantine spaces including vacated hotels and university dormitories. The goal of these measures was to reduce transmissions within family clusters and residential compounds. These measures have a direct impact on two parameters in our SIR model (2): reducing the transmission rate β and increasing the diagnosis rate $\rho .$ It is difficult to estimate the exact impacts on these parameters by these measures. We incorporated several likely scenarios of the effects of these measures by adjusting our baseline estimates of β and ρ and we plotted the resulting time courses in Fig. 6.

Fig. 6.

Predictions of the COVID-19 epidemic in Wuhan with more strict quarantine measures after February 7, 2020. Impacts of reductions in transmission rate β and increases in diagnosis rate ρ are shown in (a). Impacts of only reducing the transmission rate (b) or only increasing the diagnosis rate (c) are also shown for comparison purposes.

In Fig. 6 (a), we see that a combination of a 10% reduction in the transmission rate β and a 90% increase in the diagnosis rate ρ can effectively stop the epidemic in its tracks, force the newly diagnosed cases to decline, and significantly shorten the duration of the epidemic.

7. Potential of a second outbreak in Wuhan after the return-to-work

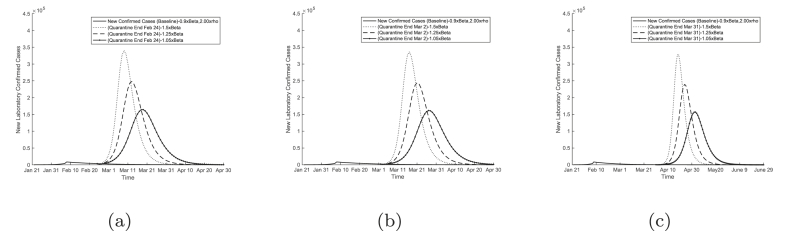
With newly diagnosed cases on the decline in Wuhan and other cities in China since February 14, an urgent task for the authorities is to decide when to allow people to go back to work. Without lifting the ban on traffic in and out of the city, we tested three hypotheses of allowing people to return to work in Wuhan at three different dates: February 24, March 2, and March 31. As shown in Fig. 7, our results predict a significant second outbreak after the return-to-work day.

Fig. 7.

Model predictions of time courses of COVID-19 epidemic in Wuhan with return to work on (a) February 24, (b) March 2, and (c) March 31, 2020.

8. Conclusions

The COVID-19 epidemics have presented China and many other countries in the world with an unprecedented public health challenge in the modern era, with a significant impact on health and public health systems, human lives and national and world economies. Mathematical modeling is an important tool for estimating and predicting the scale and time course of epidemics, evaluating the effectiveness of public health interventions, and informing public health policies. The focus of our study is to demonstrate the challenges facing modelers in predicting outbreaks of this nature and to provide a partial explanation for the wide variability in earlier model predictions of the COVID-19 epidemic.

Our study focused on the COVID-19 epidemic in Wuhan city, the epicentre of the epidemic, during a less volatile period of the epidemic, after the lock down and quarantine of the city. By comparing standard SIR and SEIR models in predicting the epidemic using the Akaike Information Criterion, we showed that, given the same dataset of confirmed cases, more complex models may not necessarily be more reliable in making predictions due to the larger number of model parameters to be estimated.

Using a simple SIR model and the dataset of newly diagnosed cases in Wuhan for model calibration, we demonstrated that there is a linkage between the transmission rate β and the case-infection ratio ρ, which resulted in a continuum of best-fit parameter values, which can produce significantly different model predictions of the epidemic. This is a hallmark of nonidentifiability, and the root cause for variabilities in model predictions. The nonidentifiability should not be interpreted as a shortcoming of transmission models; neither is it caused by the limited number of time points in data. Rather, it is caused by the lack of datasets that are independent of the conirmed cases to allow modelers to produce independent estimates of β and ρ. The reliability in model predictions depends on how rigorously the nonidentifiability is addressed in model calibration and on the choice of parameter values.

We demonstrated that Bayesian inference and an improved Markov chain Monte Carlo algorithm, the affine invariant ensemble Markov chain Monte Carlo algorithm, can significantly reduce the wide parameter ranges in the uniform prior and produce workable credible intervals, even in the presence of nonidentifiability. We showed that the estimated credible intervals for the parameters are sufficiently small to allow our credible interval for the peak time to fall within a week. We have further demonstrated that the peak time of the epidemic is much less sensitive to parameter variations than the peak values and the scale of the epidemic. This was also observed in our previous work on predicting seasonal influenza for the Province of Alberta.

We estimated the impact of the Wuhan lockdown and traffic restrictions in the city after January 23 and before February 6, 2020. We show that if the more restrictive control and prevention measures were not implemented in the city, the epidemic would peak between the end of February and first week of March of 2020. Our results can be used to inform public health authorities on what may happen if the more strict quarantine measures after February 7 were not taken.

When the more restrictive measures are incorporated into our model, including the lock down of residential buildings and compounds, the door-to-door search of suspected cases, and the quarantine of suspected cases and their close contacts in newly established hospitals and quarantine spaces, we showed that these measures can effectively stop the otherwise surging epidemic in its tracks and significantly reduce the duration of the epidemic. These findings provide a theoretical verification of the effectiveness of these measures.

We further considered the impact of the return-to-work order on different dates in February and March on the course of the outbreak. Our results show that a second peak in Wuhan is very likely even if the return-to-work happens near the end of March 2020. This may serve as a warning to the public health authorities.

Declaration of competing interest

The authors claim no conflict of interests.

Handling Editor: Dr. J Wu