Study on the motion law of aerosols produced by human respiration under the action of thermal plume of different intensities

Highlights

• •User-defined functions (UDF) are implemented for airflow velocity of nostril breathing.
• •Large eddy simulation turbulence model is used to predict the characteristics of thermal plume and particle diffusion law.
• •The difference in calorific value between different regions of the body is taken into account.
• •The main factors influencing the intensity of thermal plume and motion law of aerosols are analyzed.

Abstract

Predicting influence of human thermal plume on the diffusion of respiration-produced particles is an important issue for improving indoor air quality through eliminating infectious microbes efficiently. In this study, the Large Eddy Simulation was utilized to predict the effects of thermal plume of different intensities on particle diffusion. Three postures of the human body model and three room temperatures were considered. The results show that the convective heat transfer coefficient on the surface of the human body varies greatly with different postures. The coefficient is the largest when the model is in sitting posture, leading to the greatest heat transfer rate. Meanwhile, the thermal plume generated by bending the thigh increases the size of the facial thermal plume in horizon direction. The increase of the difference between indoor temperature and skin temperature causes an increase of the convective heat transfer of the manikin, leading to stronger airflow in front of the face. The thicker and faster the human thermal plume is, the more difficult it is penetrated by aerosols produced by nasal breathing, finally resulting in most particles distributed within 0.2 m thick under the roof.

1. Introduction

Indoor Air Quality (IAQ) is closely related to the health of building occupants, since on average, people spend more than 70 % of their time in homes, offices and other indoor environments (Zhong, Lee, & Haghighat, 2017). Nevertheless, the spread of infectious diseases in the indoor has seriously affected the IAQ and human health. Airborne transmission is the primary mode of transmission of many diseases such as tuberculosis, severe acute respiratory syndrome (SARS) and influenza (Milton, 2012; Roy & Milton, 2004). The main feature of airborne transmission is that microbes can move along the air flow and consequently infect other people in a long distance. Infectious microbes can be released through a variety of mechanisms, such as physical contact and human respiratory behaviors (Xu & Liu, 2018; Tellier, 2006; Xu, Nielsen, Liu, Jensen, & Gong, 2017). The particle sizes of these released microbes are different, resulting in atypical movement patterns (Jurelionis et al., 2015; Xie, Li, Chwang, Ho, & Seto, 2007). Microbial droplets larger than 10 μm in diameter deposit rapidly due to gravity (Jiang, Yao, Feng, Sun, & Liu, 2017), while microbial aerosols smaller than 10 μm in diameter evaporate and shrink to droplets nuclei, with their particle size further reduced. These fine microbial aerosols could follow the indoor air currents and survive for long time (Lai, Cheng, & Lim, 2005; Morawska, 2006). They diffuse around people in the air and enter people's upper respiratory tract along with their respiratory airflow, which will eventually settle in the trachea or bronchus of mortal body (Koullapis, Kassinos, Bivolarova, & Melikov, 2016; Thomas, 2013). Some microorganism aerosols with extremely small diameter can be directly deposited in the alveoli of human body (Hinds, 1999). Accordingly, the accumulation rather than effective removal of contaminants indoors can bring harm to occupants’ well-being (Hesaraki, Myhren, & Holmberg, 2015).

Respiratory behavior is the most common behavior of human to release microbial aerosol, which mostly releases aerosols with particle size range of 0.3–1.3 μm (Morawska et al., 2009; Papineni & Rosenthal, 1997; Wan, Wu, Chen, Huang, Wang, & Chen, 2014). These particles can be easily absorbed into the lower respiratory tract and therefore increases the risk of infection. When patients with communicable diseases release harmful aerosols through respiration in offices, wards, operating rooms and other places, the risk of infection of surrounding people will be increased. Therefore, it is of vital importance to better understand the diffusion behavior of aerosols generated by human respiration in order to reduce the risk of infection of susceptible population sharing the indoor environment.

Human microenvironment has a vital influence on the transmission of an airborne infectious disease. Human thermal plume (TP), as an important part of human microenvironment, has been widely studied by researchers (Licina, Pantelic, Melikov, Sekhar, & Tham, 2014; Melikov, 2015; Zukowska, Melikov, & Popiolek, 2012). Human TP refers to the airflow rising along the boundary of the human due to the temperature difference between the surface of the human and the surrounding air and the thermal buoyancy of the air. The maximum speed of TP is usually about 0.45 m above the head, with a value of about 0.24 m/s (Craven & Settles, 2006; Li, Liu, Wang, Jiang, & Cao, 2017; Sørensen & Voigt, 2003). TP carries particles from the lower part of the body into the respiratory area (Brohus & Nielsen, 1996), and also prevent particles generated by human respiration from penetrating out (Nielsen, Buus, Winther, & Thilageswaran, 2008). Human TP may have a positive impact on the diffusion of aerosols in a ventilated room, as it may make the dispersion of particulate matter more intense (Salmanzadeh, Zahedi, Ahmadi, Marr, & Glauser, 2012). Many previous studies have shown that the TP has a significant impact on the diffusion of particles. However, the quantitative relationship between the intensity of the TP and the degree of influence on particles has seldom been studied. The TP at higher room temperature has different characteristics from that at lower room temperature (Ge, Li, Inthavong, & Tu, 2013; Voelker, Maempel, & Kornadt, 2014), so it may have distinct effects on the diffusion law of particles. Therefore, the study of different intensities of TP is of huge significance to the study of the diffusion of aerosol produced by respiration.

Computational Fluid Dynamics (CFD) simulation is an economical and effective method to solve fluid flow problems. With the improvement of computer power, Large Eddy Simulation (LES) turbulence model has attracted the attention of computational fluid mechanists and related areas researchers in recent years. And good application results have been obtained in various fields (Hu, Ohba, & Yoshie, 2008; Riber, Moureau, García, Poinsot, & Simonin, 2009; Tian, Tu, Yeoh, 2006). In this study, the LES turbulence model was used to predict the motion of particulate matter produced by human sine breathing by considering three common postures which are standing, sitting and lying, as well as three room temperatures which are 24 ℃, 27 ℃ and 30 ℃. This study provides theoretical insights and data support for ventilation design.

2. Mathematical model

2.1. LES model

The eddy current at different scales constitute a turbulent flow field. And the difference in the sizes of these vortices also leads to their distinct roles in the flow field. Larger-scale vortices have a profound influence on the average flow, such as the diffusion of turbulence, the exchange of heat, mass, and momentum. While small-scale vortices mainly play a role in dissipating function and affect various variables through dissipation pulsations. The shape and boundary conditions of the flow field influence the large-scale vortex. So, it has obvious anisotropy, while the small-scale vortex is almost not subject to the boundary conditions and flow field size, having approximate isotropy. Therefore, it is easier to establish a general model to simulate. LES distinguishes the large eddy from the small eddy, simulating large eddies by the direct solution to the Navier-Stokes (N-S) equation, and small eddies in the universal subgrid model.

For incompressible fluids, the filtered LES continuity equation is as follows:

$$\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial x_j}\left(\rho \overline{u_i}\right)=0$$ (1)

Where u denotes the vector form of the velocity, ρ denotes the density in kg/m³, and t denotes the time. After filtering, we also get the following momentum equations:

$$\frac{\partial \left(\rho \overline{u_i}\right)}{\partial t}+\frac{\partial \left(\rho \overline{u_i}\overline{u_j}\right)}{\partial x_j}=-\frac{\partial \overline{p}}{\partial x_i}+\frac{\partial {\sigma }_{ij}}{\partial x_j}-\frac{\partial {\tau }_{ij}}{\partial x_j}$$ (2)

Where σ_ij is the stress tensor due to molecular viscosity and τ_ij is the subgrid stress, which can be expressed by the following equation:

$${\sigma }_{ij}=\mu \left(\frac{\partial \overline{u_i}}{\partial x_j}+\frac{\partial \overline{u_j}}{\partial x_i}\right)-\frac{2}{3}\mu \frac{\partial \overline{u_k}}{\partial \overline{x_k}}{\delta }_{ij}$$ (3)

$${\tau }_{ij}=\rho \overline{u_i{u}_j}-\rho \overline{u_i}\overline{u_j}$$ (4)

The filtered energy equation is as follows:

$$\frac{\partial \rho \overline{h_s}}{\partial t}+\frac{\partial \rho \overline{u_i}\overline{h_s}}{\partial x_i}-\frac{\partial \overline{p}}{\partial t}-\overline{u_j}\frac{\partial \overline{p}}{\partial x_i}-\frac{\partial }{\partial x_i}\left(\lambda \frac{\partial \overline{\text{T}}}{\partial x_i}\right)=-\frac{\partial }{\partial x_j}\left[\rho \left(\overline{u_i{h}_s}-\overline{u_i}\overline{h_s}\right)\right]$$ (5)

Among them, h_s and λ are Sensible heat enthalpy and thermal conductivity, respectively. The subgrid enthalpy flux terms in the above equation are approximated using gradient assumptions:

$$\rho \left(\overline{u_i{h}_s}-\overline{u_i}\overline{h_s}\right)=-\frac{{\mu }_{\text{SGS}}{c}_p}{{\mathrm{Pr}}_{\text{SGS}}}\frac{\partial \overline{T}}{\partial x_j}$$ (6)

Where μ _SGS is the subgrid viscosity and Pr_SGS is the subgrid Prandtl number, usually set to a constant of 0.85 (Cheng & Tak, 2006; Kays, 1994).

The original and dynamic Smagorinsky-Lilly models are essentially algebraic models in which subgrid-scale stresses are parameterized using the resolved velocity scales. The underlying assumption is the local equilibrium between the transferred energy through the grid-filter scale and the dissipation of kinetic energy at small subgrid scales. The subgrid-scale turbulence can be better modeled by accounting for the transport of the subgrid-scale turbulence kinetic energy. Wall-Adapting Local Eddy-viscosity (WALE) model is designed to return the correct wall asymptotic behavior for wall bounded flows (Ben-Nasr, Hadjajdj, Chaudhuri, & Shadloo, 2017). So that, we chose the WALE model as the subgrid model of this simulation, and its control equation is as follows (Nicoud & Ducros, 1999):

The eddy viscosity in the WALE model is modeled by:

$${\mu }_t=\rho L_s^2\frac{{\left(S_{ij}^d{S}_{ij}^d\right)}^{3/2}}{{\left(\overline{S_{ij}}\overline{S_{ij}}\right)}^{5/2}+{\left(S_{ij}^d{S}_{ij}^d\right)}^{5/4}}$$ (7)

L_s is the mixed length of the subgrid, and it is expressed with the Sd ij in the WALE model as follows:

$$L_s=\text{min}\left(\kappa d,C_w{V}^{1/3}\right)$$ (8)

$$S_{ij}^d=\frac{1}{2}\left({\overline{g}}_{ij}^2+{\overline{g}}_{ji}^2\right)-\frac{1}{3}{\delta }_{ij}{\overline{g}}_{kk}^2,{\overline{g}}_{ij}^2=\frac{\partial \overline{u_i}}{\partial x_j}$$ (9)

Where κ is the von Kármán constant, κ≈ 0.40, d is the distance from the nearest wall, and C_w is the constant 0.325.

2.2. Discrete phase model

The discrete phase model predicts the trajectory of the discrete phase particles (or droplets or bubbles) by adding force equilibrium on the particles in the Lagrange reference frame. This equilibrium relation is equivalent to the balance between the inertial force and the mass force on the particle, which is expressed by the following equation:

$$\frac{\text{d}{u}_p}{dt}=F_D\left(u-u_p\right)+\frac{g\left({\rho }_p-\rho \right)}{{\rho }_p}+F$$ (10)

Where F is the additional acceleration term, F_D(u-u_p) is the drag force to which the unit particle mass is subjected. F_D can be expressed by the following equation:

$$F_D=\frac{18\mu }{{\rho }_p{d}_p^2}\frac{C_{D}Re}{24}$$ (11)

Additional forces can also be added in Eq. (10), this study neglecting pressure gradient forces, Bassett forces, and virtual mass forces, with a focus on Thermophoretic Force and Saffman Lift Forces.

Thermophoresis is a force that arises from asymmetrical interaction of a particle with the surrounding gas molecules due to a temperature gradient. In simple terms, the particle will be repelled away from a hot surface and attracted to a cold surface. Tyndall first described the phenomenon in 1870 when he observed a dust free zone in a dusty gas around a hot body (Reinhardt & Kern, 2018). In Eq. (10), thermophoretic effects on particles can be selectively included in the additional acceleration (force/unit mass) term:

$$F=-D_{T,p}\frac{1}{m_{p}T}\nabla T$$ (12)

Where D_{T, p} is the coefficient of thermophoresis, which we define as Talbot's suggested form (Talbot, Cheng, Schefer, & Willis, 1980):

$$D_{T,p}=\frac{6\pi d_p{u}^2{C}_s\left(K+C_{t}Kn\right)}{\rho \left(1+3C_{m}Kn\right)\left(1+2K+2C_{t}Kn\right)}$$ (13)

Where K_n is the Knudsen number and can be expressed as K_n = 2λ/d_p; λ is the free path of the fluid; K = k/k_p where k is the thermal conductivity of the fluid based on translational energy, expressed as 15/4μR; and k_p is the heat of the particle Conductivity; C_s, C_t, C_m are constants, 1.17, 2.18, 1.14, respectively; m_p is the mass of the particulate matter; T is the local fluid temperature; μ is the viscosity of the fluid.

The Saffman force describes the lifting force of the particles in the shear flow, which is generalized by the expression provided by Saffman:

$$F=\frac{2K{\nu }^{1/2}\rho d_{ij}}{{\rho }_p{d}_p{\left(d_{lk}{d}_{kl}\right)}^{1/4}}\left(u-u_p\right)$$ (14)

Where K = 0.594 and d_ij is the deformation tensor.

3. Model descriptions

3.1. Simulated scenes

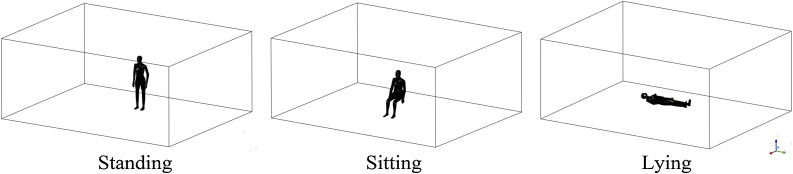
There are many public places that are crowded with people and prone to disease transmission, such as classrooms, offices, hospitals, shopping malls and schools. The common postures in these places were summarized as the main content of this study, namely sitting (school, office), standing (shopping mall) and lying (operating room, ward and dormitory). The simulated scene is a room with a width of 4.7 m, a length of 6.0 m and a height of 2.5 m. The manikin in three postures is illustrated in Fig. 1 , including standing, sitting and lying. Height of the lying manikin from the ground is 0.4 m, and the standing manikin is 0.3 m behind the center line. The heights of standing manikin and seated manikin are 1.68 m and 1.39 m. The wall surface is far enough away that it will not affect the forming of TP. We considered three different room temperatures, namely 24 ℃, 27 ℃, which are common room temperature in an air-conditioned room in summer, and 30 ℃, which is common temperature in non-air-conditioned rooms in summer. All cases are presented in Table 1 . The computational domain is large enough that the boundary effects caused by the wall around the room does not affect simulation results of the human microenvironment.

Fig. 1.

Simulation scenario.

Table 1.

Simulation cases.

Case No.	Posture	Room temperature
Case 1	Standing	24 ℃
Case 2	Standing	27 ℃
Case 3	Standing	30 ℃
Case 4	Sitting	24 ℃
Case 5	Sitting	27 ℃
Case 6	Sitting	30 ℃
Case 7	Lying	24 ℃
Case 8	Lying	27 ℃
Case 9	Lying	30 ℃

3.2. Boundary conditions

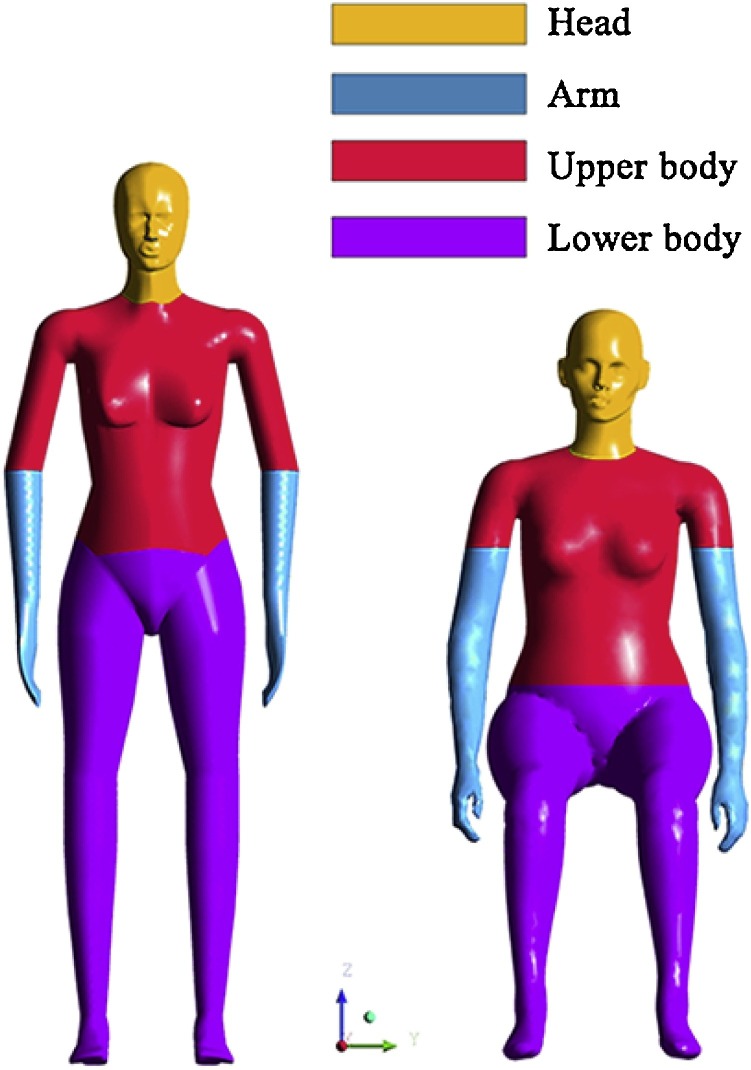
The surface temperature of different parts of the human body at the same temperature environment is different. The largest temperature difference may reach more than 3 ℃ (Werner & Reents, 1980; Zaproudina, Varmavuo, Airaksinen, & Närhi, 2008). In addition, the temperature difference between the skin and the clothing of a person is even larger. Therefore, we divided the manikin into four temperature regions, as showed in Fig. 2 . We assumed that the head and arms are exposed to the environment. And the rest of the body is covered by clothing. The temperatures of the four zones in three room temperatures are given in Table 2 . All the manikin surface temperatures shown in the table are set based on the results of previous experimental studies (Werner & Reents, 1980; Zaproudina et al., 2008), while the outer surface temperature of clothing is set as the average of manikin surface temperature and room temperature.

Fig. 2.

Division of the manikin surface.

Table 2.

Manikin surface temperature setting.

Section		Head	Arm	Upper body	Lower body	Breathing air
Temperature Setting (℃)	room temperature for 24 ℃	33 (Zaproudina et al., 2008)	31 (Zaproudina et al., 2008)	27	28	35
	room temperature for 27 ℃	33.5 (Werner & Reents, 1980)	32 (Werner & Reents, 1980)	29	30	35
	room temperature for 30 ℃	34 (Werner & Reents, 1980)	33 (Werner & Reents, 1980)	31	32	35

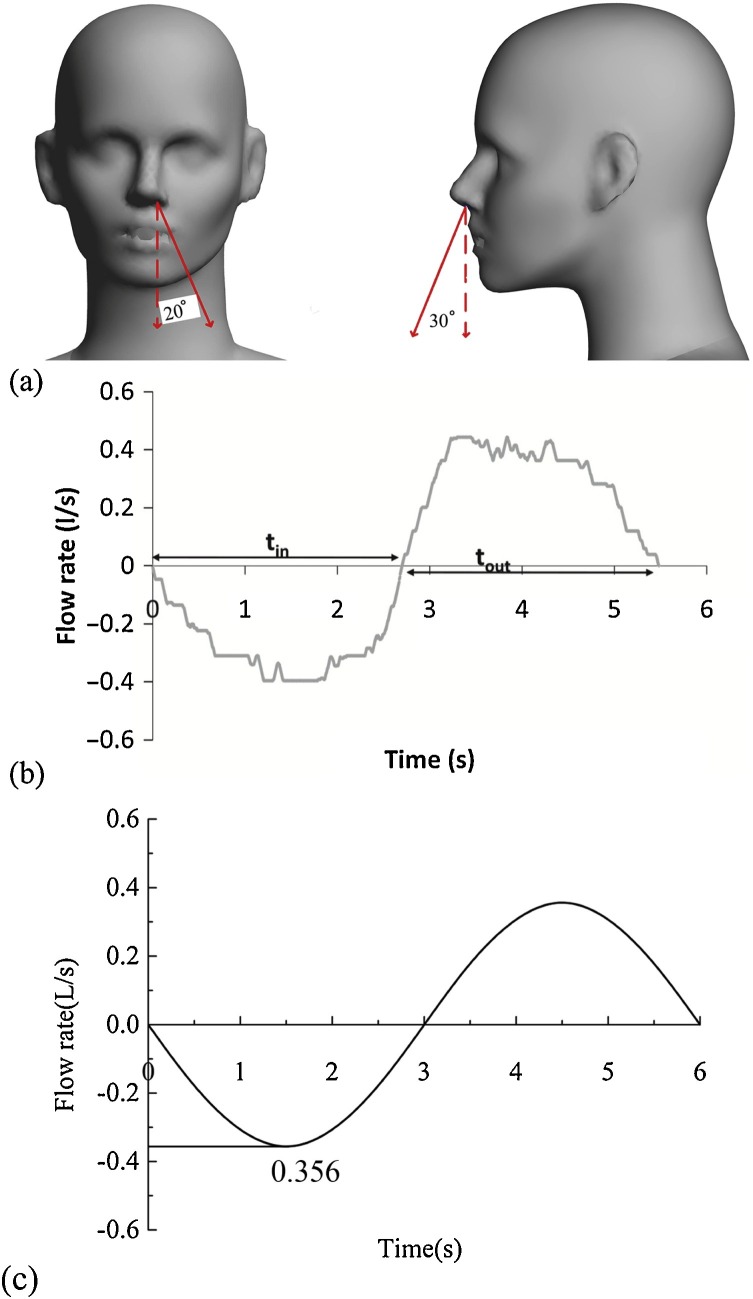
The CFD software ANSYS 17.0 was utilized to simulate the breathing airflow and the aerodynamic effects of human TP. The setting of nostril boundary conditions is crucial to the outcome of respiratory airflow (Zhang et al., 2019). Gupta, Lin, and Chen (2010) measured the nostril area of the human body as 0.56 ± 0.1 cm², respiratory volume as 13.33 L/min, and the respiratory frequency as 12/min. Xu et al. (2015), Xu et al. (2017) measured the respiratory rate of nasal respiration 10/min. Respiratory boundary conditions of this study are determined according to the previous experimental results, and the exhalation angle is shown in Fig. 3 (a). The function of respiratory velocity against time is a sine function, expressed as V = −2.8 sin (1.04t), where V is respiratory velocity, m/s; t is time, s. The above equation is obtained by simplifying the experimental results, and the simplification process is shown in Fig. 3(b) and (c). We added the above equation to the nostril boundary condition using the User-defined function, so that the nasal breathing speed changes following the sinusoidal curve. The air density is approximated by Boussinesq, and the settings of other boundary conditions are shown in Table 3 .

Fig. 3.

(a) Breathing angle setting (b) Flow generated over time for a subject for normal breathing (Gupta et al., 2010) (c) Flow generated over time as a simulated manikin breathes.

Table 3.

Setting of boundary conditions.

Boundary	Setting
Nostril area(single)	0.636 cm2 (Gupta et al., 2010)
Respiratory rate	10/min
breathing capacity	5.98 L/min (Bjørn & Nielsen, 2002)
Particle diameter	0.3−1 μm (Morawska et al., 2009; Papineni & Rosenthal, 1997; Wan et al., 2014)
Particle density	1.2 × 103 kg/m3
Particle released number	50/s
Coefficient of thermal expansion of air	0.0036 (1/℃)
Particle release time	0−30 s

The time step is defined as 0.02 s, and the solution method adopted the Pressure Implicit with Split Operator algorithm, and the maximum number of iterative steps is set at 20. The second-order upwind method is used for the spatial discretization of momentum and energy. Second order implicit method is used for transient formulation. Activated the warped-face Gradient Correction option to improve simulation accuracy for low-quality grids.

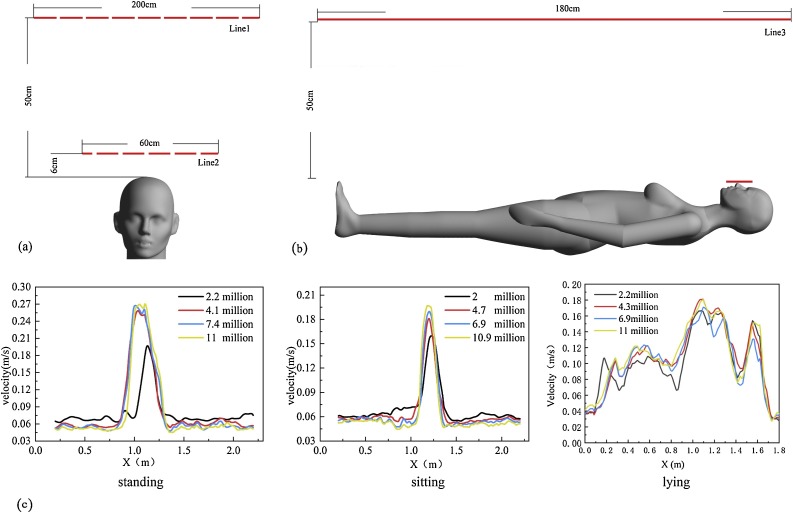
3.3. Grid independence test

In order to save computing time and ensure the accuracy of simulation, the independence test of the number of grids is carried out before simulation. The number of grids is divided into four levels, including 2.2 million, 4.1 million, 7.4 million and 11 million in the standing condition, 2 million, 4.7 million, 6.9 million and 10.9 million in the sitting condition, and 2.2 million, 4.3 million, 6.9 million and 11.05 million in the lying condition. The ratio of mesh sizes of different parts of the computational domain is guaranteed to be the same when different number of grids is divided. So the mesh quality of different number of grids is similar. The velocity results of line 1 in Fig. 4 (a) and line 3 in Fig. 4(b) are used to detect the grid independence of the three postures, and the results are shown in Fig. 4(c).

Fig. 4.

Grid independence test (a) for sitting and standing mannequin (b) for lying down model (c) Test result.

The results show that the simulation results are quite different when the number of grids increases from about 2 million to about 4 million in all three postures. When the number of grids increased from about 4 million to about 7 million, the differences become small. Therefore, 4.1 million, 4.7 million and 4.3 million grids are selected to simulate standing, sitting and lying cases, respectively. The grid size of each part of the computational domain is set as follows, nostril: 0.001 m; face: 0.002 m; head: 0.004 m; arm: 0.005 m; upper body: 0.008 m; lower body: 0.007 m; wall: 0.1 m; mesh growth rate: 1.2. At the same time, such grid division ensures that Y + of 95 % or more grids of human wall surface and wall is less than 1, providing the most support for LES.

3.4. Model validation

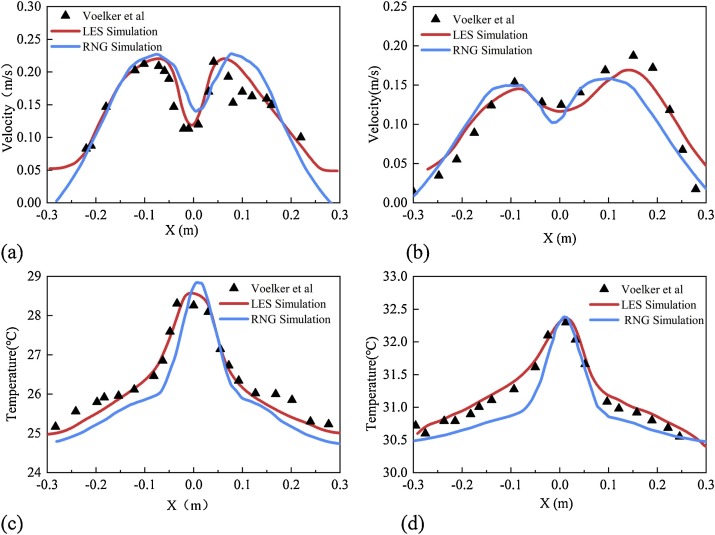
It is necessary to verify the accuracy of the LES turbulence model before the study. Voelker et al. (2014) used four measurement and statistical methods to conduct experimental studies on human TP, providing effective data for our comparison. In addition, the RNG k-epsilon model is also compared. All the settings for the RNG k-epsilon model were the same as those for the LES, and the near wall treatment was set as the standard wall equation, taking full buoyancy effect into account. The velocity and temperature results on the line 2 in Fig. 4 in the case of sitting manikin at room temperature for 24 ℃ and 27 ℃ are used to compare with the experimental results. The continuous results of 60 s–65 s in the simulation are averaged, and the comparison results are shown in Fig. 5 . The velocity and temperature results of both LES and RNG models fits well to the experimental results. The minor mismatches may be caused by the difference between the simulation and the human model used in the experiment. When looked in detail, LES model seems to be better than the RNG model.

Fig. 5.

Simulation model validation results (a) Comparison of velocity results at room temperature 24 ℃ (b) Comparison of velocity results at room temperature 30 ℃ (c) Comparison of temperature results at room temperature 24 ℃ (d) Comparison of temperature at room temperature 24 ℃.

4. Results

4.1. Surface heat transfer rate

Table 4 shows the area and heat flux of different areas of manikin in 9 cases. There are many ways of heat dissipation, such as radiation heat dissipation and convection heat transfer. The TP is mainly caused by convective heat transfer. The heat flow generated by convective heat transfer is shown in the table. Room temperature and posture affect the heat transfer rate to some extent. The greater the difference between human surface temperature and indoor temperature is, the greater the total heat transfer rate will be. When the room temperature is 24 ℃, the heat transfer rate of manikin in case 1, case 4 and case 7 are 15.82 W, 26.46 W and 19.48 W, respectively. When the room temperature is 30 ℃, the heat transfer rate of manikin in case 3, case 6 and case 9 are 4.98 W, 7.19 W and 6.29 W, respectively. The different postures mainly lead to the different convective heat transfer coefficients between the manikin surface and the air, which leads to the difference in the total heat transfer rate. Among the three postures, the convective heat transfer coefficient of the body surface is the largest in the sitting posture and the smallest in the standing posture.

Table 4.

Area and heat transfer rate of each section of the manikin.

Section		Lower body	Upper body	Head	Left hand	Right hand	Total
Area(m2)	Standing	0.72	0.48	0.13	0.08	0.08	1.49
	Sitting	0.79	0.43	0.13	0.12	0.12	1.60
	Lying	0.72	0.48	0.13	0.08	0.08	1.49
Heat transfer rate(W)	Case 1	4.90	2.09	4.12	2.06	2.15	15.82
	Case 2	3.00	1.07	3.19	1.34	1.34	9.95
	Case 3	1.36	0.41	1.75	0.71	0.74	4.98
	Case 4	9.65	3.47	5.58	3.89	3.86	26.46
	Case 5	4.54	1.29	3.19	2.29	2.26	13.59
	Case 6	2.13	0.57	1.83	1.33	1.31	7.19
	Case 7	6.49	3.79	4.17	2.49	2.54	19.48
	Case 8	3.96	2.29	2.79	1.71	1.69	12.46
	Case 9	1.79	1.01	1.59	0.94	0.94	6.29

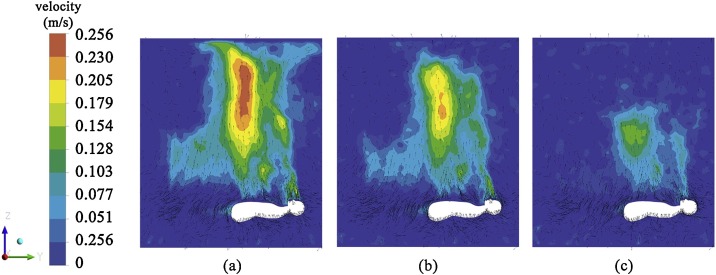
4.2. Standing manikin case

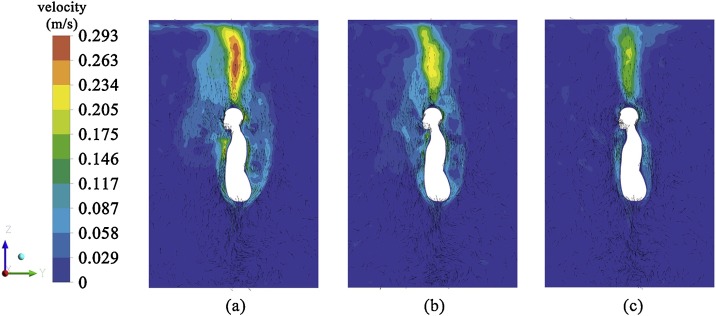
Fig. 6 shows the TP velocity contours and vector diagram of case 1, case 2 and case 3. The TP velocity is getting lower by increasing the room temperature. The maximum TP velocity is at a height of 0.45 m above the head, which is the same as previous experimental and simulation studies (Craven & Settles, 2006; Li et al., 2017; Sørensen & Voigt, 2003). The maximum velocity value is 0.293 m/s when room temperature is 24 ℃, and the smaller velocity value is 0.22 m/s and 0.19 m/s when room temperature is 27 ℃ and 30 ℃, respectively.

Fig. 6.

Velocity contour and vector diagram of TP produced by standing manikin (a) Case 1 (b) Case 2 (c) Case 3.

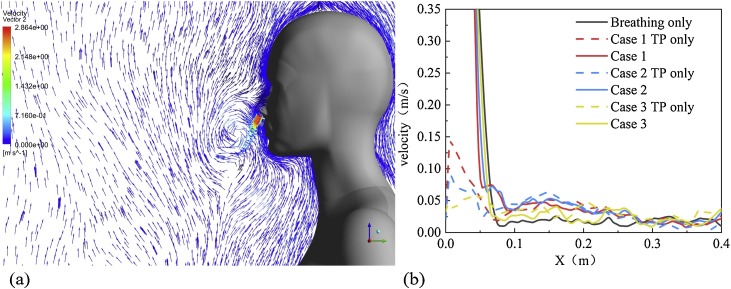
Fig. 7 shows the results of the interaction between respiratory airflow and TP produced by the standing manikin. The velocity vector diagram of airflow generated in the exhalation process of breathing under the influence of TP is shown in Fig. 7(a). The influence of TP on respiratory airflow is very great. When the airflow jets from the nostril at a distance of 5 cm, it moves upward and form a small vortex in front of the face. Three kinds of airflow at room temperature, namely exhalation airflow as pure breathing, pure TP and mixed airflow of two kinds of airflow, are projected on the X-axis along the velocity value of breathing direction and compared, the results are shown in Fig. 7(b). The TP velocity near the body surface also decreases with the increasing of room temperature. The values of case 1, case 2 and case 3 are 0.15 m/s, 0.09 m/s and 0.05 m/s, respectively. The thickness of the TP at three cases is similar, which attenuates from about 0.28 m to less than 0.025 m/s. When the room temperature is 24 ℃ and 27 ℃, the respiratory airflow is greatly affected by TP. When the room temperature is 30 ℃, whether there is TP or not, the respiratory airflow has a similar attenuation trend.

Fig. 7.

Interaction between human respiratory airflow and TP in standing posture (a) Velocity vector (b) the velocity change in different situations along the direction of exhalation and outflow.

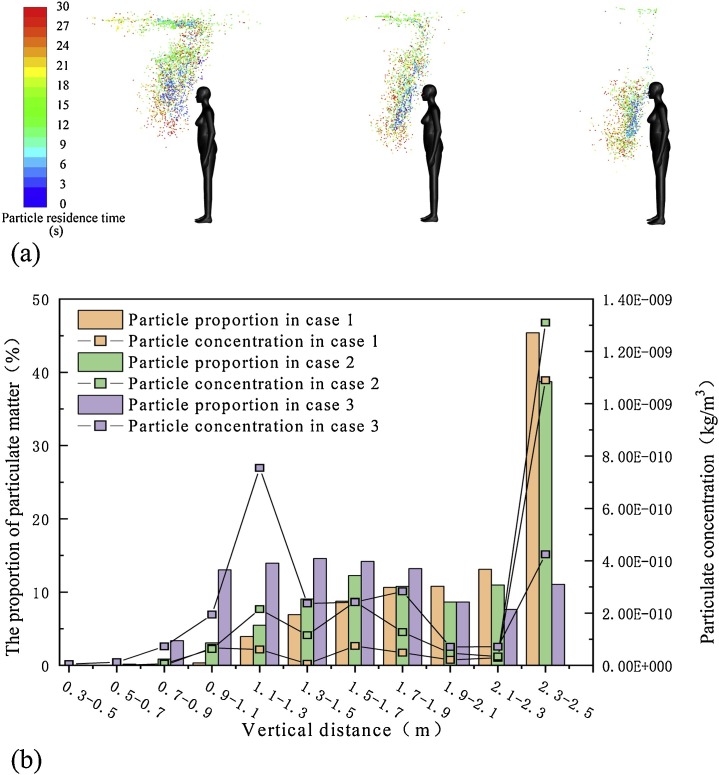
Fig. 8 (a) shows the distribution of particles generated by standing manikin at 60 s at different room temperature. The lateral diffusion of the particles is not violent. Most of the particles mainly follow the direction of TP upward diffusion. The lower the room temperature is, the more particles are concentrated near the roof. The higher the room temperature is, the more particles are concentrated in front of chest with the manikin. To describe the distribution of this motion, the distribution of the number proportion and concentration of particles along the vertical direction is shown in Fig. 8(b). Due to the high concentration of particles around the nostrils in 30 s, the particle diffusion results in 60 s is adopted. The results show that at room temperature of 24 ℃, the number of particles in the range of 2.3–2.5 m accounts for 45 % of the total. While at room temperature of 30 ℃, 11.5 % of the particles are distributed near the roof, and 70 % of the particles are distributed in the height range of 0.9–1.9 m. The diffusion distribution of particles at room temperature of 27 ℃ is similar to that at room temperature of 24 ℃. For the maximum concentration of particulate matter, the condition of 24 ℃ at room temperature and 27 ℃ at room temperature appeared near the roof. However, the maximum concentration of particulate matter at room temperature of 30 ℃ is in the range of 1.1–1.3 m. The maximum concentrations in case 1, case 2 and case 3 are 2.74e-9 kg/m³, 2.28 e-9 kg/m³ and 9.85 e-9 kg/m³, respectively.

Fig. 8.

Distribution of particulate matter in standing manikin (a) Diffusion results of particulate in case 1–3 at 30 s (b) Vertical distribution of the number and concentration of particles in case 1–3.

4.3. Sitting manikin case

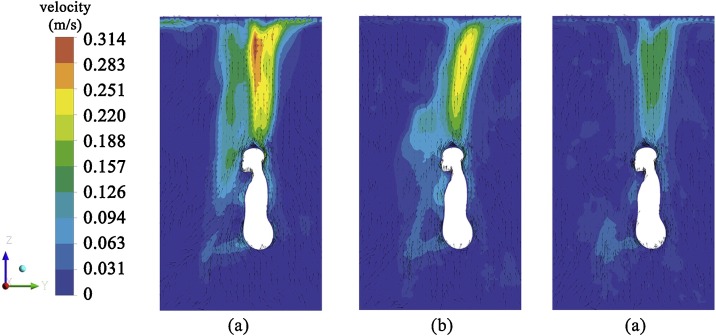
Fig. 9 shows the TP velocity contour and vector diagram of case 4–6 at 60 s. Similar to standing case, TP velocity decreases as room temperature increases. The difference is that the maximum TP velocity in all three kinds of room temperatures is at a height of 0.65 m above the head. Maximum value at 24 ℃ is 0.314 m/s. It should be noted that the TP in front of the face and chest produced by the sitting manikin is thicker than it is in the standing posture, due to the interference caused by leg flexing.

Fig. 9.

Velocity contour and vector diagram of TP (a) Case 4 (b) Case 5 (c) Case 6.

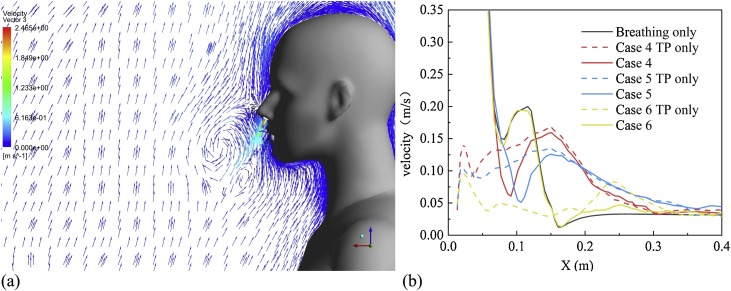
Fig. 10 shows the interaction between respiratory airflow and TP in the sitting manikin. Similar to the results of the standing manikin, respiratory airflow generates a vortex in front of face, and the loss of kinetic energy leads to a rapid decline in the exhalation velocity. The velocity value in the direction of exhalation is compared with TP and exhalation airflow of three kinds of room temperature in Fig. 10(b). The velocity of TP in front of the face is similar to that of standing case. However, after a short decline, the velocity of TP at room temperature of 24 ℃ and 27 ℃ rises to 0.17 m/s and 0.13 m/s respectively at 0.15 m from the human surface, which is due to the positive effect of leg bending on the chest TP. As a result, the TP increased in thickness to about 0.36 m in the sitting posture, 28 % thicker than 0.28 m in the standing posture. At room temperature of 30 ℃, like standing posture, the influence of TP is still small.

Fig. 10.

Interaction between human respiratory airflow and TP in sitting posture (a) velocity vector (b) the velocity attenuation in different situations along the direction of exhalation and outflow.

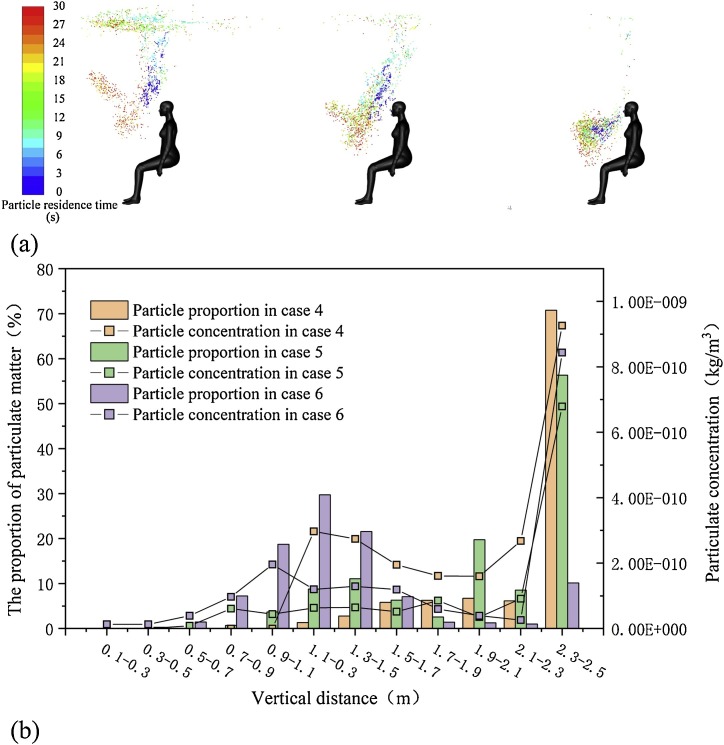
Fig. 11 (a) shows the indoor distribution of particles generated by sitting human respiration for 30 s. The colder the room temperature is, the more particles are clustered around the roof, while others spread diagonally in front of the body. TP from bending thigh are responsible for the lateral diffusion of these particles. Fig. 11(b) shows the distribution of the number proportion and concentration of particles in the vertical direction. Similar to the distribution results of particles generated by standing manikin, when the room temperature is 24 ℃ and 27 ℃, the majority of particles gather near the ceiling, which is a range of 2.3–2.5 m high. However, this ratio is much higher than standing, reaching 72 % and 56 %, respectively. When the room temperature is 30 ℃, the particles tend to gather in the height range of 1.1–1.3 m, and the number of particles on the roof counts for only 9 %. The concentration distribution of particulate matter is similar to that of standing posture.

Fig. 11.

Particle diffusion results in case 4–6 (a) Distribution of particle in case 4–6 (b) The distribution of particle quantity and concentration along the vertical direction in case 4–6.

4.4. Lying manikin case

Fig. 12 shows the velocity contour and vector diagram of the TP generated by the lying manikin. The velocity of the plume increases with the difference between the manikin’s surface temperature and room temperature. The maximum value of TP appears at the height of about 1.3–1.5 m above the manikin, and the maximum values of three kinds of room temperature are 0.256 m/s, 0.205 m/s and 0.159 m/s, respectively. The maximum speed and range of the TP produced by the lying body are much smaller than those of the previous two positions. Because the lying position does not provide the process of TP accumulation.

Fig. 12.

Velocity contour and vector diagram of TP (a) Case 7 (b) Case 8 (c) Case 9.

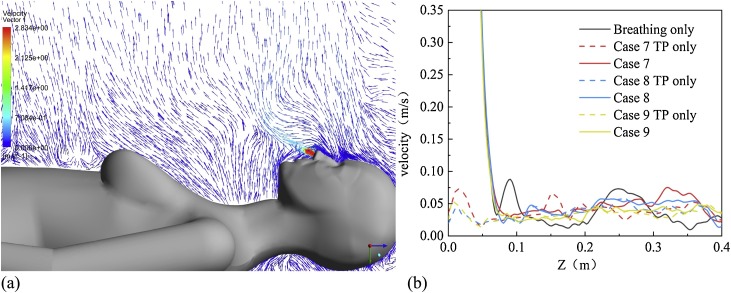
Fig. 13 (a) shows the results of the velocity direction of TP and respiratory airflow in the lying manikin. It can be seen from the figure that the respiratory airflow only slightly changes the flow direction angle under the influence of the TP. Three kinds of air flows at room temperature, namely exhalation flow in pure breathing, TP flow and mixed air flows of two kinds of air flows, are projected on the Z-axis along the breathing direction for comparison, and the results are shown in Fig. 13(b). At three kinds of room temperatures, the velocity of TP near the skin was 0.75 m/s, 0.4 m/s and 0.5 m/s, respectively, which was much smaller than the other two postures. The TP produced by the manikin in the lying position is similar to the flow direction of the respiratory airflow. The exhaled air flows for some distance and then mixes with the TP to move upward.

Fig. 13.

Interaction between human respiratory airflow and TP in lying posture (a) velocity vector (b) the velocity attenuation in different situations along the direction of exhalation and outflow.

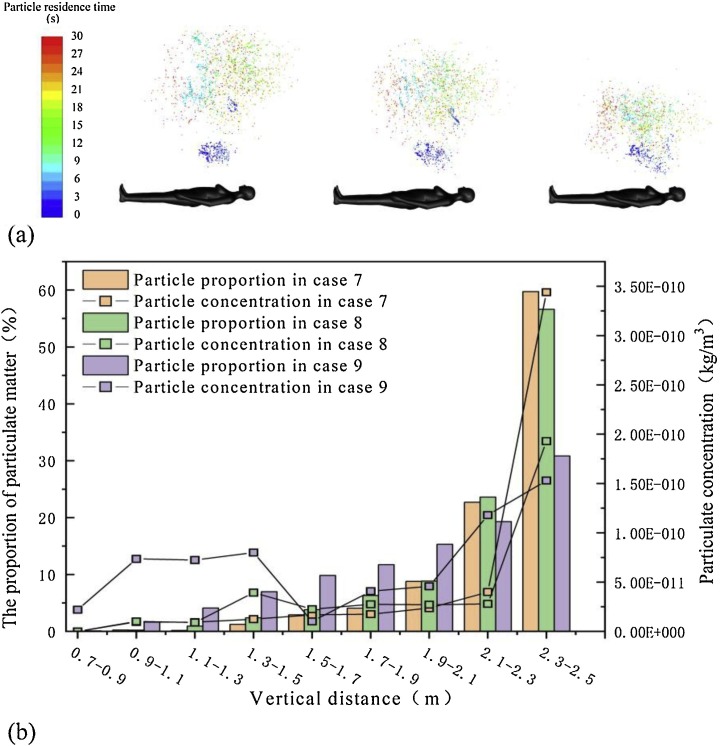
Fig. 14 (a) shows the diffusion results of the particulate matter generated by lying flat human breathing at 30 s. The particle is released from the nostril, travels in the direction of the airflow to the chest, and then diffuses upwards. The diffusion velocity of the particle is directly related to the airflow velocity of TP. The higher the velocity is, the farther the diffusion distance is, and the larger the diffusion velocity is. The particles produced by lying on your back spread more widely than the other two positions because of the larger range of TP. Similar to the distribution of the particles in the first two positions, the lower the room temperature is, the more the particles diffuse upward. However, despite the fact that at room temperature of 30 ℃, the proportion of particles near the roof is still very high, at 32 %. The particulate matter near the roof counts for 61 % and 58 % in case 7 and case 8, respectively. The distribution of particle concentration has the same rule as the distribution of particle number. Maximum concentrations in case 7–9 are all found near the roof 3.4e-10 kg/m³, 1.9e-10 kg/m³ and 1.5e-10 kg/m³, respectively.

Fig. 14.

Particle diffusion results in case 7–9 (a) Distribution of particle in case 7–9 (b) The distribution of particle quantity and concentration along the vertical direction in case 7–9.

5. Discussion

This study provides basic knowledge for understanding the characteristics of airflow around manikin, the diffusion of particulate matters and the practical significance of optimal ventilation design, etc. It also confirms the previous researches, that is, the velocity of human TP decreases with the decrease of temperature difference between human surface and surrounding air.

Licina et al. (2014) reported a more detailed experimental study on TP, and obtained that the manikin in a sitting position generates more heat, which is similar to our simulation results. Based on the analysis they got this phenomenon is due to the effect of the TP produced by the thighs. However, we propose another explanation. TP is produced by convection of heat transfer between the surface of the manikin and the indoor air. The basic equation for convective heat transfer, Newton's law of cooling is as follows:

q = h(t_w − t_f) (15)

Where q is heat flux, W/m², h is convective heat transfer coefficient, W/m²⋅k, t _w is solid wall temperature, k, t _f is fluid characteristic temperature, k. According to Newton's law of cooling, convection heat transfer is determined by the difference between solid surface temperature and fluid temperature and the convection heat transfer coefficient. According to the heat flow results in this study, the thermal conductivity per unit area of different postures is different at the same room temperature. For example, when the room temperature is 24 ℃, the heat flux of the manikin in three postures is 10.63 W/m², 16.55 W/m² and 13.09 W/m², respectively. Therefore, different postures mainly lead to the change of convective heat transfer coefficient, which leads to the difference of human heat flux.

The change of heat flux caused by postures mainly affects the influence range of TP, but has no direct influence on the velocity value of TP near human surface. At the same room temperature, the thermal conductivity of a sitting body is 1.6 times than that of a standing body. But the TP velocity near the surface of the body in the two positions is not significantly different. When the room temperature is 24 ℃, the TP velocity near the surface of the sitting body is 0.15 m/s, with the same value which is 0.15 m/s for the standing posture. The influence range of the three poses is very different. Here, the influence range is defined as the cross-sectional area of the plane XOY. The influence range of the TP generated by the lying manikin is the largest, followed by the sitting posture and finally the standing posture.

Another factor that affects thermal conductivity is the room temperature. The difference in thermal conductivity at room temperature is very large. However, the difference of thermal conductivity caused by the difference of room temperature mainly affects the TP velocity near the manikin surface, but has little effect on the influence range of the TP. At different room temperature, the TP velocity was significantly different near the surface of manikin.

Differences in posture from room temperature lead to differences in the surface thermal conductivity of the body, which in turn leads to differences in the range and velocity of the plume. We call the ability of TP to carry particles upward movement as TP intensity. The intensity of TP is mainly affected by the surface thermal conductivity of manikin. According to the results of particle distribution, the velocity and influence range of TP both affect the velocity and quantity of particle upward diffusion to some extent. The higher the velocity of the TP is, the larger the influence range of the TP is. The greater the flux of the TP and the stronger the TP.

Previous studies have shown that aerosols smaller than 45 μm have very short evaporation and cooling times (Chen & Zhao, 2010), and very long deposition times, which can exceed 360 s (Wan, Chao, Ng, Sze to, & Yu, 2007). Therefore, according to the diffusion law of particulate matter, the selection of appropriate ventilation can reduce its indoor stay time. When the room temperature is 24 ℃ and 27 ℃, the distribution of particulate matter generated by standing and sitting for human respiration is characterized by a higher concentration and more quantity near the roof. In order to eliminate these particles, the primary task of ventilation is to prevent the particles from returning to the breathing area, and the second is to effectively organize the airflow distribution around the roof to remove the vast majority of pollutants. Therefore, it is possible to produce positive effects by applying the displacement ventilation in the above situation. At room temperature of 30 ℃, the TP of manikin has very little influence on respiratory airflow, and the particle hardly changes with the movement track of respiratory airflow. Sitting and standing manikin at this room temperature particle tends to gather in the chest, producing a higher concentration. In this case, it is more efficient and energy saving to deal with the distributed particles by local exhaust. The particles produced by people lying flat on their backs are usually more evenly distributed, with no particularly high concentration areas. In this case, mixed ventilation can reduce the overall concentration of particulate matter in the room and achieve the effect of energy-saving.

Despite discussed, the study does not take into account the detailed state of human dress. The convective heat exchange and TP effects are different when the manikin is wearing different clothes, and the impact on particulate matter is also different. In addition, this paper only considers the situation that people are at rest and do not move. In fact, the micro movement of manikin is carried out all the time. The influence of this micro movement on TP and even particles needs to be further studied. In the discussion, although the elimination of particulate matter generated by different ventilation forms has been simply predicted, the actual effects still need to be further studied.

6. Conclusions

In this paper, a LES turbulence model was used to simulate the diffusion of microbial particles produced by female human respiration under the influence of TP. By analyzing and summarizing the diffusion characteristics from convective heat transfer, the interaction between TP and respiratory airflow and the diffusion data of particles, the following conclusions were drawn:

• (1)Different postures mainly affect the convective heat transfer coefficient on the surface of human body, which leads to differences in the thermal conductivity of the human body. Such differences mainly affect the range instead of velocity of TP.
• (2)The difference in room temperature directly affects the convective heat transfer on the surface of human body, causing a huge difference in the velocity of TP near the surface of the human body. At different room temperature, the difference of thermal conductivity of human surface can be 3–4 times, and the difference of TP velocity can be 1–2 times.
• (3)The difference in the ability of TP to carry particles upward is mainly caused by the difference in heat flux. The greater the heat flux is, the greater the air flow flux of the plume is, and the greater the ability of the plume is to carry particles upward.
• (4)When the room temperature is 24 ℃ and 27 ℃, the TP generated by the human body in the standing and sitting positions has a strong ability to interfere with the respiratory airflow, and the respiratory airflow can hardly penetrate the TP. At room temperature of 30 ℃, some particles can pass through the TP with the respiratory airflow. TP produced by the lying manikin slightly changes the direction of particle movement and promotes particle diffusion.

The study was verified by experimental results under similar conditions, but the main conclusions of the simulation were not verified by relevant experiments. Further studies are needed to verify the diffusion results of particulate matter. In addition, the influence extent of human motion on the formation of thermal plume is also worthy being investigated. These will be of great interest in our future work.

Declaration of Competing Interest

We declare that we have no financial and personal relationships with other people or organizations that can inappropriately influence our work, there is no professional or other personal interest of any nature or kind in any product, service and/or company that could be construed as influencing the position presented in, or the review of, the manuscript entitled, “Study on the motion law of aerosols produced by human respiration under the action of thermal plume of different intensities”.