Active learning narrows achievement gaps for underrepresented students in undergraduate science, technology, engineering, and math

Significance

Achievement gaps increase income inequality and decrease workplace diversity by contributing to the attrition of underrepresented students from science, technology, engineering, and mathematics (STEM) majors. We collected data on exam scores and failure rates in a wide array of STEM courses that had been taught by the same instructor via both traditional lecturing and active learning, and analyzed how the change in teaching approach impacted underrepresented minority and low-income students. On average, active learning reduced achievement gaps in exam scores and passing rates. Active learning benefits all students but offers disproportionate benefits for individuals from underrepresented groups. Widespread implementation of high-quality active learning can help reduce or eliminate achievement gaps in STEM courses and promote equity in higher education.

Abstract

We tested the hypothesis that underrepresented students in active-learning classrooms experience narrower achievement gaps than underrepresented students in traditional lecturing classrooms, averaged across all science, technology, engineering, and mathematics (STEM) fields and courses. We conducted a comprehensive search for both published and unpublished studies that compared the performance of underrepresented students to their overrepresented classmates in active-learning and traditional-lecturing treatments. This search resulted in data on student examination scores from 15 studies (9,238 total students) and data on student failure rates from 26 studies (44,606 total students). Bayesian regression analyses showed that on average, active learning reduced achievement gaps in examination scores by 33% and narrowed gaps in passing rates by 45%. The reported proportion of time that students spend on in-class activities was important, as only classes that implemented high-intensity active learning narrowed achievement gaps. Sensitivity analyses showed that the conclusions are robust to sampling bias and other issues. To explain the extensive variation in efficacy observed among studies, we propose the heads-and-hearts hypothesis, which holds that meaningful reductions in achievement gaps only occur when course designs combine deliberate practice with inclusive teaching. Our results support calls to replace traditional lecturing with evidence-based, active-learning course designs across the STEM disciplines and suggest that innovations in instructional strategies can increase equity in higher education.

In industrialized countries, income inequality is rising and economic mobility is slowing, resulting in strains on social cohesion (1). Although the reasons for these trends are complex, they are exacerbated by the underrepresentation of low-income and racial and ethnic minority students in careers that align with the highest-lifetime incomes among undergraduate majors: the science, technology, engineering, and mathematics (STEM) and health disciplines (2–4). Underrepresentation in STEM is primarily due to attrition. Underrepresented minority (URM) students in the United States, for example, start college with the same level of interest in STEM majors as their overrepresented peers, but 6-y STEM completion rates drop from 52% for Asian Americans and 43% for Caucasians to 22% for African Americans, 29% for Latinx, and 25% for Native Americans (5). Disparities in STEM degree attainment are also pronounced for low-income versus higher-income students (6, 7).

Poor performance, especially in introductory courses, is a major reason why STEM-interested students from all backgrounds switch to non-STEM majors or drop out of college altogether (8–10). Underrepresentation occurs because URM and low-income students experience achievement gaps—examination scores that are lower on average than their overrepresented peers in “gateway” STEM courses, along with failure rates that are higher (11, 12). In some cases, these disparities occur even when researchers control for prior academic performance—meaning that underrepresented students are underperforming relative to their ability and preparation (12). Achievement gaps between overrepresented and underrepresented students have been called “one of the most urgent and intractable problems in higher education” (ref. 13, p. 99).

Previously, most efforts to reduce achievement gaps and increase the retention of underrepresented students in STEM focused on interventions that occur outside of the courses themselves. For example, supplementary instruction programs are sometimes offered as optional companions to introductory STEM courses that have high failure rates. These supplemental sections are typically facilitated by a graduate student or advanced undergraduate, meet once a week, and consist of intensive group work on examination-like problems. Although most studies on supplemental instruction do not report data that are disaggregated by student subgroups, several studies have shown that low-income or URM students—hereafter termed students from minoritized groups in STEM, or MGS—gain a disproportionate benefit (SI Appendix, Table S1). Unfortunately, almost all studies of supplementary instruction fail to control for self-selection bias—the hypothesis that volunteer participants are more highly motivated than nonparticipants (refs. 14 and 15, but see ref. 16). A second widely implemented approach for reducing performance disparities provides multifaceted, comprehensive support over the course of a student’s undergraduate career. These programs may include summer bridge experiences that help students navigate the transition from high school to college, supplementary instruction for key introductory courses, financial aid, early involvement in undergraduate research, mentoring by peers and/or faculty, and social activities (SI Appendix, Table S2). Although these systemic programs have recorded large improvements in STEM achievement and retention for underrepresented students (17, 18), they are expensive to implement, depend on extramural funding, and are not considered sustainable at scale (19). A third approach that occurs outside of normal course instruction consists of psychological interventions that are designed to provide emotional support. Some of these exercises have also shown disproportionate benefits for underrepresented students (SI Appendix, Table S3).

Can interventions in courses themselves—meaning, changes in how science is taught—reduce achievement gaps and promote retention in STEM? A recent metaanalysis concluded that, on average, active learning in STEM leads to higher examination scores and lower failure rates for all students, compared to all students in the same courses taught via traditional lecturing (20). However, several reports from undergraduate biology courses also suggest that innovative course designs with active learning can reduce or even eliminate achievement gaps for MGS (12, 21–24). Is there evidence that active learning leads to disproportionate benefits for students from MGS across a wide array of STEM disciplines, courses, instructors, and intervention types? If so, that evidence would furnish an ethical and social justice imperative to calls for comprehensive reform in undergraduate STEM teaching (25).

Our answer to this question is based on a systematic review and individual-participant data (IPD) metaanalysis of published and unpublished studies on student performance. The studies quantified either scores on identical or formally equivalent examinations or the probability of passing the same undergraduate STEM course under active learning versus traditional lecturing (Materials and Methods). The contrast with traditional lecturing is appropriate, as recent research has shown that this approach still dominates undergraduate STEM courses in North America (26). In addition, passive and active approaches to learning reflect contrasting theories of how people learn. Although styles of lecturing vary, all are instructor-focused and grounded in a theory of learning that posits direct transmission of information from an expert to a novice. Active learning, in contrast, is grounded in constructivist theory, which holds that humans learn by actively using new information and experiences to modify their existing models of how the world works (27–30).

To be admitted to this study, datasets needed to disaggregate student information by race and ethnicity (or URM status) or by students’ socioeconomic status (e.g., by means of Pell Grant eligibility). These data allowed us to identify students from MGS. Although combining low-income and URM students devalued the classroom experiences of individual students or student groups, the combination is common in the literature (6, 31), represents the student groups of most concern to science policy experts (31), and increased the statistical power in the analysis by using student categories that may be reported differently by researchers, but often overlap (6, 10).

Our literature search, coding criteria, and data gathering resulted in datasets containing 1) 9,238 individual student records from 51 classrooms, compiled in 15 separate studies, with data from identical or formally equivalent examinations (32); and 2) 44,606 individual student records from 174 classrooms, compiled in 26 separate studies, with data on course passing rates, usually quantified as 1 minus the proportion of D or F final grades and withdrawals (33).

IPD metaanalyses, based on datasets like ours, are considered the most reliable approach to synthesizing evidence (34, 35). We analyzed the data using one-step hierarchical Bayesian regression models (Materials and Methods and SI Appendix, SI Materials and Methods). Below, we report the mean of the posterior distribution as well as the 95% credible intervals (CIs) for each estimate. The interpretation of the 95% CIs is “95% of the time, the estimate falls within these bounds.”

Results

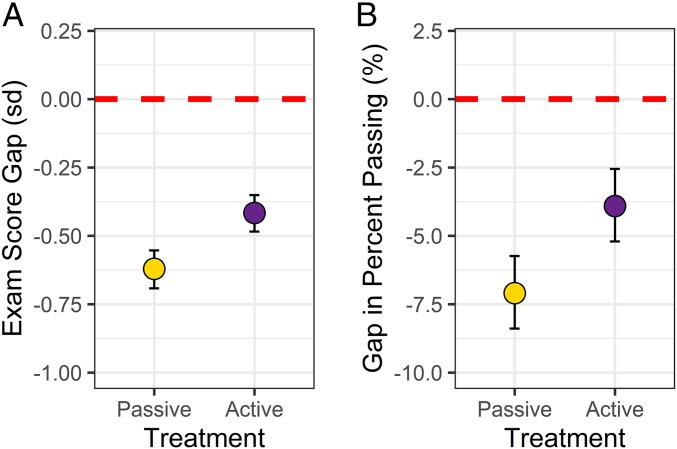
We found that, on average, the standardized achievement gap between MGS and non-MGS students on identical or formally equivalent examinations was −0.62 SDs in courses based on traditional lecturing (95% CI: −0.69 to −0.55). In courses that included active learning, this gap was −0.42 SDs (95% CI: −0.48 to −0.35) (Fig. 1A and SI Appendix, Table S4). Across many courses and sections, this represents a 33% reduction in achievement gaps on examinations in the STEM disciplines. Although students from MGS experience lower examination scores on average than students from non-MGS across both instructional types, the disparity is significantly reduced when instructors employ active learning.

Fig. 1.

Average achievement gaps are smaller in active-learning classes than traditional-lecturing classes. (A) Model-based estimates for the average achievement gaps in examination scores across STEM for students from MGS versus non-MGS under traditional lecturing (gold) and active learning (purple). The data are in units of SDs (SI Appendix, SI Materials and Methods). (B) Model-based estimates for the average achievement gaps in percentage of students passing a STEM course for students from MGS versus non-MGS. In both graphs, points show averages and the vertical bars show 95% Bayesian CIs; the dashed horizontal lines represent no gap in performance.

Furthermore, we find that, on average, students from MGS pass at lower rates than students from non-MGS by 7.1% (95% CI: −8.4% to −6.6%) with traditional lecturing. The difference in passing is reduced to only −3.9% (95% CI: −5.2% to −2.5%) with active learning (Fig. 1B and SI Appendix, Table S5). When compared to traditional lecturing across an array of disciplines, courses, and sections, active learning reduced the gap in probability of passing between students from MGS versus students from non-MGS by 45%.

A more granular analysis of changes in achievement gaps shows extensive variation among studies (Fig. 2). In 10 of the 15 studies with examination score data, students from MGS showed disproportionate gains under active learning relative to students from non-MGS (Fig. 2A). In 8 of these 10 cases, students from MGS still perform less well than students from non-MGS in both treatments, although achievement gaps shrink. The data from the remaining five studies show that active learning benefitted students from non-MGS more than students from MGS, in terms of performance on identical examinations. The analysis of passing rate data shows a similar pattern, with students from MGS showing a disproportionate reduction in failure rates in 15 of the 26 studies. In the remaining 11 studies, active learning benefitted students from non-MGS more than students from MGS in terms of lowering failure rates.

Fig. 2.

The magnitude of achievement gaps in active-learning (AL) versus passive-learning (PL) classes varies among studies. Each data point represents a single course; the majority of active-learning courses narrowed the achievement gap. In both panels, the red dashed 1:1 line indicates no difference in the gap between active and passive learning; the white area above the line indicates courses where the gap narrowed. (A) The Upper Left quadrant indicates studies where gaps in examination scores reversed, from students from non-MGS doing better under lecturing to students from MGS doing better under active learning. The Upper Right quadrant represents studies where gaps in examination scores favored students from MGS under both traditional lecturing and active learning. The Bottom Left quadrant signifies studies where students from non-MGS averaged higher examination scores than students from MGS under both passive and active instruction. The Bottom Right quadrant denotes studies where students from non-MGS outperformed students from MGS under active learning, but students from MGS outperformed students from non-MGS under traditional lecturing. Both axes are in units of SDs and indicate difference in performance between MGS and non-MGS students. (B) The Upper Left quadrant indicates studies where gaps in the probability of passing favored students from non-MGS under lecturing but MGS under active learning. The Upper Right quadrant represents studies where the probability of passing was higher for students from MGS versus non-MGS under both passive and active learning. The Lower Left quadrant signifies studies where students from MGS were less likely to pass than students from non-MGS under both modes of instruction. The Lower Right quadrant denotes studies where students from MGS were more likely than non-MGS to pass under traditional lecturing but less likely than non-MGS to pass under active learning. Both axes are percent passing and indicate the difference in performance between MGS and non-MGS students.

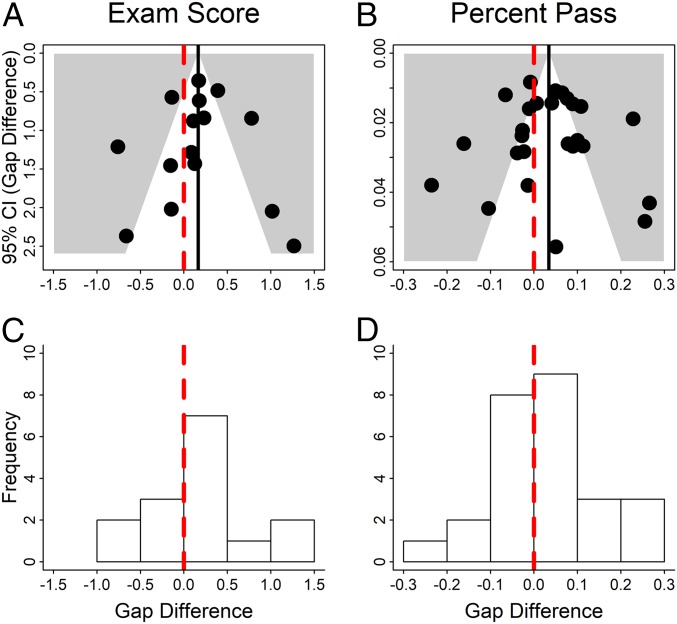
Sensitivity analyses indicate that our results were not strongly influenced by unreasonably influential studies (SI Appendix, Fig. S2) or sampling bias caused by unpublished studies with low effect sizes—the file drawer effect. The symmetry observed in funnel plots for examination score and passing rate data, and the approximately Gaussian distributions of the changes in gaps in each study, each suggest that our sampling was not biased against studies with negative, no, or low effect sizes (Fig. 3).

Fig. 3.

Results appear robust to sampling bias. Funnel plots were constructed with the vertical axis indicating the 95% CI for the difference, under active learning versus lecturing, in (A) examination score gaps or (B) passing rate gaps, and the horizontal axis indicating the change in gaps. The dashed red vertical line shows no change; the solid black line shows the average change across studies. The histograms show data on (C) examination scores (in SDs) and (D) percent passing. The vertical line at 0 shows no change in the achievement gap. If the analyses reported in this study were heavily impacted by the file drawer effect, the distributions in A–D would be strongly asymmetrical, with low density on the lower left of each funnel plot and much less density to the left of the no-change line on the histograms.

Some of the observed variation in active learning’s efficacy in lowering achievement gaps can be explained by intensity—the reported percentage of class time that students spend engaged in active-learning activities (SI Appendix, Table S6). For both examination scores and passing rates, the amount of active learning that students do is positively correlated with narrower achievement gaps: Only classes that implement high-intensity active learning narrow achievement gaps between students from MGS and non-MGS (Fig. 4). In terms of SDs in examination scores, students from MGS vs. non-MGS average a difference of −0.48 (95% CI: −0.60 to −0.37) with low-intensity active learning, but only −0.36 (95% CI: −0.45 to −0.27) with high-intensity active learning (Fig. 4A and SI Appendix, Table S7). These results represent a 22% and 42% reduction, respectively, in the achievement gap relative to traditional lecturing. Similarly, on average, differences in passing rates for students from MGS vs. non-MGS are −9.6% (95% CI: −11.0% to −8.2%) with low-intensity active learning, but only −2.0% (95% CI: −3.3 to 0.63%) with high-intensity active learning (Fig. 4B and SI Appendix, Table S8). These changes represent a 16% increase and a 76% reduction, respectively, in the achievement gap relative to passive learning.

Fig. 4.

Treatment intensity is positively correlated with narrower gaps. High-intensity active-learning courses have narrower achievement gaps between MGS and non-MGS students. In both graphs, points show averages and the vertical bars show 95% Bayesian CIs; the dashed horizontal lines represent no gap in performance. (A) Examination score gap. (B) Gap in percent passing. Intensity is defined as the reported proportion of time students spent actively engaged on in-class activities (SI Appendix, SI Materials and Methods).

Other moderator analyses indicated that class size, course level, and discipline—for fields represented by more than one study in our dataset—did not explain a significant amount of variation in how achievement gaps changed (SI Appendix, Tables S9–S11). Although regression models indicated significant heterogeneity based on the type of active learning implemented, we urge caution in interpreting this result (SI Appendix, Tables S12 and S13). Active-learning types are author-defined and currently represent general characterizations. They are rarely backed by objective, quantitative data on the course design involved, making them difficult to interpret and reproduce (SI Appendix).

Discussion

Earlier work has shown that all students benefit from active learning in undergraduate STEM courses compared to traditional lecturing (20). The analyses reported here show that across STEM disciplines and courses, active learning also has a disproportionately beneficial impact for URM students and for individuals from low-income backgrounds. As a result, active learning leads to important reductions in achievement gaps between students from MGS and students from non-MGS in terms of examination scores and failure rates in STEM. Reducing achievement gaps and increasing the retention of students from MGS are urgent priorities in the United States and other countries (36–38).

Our results suggest that, for students from MGS, active learning’s beneficial impact on the probability of passing a STEM course is greater than its beneficial impact on examination scores. Course grades in most STEM courses are largely driven by performance on examinations, even in active-learning courses that offer many nonexam points (39). As a result, achievement gaps on examinations often put underrepresented students in a “danger zone” for receiving a D or F grade or deciding to withdraw. On many campuses, median grades in introductory STEM courses range from 2.5 to 2.8 on a 4-point scale—equivalent to a C+/B− on a letter scale. In these classes, a final grade of 1.5 to 1.7 or higher—a C− or better—is required to continue in the major. If URM or low-income students have average examination scores that are 0.4 to 0.6 grade points below the scores of other students (12), then underrepresented students are averaging grades that are in or under the 2.0 to 2.4 or C range—putting many at high risk of not meeting the threshold to continue. As a result, even a small increase in examination scores can lift a disproportionately large number of URM and low-income students out of the danger zone where they are prevented from continuing. The boost could be disproportionately beneficial for students from MGS even if average grades are still low, because URM students in STEM are less grade-sensitive and more persistent, on average, than non-URMs (11, 40). This grittiness may be based on differences in motivation, as students from MGS are more likely than students from non-MGS to be driven by a commitment to family and community (41–43).

It is critical to realize, however, that active learning is not a silver bullet for mitigating achievement gaps. In some of the studies analyzed here, active learning increased achievement gaps instead of ameliorating them. Although the strong average benefit to students from MGS supports the call for widespread and immediate adoption of active-learning course designs and abandonment of traditional lecturing (23, 36), we caution that change will be most beneficial if faculty and administrators believe that underrepresented students are capable of being successful (44) and make a strong commitment to quality in teaching. Here, we define teaching quality as fidelity to evidence-based improvements in course design and implementation. Fidelity in implementation is critical, as research shows that it is often poor (45–47). In addition, faculty who are new to active learning may need to start their efforts to redesign courses with low-intensity interventions that are less likely to improve student outcomes (Fig. 4). If so, the goal should be to persist, making incremental changes until all instructors are teaching in a high-intensity, evidence-based framework tailored to their courses and student populations (12, 39, 48).

We propose that two key elements are required to design and implement STEM courses that reduce, eliminate, or reverse achievement gaps: deliberate practice and a culture of inclusion. Deliberate practice emphasizes 1) extensive and highly focused efforts geared toward improving performance—meaning that students work hard on relevant tasks, 2) scaffolded exercises designed to address specific deficits in understanding or skills, 3) immediate feedback, and 4) repetition (49). These are all facets of evidence-based best practice in active learning (38, 50, 51). Equally important, inclusive teaching emphasizes treating students with dignity and respect (52), communicating confidence in students’ ability to meet high standards (53), and demonstrating a genuine interest in students’ intellectual and personal growth and success (54, 55). We refer to this proposal as the heads-and-hearts hypothesis and suggest that the variation documented in Fig. 2 results from variation in the quality and intensity of deliberate practice and the extent to which a course’s culture supports inclusion.

We posit that these head-and-heart elements are especially important for underrepresented students, who often struggle with underpreparation due to economic and educational disparities prior to college (55), as well as social and psychological barriers such as stereotype threat and microaggressions (56, 57). Our heads-and-hearts hypothesis claims that the effect of evidence-based teaching and instructor soft skills is synergistic for underrepresented students, leading to the disproportionate gains that are required to reduce achievement gaps (36, 57).

Why might deliberate practice and inclusive teaching be particularly effective for MGS? Our answer relies on three observations or hypotheses.

• 1)If students from MGS have limited opportunities for quality instruction in STEM prior to college compared to students from overrepresented groups, they could receive a disproportionate benefit from the extensive and scaffolded time on task that occurs in a “high-intensity” active-learning classroom. Data on the impact of active-learning intensity reported here is consistent with this deliberate practice element of the heads-and-hearts hypothesis.
• 2)For students from MGS, the popular perception of STEM professionals as white or Asian males, the fact of underrepresentation in most STEM classrooms, stereotype threat, and microaggressions in the classroom can all raise the questions, “Do I belong here?” and “Am I good enough?” All students benefit from classroom cultures that promote self-efficacy, identity as a scientist, and sense of belonging in STEM (58), and students in active-learning course designs that reduced or eliminated achievement gaps have reported an increased sense of community and self-efficacy compared to their peers in the lecture-intensive version of the same course (22, 23). Similarly, recent research on 150 STEM faculty indicated that the size of achievement gaps is correlated with instructor theories of intelligence. Small gaps are associated with faculty who have a growth or challenge mindset, which emphasizes the expandability of intelligence and is inclusion-oriented, while larger gaps are correlated with faculty who have a fixed mindset, which interprets intelligence as innate and immutable and is therefore exclusion or selection-oriented (44). It is not yet clear, however, whether a change in classroom culture occurs in active-learning classrooms because of the emphasis on peer interaction, changes in student perception of the instructor, or both.
• 3)Synergy between deliberate practice and inclusive teaching could occur if a demonstrated commitment to inclusion in an active-learning classroom inspires disproportionately more intense effort from students from MGS. In support of this claim, a general chemistry companion course that used psychological interventions to address belonging, stereotype threat, and other issues, combined with evidence-based study skills training and intensive peer-led group problem-solving, narrowed achievement gaps while controlling for self-selection bias (16).

Explicit and rigorous testing of the heads-and-hearts hypothesis has yet to be done, however, and should be a high priority in discipline-based education research.

Our conclusions are tempered by the limitations of the study’s sample size. Although our search and screening criteria uncovered 297 studies of courses with codable data on the overall student population, we were only able to analyze a total of 41 studies with data on students from MGS. Based on this observation, we endorse recent appeals for researchers to disaggregate data and evaluate how course interventions impact specific subgroups of students (13, 22, 34, 59, 60). Because our analyses of moderator variables are strongly impacted by sample size, we urge caution in interpreting our results on class size, course level, and discipline. Our data on type of active learning are also poorly resolved, because publications still routinely fail to report quantitative data on the nature of course interventions, such as records from classroom observation tools (e.g., ref. 61 and SI Appendix, Table S12). We are also alert to possible sampling bias in terms of instructor and institution type (SI Appendix). If many or most of the researchers who contributed data to the study also acted as instructor of record in the experiments, they may not be representative of the faculty as a whole. Specifically, they may be more likely than most peers to be both well-versed in the literature on evidence-based teaching and highly motivated to support student success. Finally, the existing literature overrepresents courses at research-intensive institutions and underrepresents teaching-intensive institutions. Our recommendation to pursue active learning in all STEM courses is tempered by the dearth of evidence from the community college context, where over 40% of all undergraduates—and a disproportionate percentage of students from MGS—actually take their introductory courses (62, 63).

Efforts to increase study quality and to intensify research on innovations that reduce achievement gaps should continue. Researchers have noted that “One is hard pressed to find a piece in academic or popular writings in the past century that does not use the word crisis to describe inequities in educational attainment” (ref. 37, p. 1; emphasis original). The data reported here offer hope in the form of a significant, if partial, solution to these inequities. Reforming STEM courses in an evidence-based framework reduces achievement gaps for underrepresented students and increases retention in STEM course sequences—outcomes that should help increase economic mobility and reduce income inequality.

Materials and Methods

Following earlier work, we define traditional lecturing as continuous exposition by the instructor with student involvement limited to occasional questions; we define active learning as any approach that engages students in the learning process through in-class activities, with an emphasis on higher-order thinking and group work (20, 64, 65).

The protocol for this study, presented in the PRISMA-P format (66) and including annotations regarding modifications that occurred during the course of the research, is available in SI Appendix, SI Materials and Methods. SI Appendix, Fig. S1 provides data on the number of sources that were found and evaluated at each step in the study. In brief, we screened 1,659 papers and other sources that were published or completed between 2010 to 2016 and coded 1,294 that compared active- versus passive-learning classrooms. We then contacted the authors of 210 sources that met the criteria for admission along with the authors of 187 sources included in an earlier metaanalysis (20). We received data disaggregated by student MGS status from 41 studies to include in our analysis.

Literature Search.

We searched both gray and the peer-reviewed literature for studies conducted or published from January 1, 2010, to June 30, 2016 that reported data on undergraduate performance in the same STEM course under traditional lecturing versus any form or intensity of active learning. We used five methods: hand-searching of journals, database searches, snowballing, mining reviews and bibliographies, and contacting researchers—both selected individuals and the broader community via listservs composed of educational researchers in each STEM discipline (refs. 67–69 and SI Appendix, SI Materials and Methods). For research conducted or published prior to 2010, we relied on studies admitted to a recent metaanalysis on how active learning impacts the performance of all students, using work that had been conducted prior to that date (20). That study used a search strategy and coding criteria that were almost identical to the approach used here (SI Appendix, SI Materials and Methods).

Criteria for Admission.

The study protocol established criteria for admitting research for potential coding (SI Appendix); these criteria were not modified in the course of the study (70). To be considered for coding, sources had to 1) contrast any form and intensity of active learning with traditional lecturing, in the same undergraduate course and at the same institution; 2) involve undergraduates in a regularly scheduled course; 3) focus on interventions that occurred during class time or recitation/discussion sections; 4) treat a course in astronomy, biology, chemistry, computer science, engineering (all fields), environmental science, geology, mathematics, nutrition or food science, physics, psychology, or statistics; and 5) include data on course assessments or failure rates.

During the original search, papers were collected based on information in the title and abstract. One of the coauthors (S.F.) then screened all of these papers against the five criteria for admission, based on evaluating information in the introduction, methods section, and any figures or tables. In cases that were ambiguous, the paper was referred to coders for a final check on criteria for admission.

Coding.

Each paper admitted to the coding step was evaluated independently by two of the coauthors. Coders then met to reach consensus on coding decisions for each element in the coding form established in the study protocol (SI Appendix).

In addition to making a final evaluation on the five criteria for admission, coders had to reach consensus on the data used in moderator analyses, including the STEM discipline, course level (introductory versus upper division), intensity of the active-learning intervention in terms of the percentage of class time devoted to student-centered activities (SI Appendix, Table S6), the type of active learning involved (SI Appendix, Table S12), and the class size.

Coders also evaluated information designed to minimize both within-study bias and across-study bias (66, 71):

• 1)To control for the impact of time on task, we excluded studies where class time per week was longer in the active-learning treatment.
• 2)To control for the impact of class size on performance, average class size could not differ by more than 25% of the larger class, unless the active-learning section was larger.
• 3)To control for examination equivalence, the assessment coded as an outcome variable had to be identical, formally equivalent as judged by an independent analysis performed by experts who were blind to the hypothesis being tested, or made up of questions drawn at random from a common test bank. We relaxed this criterion for studies that reported failure rates as an outcome variable, as a previous analysis showed that admitting studies with missing data on examination equivalence did not change conclusions regarding failure rates (20). In addition, faculty and administrators are often concerned about increasing pass rates in courses with traditionally high percentages of failing students, irrespective of changes in the type of assessment. Coders recorded the index of failure that was reported, which was usually DFW (D or F grades or a withdrawal) but sometimes one or a combination of those three outcomes (e.g., DF, or only F).
• 4)To control for student equivalence, either students had to be assigned to treatments at random or, for quasirandom studies, reports had to include data on the students in each treatment group—for example, their entrance examination scores, high school or college grade point averages, content-specific pretests, or other direct measures of academic preparedness and ability. We retained studies in which there was no statistically significant difference in the indices or in which students in the active-learning treatment were less well prepared, on average.
• 5)To assess the impact of instructor ability or experience on performance, the instructors in the treatments were coded as either identical, drawn at random from a pool, or within a group of four or more in both treatments (i.e., both were team taught).
• 6)If a study reported outcomes from multiple sections or classrooms of either the treatment or the control, coders reported performance from each section. Our statistical models accounted for the nonindependence of these data by standardizing examination scores, including an author main effect for data on passing rates, and including an Author–Section–Course random effect (SI Appendix).
• 7)To avoid pseudoreplication when a single study reported the results of multiple experiments—for example, of how studio course designs impacted student performance in more than one course—the coders identified comparisons of treatment and control conditions that were independent in terms of course or institution. Our models also controlled for nonindependence with an Author–Course fixed effect and/or an Author–Section–Course random effect (Materials and Methods).

If studies met the five admission criteria and the seven quality criteria just listed, but did not disaggregate data for overrepresented students versus URMs and/or low-income students, we contacted the authors by email to request their raw data on student outcomes and demographics. If the studies reported outcomes for student subpopulations but only in terms of means and SEs, we also contacted the authors to obtain raw, by-student data. Finally, we contacted authors if missing data were needed to complete other aspects of coding. In total, we contacted the authors of 297 studies, each of which met the criteria above. SI Appendix, Fig. S1 summarizes the number of papers screened, coded, and admitted.

As a final quality control step, one of the coauthors (M.J.H.) checked all studies and all codes against the original publication to resolve any inconsistencies or ambiguities, consulting with a second coauthor (E.T.) to resolve any uncertainty.

Instructors who shared data had institutional review board approval to do so from the source institution. All data were received with all personal and other identifiers removed.

Data Analysis.

The dataset used in the final analyses contained 9,238 student records from 15 independent studies with data from identical or formally equivalent examinations (32). Each study represented a specific course and active-learning intervention; the data came from five different STEM disciplines and included both introductory and upper level courses (SI Appendix, Table S14a). Because most studies reported data from multiple sections of the active-learning and/or traditional-lecture treatment, the data were clustered into 51 course sections. We used hierarchical models to account for the nonindependence of student groups (MGS and non-MGS) from a single classroom (ref. 72 and SI Appendix).

The final dataset also included records on 44,606 students from 26 independent studies with data on failure rates (33). The failure rate studies represented six different STEM disciplines and included both introductory and upper level courses (SI Appendix, Table S14b). Because most studies reported data from multiple sections of the active-learning and/or traditional-lecture treatment, the failure rate data were clustered into 174 course sections.

To estimate how much treatment affected achievement gaps between students from MGS and non-MGS, we fit models predicting student performance metrics (examination scores [y₁] and percentage passing [y₂]) in multilevel linear models, implemented in a hierarchical Bayesian framework. For the first outcome, we modeled the test score of each student i in section j and course k. To account for differences in the distribution of test scores across courses, we standardized these scores by each course k to produce a standardized test score (z score) for each student, $y_{1ijk}$; the assumption is that a 1-SD increase in test scores is comparable across courses. We then modeled these standardized examination scores (Eqs. 1 and 2) as a function of treatment at the section level (passive vs. active), ${\text{Trt}}_{jk}$, MGS status at the student level, ${\text{MGS}}_{ijk}$, and their interaction, clustering the errors by each combination of section j and course k:

$$y_{1ijk}\sim N\left({\mu }_{ijk},{\sigma }_{jk}^2\right),$$ [1]

$${\mu }_{ijk}={\beta }_0+{\beta }_1{\text{MGS}}_{ijk}+{\beta }_2{\text{Trt}}_{ijk}+{\beta }_3{\text{MGS}}_{ijk}\times {\text{Trt}}_{ijk}.$$ [2]

The coefficient of interest in Eq. 2, ${\beta }_3$, can be interpreted as the expected difference between active and passive classrooms in the achievement gap between students from MGS and non-MGS. Note that the reference category in Figs. 1A and 4A is close to the mean overall.

For the second outcome, passing rate, we modeled the percentage of students who passed from each student group g (MGS and non-MGS) in section j and course k, $y_{2gjk}$. It is not possible to standardize this outcome, so we accounted for differences in the distribution of passing rates $\left(y_{2gjk}\right)$ across classrooms by including an author effect and accounted for initial differences in achievement gaps in each author’s classroom by including interactions between the author of the study that includes course k, ${\text{Auth}}_k$, and student-level MGS status, ${\text{MGS}}_{gjk}$ (Eqs. 3 and 4). See SI Appendix for data justifying the decision to treat percent passing as a normally distributed variable.

$$y_{2gjk}\sim N\left({\mu }_{gjk},{\sigma }_{jk}^2\right),$$ [3]

$${\mu }_{gjk}={\beta }_0+{\beta }_1{\text{MGS}}_{gjk}+{\beta }_2{\text{Trt}}_{gjk}+{\beta }_3{\text{MGS}}_{gjk}\times {\text{Trt}}_{gjk}+{\beta }_4{\text{Auth}}_{gjk}\times {\text{MGS}}_{gjk}.$$ [4]

As before, the coefficient of interest in Eq. 4, ${\beta }_3$, can be interpreted as the expected difference between active and passive classrooms in the achievement gap between MGS and non-MGS students.

The gaps reported above and in the figures were calculated as MGS performance minus non-MGS performance, as is common in reporting gaps between underrepresented and overrepresented groups. Specifically, gaps in passive classrooms were calculated as follows:

$$\mathrm{Ga}{\mathrm{p}}_{\mathrm{passive}}=\left({\beta }_0+{\beta }_1\right)-{\beta }_0.$$ [5]

Gaps in active classrooms were calculated as follows:

$$\mathrm{Ga}{\mathrm{p}}_{\mathrm{active}}=\left({\beta }_0+{\beta }_1+{\beta }_2+{\beta }_3\right)-\left({\beta }_0+{\beta }_2\right).$$ [6]

Because these gaps were calculated using all 1,000 iterations from each of the four Markov chain Monte Carlo (MCMC) chains, the CIs around the gaps were calculated from all of the iterations as well.

To test the effects of active-learning intensity and other moderators on examination scores and percent passing, we fit models with a three-way interaction generalized as Trt × MGS × Moderator (SI Appendix). The coefficient on this three-way interaction is an indication of the size of the relative gap conditioned by the moderator in question. The performance of different students in these conditions can be calculated by summing coefficients in a similar manner as above; gaps can be calculated by subtracting non-MGS performance from MGS performance.

We modeled IPD for examination scores and individual section data for passing rates, instead of summarized or aggregated data from each study (34, 35, 73–76). IPD metaanalyses are considered the gold standard in metaanalyses because they afford several advantages over typical metaanalyses, which rely on group means or other types of aggregated data to calculate effect sizes. First, IPD metaanalyses provide substantially more statistical power. This increased power is particularly important for subgroups that are numerically small in any single study; our data on underrepresented students are notable in this regard (73, 74). Second, using IPD allowed us to implement consistent statistical methods across studies. For example, we were able to control for aggregation bias, which few published studies are able to do (35), by fitting multilevel models to account for 1) student nonindependence within classes and 2) the presence of data on multiple iterations of the same lecturing or active-learning treatment (Eqs. 2 and 4). Finally, by combining IPD from several studies, we were able to test novel hypotheses that cannot be tested with single studies alone, such as the effect of active-learning intensity.

We fit models in a hierarchical Bayesian framework, with unique sections of each course as a random effect. A course-section random effect accounts for the nonindependence of observations on multiple students or student groups from each section from each course (72). Note that in our dataset, a single author always contributed multiple sections (at a minimum passive and active treatments) and, in a couple of cases, multiple courses. Leave-one-out cross-validation model selection using loo and looic (76) in R package loo (77), on models that did not include author fixed effects, favored a section random intercept over more complex random-effects structures, including ones that accounted for nonindependence within authors (SI Appendix, Table S15 and S16). Furthermore, the variance parameters from the model that accounts for both section and author (0.161 and 0.048, respectively) confirmed that the addition of the author random intercept does not explain substantial additional variation. Finally, the residuals of the favored model (section random intercept only) do not vary systematically by author (SI Appendix, Table S17). Posterior predictive checks demonstrated that the model fit the data well (SI Appendix, Fig. S4).

Hierarchical Bayesian regression with a section random effect, in combination with weighting the percent passing estimates by the number of students of each type in each section, allows us to “borrow strength” across sections, while honoring the amount of information provided by each section. Finally, the Bayesian framework provides increased accuracy for comparisons between multiple groups by summarizing Bayesian posterior probabilities (78).

We fit all models in R, version 3.5.3 (79), using the rstanarm package (80). We used weakly informative default priors centered at mean 0 and SD 10. We ran three parallel MCMC chains of 1,000 each after burn-in time of 1,000 iterations, which was sufficient to ensure convergence, as judged by visual inspection of the chain histories and the Gelman–Rubin statistic (Rhat = 1.0 for all parameters in all models; ref. 81).

We also conducted sensitivity analyses to check for biases in our IPD. Specifically, we used visual inspection of funnel plot symmetry and the distribution of mean change in the achievement gap to assess the impact of the file drawer effect (Fig. 3), and leave-one-study-out analyses to test for undue impacts from single studies (SI Appendix, Fig. S3).

Data Availability.

All data used in the analyses are available at https://github.com/ejtheobald/Gaps_Metaanalysis.