Head Rotational Kinematics, Tissue Deformations, and Their Relationships to the Acute Traumatic Axonal Injury

Abstract

Head rotational kinematics and tissue deformation metrics obtained from finite element models (FEM) have the potential to be used as traumatic axonal injury (TAI) assessment criteria and headgear evaluation standards. These metrics have been used to predict the likelihood of TAI occurrence; however, their ability in the assessment of the extent of TAI has not been explored. In this study, a pig model of TAI was used to examine a wide range of head loading conditions in two directions. The extent of TAI was quantified through histopathology and correlated to the FEM-derived tissue deformations and the head rotational kinematics. Peak angular acceleration and maximum strain rate of axonal fiber and brain tissue showed relatively good correlation to the volume of axonal injury, with similar correlation trends for both directions separately or combined. These rotational kinematics and tissue deformations can estimate the extent of acute TAI. The relationships between the head kinematics and the tissue strain, strain rate, and strain times strain rate were determined over the experimental range examined herein, and beyond that through parametric simulations. These relationships demonstrate that peak angular velocity and acceleration affect the underlying tissue deformations and the knowledge of both help to predict TAI risk. These relationships were combined with the injury thresholds, extracted from the TAI risk curves, and the kinematic-based risk curves representing overall axonal and brain tissue strain and strain rate were determined for predicting TAI. After scaling to humans, these curves can be used for real-time TAI assessment.

1. Introduction

Traumatic brain injury (TBI) is a major cause of cognitive and behavioral deficits in the U.S. and worldwide and occurs in a variety of sports incidents, falls, or automotive accidents. The main driving cause of TBI is recognized to be the brain tissue deformations and axonal stretch caused by rapid head rotations and head biomechanical loadings [1]. The axonal and brain tissue deformation responses due to head rotational kinematic loadings can be quantified by reconstruction simulations using biofidelic brain finite element models (FEM). Therefore, rotational kinematics and FEM-derived tissue deformation metrics have the potential to predict and/or assess the risk of occurrence and extent of TBI at different accidental events and thus to be used as design criteria and evaluation standards for protective headgears. An important question is that whether and how accurately these metrics can estimate the risk and extent of TBI especially in case of diffuse microscopic damage such as traumatic axonal injury (TAI). TAI is one of the common pathological features of TBI, but it is a diffuse microscopic damage and the definite determination of its location and extension is still challenging in the clinical setting. Therefore, a practical approach to answer this question is to use animal models of TBI, in which the precise location and extent of TAI can be quantified through microscopic histopathology analysis after sacrifice.

Most of the current metrics used to evaluate the TBI mitigation performances of headgears in laboratory testing or to assess the TBI risk on-field through wearable sensor measurements are based on head kinematics while the TBI thresholds—determined by in vivo and in vitro studies, which assess the actual damage—are mainly based on tissue deformations. Therefore, other important questions are: whether and what relationships exist between head kinematic metrics and underlying axonal fiber and/or brain tissue deformations; and whether and how these relationships are dependent on head kinematic characteristics and rotational directions. In order to answer these questions and find kinematic metrics that are predictive of TBI, the relationships between kinematic metrics and tissue deformations need to be fully elucidated. There has been research investigating the relationships between the brain tissue strain and head impact kinematic parameters, but the effect of the head rotational kinematic characteristics on the underlying deformation rate, which has been shown by many in vitro and in vivo studies to greatly affect the extent of neuro-axonal injury [2–5], has not yet been explored. These relationships should be explored over a wide range of loading conditions and at different rotational directions to provide a generalized understanding of how the characteristic of head kinematics affects the axonal fiber and brain tissue deformation and deformation-rate responses. Such an investigation is important because head kinematic parameters of different sports such as soccer, American football, hockey, boxing, rugby, Australian football, and accidental events such as fall have demonstrated different characteristics in terms of magnitude and duration of brain motions within the skull [1,6–13]. For examples, as shown in Fig. 1, some accidental events such as standing fall, falls to ice in hockey, and unhelmeted head-to-head impacts in boxing produce high kinematic values in short duration while helmeted head impacts in football or head to padded shoulder/elbow impacts in hockey produces lower peak magnitude and longer duration [6–13]. Also, some studies have shown brain vulnerabilities to be dependent on head rotational direction [14–16]. A practical approach to answer abovementioned questions and determined such generalized relationships is to perform an FEM parametric study over a wide range of head angular loadings with different angular acceleration and angular velocity magnitudes at various rotational directions. These generalized relationships can better tailor head protection strategies and headgear design criteria and evaluation standards for each sport or accidental event according to their specific head impact loading characterizations.

Fig. 1.

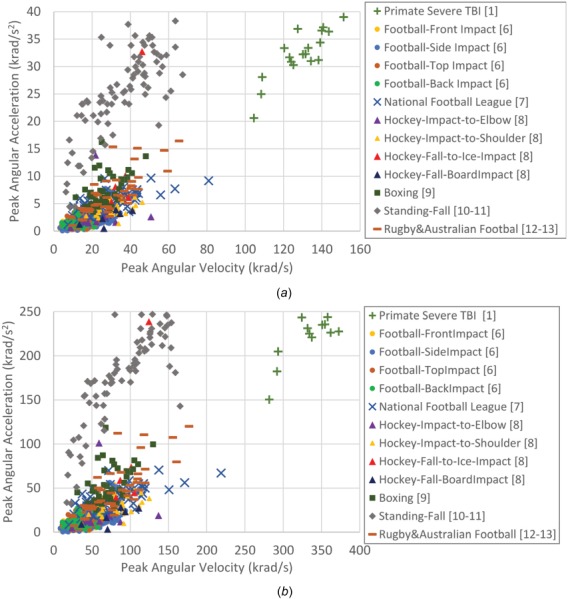
Examples of sport- or fall-related human head impact kinematics measured on-field [6,7,9] or reconstructed in laboratory [8,10–13] and primate TBI experiments that were previously performed for severe diffuse axonal injury [1] in (a) human scale and (b) all mass scaled to pig

In addition, these generalized relationships can be coupled with tissue injury thresholds determined from risk curves, commonly generated from animal experimental studies resulting in injury occurrence, to develop kinematic-based TBI criteria that are inspired by axonal/brain tissue deformation responses. There have been previous efforts to develop such injury tolerance criteria for severe diffuse axonal injury by linking head rotational loading conditions and brain tissue strain using analytical and physical skull models [1]. With advancements in imaging and computational modeling techniques, the biofidelity of the brain FEMs has improved, which makes the calculation of deformation response along the axonal tracts possible. In addition, many recent in vitro and in vivo studies, that examined the effect of strain and strain-rate on neuro-axonal damage, suggested that the extent of TBI is dependent not only on strain but also on strain rate. Therefore, there is a need to investigate and develop kinematic-based risk curves inspired by tissue deformation for mild TAI based on both strain and strain rate of brain tissue and axonal fibers by taking advantage of axonal tract embedding modeling technique. Such kinematic-based curves can be used for real-time TBI assessment using wearable sensor measurements as inputs.

We previously developed and evaluated an axonal tract-embedded anisotropic pig head FEM to simulate a set of well characterized pig TBI experiments [17]. We previously showed that the FEM-derived axonal fiber and brain tissue deformation parameters can successfully predict the presence and/or absence [17] and locations of acute TAI [18] following rapid head rotation. The distinct objectives of the current study were to: (1) determine whether those axonal and brain tissue deformation parameters and/or the head kinematic parameters can give an estimation of the extent or volume of acute TAI using the same FEM and set of animal TBI experiments; (2) quantify the possible interrelationships between the head angular kinematics and the axonal/brain tissue deformations for two head rotational directions over a wide range of loading conditions by performing FEM parametric study; and (3) utilize these interrelationships to determine tissue deformation-inspired head kinematic-based risk curves of TAI over wide range of loading conditions. As a follow-up to our previous study [17], in which the overall presence or absence of TAI was examined using the finite element (FE)-derived axonal/brain tissue deformation metrics regardless of rotational direction to determine the TAI thresholds, in this study, the volume of sustained TAI throughout the brain was measured and correlated to both the head angular kinematics and the FE-derived axonal/brain tissue deformations for each rotational direction separately and the effect of head rotational direction on such correlations was investigated using the same experimental dataset. In addition, the new FEM parametric simulations performed in this study provided the opportunity to extend these correlation investigations over a wider range of head loading conditions. The results of this study can help to determine kinematic characteristics that result in high axonal/brain tissue deformations, guide innovative head protection strategies and devices, and develop real-time TBI assessment tools.

2. Methods

2.1. Pig Traumatic Brain Injury Experiments, Head Kinematic Measurements, and Traumatic Axonal Injury Pathology Assessment.

For this study, a well-established diffuse TBI pig model was used to induce TAI in pigs' brain through single rapid nonimpact head rotation [14–16,19] about sagittal or axial plane, using a pneumatic actuator, with the center of rotation at the cervical spine. The 1- or 2-months pigs were anesthetized and while maintained on isoflurane, the pigs' heads were secured by a snout clamp to an inertial loading linkage connected to the pneumatic actuator. During the experiments, the pigs' heads rotated in a sagittal plane through a 60 deg arc (n = 23) or in axial plan through a 90 deg arc (n = 19) using the inertial loading linkage connected to the pneumatic actuator. The head angular velocity was directly measured by an angular rate sensor at sample rate of 10 kHz (ARS06, Applied Technology Associates, Albuquerque, NM) using a data acquisition system (National Instruments, Austin, TX). The angular acceleration was calculated by differentiating the angular velocity trace after proper smoothing and filtration. The angular velocity traces of the pig head rotations were filtered with a fourth-order, low-pass Butterworth filter with appropriate cut-off frequency selected from the power spectral density analysis of raw signals. The average and standard deviation of the selected cut-off frequencies for these 42 datasets was 281±71 Hz. The results of the filtration process used herein were similar to the results using CFC class 180 filtration, a fourth-order Butterworth low pass filter with a cutoff frequency of 300 Hz, which is common in biomechanics filed for angular velocity analysis [20]. The peaks of filtered angular velocity trace and calculated angular acceleration trace over the entire experimental rotational duration were extracted for each of the 42 experiments and shown in Fig. 2. The time histories of the filtered angular velocity traces were also extracted to be used as input for FEM simulations. The 42 pig TBI experiments that were selected for this study contain a wide range of peak angular velocity (89.54–203.14 rad/s) and peak angular acceleration (18.43–72.36 krad/s²).

Fig. 2.

Peak angular velocity and peak angular acceleration values for the axial (n = 19) and sagittal (n = 23) pig TBI animal experiments selected for this study

All protocols for these experiments were approved by the Institutional Animal Care and Use Committee of the University of Pennsylvania, where these experiments were previously conducted. Following the TBI experiments, pigs were sacrificed at 6 h postinjury, brains were perfusion-fixed and sectioned in coronal slices at every 3 mm. Each brain section was cut into 6 μm thick slices and stained for beta-amyloid-precursor-protein, and areas with positive axonal damage profiles were identified. To quantify the extent of acute TAI, the cumulative sum of marked axonal damage areas over all the brain sections throughout the whole brain was calculated as the axonal injury volume (AIV) for each animal expressed as a percentage of cerebral volume. The animals sustained different levels of TAI with AIV ranging from 0.02% to 1.65%, which represents levels of TBI from no/very minor with no significant behavioral or cognitive deficits, to mild TBI. In summary, peak angular velocity, peak angular acceleration, angular velocity time history, and AIV were extracted from each pig TBI experiment for further analysis.

2.2. Finite Element Simulation of Pig Traumatic Brain Injury Experiments and Finite Element Model-Derived Tissue Deformations.

To calculate the brain tissue and axonal fiber deformations experienced by the pig brains during these experiments, a newly developed and evaluated anisotropic multiscale axonal tract embedded pig brain FEM [17] was used to reconstruct those experiments using their measured angular velocity traces as input loading conditions. The brain deformation response obtained from this FEM was compared with the brain deformation measured in ex vivo hemisection experiment in a high strain and strain rate condition similar to the experiments used for reconstruction in this study and relatively good statistical correlation (p-value < 0.1) was observed between them [17]. This model can predict the overall presence/absence of TAI with 73–90% accuracy rate [17]. For each reconstruction simulation, the base pig brain FEM was scaled accordingly using the mass scaling approach (${\lambda }_x=\hspace{0.17em}{\lambda }_y=\hspace{0.17em}{\lambda }_z={\left(\frac{m_{\mathrm{animal}}}{m_{\mathrm{base}}}\right)}^{1/3})\hspace{0.17em}$[21]. All simulations were performed in LS-DYNA with temporal resolution of 0.1 ms. Axial strain of every axonal element and maximum principal strain (MPS) of every brain element at each time-step (0.1 ms) were extracted from each simulation. The strain rate was then calculated as the discrete derivative of the strain time history between time points for each element. Examples of spatial distribution of axonal fiber strains for an axial and a sagittal pig experiments with similar peak angular velocity conditions at six time frames throughout the whole-time window of simulations were shown in Fig. 3.

Fig. 3.

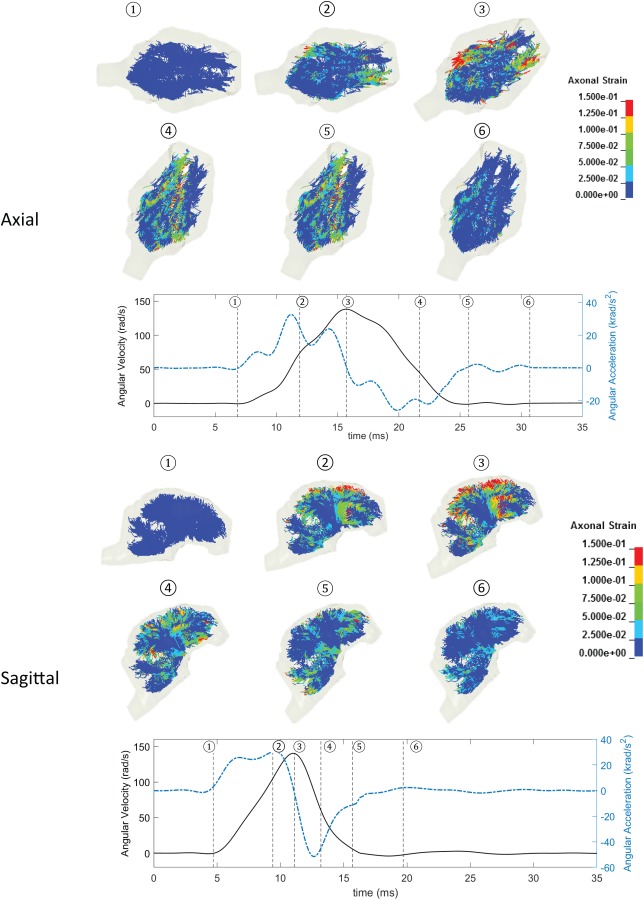
Spatial distribution of axonal fiber strains for an axial (top) and a sagittal (bottom) pig experiments with similar peak angular velocity conditions at six times frame throughout the whole-time window of simulations. Angular velocity traces (black solid lines) and angular acceleration traces (blue dashed lines) along with the six-time frames (dotted straight lines) are shown for these two examples.

For each simulation, the maximum values of stain, strain rate, and the product of strain and strain rate over the entire simulation period were calculated for each brain element and axonal fiber element. The 95th percentile maximum strain, strain rate, and strain times strain rate values, at or below which were experienced by 95% of the brain elements and axonal elements, were calculated as the overall MPS, maximum axonal strain (MAS), maximum principal strain rate (MPSR), maximum axonal strain rate (MASR), maximum principal strain times strain rate (MPSxSR), and maximum axonal strain times strain rate (MASxSR) extracted for each animal and used for further analysis. The 95th percentile maximum values were used instead of the largest (100th percentile maximum) values to eliminate any possible numerical noise.

2.3. Correlation Analysis.

Correlation analyses were performed between the kinematic parameters including peak angular velocity or peak angular acceleration extracted from the pig TBI experiments and the AIV from histopathology from each subject for each rotational direction separately and for both directions combined. Similar analyses were performed between the FEM-derived tissue deformation parameters including MAS, MPS, MASR, MPSR, MASxSR, and MPSxSR extracted from pig FEM simulations and AIV for this animal injury dataset. Correlation between AIV and each parameter was assessed using the correlation coefficient (R ²). A power function ($y=a\hspace{0.17em}{x}^b$) was employed in these analyses because this function showed higher correlation coefficients for the parameters examined than Gaussian, linear, and exponential functions. In addition, a linear surface contour was fit to the three-dimensional AIV, peak angular velocity, and peak angular acceleration results for all animals and the goodness of fit (R ²) were reported.

2.4. Finite Element Model Parametric Simulations.

In order to quantify the possible relationships between the head angular kinematics and the axonal/brain tissue deformations beyond the experimental loadings studied herein, a series of 104 simulations per direction were performed for axial and sagittal rotations for a wide range of angular loading conditions with different values of peak angular velocity and peak angular acceleration varied from 25–400 rad/s and 25–250 krad/s², respectively. This range was selected to cover the current and previous pig TBI experiments performed in our laboratory [14–16,19], sport- or fall-related human head impact kinematics measured on-field [6,7,9] or reconstructed in laboratory [8,10–13], and primate TBI experiments that were previously performed for severe diffuse axonal injury [1], all mass scaled to pig. For these parametric simulations, idealized full cycle sinusoidal angular acceleration signals were used as the loading traces. An example of these idealized traces is shown in Fig. 4(a). The head kinematic pulse durations (τ) for these parametric angular motion traces ranged from 0.6 to 100 ms. Because the parametric rotational traces were idealized full cycle sinusoidal, in which the pulse duration directly related to the peak angular velocity and acceleration values $(\frac{2\pi }{\tau }=\frac{\mathrm{peak}\hspace{0.17em}\mathrm{angular}\hspace{0.17em}\mathrm{acceleration}}{\mathrm{peak}\hspace{0.17em}\mathrm{angular}\hspace{0.17em}\mathrm{velocity}})$, only peak angular velocity and acceleration were reported from these traces. The range and distribution of loading matrix selected for the parametric simulations in this study was shown in Fig. 4(b).

Fig. 4.

(a) An example of the angular velocity and angular acceleration time histories of the idealized loadings used for FEM parametric simulations. (b) The range and distribution of loading matrix selected for the parametric simulations in this study.

Similar to the pig injury reconstruction simulations (described in Sec. 2.2), the rotational traces were applied to the rigid skull with the same center of rotation at a point in the neck, simulations were run longer than the rotational signals to let the brain to return to its initial undeformed state, and six deformation parameters including MAS, MASR, MASxSR, MPS, MPSR, and MPSxSR were extracted from each simulation. These FEM-derived deformation parameters were then related to the rotational kinematic parameters to establish kinematic-based tissue deformation response surface contour plots for both axial and sagittal rotational directions over wide range of loading conditions that were parametrically investigated in this study.

3. Results

Correlations between the kinematic parameters and sustained AIV from histopathology analysis were determined (Fig. 5). When data of the axial and sagittal directions were combined, poor correlation (R ² = 0.29) was observed between peak angular velocity and AIV (Fig. 5(a)). However, data from each of these directions separately showed fair correlation with AIV (R ² = 0.47 for sagittal and R ² = 048 for axial) and the correlation trends were dependent on the rotational direction (Fig. 5(a)). In contrary, peak angular acceleration from sagittal and axial rotations showed relatively good correlation to AIV (R ² = 0.53–0.63) with a similar trend for both directions (Fig. 5(b)), suggesting that correlation of peak angular acceleration experienced by the head and the resulting TAI may be less sensitive to the rotational directions. The multiple regression analysis for correlating the two kinematic parameters and the AIV was also performed for data from both directions combined (Fig. 5(c)). The coefficient of the peak angular acceleration parameter (0.02128) in the AIV correlation function was twenty times larger than the coefficient of the peak angular velocity (-0.00117). Power correlation analysis was also performed between FE-derived tissue deformation parameters including MAS, MPS, MASR, MPSR, MASxSR, MPSxSR, and AIV (Fig. 6). The analysis revealed relatively good correlations between MPSR and MASR with AIV (R ² = 0.48–0.56), which also were insensitive to rotational directions (Figs. 6(c) and 6(d)). On the other hand, the correlations of MPS and MAS with AIV were shown to be very different for the two rotational directions; both MPS and MAS showed high correlation with AIV for axial direction (R ² = 0.60–0.64) while no correlation was observed for sagittal direction (R ² ≤ 0.05). The correlations between MPSxSR and MASxSR with AIV (R ² = 0.36–0.57) were not as directional dependent as strain parameters and were not as directional independent as strain rate parameters.

Fig. 5.

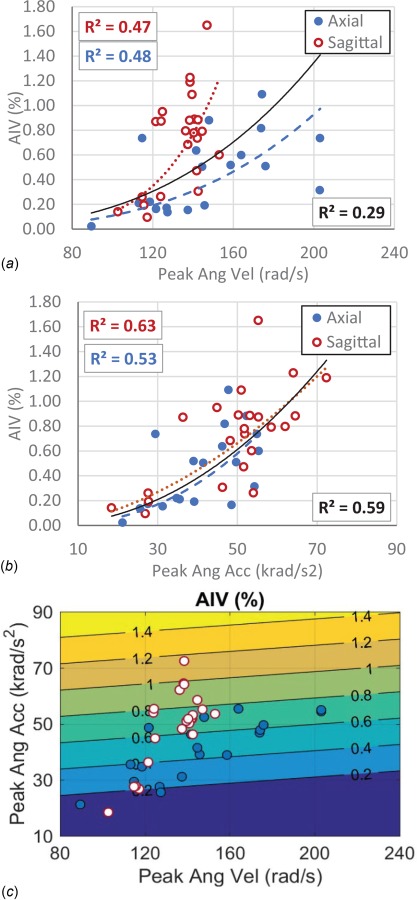
Correlation analysis between traumatic AIV and kinematic metrics including (a) peak angular velocity, (b) peak angular acceleration, and (c) combination of peak angular velocity and peak angular acceleration. The curves in graphs a and b represent the best power-fitting functions for the axial direction data (blue dashed curve), sagittal direction data (red dotted curve), and both directions combined (black solid curve). Coefficients of the power-fitting functions are also depicted in boxes in the graphs for whole dataset (right-bottom, in black), axial data (left-bottom, in blue), and sagittal data (left-top, in red). The function of the fitted AIV lines and the coefficient of correlation (R ²) in graph c are as follows: AIV (Peak Ang Vel, Peak Ang Acc) = -0.2265 - 0.00117* Peak Ang Vel + 0.02128* Peak Ang Acc), R ² = 0.52.

Fig. 6.

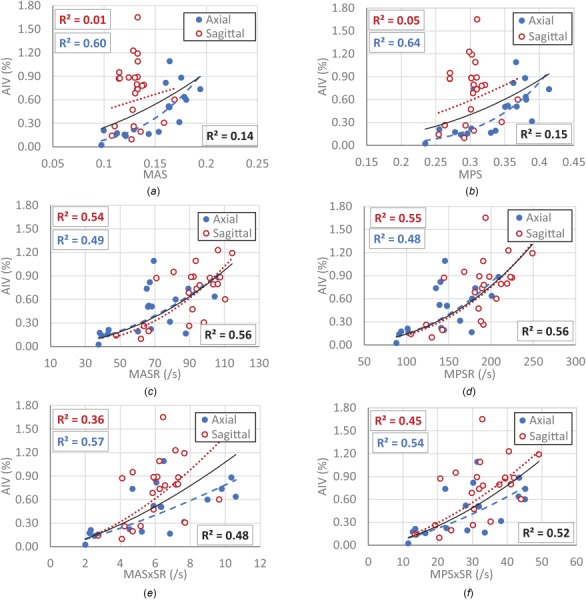
Correlation between traumatic AIV and FE-derived metrics including (a) MAS, (b) MPS, (c) MASR, (d) MPSR, (e) MASxSR, (f) MPSxSR. The curves in each graph represent the best power-fitting functions for the whole data combined (black solid curve), data with axial rotation (blue dashed curve), and data with sagittal rotation (red dotted curve). The square of the correlation coefficients (R ²) showing the goodness of fit of the power-fitting functions are also depicted in boxes in the graphs for whole dataset (right-bottom, in black), axial data (left-bottom, in blue), and sagittal data (left-top, in red).

The relationships between kinematic metrics and the axonal fiber and brain tissue deformation metrics in the pig TBI experiment dataset were also examined using linear regression analysis (Fig. 7). The results showed that, in the loading regimes and characteristics applied in the animal TBI experiments, the peak angular acceleration was highly correlated to MASR and MPSR (Figs. 7(e) and 7(k)) for both axial (R ² = 0.67–0.73) and sagittal (R ² = 0.92–0.96) rotations, and the trend of the correlations were similar for both rotational directions. The linear correlation between the peak angular velocity and MPS (R ² = 0.57–0.75) and MAS (R ² = 0.43–0.67) were also relatively good and the correlation trends were similar for both directions (Figs. 7(a) and 7(g)). However, peak angular acceleration showed correlation to MPS (R ² = 0.82) and MAS (R ² = 0.78) only for axial direction, but not for sagittal direction.

Fig. 7.

Correlation between FE-derived metrics including ((a) and (d)) MAS, ((b) and (e)) MASR, ((c) and (f)) MASxSR, ((g) and (j)) MPS, ((h) and (k)) MPSR, and ((i) and (l)) MPSxSR and rotational kinematic metrics including peak angular velocity and peak angular acceleration for axial (blue dashed lines) and sagittal (red dotted lines) rotational directions. The goodness of the fit (R ²) are depicted in the boxes in the graphs for axial data (left-bottom boxes, in blue) and sagittal data (left-top boxes, in red).

To explore the relationships between head rotational kinematic metrics and the axonal/brain tissue metrics beyond the loading range and characteristics applied in the animal experiments, a matrix of head rotational movements over a wide range of possible loading conditions and characteristics observed in different sports and head impact accidental events were parametrically simulated, as described in Sec. 2.4, for axial and sagittal directions. It should be noted that same loading traces were used for both axial and sagittal simulations. The relationships between axonal fiber and brain tissue deformation metrics including MAS, MASR, MASxSR, MPS, MPSR, and MPSXSR and rotational kinematic metrics including peak angular acceleration and peak angular velocity were determined through surface fitting and resulted in high goodness of fit (R ² ≥ 0.99). The surface contour curves were given in Fig. 8. Each contour curve represents a constant level of a tissue deformation metric as a function of peak angular acceleration and peak angular velocity applied to the head.

Fig. 8.

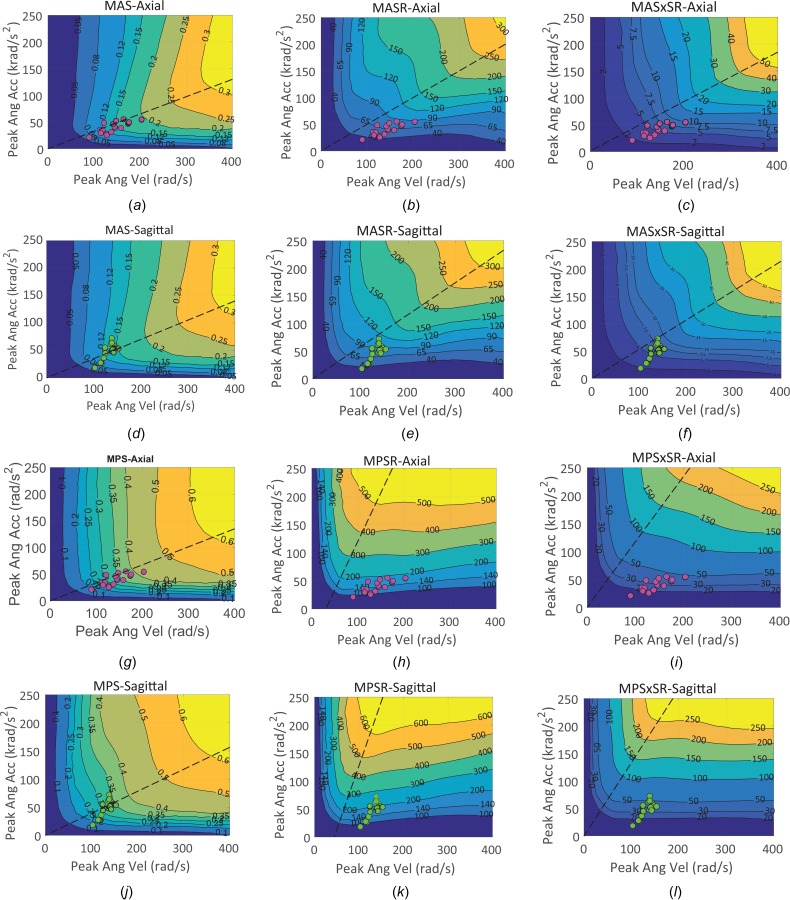
Relationships between the FE-derived tissue deformation metrics including MAS, MASR, MASxSR, MPS, MPSR, and MPSxSR and head kinematic parameters including peak angular acceleration and peak angular velocity for axial ((a)–(c) and (g)–(i)) and sagittal directions ((d)–(f), and (j)–(l)). The axial (pink markers) and sagittal (green markers) pig TBI experiments were also shown on the tissue deformation contours. An approximate partitioning line around which the concavity of the contour lines changed was drawn with black dashed line in each plot.

These kinematic-based tissue deformation contour curves were also combined with the results of the TAI risk curves that we previously developed [17] and contour curves corresponding to 10%, 25%, 50%, 75%, and 90% likelihood of sustaining TAI for both axial and sagittal directions (Fig. 9) were derived for all of the six tissue deformation metrics used in this study. The 10–90% tissue injury threshold values, extracted from the previously developed binary logistic regression TAI risk curves [17], are given in Table 1. In addition, the kinematic-based TAI risk curves at the 50% likelihood were compared between strain and strain-rate related parameters for axial and sagittal as shown in Fig. 10 (top row). These results were scaled to the human head kinematics using mass scaling approach $({\lambda }_{\omega }=({\frac{m_{\mathrm{pig}-\mathrm{brain}}}{m_{\mathrm{human}-\mathrm{brain}}})}^{\frac{1}{3}}=0.370, {\lambda }_{\alpha }=({\frac{m_{\mathrm{pig}-\mathrm{brain}}}{m_{\mathrm{human}-\mathrm{brain}}})}^{\frac{2}{3}}=0.137)$. In some loading conditions, strain-related TAI risk curves were more conservative while in many other loading conditions the strain-rate-related TAI risk curves were more conservative. For example, at the same peak angular acceleration, strain rate-related curves were predicted TAI at lower peak angular velocity than strain-related curves.

Fig. 9.

The FEM-derived tissue deformation inspired kinematic based TAI risk curves. The curves in each graph represent the 10%, 25%, 50%, 75%, and 90% likelihood of TAI based on (a) MAS, (b) MPS, (c) MASR, (d) MPSR, (e) MASxSR, and (f) MPSxSR and tissue deformation metrics for sagittal (red solid lines) and axial (blue dashed lines) rotational directions.

Table 1.

Averages of the FE-derived tissue deformation TAI thresholds derived from the 50-repetitions fivefold binary logistic regression risk curves [17]

Pig dataset	10% likelihood threshold	25% likelihood threshold	50% likelihood threshold	75% likelihood threshold	90% likelihood threshold
MAS	0.089	0.1048	0.1207	0.1365	0.1524
MASR (s−1)	47.03	56.7	66.4	76.1	85.8
MASxSR (s−1)	3.5	4.2	4.9	5.4	6.3
MPS	0.2298	0.2575	0.2852	0.3129	0.3405
MPSR (s−1)	103.49	122.12	140.76	156.39	178.03
MPSxSR (s−1)	17.1	21.0	24.9	28.8	32.7

Fig. 10.

50% tissue deformation inspired kinematic-based TAI injury risk curve as a function of peak angular acceleration and peak angular velocity derived based on axonal fiber deformation metrics (left plots) including MAS (solid line), MASR (dashed), and MASxSR (dashed–dotted) and brain tissue deformation metrics including MPS (solid line), MPSR (dashed), and MPSxSR (dashed–dotted) for pig. Similar curves for human were generated by mass scaling of pig to human kinematics. In all plots, the solid gray areas illustrate the kinematic conditions that passed 50% risk of TAI using both strain and strain-rate tissue deformation metrics and patterned areas illustrate the areas that strain and strain-rate metrics predict injury differently.

4. Discussion

4.1. Correlation of Tissue Deformation Responses and Head Rotational Kinematics With the Extent of Traumatic Axonal Injury.

Several kinematic-based and FEM-derived tissue metrics have been proposed over the years [17,22–24]; however, the correlations of these metrics with the extent of TBI have not been investigated, mainly due to the paucity of detailed volume and extent of injury data in real-world head trauma and many animal studies. In this study, a well-characterized pig model of TBI was used to apply a wide range of rotational loading in axial and sagittal directions to the pigs' heads and the volume of axonal damage was precisely quantified acutely (≤6h) after the head rotations. The AIV were then correlated with head kinematic metrics including peak angular acceleration and peak angular velocity and with FEM-derived tissue metrics including MAS, MASR, MASxSR, MPS, MPSR, and MPSxSR. The AIV showed higher correlation to peak angular acceleration than peak angular velocity. For instance, in the two cases experiencing similar peak angular velocity (∼150 rad/s) as shown in Fig. 3, the sagittal case, which had higher peak angular velocity (52 krad/s²) sustained larger AIV (0.78%) in comparison to the axial case (AIV = 0.15%), which had smaller peak angular acceleration (31 krad/s²). In addition, the AIV showed higher correlation to the axonal fiber and brain tissue strain-rate related metrics (MASR and MPSR, R ² = 0.56, and MASxSR and MPSxSR, R ² = 0.48–0.52) than the strain-related metrics (MAS and MPS, R ² ≤ 0.15) for all data combined. Similar correlation trends were observed between MASR and MPSR with AIV for both rotational directions. These results suggest that the tissue deformation rates are better for estimating the extent of TAI than the tissue deformation responses. Notably, the most common FEM-derived tissue metrics used in injury biomechanics to assess the likelihood of TBI and concussion are MPS, cumulative strain damage measure, and more recently MAS that are based on the axonal/brain tissue strain [25–28] and do not incorporate the rate of tissue deformations. The results of this study stress the importance of including strain rate-based tissue injury metrics for assessment of TBI in future studies.

The TBI metrics are commonly developed based on binary injury data to assess absence or presence of TBI. However, the relatively good correlations of peak angular acceleration, MASR and MPSR with AIV observed in this study suggest that these metrics are good candidates for estimating the extent of TBI. Moreover, the correlations of the FEM-derived axonal fiber and brain tissue strain-rates and peak angular acceleration with the extent of TAI were shown to be less sensitive to rotational direction, at least in the head rotational kinematic ranges and characteristics applied in this study which, when scaled to humans, are similar to the head impact conditions measured in sports such as football and hockey. The similar trends of the correlation of these metrics to AIV for different rotational directions make them good candidates for assessment of TBI in the real-world head trauma where the head impact incidents are mostly multidirectional.

4.2. Generalized Relationships Between Tissue Deformation Responses and Head Rotational Kinematics.

There have been studies investigating the relationships between the brain tissue strain and head impact kinematics [14,17,22–24,29] but the effect of the head kinematic characteristics on the underlying tissue strain-rate, which has been shown by many in vitro and in vivo studies [2–5] to highly affect the extent of neuro-axonal injury, has not been yet determined. In this study, we experimentally and parametrically investigated and demonstrated the relationships between head angular velocity and acceleration to strain, strain rate, and product of strain and strain rate of axonal fiber and brain tissue over a wide range of possible head kinematic conditions. The results, shown in Figs. 7 and 8, illustrated that both head angular velocity and acceleration affect the underlying deformation responses (strain and strain-rate related parameters) of the axonal fiber bundles and brain tissue and thus the knowledge of both of these kinematic metrics can help to better predict the risk of brain injury at different head loading conditions.

The generalized kinematic-based tissue deformation surface plots (Fig. 8), obtained through parametric simulations herein, can explain the correlation results, and their directional similarities or differences, that were observed in the pig TBI experiments (Figs. 5–7) as explained in Sec. 4.1. These plots show that the relationships between head kinematic and underlying tissue deformations are dependent on head loading conditions and overall are nonlinear. However, in some loading conditions, linear relationships may be observed similar to some relationships shown in Fig. 7 for experimental dataset in this study. These generalized relationships may also be dependent on other factors such as modeling technique and material models and properties; however, investigation of the effect of these factors was outside the scope of this study. The common feature in the kinematic-based tissue deformation surface plots (Figs. 8(a)–8(l)) was a partitioning line around, which the concavity of the contour lines changed. The contour curves were more tilted toward vertical lines on the left side of this line where short duration loadings were located and the MAS, MPS, MASR, MPSR, MASxSR, and MPSxSR responses were dominated by the change in peak angular velocity. In contrast, on the right side of the partitioning line where the long duration loadings were located, the contour curves were more horizontally oriented, and the deformation responses were dominated by the changes in peak angular acceleration. Along this partitioning line, the tissue deformation responses were correlated to both peak angular velocity and peak angular acceleration. The previous studies that modeled the strain response of brain tissue to the rotational head motion by a single‐degree‐of‐freedom mechanical system determined that the slope of the partitioning line for MPS contour curves was inversely related to the natural frequency of such a system [28]. Interestingly, all of our axial pig TBI experiments were along the partitioning line of the MAS and MPS contours, obtained from parametric study, for axial direction (Figs. 8(a) and 8(g)), which confirmed that the MAS and MPS responses of the pig axial TBI experiments correlated to both peak angular velocity and peak angular acceleration (Figs. 7(a), 7(d), 7(g), 7(j), R ² = 0.67–0.82). On the other hand, the majority of our sagittal pig TBI experiments were located on the left side of the MAS/MPS contour partitioning line for sagittal direction (Figs. 8(d) and 8(j)), which explains why higher correlations were observed between MPS/MAS with peak angular velocity (Figs. 7(a) and 7(g), R ² = 0.43 and 0.57) than with peak angular acceleration (Figs. 7(d) and 7(j), R ² = 0.06 and 0.11). In contrast, the strain-rate results of all the pig TBI experiments (axial and sagittal) were located on the right side of the partitioning line of the parametric MASR/MPSR response contours which explains why the MASR and MPSR responses of the pig axial TBI experiments were correlated more to the peak angular acceleration (R ² = 0.92–0.96 and R ² = 0.68–0.73) than to the peak angular velocity (R ² = 0.55–0.71 and R ² = 0.22–0.26) for both axial and sagittal directions. Overall, the partitioning lines for MASR and MPSR contours were more tilted toward the peak angular acceleration axis; thus the strain rate-related metrics were more correlated to the peak angular acceleration than peak angular velocity for all the pig TBI experiments and head impacts measured in real-world trauma (Fig. 1). The partitioning lines for MAS and MPS contours were more tilted toward the peak angular velocity axis. The rotational loading conditions examined experimentally in this study, and many head impacts measured in real-world trauma (Fig. 1) are located either on or on the left side of the MAS/MPS partitioning line and thus their MAS and MPS responses are expected to be either more dependent on peak angular velocity than peak angular acceleration or dependent on both.

The directional differences in the sustained TAI that were observed in the pig TBI experiments in this study might have been caused by the difference in the kinematic characteristics of the applied head loadings for axial and sagittal pig TBI experiments and/or the brain anatomy and inertial differences in axial and sagittal planes. Overall, in terms of head loading characteristics, the sagittal pig TBI experiments had higher ratio of peak angular acceleration to peak angular velocity than the axial pig TBI experiments (Fig. 2) because they went through a shorter angular trajectory (60 deg for sagittal compared to 90 deg for axial) due to anatomical restriction. Comparing the kinematic-based deformation curves obtained from parametric simulations (Figs. 8 and 9) between sagittal and axial directions, in which the same loading characteristics were applied for both directions, showed similar or slightly higher overall strains and strain rates for sagittal rotations than axial rotations. These results suggest that the higher injury susceptibility for sagittal direction in comparison to axial direction as observed in this pig model of TBI in many studies [14–16] was highly affected by the difference in the kinematic characteristics of the loading conditions applied in these two directions.

Overall, determining generalized head kinematic and tissue deformation relationships is particularly important because each head impact incident produces distinct kinematic loading characteristics in terms of magnitude and duration, which can result in specific levels of tissue deformation and deformation rates. For example, many short duration events such as head impacts in boxing or fall-related head impacts occur more on the left side of the MAS/MPS partitioning line where the tissue strain responses were expected to be more dominated by peak angular velocity than peak angular acceleration. These generalized head kinematic and tissue deformation relationships obtained in this study can guide tailoring headgear design and evaluation criteria for different sports or accidental events based on their specific head kinematic conditions. Different head protection can also change the head kinematic characteristics and thus influence axonal/brain tissue deformations due to impacts. For example, the ratio of peak angular acceleration to peak angular velocity was shown to decrease from unprotected to helmeted and then to well-padded impact conditions such as head impacts to elbow and shoulder pads [30].

4.3. Tissue Deformation Inspired Head Kinematic-Based Traumatic Axonal Injury Risk Curves.

Although the magnitude and rate of axonal and brain tissue deformations have been shown to be the leading cause of TBI, the TBI risk metrics are commonly based on head kinematics, as these metrics have the advantage of low computational cost and capability of real-time assessment of potential injury. In this study, the generalized tissue deformation surface contours were combined with the tissue injury thresholds extracted from the traditional risk curves, recently developed using the same dataset and the anisotropic axonal tract embedded brain FEM for predicting likelihood of TAI occurrence [17]. Then the kinematic-based risk curves representing overall axonal and brain tissue strain, strain rate, and strain times strain rate were determined for 10% to 90% likelihood of sustaining TAI for pigs. These curves were then scaled to human kinematics.

These kinematic-based tissue-deformation-inspired risk curves for axial and sagittal directions were similar in some head loading conditions and slightly different at other loading conditions (Fig. 9). Overlapping the kinematic-based strain, strain rate, and strain times strain rate-related TAI risk curves over the wide range of head kinematics mainly emphasizes the importance of head impact loading characteristics on TBI assessments. The kinematic-based tissue strain and strain-rate inspired risk curves were quite different at some kinematic ranges and characteristics. At the loading conditions with short time durations and thus higher ratio of peak angular acceleration to peak angular velocity, the strain rate-related TAI curves (MASR, MASxSR, MPSR, and MPSxSR) predicted injury at smaller peak angular velocity than the strain-related curves (Fig. 10). However, the strain-related metrics were slightly more conservative than strain rate-related curves for long duration head impact events (Fig. 10). Interestingly, some of the head kinematics in different sports measured in real-world incidents fall at the intersection of the strain and strain rate-related TAI risk curves, scaled to humans (Figs. 10(c) and 10(d)). When only the data along this intersection are used for TBI and concussion risk development, similar prediction performance of tissue strain and strain rate may be found. Additional kinematic and injury data, particularly at the loading conditions where the kinematic-based strain and strain rate-related curves are more disperse, are important to be included and can help to better guide TBI assessment and the risk curve development process.

4.4. Limitations and Directions for Future Research.

In this study, parametric simulations were performed unidirectionally using idealized full cycle sinusoidal angular traces. Although the sinusoidal traces are common signals for parametric studies in the injury biomechanics field, these signals may not capture all the complexity and characteristics of head impact kinematics in real-world incidents. Therefore, the effect of different signal shapes in a range of possible multidirectional head motion conditions on the relationships between head kinematics and underlying tissue deformations in real-world trauma deserves to be explored in future studies. Furthermore, in this study, the kinematic-based tissue response plots and injury curves were developed for the overall maximum strain and strain rate experienced by brain tissue and axonal fiber tracts during a head rotational movement and cannot estimate the brain regional deformation responses. Future studies should investigate the relationships of head kinematics to the regional (or region-specific) tissue responses. In addition, the kinematic ranges and characteristics of the pig TBI experiments used for this study and other studies using this pig model of TBI mainly fell on or very close to the MAS/MPS partitioning line. Although, these experiments when scaled to humans cover some loading conditions in real-world trauma, the head loading conditions in different sports, falls, or automotive-related head impact incidents occur at wide kinematic ranges and characteristics. Animal experiments with head kinematics beyond this study are worthy to be investigated in future TBI studies for development of more generalized metrics and risk curves.

Funding Data

• •Biomechanics Consulting and Research, LLC (BioCore, LLC).
• •National Institutes of Health (R01NS097549 and R56NS055951; Funder ID: 10.13039/100000002).