Association of Placental Jets and Mega-Jets With Reduced Villous Density

Abstract

Spiral arteries (SAs) lie at the interface between the uterus and placenta, and supply nutrients to the placental surface. Maternal blood circulation is separated from the fetal circulation by structures called villous trees. SAs are transformed in early pregnancy from tightly coiled vessels to large high-capacity channels, which is believed to facilitate an increased maternal blood flow throughout pregnancy with minimal increase in velocity, preventing damage to delicate villous trees. Significant maternal blood flow velocities have been theorized in the space surrounding the villi (the intervillous space, IVS), particularly when SA conversion is inadequate, but have only recently been visualized reliably using pulsed wave Doppler ultrasonography. Here, we present a computational model of blood flow from SA openings, allowing prediction of IVS properties based on jet length. We show that jets of flow observed by ultrasound are likely correlated with increased IVS porosity near the SA mouth and propose that observed mega-jets (flow penetrating more than half the placental thickness) are only possible when SAs open to regions of the placenta with very sparse villous structures. We postulate that IVS tissue density must decrease at the SA mouth through gestation, supporting the hypothesis that blood flow from SAs influences villous tree development.

1. Introduction

The uterine SAs play a key role in the supply of nutrients to the placenta in pregnancy. They are dynamically converted in early gestation via an invasion of placental cells called trophoblasts that extend out from the developing placenta and invade the decidualized maternal endometrium (decidua) in which the SAs reside. At the start of pregnancy, the SAs are narrow tortuous vessels surrounded by a functional smooth muscle layer. However, in the early stages of pregnancy (typically from 5 to 18 weeks [1,2]), the SAs are invaded by trophoblasts, which destroy the musculoelastic tissue in the walls of the SAs (see Refs. [2–4] for reviews of the process). Figure 1(a) shows typical remodeling of a SA; as trophoblast colonize the artery they act to both transiently plug the arterial lumen, and to transform the arteries into wide funnel-like structures. Figure 1(b) shows a schematic of hypothesized blood flow through the IVS from a transformed SA. The remodeled SA shape is thought to allow significant volumetric blood flow with low flow velocities and pressure to prevent any damage to the delicate villous structure. Inadequate conversion of the SAs and pathology of the placental tissue distal to these arteries has been linked to pathologies such as pre-eclampsia [5,6], intrauterine growth restriction (IUGR) [5,7], and preterm birth [6]. However, there is some debate as to how SA blood flow influences the placenta in pathology, with mechanical stress [8], and oxidative stress due to ischemia–reperfusion injury because of a retention of smooth muscle [8,9], being cited as possible explanations.

Fig. 1.

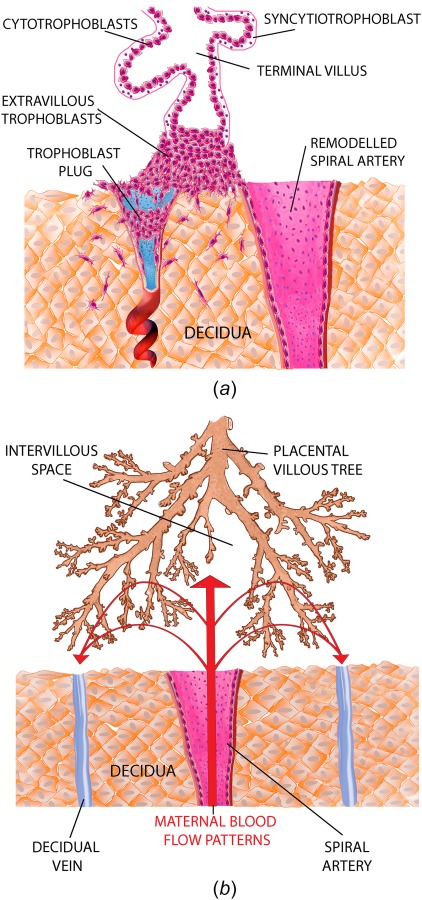
(a) The progression of SA remodeling. At the start of pregnancy SAs are small tortuous vessels and they are progressively remodeled by trophoblast to have large funnel-like openings. (b) Flow from SAs enters the intervillous space and supplies placental tissue with nutrients. Inadequate SA remodeling has been theorized to induce an excessive blood flow velocity and pressure on the placental tissue.

As the extent of SA remodeling in humans is relatively unique within the animal kingdom, and studies in humans are limited by obvious ethical constraints, most studies of SA remodeling in early pregnancy are conducted in vitro using histological sections [1,5,7]. The SAs are small and tortuous; limited measurements have been made but published values are approximately 400 μm diameter [8]. Reliable ultrasonographic measurement of blood flow at the interface between the uterine circulation and the placenta has therefore been difficult to achieve. However, in recent years, a validated ultrasonographic method to measure flow velocities at the SA opening, and to estimate the distance that blood flow penetrates into the IVS, has been developed [10,11]. Using this methodology, the blood flow from typical SAs has been described as “jets.” The width of a jet is assumed to correlate with the size of a SA opening. These jets of flow appear to resemble the patterns of flow into the IVS that have been previously estimated from histological specimens and simple computational models [8]. Typically, three or four jets of interest are measured in an individual, but in some individuals, attempts have been made to measure each SA jet. In these cases between 29 and 32, jets with similar flow properties were measured in individuals [10].

In addition to jets of flow that appear to correspond to normal SA remodeling observed in histology, ultrasound also identifies “mega-jets” of flow into the IVS. These mega-jets appear to penetrate further into the placenta than normal jets and frequently terminate in placental lakes (low density regions of the placenta with little blood circulation) [11]. The origin of the mega-jets is uncertain, but they may arise from the accumulation of multiple SAs feeding into one opening producing a higher than usual flow rate [11]. The relationship between mega-jets and placental tissue is also uncertain. For example, as their association with placental lakes increases over pregnancy, do high flow jets influence the development of the placental villous structure regionally?

Simple computational models have been used previously to understand the nature of blood flow from SA openings [8], but these models neglected the tissue lying distal to the SAs. At term, blood flow in the IVS has previously been modeled as flow through a porous medium [12,13]. Some studies have assumed uniform porosity and others allowed for “cavities” near to the SA opening, reflecting the possible interaction between SAs and the placental tissue. However, all studies considered the SA opening to be a point source. To our knowledge, no one has examined on how a change in dimension of the SA that is predicted to occur as a result of vessel remodeling, influences the jet-like flows or how these flows are influenced by changes in placental tissue density with gestation, nor the potential differences in jets or mega-jets that are observed in ultrasonography. Here, we present a computational model of flow from the opening of a maternal SA into a placentome through gestation. We show how an increase in placental tissue density through pregnancy results in an overall decrease in penetration of blood from the maternal SAs to the placenta, despite an increase in overall blood flow rates. We also postulate how the volume fraction occupied by villous trees (ψ), or the presence and size of a central cavity, may be indicated by ultrasonographic placental jet properties.

2. Materials and Methods

2.1. Geometric Model.

We consider blood flow in a single placentome (a placental functional unit supplied by a single SA), which in previous computational models has been assumed to be a two-dimensional square [12,14] and a hemisphere [13]. We assume a cuboidal placentome shown in Fig. 2, which implicitly assumes that the placenta can be approximated as uniform in width over the area comprising a single placentome. We assume that the placentome has thickness Z_L, and dimensions (X_L, Y_L) in its cross section parallel to its basal and chorionic plates, and there are n_p placentomes that make up the placenta. The value of n_p is dependent on the number of SAs and ranges from 30 to 100 [15,16]. Total placental volume [17] and thickness (Z_L) [18] have been calculated through gestation, and assuming each SA supplies an equal volume of placenta, and that X_L = Y_L allows determination of the dimensions of an average placentome through gestation.

Fig. 2.

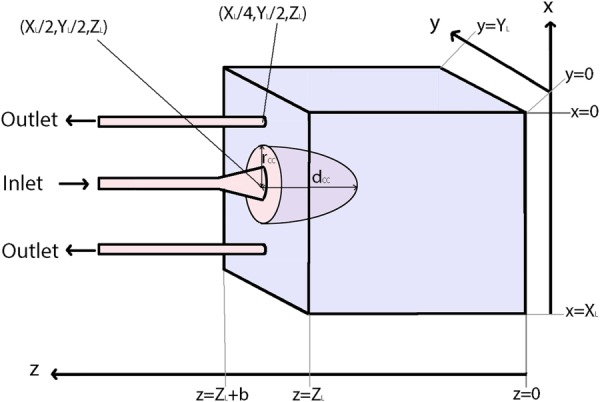
A schematic of the idealized placentome represented in our model. Geometric parameters are dependent on gestational age.

There have been few quantitative studies on the size and number of uterine veins that drain maternal blood from the placenta. Therefore, we follow previous studies [14] and assume that each SA is accompanied by two decidual veins (DVs) draining the placentome. We model the SA opening following Burton et al. [8] as a cylindrical tube with a funnel-shaped opening supplying the placentome with blood. The SA is located at the center of the placentome ($X_L/2,\hspace{0.17em}{Y}_L/2$, Z_L), and the veins are placed symmetrically with respect to the SA along a line joining the artery to the center of the placentome edge (Fig. 2). Assuming that the SA is remodeled along a distance b, then SA radius (r) in the remodeled section, between z = Z_L and $z=Z_L+b$, is assumed to follow $r=r_0+c(Z_L+b-z)$, where r₀ is the radius of the unremodeled portion of the SA, and c is a constant [8]. There are few measurements in the literature of venous caliber, and so, the radius of the draining veins is assumed to equal the radius of the unremodeled part of the SA r₀.

2.1.1. Central Cavity.

A “central cavity,” or villus-free region near the spiral artery opening, is included in the model geometry by assuming a hemi-ellipsoid at the mouth of the SA to be devoid of tissue (Fig. 2). The major axis of the central cavity is along the z-axis and centered on the SA mouth. The short-axis radius of the central cavity (r_CC) is assumed constant in the x–y plane, and as the radius of the central cavity is unknown two values were considered. The first assumes that the central cavity sits directly around the mouth of the SA, and the second assumes that the central cavity sits a constant 0.5 mm beyond the opening of the SA. The depth of the central cavity (d_CC) is unknown and thus varied from zero length (no central cavity) to the entire thickness of the placenta.

2.1.2. Changes in Placental Tissue Through Gestation.

The tissue within the placentome beyond the opening of the SAs comprises the villous tree (a branching network of tissue containing placental arteries and veins) and intervillous space (IVS). This portion of the placentome is modeled as a porous medium with uniform and isotropic hydraulic permeability (k) and porosity $\varphi =1-\psi$, where ψ is the volume fraction (the ratio of tissue space to IVS in the placenta). Placental tissue density or the volume fraction of placenta that is occupied by tissue, is known to increase with gestational age (GA) [19]. The effective k of placental tissue at term is estimated following Chernyavsky et al. [13] to be approximately 10⁻¹⁰ m² using

$$k=\frac{d^2}{180}\frac{{(1-\psi )}^3}{{\psi }^2}$$ (1)

where d is an average diameter of a villus in the IVS.

To estimate the change in ψ with gestation, we assume that d remains constant and that tissue density can act as a proxy for volume fraction. Boyd and Hamilton [20] measured placental weight (converted here to volume by assuming tissue density of 1000 kg m⁻³) with gestation, and de Paula et al. [17] estimated in vivo placental volume with gestation. The relative changes in volume fraction can then be estimated by dividing normal placental weight by placental volume at each gestational age. A polynomial fit to literature data gives us an equation for ψ as a function of gestational age (GA, in weeks, R²= 0.99) as

$$\psi (\text{GA})=\alpha (\text{GA}){\psi }_{\text{term}}$$ (2)

where

$$\alpha (\text{GA})=-0.0007{\text{GA}}^2+0.062\text{GA}-0.39$$ (3)

So, at the 12th week of gestation, ψ is expected to be 45% of its value at term. This is reflected in power Doppler images, scanning electron micrographs, and histological sections through gestation presented by Konje et al. [19] and translates to k at 12 weeks being almost 10 times the value at term. Note that the volume fractions which are calculated using Eq. (2) (or corresponding porosities $\varphi =1-\psi$) are average values over the whole placenta. When a central cavity is present, the porosity of tissue in the IVS away from the central cavity is adjusted based on central cavity volume such that the average tissue volume (and thus porosity) of the placenta is constant between simulations.

2.2. Model Construction and Solution.

The model was formulated in the computational fluid dynamics software ansys-fluent (Ansys, Inc., Version 14.0, Canonsburg, PA). The geometry of the model as shown in Fig. 2 was constructed and meshed in ansys icem cfd^TM (Ansys, Inc., Version 14.0), with mesh resolution determined by convergence tests. The model geometry was split into two regions, a composite fluid-tissue region comprising the IVS ($z<Z_L$, less the central cavity) and a region in which fluid flow is unimpinged by the villous structure ($z>Z_L$, plus the central cavity). We solve for steady-state, laminar flow, assuming that blood is an incompressible Newtonian liquid. In general, the situations simulated here have an upstream flow velocity (in the unremodeled portion of the SA) of 0.5–4 m s⁻¹, which is consistent with Burton et al. [8]. This results in Reynolds numbers of 70–550, which suggests a laminar flow assumption is reasonable. In the porous region, Darcy flow is solved

$$\mathbf{U}=-\frac{k}{\mu }\nabla P,\hspace{1em}\nabla ·\mathbf{U}=0$$ (4)

where U is blood velocity, μ is the viscosity of blood, and P is blood pressure. In the villus-free region, the Navier–Stokes and continuity equations are solved

$$(\mathbf{U}·\mathbf{\nabla })\mathbf{U}=-\frac{1}{\rho }\mathbf{\nabla }\mathit{P}+\mu {\mathbf{\nabla }}^2\mathbf{U},\hspace{1em}\mathbf{\nabla }·\mathbf{U}=0$$ (5)

where ρ is the density of blood. Solutions were obtained with 100 iterations and a residual target of 1 × 10⁻⁴, and convergence was checked via both a check of mass flow balance (i.e., flow into the system equals flow out), and further convergence checks for mesh resolution. Blood velocity at the SA opening was defined as the average velocity across the SA mouth at z = Z_L.

2.3. Boundary Conditions.

At the inlet of the SA, for simplicity, we assume a fully developed laminar flow and a parabolic flow velocity profile. The flow velocity at the inlet is adjusted to match ultrasound measured flow average velocity at the SA opening to the IVS. At the venous outlets, pressure was fixed at a constant 0 Pa. The interface between the villus-free and porous medium domains was defined in ansys-fluent as an “interior” boundary, which means that continuity of parameters (velocity and pressure) is ensured at this interface.

At the chorionic and decidual surfaces (z = 0 and z = Z_L), a no-slip condition is assumed as these surfaces are a physical barrier to flow. At the boundaries at the periphery of the placentome ($x=0,X_L$ and $y=0,Y_L$), no-slip conditions were also assumed, which tacitly assumes that placentomes are separated by physical boundaries (septa). To test the impact of this assumption on the model, the geometry was extended to multiple placentomes fed by different spiral arteries, predictions of jet length were unaffected by this assumption.

2.4. Model Parametrization.

Model parameters which are not changed with gestation are summarized in Table 1, and those that change with gestational age are shown in Table 2. To define SA funnel dimensions, the inlet radius r₀ is fixed at 200 μm following Burton et al. [8] and b and c are model variables, with c adjusted to match SA opening radii measured by ultrasound through gestation [10,11]. A range of ψ and d at term is available in the literature for normal placentas [22,23]. This leads to a range of placental permeabilities, k, and the nominal value for this parameter is set following [13].

Table 1.

Nominal parameter values and ranges from the literature

Parameter	Value	Range	References
np, number of placentomes	100	30–100	[15,16]
r0, undilated SA radius (μm)	200	—	[8]
b, depth of spiral artery remodeling (m)	0.003	—	[8]
d, average villous diameter (μm)	70	50–70	[34]
ψterm, volume fraction	0.3	0.3–0.7	[22,23]
${\varphi }_{\text{term}}$, porosity	0.7	0.3–0.7	[22,23]
k, permeability at term (m2)	1 × 10−10	7.65 × 10−12 to 1 × 10−10	Calculated from d, ψterm
Blood viscosity (μ, Pa · s)	0.003	—	[21]
Blood density (ρ, kg m−3)	1056	—	[21]

Table 2.

Model parameters estimated from the literature to describe the size and structure of an “average” placentome through gestation, 95% confidence values are given where available

Gestation (weeks)	12	15	20	25	30	35	References
Placental volume (L)	0.108	0.147	0.206	0.243	0.329	0.390	[17]
Range of 10th to 90th percentile (L)	0.070–0.154	0.088–0.210	0.118–0.304	0.136–0.361	0.178–0.493	0.208–0.587
Placental thickness, ZL (mm)	10	12	16	19	22	24	[18,35]
x- and y-direction dimension, XL, YL (mm)	10.4	10.9	11.3	11.6	12.2	12.7	See text
Width of jet mouth (mm)	1.96	2.56	3.30	3.75	3.90	3.76	[10,11]
95% confidence range (mm)	1.46–2.44	2.01–3.08	2.46–4.11	2.53–4.96	2.30–5.52	1.75–5.76
Mean velocity at SA mouth (m/s)	0.51	0.43	0.33	0.25	0.19	0.14	[10,11]
95% confidence range (mm)	0.36–0.71	0.32–0.58	0.26–0.41	0.20–0.30	0.15–0.23	0.11–0.18
Average porosity, $\varphi$	0.92	0.89	0.83	0.79	0.77	0.74	See text

2.4.1. Sonographic Measurements.

A previous pulsed wave Doppler ultrasonography study measured SA mouth width, jet length, and jet flow velocity (at the level of the opening of the SA mouth) in 52 normal singleton pregnancies [11]. A full statistical analysis is given in the original study [11]. Participants were recruited at 11 + 0 weeks and 13 + 6 weeks gestation (weeks + days). All 52 pregnancies had uterine artery Doppler results within the normal range at 23 weeks. Placental weight at birth was 0.63 kg (range 0.38–0.87 kg) and all placental weights lay within 1.5 standard deviations of the mean for gestation (according to a study reporting placental weight results for 3434 cases [24]). Mean values of jet mouth width and velocities through gestation are given in Table 2, along with ranges of the 95% confidence intervals for each parameter at that gestation.

2.4.2. Jet Length.

Jet length was defined by assessing the blood flow velocity through the IVS along the centerline of the SA. For consistency with ultrasonography [11,25], this point was defined as the point at which blood flow velocity drops below 1 × 10⁻¹ m s⁻¹ (10 cm s⁻¹).

3. Results

The model was solved first with nominal parameters as defined in Tables 1 and 2, no central cavity (d_CC = 0), and with mean velocity at the SA mouth fixed at the mean velocity, and maximum and minimum velocities in the 95% confidence range. Figure 3 shows the predicted jet length, and ultrasound measured jet length under these conditions. The model, with its nominal parameters underpredicts measured values of jet length except in early gestation. At week 12 of gestation, model predictions lie near the center of the confidence band for ultrasound measured length, and at 15 weeks, predicted values lie at the lower end of the confidence band for ultrasound measured length. Changes in SA mouth flow velocity have a progressively reduced impact on model predictions of jet length (as indicated by the error bars in Fig. 3) and increasing velocity within feasible ultrasound measured bounds is not sufficient to predict the range of jet length observed. Ultrasound measured jet velocities and lengths are not related (Fig. 4) suggesting that longer jets are not simply reflective of faster moving blood.

Fig. 3.

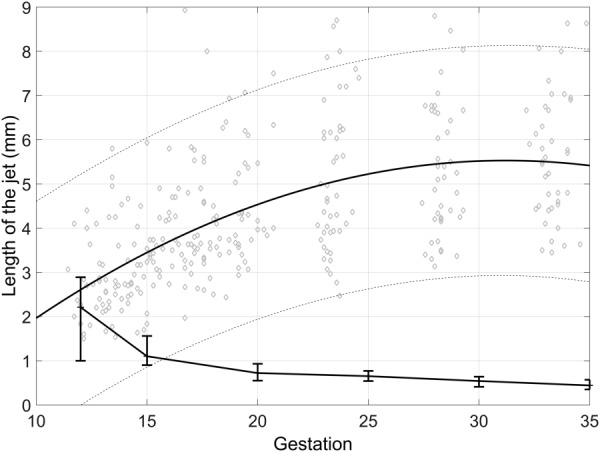
Ultrasonographic measurements of jet length in normal pregnancies (solid line, dashed lines represent 95% confidence intervals, from Ref. [11] compared with jet length predicted by the model with ultrasound measured flow velocities at the SA mouth (crosses represent predictions at nominal parameters for each gestation, error bars represent jet length predicted at minimum and maximum of 95% confidence range for velocity at SA mouth). The model underpredicts jet length at all but the earliest gestation. Note that the predicted jet length at 35 weeks is small, but nonzero, and the level of jet length is defined as flow velocity less than 1 × 10⁻¹ m s⁻¹ for consistency with ultrasound, so there is still circulation predicted in the IVS under these conditions.

Fig. 4.

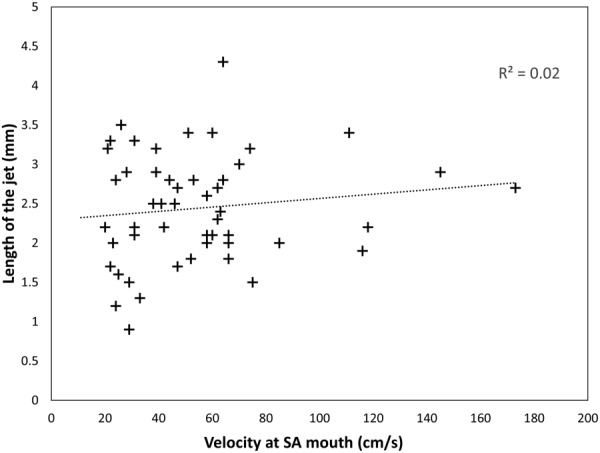
The relationship between ultrasonographic measurements of length and jet mouth velocity at 11 + 0 to 13 + 6 weeks of pregnancy. Trends are similar at later stages of pregnancy. There is no significant relationship between the two parameters. This lack of relationship, and the predictions that flow velocity at the SA mouth must be much higher than ultrasound measured values to predict accurate jet length, suggest that the density of villous tissue distal to the SA mouth must be a primary determinant of jet penetration.

To assess the influence of uncertainty in parameter estimation, we resimulated the model under conditions representing the extremes of parameter ranges to determine how results were influenced in each case. The model for the 12 week placenta (GW = 12) was used as a baseline for comparison.

3.1. Placentome Dimensions.

There is significant variability in placental volume throughout gestation, and this variability appears to be predominantly in the thickness of the placenta Z_L [26]. Holding all other parameters constant, the placental thickness Z_L was reduced to half its baseline value at GW = 12 (5 mm) to represent the range of physiological placental thickness. With Z_L = 10 mm, the length of the jet was predicted to be 2.21 mm. When placental thickness was reduced to Z_L = 5 mm, the length of the jet was reduced to 2.07 mm. Reducing Z_L still further, to a location that was nonphysiological but at which the chorionic plate might be expected to influence hemodynamics, resulted in a further reduced jet length (1.98 mm). In most cases, where jet length is significantly less than the thickness of the placenta, the parameter Z_L has only a small effect on predicted jet length. The effect of Z_L is to decrease jet length rather than the increase required to match data in Fig. 3.

3.2. Decidual Vein Location.

The location of the decidual veins (DVs) with respect to the SA was varied with veins located at (a) the periphery of the placenta (x = ±0.00479), and (b) immediately adjacent to the SA (x = $\mp$0.001). Neither simulation resulted in a significant change in jet length, but this change did influence flow velocities near the periphery of the placenta with peripheral DVs resulting in higher peripheral flow velocities near the drainage area.

3.3. Spiral Artery Dimensions.

The width of the spiral artery mouth was taken from ultrasound data [11,25]. Increasing the mouth width decreases jet length. Increasing the unknown parameter, b, representing the depth of spiral artery remodeling decreases the jet length. Simulating with b representing the maximum depth of remodeling (7 mm) results in a decrease in penetration of 1.41 mm. The normal extension of trophoblast invasion reaches to inner third of myometrial thickness [8]. The decidual thickness varies between 5 and 11 mm from person to person [27,28]. While the measurements of the myometrial layer give a range of 6–10 mm [29,30]. Therefore, the remodeled part of SA is expected to extend 7–14 mm into the decidual–myometrial tissue from the IVS. Our simulation using a 7 mm depth of remodeling has shown that the jet length decreases in comparison to 3 mm depth of remodeling. Further increasing the depth of SA remodeling decreases the penetration length further.

3.4. Pulsatility.

The pulsatility index of spiral arteries decreases with gestation [10,11]. However, flow in the system is pulsatile. Assuming a heart rate of 80–90 beats per minute for a pregnant woman, the Strouhal number and Womersley numbers for the SA are small at o(10⁻³) and o(10⁻¹), respectively. This suggests that a steady-state approximation of the system is appropriate. To check this assumption, a pulsatile simulation using nominal model parameters was conducted at 12 weeks of gestation using peak systolic and end diastolic flow velocities measured in ultrasound. Maximum jet length over a heart beat predicted by the pulsatile model and jet length predicted by the steady model differed by 0.1 mm.

3.5. Velocity.

The model was parametrized using the average velocity of a jet at its mouth from ultrasound data [10,11]. There is variation in this velocity. To assess the impact of this variation, at each gestational week, simulations were conducted using the maximum and minimum values of velocity from ultrasound. These simulations are reflected by the error bars in Fig. 3. While an increase in jet mouth velocity does increase jet length, this is not sufficient to explain the difference between model predicted and ultrasound jet lengths in Fig. 3.

4. Tissue Properties Distal to Jets

The results outlined in Sec. 3, taken together suggest that low tissue fraction at the mouth of the SA must contribute to the presence of ultrasound jets in the placenta, as changing each of the other model parameters within reasonable bounds was not sufficient to increase predicted jet length to measured values. Variation in placental tissue density was represented by (1) simulating a change in tissue volume fraction through the whole placentome, and (2) by assuming a central cavity at the mouth of the spiral artery. To predict the placental tissue properties required for our model to predict ultrasound measured jet length, for a given jet mouth velocity, blood flow in the placentome was resimulated using the data in Tables 1 and 2, with inlet flow velocity to match mean ultrasonographic data, and either the volume fraction of the placentome altered, or length of the central cavity increased, until the desired jet length is reached. Table 3 and Fig. 5 show the results of these simulations to predict both jets and mega-jets (jet length equal to half of the placental thickness). Figure 5 shows for observed jets and mega-jets to occur, the tissue density at the SA mouth must decrease significantly with gestation, or the length of a villus-free central cavity must increase with gestation.

Table 3.

Model volume fractions and cavity lengths required to achieve mean SA jet and mega-jet properties through gestation. The model predicts that a significant reduction in tissue volume fraction distal to the SA opening or an increase in cavity length is required to see jets as gestation progresses.

Gestation (weeks)	Target jet length (mm)	Target mega-jet length (mm)	Volume fraction (ψ) for jet	Volume fraction (ψ) for mega-jet	Cavity length for jet (mm)	Cavity length for mega-jet (mm)
12	2.73	5.0	0.07	0.04	0.67	3.6
15	3.13	6.0	0.06	0.03	1.87	5.15
20	4.51	8.0	0.05	0.03	4.01	7.80
25	5.01	8.5	0.04	0.02	4.94	8.68
30	5.50	11.0	0.03	0.01	5.62	11.55
35	5.32	12.0	0.02	0.01	5.63	12.91

Fig. 5.

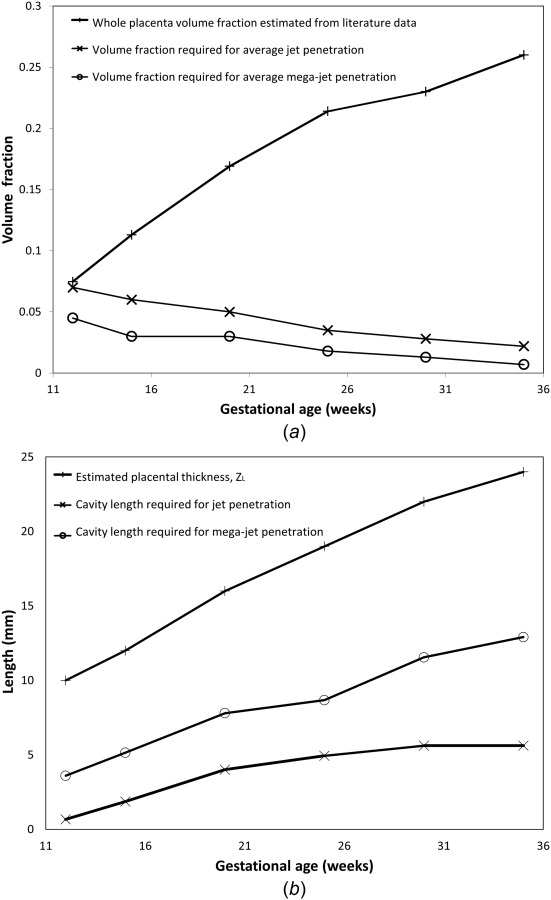
(a) The predicted volume fraction of the villous tissue required to generate a jet with average jet lengths, a mega-jet and a comparison to the whole placenta tissue volume fraction determined from literature data. (b) The predicted length of a villus-free cavity required to produce jets and mega-jets compared to average placental thickness. Both predictions suggest a reduced tissue density, compared with the whole placenta average, at the opening of SA where significant jets are observed, particularly in the later stages of gestation.

The effect of reducing the volume fraction of tissue distal to the SA opening for a given upstream flow velocity is shown in Fig. 6. This figure shows model predictions of average blood flow velocity in the SA and into the intervillous space distal to the SA at 25 weeks of gestation for an average placental volume fraction ψ = 0.21 and a low volume fraction ψ = 0.02. Both simulations show a similar pressure profile through the SA, but the lower the volume fraction (the less tissue distal to the SA) the higher the jet length. Incorporating a central cavity produces similar results, with an increase in cavity size allowing increased penetration of blood. The major difference between the two approaches for reducing tissue density at the SA mouth is that when a central cavity is included flow velocity decreases rapidly as blood penetrates into the tissue filled space distal to the central cavity. The site of highest resistance, and thus, pressure drop in the SA in the undilated portion of the spiral artery is far more significant than in the dilated portions, pressure variations in the dilated and undilated are consistent with Burton et al.'s [8] Poiseuille flow approximation to hemodynamics in the SA for flow rates of the same magnitude.

Fig. 6.

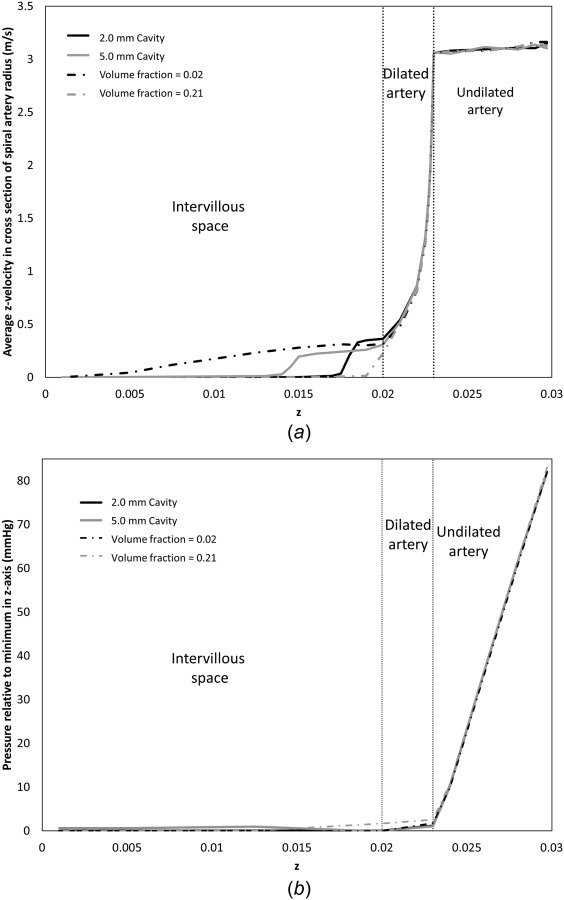
Model predictions of (a) average blood flow velocity through the SA and into the placental tissue in a region of the same diameter as the opening of the SA, and (b) average blood pressure in a spiral artery cross section relative to minimum pressure along the z-axis at 25 weeks gestation. Results shown represent a placentome with a 2 mm central cavity (average ψ = 0.21), a 5 mm central cavity (average ψ = 0.21), no central cavity (average ψ = 0.21), and a homogenously reduced tissue volume fraction (ψ = 0.02). All simulations have the same fixed inlet velocity. Visible jet length is sensitive to the structure of villous tissue distal to the SA opening.

Mega-jets of blood flow from SAs into the intervillous space have been described in normal pregnancies and are defined as a visible blood flow traveling more than 50% of the placental thickness [10,11]. In these studies, there was no significant difference found in peak systolic jet velocity with mega-jets compared to standard jet [11]. The porosities required to predict mega-jets are given in Table 3. Therefore, in order to predict the jet and mega-jet length observed by Doppler ultrasonography, the volume fraction of villous trees must decrease compared with the average (whole) placenta value derived from the literature, or a central cavity of increasing length must develop through gestation as shown in Fig. 5.

The extent to which jet length may be indicative of the presence and size of a central cavity was investigated. The short-axis radius of the central cavity did not influence jet penetration. Figure 7(a) shows the effect of cavity long axis length on jet length at 35 weeks. Up to a cavity major-axis length of approximately 12 mm, the length of the jet is approximately equal to the length of the cavity at this gestation. However, for larger cavities, the jet length no longer extends the full length of the cavity. At 35 weeks of gestation, the average jet length is 5.32 mm and, assuming an average placental thickness of 24 mm, the minimum length for a jet to be defined as a mega-jet is approximately 12 mm, with a maximum recorded length at 35 weeks gestation of 17.4 mm [11]. These lengths are shown in Fig. 7 for reference. For most standard jets, our model predicts that the jet length is reflective of the size of the central cavity. However, mega-jets may be associated with cavities that are longer than measured jet length, which is consistent with the higher frequency of occurrence of mega-jets in the vicinity of placental “lakes” [11]. This relationship between cavity length and jet length holds true from approximately 20 weeks of gestation. Prior to 20 weeks the model predicts that, in general, a jet or mega-jet can penetrate into the IVS beyond the central cavity (Fig. 7(b)), because, in average, the tissue is more porous in early gestational ages.

Fig. 7.

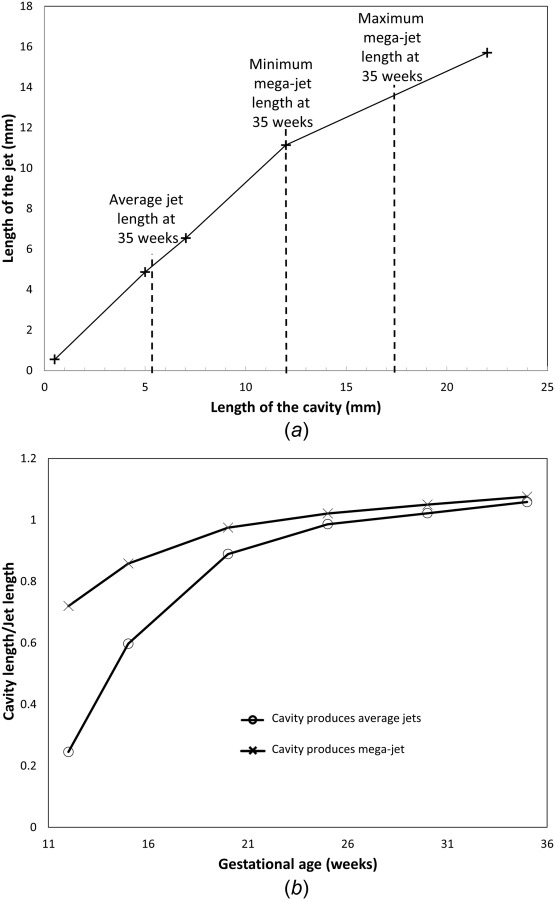
(a) The predicted jet length for a given central cavity long axis dimension at 35 weeks gestation. Average jet length is given along with an expected range for mega-jet lengths based on data from Collins et al. [11]. Jet length is predicted to follow the size of the central cavity up to a maximum value at which the jet length becomes reduced compared with the length of the central cavity (the effect of reaching the porous placental tissue is no longer the dominant determinant of jet penetration). (b) The predicted proportion of jet length that must be comprised of a villus-free cavity to predict a jet and mega-jet through gestation. Early in gestation blood is able to penetrate significantly beyond the length of the cavity, however from approximately 20 weeks jet length becomes indicative of cavity length.

Variation of model parameters across physiological ranges, and assessment of steady versus pulsatile flow shows that placentome dimensions, decidual vein location and pulsatility do not influence jet length significantly. Most changes to model parameters acted to decrease rather than increase jet length. The key parameters that influence our model are jet velocity (which is input from ultrasound) and IVS tissue porosity.

4.1. Jet Fluid Dynamic Behavior.

An interesting feature of our predicted 3D flow dynamics in the remodeled part of the SAs, is that flow separation can occur in the dilated part of the spiral arteries. This results in a flow profile more akin to a true jet than the gradual decrease in flow velocity as predicted in the 2D model developed by Burton et al. [8]. An analysis of model predictions suggests that this phenomenon occurs when the ratio of dilation length to width is approximately 0.5 (when the dilation of the artery is 30 deg or greater), or if flow velocity in the unremodeled portion of the SA is greater than 1.5 m s⁻¹. This velocity is at the high end of estimated physiological values but not impossible, it reflects a Reynolds number entering the dilated part of the SA of approximately 1500. From an engineering perspective, this behavior is similar to the problem of a diffuser [31], where flow separation can be shown to occur at high separation angles, and high Reynolds numbers. In this case, blood flow retains the width and velocity of the upstream (unremodeled) SA. Using the geometrical description of Burton et al. to describe the opening of the SA results in a sharp change in artery diameter at the remodeled part, however, this result is not dependent on this geometric feature and remains when the geometry of the model is altered to include a curved dilation with a smooth arterial wall through the dilation. Whether or not this occurs in the physiological situation is unknown, and this type of flow dynamic may not be determinable by ultrasonography, where if the uterine placental boundary is well identified, this type of jet would likely present as a narrow opening into the placental space.

5. Discussion

In this study, we have presented a computational model of flow at the interface between a SA and placental tissue and compared it to ultrasonographic data describing jets and mega-jets of flow at this interface. In general, our predictions of flow dynamics at this interface are consistent with ultrasonography, where a typical jet waveform is seen as predominantly unidirectional with some flow in directions away from the main axis [10]. Model predictions of pressure gradients within the spiral artery and intervillous space are also consistent with previous models of spiral artery hemodynamics [8], as shown in Fig. 6(b). Our model suggests that the length that a blood flow jet can penetrate into the IVS is primarily dependent on the tissue properties at the opening of the SA and that high penetration jets and mega-jets are most likely associated with low density tissue distal to the SAs or with the concept of a central cavity, or a villus-free space where the SA opens to the placental tissue [8,32]. Based on the average porosity of the placenta calculated from the literature, it appears that this villus-free space is not required for jets to be observed in early pregnancy (12 weeks), but that a decreasing tissue density distal to the SA occurs as pregnancy progresses. This is consistent with the idea that high blood flow at the SA mouth at 12 weeks impedes villus development into that region, and that the central villus cavity allows blood to be carried through to the distal portion of the placental tissue before being dispersed into villous tissue [33,34]. The model predicts that cavity size is likely reflective of jet length for most jet lengths, from 20 weeks of gestation, although some mega-jets may be associated with cavities that are longer than observed jet lengths.

Tissue volume fraction is known to change regionally in the placenta and there is significant heterogeneity in structure between villi and placentomes within the same placenta particularly in the later stages of gestation [32,35,36]. For example, peripheral placentomes typically have less mature (less dense) villous architecture than central villi [35], but there are limited quantitative data describing within placenta variability in tissue density. The presence of a central cavity at the mouth of spiral arteries is most often described in studies at term [32], although there is little data on the presence or size of central cavities in early gestation, and the placentome is considered relatively homogeneous until the development of mature intermediate villi at the end of the second trimester (approximately 20 weeks) [35]. Thus, in this study, heterogeneity in placental tissue density was represented by (1) simulating a change in tissue volume fraction through the whole placentome, and (2) by assuming a central cavity at the mouth of the spiral artery. The first of these approaches represents possible heterogeneity in tissue volume fraction between placentomes and the second represents within placentome heterogeneity in tissue volume fraction. The model suggests that a completely homogeneous placenta could have jet-like flow profiles at week 12, but later in gestation, the predictions of volume fraction to produce jets and mega-jets become unphysiologically low, and a central cavity must develop to allow penetration of blood deep into the IVS. The model simulations suggest that this cavity becomes more important to placental hemodynamics as gestation progresses, which agrees with evidence of increased heterogeneity in placental tissue as the placenta matures [35]. Homogeneous reductions in volume fraction result in a slow decrease in blood velocity through the IVS, whereas the inclusion of a central cavity allows high blood flow to penetrate far into the IVS before a relatively rapid decrease in velocity as blood penetrates into dense villous tissue (Fig. 6). Thus, the development of a central cavity allows increased blood penetration with lower flow velocities (and so stress) in the villous tissue region.

The model predictions suggest that blood circulates slowly around villous tissue in high density regions of placental villi while low density regions of placental villi develop under the influence of the higher blood flow near the openings of SAs at 12 weeks of gestation (the remodeling process continues up to 18 weeks of gestation) and allow flow to penetrate through the IVS reaching villous tissue throughout its thickness. In a study on the effects of utero-placental blood flow in the pathogenesis of pre-eclampsia, Hutchinson et al. [37] showed that for a constant density of villous trees (term placentas collected from normal healthy pregnancies) increasing the blood flow will result in deeper perfusion of blood into the IVS. In their experiment, in vitro placental perfusions were conducted using polythene tubes as replacement for the maternal SA. The blood penetration into the IVS arising from the artificial tubes used does not necessarily correspond to high and low density regions of tissue and can be increased if the injection velocity is high. This finding is in agreement with implications of our model. To get desired penetration to predict jets and mega-jets, a manipulation to the inlet flow could result in variation of jet length for a constant porosity. Moreover, Hutchinson et al. observed widespread damage to the villus syncytiotrophoblast as a consequence of high blood flow. As a result, they anticipated greater villous architecture change proximal to cannulae in vitro or SAs in vivo. This result is also consistent with our prediction of existence of low density regions of villous tissue proximal to regions of slightly high blood flow at the entrance of jets or mega-jets.

In our model, the depth of jet penetration into the IVS is most dependent on three factors: (1) the width of the SA opening, which decreases the mean velocity of flow reaching the IVS as it widens [8], (2) the flow rate in the upstream portion of the SA, which also influences velocity and potentially increases with gestational age, and (3) the density of tissue in the IVS distal to the SA opening whether this is applied homogeneously or by explicitly including a central cavity. While significant dilation has been observed in individual SAs [8], measurement of this parameter in large numbers of arteries and over gestation has to date not been possible. Therefore, in this model, ultrasound measured jet width is assumed to be representative of SA mouth width at each stage of gestation. Increasing the mouth width results in decreased penetration (reduced mouth flow velocities) and decreasing the mouth width increases predicted IVS penetration. Changing the width of the SA opening within physiologically estimated ranges in our model is not sufficient to predict realistic jet length.

Predictions of the volume fraction of placental villi in the IVS required to predict a given jet length and jet mouth blood flow velocity show that after 12 weeks of gestation, for an average ultrasonographically observed jet, the villus density at the SA opening must stay approximately constant or slightly decrease with gestation. This suggests that from the onset of significant flow from the SAs (from around 12 weeks of gestation) there is an interaction between maternal blood and the developing villous trees in normal pregnancy that leads to sparse tree development in these regions. Simulations with a central cavity, but physiological average tissue density away from the SA opening were consistent with this hypothesis. If a tissue free region exists at the mouth of the spiral artery, our model predicts that jet length follows the length of this cavity, up to a maximum penetration. The existence of a central cavity would potentially allow increased oxygen delivery to villi distal to the spiral arteries as jets can transport oxygen rich blood further through the IVS. The formation of mega-jets would require further decreases in local villus density, a longer central cavity and/or increased blood flow velocity. A previous modeling study has predicted that areas of decreased villus density (a central cavity) do facilitate transport of oxygen or nutrients to the distal portions of the placenta and that an “intermediate” cavity size provides the optimal rate of nutrient exchange between the maternal and placental circulations [13]. This implies that jet penetration into the IVS is beneficial to nutrient exchange but high levels of penetration may not be ideal (jets may be seen as preferential to mega-jets in terms of nutrient exchange).

In ultrasound studies, placental lakes (low or zero flow regions, with low tissue density) can be observed in the vicinity of mega-jets [11]. In early stages of pregnancy, more women with only mega-jets or only placental lakes are observed, but as gestation increases the number of women with both mega-jets and lakes increases [11]. While these ultrasound studies could not determine a direct relationship between mega-jets and lake formation, the association between the two suggests that the hemodynamics of mega-jets could cause the formation of lakes, and our model predictions support this hypothesis. Mega-jets seem to be normal components of pregnancy, and the high blood flow from these mega-jets could occur following the convergence of more than one SA to produce a high flow region. Both ultrasound and model data suggest that this influences the development of the delicate circulatory system of the IVS and consequently allows blood to travel further into the IVS. Our model suggests this may be the case in both standard and mega-jets but to a different extent in each.

Our model is parametrized for normal pregnancies. There are limited quantitative data on SA remodeling in pathological pregnancies, although in many pathologies it appears that the SAs are incompletely remodeled [5,7]. This means that blood must flow through a narrower arterial opening into the IVS. As described by Burton et al. [8], this means a higher blood velocity at the interface between the SA and the IVS and a greater potential for a decreased IVS tissue density at this interface. Our results suggest that even in normal pregnancies, sparse regions of IVS occur, suggesting that this allows increased penetration of oxygen rich blood into the IVS. Investigation of jet properties in small for gestational age pregnancies have been conducted by pulsed wave Doppler ultrasonography [10], with small for gestational age in this study being defined as <10th centile on customized growth charts. However, assessments of jet properties have not been conducted in large numbers of subjects. The data showed on average a decrease in jet length and a slight but not significant increase in jet mouth velocity in small for gestational age pregnancies (Fig. 24 from Ref. [25]). The appearance of mega-jets and lakes occurred significantly later in gestation in the small for gestational age pregnancies than for average for gestational age pregnancies [25]. The model would suggest that in these pregnancies, as blood flow velocities are similar or elevated to average for gestational age pregnancies, that the villous tissue acts as more of a barrier to jet flow. Small for gestational age pregnancies are known to produce villous trees with reduced small vessel branching, as well as altered composition [38]. Small for gestational age pregnancies also appear to have reduced IVS volume when compared to average for gestational age pregnancies [38]. This may explain a reduced jet length, however, the question of whether jet properties are related to this aspect of placental morphometry in small for gestational age pregnancies remains a question for future studies. The model suggests, at least early in pregnancy, that either high velocity flows from poorly remodeled SAs damage the placental tissue making it more of a barrier to flow, or that there is a fundamental difference in IVS properties in small for gestational age pregnancies.

In a previous three-dimensional color power angiography (CPA) study [19], maternal jets crossing the whole way through the placental thickness were observed reaching the chorionic plate at 13 weeks gestation. In this study, jets become more slender over gestation until 38 weeks when they could be traced only up to half of the way into the placental thickness. As placental thickness increases with gestation, this is equivalent to an approximate constancy in jet penetration length through gestation. On the other hand, our data shows that jet length increases with developing gestation [11]. This may be influenced by the measurement technique. In the future, our model can potentially be parametrized to describe individual jets, or expanded to the whole placenta, to determine whether the properties of arterial jets in an individual could influence the transit of maternal blood through the IVS and thus, placental exchange capacity.

Ultrasonographic data suggests a decrease in jet mouth velocity and an increase in jet length through pregnancy, which may seem inconsistent. Our model shows the same trend in mean velocity of flow at the jet mouth, as ultrasonographic measurement is conducted over the width of the remodeled end of the SA. The peak flow velocity occurs at the center of the SA opening with flow velocity decreasing to the wall of the artery. Assuming that the width of the SA opening increases through gestation, along with remodeling, the peak velocity of flow can increase, leading to an increased jet length, while average flow velocity through a cross section decreases.

5.1. Model Limitations.

We have assumed blood flow to be laminar, steady, and Newtonian. Reynolds numbers for the problem of 70–550 suggest a laminar flow assumption is reasonable. As described in Sec. 4.1, some SAs may have higher Reynolds numbers (up to around 1500), so may begin to approach the turbulent regime, but these are few in number in the analyzed ultrasound data-set, so the laminar approximation is valid for most SAs. Blood is known to be non-Newtonian but the size of blood vessels considered (>200 μm) makes a Newtonian assumption reasonable in the unobstructed vessels. Pore size in the IVS has been estimated to be 70–90 μm, which is much larger than a red blood cell, justifying the assumption of a Newtonian fluid in this part of the domain. Finally, flow in the SAs is pulsatile, with decreasing pulsatility through gestation. Simulations of pulsatile flow did not significantly impact on predictions. Similarly, the Darcy flow equations are a simplification for flow in a porous medium, and they are only applicable when inertial effects are negligible. While this is likely true for a steady flow of the velocities observed in the intervillous space, sudden “bursts” of blood penetration into the intervillous space have been observed [8]. In these cases, inertia would become important and the Darcy–Brinkman equation would be a more appropriate governing equation for blood flow.

The SAs were assumed to be straight tubes prior to their dilated openings, following Burton et al. [8]. Inlet flow profiles were assumed to be fully developed (parabolic). The spiral arteries and the more proximal radial vessels are known to be tortuous, thus, the assumption of a straight spiral artery will underestimate spiral artery resistance. The tortuosity of the vessels will also likely result in a velocity profile that is not symmetric, and this is not reflected here. The true inlet velocity profile is unknown, and difficult to measure, therefore, a modeling assumption must be made at this level. In general, the less tortuous the uterine vessels the more realistic this assumption will be. Reconstructions of spiral arteries [39] suggest that as gestation progresses, possibly from 20 weeks and certainly at term, the spiral arteries become less tortuous. However, there are few quantitative descriptions of the extent of tortuosity in human spiral arteries at present. These modeling assumptions are likely to over-predict jet length, so although more accurate representations of spiral artery tortuosity would improve model predictions of flow profiles, they are unlikely to change the main outcomes of our predictions.

Our geometric description of the placentome is idealized, and while consistent with previous modeling studies [8,12,14], it does not reflect the true configuration of the placental interface. Some modeling studies have considered the placentome as a hemisphere [13,14], which may be considered more reflective of a cotyledon. We also simulated this configuration with the same volume as our cuboidal domain. As jets do not penetrate close to the placentome boundaries, there were no significant differences in model predictions. Geometrical accuracy could potentially be improved by incorporation of data from cast based studies, or modeling a whole placenta with SA location and size determined from ultrasound. The ratio of SAs to decidual veins is still unknown, so despite most modeling studies assuming two veins to each artery, an investigation into this configuration would provide additional accuracy. Each of these geometric improvements would increase computational expense for this model, and despite its geometric simplicity, this model provides important predictions regarding the nature of blood flow at the uteroplacental interface.

5.2. Conclusions.

In this study, we made a virtual model of a placentome within which we can predict blood pressure, speed, and penetration length into the IVS in three dimensions. During gestation, the placental thickness increases and placental villi continue to branch and elongate to make the placenta less porous on average. Meanwhile, the SAs transform into nonvasoactive vessels with a wide openings into the IVS in order to provide the placenta and fetus with increasing levels of nutrients and oxygen. While the increased branching and density of villous trees make it harder for the blood to penetrate the IVS, a healthy pregnancy requires maximal transmission of placental blood to the deeper points of the IVS to ensure exchange across all placental villi. Our model predicts that free spaces must develop distal to the SAs among the villous trees' branches for blood to penetrate as far as measured in Doppler ultrasonography (in jets). Our model predicts that a mega-jet requires hollow spaces with almost no villous tree branching, particularly late in pregnancy. This suggests that the villous structure potentially develops under influence from SA blood flow to allow penetration of nutrient rich blood effectively through the thickness of the villous tissue.