Abstract
Magnetic resonance elastography (MRE) has emerged as a sensitive imaging technique capable of providing a quantitative understanding of neural microstructural integrity. However, a reliable method for the quantification of the anisotropic mechanical properties of human white matter is currently lacking, despite the potential to illuminate the pathophysiology behind neurological disorders and traumatic brain injury. In this study, we examine the use of multiple excitations in MRE to generate wave displacement data sufficient for anisotropic inversion in white matter. We show the presence of multiple unique waves from each excitation which we combine to solve for parameters of an incompressible, transversely isotropic (ITI) material: shear modulus, , shear anisotropy, , and tensile anisotropy, . We calculate these anisotropic parameters in the corpus callosum body and find the mean values as = 3.78 kPa, = 0.151, and = 0.099 (at 50 Hz vibration frequency). This study demonstrates that multi-excitation MRE provides displacement data sufficient for the evaluation of the anisotropic properties of white matter.
Keywords: magnetic resonance elastography, brain, stiffness, anisotropy, white matter
Introduction
Imaging methods for noninvasively characterizing the microstructural health and integrity of white matter make up an important area of research for understanding various neuropathologies. These include traumatic brain injury, which often involves diffuse axonal injury caused by shearing of white matter due to linear or rotational accelerations of the head. In addition to common metrics of damage or degeneration of white matter tracts, most notably from diffusion magnetic resonance imaging (MRI) [1–4], mechanical properties of the brain measured with magnetic resonance elastography (MRE) [5–9] also appear sensitive to white matter tissue health. Previous work has shown that MRE can detect mechanical alterations in several neurological diseases including multiple sclerosis [10–12], Alzheimer's disease [13,14], and Parkinson's disease [15], and animal studies have demonstrated correlations between these properties with tissue microstructure such as axonal myelination [16,17]. However, most MRE studies use methods that assume the brain is mechanically isotropic [6,18,19], though the fibrous nature of white matter, comprising bundles of aligned axons, gives rise to anisotropic, directionally dependent mechanical properties [20–23]. As such, anisotropic MRE methods are likely needed to improve accuracy, sensitivity, and reliability of white matter mechanical property measurements.
Several anisotropic MRE analysis methods have been proposed, which generally vary in the underlying anisotropic material model and thus the number of parameters to be estimated. One anisotropic model used in MRE considers white matter as an incompressible, transversely isotropic (ITI) material with both shear and tensile anisotropy [24–26]. The three parameters of this model can be estimated through the speed of waves propagating in different directions relative to the fiber direction, which can be separated into “slow” and “fast” components based on their propagation and polarization [27]. Two separate methods have been proposed to estimate these parameters from MRE data: one based on filtering data based on the presence of slow or fast waves [27] and a separate method using displacements at multiple frequencies [28]. The three-parameter ITI model provides a minimal model to accurately describe the behavior of white matter in a small number of parameters to be estimated. Additional anisotropic MRE methods include a two-parameter model that includes only shear anisotropy [29], which has been used to characterize breast tissue [29] and skeletal muscle [30], and a nine-parameter model that does not assume near-incompressibility of tissue [31], which has been used to examine white matter tracts [32].
These anisotropic MRE methods all vary in the complexity of their material model and details of their inversion algorithm; however, they all depend on having sufficient displacement data to estimate parameters. In general, there must be sufficient deformation in multiple directions to calculate the direction-dependent mechanical behavior of white matter [31]. Tweten et al. [33] described requirements for accurate estimation of the three parameters of the ITI model that include having slow and fast waves present in multiple propagation directions. To ensure that these requirements are met for anisotropic MRE of white matter, we propose to use multi-excitation MRE to capture distinct displacement fields [34]. Anderson et al. [34] first used multi-excitation MRE in the human brain and observed differences in recovered properties up to approximately 25% in several white matter tracts, which is likely due to differences in wave propagation arising from excitation location, making this a promising approach for use with anisotropic inversion.
The primary objective of this paper is to measure wave propagation in the brain from multi-excitation MRE to assess whether data requirements for anisotropic property estimation in white matter are met. By directionally filtering the MRE displacement data, we isolate distinct, independent propagating shear waves. We then identify the dominant (primary) and secondary directions of wave propagation, based on relative amplitudes of filtered components. We classify voxels in white matter based on whether they meet minimum data requirements and show that multi-excitation MRE results in more voxels with sufficient displacement information. Finally, we demonstrate that combining wave information from multiple excitations allows us to estimate the three parameters of the ITI model.
Methods
Slow and Fast Wave Propagation in Incompressible, Transversely Isotropic Materials.
The three independent material parameters that determine the behavior of ITI materials are substrate shear modulus, , shear anisotropy, , and tensile anisotropy, , which are based upon the shear modulus and tensile modulus of the material in two directions: parallel ( and ) and perpendicular ( and ) to the fibers. These parameters are described by the following equations:
| (1) |
| (2) |
| (3) |
In an ITI material, shear waves with a given propagation direction, , can be either “slow” (transverse) or “fast” (quasi-transverse) waves, which have separate polarization directions. These components are determined by relative to the fiber direction, , and the angle between them, . The polarization direction of the slow wave, , is perpendicular to and (Eq. (4)), while the polarization of the fast wave, , is perpendicular to and (Eq. (5))
| (4) |
| (5) |
The slow and fast wave speeds, and , are determined from the three material parameters and the angle of propagation relative to fiber direction (θ). The slow wave speed depends on the shear modulus, material density, ρ, and shear anisotropy, (Eq. (6)), while the fast wave speed also depends on tensile anisotropy, (Eq. (7))
| (6) |
| (7) |
Magnetic resonance elastography is potentially well-suited to quantify the three anisotropic material parameters, as wave speed, propagation direction, and fiber direction are obtainable through MRE and MRI (i.e., using diffusion tensor imaging, DTI). However, solving for these parameters requires sufficient displacement data, as described by Tweten et al. [33]. Specifically, there should be (1) multiple slow and fast waves in multiple directions and (2) each wave amplitude must have sufficient signal, i.e., at least 20% of the total original amplitude. Voxels with displacement data that meet these criteria should provide sufficient information for estimating the anisotropic parameters.
Data Acquisition.
Four healthy subjects (3/1 M/F; 22–32 yr old) provided informed, written consent and participated in the study approved by our Institutional Review Board. Each participant was scanned using a Siemens 3 T Prisma MRI scanner with 20-channel head coil. Vibrations at 50 Hz were generated by an active pneumatic driver (Resoundant, Inc., Rochester, MN) and delivered to the head with two passive drivers: a pillow-driver placed behind the head for anterior–posterior (AP) excitation, and a paddle-driver placed against the temple for left-right (LR) excitation, as shown in Fig. 1. Separate MRE scans were acquired for AP and LR excitations. The acquisition employed an echoplanar-imaging sequence with the following parameters: 3 × 3 × 3 mm3 isotropic voxels; field-of-view = 240 × 240 mm2; 48 slices; repetition time (TR)/echo time (TE) = 6720/65 ms. Auxiliary scans included DTI with resolution and field-of-view matched to MRE to estimate white matter fiber direction and T 1-weighted anatomical image at 0.9 mm3 isotropic resolution to localize white matter tracts. DTI scan parameters were included: TR/TE = 4800/60 ms; b = 1000 s/mm2; 30 noncolinear direction. T 1-weighted anatomical scan parameters included: field-of-view = 256 × 256 mm2; slices = 176; TR/TE/inversion time (TI) = 2080/4.45/1050 ms.
Fig. 1.
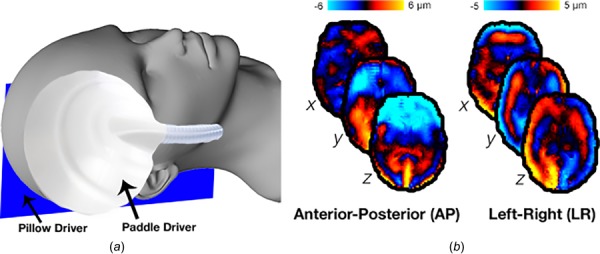
Overview of multi-excitation MRE: (a) positioning of pillow driver for AP excitation and paddle-driver for LR excitation; (b) representative wave fields from AP and LR excitations, shown as their x, y, and z components
Individual Wave Identification.
We directionally filtered [35] each MRE displacement field to determine dominant directions of wave propagation [36,37]. Each wave field was directionally filtered in 300 directions across the surface of a sphere, with a spherical bandpass filter (4.2–166.7 m−1) applied in all directions. In each voxel, the primary wave direction was determined as the filter direction in which the filtered field retained the highest energy. We also identified a secondary wave direction as the filter direction which retained the next greatest energy in the filtered field, and that differed by at least 30 deg from the primary direction. From this analysis, we identified primary () and secondary () wave propagation directions at every voxel for both AP and LR excitations.
We then isolated the slow and fast shear waves in each of the primary and secondary directions. We determined the polarization directions of each slow and fast wave based on propagation direction (primary and secondary, n = 1,2) and fiber direction (Eqs. (8) and (9)). Slow and fast waves were then reconstructed by projecting the directionally filtered wave field, , onto the polarization direction (Eqs. (10) and (11))
| (8) |
| (9) |
| (10) |
| (11) |
Using the analysis above, there are eight possible wave fields (AP/LR, primary/secondary, slow/fast) that can be used to meet the criteria for successful anisotropic inversion. We determined if a voxel had sufficient data to meet these criteria if there were at least two slow waves and two fast waves with amplitude greater than 20% of the original motion amplitude and with propagation directions different by at least 15 deg [33]. We considered the number of voxels that met these criteria using both single excitations (AP or LR) and multiple excitations together (AP + LR).
Anisotropic Parameter Estimation.
In order to demonstrate that individual waves from multi-excitation MRE can be used to estimate anisotropic material parameters, we estimated , , and using an overdetermined system of equations (Eq. (12)). Specifically, we considered the relationships for both slow and fast wave speeds (Eqs. (6) and (7)) separately for each of the primary and secondary waves included in each excitation. This resulted in a system of eight equations comprising two polarizations (slow and fast) for each of two wave propagation directions (primary and secondary) for each of two excitations (AP and LR). Since the material parameters , , and are the same in each case, this system of equations can be solved to generate property estimates
| (12) |
Solving this system of equations requires estimates of the wave speed for each individual wave field, which we perform for each voxel. First, for a given voxel—i.e., —we directionally filtered the wave field from AP or LR excitation in the direction of the primary or secondary wave at that voxel (Fig. 2(a)), and then projected onto the slow or fast polarization direction to create an isolated wave field (Fig. 2(b))—e.g., . This wave field is input to the local direct inversion algorithm [38] to estimate the wave speed—e.g., —from which we extract the value only at the voxel of interest . This process is repeated for each voxel and for each of the additional wave fields, as seen in Fig. 2(c). Each of the angles, θ, describing the relationship between propagation direction and fiber angle were computed for each individual primary and secondary wave by This results in a system of equations (Eq. (12)) at each voxel. We use a least squares solution of this system at each voxel, including only the isolated wave fields that meet the amplitude threshold (see above), to estimate , , and at each voxel. We constrained values of to be positive between 0 and 8 kPa and left the other parameters unconstrained in the solution.
Fig. 2.
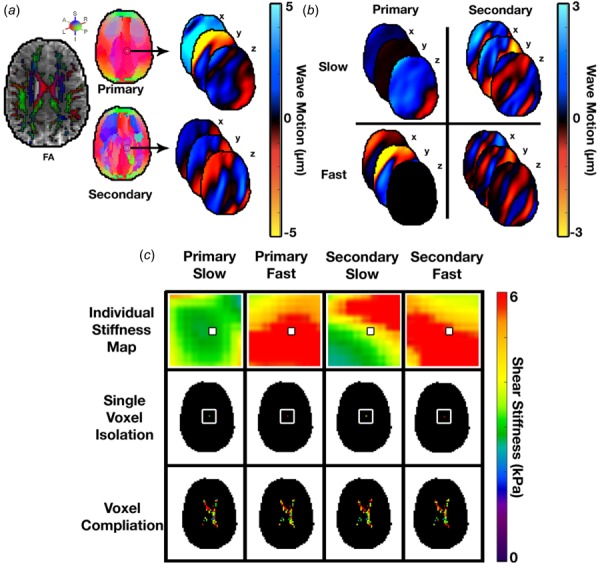
The approach used to determine voxelwise stiffness estimates from individual wave fields: (a) directional filters, based on the primary and secondary directions of a specific voxel, are applied to the wave field over the entire brain, providing two (primary and secondary) filtered fields; (b) slow and fast shear waves in those primary and secondary directions; (c) isolated section, outlined by the white box, of the stiffness map estimated for each of the slow and fast waves, at every voxel, and the stiffness map created by compiling results from individual inversions
Analysis.
We analyzed wave propagation throughout the brain, in white matter, and in an individual white matter tract—the body of the corpus callosum, which was chosen as it has highly aligned fibers and thus is likely to behave like an ITI material. The white matter mask was created using the FMRIB Automated Segmentation Tool (FAST) in the FMRIB Software Library (FSL) [39] to segment the T 1-weighted MPRAGE, which was then registered to the MRE data. Only voxels with fractional anisotropy (FA) > 0.25 from DTI were included. A white matter atlas in standard-space [40] was registered to the MRE data using the FMRIB Linear Image Registration Tool (FLIRT) in FSL [41] to create a mask of the corpus callosum body.
Results
Figure 3 depicts the identification of individual primary and secondary wave directions at each voxel throughout the brain. We plot the energy of the directionally filtered displacement field on a sphere; the maxima on the surface (“hot spots”), correspond to the dominant (primary and secondary) propagation directions. The two spheres show clearly that the AP and LR excitations result in different wave propagation directions at a single voxel. Figure 3(b) shows that the primary and secondary wave directions differ across the brain. Additionally, they are compared with the “average” propagation which is the weighted average of directions based on energy in each filter direction, which has been used previously to describe propagation direction [36]. Figure 3(c) compares the amplitudes of the primary and secondary waves, as well as the ratio between the two. Almost every voxel in the brain has a primary and secondary wave of at least 20% of the total wave amplitude: 98.8% of voxels from AP excitation and 99.2% of voxels from LR excitation had two waves above this threshold. Sharp discontinuities in wave direction are notable where two waves intersect and change their identification from primary to secondary, and vice versa. These regions are also reflected in the amplitude measurements where the two waves are of nearly identical amplitude.
Fig. 3.
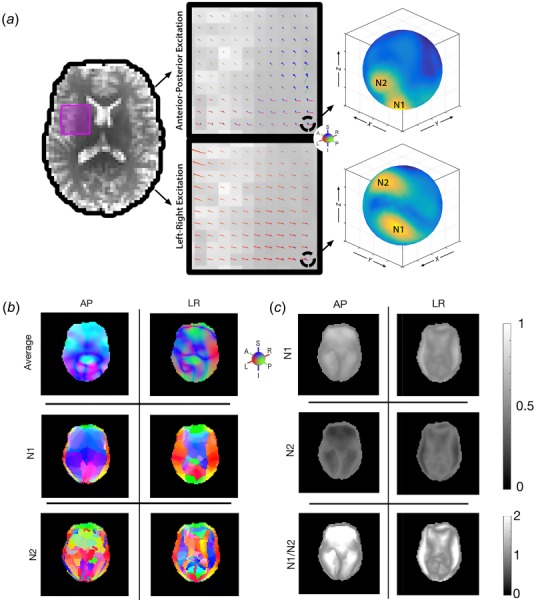
Illustration of individual wave propagation directions: (a) primary () and secondary () wave propagation directions for both AP and LR excitations within a single voxel. Note the spheres have different orientations between the two excitations; (b) average wave direction throughout the brain along with primary and secondary wave directions for both AP and LR excitations; (c) amplitudes of the primary and secondary waves and the ratio of the two for both AP and LR excitations.
Slow and fast waves were isolated in each of the individual primary and secondary wave directions. Figure 4 shows which voxels fit the criteria for anisotropic inversion based on the slow and fast waves from single (AP or LR) and multiple (AP + LR) excitations. Combining both excitations results in a substantially greater number of voxels that meet the minimum criteria compared to single excitations (Fig. 4(c)). Overall, 68.7% of white matter voxels meet the criteria from multiple excitations, and an even higher 73.8% meet the criteria in the corpus callosum body, while many fewer voxels met these criteria for single excitations (29–37% in each region for both AP and LR).
Fig. 4.
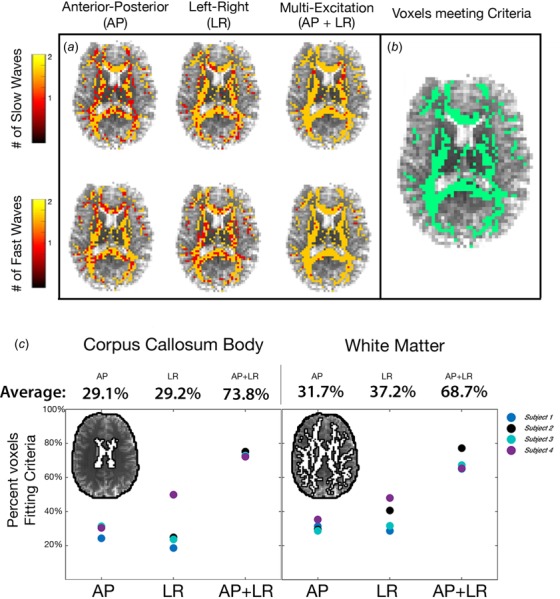
Overview of displacement data sufficient for anisotropic inversion in white matter: (a) number of slow and fast waves in each voxel for single excitations (AP or LR) and multiple excitations (AP+LR), and (b) white matter voxels with data meeting the minimum inversion criteria from both excitations. (c) Percentage of voxels across white matter and in the corpus callosum body, an individual white matter tract that fit the criteria for each excitation.
Using each of the slow and fast waves for each voxel that met the criteria, we solved the system of equations and estimated the three anisotropic parameters, , , and , in the corpus callosum body. Figure 5 shows the distributions of parameter values from each subject and all subjects pooled together. We found the mean = 3.78 kPa (95% CI: 3.67–3.90 kPa), mean = 0.151 (95% CI: 0.116–0.186), and mean = 0.099 (95% CI: 0.063–0.134). Figure 5(d) illustrates the relationship between and in each voxel, showing a weak positive correlation between the two (r = 0.38).
Fig. 5.
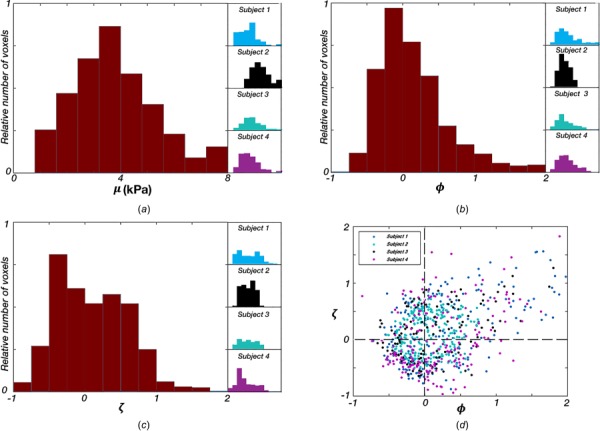
Distribution of anisotropic parameters (a) substrate shear modulus, , (b) shear anisotropy, , and (c) tensile anisotropy, , in the corpus callosum body for each subject and all subjects pooled together; (d) relationship between and in each voxel across all subjects (r = 0.38)
Discussion
In this paper, we examined the use of multi-excitation MRE to provide sufficient displacement data to estimate anisotropic mechanical parameters of the brain in vivo. This study builds on, and quantitatively extends, our previous observation that separate excitation directions in MRE give rise to different property estimates in white matter [34], which are presumably due to different propagation and polarization directions from each excitation.
By directionally filtering the MRE displacement fields in the brain, we were able to identify multiple shear waves with different propagation directions in most voxels. This is the first study to demonstrate the presence of at least two (primary and secondary) directions of wave propagation throughout the brain. In brain MRE, shear deformations are generated from the skull [36], and thus, the existence of many different source points likely gives rise to the multiple waves. Shear waves are also likely to originate from the Falx and Tentorium [36], which are stiff membranes between the cerebral hemispheres and the cerebrum and cerebellum, and perhaps even from the brainstem, which can move independently of the brain [42].
The two different excitation methods, AP and LR, lead to motion patterns that are distinct but share some common features. AP-excited primary wave propagation is predominantly in the z-direction (superior-inferior), while LR motion excites primary wave propagation predominantly in the x-direction (left-right). In both cases, there are sharp discontinuities in propagation direction away from the skull where the primary and secondary waves cross (and thus swap their identification). At these crossover regions, two waves exist with similar amplitude. The two excitations result in greater differences in secondary wave direction at the center of the brain where the propagating waves excited by contact with the cranium have converged and mix with waves from internal sources. These waves also dampen and lose amplitude causing the estimation of secondary waves in the center of the brain to be more affected by noise. In future work, these waves might be tracked individually back to their source points to better identify and characterize propagating waves, and potentially identify additional waves that may be useful in improving anisotropic MRE inversion.
By using multiple excitations, more propagation directions are generated, which increases the number of voxels that meet the minimum criteria for anisotropic inversion.
Single excitations (AP or LR) led to a much lower percentage of voxels that met the criteria as compared to the combination of multiple excitations (AP + LR). Thus, using multiple excitations likely increases the ability to determine the anisotropic properties of white matter at the individual tract or voxel level. However, two excitations did not provide sufficient data in every white matter voxel or across an entire white matter tract, and thus additional excitations providing unique displacement data may be required to completely map anisotropic tissue parameters at the voxel level throughout the brain. To combat the commensurate increase in scan time necessary for additional excitations, accelerated data collection may be required, perhaps through simultaneous acquisition of MRE displacement directions [43–45].
We demonstrated that multiple wave fields may be used to estimate anisotropic parameters in white matter by determining the wave speeds of individual slow and fast waves. In the corpus callosum body, we found the mean shear stiffness of 3.78 kPa. This estimate is slightly higher than two other recent estimates that used a different inversion technique without considering anisotropy [34,46], which may account for differences we observe in this work. We found mean shear anisotropy of 0.151, indicating that the shear modulus is 15.1% higher for shear in planes parallel to the fiber direction compared to planes normal to the fibers. We also found mean tensile anisotropy of 0.099, indicating that the elastic modulus is 9.9% higher parallel to the fiber direction. The recovered and values in each voxel were positively correlated indicating that the degree of shear and tensile anisotropy increases together, as we may expect for fibrous material like brain white matter.
Our estimate of is smaller than a similar report of in porcine white matter between 0.27 and 0.34 as reported by Schmidtet al. [24]. However, both and are more similar to equivalent parameters in the in vivo human corticospinal tract of = 0.14 and = 0.06 as reported by Romanoet al. [31]. The true in vivo parameters are potentially higher, indicating greater anisotropy, based on ex vivo mechanical testing [20], and the incomplete contrast recovery in our preliminary estimates is likely due to methodological factors. For instance, the resolution used in this study is lower than used in previous studies of white matter tracts [34,46,47], which likely impacts the accuracy and reliability of property maps in these small regions [48,49]. Ideally, future investigations should adopt higher resolution imaging methods to better resolve individual white matter tracts.
Additionally, while this initial attempt to estimate anisotropic parameters showed promising results, we also acknowledge several limitations. First, we used a direct inversion method to process individual wave fields. Direct inversion methods assume local tissue homogeneity [6] and thus introduce uncertainty at tissue boundaries, which is exacerbated by lower spatial resolution. Inversion methods specifically designed to model white matter anisotropy, such as the waveguide MRE method [31], may be potentially combined with multi-excitation MRE to provide more robust parameter estimates. Additionally, the nonlinear inversion method [19,50], which explicitly models tissue as a heterogeneous material and has been applied successfully to estimate local brain properties [46,49], may improve accuracy of measures in specific white matter tracts if formulated to include anisotropy. Advanced inversion methods will also allow us to incorporate data from multiple frequencies and model viscoelastic behavior of the anisotropic white matter [28,51]. More robust methods for LR excitation or additional excitations may improve feasibility and comfort in participants. Yin et al. [52] have previously used multiple active pneumatic drivers, in addition to multiple passive drivers arrayed around the head, in order to excite the brain in several directions; though the use of multiple active drivers can potentially lead to prohibitive equipment costs. Finally, future studies are needed to evaluate the consistency and reliability of parameter estimates through phantom studies, repeated measurements in healthy brains [46,49,53], and studies with a larger number of subjects to determine sensitivity to pathology.
Conclusions
This study is the first to investigate the use of multi-excitation MRE to estimate anisotropic parameters (, , and ) of an ITI material model of white matter. We found that each excitation results in distinct shear waves, in at least two propagation directions, and both “slow” (pure shear) and “fast” (quasi-shear) polarizations. Thus, by combining AP and LR excitations, shear wave data from most voxels in white matter was sufficient for anisotropic inversion. We demonstrated that by isolating individual waves and calculating their wave speeds we could estimate the three anisotropic parameters and recover values consistent with previous reports in white matter. Overall, these results suggest that multi-excitation MRE is a promising technique for providing data for anisotropic inversion and that this approach can be used in future work to more accurately and reliably map the mechanical properties of brain white matter in vivo.
Contributor Information
Daniel R. Smith, Department of Biomedical Engineering, University of Delaware, Newark, DE 19716
Charlotte A. Guertler, Department of Mechanical Engineering and Material Science, Washington University, St. Louis, MO 63130
Ruth J. Okamoto, Department of Mechanical Engineering and Material Science, Washington University, St. Louis, MO 63130
Anthony J. Romano, Naval Research Laboratory, Code 7160, Washington, DC 20375
Philip V. Bayly, Department of Mechanical Engineering and Material Science, Washington University, St. Louis, MO 63130
Curtis L. Johnson, Department of Biomedical Engineering, University of Delaware, Newark, DE 19716 e-mail: clj@udel.edu .
Funding Data
Office of Naval Research (Grant Nos. N00014-17-P-7001, N00014-18-P-7004, and N00014-18-1-2018; Funder ID: 10.13039/100000006).
Delaware INBRE Program (Grant No. P20-GM103446).
National Institutes of Health (Grant Nos. R01-EB027577 and R01-NS055951; Funder ID: 10.13039/501100000272).
National Science Foundation (Grant No. CMMI-1727412; Funder ID: 10.13039/100000001).
References
- [1]. Aoki, Y. , Inokuchi, R. , Gunshin, M. , Yahagi, N. , and Suwa, H. , 2012, “Diffusion Tensor Imaging Studies of Mild Traumatic Brain Injury: A Meta-Analysis,” J. Neurol. Neurosurg. Psychiatry, 83(9), pp. 870–876. 10.1136/jnnp-2012-302742 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2]. Wozniak, J. R. , Krach, L. , Ward, E. , Mueller, B. A. , Muetzel, R. , Schnoebelen, S. , Kiragu, A. , and Lim, K. O. , 2007, “Neurocognitive and Neuroimaging Correlates of Pediatric Traumatic Brain Injury: A Diffusion Tensor Imaging (DTI) Study,” Arch. Clin. Neuropsychol., 22(5), pp. 555–568. 10.1016/j.acn.2007.03.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3]. Rutgers, D. R. , Fillard, P. , Paradot, G. , Tadié, M. , Lasjaunias, P. , and Ducreux, D. , 2008, “Diffusion Tensor Imaging Characteristics of the Corpus Callosum in Mild, Moderate, and Severe Traumatic Brain Injury,” Am. J. Neuroradiol., 29(9), pp. 1730–1735. 10.3174/ajnr.A1213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Niogi, S. N. , Mukherjee, P. , Ghajar, J. , Johnson, C. , Kolster, R. A. , Sarkar, R. , Lee, H. , Meeker, M. , Zimmerman, R. D. , Manley, G. T. , and McCandliss, B. D. , 2008, “Extent of Microstructural White Matter Injury in Postconcussive Syndrome Correlates With Impaired Cognitive Reaction Time: A 3T Diffusion Tensor Imaging Study of Mild Traumatic Brain Injury,” Am. J. Neuroradiol., 29(5), pp. 967–973. 10.3174/ajnr.A0970 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Muthupillai, R. , Lomas, D. J. , Rossman, P. J. , Greenleaf, J. F. , Manduca, A. , and Ehman, R. L. , 1995, “Magnetic Resonance Elastography by Direct Visualization of Propagating Acoustic Strain Waves,” Science, 269(5232), pp. 1854–7. 10.1126/science.7569924 [DOI] [PubMed] [Google Scholar]
- [6]. Manduca, A. , Oliphant, T. E. E. , Dresner, M. A. A. , Mahowald, J. L. L. , Kruse, S. A. A. , Amromin, E. , Felmlee, J. P. P. , Greenleaf, J. F. F. , and Ehman, R. L. L. , 2001, “Magnetic Resonance Elastography: Non-Invasive Mapping of Tissue Elasticity,” Med. Image Anal., 5(4), pp. 237–254. 10.1016/S1361-8415(00)00039-6 [DOI] [PubMed] [Google Scholar]
- [7]. Mariappan, Y. K. , Glaser, K. J. , and Ehman, R. L. , 2010, “Magnetic Resonance Elastography: A Review,” Clin. Anat., 23(5), pp. 497–511. 10.1002/ca.21006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8]. Sack, I. , Beierbach, B. , Hamhaber, U. , Klatt, D. , and Braun, J. , 2008, “Non-Invasive Measurement of Brain Viscoelasticity Using Magnetic Resonance Elastography,” NMR Biomed., 21(3), pp. 265–271. 10.1002/nbm.1189 [DOI] [PubMed] [Google Scholar]
- [9]. Hiscox, L. V. , Johnson, C. L. , Barnhill, E. , McGarry, M. D. J. , Huston, J. , van Beek, E. J. R. , Starr, J. M. , and Roberts, N. , 2016, “Magnetic Resonance Elastography (MRE) of the Human Brain: Technique, Findings and Clinical Applications,” Phys. Med. Biol., 61(24), pp. R401–R437. 10.1088/0031-9155/61/24/R401 [DOI] [PubMed] [Google Scholar]
- [10]. Sandroff, B. M. , Johnson, C. L. , and Motl, R. W. , 2017, “Exercise Training Effects on Memory and Hippocampal Viscoelasticity in Multiple Sclerosis: A Novel Application of Magnetic Resonance Elastography,” Neuroradiology, 59(1), pp. 61–67. 10.1007/s00234-016-1767-x [DOI] [PubMed] [Google Scholar]
- [11]. Streitberger, K.-J. , Sack, I. , Krefting, D. , Pfüller, C. , Braun, J. , Paul, F. , and Wuerfel, J. , 2012, “Brain Viscoelasticity Alteration in Chronic-Progressive Multiple Sclerosis,” PLoS One, 7(1), p. e29888. 10.1371/journal.pone.0029888 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12]. Wuerfel, J. , Paul, F. , Beierbach, B. , Hamhaber, U. , Klatt, D. , Papazoglou, S. , Zipp, F. , Martus, P. , Braun, J. , and Sack, I. , 2010, “MR-Elastography Reveals Degradation of Tissue Integrity in Multiple Sclerosis,” Neuroimage, 49(3), pp. 2520–2525. 10.1016/j.neuroimage.2009.06.018 [DOI] [PubMed] [Google Scholar]
- [13]. Murphy, M. C. , Curran, G. L. , Glaser, K. J. , Rossman, P. J. , Huston, J. , Poduslo, J. F. , Jack, C. R. , Felmlee, J. P. , and Ehman, R. L. , 2012, “Magnetic Resonance Elastography of the Brain in a Mouse Model of Alzheimer's Disease: Initial Results,” Magn. Reson. Imaging, 30(4), pp. 535–539. 10.1016/j.mri.2011.12.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Murphy, M. C. , Huston, J. , Jack, C. R. , Glaser, K. J. , Manduca, A. , Felmlee, J. P. , and Ehman, R. L. , 2011, “Decreased Brain Stiffness in Alzheimer's Disease Determined by Magnetic Resonance Elastography,” J. Magn. Reson. Imaging, 34(3), pp. 494–498. 10.1002/jmri.22707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Lipp, A. , Trbojevic, R. , Paul, F. , Fehlner, A. , Hirsch, S. , Scheel, M. , Noack, C. , Braun, J. , and Sack, I. , 2013, “Cerebral Magnetic Resonance Elastography in Supranuclear Palsy and Idiopathic Parkinson's Disease,” NeuroImage Clin., 3, pp. 381–387. 10.1016/j.nicl.2013.09.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16]. Schregel, K. , Wuerfel, E. , Garteiser, P. , Gemeinhardt, I. , Prozorovski, T. , Aktas, O. , Merz, H. , Petersen, D. , Wuerfel, J. , and Sinkus, R. , 2012, “Demyelination Reduces Brain Parenchymal Stiffness Quantified In Vivo by Magnetic Resonance Elastography,” Proc. Natl. Acad. Sci. U. S. A., 109(17), pp. 6650–6655. 10.1073/pnas.1200151109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Weickenmeier, J. , de Rooij, R. , Budday, S. , Steinmann, P. , Ovaert, T. C. , and Kuhl, E. , 2016, “Brain Stiffness Increases With Myelin Content,” Acta Biomater., 42, pp. 265–272. 10.1016/j.actbio.2016.07.040 [DOI] [PubMed] [Google Scholar]
- [18]. Oliphant, T. E. , Manduca, A. , Ehman, R. L. , and Greenleaf, J. F. , 2001, “Complex-Valued Stiffness Reconstruction for Magnetic Resonance Elastography by Algebraic Inversion of the Differential Equation,” Magn. Reson. Med., 45(2), pp. 299–310. [DOI] [PubMed] [Google Scholar]
- [19]. McGarry, M. D. J. , Van Houten, E. E. W. , Johnson, C. L. , Georgiadis, J. G. , Sutton, B. P. , Weaver, J. B. , and Paulsen, K. D. , 2012, “Multiresolution MR Elastography Using Nonlinear Inversion,” Med. Phys., 39(10), pp. 6388–6396. 10.1118/1.4754649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Feng, Y. , Okamoto, R. J. , Namani, R. , Genin, G. M. , and Bayly, P. V. , 2013, “Measurements of Mechanical Anisotropy in Brain Tissue and Implications for Transversely Isotropic Material Models of White Matter,” J. Mech. Behav. Biomed. Mater., 23, pp. 117–132. 10.1016/j.jmbbm.2013.04.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21]. Feng, Y. , Okamoto, R. J. , Genin, G. M. , and Bayly, P. V. , 2016, “On the Accuracy and Fitting of Transversely Isotropic Material Models,” J. Mech. Behav. Biomed. Mater., 61, pp. 554–566. 10.1016/j.jmbbm.2016.04.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22]. Feng, Y. , Lee, C.-H. , Sun, L. , Ji, S. , and Zhao, X. , 2017, “Characterizing White Matter Tissue in Large Strain Via Asymmetric Indentation and Inverse Finite Element Modeling,” J. Mech. Behav. Biomed. Mater., 65, pp. 490–501. 10.1016/j.jmbbm.2016.09.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23]. Feng, Y. , Qiu, S. , Xia, X. , Ji, S. , and Lee, C.-H. , 2017, “A Computational Study of Invariant I5 in a Nearly Incompressible Transversely Isotropic Model for White Matter,” J. Biomech., 57, pp. 146–151. 10.1016/j.jbiomech.2017.03.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24]. Schmidt, J. L. , Tweten, D. J. , Badachhape, A. A. , Reiter, A. J. , Okamoto, R. J. , Garbow, J. R. , and Bayly, P. V. , 2018, “Measurement of Anisotropic Mechanical Properties in Porcine Brain White Matter Ex Vivo Using Magnetic Resonance Elastography,” J. Mech. Behav. Biomed. Mater., 79, pp. 30–37. 10.1016/j.jmbbm.2017.11.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25]. Feng, Y. , Clayton, E. H. , Chang, Y. , Okamoto, R. J. , and Bayly, P. V. , 2013, “Viscoelastic Properties of the Ferret Brain Measured In Vivo at Multiple Frequencies by Magnetic Resonance Elastography,” J. Biomech., 46(5), pp. 863–870. 10.1016/j.jbiomech.2012.12.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26]. Schmidt, J. L. , Tweten, D. J. , Benegal, A. N. , Walker, C. H. , Portnoi, T. E. , Okamoto, R. J. , Garbow, J. R. , and Bayly, P. V. , 2016, “Magnetic Resonance Elastography of Slow and Fast Shear Waves Illuminates Differences in Shear and Tensile Moduli in Anisotropic Tissue,” J. Biomech., 49(7), pp. 1042–1049. 10.1016/j.jbiomech.2016.02.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Tweten, D. J. , Okamoto, R. J. , Schmidt, J. L. , Garbow, J. R. , and Bayly, P. V. , 2015, “Estimation of Material Parameters From Slow and Fast Shear Waves in an Incompressible, Transversely Isotropic Material,” J. Biomech., 48(15), pp. 4002–4009. 10.1016/j.jbiomech.2015.09.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28]. Guo, J. , Hirsch, S. , Scheel, M. , Braun, J. , and Sack, I. , 2016, “Three-Parameter Shear Wave Inversion in MR Elastography of Incompressible Transverse Isotropic Media: Application to In Vivo Lower Leg Muscles,” Magn. Reson. Med., 75(4), pp. 1537–1545. 10.1002/mrm.25740 [DOI] [PubMed] [Google Scholar]
- [29]. Sinkus, R. , Tanter, M. , Catheline, S. , Lorenzen, J. , Kuhl, C. , Sondermann, E. , and Fink, M. , 2005, “Imaging Anisotropic and Viscous Properties of Breast Tissue by Magnetic Resonance-Elastography,” Magn. Reson. Med., 53(2), pp. 372–387. 10.1002/mrm.20355 [DOI] [PubMed] [Google Scholar]
- [30]. Green, M. A. , Geng, G. , Qin, E. , Sinkus, R. , Gandevia, S. C. , and Bilston, L. E. , 2013, “Measuring Anisotropic Muscle Stiffness Properties Using Elastography,” NMR Biomed., 26(11), pp. 1387–1394. 10.1002/nbm.2964 [DOI] [PubMed] [Google Scholar]
- [31]. Romano, A. , Scheel, M. , Hirsch, S. , Braun, J. , and Sack, I. , 2012, “In Vivo Waveguide Elastography of White Matter Tracts in the Human Brain,” Magn. Reson. Med., 68(5), pp. 1410–1422. 10.1002/mrm.24141 [DOI] [PubMed] [Google Scholar]
- [32]. Romano, A. , Guo, J. , Prokscha, T. , Meyer, T. , Hirsch, S. , Braun, J. , Sack, I. , and Scheel, M. , 2014, “In Vivo Waveguide Elastography: Effects of Neurodegeneration in Patients With Amyotrophic Lateral Sclerosis,” Magn. Reson. Med., 72(6), pp. 1755–1761. 10.1002/mrm.25067 [DOI] [PubMed] [Google Scholar]
- [33]. Tweten, D. J. , Okamoto, R. J. , and Bayly, P. V. , 2017, “Requirements for Accurate Estimation of Anisotropic Material Parameters by Magnetic Resonance Elastography: A Computational Study,” Magn. Reson. Med., 78(6), pp. 2360–2372. 10.1002/mrm.26600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34]. Anderson, A. T. , Van Houten, E. E. , McGarry, M. D. , Paulsen, K. D. , Holtrop, J. L. , Sutton, B. P. , Georgiadis, J. G. , and Johnson, C. L. , 2016, “Observation of Direction-Dependent Mechanical Properties in the Human Brain With Multi-Excitation MR Elastography,” J. Mech. Behav. Biomed. Mater., 59, pp. 538–546. 10.1016/j.jmbbm.2016.03.005 [DOI] [PMC free article] [PubMed]
- [35]. Manduca, A. , Lake, D. S. , Kruse, S. A. , and Ehman, R. L. , 2003, “Spatio-Temporal Directional Filtering for Improved Inversion of MR Elastography Images,” Med. Image Anal., 7(4), pp. 465–473. 10.1016/S1361-8415(03)00038-0 [DOI] [PubMed] [Google Scholar]
- [36]. Clayton, E. H. , Genin, G. M. , and Bayly, P. V. , 2012, “Transmission, Attenuation and Reflection of Shear Waves in the Human Brain,” J. R. Soc. Interface, 9(76), pp. 2899–910. 10.1098/rsif.2012.0325 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37]. Okamoto, R. J. , Romano, A. J. , Johnson, C. L. , and Bayly, P. V. , 2019, “Insights Into Traumatic Brain Injury From MRI of Harmonic Brain Motion,” J. Exp. Neurosci., 13, p. 117906951984044. 10.1177/1179069519840444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38]. Okamoto, R. J. , Clayton, E. H. , and Bayly, P. V. , 2011, “Viscoelastic Properties of Soft Gels: Comparison of Magnetic Resonance Elastography and Dynamic Shear Testing in the Shear Wave Regime,” Phys. Med. Biol., 56(19), pp. 6379–6400. 10.1088/0031-9155/56/19/014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Jenkinson, M. , Beckmann, C. F. , Behrens, T. E. J. , Woolrich, M. W. , and Smith, S. M. , 2012, FSL, Neuroimage, 62(2), pp. 782–790. 10.1016/j.neuroimage.2011.09.015 [DOI] [PubMed] [Google Scholar]
- [40]. Mori, S. , Oishi, K. , Jiang, H. , Jiang, L. , Li, X. , Akhter, K. , Hua, K. , Faria, A. V. , Mahmood, A. , Woods, R. , Toga, A. W. , Pike, G. B. , Neto, P. R. , Evans, A. , Zhang, J. , Huang, H. , Miller, M. I. , van Zijl, P. , and Mazziotta, J. , 2008, “Stereotaxic White Matter Atlas Based on Diffusion Tensor Imaging in an ICBM Template,” Neuroimage, 40(2), pp. 570–582. 10.1016/j.neuroimage.2007.12.035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41]. Jenkinson, M. , Bannister, P. , Brady, M. , and Smith, S. , 2002, “Improved Optimization for the Robust and Accurate Linear Registration and Motion Correction of Brain Images,” Neuroimage, 17(2), pp. 825–41. 10.1006/nimg.2002.1132 [DOI] [PubMed] [Google Scholar]
- [42]. Ji, S. , and Margulies, S. S. , 2007, “In Vivo Pons Motion Within the Skull,” J. Biomech., 40(1), pp. 92–99. 10.1016/j.jbiomech.2005.11.009 [DOI] [PubMed] [Google Scholar]
- [43]. Klatt, D. , Johnson, C. L. , and Magin, R. L. , 2015, “Simultaneous, Multidirectional Acquisition of Displacement Fields in Magnetic Resonance Elastography of the In Vivo Human Brain,” J. Magn. Reson. Imaging, 42(2), pp. 297–304. 10.1002/jmri.24806 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44]. Nir, G. , Sahebjavaher, R. S. , Sinkus, R. , and Salcudean, S. E. , 2015, “A Framework for Optimization-Based Design of Motion Encoding in Magnetic Resonance Elastography,” Magn. Reson. Med., 73(4), pp. 1514–1525. 10.1002/mrm.25280 [DOI] [PubMed] [Google Scholar]
- [45]. Guenthner, C. , Runge, J. H. , Sinkus, R. , and Kozerke, S. , 2018, “Analysis and Improvement of Motion Encoding in Magnetic Resonance Elastography,” NMR Biomed., 31(5), p. e3908. 10.1002/nbm.3908 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46]. Johnson, C. L. , McGarry, M. D. J. , Gharibans, A. A. , Weaver, J. B. , Paulsen, K. D. , Wang, H. , Olivero, W. C. , Sutton, B. P. , and Georgiadis, J. G. , 2013, “Local Mechanical Properties of White Matter Structures in the Human Brain,” Neuroimage, 79, pp. 145–152. 10.1016/j.neuroimage.2013.04.089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47]. Guo, J. , Hirsch, S. , Fehlner, A. , Papazoglou, S. , Scheel, M. , Braun, J. , and Sack, I. , 2013, “Towards an Elastographic Atlas of Brain Anatomy,” PLoS One, 8(8), p. e71807. 10.1371/journal.pone.0071807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48]. Johnson, C. L. , McGarry, M. D. J. , Van Houten, E. E. W. , Weaver, J. B. , Paulsen, K. D. , Sutton, B. P. , and Georgiadis, J. G. , 2013, “Magnetic Resonance Elastography of the Brain Using Multishot Spiral Readouts With Self-Navigated Motion Correction,” Magn. Reson. Med., 70(2), pp. 404–412. 10.1002/mrm.24473 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49]. Johnson, C. L. , Schwarb, H. , D.J. McGarry, M. , Anderson, A. T. , Huesmann, G. R. , Sutton, B. P. , and Cohen, N. J. , 2016, “Viscoelasticity of Subcortical Gray Matter Structures,” Hum. Brain Map., 37(12), pp. 4221–4233. 10.1002/hbm.23314 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50]. Solamen, L. M. , McGarry, M. D. , Tan, L. , Weaver, J. B. , and Paulsen, K. D. , 2018, “Phantom Evaluations of Nonlinear Inversion MR Elastography,” Phys. Med. Biol., 63(14), p. 145021. 10.1088/1361-6560/aacb08 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51]. Testu, J. , McGarry, M. D. J. , Dittmann, F. , Weaver, J. B. , Paulsen, K. D. , Sack, I. , and Van Houten, E. E. W. , 2017, “Viscoelastic Power Law Parameters of In Vivo Human Brain Estimated by MR Elastography,” J. Mech. Behav. Biomed. Mater., 74, pp. 333–341. 10.1016/j.jmbbm.2017.06.027 [DOI] [PubMed] [Google Scholar]
- [52]. Yin, Z. , Sui, Y. , Trzasko, J. D. , Rossman, P. J. , Manduca, A. , Ehman, R. , and Huston, J. , 2018, “In Vivo Charazterization of 3D Skull and Brain Motion Using MR Elastography With Multi-Excitation Head Driver,” 2018 Joint Annual Meeting ISMRM-ESMRMB, Paris, France, June 16–21, Abstract 8309. [Google Scholar]
- [53]. Murphy, M. C. , Huston, J. , Jack, C. R. , Glaser, K. J. , Senjem, M. L. , Chen, J. , Manduca, A. , Felmlee, J. P. , and Ehman, R. L. , 2013, “Measuring the Characteristic Topography of Brain Stiffness With Magnetic Resonance Elastography,” PLoS One, 8(12), p. e81668. 10.1371/journal.pone.0081668 [DOI] [PMC free article] [PubMed] [Google Scholar]


