Abstract
Characterization of the biomechanical behavior of the optic nerve head (ONH) in response to intraocular pressure (IOP) elevation is important for understanding glaucoma susceptibility. In this study, we aimed to develop and validate a three-dimensional (3D) ultrasound elastographic technique to obtain mapping and visualization of the 3D distributive displacements and strains of the ONH and surrounding peripapillary tissue (PPT) during whole globe inflation from 15 to 30 mmHg. 3D scans of the posterior eye around the ONH were acquired through full tissue thickness with a high-frequency ultrasound system (50 MHz). A 3D cross-correlation-based speckle-tracking algorithm was used to compute tissue displacements at ∼30,000 kernels distributed within the region of interest (ROI), and the components of the strain tensors were calculated at each kernel by using least square estimation of the displacement gradients. The accuracy of displacement calculation was evaluated using simulated rigid-body translation on ultrasound radiofrequency (RF) data obtained from a porcine posterior eye. The accuracy of strain calculation was evaluated using finite element (FE) models. Three porcine eyes were tested showing that ONH deformation was heterogeneous with localized high strains. Substantial radial (i.e., through-thickness) compression was observed in the anterior ONH and out-of-plane (i.e., perpendicular to the surface of the shell) shear was shown to concentrate in the vicinity of ONH/PPT border. These preliminary results demonstrated the feasibility of this technique to achieve comprehensive 3D evaluation of the mechanical responses of the posterior eye, which may provide mechanistic insights into the regional susceptibility in glaucoma.
1. Introduction
Glaucoma is a neurodegenerative disease and one of the leading causes of irreversible blindness worldwide [1]. The initial axonal damage in glaucoma is thought to occur within the optic nerve head (ONH), particularly at the level of the lamina cribrosa (LC), which is a mesh-like structure composed of collagen beams through which the axons traverse the scleral canal [2,3]. High intraocular pressure (IOP) is known as a primary risk factor for glaucoma onset and progression. Studies have confirmed the benefit of lowering IOP in glaucoma patients, even in those without an overtly high IOP [4,5]. IOP-related mechanical insult is likely a driving force in the disease process of glaucoma [6–8]. Characterization of the biomechanical behavior of the ONH in response to IOP elevation is thus important for understanding glaucoma susceptibility.
Measuring ONH deformation is a challenging task given its complex tissue composition and structure. Important efforts have been made in recent years using various imaging modalities to measure ONH deformation, including histomorphometry [9], confocal microscopy [10], optical coherence tomography [11–14], microcomputed tomography [15], second harmonic generation (SHG) imaging [16,17], and electron speckle pattern interferometry [18,19]. High-resolution images can be generated using these techniques, but tissue penetration depth and/or displacement sensitivity are often limited. Our laboratory has developed a high-frequency ultrasound elastography technique to quantify the deformation of ocular tissues, including the cornea [20,21], sclera [22,23], and ONH [24,25]. High-frequency ultrasound imaging at 50–55 MHz has a unique combination of field of view (up to 10 mm), penetration depth (1–2 mm), and spatial resolution (10 s of micrometers) which allows us to image the ONH and the surrounding peripapillary tissue (PPT) simultaneously and through the entire tissue depth with excellent contrast. Our previous studies have reported an accuracy of less than 10% error for a 0.5 μm vertical (i.e., the direction of sound propagation) displacement using correlation-based high-frequency ultrasound speckle tracking (center frequency = 55 MHz) [21]. This technique detects strains down to 0.01% vertically and 0.025% horizontally (i.e., the direction perpendicular to sound propagation) with an error less than 10% comparing calculated and true strains using simulated radiofrequency (RF) data [21].
Using this tool, we have reported 2D ultrasound elastography mapping of the deformation of ONH and PPT in porcine [24] and human donor eyes [25], showing a through-thickness compression concentrated in the anterior ONH and a posterior bending/shear concentrated in the peripheral ONH and the PPT near the scleral canal. Our 2D studies only evaluated one transverse cross section of the posterior eye. In this study, we aimed to apply a three-dimensional (3D) ultrasound elastographic technique to obtain more comprehensive mapping and visualization of the displacements and strains within and around the ONH during IOP elevation in porcine globes. The 3D elastography method was further developed to include calculations of strains in a spherical coordinate system that coincides with the anatomy of the posterior eye. In addition, we validated the displacement and strain accuracy of the 3D speckle tracking method for tissue regions with heterogeneous properties as seen in the posterior eye, using simulated displacements and finite element (FE) modeling.
2. Method
2.1. Experimental Testing in Porcine Eyes.
Three porcine globes from animals between 4 and 6 months old were obtained from a U. S. Department of Agriculture-approved abattoir under Hazard Analysis and Critical Control Point guidelines (SiouxPreme Packing Co., Sioux City, IA). The globes were immersed in saline and kept cold at 4 °C during shipping, and all eyes were tested within 48 h post mortem at room temperature. The optic nerve was trimmed to be flush with the sclera for ultrasound imaging of the ONH from the posterior side (Fig. 1). Whole globes were mounted in a custom-built holder with the ONH facing up. Two spinal needles were inserted near the equator of the globe and secured the eye to the holder (Fig. 1(a)). Two 20 G needles were inserted into the anterior chamber of the eye from the corneal limbus, one connected to a programmable syringe pump (Ph.D. Ultra, Harvard Apparatus, Holliston, MA) to control IOP, and the other connected to a pressure sensor (P75, Harvard Apparatus, MA) to continuously record IOP. The eye holder was immersed in 0.9% saline to maintain tissue hydration and facilitate propagation of ultrasound waves.
Fig. 1.
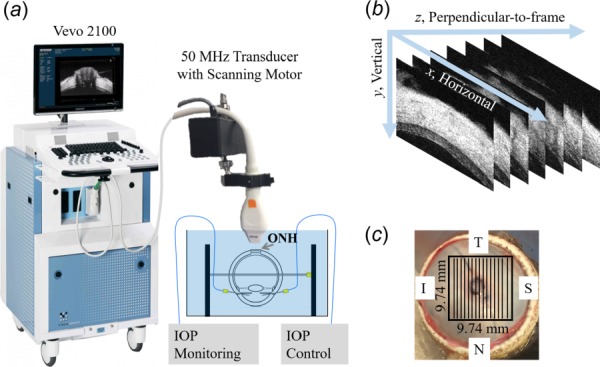
(a) Experimental setup for inflation testing with ultrasound imaging of the ONH and surrounding peripapillary tissues. IOP = intraocular pressure. (b) Imaged volume composed of stacked 2D ultrasound frames. (c) Posterior view of an eye showing trimmed optic nerve and the scanned region (black box). T = temporal, S = superior, N = nasal, I = inferior.
The globes were first preconditioned with 20 pressure cycles from 15 to 30 mmHg at 2 s per cycle, and then equilibrated at 15 mmHg for 30 min prior to inflation testing. Inflation tests were performed from a baseline IOP of 15 mmHg, and raised to 17, 19, 22, 25, and 30 mmHg. At each IOP level, a 3D ultrasound scan was acquired by using a Vevo 2100 ultrasound imaging system (50 MHz, FUJIFILM VisualSonics, Inc., Toronto, Canada). During image acquisition, each frame of RF data was sampled with an interval of 1.5 μm in the vertical direction and 19 μm in the horizontal direction. For posterior eye 3D scanning, each frame was 5 mm (vertical) by 9.74 mm (horizontal) in size. 307 frames with a step size of 32 μm (total width of 9.74 mm, perpendicular-to-frame) were acquired to build the 3D volume (Fig. 1(b)), and the scans covered a 9.74 × 9.74 mm2 region of the posterior eye centered at the ONH (Fig. 1(c)). The transverse frame was oriented either along the nasal-temporal or the superior–inferior meridians and was randomized among tested eyes.
2.2. Three-Dimensional Ultrasound Speckle Tracking.
Three-dimensional correlation-based ultrasound speckle tracking has been developed and reported previously [22]. Briefly, speckle tracking was performed at the level of the radiofrequency data which are digitized voltage values corresponding to the amplitude of the received ultrasound signal. A region of interest (ROI) was defined within the scanned volume at the reference/baseline IOP by fitting two concentric spheres that matched approximately the anterior and posterior surface of the sclera (more details are described Sec. 2.3). It is noted that the retina was largely excluded from the speckle tracking ROI in this study. Within the ROI, the RF data were divided into kernels, each containing 51 × 31 × 31 voxels (vertical × horizontal × perpendicular-to-frame), or approximately 75 μm × 570 μm × 960 μm in size. This kernel size was chosen because our previous studies showed that it achieves the best combination of accuracy and signal-to-noise ratio for strain estimation in all directions [22]. The kernels were overlapped by 50% to improve spatial resolution of the strain image [26], resulting in about 30,000 kernels within the ROI. To compute the displacements of each kernel, normalized cross-correlation coefficient was used to evaluate the similarity of the speckle patterns in volumes acquired at successive IOPs within a designated search window. The kernel center corresponding to the maximum correlation coefficient was used as the new location of the kernel, and spline interpolation was used to achieve subvoxel resolution.
2.3. Three-Dimensional Strain Estimation and Coordinate Transform.
The displacement vectors were calculated in Cartesian coordinates with components denoted as , where x is the horizontal direction, y is the vertical direction, and z is the perpendicular-to-frame direction. The displacement gradients were obtained by a 3D least squares method based on the measured displacement data [27]
| (1) |
where is the local intercept constants used during fitting. After obtaining all the displacement gradients (, the Green strain tensor components (with quadratic terms) were calculated as follows:
| (2) |
| (3) |
Other components of the Cartesian strain tensor , , ,,, and were determined likewise. To convert the Cartesian coordinate to the spherical coordinate system that better corresponds to the anatomy of the posterior eye, two concentric spherical shells were fitted to the region of ONH and peripapillary tissue at the baseline IOP. The outer surface of the shell was reconstructed by manually selecting five points on the posterior boundary of peripapillary sclera in each selected scan at the kernel center of the ultrasound frames. A sphere was fitted to a total of 105 spatial points on the outer shell surface. Similarly, the inner surface of the shell was fitted with a sphere that shares the same center as the outer shell surface and matches the anterior boundary of the scanned peripapillary sclera. The spherical coordinate system has base vectors denoted as , as shown in Fig. 2, where is the circumferential direction, is the meridional direction, and is the radial direction (through-thickness direction). The transformations between spherical strain tensor and Cartesian strain tensor take the form in matrix
| (4) |
Fig. 2.
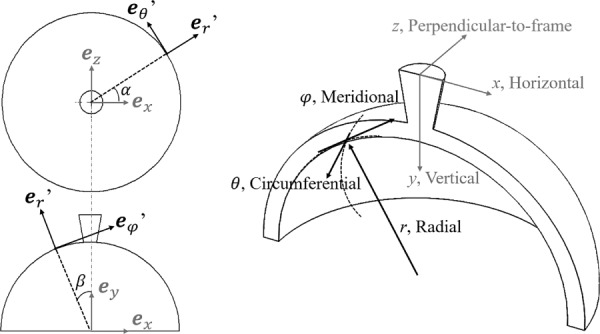
Definition of the spherical coordinate system in the region of ONH and peripapillary tissue and the Cartesian coordinate system based on transducer scanning directions in the experiments
where the components of the transformation matrix are
| (5) |
where is the Cartesian base vector, is the azimuth angle (in the direction) and is the elevational angle (in the direction).
2.4. Evaluation of Displacement Accuracy Using Simulated Rigid-Body Translation.
We have previously evaluated the accuracy of the 3D ultrasound speckle tracking algorithm in displacement calculations using simulated ultrasound RF data with uniform echogenicity [22]. The posterior eye has a heterogeneous appearance in ultrasound signal intensity, with the ONH having much weaker echogenicity than the PPT. To test whether the displacement calculations were consistent across regions of different echo strengths, the 3D ultrasound RF data of a posterior porcine eye was used to simulate rigid-body translation. The volume was translated by a uniform amount of 0, 1, and 2 voxels in each coordinate direction. The displacements were calculated using the 3D speckle tracking algorithm described in Sec. 2.2 and compared with the intended displacements.
2.5. Evaluation of Strain Accuracy Using Finite Element Simulation.
Finite element models were used to generate distributive displacement data and strain data in spherical thin shell structures inflated from 15 to 25 mmHg. A spherical thin shell with a uniform thickness of 0.9 mm and an internal radius of 11.0 mm (typical dimensions of porcine posterior eyes estimated from ultrasound scans) was built and meshed with eight-node structural solid element (SOLID185, Ansys, Inc., PA). The shell material was assumed isotropic, homogeneous, and near-incompressible with a modulus of 5 MPa. To optimize the simulation efficiency and accuracy, a mesh convergence study was conducted. A mesh with 40,500 elements was chosen for the homogeneous shell. One eighth of the sphere was modeled with assumption of axisymmetry. The node coordinates (x, y, z) and the corresponding displacements () from the FE model were imported into our strain estimation algorithm (Eqs. (1)–(3)) to calculate the components of the Cartesian strain tensor , , ,, and at each node. The calculated strains were compared with those obtained from the FE model output. Similarly, a thin shell with a 4.7 mm inclusion (size of porcine ONH estimated from ultrasound scans) of more compliant material (modulus = 1 MPa) was built to simulate a non-homogeneous structure like the posterior eye and a mesh with 42,000 elements was used based on convergence study. The spherical strain tensor components , , ,, and of each node obtained from FE simulation were also compared with those calculated from the coordinate transform (Cartesian-to-Spherical) algorithm (Eqs. (4)–(5)).
3. Results
The calculated displacements based on 3D speckle tracking of the RF data obtained by scanning a porcine posterior eye were −0.0049±0.0059, −0.0011±0.0101, and −0.0037±0.0163 voxels (about −0.093 μm, −0.0017 μm, and −0.11 μm) for 0 voxel uniform translation in the x, y, z directions. The same absolute errors were found for uniform translations of 1 or 2 voxels, similar to our previous results using simulated RF data of a uniform sclera-like structure [22]. The small displacement errors were randomly distributed in the volume, and not different in regions of ONH, PPT, or the transition between the two.
Strain estimations from the least-square methods we developed agreed well with the output of the FE model. An example of the horizontal strain is shown in Fig. 3. In the homogeneous shell, the strains ranged from to , while in the inhomogeneous shell the strain ranged from to . The absolute differences between the estimated strains and the FE model outputs were very small for the homogeneous shells, with mean and standard deviation of ± . The difference maps showed minimal difference (green color) throughout the volume comparing the strains at each kernel. For the inhomogeneous shell with a weaker inclusion, the absolute differences were also small, with mean and standard deviation of ±. At the boundary between the weaker inclusion and the stiffer shell, there appeared a region of small difference (light blue). The average absolute strain difference in this transition region was , about 4% of the actual strain in this region. All other strain components yielded similar outcome and are not shown.
Fig. 3.
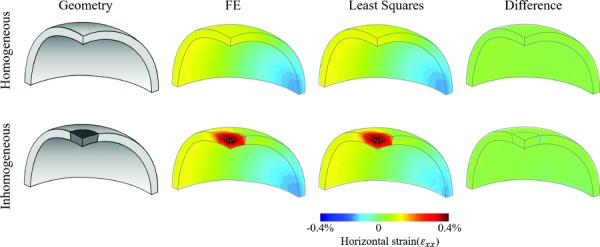
Geometry of a homogeneous thin shell (top row) and one with a weaker inclusion at the top center (dark gray and bottom row), and the corresponding maps of horizontal strains obtained from least squares estimation and FE modeling. Difference maps were generated to compare the strains at each node.
Spherical strains converted from those in Cartesian coordinates matched well with the spherical strains directly outputted from the FE model. With radial strains ranging from to and to for the homogeneous shell and the inhomogeneous shell, respectively, and the absolute strain differences were ± and ±, respectively. All other strain components yielded similar outcome and are not shown.
Three-dimensional maps of displacements and strains at 30 mmHg in a representative porcine eye are presented in Fig. 4. The ONH region had substantially larger vertical displacement as compared to the surrounding peripapillary tissue. Negative radial strains , indicating through-thickness compression, were seen within the volume except for the posterior portion of the ONH. Higher meridional strain , circumferential-radial shear , and meridional-radial shear were observed in the vicinity of the conjunction of the ONH and PPT than the rest of the volume. Circumferential strain and circumferential-meridional shear were minimal throughout the scanned volume. These patterns were similar in all tested porcine eyes.
Fig. 4.
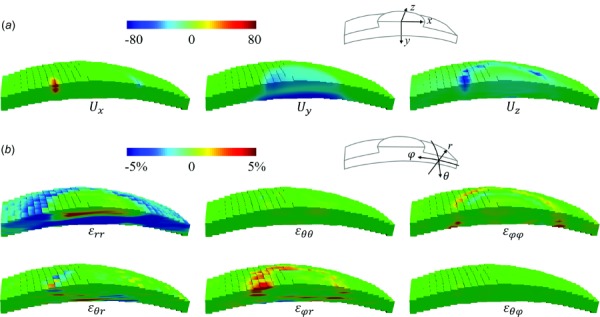
(a) Displacements at 30 mmHg in the scanned volume of a porcine posterior eye. (b) Strains of the same eye in spherical coordinates. Note that the retina has been largely excluded from the ROI.
The 2D cross-sectional view of the vertical displacements in the center frame of the scanned volumes is shown in Fig. 5. Different magnitudes of ONH posterior displacement were observed in different eyes, but in all eyes the ONH displaced more posteriorly relative to the surrounding PPT when inflated to 30 mmHg.
Fig. 5.
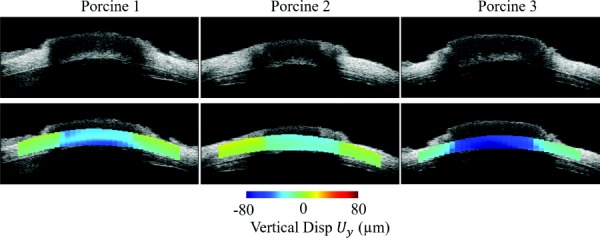
Cross-sectional view of the vertical displacement () maps for the three measured porcine eyes at 30 mmHg. Negative displacement corresponds to posterior movement. The ONH moved more posteriorly than the PPT in all eyes despite different magnitudes.
Figure 6 shows the cross-sectional views of radial strain , meridional strain and shear strain in the coronal (en face) and transverse (both superior–inferior and nasal-temporal) cross section in a tested porcine eye. All three types of strains appeared heterogeneous and higher strains were localized.
Fig. 6.
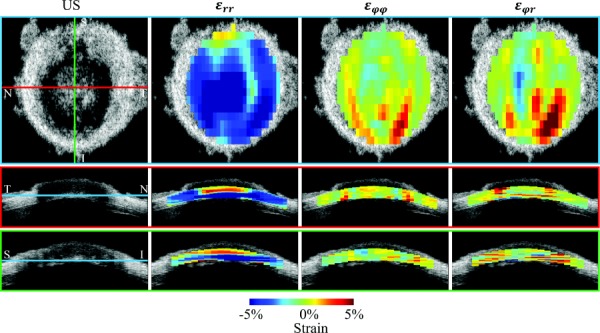
Top row shows the strain distribution in a coronal section (en-face view) at a depth indicated by the blue lines shown in the corresponding ultrasound images (US) below. Middle and bottom rows show the transverse views corresponding to the red and green lines in the ultrasound image in the top row. Substantial radial strains appeared to distribute across the cross section and were largely compressive. Meridional strain and shear strain appeared to concentrate in the ONH and PPT conjunction, and through a certain depth. All strains were from a representative porcine eye during inflation from 15 mmHg to 30 mmHg. Strains were plotted at the level of kernels without smoothing.
Since the strains were not uniform in magnitude throughout the volume, a further analysis was performed to evaluate the number and percentage of kernels that had strains larger than 3%. Table 1 shows the results for each type of strains within the ROI volume in each tested porcine eye. Radial strains had the largest percentage of kernels with strains over 3%, while circumferential strains were minimal throughout the volume.
Table 1.
Percentage of kernels with a strain magnitude greater than 3%
| Percentage % | Radial | Circumferential | Meridional | Shear | Shear | Shear |
|---|---|---|---|---|---|---|
| Porcine 1 | 32.44 | 0.06 | 1.96 | 7.95 | 4.17 | 0.13 |
| Porcine 2 | 46.58 | 0.23 | 4.72 | 13.56 | 11.23 | 0.17 |
| Porcine 3 | 27.63 | 0.79 | 8.21 | 19.74 | 16.12 | 0.52 |
The ONH region was also manually segmented out in frame images acquired at the reference pressure based on signal intensity difference between the ONH and the surrounding PPT [24,25], since the collagenous sclera is more echogenic than the neural tissue within the ONH. The average strains within the ONH region increased from 15 to 30 mmHg and the increase was approximately linear within this range of pressure (Fig. 7).
Fig. 7.
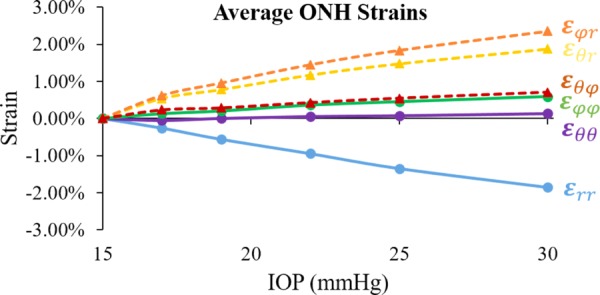
Average strains (n = 3) within the porcine ONH during inflation
4. Discussion
A high-frequency ultrasound elastographic technique was developed in this study to obtain 3D characterization of displacements and strains in the ONH and the surrounding PPT during IOP elevation. The accuracy of displacement and strain calculations were evaluated using simulations and finite element models. Using this technique, we quantified the inflation response of the porcine ONH and PPT and mapped out all components of the 3D displacements and strains through full tissue thickness.
The overall deformation patterns in 3D resembled those previously reported in 2D studies [24]. First, substantial compression (i.e., negative radial strain ) appeared a dominant deformation mode of the anterior ONH across all quadrants of the eye, while the posterior ONH experienced less compression and even expansion in the through-thickness direction (i.e., positive radial strain) (Fig. 4). This might be due to tissue permeability and swelling [28,29], and was consistent with our previous 2D findings [24]. Previous phase-contrast microcomputed tomography imaging reported a similar trend of decreasing compressive strains within the LC from anterior to posterior [15]. The large penetration depth and high displacement sensitivity of high-frequency ultrasound allowed us to resolve the changes in radial strains through tissue thickness, which is difficult with other techniques such as optical coherence tomography or SHG. The porcine LC was located in the anterior region of the ONH, as shown in our histology results in a previous study [24] and reported by others [30,31]. This may suggest that the LC was under compression in the porcine eye during IOP elevation. In the 2D study of human eyes, we also found anterior concentration of compression within the ONH [25], but it remains unclear whether LC was within the region of compression in the human eye [32]. Nonetheless, it is likely that the through-thickness compression in the anterior ONH may directly impact axonal transport [33,34], astrocyte reactivity [35,36] and capillary blood flow [37] in this critical site of glaucomatous injury. Future studies are needed to further investigate these impacts on the cellular and microstructural level.
The 3D view of strain distribution (Fig. 4) showed that high out-of-plane shear strains were clustered in the peripheral ONH, a phenomenon also found in our previous 2D study in porcine eyes [24]. The 3D technique allowed us to evaluate all components of the strain tensor, and the results showed that the three different types of shears appeared to have different magnitudes. To our best knowledge, this is the first report of all three shear components within the ONH. Previous SHG methods have reported in-plane shear, but had difficulty determining the out-of-plane responses due to the limited field of view in that direction [16,17]. Our results showed that the out-of-plane shear was more substantial than the other two shear components, while the in-plane shear was minimal (Fig. 4 and Table 1). Peripheral concentration of shear within the ONH was also observed in human donor eyes [25]. The substantially higher shear at the peripheral ONH may underlie the higher susceptibility of the peripheral optic nerve axon bundles characteristic to glaucoma. This transition region between ONH and PPT is also where disk hemorrhage and LC defects often occur, suggesting that out-of-plane shear could be potentially linked to these localized damages. A more detailed evaluation of the strain maps within the en-face view of the ONH (Fig. 6) showed that shear strain was not evenly distributed in the different quadrants. For example, in the porcine eye shown in Fig. 6, the shear strains were concentrated in the inferior-temporal quadrant. Future studies in a larger sample size are needed to analyze regional variations and potential link to earlier glaucomatous damage in certain regions [18,38,39].
With the 3D technique, we were able to determine both the circumferential and the meridional strains (Fig. 4). Although both of these in-plane strains were small, the meridional strains appeared to be larger and localized in the ONH/PPT junction, while the circumferential strains were minimal throughout the volume likely due to the collagen annulus ring surrounding the ONH [40,41].
As discussed above, one primary feature we observed about ONH deformation was the heterogeneity through the volume and the local concentrations of high strains. It is, therefore, important to validate the strain measurements and calculations in a heterogeneous structure like the posterior eye. We have previously evaluated the 3D displacement accuracy with simulated ultrasound RF data for a homogeneous structure with strong, sclera-like echogenicity [22]. The echogenicity of the posterior eye is not uniform and the ONH has weaker echogenicity than that of sclera due to its more complex structure and the presence of noncollagenous tissues. Our results from translating an experimentally acquired posterior eye RF volume data showed that the displacement accuracy of the 3D speckle tracking algorithm remained very high throughout the volume, similar to what we found previously using simulated RF data from a homogeneous model [22]. We previously evaluated the 3D strain accuracy using Field II simulation [42,43] to generate reference ultrasound RF volumes and those deformed at different levels of uniform strains. In this study, we evaluated strain accuracy by comparing with the outputs of finite element models at each kernel. Our results showed very small difference, comparing kernel to kernel, between the least squares estimated strains using our algorithm, and the calculations from the FE models. It is noted that the slightly larger error in the inhomogeneous shell model at the boundary between the weaker inclusion and the stiffer shell was much smaller than the strains we saw experimentally during porcine eye inflation, thus unlikely to cause significant error in this region.
This study has a few limitations. First, ex vivo testing could not fully represent the in vivo configuration, including the absence of cerebrospinal fluid pressure (CSFP), central retinal artery blood pressure, and tension on the optic nerve. Sensitivity study of the ONH biomechanical environment with computational models suggested that the overall effect of blood pressure is about 600 times smaller than that of IOP [44]. Optic nerve tension may have a strong influence on LC displacement but experimental data on how it interacts with IOP are yet to be obtained. CSFP may also have a significant effect but current computational and experimental studies showed that the effect was mostly concentrated posterior to the LC [45,46]. Nonetheless, future studies are needed to evaluate how changes in CSFP and optic nerve tension may modify the 3D strain response we observed in this study. Another limitation is the small sample size. This study focused on the 3D method validation with initial, proof-of-concept results on the biomechanical behavior of porcine globes to demonstrate the feasibility of this approach. 3D inflation responses of human ONH are currently being acquired and analyzed in our laboratory, to generate a more comprehensive analysis of the regional variations, including quadrant- and depth-dependent variations in ONH mechanical response to IOP. Third, a limited pressure range (from 15 to 30 mmHg) was used in the experiments. Although this range provides information of how the eye deforms from normal to elevated pressure, the strains were not calculated from an unloaded state. The average strains (averaged over the entire measured volume within the ONH) showed a nearly linear relationship to IOP (Fig. 7). Our previous 2D study showed that all strains (through-thickness, in-plane and shear) within the ONH increased nonlinearly when IOP was elevated from 5 to 30 mmHg [24]. Fourth, ultrasound imaging, even at the high frequency used in this study, has a limited spatial resolution. Our system has an axial resolution of 30 μm and a lateral resolution of 65 μm. This makes it impossible to resolve very small structures such as LC beams in the ultrasound images, while optical methods such as SHG has an advantage.
In summary, a 3D ultrasound speckle tracking technique has been successfully implemented and validated to quantify the deformation of porcine ONH. This technique has a greater penetration than achievable with optical techniques, offering an opportunity to image the responses through the full thickness of the posterior ocular shell. The validation studies confirmed a very high displacement and strain accuracy, enabled by RF data analysis of high-frequency ultrasound. These preliminary results demonstrated the feasibility of this technique to achieve comprehensive 3D evaluation of the mechanical responses of the posterior eye.
Contributor Information
Yanhui Ma, Department of Biomedical Engineering, Ohio State University, 1080 Carmack Road, Columbus, OH 43210 e-mail: ma.1634@osu.edu .
Elias Pavlatos, Department of Biomedical Engineering, Ohio State University, 1080 Carmack Road, Columbus, OH 43210 e-mail: pavlatos.2@osu.edu .
Keyton Clayson, Department of Biomedical Engineering, Ohio State University, 1080 Carmack Road, Columbus, OH 43210 e-mail: clayson.2@osu.edu .
Sunny Kwok, Department of Biomedical Engineering, Ohio State University, 1080 Carmack Road, Columbus, OH 43210 e-mail: kwok.55@osu.edu .
Xueliang Pan, Department of Biomedical Informatics, Ohio State University, 1800 Cannon Drive, Columbus, OH 43210 e-mail: jeff.pan@osumc.edu .
Jun Liu, Department of Biomedical Engineering, Ohio State University, 1080 Carmack Road, Columbus, OH 43210 e-mail: liu.314@osu.edu .
Funding Data
National Institutes of Health (NIH; Bethesda, MD, USA) (Grant Nos. RO1EY020929 and NIH RO1EY025358; Funder ID: 10.13039/100000053).
References
- [1]. Quigley, H. A. , 1996, “Number of People With Glaucoma Worldwide,” Br. J. Ophthalmol., 80(5), pp. 389–393. 10.1136/bjo.80.5.389 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2]. Nickells, R. W. , Howell, G. R. , Soto, I. , and John, S. W. M. , 2012, “Under Pressure: Cellular and Molecular Responses During Glaucoma, A Common Neurodegeneration With Axonopathy,” Annu. Rev. Neurosci., 35(1), pp. 153–179. 10.1146/annurev.neuro.051508.135728 [DOI] [PubMed] [Google Scholar]
- [3]. Quigley, H. A. , Addicks, E. M. , Green, W. R. , and Maumenee, A. E. , 1981, “Optic Nerve Damage in Human Glaucoma—II: The Site of Injury and Susceptibility to Damage,” Arch. Ophthalmol., 99(4), pp. 635–649. 10.1001/archopht.1981.03930010635009 [DOI] [PubMed] [Google Scholar]
- [4]. Anderson, D. R. , Drance, S. M. , and Schulzer, M. , 1998, “Comparison of Glaucomatous Progression Between Untreated Patients With Normal-Tension Glaucoma and Patients With Therapeutically Reduced Intraocular Pressures,” Am. J. Ophthalmol., 126(4), pp. 487–497. 10.1016/S0002-9394(98)00223-2 [DOI] [PubMed] [Google Scholar]
- [5]. Heijl, A. , Leske, M. C. , Bengtsson, B. , Hyman, L. , Bengtsson, B. , and Hussein, M. , 2002, “Reduction of Intraocular Pressure and Glaucoma Progression: Results From the Early Manifest Glaucoma Trial,” Arch. Ophthalmol., 120(10), pp. 1268–1279. 10.1001/archopht.120.10.1268 [DOI] [PubMed] [Google Scholar]
- [6]. Burgoyne, C. F. , Downs, J. C. , Bellezza, A. J. , Suh, J.-K. F. , and Hart, R. T. , 2005, “The Optic Nerve Head as a Biomechanical Structure: A New Paradigm for Understanding the Role of IOP-Related Stress and Strain in the Pathophysiology of Glaucomatous Optic Nerve Head Damage,” Prog. Retin. Eye Res., 24(1), pp. 39–73. 10.1016/j.preteyeres.2004.06.001 [DOI] [PubMed] [Google Scholar]
- [7]. Campbell, I. C. , Coudrillier, B. , and Ethier, C. R. , 2014, “Biomechanics of the Posterior Eye: A Critical Role in Health and Disease,” ASME J. Biomech. Eng., 136(2), p. 21005. 10.1115/1.4026286 [DOI] [PubMed] [Google Scholar]
- [8]. Downs, J. C. , 2015, “Optic Nerve Head Biomechanics in Aging and Disease,” Exp. Eye Res., 133, pp. 19–29. 10.1016/j.exer.2015.02.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Yang, H. , Downs, J. C. , Sigal, I. A. , Roberts, M. D. , Thompson, H. , and Burgoyne, C. F. , 2009, “Deformation of the Normal Monkey Optic Nerve Head Connective Tissue After Acute IOP Elevation Within 3-D Histomorphometric Reconstructions,” Invest. Ophthalmol. Vis. Sci., 50(12), pp. 5785–5799. 10.1167/iovs.09-3410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Albon, J. , Purslow, P. P. , Karwatowski, W. S. S. , and Easty, D. L. , 2000, “Age Related Compliance of the Lamina Cribrosa in Human Eyes,” Br. J. Ophthalmol., 84(3), pp. 318–323. 10.1136/bjo.84.3.318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11]. Fazio, M. A. , Clark, M. E. , Bruno, L. , and Girkin, C. A. , 2018, “In Vivo Optic Nerve Head Mechanical Response to Intraocular and Cerebrospinal Fluid Pressure: Imaging Protocol and Quantification Method,” Sci. Rep., 8(1), p. 12639. 10.1038/s41598-018-31052-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12]. Girard, M. J. A. , Beotra, M. R. , Chin, K. S. , Sandhu, A. , Clemo, M. , Nikita, E. , Kamal, D. S. , Papadopoulos, M. , Mari, J. M. , Aung, T. , and Strouthidis, N. G. , 2016, “In Vivo 3-Dimensional Strain Mapping of the Optic Nerve Head Following Intraocular Pressure Lowering by Trabeculectomy,” Ophthalmology, 123(6), pp. 1190–1200. 10.1016/j.ophtha.2016.02.008 [DOI] [PubMed] [Google Scholar]
- [13]. Wang, B. , Tran, H. , Smith, M. A. , Kostanyan, T. , Schmitt, S. E. , Bilonick, R. A. , Jan, N.-J. , Kagemann, L. , Tyler-Kabara, E. C. , Ishikawa, H. , Schuman, J. S. , Sigal, I. A. , and Wollstein, G. , 2017, “In-Vivo Effects of Intraocular and Intracranial Pressures on the Lamina Cribrosa Microstructure,” PLoS One, 12(11), p. e0188302. 10.1371/journal.pone.0188302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Wei, J. , Yang, B. , Voorhees, A. P. , Tran, H. , Brazile, B. , Wang, B. , Schuman, J. , Smith, M. A. , Wollstein, G. , and Sigal, I. A. , 2018, “Measuring In-Vivo and In-Situ Ex-Vivo the 3D Deformation of the Lamina Cribrosa Microstructure Under Elevated Intraocular Pressure,” Proc. SPIE, 10496, p. 1049611. 10.1117/12.2291243 [DOI] [Google Scholar]
- [15]. Coudrillier, B. , Geraldes, D. M. , Vo, N. T. , Atwood, R. , Reinhard, C. , Campbell, I. C. , Raji, Y. , Albon, J. , Abel, R. L. , and Ethier, C. R. , 2016, “Phase-Contrast Micro-Computed Tomography Measurements of the Intraocular Pressure-Induced Deformation of the Porcine Lamina Cribrosa,” IEEE Trans. Med. Imaging, 35(4), pp. 988–999. 10.1109/TMI.2015.2504440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16]. Midgett, D. E. , Pease, M. E. , Jefferys, J. L. , Patel, M. , Franck, C. , Quigley, H. A. , and Nguyen, T. D. , 2017, “The Pressure-Induced Deformation Response of the Human Lamina Cribrosa: Analysis of Regional Variations,” Acta Biomater., 53, pp. 123–139. 10.1016/j.actbio.2016.12.054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Sigal, I. A. , Grimm, J. L. , Jan, N.-J. , Reid, K. , Minckler, D. S. , and Brown, D. J. , 2014, “Eye-Specific IOP-Induced Displacements and Deformations of Human Lamina Cribrosa,” Invest. Ophthalmol. Vis. Sci., 55(1), pp. 1–15. 10.1167/iovs.13-12724 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Fazio, M. A. , Grytz, R. , Bruno, L. , Girard, M. J. A. , Gardiner, S. , Girkin, C. A. , and Downs, J. C. , 2012, “Regional Variations in Mechanical Strain in the Posterior Human Sclera,” Invest. Ophthalmol. Vis. Sci., 53(9), pp. 5326–5333. 10.1167/iovs.12-9668 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Grytz, R. , Fazio, M. A. , Girard, M. J. A. , Libertiaux, V. , Bruno, L. , Gardiner, S. , Girkin, C. A. , and Downs, J. C. , 2014, “Material Properties of the Posterior Human Sclera,” J. Mech. Behav. Biomed. Mater., 29, pp. 602–617. 10.1016/j.jmbbm.2013.03.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Clayson, K. , Pavlatos, E. , Ma, Y. , and Liu, J. , 2017, “3D Characterization of Corneal Deformation Using Ultrasound Speckle Tracking,” J. Innov. Opt. Health Sci., 10(06), p. 1742005. 10.1142/S1793545817420056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21]. Pavlatos, E. , Chen, H. , Clayson, K. , Pan, X. , and Liu, J. , 2018, “Imaging Corneal Biomechanical Responses to Ocular Pulse Using High-Frequency Ultrasound,” IEEE Trans. Med. Imaging, 37(2), pp. 663–670. 10.1109/TMI.2017.2775146 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22]. Perez, B. C. , Pavlatos, E. , Morris, H. J. , Chen, H. , Pan, X. , Hart, R. T. , and Liu, J. , 2016, “Mapping 3D Strains With Ultrasound Speckle Tracking: Method Validation and Initial Results in Porcine Scleral Inflation,” Ann. Biomed. Eng., 44(7), pp. 2302–2312. 10.1007/s10439-015-1506-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23]. Pavlatos, E. , Perez, B. C. , Morris, H. J. , Chen, H. , Palko, J. R. , Pan, X. , Weber, P. A. , Hart, R. T. , and Liu, J. , 2016, “Three-Dimensional Strains in Human Posterior Sclera Using Ultrasound Speckle Tracking,” ASME J. Biomech. Eng., 138(2), p. 21015. 10.1115/1.4032124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24]. Pavlatos, E. , Ma, Y. , Clayson, K. , Pan, X. , and Liu, J. , 2018, “Regional Deformation of the Optic Nerve Head and Peripapillary Sclera During IOP Elevation,” Invest. Ophthalmol. Vis. Sci., 59(8), pp. 3779–3788. 10.1167/iovs.18-24462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25]. Ma, Y. , Pavlatos, E. , Clayson, K. , Pan, X. , Kwok, S. , Sandwisch, T. , and Liu, J. , 2019, “Mechanical Deformation of Human Optic Nerve Head and Peripapillary Tissue in Response to Acute IOP Elevation,” Invest. Ophthalmol. Vis. Sci., 60(4), pp. 913–920. 10.1167/iovs.18-26071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26]. Tang, J. , and Liu, J. , 2012, “Ultrasonic Measurement of Scleral Cross-Sectional Strains During Elevations of Intraocular Pressure: Method Validation and Initial Results in Posterior Porcine Sclera,” ASME J. Biomech. Eng., 134(9), p. 91007. 10.1115/1.4007365 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Kallel, F. , and Ophir, J. , 1997, “A Least-Squares Strain Estimator for Elastography,” Ultrason. Imaging, 19(3), pp. 195–208. 10.1177/016173469701900303 [DOI] [PubMed] [Google Scholar]
- [28]. Flage, T. , 2009, “Permeability Properties of the Tissues in the Optic Nerve Head Region in the Rabbit and the Monkey: An Ultrastructural Study,” Acta Ophthalmol., 55(4), pp. 652–664. 10.1111/j.1755-3768.1977.tb05663.x [DOI] [PubMed] [Google Scholar]
- [29]. Ayyalasomayajula, A. , Park, R. I. , Simon, B. R. , and Vande Geest, J. P. , 2016, “A Porohyperelastic Finite Element Model of the Eye: The Influence of Stiffness and Permeability on Intraocular Pressure and Optic Nerve Head Biomechanics,” Comput. Methods Biomech. Biomed. Eng., 19(6), pp. 591–602. 10.1080/10255842.2015.1052417 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30]. Fatehee, N. , Yu, P. K. , Morgan, W. H. , Cringle, S. J. , and Yu, D.-Y. , 2011, “Correlating Morphometric Parameters of the Porcine Optic Nerve Head in Spectral Domain Optical Coherence Tomography With Histological Sections,” Br. J. Ophthalmol., 95(4), pp. 585–589. 10.1136/bjo.2010.188441 [DOI] [PubMed] [Google Scholar]
- [31]. Chien, J. L. , Ghassibi, M. P. , Mahadeshwar, P. , Li, P. , Liebmann, J. M. , Ritch, R. , Milman, T. , and Park, S. C. , 2017, “A Novel Method for Assessing Lamina Cribrosa Structure Ex Vivo Using Anterior Segment Enhanced Depth Imaging Optical Coherence Tomography,” J. Glaucoma, 26(7), pp. 626–632. 10.1097/IJG.0000000000000685 [DOI] [PubMed] [Google Scholar]
- [32]. Girkin, C. A. , Fazio, M. A. , Yang, H. , Reynaud, J. , Burgoyne, C. F. , Smith, B. , Wang, L. , and Downs, J. C. , 2017, “Variation in the Three-Dimensional Histomorphometry of the Normal Human Optic Nerve Head With Age and Race: Lamina Cribrosa and Peripapillary Scleral Thickness and Position,” Invest. Ophthalmol. Vis. Sci., 58(9), pp. 3759–3769. 10.1167/iovs.17-21842 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33]. Chidlow, G. , Ebneter, A. , Wood, J. P. M. , and Casson, R. J. , 2011, “The Optic Nerve Head is the Site of Axonal Transport Disruption, Axonal Cytoskeleton Damage and Putative Axonal Regeneration Failure in a Rat Model of Glaucoma,” Acta Neuropathol., 121(6), pp. 737–751. 10.1007/s00401-011-0807-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34]. Quigley, H. A. , McKinnon, S. J. , Zack, D. J. , Pease, M. E. , Kerrigan–Baumrind, L. A. , Kerrigan, D. F. , and Mitchell, R. S. , 2000, “Retrograde Axonal Transport of BDNF in Retinal Ganglion Cells is Blocked by Acute IOP Elevation in Rats,” Invest. Ophthalmol. Vis. Sci., 41(11), pp. 3460–3466. [PubMed] [Google Scholar]
- [35]. Tehrani, S. , Davis, L. , Cepurna, W. O. , Choe, T. E. , Lozano, D. C. , Monfared, A. , Cooper, L. , Cheng, J. , Johnson, E. C. , and Morrison, J. C. , 2016, “Astrocyte Structural and Molecular Response to Elevated Intraocular Pressure Occurs Rapidly and Precedes Axonal Tubulin Rearrangement Within the Optic Nerve Head in a Rat Model,” PLoS One, 11(11), p. e0167364. 10.1371/journal.pone.0167364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Wang, R. , Seifert, P. , and Jakobs, T. C. , 2017, “Astrocytes in the Optic Nerve Head of Glaucomatous Mice Display a Characteristic Reactive Phenotype,” Invest. Ophthalmol. Vis. Sci., 58(2), pp. 924–932. 10.1167/iovs.16-20571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37]. Yarmohammadi, A. , Zangwill, L. M. , Diniz-Filho, A. , Suh, M. H. , Manalastas, P. I. , Fatehee, N. , Yousefi, S. , Belghith, A. , Saunders, L. J. , Medeiros, F. A. , Huang, D. , and Weinreb, R. N. , 2016, “Optical Coherence Tomography Angiography Vessel Density in Healthy, Glaucoma Suspect, and Glaucoma Eyes,” Invest. Ophthalmol. Vis. Sci., 57(9), pp. OCT451–OCT459. 10.1167/iovs.15-18944 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38]. See, J. L. S. , Nicolela, M. T. , and Chauhan, B. C. , 2009, “Rates of Neuroretinal Rim and Peripapillary Atrophy Area Change: A Comparative Study of Glaucoma Patients and Normal Controls,” Ophthalmology, 116(5), pp. 840–847. 10.1016/j.ophtha.2008.12.005 [DOI] [PubMed] [Google Scholar]
- [39]. Hammel, N. , Belghith, A. , Bowd, C. , Medeiros, F. A. , Sharpsten, L. , Mendoza, N. , Tatham, A. J. , Khachatryan, N. , Liebmann, J. M. , Girkin, C. A. , Weinreb, R. N. , and Zangwill, L. M. , 2016, “Rate and Pattern of Rim Area Loss in Healthy and Progressing Glaucoma Eyes,” Ophthalmology, 123(4), pp. 760–770. 10.1016/j.ophtha.2015.11.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40]. Grytz, R. , Meschke, G. , and Jonas, J. B. , 2011, “The Collagen Fibril Architecture in the Lamina Cribrosa and Peripapillary Sclera Predicted by a Computational Remodeling Approach,” Biomech. Model. Mechanobiol., 10(3), pp. 371–382. 10.1007/s10237-010-0240-8 [DOI] [PubMed] [Google Scholar]
- [41]. Pijanka, J. K. , Coudrillier, B. , Ziegler, K. , Sorensen, T. , Meek, K. M. , Nguyen, T. D. , Quigley, H. A. , and Boote, C. , 2012, “Quantitative Mapping of Collagen Fiber Orientation in Non-Glaucoma and Glaucoma Posterior Human Sclerae,” Invest. Ophthalmol. Vis. Sci., 53(9), pp. 5258–5270. 10.1167/iovs.12-9705 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42]. Jensen, J. A. , and Svendsen, N. B. , 1992, “Calculation of Pressure Fields From Arbitrarily Shaped, Apodized, and Excited Ultrasound Transducers,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 39(2), pp. 262–267. 10.1109/58.139123 [DOI] [PubMed] [Google Scholar]
- [43]. Jensen, J. A. , 1996, “Field: A Program for Simulating Ultrasound Systems,” Tenth Nordic Baltic Conference Biomedical Imaging, Tampere, Finland, Vol. 4, pp. 351–353. [Google Scholar]
- [44]. Hua, Y. , Voorhees, A. P. , and Sigal, I. A. , 2018, “Cerebrospinal Fluid Pressure: Revisiting Factors Influencing Optic Nerve Head Biomechanics,” Invest. Ophthalmol. Vis. Sci., 59(1), pp. 154–165. 10.1167/iovs.17-22488 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45]. Feola, A. J. , Coudrillier, B. , Mulvihill, J. , Geraldes, D. M. , Vo, N. T. , Albon, J. , Abel, R. L. , Samuels, B. C. , and Ethier, C. R. , 2017, “Deformation of the Lamina Cribrosa and Optic Nerve Due to Changes in Cerebrospinal Fluid Pressure,” Invest. Ophthalmol. Vis. Sci., 58(4), pp. 2070–2078. 10.1167/iovs.16-21393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46]. Feola, A. J. , Myers, J. G. , Raykin, J. , Mulugeta, L. , Nelson, E. S. , Samuels, B. C. , and Ethier, C. R. , 2016, “Finite Element Modeling of Factors Influencing Optic Nerve Head Deformation Due to Intracranial Pressure,” Invest. Ophthalmol. Vis. Sci., 57(4), pp. 1901–1911. 10.1167/iovs.15-17573 [DOI] [PubMed] [Google Scholar]


