Membrane vesiculation induced by proteins of the dengue virus envelope studied by molecular dynamics simulations

Abstract

Biological membranes are continuously remodeled in the cell by specific membrane-shaping machineries to form, for example, tubes and vesicles. We examine fundamental mechanisms involved in the vesiculation processes induced by a cluster of envelope (E) and membrane (M) proteins of the dengue virus (DENV) using molecular dynamics simulations and a coarse-grained model. We show that an arrangement of three E-M heterotetramers (EM₃) works as a bending unit and an ordered cluster of five such units generates a closed vesicle, reminiscent of the virus budding process. In silico mutagenesis of two charged residues of the anchor helices of the envelope proteins of DENV shows that Arg-471 and Arg-60 are fundamental to produce bending stress on the membrane. The fine-tuning between the size of the EM₃ unit and its specific bending action suggests this protein unit is an important factor in determining the viral particle size.

Introduction

The mechanisms of membrane remodeling in the cell constitute a fundamental problem in molecular biology [1] with important applications in different areas of science and technology, such as nanomedicine, synthetic molecule carriers, new vaccine development, and material sciences [2–6]. Biological membranes consist of phospholipid bilayers with embedded integral and peripheral proteins that can rotate and translate laterally. Membranes may attain curvature as a consequence of asymmetry imposed by its own constituents, such as cholesterol, or by the presence of external molecules, such as proteins that can insert hydrophobic domains into one side of the bilayer with membrane-piercing $\alpha$-helices [7]. This type of helix can hook the opposite side of the membrane and produce a local constriction on membrane thickness or they may act as scaffolds for membrane curvature [1, 8, 9]. Moreover, domains of different lipids or clusters of proteins, as well as the boundaries of an open membrane, may produce lines of tension that introduce extra forces on the membrane [10, 11].

Replication of enveloped viruses comprises several steps controlled by specific proteins. These include local membrane bending [1] followed by virus budding and final membrane scission, in which the virion is detached from the cellular membrane [12]. Specifically, the dengue virus (DENV) [13, 14] is coated by replicas of two proteins, namely envelope (E) and membrane (M) proteins, forming 90 E-M heterotetramers (2 E  +  2 M) that cover a spherical phospholipid membrane. The E protein presents a soluble ectodomain (sE) and a transmembrane domain (TMD) that acts as an anchor. The M protein resides under the E protein shell, practically immersed in the virus membrane (figures 1(A) and (B)). The transmembrane domain of the E-M heterotetramer is subdivided into stem and anchor helices (figure 1(A)); the stem helices have a polar/nonpolar surface pattern and are all accommodated at one side of the bilayer surface, while the anchors, mostly hydrophobic, present polar residues only at their distal loops [14–16]. Theses loops connect two helices of the E protein (ET1; ET2) and two helices of the M protein (MT1; MT2).

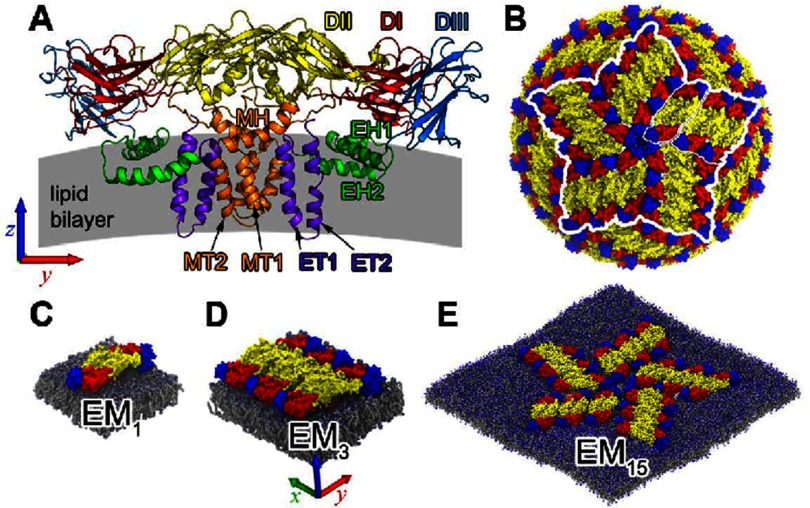
Figure 1.

Envelope (E) and membrane (M) proteins of the dengue virus (DENV). (A) Structures of the EM heterotetramer (two E and two M) of DENV: domain I (DI, red), domain II (DII, yellow), and domain III (DIII, blue) are the three domains collectively called ectodomain of E. The TMD is composed of (i) stem: six helices (two sets each of EH1, EH2, and MH) partially embedded into the bilayer, and (ii) anchor: eight membrane-piercing helices (two sets each of ET1, ET2, MT1, and MT2). (B) Structural surface of DENV as crystallographically determined; note the fivefold axis at the center of the figure (blue circle-like spot). White lines highlight the three systems considered here, composed of one (EM₁), three (EM₃), and fifteen (EM₁₅) EM heterotetramers. (C) EM₁ system: one EM heterotetramer anchored in a flat continuous membrane connected with its images through the periodic boundary conditions. (D) The EM₃ system corresponds to three EM₁ shaped as an irregular rhombus also planted parallel into the flat ‘continuous’ membrane. (E) In turn, the EM₁₅ system (shown in smaller scale here) consists of five groups of EM₃, facing each other in a rotationally symmetric fashion, embedded into a flat open membrane patch of size 59  ×  59 nm². It reproduces a planar version of the cluster of fifteen EM heterotetramers around the fivefold axis of the icosahedral symmetry of the DENV.

A set of high-resolution structures of the DENV-2 envelope proteins [14, 15, 17] allows us to use molecular dynamics (MD) simulations to investigate the effects of protein-protein and protein-membrane interactions in the generation of membrane-bending forces. Here, we examine deformations induced on a host-like phospholipid bilayer [18] (see Methods section) in a progressive way, through three distinct oligomerization states of E-M proteins, namely: one (EM₁), three (EM₃), and fifteen (EM₁₅) heterotetramers (figures 1(C)–(E)). Essentially, this work concerns the description and analysis of the membrane bending and vesiculation mechanisms induced by the envelope proteins of the DENV. The EM₁₅ system emulates a fragment of the DENV envelope: it is composed of an open membrane patch of 59  ×  59 nm² encrusted by 1/6 of the outer structural proteins of DENV immersed in solvent particles, amounting to the equivalent of three million atoms.

Our results show that the E-M heterotetramer architecture has a key topological and physicochemical characteristic that ultimately breaks the planar symmetry of the bilayer and generates forces capable of modifying the overall bilayer shape. We present in silico mutagenesis experiments that corroborate the notion that the membrane-bending forces are a consequence of the phospholipid rearrangement triggered by the relatively short length of the TMD of the E-M proteins. As more E-M heterotetramers are assembled in a symmetric setup, the resulting curvature in the planar phospholipid bilayer leads to a self-assembled vesicle, impelled by the accumulated mechanical stress imposed by the proteins and also by a line of tension along the membrane boundary.

Methods

Molecular dynamics (MD) simulation and analysis

All MD simulations in this work were performed using the GROMACS 4 package [19]; the CHARMM36c [20] force field with cholesterol parameters [21] and TIP3P water [22] was used to supply the energy function for all-atom (AA) MD simulations. The MARTINI [23] model was used for the coarse-grained (CG) modeling. All bilayers in this work emulate the phospholipid composition of the DENV membrane [24]. The method described in Hsin et al [25] was employed to evaluate the bilayer curvature. Analyses, visualization, and preparation of figures were performed through the following tools: GROMACS, VMD [26], and open-source PyMol [27]. The complete methodology is described in the separated topics below.

System preparation: general aspects

All atom simulations for EM₁ and EM₃ systems and CG ‘simulations’ for EM₃ and the large EM₁₅ system were performed. We write ‘simulations’ since the CG energy function is a mixture between enthalpy and entropy. This mix-up leads to the problem that the ‘forces’ in a CG model include the time derivative of the entropy (the same goes for implicit solvent models). Hence CG can not be used to generate simulation trajectories, the resulting ensemble is not a Boltzmann ensemble and the concept of time is ill-defined. CG ‘simulations’ should therefore be considered as an algorithm to search the free energy landscape. For readability we leave out the ‘’ in the remainder of the text.

The phospholipid composition of the bilayer model follows the actual ratios in DENV, derived from the mosquito lipidome [24]: POPC (1-palmitoyl-2-oleoyl-sn-glicero-3-phosphatidylcholine), 60%; POPE (1-palmitoyl-2-oleoyl-sn-glicero-3-phosphatidylethanolamine), 20%; and POPS (1-palmitoyl-2-oleoyl-sn-glicero-3-phosphatidylserine), 10%. The remaining 10% corresponds to the cholesterol fraction, as found on mammalian RER membranes [28]. The system’s net charge was neutralized by the addition of Na⁺ and Cl⁻ counter ions at the ionic strength of 150 mM.

The geometry of molecules and their interactions were optimized after protein embedding by performing energy minimization with the steepest descent method. Position restraints were applied to a set of system-dependent atoms during equilibration runs. A Maxwell–Boltzmann distribution was used to generate the initial velocities of the atoms at a temperature of 310 K and thermal stabilization was achieved using the Berendsen thermostat [29]. The cutoffs of nonbonded interactions were set to 1.0 nm for AA simulations or 1.2 nm for CG simulations. Long-range electrostatic interactions were dealt with using the particle-mesh Ewald method, with sixth order interpolation. Bonds containing hydrogen atoms were constrained by the LINCS [30] algorithm, except when minimizing the potential energy of CG beads in the presence of polarizable water [31].

We used the replacement method for protein insertion [32] in all cases; the AA bilayers were equilibrated prior the insertion, while the CG bilayers were equilibrated after protein insertion using position restraints on the protein. For the AA equilibration steps we used the Berendsen algorithm [29] to control both temperature (310 K) and pressure (1 bar); for production we used the Berendsen barostat to control surface tension (NPγT ensemble, γ  =  0) and V-rescale [33] for temperature coupling. Periodic boundary conditions in a semi-isotropic regime were applied in EM₁ and EM₃ systems; the membrane covered the entire cross-section of the simulation box. Open membrane patches were used for the larger EM₁₅ system, and this was simulated with isotropic periodic boundary conditions. The time step for leap-frog algorithm integration was set to 1 femtosecond (fs) and 20 fs for AA and CG simulations, respectively. For consistency with other literature all reported MD-times for CG simulations were multiplied by a factor of four to represent an estimate of real time [23], however with the caveat noted above that there is no time in CG simulations. Analyses of bilayer curvature were performed with a method described by Jen Hsin [25] who kindly provided a script for this purpose.

EM₁ system

The EM₁ system is a heterotetramer composed of a single set of two E and two M proteins embedded in a flat bilayer patch measuring 14.8  ×  14.8 nm² and with a thickness of about 4 nm. Periodic boundary conditions were employed to emulate a continuous membrane (figure 1(C)), by replication of the original square patch in the x- and y-direction.

The AA model of the DENV E-M heterotetramer (serotype 2) was obtained from the RCSB Protein Data Bank [34] under the accesion code 3J27 [14]. This model is derived from an electron microscopy structure with resolution of 3.5 Å and contains all amino acids of the native E and M proteins. We extracted the atoms that correspond to one E-M heterotetramer and added all missing hydrogen atoms. Then, we performed a steepest-descent energy minimization, removing eventual steric impairments on the structure.

The lipid bilayer was assembled with aid of the membrane builder module from CHARMM-GUI [35]. The resulting bilayer initially contained 800 phospholipid and cholesterol molecules equally divided between its upper and lower layers. First, we removed all overlapping phospholipid acyl chains with a series of steepest-descent energy minimizations in conjunction with the inflategro script [32]. Then, we solvated the bilayer with the TIP3P CHARMM water model [36] with a water/lipid weight ratio (%wtH₂O) above the phase transition threshold of the liquid crystal state (Lα), with an experimental value [32] of 32.5. In order to equilibrate the solvent layer at the interface of the membrane, we performed a 5 ns equilibration in the NVT ensemble using position restraints on the phosphor atoms of the lipids to allow diffusion only in the xy plane.

Another 10 ns thermalization under the NPT ensemble without restraints was performed, adjusting the box to yield a system pressure of 1 bar using the Berendsen barostat [29] with τ_P  =  1 ps. In the final step, we adjusted the surface tension to zero under the NPγT ensemble with the Berendsen algorithm for 60 ns. The temperature of the system was maintained within the physiological threshold and above the transition temperature of the bilayers components to achieve the Lα phase of a typical biological membrane. The expected reference properties were confirmed by establishing the approximate area per lipid of 0.55 nm², the average bilayer thickness of 4.3 nm and the characteristic order of the lipids acyl chains, as described by the lipid deuterium order parameter and electronic density of the system. After protein embedding, a 10 ns equilibrium run was performed with restraints on the heavy atoms of the protein, allowing the bilayer to fully embed the TMD. Then, we proceeded with the production run of 100 ns under the NPγT ensemble.

EM₃ systems

To obtain the EM₃ system, the coordinates of three neighboring heterotetramers in the biological assembly were extracted from the same cryo-EM structure used for EM₁. The three heterotetramers were put in the same plane of reference, obtaining a planar configuration. To accommodate these three heterotetramers, a larger bilayer fitting a box 20.8  ×  14.6  ×  13.8 nm³ was taken from the previously equilibrated membrane and an additional layer of water was added, yielding $\mathrm{\%}\mathrm{w}{\mathrm{t}}_{{\mathrm{H}}_2\mathrm{O}}$ ~ 91. Then a 60 ns NPγT equilibration was carried out with the same parameters as the smaller bilayer to thermalize the system. Finally, we proceeded with the production run of 100 ns under the NPγT ensemble.

To convert the AA EM₃ configuration to a CG model, we employed the martinyze script [23]. The lipid bilayer and solvated box, with polarizable water [31], was built with MARTINI’s insane script [23]. The first step in the process of embedding the TMD into the bilayer consisted of the alignment of both geometrical centers of the proteins and bilayer in the XY-plane. Next, the TMD were adjusted along the Z-axis as close as possible to the bilayer depth described in the cryo-EM structure. At this stage, all overlapping non-protein molecules within a distance smaller than 1.2 Å of the heterotetramer were removed. After the addition of Na⁺ and Cl⁻ to achieve the desired ionic strength and electroneutrality, we proceeded to a steepest-descent energy minimization, and the resulting system was used as the starting conformation for a 10 ns NVT step in which protein atoms were restrained in their positions and the phosphor atoms of each phospholipid were allowed to laterally diffuse through the membrane. Then, all restrictions were released and the 100 ns production run started.

Two CG EM₃ systems for in silico mutation simulations were prepared: one consisted of a single mutation from Arg-471 to Ala in the E protein and the other with an extra mutation of Arg-60 to Ala in the M protein. These substitutions were performed directly on the heterotetramers on the starting structure of the AA EM₃, using the mutagenesis tool of Pymol [27]. Then, the resulting AA file was converted to a CG system model with the martinize script [23]. From there, all steps were identical to the CG EM₃ system assembly, equilibration, and production of 100 ns.

EM₁₅ system

The EM₁₅ system was built on an open membrane patch of area 59  ×  59 nm², consisting of 8008 lipids and 856 cholesterol molecules, in a box of size 62.9  ×  62.9 nm². The number of lipids molecules and cholesterol molecules in the upper layer was about 22% less than in the lower layer, due to the surface area $S_{\mathrm{p}}$ occupied by the protein cluster. Five EM₃ structures constituted the building blocks of the EM₁₅ system, forming a cluster of 15 E-M heterotetramers. Note that six such raft-like domains are needed to cover the entire DENV (figures 1(B) and (E)). The lines coming out from the DENV five fold symmetry axis and passing through domain II of the ectodomain of protein E of each EM₃ (figures 1(B) and (E), colored yellow), define the five arms of the EM₁₅ system. Each EM₃ block bends the membrane along each arm of the EM₁₅ cluster.

The E-M heterotetramers are initially arranged as a planar projection of the coordinates of the fivefold pore of the cryo-EM structure, figure 1(E). They correspond to the five CG EM₃ initial systems, as described above, with each EM₃ structure successively rotated by 72° around its Z-axis, with respect to the preceding structure. After embedding the proteins into the bilayer and removing all overlapping molecules of the membrane, we proceeded with the same equilibration steps described in the CG EM₃ bilayer, and another 10 ns of NPT run with protein coordinates fully restrained, allowing the stabilization of pressure to the NVT production run, for 150 ns (CG time).

Results and discussion

Origin of bending forces

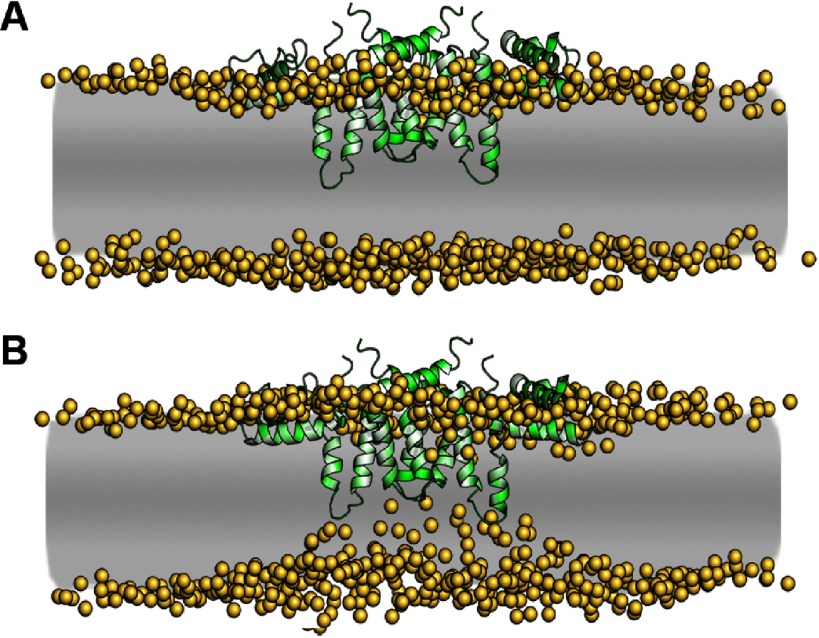
The E and M proteins of Flavivirus have two short bisected helices. In the case of DENV, the anchor helices ET1 and ET2 are 16 and 17 residues long, respectively, whereas they are only 12 and 14 residues long for MT1 and MT2, respectively. Initially, the TMD of the E-M proteins was aligned closely to the upper layer of a continuous membrane (figure 2(A); see also the Methods section); this configuration is thermodynamically unfavorable because the anchor helices, which are relatively short, have their polar loops in a hydrophobic environment (the middle portion of the membrane). Therefore, a prompt rearrangement of the lipids molecules and cholesterol molecules takes place, producing a local constriction on the membrane: the bottom layer is attracted by the polar tip of the anchor helices, pulling down the whole TMD, which gets embedded deeper into the membrane, pressuring the upper monolayer. Promptly, the E-M heterotetramer becomes attached to the membrane through the amphipathic EH1, EH2, and MH helices. Concomitantly, the lipid rearrangement leads to a number of polar phosphate groups from the bottom layer to move toward the polar helices’ loops. After about 50 ns, the system is stabilized in a conformation that shows an upper planar layer and a bottom layer containing an indentation right below the TMD (figure 2(B)), which leads to a locally reduced thickness of the bilayer. This is in good agreement to the experimental observation made using cryo-electron microscopy that the membrane thickness is reduced by the transmembrane helices of E and M [14].

Figure 2.

Evolution of the interplay between the EM heterotetramer and membrane. (A) The initial conformation corresponding to the embedding of the TMD of the EM heterotetramer, placing the amphipathic stem helices (EH1, EH2 and MH) inside the hydrophobic lipid matrix of the membrane, a thermodynamically unfavorable condition—the golden spheres represent the polar heads of phospholipid molecules. (B) pronounced indentation on the lower phospholipid layer caused by the TMD.

A cluster of three EM heterotetramers induces a defined bilayer curvature

Simulations of the AA EM₃ system, which consists of a continuous bilayer over which the EM heterotetramers are positioned as they are found in the mature form of DENV [37] (figure 1(D), details in the Methods section), reveal an intensified curvature of the membrane bilayer, exclusively pronounced in the direction perpendicular to the longest axis of an EM heterotetramer (figures 1(A) and 3(A), labeled here as the y-axis direction). In turn, along the x-direction, the overall curvature is practically zero (figure 3(B)). The local radius of curvature $R_{\mathrm{C}}$ observed along the y-axis, just at the middle of the protein cluster, converges asymptotically to the actual radius of the mature DENV particle [14] $R_{\mathrm{v}\mathrm{i}\mathrm{r}\mathrm{u}\mathrm{s}}\approx$ 25 nm (figure 3(C), full symbols). $R_{\mathrm{C}}$ corresponds to the average between the internal and external bilayer radii of curvatures. This result suggests that, by imposing a defined curvature upon the membrane, the transmembrane helices of the EM₃ cluster may be a key factor in determining the virus size as well as the number of its envelope components.

Figure 3.

Membrane curvature produced by the EM₃ system (a trimer of EM heterotetramers). (A) Full all-atom simulation of three aligned EM heterotetramers as in the DENV native conformation (each colored in different shades of green for distinction). After 100 ns the system reaches stable conformation, with the membrane bilayer keeping an asymmetric curvature exclusively along a specific direction (y-axis). (B) The same, but with view orientation along the x-axis of the simulation box: the overall curvature is practically zero. (C) Evolution of the radius of curvature, represented by the two layer local average about the protein cluster center: all-atom (AA) simulation (full symbols) and coarse-grained (CG) model (open symbols) of the EM₃ system. Both methods reproduce the same anisotropic curvature in the y-axis direction, corresponding to the DENV radius (25 nm). The gain in performance using the CG method is about 18 times faster.

The fundamental role of two arginine residues

The membrane curvature for the wild-type EM₃ was reproduced using a CG approach (figure 3(C), open symbols), resulting in a 18-fold lower computational cost. This was exploited to verify the effect of mutating two positively charged residues on the ability of the EM₃ system to bend the membrane. Arg-471 and Arg-60 are located at the loops of the anchor proteins (figure 1(A)) and were changed as (i) a single mutation of Arg-471 to Ala; and (ii) double mutation of both Arg-471 and Arg-60 to Ala.

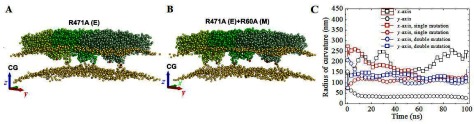
The mutants resulted in a drastically reduced attraction of the lower layer by the anchor loops and the curvature imposed by the wild-type EM₃ system is not observed in the mutants (figure 4). This suggests that these two arginines are fundamental for the function of the envelope proteins. Without them, the EM₃ heterotetramer loses its capacity to impose a curvature upon the membrane, which could impair virus assembly and budding.

Figure 4.

In silico mutagenesis of the EM₃ system: the arginine-to-alanine replacement eliminates the bending capability of the EM heterotetramers. (A) When only the Arg-471 in E protein is replaced (colored in red), the membrane curvature becomes instable in both x- and y-axes (square and circle colored red in (C)), oscillating around a much larger radius of curvature. (B) On the other hand, when both Arg-471 in E and Arg-60 in M protein are substituted, the membrane curvature becomes totally undefined (square and circle colored blue in (C)) changing randomly in both x and y directions. (C) Evolution of the radius of curvature (CG simulation). Blue symbols, double mutations: R471  +  R60A; read symbols, single mutations: R471A; and black symbols: no mutation. Note that only the wild case produces a defined anisotropic curvature in the y-direction as in the AA simulation (figures 3(A) and (C)).

Total vesiculation of an open membrane patch induced by 15 EM heterotetramers

The EM₁₅ system consists of five EM₃ structures, forming a cluster of fifteen EM heterotetramers, accounting for one sixth of the domains covering DENV. The EM₃ elements are arranged as a planar version of the cluster of proteins around the fivefold axis of DENV (compare figures 1(B) and (E)). The orientation of the curved surface of each EM₃ element (y-direction, figures 1(A) and 3(A)) is perpendicular to its correspondent arm. The EM₁₅ system is built on an open membrane patch (more details in the Methods section).

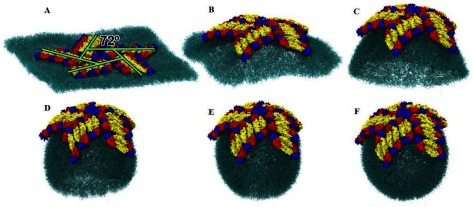
The first change in the morphology of the open membrane patch is that the edges, initially shaped like a square wafer (figure 5(A)), begin to round of in order to reduce the contact area between the hydrophobic tail of the lipids and water (figure 5(B)). Concomitantly, the EM₁₅ system starts to impose a specific curvature on the membrane, breaking its initial symmetry (upper and lower different leaflet curvatures), which is minimized by transferring lipid molecules from the lower into the upper layer. Tension is also accumulated along the membrane rounded edge, which forces to reduce its perimeter; see Movie-1 and 2, in supplementary material (stacks.iop.org/JPhysCM/29/504002/mmedia). Therefore, the bilayer evolves continually as a spherical cap (figures 5(D) and (E)) until the point in which its opening becomes sufficiently small to allow thermal fluctuations to fuse the membrane (figure 5(F)). This process generates a vesicle of external, internal and average radii of $R_{\mathrm{o}\mathrm{u}\mathrm{t}}=17.3\mathrm{n}\mathrm{m}$, $R_{\mathrm{i}\mathrm{n}}=13.3\mathrm{n}\mathrm{m}$ and $R=15.3\mathrm{n}\mathrm{m}$.

Figure 5.

The vesiculation process. (A) The EM₁₅ setup: fifteen EM heterotetramers on a flat membrane patch of 59  ×  59 nm². (B) After 80 ns the membrane already shows a defied curvature, induced by the protein-membrane interplay and by the line of tension around the membrane. (C) The curvature grows systematically and about 240 ns later, a parabolic-like cap is formed. At this stage, the protein-membrane interaction reaches a steady conformation and thereafter, the vesiculation evolutes exclusively under action of the line tension. (D) and (E) As time goes on, the membrane curvature continues to decline. Note that the curvature determined by the protein-membrane interaction (on the top of the sphere) is smaller than the curvature determined by the rest of the membrane. (F) The vesicle reaches a final stable size (external radius of 17.3 nm) at about 440 ns. A comparison between parts (C) and (F) can show how the radius of curvature decreased.

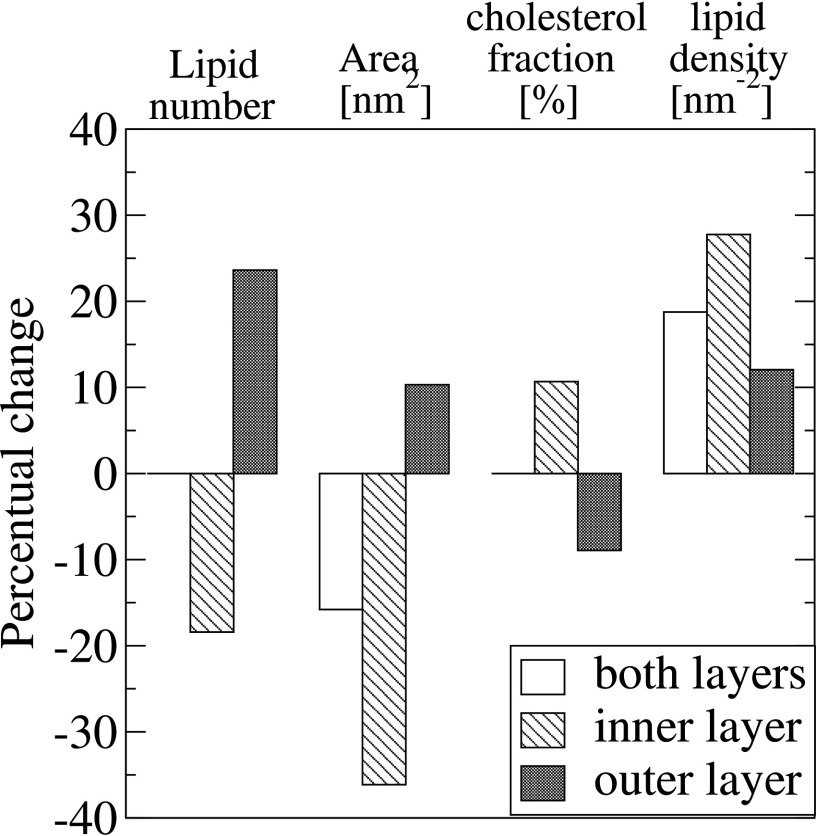
The composition and the surface density of molecules on the membrane layers change notably during the vesiculation process due to migration of lipids from the inner layer, which lost 18% of its lipids, to the outer layer, which received additional 24% of its initial number of lipids (figure 6). The overall impact of such migration is a decrease of 16% in the total area occupied by all lipids and, as one would expect, a corresponding increase in 19% in lipid density in the whole vesicle. This behavior is, however, asymmetric between the layers: while the inner layer area decreases 36% and its density—defined as the number of lipid head groups per unit area of the membrane—increases 28%, the outer layer shows a different behavior due to the large number of lipids that it accepted during vesiculation; its area expanded by 10% and its lipid density also increased by 12% (figure 6). Cholesterol specifically localizes in the inner layer, where its proportion is 11% higher than in the open patch (figure 6).

Figure 6.

Changes in the membrane layers composition (%) during the observed vesiculation process, in which the number of lipids and cholesterol molecules are preserved in the membrane. The lipid number and area of the outer (dark columns) and inner (hatched columns) layers change asymmetrically: the outer becomes bigger than inner layer, but the lipid density increases in both, markedly in the inner (28.6%). The cholesterol fraction (#chol/#lipids) increases in the inner and diminishes in the outer layer, but the density of lipids incresses in both layers.

Even though this is a large overall change on the membrane surface area, no elastic energy is stored due to membrane deformation because the bilayer is no longer symmetric—a spontaneous curvature was generated during the vesiculation process.

Conclusion

In this work we used molecular dynamics simulations and a coarse-grained model to investigate some aspects of how protein-lipid interactions can shape membranes. The origin of membrane-bending forces was identified by analyzing the behavior of EM, an heterotetramer containing two dimers of the E and M proteins from DENV. This system was considered in three progressively higher oligomerization states assembled in a host-like model membrane.

The structural organization of the EM₃ system—composed by three heterotetramers EM—acts as a anisotropic bending unit for the dengue virus envelope, mainly due to the fact that it can locally reduce the thickness of the membrane with its short transmembrane helices, imposing a specific radius of curvature to the membrane that, locally, at the center of the EM₃ cluster, is similar to that of the DENV, R_virus 25 nm. This suggests that the EM₃ unit may be the main determinant of the viral particle size. In silico mutagenesis experiments point out that residues Arg-471 and Arg-60 are the responsible for locally reducing the thickness of the bilayer. It will be interesting to see to which extent these specific mutations can impair virus assembly and budding in vitro or in vivo.

Our simulations show that just a fraction of the envelope proteins of DENV, the EM₁₅ system, which corresponds to one sixth of the viral envelope, is competent to induce complete vesiculation of an open membrane patch. The topological pentagonal arrangement of five EM₃ units, acting in concert, imposes a specific curvature R⁻¹ to the membrane, breaking its initial symmetry and creating stress in the membrane. Then, the process evolutes spontaneously: the resulting elastic energy is minimized by the systematic migration of lipids from the lower into the upper layer. The lipid transfer is processed exclusively through the edge creating tension along the edge. Such tension is released by continuous reduction of the spherical cap perimeter in formation, and concurrently more lipids are moved to the external layer.

The local curvature $R_{\mathrm{v}\mathrm{i}\mathrm{r}\mathrm{u}\mathrm{s}}^{-1}$ that the EM₁₅ structure seems to impose to the membrane approaches to that of DENV spherical surface. However, $R_{\mathrm{v}\mathrm{i}\mathrm{r}\mathrm{u}\mathrm{s}}^{-1}$ is larger than the curvature of the vesicle at the simulation end—as one can see by direct inspection of figures 5(D)–(F), since that the vesicle size is limited by the amount of lipids in the initial path.

In short, the vesiculation process studied in this work revels the role of the envelop proteins of DENV in the mechanism of membrane shaping, and the extensive effect the forces of such proteins on the lipid membrane creating enough stress that eventualy transform a flat membrane in an almost perfect sphere tension free.