TensorCalculator: exploring the evolution of mechanical stress in the CCMV capsid

Abstract

A new computational methodology for the accurate numerical calculation of the Cauchy stress tensor, stress invariants, principal stress components, von Mises and Tresca tensors is developed. The methodology is based on the atomic stress approach which permits the calculation of stress tensors, widely used in continuum mechanics modeling of materials properties, using the output from the MD simulations of discrete atomic and $C_{\alpha }$-based coarse-grained structural models of biological particles. The methodology mapped into the software package TensorCalculator was successfully applied to the empty cowpea chlorotic mottle virus (CCMV) shell to explore the evolution of mechanical stress in this mechanically-tested specific example of a soft virus capsid. We found an inhomogeneous stress distribution in various portions of the CCMV structure and stress transfer from one portion of the virus structure to another, which also points to the importance of entropic effects, often ignored in finite element analysis and elastic network modeling. We formulate a criterion for elastic deformation using the first principal stress components. Furthermore, we show that von Mises and Tresca stress tensors can be used to predict the onset of a viral capsid’s mechanical failure, which leads to total structural collapse. TensorCalculator can be used to study stress evolution and dynamics of defects in viral capsids and other large-size protein assemblies.

1. Introduction

In the past decade, rapid development of experimental techniques, namely dynamic force spectroscopy, made available a new research methodology to investigate the mechanical properties of biological matter [1–3]. Applied to large biological supramolecular complexes, such as viruses, microtubules, micro- and nanocompartments, and small cellular organelles [4–7], dynamic force spectroscopy has enabled researchers to interrogate these large-size biological protein assemblies mechanically, to probe the limits of their mechanical strength, and to gather valuable information about their nanomechanical characteristics, including the critical deformation, Youngs modulus, shear modulus, flexural rigidity, etc [6, 8–17]. Although a considerable amount of experimental effort has been expended to understand how the mechanical response of biological particles depends on their compressive-force induced deformation, many difficulties remain, e.g. regarding the interpretation of force-deformation spectra [18]. Experimental resolution in the state-of-the-art single-molecule forced-deformation assays do not allow researchers to extract the molecular level structural details underlying dynamic transitions in biological particles, such as buckling and structural collapse.

The past decade has witnessed rapid progress in the development of computational methods for modeling large biological assemblies to understand their unique physico-chemical properties (e.g. stiffening, softening, buckling, etc). Among these are: finite element analysis (FEA) [14, 19–21], explicit and implicit solvent molecular dynamics (MD) simulations [22–24], elastic network modeling (ENM) [25–27], and various coarse-graining (CG) techniques [28–33]. However, these approaches have exhibited a number of drawbacks. For example, FEA and ENM approaches do not take into account the discrete nature of biological particles’ structures, such as a virion (formed by self-assembly of capsid proteins) or a microtubule (built by laterally and longitudinally assembled head-to-tail linked $\alpha \beta$-tubulin dimers). Because these approaches do not have a thermostat, they cannot capture the stochastic nature of biological particles’ mechanical deformation and collapse. The all-atom MD simulations account for the discreteness and stochastic variation of the particles’ structures, but owing to their immense system size the all-atom MD schemes do not allow researchers to follow the dynamics of particles in the biologically relevant timescale. Langevin simulations of particles’ nanoindentation, in conjunction with some of the coarse-grained models, employ force-loading rates three orders of magnitude faster than their experimental counterparts [28, 31], and so the results of experiments in vitro and in silico cannot be compared.

To overcome these limitations, we have developed a new computational methodology which allows for nanomanipulation of biological particles in silico [34–36]. This approach utilized the simple, yet accurate $C_{\alpha }$-based coarse-grained self-organized polymer (SOP) model [37, 38] and Langevin dynamics to simulate the force loading experiments on a computer, obtaining a high-resolution detailed molecular picture of the entire indentation process, while also allowing extraction of important mechanical and thermodynamic characteristics of the system, not accessible from experiment [6, 24, 36, 39]. The SOP model is a simplified native-topology based model of biomolecules which has been used to explore the mechanical properties of protein assemblies [24, 36, 39]. The  ∼10–100 fold computational acceleration attainable on graphics processing units (GPUs) with SOP-GPU software allows for using the experimental force protocol and reaching biologically relevant timescales up to hundreds of milliseconds [34, 40, 41], which makes the results comparable with the experimental data. This approach to forced indentation in silico has been successfully applied to study the biomechanics of a range of biological particles, including CCMV virus capsids [36], microtubules [24] and nanocompartment encapsulin [6].

In this work we extended the capabilities of our methodology by developing the TensorCalculator software package. This software enables researchers to compute the stress distribution in biological matter using the results of MD simulations. The approach utilizes an idea of ‘local atomic stress’, i.e. when the stress is represented by the derivative of the total atomic forces acting on a particular atom along different directions. Taking the average over all the interactions involving this atom mimics the integration over all the forces acting on an arbitrary volume element [42]. This approach was first introduced by Basinski [43] for the calculation of shear stress in a simple body-centered cubic lattice. Shortly thereafter, Hardy derived this stress measure in a more general form [44], which later was adapted by researches in their studies of material properties of crystalline substances [45–47] and amorphous structures [48]. Ishikura et al used this concept in conjunction with the MD simulations and all-atom force field to calculate the atomic forces and local atomic stresses in short polypeptide chains [49]. To our knowledge, there has been only a single study [50], in which this approach was used to compute the stress distribution in viral shells.

The dynamics of biological particles evolve on multidimensional energy landscapes. In AFM-based single-particle compressive-force experiments, the particle’s dynamics is projected along the direction of particle deformation (‘reaction coordinate’), which limits the information obtainable. The force-deformation spectra reveal the critical forces and critical deformations for the collapse transition, but offer little insight as to what caused the transition and do not provide structural details. Here, we show that dynamic evolution of biological particles can be illuminated by considering the propagation and distribution of mechanical stress in the particle’s structure. We use cowpea chlorotic mottle virus (CCMV) as a suitable model system since it was extensively studied previously by us [36, 51] and other research groups [20, 27, 31, 52]. We explore the rich dynamics of stress distribution in the CCMV shell tested mechanically by considering the most common stress measures used to describe properties of materials, including the first principal stress, von Mises shear stress, and Tresca shear stress [53, 54]. Our results raise questions regarding some of the theoretical approaches used to model the dynamics of biological particles, including finite element analysis and elastic network models, in which stochastic fluctuations and entropic effects are ignored. We also formulate for soft biological particles like CCMV the yield condition in terms of the first principal stress components, and the failure criterion in terms of von Mises stress or Tresca stress.

2. Materials and methods

2.1. Self-organized polymer (SOP) model of a polypeptide chain

We employed the native topology $C_{\alpha }$-based self organized polymer (SOP) model of a polypeptide chain [37, 38]. In the SOP model, each protein residue is represented by a bead, positioned at the residue’s $C_{\alpha }$-atom. The explicit form of the total potential energy U_SOP (force field) expressed in terms of the coordinates of the $C_{\alpha }$-atoms $\{r_i\}=r_1,r_2,\dots ,r_N$ of residues 1, 2, …, N is given by

$${\displaystyle \begin{array}{l}{\displaystyle U_{\mathrm{S}\mathrm{O}\mathrm{P}}=U_{\mathrm{F}\mathrm{E}\mathrm{N}\mathrm{E}}+U_{\mathrm{N}\mathrm{B}}^{\mathrm{N}\mathrm{A}\mathrm{T}}+U_{\mathrm{N}\mathrm{B}}^{\mathrm{R}\mathrm{E}\mathrm{P}}.}\end{array}}$$ 1

In equation (1), the first term is the finite extensible nonlinear elastic (FENE) potential, which describes the backbone chain connectivity (i.e. the covalent bonds holding a polypeptide chain together) [37, 38]:

$${\displaystyle \begin{array}{l}{\displaystyle U_{\mathrm{F}\mathrm{E}\mathrm{N}\mathrm{E}}=-{\displaystyle \sum _{i=1}^{N-1}}\frac{k}{2}{R}_0\log [1-\frac{(r_{i,i+1}-r_{i,i+1}^0{)}^2}{R_0^2}]}\end{array}}$$ 2

where k  =  14 N m⁻¹ is the spring constant, and the tolerance in the change of the covalent bond distance is R₀  =  2 Å. The distance between the next-neighbor residues i and i  +  1, is r_i,i+1, and $r_{i,i+1}^0$ is its value in the native structure.

In equation (1), the second and third terms represent all the non-bonded interactions between amino acids, which include the residue–residue contacts stabilizing the native (folded) state ($U_{\mathrm{N}\mathrm{B}}^{\mathrm{N}\mathrm{A}\mathrm{T}}$; see equation (3) below) and all non-native interactions between residues that do not form contacts in the native state (see equation (4) for $U_{\mathrm{N}\mathrm{B}}^{\mathrm{R}\mathrm{E}\mathrm{P}}$ below). To describe the native interactions, we use the attractive Lennard-Jones potential [37, 38]:

$${\displaystyle \begin{array}{l}{\displaystyle U_{\mathrm{N}\mathrm{B}}^{\mathrm{N}\mathrm{A}\mathrm{T}}={\displaystyle \sum _{i=1}^{N-3}}{\displaystyle \sum _{j=i+3}^N}{\epsilon }_h[{\left(\frac{r_{ij}^0}{r_{ij}}\right)}^{12}-2{\left(\frac{r_{ij}^0}{r_{ij}}\right)}^6]{\mathrm{\Delta }}_{ij}.}\end{array}}$$ 3

In equation (3) above, we assume that if the non-covalently linked residues i and j ($|i-j|>$ 2) are within the cut-off distance of 8 Å in the native state, then ${\mathrm{\Delta }}_{ij}=$ 1; and ${\mathrm{\Delta }}_{ij}=$ 0 otherwise. The prefactor ${\epsilon }_h$ quantifies the strength of the non-bonded (non-covalent) interactions.

The third term in equation (1) accounts for the non-bonded interactions, which include the non-native interactions (for which ${\mathrm{\Delta }}_{ij}=0$ in equation (3)) and the interactions between residues i, i  +  1, and i  +  2, which constrains bond angles and models bending flexibility of a polypeptide chain. All the non-native non-bonded interactions are treated as repulsive using the repulsive form of Lennard-Jones potential [37, 38]:

$${\displaystyle \begin{array}{l}{\displaystyle U_{\mathrm{N}\mathrm{B}}^{\mathrm{R}\mathrm{E}\mathrm{P}}={\displaystyle \sum _{i=1}^{N-3}}{\displaystyle \sum _{j=i+3}^N}{\epsilon }_l{\left(\frac{r_{ij}^0}{r_{ij}}\right)}^6(1-{\mathrm{\Delta }}_{ij})+{\displaystyle \sum _{i=1}^{N-2}}{\epsilon }_l{\left(\frac{{\sigma }_l}{r_{i,i+1}}\right)}^6.}\end{array}}$$ 4

In equation (4) above, the second term takes into account self-avoidance of a polypeptide chain. The constant parameters ${\epsilon }_l$ and ${\sigma }_l$ define the strength and the range of repulsion. We set ${\epsilon }_l=$ 1 kcal mol⁻¹ and ${\sigma }_l=$ 3.8 Å [37, 38].

2.2. Langevin dynamics simulations

The dynamics of the system are obtained by propagating forward in time numerically the Langevin equations of motion for each $C_{\alpha }$-particle’s position r_i (i  =  1, …, N) in the overdamped (high-friction or Brownian) limit:

$${\displaystyle \begin{array}{l}{\displaystyle \gamma \frac{\mathrm{d}{r}_i}{\mathrm{d}t}=-\frac{\mathrm{\partial }{U}_{\mathrm{S}\mathrm{O}\mathrm{P}}}{\mathrm{\partial }{r}_i}+g_i(t).}\end{array}}$$ 5

In equation (5) above, U_SOP is the total potential energy of a biological particle (see equation (1)), g_i(t) is the Gaussian distributed zero-average random force, and γ is the friction coefficient. To generate the Brownian dynamics for a system in question, the equations of motion (equation (5)) for each $C_{\alpha }$-atom are propagated forward with the time step $\mathrm{\Delta }t=$ 0.08${\tau }_H$, where ${\tau }_H=\zeta {\epsilon }_h{\tau }_L/k_{\mathrm{B}}T$ is the characteristic time of a spherical particle’s motion in the overdamped limit. Here, ${\tau }_L=(m{a}^2/{\epsilon }_h){}^{1/2}=$ 3 ps is the characteristic time for the underdamped motion of a particle of mass $m\approx 3\times {10}^{-22}$ g (average amino acid residue mass) and radius $a\approx 5$ Å (average size of amino acid), and parameter ${\epsilon }_h$ sets the energy scale. Also, $\zeta =$ 50.0 is the dimensionless friction constant for amino acid residue in water ($\eta =\zeta m/{\tau }_L$), and $k_{\mathrm{B}}T$ is temperature [35, 55]. To perform simulations, we set T  =  298 K and we used the bulk water viscosity, which corresponds to the friction coefficient $\eta =7.0\times {10}^5$ pN ps nm⁻¹. Corresponding to this choice of physical parameters, we set $\mathrm{\Delta }t=$ 40 ps in the simulations.

2.3. Nanoindentation in silico

To deform virus particles, we used our recently developed approach to nanoindentation in silico [35]. Briefly, the particle is resting on the substrate surface represented by a dense network, which interacts with the virus particle through the Lennard-Jones potential:

$${\displaystyle \begin{array}{l}{\displaystyle U_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}={\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^M}{\epsilon }_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}[{\left(\frac{{\sigma }_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}}{r_i-r_j^{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}}\right)}^{12}-2{\left(\frac{{\sigma }_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}}{r_i-r_j^{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}}\right)}^6].}\end{array}}$$ 6

In equation (6), $r_j^{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}$ is the position of the jth surface bead ($j=1,2,\dots ,M$) and ${\sigma }_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}=10.0$ Å. The parameter ${\epsilon }_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}$ controls the strength of adsorption forces holding the particle on the surface, and it can be adjusted to model weak, medium and strong adsorption. Following our previous work [36], in our simulations we set ${\epsilon }_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}=0.2$ kcal mol⁻¹ to mimic weak adsorption of the CCMV particle.

The cantilever base is represented by a virtual particle connected by a harmonic spring with the spherical bead of radius R_tip mimicking the cantilever tip (indenter). The tip interacts with the virus particle via the repulsive Lennard-Jones potential:

$${\displaystyle \begin{array}{l}{\displaystyle U_{\mathrm{t}\mathrm{i}\mathrm{p}}={\displaystyle \sum _{i=1}^N}{\epsilon }_{\mathrm{t}\mathrm{i}\mathrm{p}}{\left(\frac{{\sigma }_{\mathrm{t}\mathrm{i}\mathrm{p}}}{|r_i-r_{\mathrm{t}\mathrm{i}\mathrm{p}}|-R_{\mathrm{t}\mathrm{i}\mathrm{p}}}\right)}^6}\end{array}}$$ 7

which produces an indentation on the virus particle’s outer surface. In equation (7), r_i and r_tip are coordinates of the ith virus residue and the center of the tip, respectively; ${\epsilon }_{\mathrm{t}\mathrm{i}\mathrm{p}}=$ 1.0 kcal mol⁻¹, and ${\sigma }_{\mathrm{t}\mathrm{i}\mathrm{p}}=$ 1.0 Å. For the cantilever tip, we solve the following Langevin equation:

$${\displaystyle \begin{array}{l}{\displaystyle \gamma \frac{\mathrm{d}{r}_{\mathrm{t}\mathrm{i}\mathrm{p}}}{\mathrm{d}t}=-\frac{\mathrm{\partial }{U}_{\mathrm{t}\mathrm{i}\mathrm{p}}(r_{\mathrm{t}\mathrm{i}\mathrm{p}})}{\mathrm{\partial }{r}_{\mathrm{t}\mathrm{i}\mathrm{p}}}+\kappa [(r_{\mathrm{t}\mathrm{i}\mathrm{p}}^0-{\nu }_{f}t)-r_{\mathrm{t}\mathrm{i}\mathrm{p}}].}\end{array}}$$ 8

In equation (8), κ is the cantilever stiffness, ${\nu }_f$ is the cantilever base velocity, $r_0^{\mathrm{t}\mathrm{i}\mathrm{p}}$ is the initial position of the tip center, and the friction coefficient γ corresponds to the viscosity $\eta =7.0\times {10}^6$ pN ps nm⁻¹. To generate the dynamics of a biological particle, we solved numerically equations (1) and (5)–(7) for the biological particle (CCMV shell), and equations (7) and (8) for the indenter (spherical tip).

2.4. Model systems

2.4.1. CCMV shell.

As a suitable model system, we used the SOP-based coarse-grained reconstruction of an empty capsid of cowpea chlorotic mottle virus (CCMV; protein data bank (PDB) entry: 1CWP [56]) described in detail in our previous study [36]. The CCMV shell consists of 180 identical single subunit capsid proteins. The 19.5 KDa (190 amino acid sequence) capsid proteins self-assemble into 12 pentameric and 20 hexameric structures (pentons and hexons) which form an icosahedral virus capsid (protein shell with the triangulation number T  =  3). The empty CCMV capsid is 28.6 nm in diameter, with an average shell thickness of 2.8 nm [56]. This thick shell comprises a total of 60 trimeric structural units and exhibits a pentameric symmetry at the 12 vertices (pentameric capsomers) and hexameric symmetry at the 20 faces (hexamer capsomers) of the icosahedron. The SOP model parameterization for CCMV shell is presented in our previous study [36].

2.4.2. WW-domain.

For benchmark testing of the TensorCalculator software, we used the $C_{\alpha }$-based SOP model of the WW-domain—a short polypeptide chain composed of 34 amino acid residues (PDB entry: 1PIN [57]) described in more detail in our previous study [58, 59]. The WW-domain forms an all-β-sheet structure (figure 1). The mechanical unraveling of the WW-domain is described by the reversible single-step kinetics of unfolding, $F\leftrightarrow U$, from the folded state F to the unfolded state U. The SOP model parameterization of the WW domain is presented in our previous study [58, 59].

Figure 1.

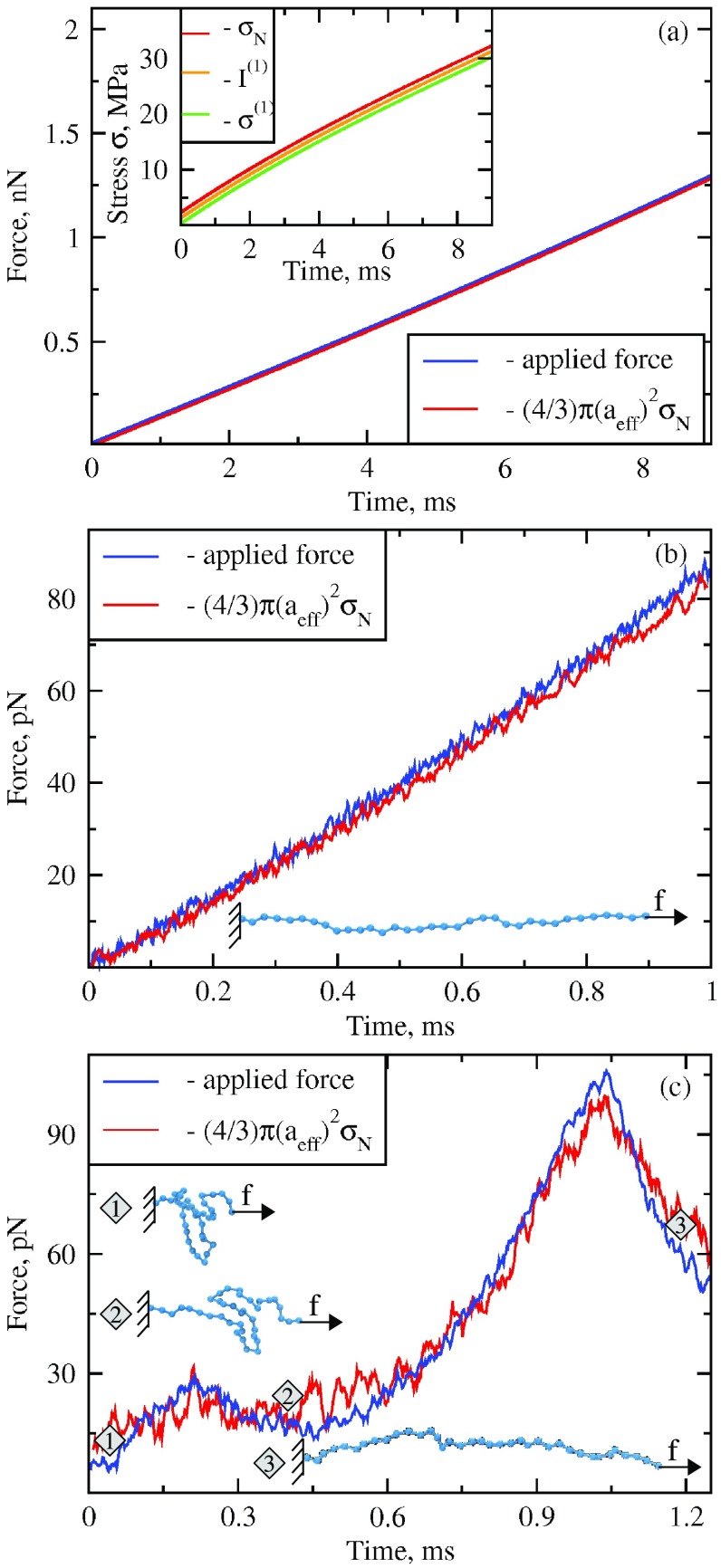
Dynamics of tension from protein forced unfolding experiments in silico (for colored figure go online). Panel (a): the profiles of applied time-dependent pulling force $f(t)$ (blue curve) and the unfolding force obtained from the average normal stress ($F=(4/3)\pi a_{\mathrm{e}\mathrm{f}\mathrm{f}}^2\sigma$; red curve) from the simulations of forced unfolding of the bead-spring chain (beads connected by harmonic springs) at zero temperature, T  =  0 K. The inset shows the profiles of the normal stress (red curve), the first invariant (orange curve) and the first principal stress (green curve). Panel (b): the profiles of applied time-dependent pulling force $f(t)$ (blue curve) and the normalized average normal stress (tension; red curve) for a bead-spring chain from the simulations of forced unfolding at finite temperature, T  =  300 K. Panel (c): the profile of applied force (blue curve) and normalized average normal stress (tension; red curve) for the WW-domain from the simulations of forced unfolding of WW-domain at finite temperature, T  =  300 K. Structural snapshots 1–3, which correspond to the equally numbered regions of the force-time curves, show WW-domain in the native folded state (snapshot 1), in the partially stretched state (snapshot 2), and in the fully unfolded state (snapshot 3) as observed in the pulling simulation.

2.5. Force protocol

2.5.1. Nanoindentation of CCMV shell.

To mimic the dynamic force-ramp conditions utilized in AFM nanoindentation experiments on the CCMV shell, we set the cantilever base to move towards an immobilized particle (CCMV shell) with a constant velocity ${\nu }_f$ thereby exerting the compressive force $\mathbf{f}=f(t)\mathbf{n}$ in the direction $\mathbf{n}$ perpendicular to the particle surface. The force magnitude f(t)  =  r_ft increases linearly in time t with the loading rate $r_f=\kappa {\nu }_f$. To indent the CCMV capsid, we used the cantilever tip radius $R_{\mathrm{t}\mathrm{i}\mathrm{p}}=$ 20 nm, ${\nu }_f=$ 1.0 μm s⁻¹, and $\kappa =$ 50 pN nm⁻¹ [36].

2.5.2. Protein forced unfolding.

To mechanically unravel the bead-and-spring chain and the WW domain, we employed the dynamic force ramp. The linearly increasing time-dependent pulling force $\mathbf{f}=f(t)\mathbf{n}$ was applied to the N-terminus, whereas the C-terminus was constrained. The force magnitude is given by $f(t)=\kappa ({\nu }_{f}t-\mathrm{\Delta }x)$, where $\mathrm{\Delta }x$ is the displacement of a pulled bead from its initial position [40], ${\nu }_f=$ 0.01 μm s⁻¹, and $\kappa =$ 100 pN nm⁻¹ [58, 59].

3. Results

3.1. TensorCalculator software

3.1.1. Atomic stress tensor.

To compute the distribution of mechanical stresses in a molecular system in question, TensorCalculator uses the local atomic stress first described by Delph [46] and Ishikura et al [49]. Without a kinetic term in a vector form, a stress for the ith particle ($C_{\alpha }$-atom) reads:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathit{\sigma }}_i=\frac{1}{2{\mathrm{\Omega }}_i}{\displaystyle \sum _{j\ne i}}{\mathbf{F}}_{ij}\otimes {\mathbf{r}}_{ij}.}\end{array}}$$ 9

In equation (9), ${\mathbf{F}}_{\mathbf{i}\mathbf{j}}$ is a total (pairwise) force, acting on atom i due to atom j, ${\mathbf{r}}_{\mathbf{i}\mathbf{j}}\mathbf{=}{\mathbf{r}}_{\mathbf{i}}\mathbf{-}{\mathbf{r}}_{\mathbf{j}}$ is the distance between particles i and j, ${\mathrm{\Omega }}_i$ is the local atomic volume, and $\otimes$ denotes the tensor product. In equation (9), the summation over atomic forces extends over all the atoms within the interaction range, defined by the cut-off distance. We used the 8 Å cut-off distance for the native interactions ($U_{\mathrm{N}\mathrm{B}}^{\mathrm{N}\mathrm{A}\mathrm{T}}$; see equation (3)) and the 20 Å cut-off for the repulsive interactions ($U_{\mathrm{N}\mathrm{B}}^{\mathrm{R}\mathrm{E}\mathrm{P}}$; see equation (4)). In the coarse-grained representation of the molecule, equation (9) is used to calculate the local stress for each amino acid residue ($C_{\alpha }$-atom). The total molecular force acting on the ith amino acid is calculated by taking the derivative of the potential energy U_SOP (equation (1)). In terms of its components, the stress tensor for the ith particle is given by

$${\displaystyle \begin{array}{l}{\displaystyle {\sigma }_i^{\alpha \beta }=-\frac{1}{2{\mathrm{\Omega }}_i}{\displaystyle \sum _{j\ne i}}\frac{\mathrm{\partial }{U}_{\mathrm{S}\mathrm{O}\mathrm{P}}(r)}{\mathrm{\partial }{r}_{ij}}\frac{r_{ij}^{\alpha }{r}_{ij}^{\beta }}{r_{ij}}}\end{array}}$$ 10

where $\alpha ,\beta =x,y,z$ denote components in 3D space. In its original form, equation (10) also has the second term which accounts for the interaction between the exterior particles and interior particles included in the volume ${\mathrm{\Omega }}_i$ [46]. Here, we use a larger volume for better averaging within the 20 Å cut-off radius. On this scale of length, we approach the continuum limit and the second term becomes negligible. In equation (10), ${\mathrm{\Omega }}_i$ is the local atomic volume, which can be calculated as [48]:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{\Omega }}_i=\frac{4\pi }{3}{a}_i^3\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}{a}_i=\frac{{\displaystyle \sum _{j\ne i}}1/r_{ij}}{2{\displaystyle \sum _{j\ne i}}1/r_{ij}^2}.}\end{array}}$$ 11

Here a_i is an ‘effective radius’ of the ith particle, which in our case is equal to the cut-off radius (≈20 Å). The stress tensor ${\sigma }_{\alpha \beta }$ (equation (10)) gives the distribution of internal stresses in a material [60].

3.1.2. Stress tensor characteristics.

The stress tensor is a second rank tensor with the components dependent upon the choice of coordinate system. However, there are sets of scalar quantities associated with the tensor, which do not change upon the transformation of coordinates. For the stress tensor, these quantities are three stress invariants, as well as three principal stress components. To obtain these quantities, we need to rewrite a stress tensor as a $3\times 3$ matrix, and then to solve the corresponding characteristic equation [61], which reads:

$${\displaystyle \begin{array}{l}{\displaystyle |\mathit{\sigma }-\lambda \mathbf{1}|=-{\lambda }^3+I^{(1)}{\lambda }^2-I^{(2)}\lambda +I^{(3)}=0.}\end{array}}$$ 12

In equation (12), $\mathbf{1}$ is the identity matrix, and

$${\displaystyle \begin{array}{ll}{\displaystyle I^{(1)}}& ={\displaystyle \sum _{\alpha }}{\sigma }^{\alpha \alpha }\\ I^{(2)}& ={\displaystyle \sum _{\alpha \beta }}({\sigma }^{\alpha \alpha }{\sigma }^{\beta \beta }-{\sigma }^{\alpha \beta }{\sigma }^{\beta \alpha })\\ I^{(3)}& =det(\mathit{\sigma }).\end{array}}$$ 13

The quantities I⁽¹⁾, I⁽²⁾, and I⁽³⁾ in equation (13) are called the stress invariants, and in the equation for I⁽³⁾, $det$ denotes the determinant of matrix $\mathit{\sigma }$. The roots of characteristic equation (12), i.e. $\lambda =\{{\lambda }^{(1)},{\lambda }^{(2)},{\lambda }^{(3)}\}$, are the eigenvalues of the stress tensor. These are related to the three principal stress components as follows:

$${\displaystyle \begin{array}{ll}{\displaystyle {\sigma }_i^{(1)}}& =max\{{\lambda }_i^{(1)},{\lambda }_i^{(2)},{\lambda }_i^{(3)}\}\\ {\sigma }_i^{(3)}& =min\{{\lambda }_i^{(1)},{\lambda }_i^{(2)},{\lambda }_i^{(3)}\}\\ {\sigma }_i^{(2)}& ={\lambda }_i^{(1)}+{\lambda }_i^{(2)}+{\lambda }_i^{(3)}-{\sigma }_i^{(1)}-{\sigma }_i^{(3)}.\end{array}}$$ 14

The first invariant I⁽¹⁾ is related to a hydrostatic pressure p  =  I⁽¹⁾/3, whereas the other two invariants I⁽²⁾ and I⁽³⁾ have no obvious physical meaning. The combination of the stress invariants, also known as the von Mises shear stress ${\sigma }^{vM}$ defines the magnitude of the shear stress:

$${\displaystyle \begin{array}{l}{\displaystyle {\sigma }^{vM}={[(I^{(1)}{)}^2-3I^{(2)}]}^{1/2}.}\end{array}}$$ 15

The first principal stress ${\sigma }^{(1)}$ is related to the maximum tensile stress, whereas the third principal stress ${\sigma }^{(3)}$ corresponds to the maximum compressive stress. Knowing the principal stress components allows for the calculation of the Tresca stress:

$${\displaystyle \begin{array}{l}{\displaystyle {\sigma }^{\mathrm{T}\mathrm{r}}=\frac{{\sigma }^{(1)}-{\sigma }^{(3)}}{2}.}\end{array}}$$ 16

TensorCalculator computes the first stress invariant $I_i^{(1)}$ (equation (13)), the first principal stress ${\sigma }_i^{(1)}$ (equation (14)), the von Mises stress ${\sigma }_i^{vM}$ (equation (15)), and the Tresca stress ${\sigma }_i^{\mathrm{T}\mathrm{r}}$ (equation (16)) for each amino acid $i=1,2,\dots ,N$.

3.1.3. Using TensorCalculator.

The TensorCalculator package is an extension of the SOP-GPU software developed previously in our group [40] for performing the Langevin dynamics of biomolecules in a coarse-grained representation. As an input, TensorCalculator uses (i) the structure file (in the PDB format), which carries information about the particles’ coordinates, (ii) the topology file (in the GROMACS topology format [62, 63]), which contains information about the residue–residue interactions, and iii) the simulation trajectory (i.e. simulation output in the CHARMm-DCD binary format [64]). TensorCalculator reads the system coordinates for each time-frame from the DCD trajectory file and calculates the distribution of instantaneous amino acid stresses for system’s conformation in each frame using equations (1)–(4) and (10). TensorCalculator outputs dynamics of varying stress values for each amino acid along a simulation trajectory. Since calculations of the atomic tensors are based on the SOP force field, TensorCalculator is fully compatible with the simulation output obtained from Langevin dynamics (LD) simulations with the SOP force field.

TensorCalculator can also work with any other type of trajectory, as long as the input files are in the correct format. The code has a modular architecture, which allows for addition of any potential energy term (force field) without affecting other computational modules. TensorCalculator can operate in two modes. In the first mode, it computes the atomic stress tensors for an existing simulation input (LD run). In this mode, TensorCalculator produces the TNSR output file. The TNSR file is a text file with the strings format similar to that used in PDB; however, instead of coordinate values for each particle it contains stress tensor components per particle for each trajectory frame (moment of time). This is the most time consuming part of the program, and it needs to be done only once. In the second mode, TensorCalculator produces different outputs with the stress tensor components reported as scalar quantities. It prints out the average values of the stress invariants, the principal components, and von Mises stress and Tresca stress along the simulation trajectory.

TensorCalculator produces an output file for visualization of the first invariant, first principal component and von Mises/Tresca stresses. The output file for visualization uses the PDB file format to write out the scalar stress quantities in the last four columns per $C_{\alpha }$-atom for each frame of trajectory. TensorCalculator works in conjunction with the visual molecular dynamics (VMD) package [65] and our own lab-written scripts (available in TensorCalculator repository). Calculation of the scalar stress quantities for visualization and graphics can be done independently from stress tensors’ calculations, as long as the input TNSR file is provided. Therefore, TensorCalculator allows for a quick recalculation as many times as necessary, e.g. for different averaging options (cut-offs). Since the values of stress tensors per $C_{\alpha }$-atom can fluctuate significantly both in space and time, different types of averaging can be tried in order to make visualization and graphical representation smooth and continuous. The running average can be chosen in order to smooth out the stress fluctuations along the trajectory. In addition, different types of averaging over the particles can be specified, e.g. averaging over the structure segments or within a cut-off radius, in order to obtain a smooth and continuous stress gradient. Examples of configuration files for running the TensorCalculator software package for several model systems are provided in the code repository (https://github.com/BarsegovGroup/TensorCalculator.git).

3.1.4. Benchmark tests of numerical accuracy.

Before using the first stress invariant $I_i^{(1)}$, the first principal stress ${\sigma }_i^{(1)}$, von Mises stress ${\sigma }_i^{vM}$, and Tresca stress ${\sigma }_i^{\mathrm{T}\mathrm{r}}$ to describe the dynamics of stress propagation and distribution in the CCMV virus particle, we performed benchmark testing of the TensorCalculator software. First, we carried out test calculations of the atomic stress tensors using a trajectory of protein forced unfolding for a generic polypeptide, which consists of 34 beads connected by harmonic springs. The potential energy of this simple bead-and-spring model is given by the FENE potential (see equation (2)). The dynamics of the system was described by solving the Langevin equations of motion for each bead (equation (5)) at T  =  0 K and T  =  300 K. For the simulations at finite temperature T  =  300 K, we completed 100 simulation runs, and the final result was averaged over all 100 trajectories due to thermal fluctuations (see Materials and Methods for the protocol of force application). At zero temperature T  =  0 K, a single simulation run needs to be completed (no thermal fluctuations).

Using the results of pulling simulations for the bead-and-spring chain, we calculated the atomic stress tensors for each bead and for each moment of time (every frame). The values of stress tensors were combined for all frames to probe the time-dependence of the following stress characteristics: the normal stress, stress invariants and principal components of stress as described above (see equations (13) and (14)). The normal stress (${\sigma }_N$) was obtained by projecting the tensor component along the direction of pulling (x-axis) roughly equal to a vector connecting the C- and N-termini (end-to-end vector). In figure 1(a), we display the time-dependent profiles of the stress characteristics averaged over the chain (total of 34 beads). To directly compare the stress in a molecular chain due to applied pulling force, we converted the stress quantity (given in units of Pa) into the molecular force or tension (in units of pico-Newtons) using the formula: $F=(4/3)\pi a_{\mathrm{e}\mathrm{f}\mathrm{f}}^2{\sigma }_N$, where ${\sigma }_N$ is the average normal molecular stress and $a_{\mathrm{e}\mathrm{f}\mathrm{f}}=1/N\sum a_i$ is the average radius of cross-sectional area of the chain (see equation (11)). Because the chain is formed by the beads of radius 3.4 Å, $a_{\mathrm{e}\mathrm{f}\mathrm{f}}\approx$ 3.4 Å. We see that the curve of tension F practically collapses on the curve of applied pulling force $f(t)$ (figure 1(a)). Both quantities show very good agreement at zero temperature T  =  0, and at finite temperature T  =  300 K (see figures 1(a) and (b)).

Next, we carried out the calculations of the stress measures but for the SOP model of the all-β-sheet WW-domain (see Materials and Methods) using the output from pulling simulations at T  =  300 K (a total of 100 independent runs). Figure 1(c) shows the result of comparison of mechanical tension in the WW-domain derived from the normal stress in the molecule ${\sigma }_N$ using the formula $F=(4/3)\pi a_{\mathrm{e}\mathrm{f}\mathrm{f}}^2{\sigma }_N$, and the applied pulling force $f(t)$. We see that the agreement between the molecular tension F computed with TensorCalculator and the applied pulling force $f(t)$ is excellent. Both force-time curves show force peaks, which mark the unfolding transition in the WW-domain. Small differences are due to the non-zero shear component of the stress, which is not analyzed in the context of protein forced unfolding. At the force maximum (peak force) at time $t\approx$ 1 ms, most of the protein native structure is disrupted, and so the concept of volume averaging is not valid. Hence, the discussion of stress dynamics is meaningful only before the global transitions occur in the system (e.g. unfolding of a protein or structural collapse of a virus shell). Taken together, the results of benchmark testing confirm the numerical accuracy of the stress measures computed with TensorCalculator.

3.2. Analysis of dynamics of stress propagation and distribution in CCMV shell

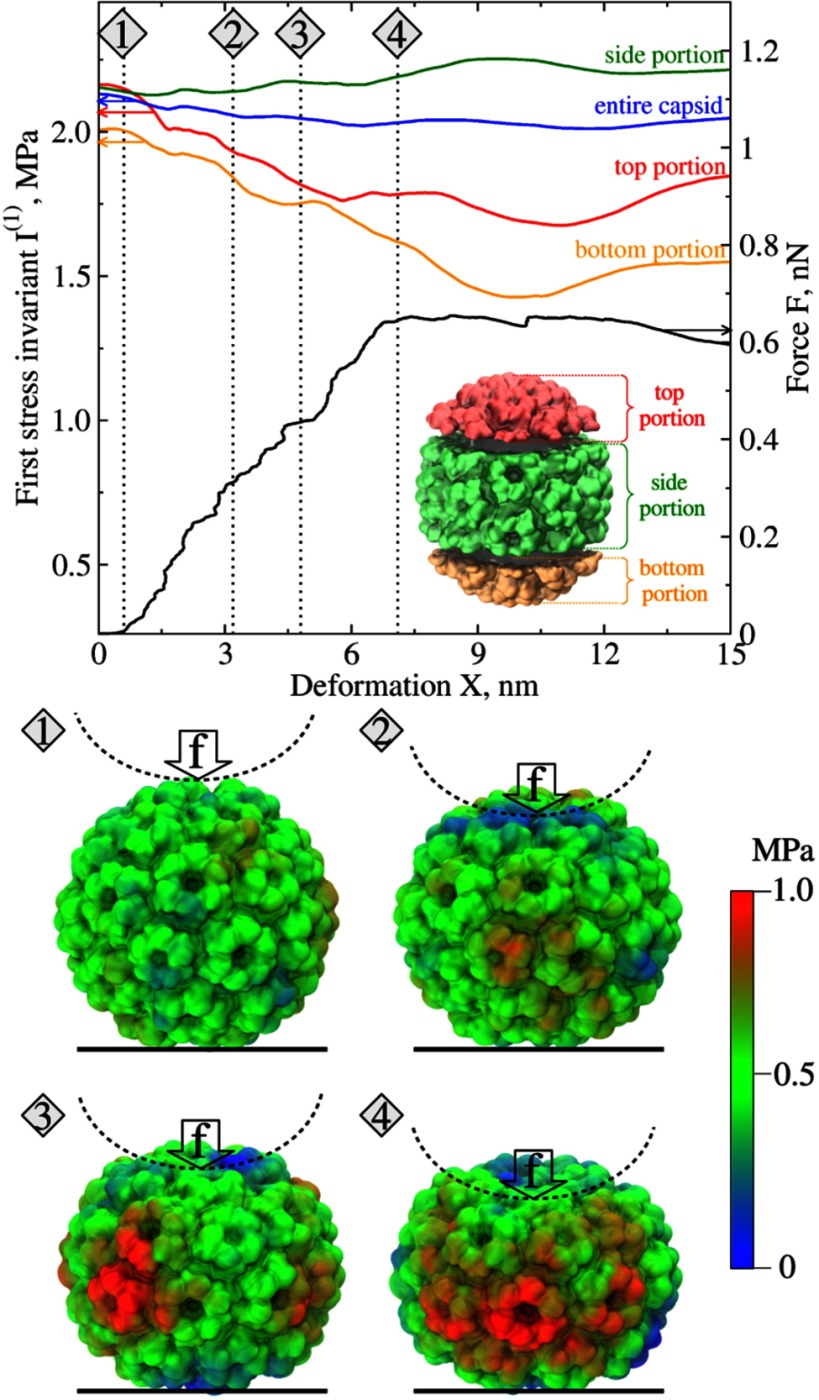
We used the results of in silico nanomanipulation with the empty CCMV protein shell, for which we performed uniaxial compression of the capsid structure as described in our previous study of CCMV dynamics [35, 36]. A total of 20 trajectories of nanoindentation of the CCMV capsid were analyzed in which a compressive force was indenting the capsid along different directions coinciding with the two-, three-, five-, quasi-two-, and quasi-three-fold symmetry axes. The results obtained were used to compute all the distributions of mechanical stress measures in the capsid structure. To visualize the dynamics of stress propagation, we profiled various stress measures as functions of particle deformation—a suitable reaction coordinate, and analyzed the surface maps of these measures. An example of the evolution of mechanical stress in the particle’s structure represented by the first stress invariant I⁽¹⁾ (equation (13)) is shown in figure 2 along with the force-deformation curve (FX-curve) for a representative trajectory of CCMV indentation along the two-fold symmetry axis.

Figure 2.

Evolution of mechanical stress in CCMV capsid from forced nanoindentation in silico (for colored figure go online). Top panel: the force (F) versus deformation (X) curve (FX-curve; black solid line) and the first stress invariants I⁽¹⁾ for an entire CCMV capsid (blue solid curve), and for the top portion (red dashed curve), bottom portion (orange curve) and side portion of CCMV capsid structure (green dashed curve) for a representative trajectory of nanoindentation of CCMV along the two-fold symmetry axis (see Materials and Methods). The stress invariants do not include contributions from the kinetic term. Bottom panel: snapshots of the capsid structure numbered 1–4 displaying the propagation and inhomogeneous distribution of the stress on the particle’s surface corresponding to X  =  0.6, 3.2, 4.8 and 7.0 nm deformations. The color code displayed on the far right shows the stress amplitude. In the snapshots, the vertical arrows indicate the direction of external compressive force and dashed semi-circles show the indenter position. Here and in figures 3–5 the results are shown for one representative trajectory of CCMV nanoindentation along the two-fold symmetry axis obtained with the cantilever tip of radius $R_{\mathrm{t}\mathrm{i}\mathrm{p}}=$ 20 nm and cantilever base velocity ${\nu }_f=$ 1.0 μm s⁻¹.

In general, the stress tensor given by equation (9) contains the kinetic energy term $1/(2{\mathrm{\Omega }}_i)m_i{\mathbf{v}}_{\mathbf{i}}\otimes {\mathbf{v}}_{\mathbf{i}}$, where m_i and ${\mathbf{v}}_{\mathbf{i}}$ are the mass and velocity of ith particle, respectively [44, 49]. However, for Langevin dynamics in the overdamped (high-friction) limit this term gives a small constant contribution. Although TensorCalculator has the option to include the contribution from kinetic energy terms in the calculation of stress measures, in this work we ignored this contribution because we focused on the stress difference in various portions of the capsid structure having similar kinetic energy. For this reason, the calculated stress tensor does not satisfy the energy conservation law [45, 46].

3.2.1. Stress dynamics in CCMV shell.

The total stress (without the kinetic contribution discussed above) remains almost constant while the particle is loaded mechanically (figure 2). This might seem counter-intuitive, since the particle is gradually loaded mechanically with the CCMV capsid response force rising up to F  =  0.65 nN as reflected by the FX-curve. In this work, we focused on elucidating the role of structural changes in various portions of CCMV structure in the dynamic evolution of mechanical stress, and so we ignored the contributions from kinetic energy terms. These terms (not included in equations (9) and (10) and (13)–(16)) describe the translocation of various portions of CCMV structure due to uniaxial compression. We defined the top and bottom portions of CCMV structure as the top and bottom particle caps with their heights equal to 30% of total particle diameter. This corresponds to 8 nm slices at the top and bottom of CCMV as measured along the axis of indentation (see inset in figure 2). The remaining part of the CCMV capsid is referred to as the side portions of the CCMV structure.

Structure analysis as well as calculation and visualization of the stress measures with TensorCalculator reveal inhomogeneous stress distribution on the particle’s surface. In the course of mechanical deformation, the CCMV capsid’s top and bottom portions interact with the cantilever tip (indenter) and the substrate surface, respectively (see snapshot 1 in figure 2). These structure portions rapidly become flat (snapshots 2 and 3) and they transmit mechanical stress to the side portions of the CCMV shell. At the same time, the CCMV capsid’s side portions bend and accumulate most of the stress in the course of compression. This is precisely reflected in the dynamics of first stress invariant I⁽¹⁾. The profiles of I⁽¹⁾ displayed in figure 2 show that corresponding to CCMV capsid deformation by X  =  7 nm, the stress invariant for top and bottom portions of CCMV structure $I_t^{(1)}$ and $I_b^{(1)}$ decrease by  ∼19% of their initial values, i.e. by $\mathrm{\Delta }{I}_t^{(1)}\approx 0.40\pm$ 0.05 MPa and $\mathrm{\Delta }{I}_b^{(1)}\approx 0.38\pm 0.07$ MPa, respectively. At the same time, the first stress invariant for the side portion of CCMV structure $I_s^{(1)}$ increases by $\mathrm{\Delta }{I}_s^{(1)}\approx$ 0.06  ±  0.03 MPa, which accounts for only  ∼3% change from its initial value. Hence, we can conclude that the stress development and redistribution from the top and bottom portions of the CCMV structure to the side portions result in the particle’s shape alteration under mechanical loading. These shape changes are reflected in stress decrease in the top and bottom portions of the capsid structure and stress accumulation in the side portion of the CCMV structure. This physical picture fully agrees with our previous finding regarding formation of multiple cracks (structure defects) in the side portion of the CCMV shell, eventually leading to the particle’s structural collapse. A supplementary movie (stacks.iop.org/JPhysCM/30/044006/mmedia) shows the appearance of red spots, which correspond to large stress accumulation far exceeding the critical values, which leads to particle collapse (see movie S1). Hence, the results obtained for CCMV show that the stress distribution and the interplay between mechanical stress components in the top, bottom and side portions of the CCMV capsid set the limits of particle mechanical strength and structural stability.

3.2.2. Effect of thermal fluctuation on stress propagation in virus shell.

The results described in the previous section demonstrate a strong correlation between the CCMV particle’s shape alteration and the dynamics of stress propagation in the protein capsid. In our previous work, we showed using nanomanipulation of the CCMV shell in silico that the virus particle’s stiffness and resistance to external mechanical factors are, in part, due to the capsomers’ gradual rearrangement and the particle’s structure remodeling near and under the indenter (cantilever tip), which also results in a large entropy increase [36]. To further address the issue of entropic effects and to probe possible interplay among the entropy changes, deformation dynamics, and stress evolution in the CCMV particle’s structure, we carried out simulations of CCMV nanoindentation at zero temperature T  =  0 K. Next, we directly compared the results at zero temperature with those obtained at finite temperature T  =  300 K.

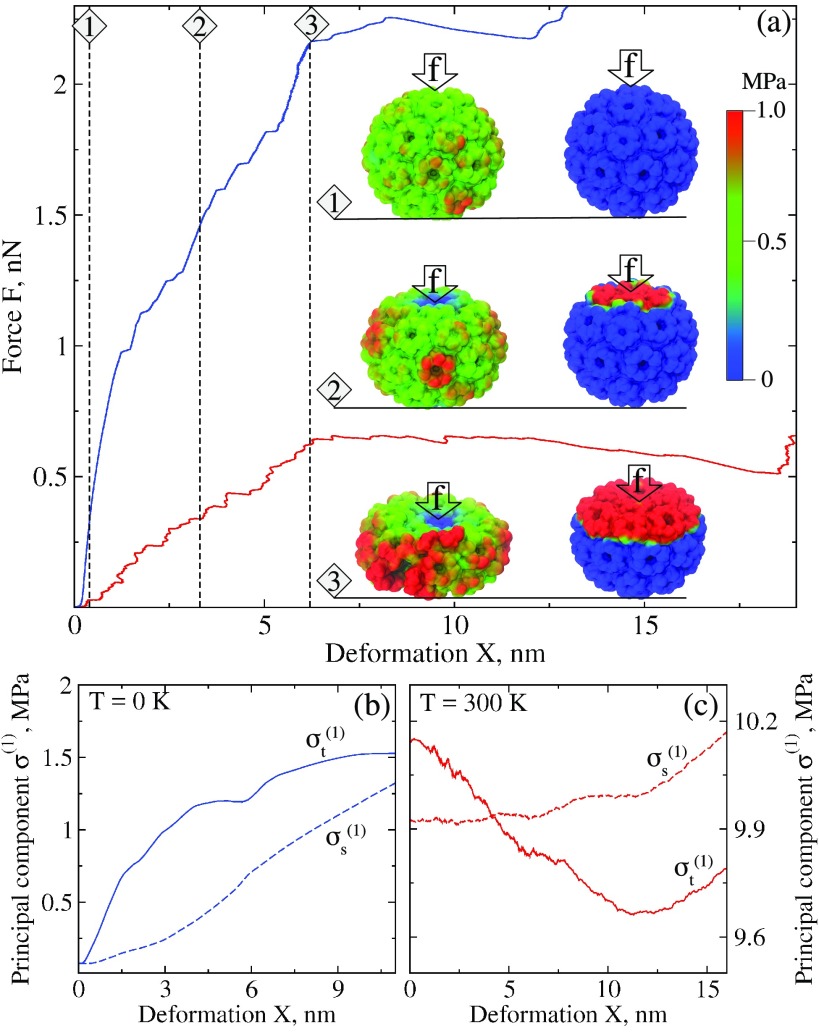
Surprisingly, the FX-curves displayed in figure 3(a) show that, unlike for the T  =  300 K case, the capsid’s structural collapse at T  =  0 K occurs at significantly higher force, i.e. F^*  =  2.25 nN at T  =  0 K versus F^*  =  0.65 nN at T  =  300 K. To understand the origin of this drastic reduction in the critical force for the CCMV shell global transition to the collapsed state, we also analyzed and compared the surface maps showing the distributions of the first principal stress component in the CCMV shell ${\sigma }^{(1)}$ at T  =  0 K and 300 K (see snapshots in figure 3(a)). Structural snapshots 1–3 which correspond to the equally numbered regions in the FX-spectra show a more rapid yet gradual change in the stress intensity at finite temperature T  =  300 K as compared to zero temperature. Interestingly, as is evident from the CCMV structure snapshots for X  =  3.3 and 6.2 nm deformation, at T  =  0 K the color (stress intensity) shows a step-wise (sudden) change as one goes from the top portion to the side portion of the CCMV structure.

Figure 3.

Nanomanipulations in silico with CCMV capsid at different temperatures (for colored figure go online). Panel (a): the FX-curves from nanoindentation experiments at zero temperature T  =  0 K (blue curve) versus finite temperature T  =  300 K (red curve) displaying a dramatic effect of thermal fluctuations on the particle’s mechanical properties. Structural snapshots numbered 1–3 show changing intensity of the CCMV surface map for the first principal stress component for the entire capsid structure ${\sigma }^{(1)}$ in the course of capsid deformation at X  =  0.4, 3.3 and 6.2 nm. Color code (same as in figure 2) is presented next to structure snapshots. More rapid propagation of mechanical stress to the side portions of the capsid structure due to thermal fluctuations (at T  =  300 K, left snapshots) leads to CCMV particle’s collapse at much lower forces. This behavior can be directly compared with the results of CCMV forced deformation without thermal fluctuation effects (at T  =  0 K, right snapshots). Here, the mechanical stress is accumulated only locally in the area around the cantilever tip, while the remaining portion of CCMV structure is unstressed. Panel (b) and (c): the profiles of the first principal stress component for the top portion ${\sigma }_t^{(1)}$ (solid curves) and side portion ${\sigma }_s^{(1)}$ (dashed curves) of the CCMV capsid structure versus deformation X obtained at zero temperature T  =  0 K (panel (b)) and finite temperature T  =  300 K (panel (c)).

The observed large differences in the stress amplitude and dynamic pattern of stress propagation in the CCMV capsid structure prompted us to analyze the first principal stress components for the top portion ${\sigma }_t^{(1)}$ and side portion ${\sigma }_s^{(1)}$ of the CCMV structure, which are displayed in figures 3(b) and (c) for zero temperature T  =  0 K and finite temperature T  =  300 K, respectively (see also supplementary movie S1). In the absence of thermal fluctuations, initially (for small deformation X) both the mechanical stress in top and side portions ${\sigma }_t^{(1)}$ and ${\sigma }_s^{(1)}$ gradually increase. Later on, at $X\approx$ 6.2 nm deformation, the slope of ${\sigma }_t^{(1)}$ decreases, which implies that the stress stored in the top portion of the CCMV shell propagates slowly to the side portion (figure 3(b); see also supplementary movie S2). Quite unexpectedly, the CCMV capsid response is dramatically different when the particle is deformed at finite temperature T  =  300 K (figure 3(c), supplementary movie S2). Here, thermal fluctuations lead to a 0.22 MPa difference between ${\sigma }_t^{(1)}$ and ${\sigma }_s^{(1)}$ at small deformations (figure 3(c)), and they introduce significant inhomogeneity in the stress distribution as is evident from the structure snapshots displayed in figure 3. In the course of indentation up to X  =  6.2 nm deformation, the stress in the top portion of the CCMV structure rapidly decreases by $\mathrm{\Delta }{\sigma }_t^{(1)}=$ 0.32 MPa, whereas the stress in the side portion of the CCMV shell increases by $\mathrm{\Delta }{\sigma }_s^{(1)}=$ 0.02 MPa until the CCMV capsid collapse occurs at X  =  6.2 nm. To summarize, the results obtained clearly demonstrate that thermal fluctuations modulate the mechanical properties of virus shells, which implies that the entropic effects are highly important.

3.2.3. First principal stress helps define the yield strength of virus particles.

The results of the previous section also indicate that the mechanical evolution of the CCMV capsid can be described in terms of the deformation-dependent dynamics of stress components for different portions of the capsid structure (i.e. top and side portions). Hence, there is a question whether these stress components can be used to determine a yield strength for a particle under study, i.e. the critical stress at which the material response to external mechanical loading changes from elastic to plastic.

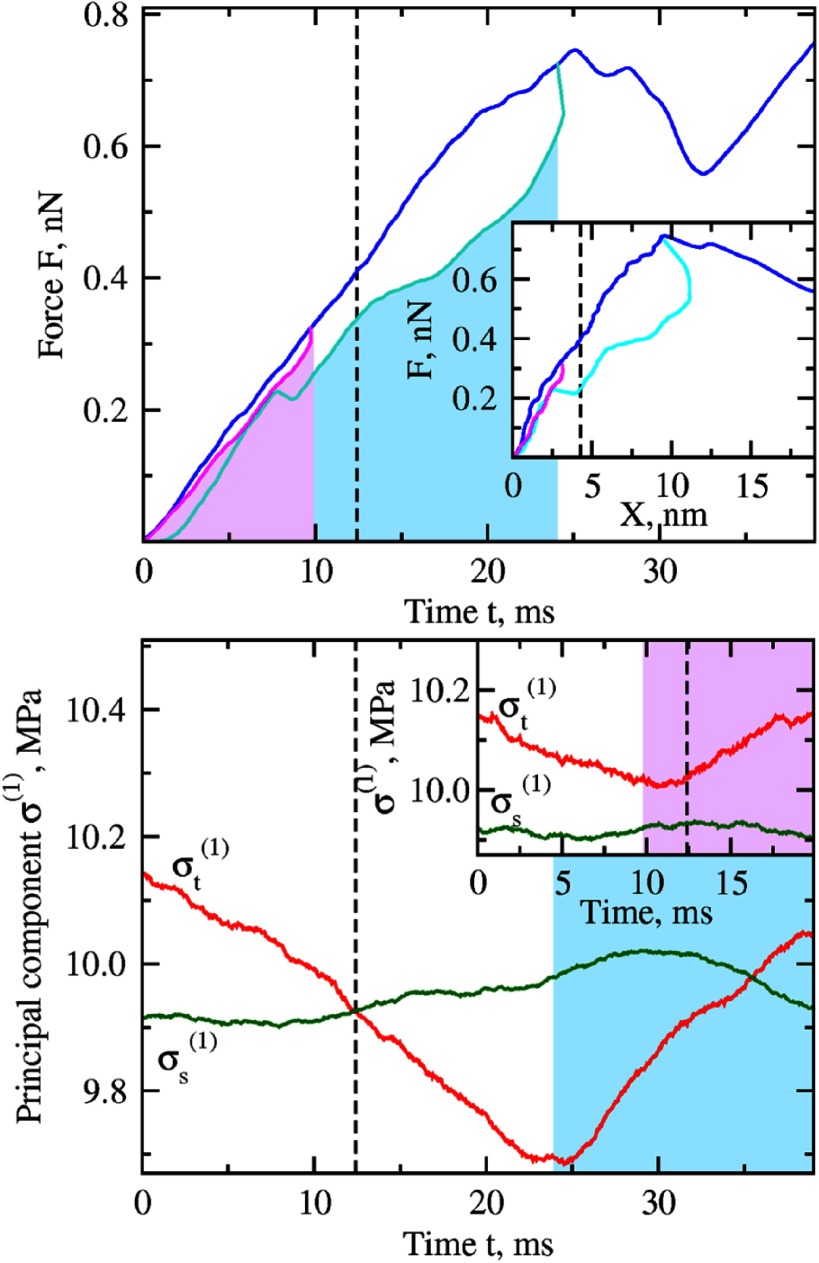
We employed nanomanipulations with the CCMV capsid in silico to probe the limit of its elasticity. In these sets of computer experiments we mechanically tested the CCMV particle by performing the simulations of forward indentation when the compressive force is ramped up, which were then followed by the simulations of backward tip retraction when the compressive force is gradually quenched to zero. The simulations of backward tip retraction were performed starting from the partially deformed structures generated in the course of forward indentation with X  =  3.8, 6.2, 7.4, and 9.5 nm deformation (see figure S2). The profiles of FX curves for two representative trajectories with X  =  3.8 and 9.5 nm deformation are shown in figure 4(a). The lack of hysteresis in the FX-curves show that the CCMV particle completely restores its initial shape in the course of force-quench tip retraction if the deformation in the forward indentation does not exceed X  =  5.0 nm deformation. However, when CCMV deformation is larger than $X⩾$ 5.0 nm, the CCMV structure is not fully restored in the course of force-quench tip retraction, which also results in the increased hysteresis as observed in the FX curves. Next, we analyzed the first principal stress components ${\sigma }^{(1)}$, which showed that for X  <  5.0 nm deformation the mechanical stress in the top portion of CCMV structure ${\sigma }_t^{(1)}$ does not decrease beyond the stress level in the side portion of CCMV capsid ${\sigma }_s^{(1)}$. Indeed, the curves of ${\sigma }_t^{(1)}$ and ${\sigma }_s^{(1)}$ displayed in the inset in figure 4(b) never cross. This result is in contrast to indentations exceeding X  =  5.0 nm deformation, for which the stress in the side portion of CCMV shell exceeds the stress in the top portion of CCMV structure as soon as the curves of ${\sigma }_t^{(1)}$ and ${\sigma }_s^{(1)}$ cross (figure 4(b)).

Figure 4.

Forward indentation and backward tip retraction for CCMV capsid in silico (for colored figure go online). Top panel: the total molecular deformation force (F) as a function of time (t) for the forward indentation (blue curve) and backward tip retraction (curves shown in magenta and cyan). The inset shows the corresponding force-deformation curves (FX-curves) for the forward deformation and backward tip retraction (color denotation is same). The areas under the Ft-curves shown in magenta and cyan areas indicate, respectively, the moments of time for backward tip retractions which correspond to the structures deformed by X  =  4 and 9 nm. Bottom panel: the average first principal stress component for the top portion ${\sigma }_t^{(1)}$ (red curve) and side portion ${\sigma }_s^{(1)}$ (green curve) of CCMV structure calculated for the full cycle of forward indentation and backward tip retraction starting from the 9 nm deformed structure. The inset shows same stress quantities calculated for the full cycle of forward indentation and backward tip retraction starting from the 4 nm deformed structure. Highlighted cyan and magenta areas denote same intervals of backward tip retraction as on the top panel. The retraction simulations for the structures obtained at X  <  4.5 nm (dashed curve) deformation exhibit almost linear (i.e. elastic) response of the capsid to mechanical perturbation (no hysteresis), while for the structures obtained after X  =  4.5 nm we observe significant dissipation of energy (large hysteresis) meaning that the particle response is plastic). The point of transition from elastic to plastic regime corresponds to the equality of the stress components for the top and side portions of CCMV capsid.

The results of analysis of the first principle stress components ${\sigma }^{(1)}$ for different elements of the CCMV shell structure clearly demonstrate that the equality of the first principal stresses in the top portion of CCMV ${\sigma }_t^{(1)}$, to which the external compressive force is applied through a cantilever tip, and the side portions, where structural defects occur and accumulate in the course of mechanical deformation ${\sigma }_s^{(1)}$, can be used to formulate a yield strength (and yield deformation) criteria for virus capsids. Here, we considered the top versus side portions of the CCMV particle, but these results also hold for the bottom versus side portions of the CCMV structure (not shown).

3.2.4. Von Mises stress and Tresca stress criteria define the critical strength of virus particles.

It has been shown that the von Mises stress tensor is a suitable measure of mechanical strength of brittle isotropic materials, whereas the Tresca stress tensor is a good measure for describing the mechanical stability of isotropic ductile materials [53, 54]. We analyzed the nanomechanics of the virus capsid from the brittle versus ductile materials science perspective using the CCMV shell as a suitable model system. To that end, we computed and analyzed the von Mises stress tensor and Tresca stress tensor for the CCMV capsid, using the output from the simulations of CCMV nanoindentation. We analyzed the profiles of these quantities as functions of particle deformation X. For simplicity, here we consider von Mises and Tresca stress tensors for the top portion and for the side portion of the CCMV structure. A comparison of von Mises and Tresca stress tensors for the bottom and side portions of the CCMV shell gave similar results (not shown).

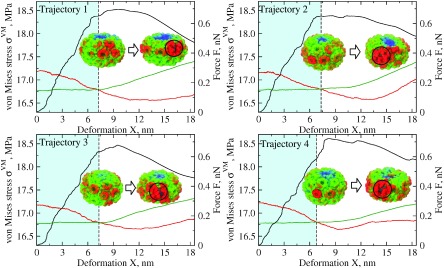
The profiles of average von Mises stress ${\sigma }^{vM}$ for the top portion and side portion of the CCMV structure are presented in Figure 5 for four representative indentation trajectories, where they are overlaid with the corresponding FX-spectra. The profiles of Tresca stress ${\sigma }^{\mathrm{T}\mathrm{r}}$ for the top and side portions of the CCMV shell overlaid with the FX-curves are shown in figure S3. For all four independent measurements, von Mises stress for the top portion of CCMV shell ${\sigma }_t^{vM}$ monotonically decreases during forced deformation by $\mathrm{\Delta }{\sigma }_t^{vM}\approx$ 0.39  ±  0.02 MPa, whereas von Mises stress for the side portion of CCMV structure ${\sigma }_s^{vM}$ slowly increases by $\mathrm{\Delta }{\sigma }_s^{vM}\approx$ 0.02  ±  0.01 MPa (figure 5). This means that the mechanical stress generated at the top by the cantilever tip rapidly propagates from the top to the sides of the CCMV shell and gradually accumulates in the side portion of the CCMV structure. As soon as the von Mises stresses for the top and side portions become equal ${\sigma }_t^{vM}={\sigma }_s^{vM}$ (see curves’ intersection in figure 5), a subsequent mechanical loading leads to ${\sigma }_s^{vM}$ being greater than ${\sigma }_t^{vM}$. From this point on, any additional stress propagation and accumulation in the side portion of CCMV results in formation of cracks, which then leads to the CCMV transition to the globally collapsed state (figure 5). Not coincidentally, the characteristic deformation X where ${\sigma }_t^{vM}={\sigma }_s^{vM}$ corresponds to the moment of time at which the indentation force begins to decrease. The force decrease signifies that the CCMV shell is starting to lose its mechanical resistance, which eventually results in the collapse transition (see FX-curves in figure 5). Hence, the characteristic deformation X at which ${\sigma }_t^{vM}={\sigma }_s^{vM}$ corresponds to the regime where the particle deformation is approaching the critical deformation $X\to X^{\ast }$. This result is consistent for all nanoindentation assays summarized in figure 5. We also analyzed the output from nanoindentation simulations for CCMV compressed along three-, five-, quasi-two- and quasi-three- fold symmetry axes and found similar results (not shown). Therefore, we conclude that the equality of von Mises stress for the top and side portions is a good predictor of the structural collapse transitions in virus shells.

Figure 5.

Dynamics of deformation (black FX-curves; right y-axes) and evolution of average von Mises stress for the top portion ${\sigma }_t^{vM}$ (red curves) and side portion ${\sigma }_s^{vM}$ (green curves) of CCMV capsid as functions of the capsid deformation X (left y-axes) (for colored figure go online). Shown in four panels are the results from four independent nanoindentations of CCMV in silico. The dashed vertical lines denote the critical deformations in the $X\approx$ 7.0–7.5 nm range, which correspond to the specific times at which all the stress from the top portion transfers to and accumulates in the side portion of the CCMV shell. These times correspond to the ${\sigma }_t^{vM}$ and ${\sigma }_s^{vM}$ curves crossing in the graphs. Subsequent force loading beyond 7.0–7.5 nm deformation leads to the stress increase in the side portions, at which point the cracks in the CCMV structure start to appear (shown in black circles). This leads to the particle’s transition into the collapsed state at $X\approx$ 9.0–9.5 nm. The snapshots display the surface maps of von Mises stress before the collapse for $X\approx$ 7.0–7.5 nm (left snapshots) and after the collapse for $X\approx$ 9.0–9.5 nm (right snapshots).

4. Discussion

Large-size biological particles such as virus shells, protein fibers, microtubule polymers, etc are composed of elementary building blocks that are formed by the association of protein domains. For example, the CCMV capsid is composed of multiple copies of a 190 amino acid long capsid protein; fibrin fibers are formed by fibrin monomers, ∼3500 residue long, organized into double-stranded fibrin protofibrils; microtubule polymers are composed of 10–13 protofilaments, each formed by  ∼1000 residue long $\alpha \beta$-tubulin dimers. Clearly then, biological particles are discrete structures and there is a more philosophical question to consider: how large can a particle be so that the concepts of continuum mechanics can be applied to describe their physical and materials properties? For example, Cauchy stress is widely used in materials science to study the physical properties of materials undergoing small deformations. On the other hand, we have demonstrated in our previous studies of the CCMV capsid [36] and microtubule polymer fragments [24] that the long-wavelength global modes, which control the displacements of entire structural subunits (i.e. hexon and penton capsomers in the CCMV shell or microtubule protofilaments in microtubules), and the symmetry of their arrangement, rather than atomic level details, determine the mechanical properties of biological particles and their response to external physical inputs. Hence, large-size biological particles do permit a continuum representation, which allows use of the apparatus of continuum mechanics to describe their properties. Yet, computational molecular modeling of biological particles requires having a discrete representation of the polypeptide chains, either atomic or simplified (coarse-grained) bead-per-residue, and so there is an issue of how continuum measures can be calculated for the discrete structures.

We have overcome this problem by employing a concept of the atomic stress tensor $\mathit{\sigma }$ defined by equations (9) and (10), which captures local deformation stresses induced in a small volume element Ω of the particle’s structure under the influence of local strain. When defined locally for all particles i  =  1, 2, …, N where N is the system size (total number of residues in the system), i.e. atoms (all-atomic modeling) or amino acid residues (coarse-grained schemes), the atomic stress tensor ${\mathit{\sigma }}_i$ provides valuable information about the distribution of internal tension in the biological material. Furthermore, since the tensor components are averaged over the volume element Ω of a large 20 Å cut-off radius, they carry information about the pair-wise particle-particle interactions between the ith particle and other particles within the cut-off sphere (see equation (11)). Therefore, the stress tensor components are piecewise continuous functions of space and time. Stress tensors are typically used in continuum mechanics to analyze the effects of small deformation. In our nanomanipulations in silico, we too use experimentally relevant slow force-loading rates, which translate to the cantilever velocities of 10⁻¹–${10}^1\mu$m s⁻¹, and so the local deformations are of low amplitude. Hence, the differences in the stress tensor components $\mathrm{\Delta }{\mathit{\sigma }}_i(\mathrm{\Delta }t)$ for two consecutive structural configurations separated by a short time interval $\mathrm{\Delta }t\approx$ 40 μs are, indeed, very small (see movie S1).

We have developed the TensorCalculator software package for the numerical calculation of the local stress tensor ${\mathit{\sigma }}_i$, the stress invariants $I_i^{(1)}$, $I_i^{(2)}$, $I_i^{(3)}$, the principal stress components ${\sigma }_i^{(1)}$, ${\sigma }_i^{(2)}$, ${\sigma }_i^{(3)}$, the von Mises stress ${\sigma }_i^{vM}$, and the Tresca stress ${\sigma }_i^{\mathrm{T}\mathrm{r}}$ given by equations (9)–(16). These are important stress measures widely used in materials science and mechanical engineering. The stress invariants are characteristics of the tensors which, unlike the tensors components, do not change upon the transformation of coordinates. The principal values characterize stress components in the direction of maximum tension or compression, and they are often used by engineers to formulate the yield and failure criteria of materials. The von Mises stress and Tresca stress are derivative quantities from the stress invariants and principal stress components. These measures are widely used in mechanical engineering to define the yield and failure criteria for brittle versus ductile materials [53, 54].

In the current version, TensorCalculator uses the coordinates and forces on the $C_{\alpha }$-atoms from the numerical output obtained using the SOP coarse-grained model. With little effort, TensorCalculator can be made compatible with the output from the all-atom MD simulations. Furthermore, the output from TensorCalculator can be made into the input for VMD software, and so the results of calculation of various stress measures can be visualized. The TensorCalculator package was successfully tested by comparing the time-dependent mechanical tension $F(t)$ in a generic bead-and-spring chain and a $C_{\alpha }$-based SOP-model of the all-β-sheet WW-domain with the applied external (time-dependent) pulling force (or ramped force) $f(t)$ obtained from the protein forced unfolding experiments in silico. The results presented in figure 1 show that the agreement between applied time-dependent force $f(t)$, which can be accessed from the pulling simulations, and time-dependent mechanical tension $F(t)$ in the bead-and-spring and SOP models, computed with TensorCalculator, agree very well. This shows a high level of numerical accuracy in the calculation of stress measures with TensorCalculator. Excellent agreement between the stress quantities known exactly and those computed with TensorCalculator has enabled us to explore the dynamics of mechanical stress in a soft capsid of cowpea chlorotic mottle virus (CCMV).

Using TensorCalculator, we computed and analyzed the distributions of mechanical stress measures in the CCMV capsid structure, including the first stress invariant $I_i^{(1)}$, the first principal component ${\sigma }_i^{(1)}$, von Mises stress tensor ${\sigma }_i^{vM}$ and Tresca stress tensor ${\sigma }_i^{\mathrm{T}\mathrm{r}}$, and profiled them as functions of the particle deformation X (figures 2–5). To visualize the results, we also constructed the CCMV surface maps of these measures using VMD (figures 2, 3, and 5, movie S1) [65]. The results obtained show that when a virus capsid is loaded mechanically, there are nontrivial stress dynamics in the CCMV particle, which results in the inhomogeneous stress distribution in various portions of the CCMV structure. Analysis of the first stress invariant $I_i^{(1)}$ (figure 2) revealed the interplay between the stress in the side portion and top portion of the CCMV shell compressed by the cantilever tip (indenter used in AFM). It turns out that, similar to energy, the mechanical stress is capable of transferring from one portion of the virus structure to another. We found that the mechanical stress created in the top portion of CCMV by the indenting tip-sphere rapidly transfers to the side portion of CCMV where it accumulates over time (figures 2–5). Another interesting finding is a strong correlation between the deformation-induced alterations in the CCMV structure and the overall shape and dynamics of stress propagation in the protein capsid.

Previously, Zandi and Reguera employed a similar approach to calculate the stress distribution in virus capsids of different symmetry types [50]. In that study, a virus particle was coarse-grained using the bead-per-capsomer representation; different capsomers were allowed to interact through the Lennard-Jones potential with different parameters for pentamers and hexamers; the equilibrium dynamics of capsomer particles was described using Monte-Carlo simulations. Zandi and Reguera analyzed stress characteristics which included different projections of the stress tensor on spherical coordinates giving the in-plane shear stress and out-of-plane radial stress. They observed inhomogeneous distribution of stresses in capsomers with large stress values attributed to the vertices and edges of icosahedra [50].

In this work, we went beyond the equilibrium dynamics of virus particles by considering stress propagation in the capsid structure subjected to external mechanical loading. Specifically, we explored the dynamics of stress propagation and accumulation in a virus shell resulting from particle’s structure alterations and shape changes as well as capsomers’ symmetry breaking. The $C_{\alpha }$-based coarse-grained modeling proved to be accurate in describing the mechanical properties of large biological assemblies [24, 35, 36, 39, 51]. This allowed us to obtain, for the first time, detailed microscopic information about the dynamics of local stresses at the amino-acid-residue level. We observed formation of ‘hot spots’, i.e. locations in the virus particle structure with the maximum stress, which result in the long run in cracks and defects (figures 2 and S1, movies S1). Although the structural model ($C_{\alpha }$-based coarse-grained SOP model) and Langevin dynamics we have utilized and the stress characteristics (stress invariants, principal stresses, von Mises and Tresca stresses) we have analyzed in this work are different from the bead-per-capsomer model and Monte-Carlo moves used by Zandi and Reguera [50], the results of their study and our own work show very good qualitative agreement. For example, we also observe inhomogeneous stress distribution in the shell structure.

In our previous studies of the nanomechanics of biological particles [18, 24, 36], we showed that the entropy changes due to structure remodeling and shape change are significant. Hence, it should be expected that thermal effects play an important role in the capsid’s evolution, and in defining the dynamics and setting the energy scale for global transitions in a virus capsid, such as buckling and structural collapse. We analyzed the effect of thermal fluctuations on the stress evolution in the CCMV capsid structure by carrying out nanoindentation measurements at zero temperature (T  =  0 K) and finite temperature (T  =  300 K). Quite surprisingly, we found that the mechanical response (as reflected by the FX-curves), the stress magnitude and the pattern of stress propagation and distribution in the virus capsid, all change with temperature (see figure 3). The area under the FX-curve recorded at a very slow force-loading rate is the reversible work w_rev, which is equal to the equilibrium Gibbs free energy change for the collapse transition $\mathrm{\Delta }{G}_{eq}$, i.e. $w_{\mathrm{r}\mathrm{e}\mathrm{v}}=\mathrm{\Delta }{G}_{eq}=\mathrm{\Delta }H-T\mathrm{\Delta }S$, where $\mathrm{\Delta }H$ and $\mathrm{\Delta }S$ are the enthalpy change and the entropy change, respectively. Hence, the entropic contribution $T\mathrm{\Delta }S$ to the free energy change $\mathrm{\Delta }G$ can be estimated by subtracting the work done on the capsid by the indenter at finite temperature from the work performed at zero temperature. For the native state as the initial state (snapshot 1 in figure 3) and the collapsed state as the final state (snapshot 3 in figure 3), we obtain from the FX-curves in figure 3 that for the CCMV structural collapse $T\mathrm{\Delta }S\approx$ 920 kcal mol⁻¹. This is almost three-fold larger than the the enthalpy change $\mathrm{\Delta }H\approx$ 370 kcal mol⁻¹.

The large entropic contributions to the free energy of mechanical deformation of biological particles raise questions about some of the theoretical methods used to model the dynamics of deformation of biological particles. For example, the finite elements analysis [20] and variances of elastic network modeling [25] analyze the potential energy changes, while the entropy changes are ignored. In a sense, this is similar to setting T  =  0 K in our nanoindentation experiments in silico. However, our results clearly demonstrate large differences in the FX-spectra collected at zero and finite temperature, as well as in the amplitude and pattern of stress evolution in the CCMV shell. For example, at T  =  0 K the mechanical stress in the top and side portions of the CCMV structure both increase, whereas at T  =  300 K the stress in the top decreases and the stress in the sides increases (figure 3). Hence, thermal fluctuations modulate the mechanical and materials properties of virus capsids, and the entropic effects are significant and not to be ignored. The importance of the entropic effects, clearly expressed in the quite different stress distributions presented for the T  =  0 K and T  =  300 K (see figure 3), suggest that investigators should be cautious in their application of continuum mechanics models, such as finite element analysis and elastic network modeling, to structural models of biological particles.

In materials science, a yield strength describes the critical stress at which the material response to an external mechanical loading changes from elastic to plastic. The meaning of the term ‘plastic’ is that above a critical value of stress (or deformation), the deformed material will never return to its original shape and will not fully restore its initial structure when the applied stress is quenched. We tested if stress measures can be used to predict the onset of plasticity in viral shells. Using TensorCalculator, we computed the first principle stress components for the top and side portions of the CCMV structure ${\sigma }_t^{(1)}$ and ${\sigma }_s^{(1)}$ and profiled them as functions of deformation time (figure 4). Our results indicate that for a small (forward) deformation the curves of ${\sigma }_t^{(1)}$ and ${\sigma }_s^{(1)}$ do not cross, and when the compressive force is gradually quenched to zero during the backward tip retraction, the CCMV capsid fully restores back its initial state (both structure and shape). However, when the deformation is large so that the curves of ${\sigma }_t^{(1)}$ and ${\sigma }_s^{(1)}$ cross, the capsid does not return back to its initial state. Hence, the relationship between the first principal stress components for the top and side portions of the viral capsid structure, i.e.

$${\displaystyle \begin{array}{l}{\displaystyle {\sigma }_t^{(1)}⩾{\sigma }_s^{(1)}}\end{array}}$$ 17

sets the limit of elastic deformation in soft viral capsids.

We also computed the von Mises stresses and Tresca stresses for the top portion, ${\sigma }_t^{vM}$ and ${\sigma }_t^{\mathrm{T}\mathrm{r}}$, and for the side portions of the CCMV structure, ${\sigma }_s^{vM}$ and ${\sigma }_s^{\mathrm{T}\mathrm{r}}$, and we profiled these quantities as functions of deformation. The results obtained show that the moment when the curves of ${\sigma }_t^{vM}$ and ${\sigma }_s^{vM}$ cross corresponds to the critical deformation X  =  X^* and critical force F  =  F^* (see force maxima in figure 5) at which the collapse transition occurs. Analysis of the results of Tresca tensor calculations gave similar results (figure S3). Hence, the relationship between von Mises stresses for the top and side portions, i.e.

$${\displaystyle \begin{array}{l}{\displaystyle {\sigma }_s^{vM}⩾{\sigma }_t^{vM}}\end{array}}$$ 18

marks the onset of the viral capsid’s structural failure.

Taken together, the results we have obtained in this study for the first principle stress components and for von Mises stress and Tresca stress components agree very well with our previous findings regarding mechanical excitation of various capsid’s degrees of freedom upon deformation [18]. Indeed, the stress in the top portion of the CCMV shell corresponds to the non-linear Hertzian deformation, whereas the stress in the side portion results in bending of beams [18].

To conclude, we have developed and tested a new computational methodology for accurate numerical calculation of the local stress measures and its derivative quantities using the output from the MD simulations of compressive force-induced nanoindentation of biological particles. This methodology employs the atomic tensor approach to computing the stress measures traditionally used in continuum mechanics for the discrete atomic or coarse-grained structures of large-size biological assemblies. We successfully applied this methodology to explore the evolution of mechanical stress in a specific example of viral capsids—the CCMV shell. Numerical subroutines have been organized into a lab-written software package called TensorCalculator, which can now be used to study the stress evolution and dynamics of defects in viral capsids and other protein assemblies tested mechanically. The TensorCalculator code is open source code and it is fully available for downloading at https://github.com/BarsegovGroup/TensorCalculator.git.