Compactness of viral genomes: effect of disperse and localized random mutations

Abstract

Genomes of single-stranded RNA viruses have evolved to optimize several concurrent properties. One of them is the architecture of their genomic folds, which must not only feature precise structural elements at specific positions, but also allow for overall spatial compactness. The latter was shown to be disrupted by random synonymous mutations, a disruption which can consequently negatively affect genome encapsidation. In this study, we use three mutation schemes with different degrees of locality to mutate the genomes of phage MS2 and Brome Mosaic virus in order to understand the observed sensitivity of the global compactness of their folds. We find that mutating local stretches of their genomes’ sequence or structure is less disruptive to their compactness compared to inducing randomly-distributed mutations. Our findings are indicative of a mechanism for the conservation of compactness acting on a global scale of the genomes, and have several implications for understanding the interplay between local and global architecture of viral RNA genomes.

1. Introduction

Genomic information of small eukaryotic viruses is typically encoded in a single-stranded nucleic acid filament (specifically, a positively-stranded RNA) rather than a double-stranded one, as is the case for larger viruses [1]. The very different flexural rigidities of single- and double-stranded nucleic acids call for different mechanisms of genome packaging inside viral capsids. Double-stranded DNA, which has a persistence length of  ∼50 nm, is inserted into a pre-formed capsid by a molecular motor, and the mature virion has to withstand a significant positive osmotic pressure as a result [2–6]. On the other hand, single-stranded (ss)RNA has a persistence length of only about 1 nm, and its self-interaction and interactions with the capsid proteins are sufficient to drive its organization into a rather compact fold, inducing a small negative osmotic pressure [6–10]. Indeed, the sizes of wild-type (WT) ssRNA genomes of icosahedral viruses are usually only slightly larger than the space available inside the proteinaceous capsid of the mature virions [11]. This implies that only a modest additional compression of the ssRNA has to be imparted by the viral coat proteins that attach and assemble around the genome to form the capsid [6, 12–15].

The pivotal role of the innate compactness of ssRNA genomes of icosahedral viruses has been elegantly demonstrated in a study by Yoffe et al [9], who have shown that random reshufflings of their genome sequences yield much larger folds compared to those of their corresponding WT sequences. A follow-up study by Tubiana et al [16] further established that even relatively mild alterations of the WT sequence in the form of synonymous mutations can be as disruptive for the overall compactness of the genome folds as complete random reshufflings. These results indicate that, just as for specific local RNA structures [17–20] and phenotypic viral proteins, the global compactness of viral ssRNA genomes too has been optimised by evolutionary mechanisms [21]. In addition, both experimental and bioinformatics studies have indicated that a key recurrent and distinctive element of compact RNA folds is the presence of hubs with high-degree branching points in their secondary structure [22, 23]. These hubs are instrumental for the organization of the RNA fold into a floret-like structure composed of several local structural moduli ($\lesssim$1000 nt long) [24, 25] and for the general control of the fold compactness [22].

A natural question, prompted by the conservation of the compactness of viral ssRNA genomes, is how exactly compactness is encoded in the genomes themselves, and what kind of mutations can erase this information—disrupting the compactness of the folds. While it has already been shown that a sufficient amount of random synonymous mutations disrupts the compactness of the folds, it is possible that genome compactness is encoded on a more local scale in specific regions of RNA. In particular, observations of Gopal et al [22] indicate that fold compactness seems to be encoded locally on a scale of $\lesssim$1000 nt. If this is indeed so, mutations targeting local regions of RNA secondary structure should consequently be able to disrupt the compactness more efficiently. It is therefore interesting to consider whether mutations concentrated on local, continuous stretches of the genome sequence or near the central branching hub of its secondary structure are more disruptive to the genome fold compactness than completely random mutations.

In the present work, we address this question for two different positive-strand ssRNA viruses, bacteriophage MS2 and Brome Mosaic virus (BMV). The genomes of the two selected viruses share several properties which make them ideally suited for this study: their folds have a highly-branched architecture [22], have comparable lengths (∼3000 nt), and are amenable to extensive numerical characterization. What is more, they are believed to assemble and bind to the viral coat proteins using two different mechanisms—non-specific (electrostatic) interactions in the case of BMV and specific packaging signals in the case of MS2 [26–29]—allowing us to observe any potential differences between the two.

We study the robustness of the sequence-structure interplay involved in determining the size of RNA folds by mutating the WT genomes of both viruses using three different mutation schemes. We mutate either continuous stretches (blocks) of nucleotides, spaced at regular intervals along the genome, or stretches of nucleotides sharing a similar distance relationship from the central branching hub of the WT fold. In addition, we also consider disperse mutations picked uniformly (stochastically) along the genome to provide a comparison with existing studies. Based on previous studies, one might expect that (local) mutations targeting the nucleotides closest to the central, high-branching hub of a fold would be the most disruptive for its compactness, and that disperse mutations would be, conversely, the least disruptive. Instead, we find that the exact opposite is true, indicating that the compactness of viral ssRNA genomes is encoded on a global scale.

2. Methods

2.1. Datasets

We study the viral genomes of two positive-strand ssRNA viruses: bacteriophage MS2 from the Leviviridae family and BMV from the Bromoviridae family. The latter has a tripartite genome, and we thus limit our considerations only to its RNA2 component, whose length (N  =  2865 nt) is comparable to the length of the MS2 genome (N  =  3569 nt). In both cases, the RNA material is co-assembled together with coat proteins (and in absence of any additional proteins) into a single virion whose capsid has a triangulation number T  =  3. Both MS2 and BMV RNA2 reference genomic sequences were obtained from the NCBI nucleotide database [30].

Secondary structures (folds) of the WT and mutated genomes of both viruses are obtained using RNAsubopt, a program included in the ViennaRNA package, version 2.1 [31]. For each RNA sequence we generate 500 folds representative of the conformational ensemble in canonical equilibrium at T  =  37 C. Since the folds are sampled according to their canonical probability, we can then use them to compute the quantities of interest (described below) and take their arithmetic average. In this way, we obtain the canonical averages of the quantities of interest, which will be denoted with $\langle \cdot \rangle$.

2.2. Maximum ladder distance (MLD)

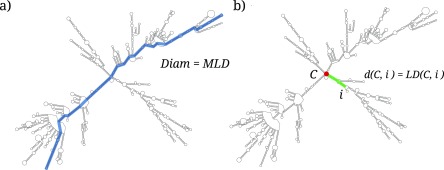
We characterize the size of the folded RNA sequences in terms of the ensemble average of the MLD. This quantity derives from graph theory and, for a given RNA secondary structure fold, it measures the largest number of distinct secondary contacts (rungs) that must be crossed to move along the sequence from any nucleotide to any other nucleotide (see figure 1(a)) [9, 32]. The average MLD, obtained by averaging over the MLD values of a canonical ensemble of RNA folds, has been shown to correlate significantly with the RNA radius of gyration, for which it therefore provides a good proxy in cases where actual structural data is not available [9].

Figure 1.

A fold of BMV RNA2, outlining (a) the contour length of the fold (given by its MLD), and (b) the distance $d(C,i)$ of nucleotide i from the center of the fold, C, defined as the LD separating the two. Panel (a) is adapted from [16], Copyright 2015, with permission from Elsevier.

2.3. Ranking nucleotides by their fold centrality

The concept of ladder distance (LD) can also be used to pinpoint the central hub from which the main branches of an RNA fold depart. In this way, we are able to rank all the nucleotides in an RNA fold in terms of their proximity to the central hub. For any nucleotide i in the fold, we compute its maximum LD to any other nucleotide, ${\mathrm{M}\mathrm{L}\mathrm{D}}^{(1)}(i)$. The superscript $(1)$ is now used to stress that the maximization is not taken over all nucleotide pairs anymore, as was the case in the previous subsection, but is limited to LDs involving the specific nucleotide i. Nucleotides with the lowest values of ${\mathrm{M}\mathrm{L}\mathrm{D}}^{(1)}$ are those with the lowest average distance to any other nucleotide, and hence constitute the center of the fold, C [33, 34]. After computing the average ${\mathrm{M}\mathrm{L}\mathrm{D}}^{(1)}$ profiles of the ViennaRNA-generated folds we can thus rank the nucleotides by the decreasing $\langle {\mathrm{M}\mathrm{L}\mathrm{D}}^{(1)}\rangle$ values, obtaining an ordered list of nucleotides ranked by increasing centrality (figure 1(b)).

2.4. Mutation schemes

We introduce a varying number of non-synonymous point mutations into the MS2 and BMV RNA2 genomes by using a stochastic (Monte Carlo) scheme introduced previously by Tubiana et al [16]. We mutate different batches of nucleotides (with batch sizes s  =  120, 180, 240, 300, 360, and 720 nt) spanning from  ∼3% to  ∼22% of the genomes. The nucleotides in the batches are picked according to three different mutation schemes described further below. For each batch we independently generate 100 mutated sequences using non-synonymous point substitutions that approximately conserve the characteristic dinucleotide frequencies of the WT genomes. More precisely, the frequencies are allowed to vary by no more that 37.5% from the WT reference values (see the supplementary material available online at stacks.iop.org/JPhysCM/30/084006/mmedia and [16]). Additionally, we verified a posteriori that the results we obtain in this way are largely unaffected by substituting the dinucleotide frequency constraint with that of mononucleotide frequency constraint, based on the Fisher–Yates shuffling algorithm [35]. Moreover, we also checked that omitting half of the mutated sequences does not significantly change our results, as demonstrated in figure S1. This confirmed a posteriori the adequacy of the statistical coverage.

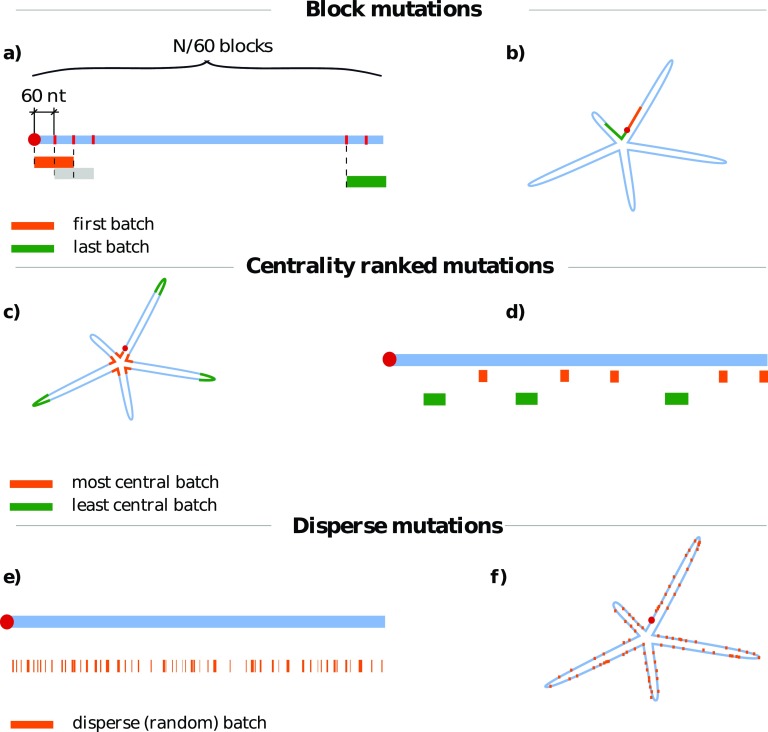
We use three different mutation schemes to select the batches of nucleotides where we introduce non-synonymous mutations. The three schemes are aimed at probing the different aspects of RNA sequence-structure interplay and their role in genome compactness. They are depicted in figure 2 and consist of:

• (i)block mutations, where a given batch of s nucleotides covers an uninterrupted, continuous stretch of the RNA sequence;
• (ii)centrality-ranked mutations, where a batch is comprised of s nucleotides that are consecutive in the centrality-ranked list. These batches are composed of nucleotides with the same average distance from the center of the fold, but are clearly not necessarily proximal in sequence space;
• (iii)disperse mutations, where the s distinct nucleotides in a batch are stochastically picked with uniform probability anywhere along the RNA sequence.

Figure 2.

(a) and (b) Block, (c) and (d) centrality-ranked, and (e) and (f) disperse mutation schemes. For each mutation scheme, a simple sketch of a linear genomic sequence is shown in blue with different mutation batches denoted below it; each color denotes a separate batch. We also show a sketch of an ideal, floret-like fold with five branches stemming from a common center. (a) and (b) Block mutations are performed by mutating the nucleotides of a sequence localized in a contiguous batch of length s (in this case, s  =  120 nt). The starting points of different batches then slide along the genome in regular intervals. Block mutations are, for the most part, located on only one strand of the folded RNA duplex. (c) and (d) Centrality-ranked mutations are performed in a similar manner, but the nucleotides are grouped in batches according to their (canonically averaged) distance from the center of the fold. This means that the batch of nucleotides with the lowest distances from the center (orange) will correspond to non-contiguous regions on the genome sequence (d), but will be spatially localized near the center of the average fold (c). The batch of nucleotides with the largest distance is shown in green. (e) and (f) Disperse mutations are obtained by randomly assigning nucleotides to batches of a certain size. These mutations show no localization on either sequence (e) or fold (f).

As the mutation schemes are aimed at testing certain aspects and hypotheses of the sequence-structure interplay, the mutation patterns considered here are not necessarily realistic from an actual evolutionary point of view. A possible exception are disperse mutations, which can model the stochastic emergence of point-wise changes during, e.g. genome replication.

For each batch size s we mutate the nucleotides in n_B  =  (N  −  s)/60  +  1 distinct batches. This number ranges from n_B  =  47 (s  =  120) to n_B  =  37 (s  =  720) in BMV RNA2, and from n_B  =  58 (s  =  120) to n_B  =  48 (s  =  720) in MS2. In the case of block mutations, the starting points of the batches are regularly spaced by 60 nucleotides along the sequence. In the case of centrality-ranked mutations, the starting points of the batches are regularly spaced by 60 nucleotides along the centrality-ranked list of nucleotides. Finally, in the case of disperse mutations, we simply pick n_B batches, each comprising s randomly-selected—though distinct—nucleotides. We also note that different batches can partially overlap, not only in the case of disperse mutations, but also in the first two schemes when the batch size s is large enough.

3. Results

Previous studies have shown that WT genomes of ssRNA viruses are significantly more compact than random RNA sequences of similar length and composition [9, 22]. Even under more stringent conditions, when a relatively small fraction of synonymous, phenotypically-neutral mutations is introduced into the WT genomes, the effect is as disruptive for the fold compactness as the introduction of completely random mutations [16]. The conclusions drawn from these studies were based on the analysis of the canonically averaged MLD of the folds’ secondary structure diagrams, $\langle \mathrm{M}\mathrm{L}\mathrm{D}\rangle$, a measure which correlates with the average gyration radius of the RNA (see Methods). The WT genomes of MS2 and BMV RNA2 embody the same general properties: their folds (see, e.g. figure 1) display a high branching propensity [22] and a low $\langle \mathrm{M}\mathrm{L}\mathrm{D}\rangle$ value, which are typical features of compact folds. Specifically, $\langle \mathrm{M}\mathrm{L}\mathrm{D}{\rangle }_{\mathrm{W}\mathrm{T}}=177\pm 12$ for BMV RNA2 and $\langle \mathrm{M}\mathrm{L}\mathrm{D}{\rangle }_{\mathrm{W}\mathrm{T}}=146\pm 18$ for phage MS2. These values are significantly lower than the $\langle \mathrm{M}\mathrm{L}\mathrm{D}\rangle$ values of random sequences of same length and similar composition, $\langle \mathrm{M}\mathrm{L}\mathrm{D}{\rangle }_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}(N=2865)=265$ and $\langle \mathrm{M}\mathrm{L}\mathrm{D}{\rangle }_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}(N=3569)=306$ [9, 16].

While we simply chose the reference WT genome for each virus from the several genomic sequences deposited in the NCBI Nucleotide database [30], this characteristic compactness is, unsurprisingly, not unique to the considered sequences. We verified this by computing the degree of compactness of several other WT genomes deposited in the Nucleotide database (five for BMV RNA2 and six for MS2). As shown in figure S2, all the WT genomes have a similar MLD distribution to the one of the reference genomes we picked. Thus, the reference WT genomes we have chosen should be representative of the larger population of viable WT genomes of these two viruses.

A question that then arises naturally when considering the sequence-structure interplay is whether mutations localized in specific regions of the RNA sequence have more impact on the fold compactness compared to ones that are uniformly distributed on the sequence. Of particular interest here are mutations clustered around high-degree branching points, or hubs, which have been recognized as key structural elements of RNA folds [22, 23]. In fact, because they have direct bearings on the hierarchical organization of the floret-like secondary structure [24, 25], they are generally deemed essential for the characteristic compactness of RNA folds. This observation motivated us to mutate blocks of nucleotides, because doing so would expectedly disrupt the branching and secondary structure modularity of the native fold, triggering a loss of its compactness.

In the following, we systematically address the impact of local mutations by introducing mutations in multiple batches of s nucleotides picked according to three different schemes: block mutations, centrality-ranked mutations, and disperse mutations. The three mutation schemes and their effects are described in detail in the Methods.

3.1. Effect of block mutations

We first study the effect of block mutations, where the nucleotides in each batch span an uninterrupted, continuous stretch of the genomic sequence. Block mutations, which target specific regions of the sequence, may seem at odds with the expectedly stochastic character of mutation. However, one should bear in mind that while mutations are expected to arise uniformly along the sequence, their fixation may not be so, and may preferentially occur in specific regions (e.g. due to epigenetic effects). The block-mutation perspective is also a natural one in the present context, where we seek to understand which aspects of the sequence-structure interplay produce the observed RNA compactness.

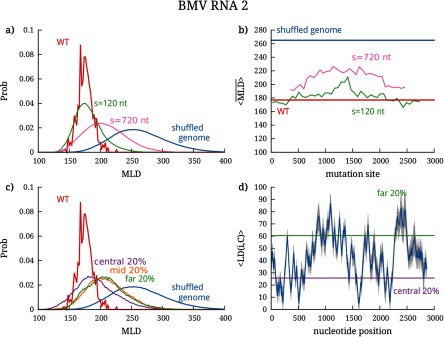
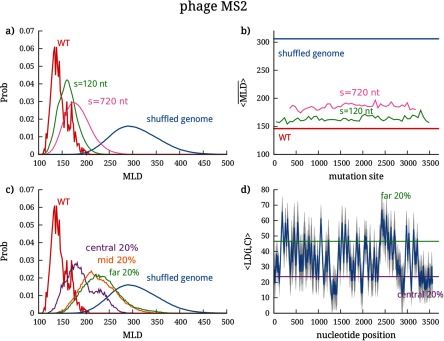
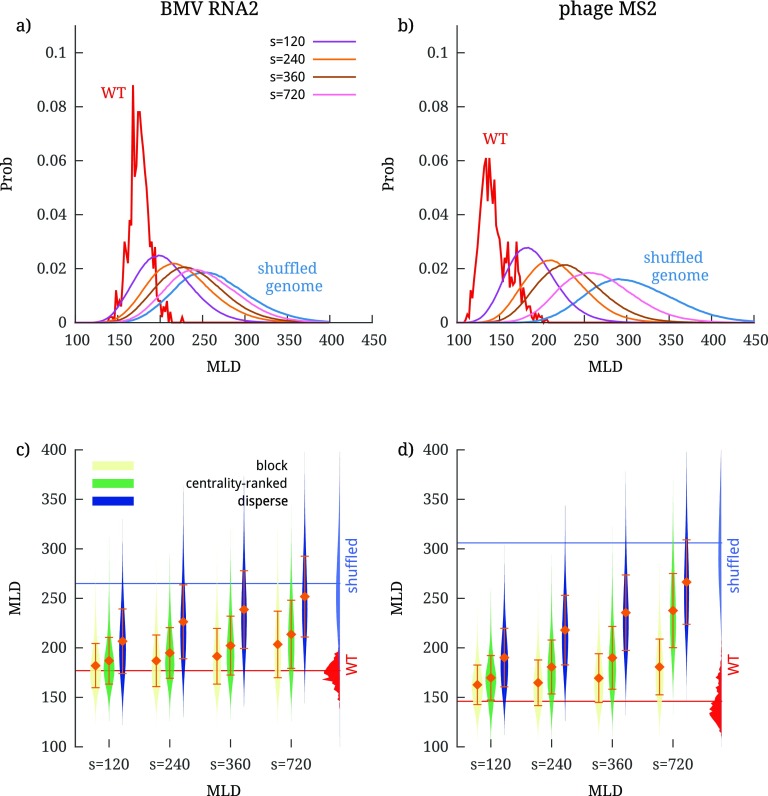
The effect of block mutations on the genome compactness—more precisely, on the MLD probability distribution—is shown in figures 3(a) and 4(a) for the cases of BMV RNA2 and phage MS2, respectively. For visual clarity, the results are presented only for two different batch sizes, s  =  120 nt and s  =  720 nt, and the distributions for other batch sizes are shown in figures S3 and S4. In addition to the MLD distributions under mutations for two different batch sizes, the figures also show the distributions for the WT genomes (calculated over the ensemble of folds populated in equilibrium) and for completely randomly-shuffled sequences.

Figure 3.

Effect of localized mutations on the compactness of the BMV RNA2 genome, as characterized by its MLD distribution. (a) MLD distribution of folds after block mutations performed in batches of 120 and 720 nt; the distributions of the WT and completely shuffled genome are shown for comparison. The effect of mutations in individual batches placed along the genome can be seen in (b), where we show the $\langle \mathrm{M}\mathrm{L}\mathrm{D}\rangle$, further averaged over the mutated sequences in each batch—$\overline{\langle \mathrm{M}\mathrm{L}\mathrm{D}\rangle }$. (c) MLD distribution of folds after centrality-ranked mutations in three different batches, chosen to contain $20\mathrm{\%}$ most central nucleotides, $20\mathrm{\%}$ least central nucleotides, and $20\mathrm{\%}$ of nucleotides with average centrality. The first two cutoffs are shown in (d), where we plot the distance of each nucleotide from the center of the fold. The blue line shows the canonically averaged distance from the center of the fold, and the gray shaded areas show the standard deviation.

Figure 4.

Effect of localized mutations on the compactness of the phage MS2 genome, as characterized by its MLD distribution. (a) MLD distribution of folds after block mutations performed in batches of 120 and 720 nt; the distributions of the WT and completely shuffled genome are shown for comparison. The effect of mutations in individual batches placed along the genome can be seen in (b), where we show the $\langle \mathrm{M}\mathrm{L}\mathrm{D}\rangle$, further averaged over the mutated sequences in each batch—$\overline{\langle \mathrm{M}\mathrm{L}\mathrm{D}\rangle }$. (c) MLD distribution of folds after centrality-ranked mutations in three different batches, chosen to contain $20\mathrm{\%}$ most central nucleotides, $20\mathrm{\%}$ least central nucleotides, and $20\mathrm{\%}$ of nucleotides with average centrality. The first two cutoffs are shown in (d), where we plot the distance of each nucleotide from the center of the fold. The blue line shows the canonically averaged distance from the center of the fold, and the gray shaded areas show the standard deviation.

We can clearly observe that increasing the batch size causes the MLD distribution to gradually move from the WT distribution to that of the randomly-shuffled genome. This progressive change is very clearly seen for BMV RNA2, whose MLD distribution broadens and shifts towards larger values as the batch size is increased from 120 to 720 nucleotides. The same shift is seen for MS2, but is quantitatively smaller in this case, a point that we shall address later. Another key feature, conveyed by panel (b) of figures 3 and 4, is that there are no sensitive regions on the sequences of the two genomes, i.e. neither of them carries a continuous stretch of sequence whose disruption would completely erase fold compactness. A final noteworthy point is that even the largest batch of mutations with s  =  720 nt (comprising  ∼20% of each genome) is not sufficient to disrupt the fold compactness, compared to the disruption achieved by a random shuffle of the entire genome. This is remarkable, as a similar percentage of more conservative (synonymous) mutations distributed randomly along the entire genome was shown to be much more disruptive, yielding the same $\langle \mathrm{M}\mathrm{L}\mathrm{D}\rangle$ value as that of a random shuffle [16].

3.2. Effect of centrality-ranked mutations

We have observed that even a significant amount of block mutations, which are concentrated on an uninterrupted stretch of genomic sequence, is less disruptive to genome compactness than a similar number of randomly-distributed synonymous mutations, which are otherwise more constrained. To further clarify these effects, we mutated nucleotides using the centrality-ranked scheme, where mutation sites are picked according to their proximity to the center of the fold, i.e. the central hub of the branched structure of the genome. Considering the distinctively large number of high-degree branching points found in WT viral RNAs [22, 23], mutations targeting nucleotides ranked by their centrality should be better able to encompass different hubs and their helices, disrupting the number of branches stemming from them in the process.

To implement this mutation scheme, we computed the average ladder distance $\langle \mathrm{L}\mathrm{D}(i,C)\rangle$ of a nucleotide i from the center of the folds C. The average is computed over the 500 folds that represent the equilibrium ensemble (see Methods). The average profile of the distance from the center and its standard deviation are shown in figures 3(d) and 4(d) for BMV RNA2 and MS2, respectively. In both cases, the profiles have well-defined features, with minima and maxima that stand out very clearly in spite of the statistical dispersion arising from the averaging over the canonical ensemble of folds. This indicates a posteriori that the relevant folds in canonical equilibrium, though different, share a similar overall architecture in terms of branching points (minima of $\langle \mathrm{L}\mathrm{D}(i,C)\rangle$) and end points of the branches (maxima of $\langle \mathrm{L}\mathrm{D}(i,C)\rangle$). From the distance profiles one can also infer the number and degree of branching points and the number and size of branches by counting the minima of $\langle \mathrm{L}\mathrm{D}(i,C)\rangle$ at a given value of LD and the separation of the minima along the sequence. The plots clearly show the presence of high-degree branching points in the region of the $20\mathrm{\%}$ most central nucleotides of the genomes of both viruses, as well as a high propensity for branching in the case of MS2⁵.

The robustness of the sites acting as roots and tips of the branching points in the canonical ensembles of WT folds of both viruses leads us to probe how the mutations targeting them can affect the compactness of the two genomes. Ranking the nucleotides according to their distance from the center of the fold enables us to group them into batches containing the nucleotides most proximal to the central hub of the fold—out of which the RNA secondary structure branches—as well as into batches containing the nucleotides furthermost from the center (see Methods). In the genomes of both viruses we thus mutate batches of nucleotides with different degrees of centrality: one batch type contains the $20\mathrm{\%}$ of the most central nucleotides, another batch type the $20\mathrm{\%}$ of the least central nucleotides, and the last batch type contains $20\mathrm{\%}$ of nucleotides with average centrality. The MLD distributions resulting from the mutations in these different batches are shown in figure 3(c) for BMV RNA2 and figure 4(c) for phage MS2.

For both viruses we observe that the resulting MLD distributions fall between the WT and the completely shuffled distributions. The support of these distributions is, in fact, largely compatible with that of block mutations discussed in the previous subsection. The most noticeable result is, however, that for the centrality-ranked mutations the largest disruption of the fold compactness is not due to the mutations targeting the most central region of the fold. This runs counter to the expectation that the central hub and the corresponding high-degree branching points of the fold would be the most crucial regions where the sequence-structure interplay would stabilize the fold compactness. Instead, the most sensitive regions appear to be those of mid- to large distance from center—and yet, even in these cases centrality-ranked mutations are not as disruptive as the random shuffling of the entire genome.

3.3. Effect of disperse mutations

It is perhaps surprising that fold compactness is only modestly perturbed both by batch mutations of nucleotides in uninterrupted blocks along the genome sequence and especially by batch mutations of nucleotides organized according to their distance from the fold center. To better understand these results, we also analyzed the effect of disperse mutations. In order to allow for a good comparison with the block and centrality-ranked mutations, we consider the same number of batches in which the mutations are performed as before: N/60, N being the genome length (see Methods).

The resulting MLD distributions of disperse mutations for various batch sizes are shown in panels (a) and (b) of figure 5. We observe that, as the batch size is increased from 120 to 720 nt, the distributions shift and broaden progressively, moving systematically from the WT distribution to that of a completely shuffled genome. This trend is completely consistent with previous studies, where mutating about $20\mathrm{\%}$ of the genome by the accumulation of random point-wise mutations completely disrupted the compactness of the WT folds and brought their $\overline{\langle \mathrm{M}\mathrm{L}\mathrm{D}\rangle }$ values to those of random RNA sequences.

Figure 5.

(a) and (b) MLD distributions of BMV RNA2 and phage MS2 genome folds after disperse mutations, and (c) and (d) a comparison of the three different mutation schemes used in the present work. The comparison is shown as violin plots of the MLD distributions for different values of batch sizes s. Each entry in the violin plots shows a (mirrored) MLD probability distribution, with the central diamonds showing the value of $\langle \mathrm{M}\mathrm{L}\mathrm{D}\rangle$ further averaged over all mutated sequences, $\overline{\langle \mathrm{M}\mathrm{L}\mathrm{D}\rangle }$, and the error bars representing the corresponding standard deviation. The MLD distributions of WT folds and shuffled sequence folds are shown on the right side of the plots for comparison.

Taking these observations together with the results for the block and centrality-ranked mutations, we can therefore conclude that disperse mutations are the most disruptive to the compactness of the WT folds of the two genomes. This intriguing result is aptly summarized by the violin plots in panels (c) and (d) of figure 5, which show how the MLD distributions of BMV RNA2 and MS2 vary with batch size for all three mutations schemes. There, it is clearly seen that the largest disruption of the MLD distributions is obtained in the case of disperse mutations, a result which would have been difficult to anticipate a priori. A possible reason behind it could involve joint disruptive effects of the mutations of nucleotides that are nearby along the sequence, yet not entirely proximal.

4. Discussion and conclusions

Previous studies have shown that WT genomes of ssRNA viruses are much more compact than random sequences of similar length and composition. It was also shown that this compactness can be destroyed by introducing a small number of synonymous mutations, usually involving between $5\mathrm{\%}$ and $20\mathrm{\%}$ of the genome. Arguably, this strong tendency for the WT fold compactness has been evolutionary promoted as it facilitates genome encapsidation. From the point of view of the sequence-structure interplay in viral RNAs, several previous works have suggested that their compactness is largely due to the atypically high number of branching points, or hubs, of their genome folds [22, 23]. This led us to the question of whether the mutations that would specifically target either batches of nucleotides that are close to the central hub of the fold or batches that span continuous stretches of its sequence could be even more disruptive to the fold compactness than random mutations.

We addressed this question by implementing three different mutation schemes, introducing non-synonymous mutations into the WT genomes of BMV RNA2 and phage MS2. First, we considered block mutations, i.e. batches of nucleotides that are continuous along the genomic sequence. Next, in the centrality-ranked scheme, we mutated batches of nucleotides at various distances (in contact space) from the central hub of the genome fold. Finally, we considered similar amounts of random mutations distributed randomly along the genome. We assessed the impact on compactness of each mutation scheme by computing the change in the MLD. The latter is a measure of the largest distance of any two nucleotides in the contact space of an RNA fold, and has been shown to be a robust proxy for the actual three-dimensional size of the RNA.

The main purpose of using different mutation schemes was to uncover potential local regions of RNA sequence or structure which would be particularly relevant for maintaining the WT fold compactness. Mutations, localized to different regions, could have a larger influence on disrupting the high-degree branching points hubs and the helices that stem from them compared to random mutations, in turn triggering large-scale reorganization of the fold and reducing its overall compactness. Contrary to this expectation, our results clearly show that the largest disruption of fold compactness is caused by disperse mutations, and targeting nucleotides either in blocks along the sequence or in batches with various degrees of centrality in the structure has significantly less impact on the compactness of the WT genomes.

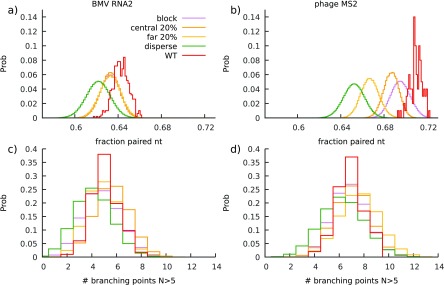
To try to clarify the reason behind the observed impact of the different mutation schemes on the MLD values of the folds, we studied their effect on other structural properties—in particular the fraction of paired nucleotides and the probability of high-degree branching points. Figures 6(a) and (b) show that while all mutation schemes produce folds with lower pairing probability than the WT one, only disperse mutations result in folds where the amount of base-pairing is significantly lower in both viruses. The number of high-degree branching points in the folds (defined as hubs with more than five branches stemming from them) is also almost unaffected by any of the mutation schemes, showing a slight decrease again only in the case of disperse mutations (figures 6(c) and (d)). Other quantities, such as the average duplex length and the number of duplexes in a fold, remain constant under different mutation schemes and compared to the WT folds. Consequently, while the reduced fraction of paired nucleotides clearly correlates with the increased impact of disperse mutations, it is difficult to argue that the change in any other structural observable could be behind our observed differences in the effects of different mutation schemes on the compactness of WT folds. It thus remains to be seen whether it is a combination of these characteristic features of RNA secondary structure, such as the number of high-degree branching points and pairing probability, that is encoded on a global scale of the fold and affected most strongly by disperse mutations, or whether there is a yet unknown global property of folds that is responsible for it.

Figure 6.

Histograms of (a) and (b) pairing probabilities of WT and mutated folds (batch size s  =  720 nt, ∼20% of the genome size) and (c) and (d) number of high-degree branching points (6 branches or more) of BMV RNA2 and phage MS2 genomes. Folds obtained with different mutation schemes result in smaller pairing probabilities compared to the WT folds; this difference is most prominent in the case of disperse mutations. Disperse mutations also tend to slightly reduce the number of high-degree branching points compared to other mutation schemes and WT sequences. Other global structural properties, such as average duplex size or average degree of branching, show no difference between the WT and mutated folds.

We note that the theoretical framework that we have used in our work is minimalistic and transparent, and hence the findings should have a more general validity beyond the two considered cases of viral genomes. At the same time, we point out here two limitations that ought to be addressed in future studies. Firstly, while the MLD has been shown to correlate well with the experimental data on RNA compactness, it is nevertheless based on a simplified description of RNA folds as planar graphs. Restricting considerations to such classes of graphs is the de facto standard for secondary structure prediction methods, because they are clearly much more amenable to extensive numerical characterization. However, it is known that as RNA length increases, the genus of the native fold (a measure of topological complexity and non-planarity) increases as well [36]. Therefore, pseudoknots and other non-planar elements may definitely be present in the WT folds of phage MS2 and BMV [37–41]. Extending considerations, as well as the definition of MLD, to such cases is underway, based on the use of McGenus, a general (non-planar) secondary structure prediction scheme [36]. Secondly, for the sake of simplicity we have neglected other elements beyond MLD that are known to be important, such as electrostatic effects and the interactions of RNA with the capsid [42–44]. These should also be included in future extensions.

In conclusion, our results elucidate an aspect that, to our knowledge, has thus far not been fully addressed—namely, the presence of joint disruptive effects when mutating nucleotides that are nearby on the genomic sequence. This is the key difference that distinguishes block and centrality-ranked mutations from the disperse ones. Our findings clearly indicate that correlations due to sequence proximity help maintain the original properties of the fold under mutations to a much greater extent than in the case when the mutations are randomly distributed all along the sequence. Based on these results, we expect that further insight into the sequence-dependent robustness of viral RNA compactness could be gleaned from mapping out the reorganization of the network of secondary structure motifs due to mutations. This point could be profitably tackled in future studies by using a systematic analysis of the folds in terms of their contact maps and the Laplacian of their associated graphs.