Improved inference of time-varying reproduction numbers during infectious disease outbreaks

Highlights

• •Real-time estimation of reproduction numbers during outbreaks can guide control.
• •Using up-to-date serial interval data and accounting for imported cases is vital.
• •We develop a framework for estimating pathogen transmissibility appropriately.
• •We demonstrate it using data from outbreaks of influenza, Ebola and MERS.
• •Our approach is implemented in R package EpiEstim and online application EpiEstim App.

Abstract

Accurate estimation of the parameters characterising infectious disease transmission is vital for optimising control interventions during epidemics. A valuable metric for assessing the current threat posed by an outbreak is the time-dependent reproduction number, i.e. the expected number of secondary cases caused by each infected individual. This quantity can be estimated using data on the numbers of observed new cases at successive times during an epidemic and the distribution of the serial interval (the time between symptomatic cases in a transmission chain). Some methods for estimating the reproduction number rely on pre-existing estimates of the serial interval distribution and assume that the entire outbreak is driven by local transmission. Here we show that accurate inference of current transmissibility, and the uncertainty associated with this estimate, requires: (i) up-to-date observations of the serial interval to be included, and; (ii) cases arising from local transmission to be distinguished from those imported from elsewhere. We demonstrate how pathogen transmissibility can be inferred appropriately using datasets from outbreaks of H1N1 influenza, Ebola virus disease and Middle-East Respiratory Syndrome. We present a tool for estimating the reproduction number in real-time during infectious disease outbreaks accurately, which is available as an R software package (EpiEstim 2.2). It is also accessible as an interactive, user-friendly online interface (EpiEstim App), permitting its use by non-specialists. Our tool is easy to apply for assessing the transmission potential, and hence informing control, during future outbreaks of a wide range of invading pathogens.

1. Introduction

Infectious disease epidemics are a recurring threat worldwide (Daszak et al., 2000; Taylor et al., 2001; Morens et al., 2004; Jones et al., 2008; Fisher et al., 2012; Allen et al., 2017; Thompson and Brooks-Pollock, 2019). A key challenge during outbreaks is designing appropriate control interventions, and mathematical models are increasingly used to guide this decision-making (Lofgren et al., 2014; Cunniffe et al., 2016; Cori et al., 2017; Morgan, 2019; Polonsky et al., 2019). Recent examples of the real-time use of models during outbreaks can be drawn from diseases of humans (e.g. the outbreaks of Ebola virus disease in West Africa in 2013–2016 (WHO Ebola Response Team, 2014) and in the Democratic Republic of the Congo in 2018-19 (The Ebola Outbreak Epidemiology Team, 2018)), animals (e.g. the epidemics of foot-and-mouth disease in 2001 and 2007 in the U.K. (Keeling et al., 2001; Ferguson et al., 2001; Keeling, 2005; Anderson, 2008)) and plants (e.g. the invasion of Italy by Xylella fastidiosa in 2013 (EFSA Panel on Plant Health, 2015; White et al., 2017)).

For control measures to be optimised, the values of the parameters governing pathogen spread must be estimated from surveillance data, and temporal changes in these values must be tracked (Merl et al., 2009; Wallinga et al., 2010; Cunniffe et al., 2015; Thompson et al., 2018). The time-dependent reproduction number, R _t, is an important parameter for assessing whether current control efforts are effective or whether additional interventions are required (Chowell and Nishiura, 2009). The value of R _t represents the expected number of secondary cases arising from a primary case infected at time t. This value changes throughout an outbreak. If the value of R _t is and remains below one, the outbreak will die out. However, while R _t is larger than one, a sustained outbreak is likely. The aim of control interventions is typically to reduce the reproduction number below one (Camacho et al., 2015).

Different formal definitions of R _t have been proposed, and a number of methods are available to estimate reproduction numbers in real-time during epidemics (Obadia et al., 2012). Fraser (2007) distinguishes between the case reproduction number and the instantaneous reproduction number. The case reproduction number represents the average number of secondary cases arising from a primary case infected at time t; this parameter therefore reflects transmissibility after time t. In contrast, the instantaneous reproduction number represents the average number of secondary cases that would arise from a primary case infected at time t if conditions remained the same after time t. The latter therefore characterises the “instantaneous” transmissibility at time t, and is more straightforward to estimate in real-time than the case reproduction number because it does not require assumptions about future transmissibility (Cori et al., 2013).

Wallinga and Teunis (2004) developed an approach to estimate the case reproduction number. They applied their method to data from the 2003 SARS epidemic, showing that the effective reproduction number decreased after control measures were implemented, with similar trends in different affected countries. Their approach involves considering all possible transmission trees consistent with the observed epidemic data, and generates an estimated value of the case reproduction number at each timestep with observed cases. This method has been applied to estimate reproduction numbers during epidemics of diseases including Ebola virus disease (Althaus, 2015; Kelly et al., 2018), Middle-East Respiratory Syndrome (MERS) (Cauchemez et al., 2014) and porcine reproductive and respiratory syndrome (Arruda et al., 2017). It has also been extended to permit inference in different settings including in populations consisting of multiple host types (Glass et al., 2011), as well as to allow estimates to be informed by other types of data (Jombart et al., 2014; Campbell et al., 2019). Because of the importance of tracking temporal changes in epidemiological parameters, software implementing the framework of Wallinga and Teunis (2004) was developed to allow such analyses to be performed (Obadia et al., 2012). Other methods to estimate reproduction numbers at the start of an epidemic are also reviewed in Obadia et al. (2012) and implemented in the same R software package R0.

Recognising that estimates of the instantaneous reproduction number may provide a superior real-time picture of an outbreak as it is unfurling, Cori et al. (2013) subsequently developed a method and software (the EpiEstim R package) for estimating the instantaneous reproduction number using branching processes. This method has been used to analyse a number of recent outbreaks (e.g. Ali et al., 2013; WHO Ebola Response Team, 2014; Ferguson et al., 2016; Kirsch et al., 2016; Nouvellet et al., 2017). As with the approach of Wallinga and Teunis (2004), it relies on two inputs: a disease incidence time series (the numbers of new observed cases at successive times) and an estimate of the distribution of serial intervals (the times between symptomatic cases in a chain of transmission).

Although the approach of Cori et al. (2013) has been used frequently, its applicability may have been limited in some contexts because of two important drawbacks. First, an estimate of the serial interval distribution may not be available early in an outbreak, or may be associated with significant uncertainty. This is particularly the case for outbreaks of emerging infections, for which the natural history is not known or is poorly characterised (Metcalf and Lessler, 2017). Second, this approach assumes implicitly that all incident cases after the first time-point arise from local transmission, i.e. it does not account for the possibility that cases (other than those appearing at the first timestep) are imported from other locations or derive from alternative host species. However, epidemiological investigations throughout outbreaks often provide valuable data that can inform the serial interval distribution (Cowling et al., 2008, 2009; Forsberg White and Pagano, 2008; Forsberg White et al., 2009) and the sources of infection of cases (Paine et al., 2010; Cori et al., 2017).

Here we extend the statistical framework of Cori et al. (2013) for estimating the time-dependent reproduction number (hereafter, when we refer to the time-dependent reproduction number in the context of our method, we are referring to the instantaneous reproduction number). Rather than relying on previous estimates of the serial interval, our method integrates data on known pairs of index and secondary cases from which the serial interval is directly estimated, with corresponding uncertainty in the serial interval fully accounted for. Our method also allows incorporation of available information on imported (as opposed to locally infected) cases. We use data from the outbreaks of H1N1 influenza in the USA in 2009 and Ebola virus disease in West Africa from 2013 to 2016 to show how directly including the latest serial interval observations can improve the precision and accuracy of estimates of the time-dependent reproduction number during an outbreak. We use data on MERS cases in Saudi Arabia from 2014 to 2015 to illustrate the importance of accounting for imported cases appropriately when quantifying transmissibility. Our approach is implemented in a new version (2.2) of the R package EpiEstim (doi: 10.5281/zenodo.3333654), as well as an online interactive user-friendly interface (EpiEstim App – accessible at https://shiny.dide.imperial.ac.uk/epiestim – doi: 10.5281/zenodo.3275999) for users that are not familiar with R statistical software.

2. Methods

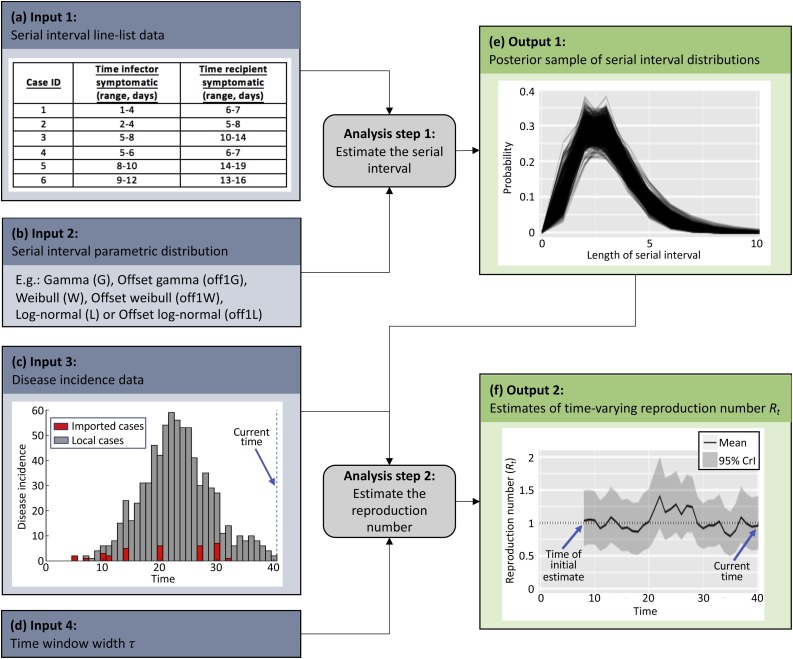
We propose a two-step procedure to estimate the time-dependent reproduction number from data informing the serial interval and from data on the incidence of cases over time (Fig. 1 ). The first step uses data on known pairs of index and secondary cases to estimate the serial interval distribution; the second step estimates the time-varying reproduction number jointly from incidence data and from the posterior distribution of the serial interval obtained in the first step.

Fig. 1.

A schematic illustrating how disease incidence time series and data on the serial interval can be combined to generate estimates of the reproduction number. Step 1. The serial interval distribution is estimated from interval-censored data on timings of symptom onset in index and secondary cases. Step 2. Estimates of the serial interval distribution are combined with disease incidence data to estimate the time-dependent reproduction number, R_t.

2.1. Estimating the serial interval distribution

The distribution of serial intervals can be estimated during an ongoing outbreak using interval-censored line list data – namely lower and upper bounds on timings of symptom onset in index and secondary cases (Cowling et al., 2009; Lessler et al., 2009) (see Fig. 1a for an example of such a dataset).

Serial interval data of this form are often collected during outbreaks, particularly in household studies from which chains of transmission can be reconstructed (Fine, 2003; Cauchemez et al., 2009; Cowling et al., 2009). Historical Ebola outbreaks provide a number of examples of this. For example, in the Ebola virus disease outbreak in the Democratic Republic of the Congo in 1995, such data were obtained from sources including hospital records and interviews with members of households with cases of Ebola (Dowell et al., 1999). Similarly, during the outbreak in Uganda in 2000, timings of symptoms were recorded throughout chains of transmission using contact tracing (Francesconi et al., 2003). Uncertainty in the reported dates, as well as lack of knowledge of the precise timings of symptom appearance even if exact dates are known, leads to interval-censored data.

Following Reich et al., 2009, Reich et al., 2016, we perform Bayesian parametric estimation of the serial interval distribution from such data using data augmentation Markov chain Monte Carlo (MCMC). In most of the analyses presented here (Fig. 2, Fig. 3, Fig. 4 ), we use a gamma distributed serial interval distribution offset by one day, although other distributions are also implemented in our R package (Fig. 1b) and in principle any parametric distribution could be used.

Fig. 2.

Estimation of the time-dependent reproduction number for an outbreak of H1N1 influenza in a New York School (Lessler et al., 2009). (a) Disease incidence time series (also see Table S1). (b) Posterior sample of serial interval distributions estimated from the interval-censored serial interval data shown in Table S2, assuming an offset gamma distributed serial interval. (c) Estimates of the reproduction number throughout the outbreak (mean (solid line) and 95% credible interval (shaded area)) obtained from the incidence data shown in (a) and the serial interval distributions shown in (b). The reproduction number was estimated on sliding windows of width τ = 6 days.

Fig. 3.

Analysis of the time-dependent reproduction number using data from the 2009 H1N1 outbreak in USA. (a) Disease incidence of H1N1 influenza from a school in Pennsylvania in 2009 (Cauchemez et al., 2011; Cori et al., 2013, see also Table S3). (b) Posterior sample of serial interval distributions (red) estimated from early serial interval data only collected in San Antonio, Texas (Morgan et al., 2010, see also Table S4), assuming an offset gamma distributed serial interval. (c) Posterior sample of serial interval distributions (black) estimated from all serial interval data collected in San Antonio, Texas (Morgan et al., 2010, see also Table S4), assuming an offset gamma distributed serial interval. (d) Estimates of the reproduction number (mean (solid lines) and 95% credible interval (shaded areas)) obtained from the incidence data shown in (a) and the serial interval distributions shown in (b) (red) and (c) (black) respectively. The reproduction number was estimated on sliding windows of width τ = 6 days. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article).

Fig. 4.

Estimates of the time-dependent reproduction number, R_t, for the early part of the 2013–2016 Ebola outbreak in Liberia (International Ebola Response Team, 2016). (a) Incidence of new confirmed and probable Ebola cases from 28^th May–31^st July 2014 (International Ebola Response Team, 2016). (b) Posterior sample of serial interval distributions estimated from nine pairs of cases between 28^th May–31^st July 2014 assuming an offset gamma distribution (blue), and a single offset gamma serial interval distribution with the same mean and standard deviation as these nine serial interval observations (yellow). (c) Estimates of R_t obtained from the incidence shown in (a) and the serial interval distributions shown in (b) (colours as in (b)). (d) Posterior sample of serial interval distributions estimated from pairs of cases up to 31^st July 2014 (blue) and up until 4^th December 2014 (red) respectively, assuming an offset gamma distribution. (e) Estimates of R_t obtained from the incidence shown in (a) and the serial interval distributions shown in (d) (colours as in (d)). Estimates of R_t were computed over four-weekly sliding windows (τ = 27 days). For the R_t estimates, the solid lines show the mean estimates and the shaded areas show the 95% credible intervals. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article).

The MCMC estimation procedure leads to a joint posterior sample for the parameters of the chosen distribution – i.e. a list of possible sets of parameter values, with each parameter set corresponding to a single step in the MCMC chain. Each parameter set, i, in the posterior sample is then converted into a discrete probability mass function $w_s^{(i)}$ (s = 0,1,2,…) as follows: the probability of the serial interval lasting 0 timesteps, $w_0^{(i)}$, is set to 0 as in Cori et al. (2013), and the probability $w_s^{(i)}$ for any other timestep s = 1,2,3,… is obtained by integrating the probability density function defined by this parameter set between s - 0.5 and s + 0.5. For each i, the function $w_s^{(i)}$ is then renormalised to sum to 1. The posterior sample of serial interval distributions, $w_s^{\left(i\right)}\left(i=1,2,\dots n\right)$ (Fig. 1e), is then used along with disease incidence time series to estimate the time-dependent reproduction number as described in the next section.

2.2. Estimating the reproduction number

The total number of incident cases arising at timestep t, $I_t$, is the sum of the numbers of incident local ($I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}}$) and imported ($I_t^{\text{i}\text{m}\text{p}\text{o}\text{r}\text{t}\text{e}\text{d}}$) cases,

$$I_t=I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}}+I_t^{\text{i}\text{m}\text{p}\text{o}\text{r}\text{t}\text{e}\text{d}}$$

We assume that, if imported cases exist, they can be distinguished from local cases, for instance through epidemiological investigations (Paine et al., 2010; Cori et al., 2017), so that $I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}}$ and $I_t^{\text{i}\text{m}\text{p}\text{o}\text{r}\text{t}\text{e}\text{d}}$ are observed at each timestep (Fig. 1c). We later discuss options for situations in which differentiation between imported and local cases is challenging.

Following Cori et al. (2013), we define the time-dependent reproduction number, R _t, as the ratio of the number of new locally infected cases at time t, $I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}}$, and the total infection potential across all infected individuals at time t, ${\text{Λ}}_t$. If there is a single serial interval distribution $w_s$ (s = 1,2,…), representing the probability of a secondary case arising a time period s after the primary case, each incident case (either local or imported) that appeared at a previous timestep t-s contributes to the current infectiousness at a relative level given by $w_s$. Therefore conditional on $w_s$, ${\text{Λ}}_t$ can be computed as ${\text{Λ}}_t(w_s)=\sum _{s=1}^t(I_{t-s}^{\text{l}\text{o}\text{c}\text{a}\text{l}}+I_{t-s}^{\text{i}\text{m}\text{p}\text{o}\text{r}\text{t}\text{e}\text{d}})w_s=\sum _{s=1}^t{I}_{t-s}{w}_s$.

Given a serial interval distribution $w_s$, data on the total number of incident cases up to the previous timestep ($I_0,I_1,\dots ,I_{t-1}$), and the time-dependent reproduction number (R_t), the expected number of incident locally infected cases at time t is

$$\mathbf{E}\left(I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}}\right|I_0,I_1,\dots ,I_{t-1},w_s,R_t)=R_t{\text{Λ}}_t{(w}_s)$$

Assuming that the number of local cases at timestep t is drawn from a Poisson distribution, the probability of observing $I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}}$ cases at timestep t is

$$\mathbf{P}\left(I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}}\right|I_0,I_1,\dots ,I_{t-1},w_s,R_t)=\frac{{(R_t{\text{Λ}}_t{(w}_s))}^{I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}}}\text{e}\text{x}\text{p}(-R_t{\text{Λ}}_t{(w}_s))}{I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}}!}$$

As in Cori et al. (2013), we make the assumption that the reproduction number is constant over a time period [t − τ, t], with τ representing the length of the time window over which R_t is estimated (Fig. 1d). The probability of observing the local incidence $I_{\text{t}-\text{τ}}^{\text{l}\text{o}\text{c}\text{a}\text{l}},I_{\text{t}-\text{τ}+1}^{\text{l}\text{o}\text{c}\text{a}\text{l}},\dots ,I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}}$ during this time period, given the reproduction number R_t and conditional on the previous incidence data $I_0,I_1,\dots ,I_{t-\text{τ}-1}$, is then

$$\mathbf{P}\left(I_{t-\tau }^{\text{l}\text{o}\text{c}\text{a}\text{l}},I_{t-\tau +1}^{\text{l}\text{o}\text{c}\text{a}\text{l}},\dots ,I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}}\right|I_0,\dots ,I_{t-\tau -1},w_s,R_t)=\prod _{k=t-\tau }^t\frac{{(R_t{\text{Λ}}_k{(w}_s))}^{I_k^{\text{l}\text{o}\text{c}\text{a}\text{l}}}\text{e}\text{x}\text{p}(-R_t{\text{Λ}}_k{(w}_s))}{I_k^{\text{l}\text{o}\text{c}\text{a}\text{l}}!}$$

Using a Bayesian framework with a gamma distributed prior for R_t as in Cori et al. (2013), the posterior distribution of R_t given past incidence data and conditional on the serial interval distribution, $w_s$, is

$$\mathbf{P}\left(R_t\right|I_0,I_1,I_2,\dots ,I_{t-\tau -1},I_{t-\tau }^{\text{l}\text{o}\text{c}\text{a}\text{l}},I_{t-\tau +1}^{\text{l}\text{o}\text{c}\text{a}\text{l}},\dots ,I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}},w_s)$$

$$\propto \mathbf{P}\left(I_{t-\tau }^{\text{l}\text{o}\text{c}\text{a}\text{l}},I_{t-\tau +1}^{\text{l}\text{o}\text{c}\text{a}\text{l}},\dots ,I_t^{\text{l}\text{o}\text{c}\text{a}\text{l}}\right|I_0,\dots ,I_{t-\tau -1},w_s,R_t\left)\mathbf{P}\right(R_t)$$

$$=\left(\prod _{k=t-\tau }^t\frac{{\left(R_t{\text{Λ}}_k\left(w_s\right)\right)}^{I_k^{\text{l}\text{o}\text{c}\text{a}\text{l}}}\text{exp}\left(-R_t{\text{Λ}}_k{(w}_s)\right)}{I_k^{\text{l}\text{o}\text{c}\text{a}\text{l}}!}\right)\left(\frac{{R_t}^{a-1}\text{exp}\left(-\frac{R_t}{b}\right)}{\mathbf{\Gamma }\left(a\right)b^a}\right)$$

$$\begin{array}{l}\propto {R_t}^{a+{\sum }_{k=t-\tau }^t{I}_k^{\text{l}\text{o}\text{c}\text{a}\text{l}}-1}\text{exp}\left(-R_t\left({\displaystyle \sum _{k=t-\tau }^t}{\text{Λ}}_k\left(w_s\right)+\frac{1}{b}\right)\right)\times \\ {\displaystyle \prod _{k=t-\tau }^t}\frac{{{\text{Λ}}_k\left(w_s\right)}^{I_k^{\text{l}\text{o}\text{c}\text{a}\text{l}}}}{I_k^{\text{l}\text{o}\text{c}\text{a}\text{l}}!}\end{array}$$

where $a$ and $b$ are the shape and scale parameters of the gamma distributed prior for R_t. We use a gamma distributed prior, conjugate to the Poisson likelihood, to obtain an analytical formulation of the posterior distribution of R_t. According to the expression above, the posterior distribution for R_t given the incidence data, conditional on the serial interval distribution $w_s$, is a gamma distribution with shape parameter $a+\sum _{k=t-\tau }^t{I}_k^{\text{l}\text{o}\text{c}\text{a}\text{l}}$ and scale parameter $\frac{1}{\sum _{k=t-\tau }^t{\text{Λ}}_k\left(w_s\right)+1/b}$.

In all our analyses here, we choose $a$ and $b$ so that the prior for R_t has mean and standard deviation equal to 5, as in Cori et al. (2013). The choice of a large standard deviation ensures that the prior is relatively uninformative, and the choice of a high mean value for the prior is conservative; i.e. if posterior estimates of R_t are below one, indicating that the epidemic is estimated to be under control, then we can be sure that this does not result from the choice of prior but is a direct result of the data.

To obtain a sample from the full posterior distribution for R_t given both the incidence and the serial interval data, we consider each possible serial interval distribution $w_s^{\left(i\right)}\left(i=1,\dots n\right)$ obtained in the previous section when the serial interval was estimated. For each $i$, we draw a sample of size $m$ from the gamma posterior distribution of R_t, given the incidence data and conditional on the serial interval distribution $w_s^{\left(i\right)}$. We thereby obtain a sample of size $n\times m$ drawn from the posterior distribution of R_t given both the incidence and serial interval data, from which the posterior mean and 95% credible intervals of R_t can be computed (Fig. 1f).

2.3. Data

We apply our method to analyse disease incidence time series and serial interval data from a number of past outbreaks, described in this section and made available, when possible, in Tables S1-S4. These are also included in our R package EpiEstim 2.2 and in the accompanying EpiEstim App online application (https://shiny.dide.imperial.ac.uk/epiestim).

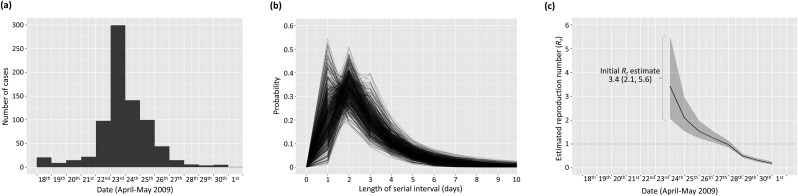
2.3.1. H1N1 influenza in a New York school (2009) – Fig. 2

From 18^th April to 1^st May 2009, an outbreak of H1N1 influenza occurred that infected more than 800 students and employees in a New York high school. The disease incidence data were shown in Fig. 1 of Lessler et al. (2009) and are reproduced in our Table S1.

Interval-censored serial interval observations were also collected from 16 pairs of cases during this outbreak, as reported in Table 2 of the Supplementary Appendix of Lessler et al. (2009), and are reproduced in Table S2 of our supplementary material.

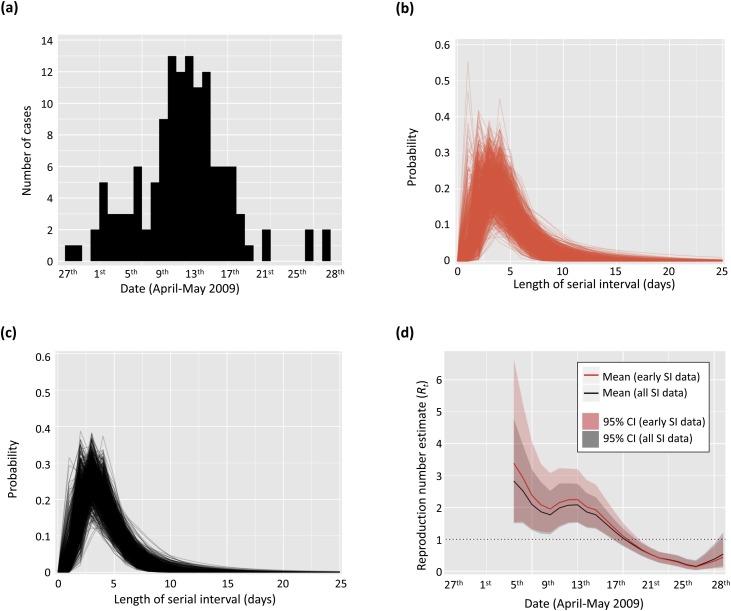
2.3.2. H1N1 influenza in a school in Pennsylvania (2009) – Fig. 3

Disease incidence data were available describing the numbers of individuals experiencing onset of acute respiratory illness in a school in Pennsylvania in April and May 2009 (Cauchemez et al., 2011). These data were included with the first version of EpiEstim (Cori et al., 2013), and are also reproduced here in Table S3.

We used these data in combination with serial interval data from the 2009 H1N1 influenza pandemic in USA (Donnelly et al., 2011). Specifically, serial interval data were collected from pairs of cases between 17^th April and 8^th May 2009, and were reported in Table 1 of Morgan et al. (2010). We converted the dates of infection of index/secondary cases into intervals to account for uncertainty in the precise timings of infection on the days concerned: for example, for an index case on 18^th April and a secondary infection on 25^th April, the length of the serial interval was between 6–8 days (Table S4). We performed analyses including cases from early in the outbreak (where the primary case occurred in the range 17^th–24^th April 2009), as well as using data from the whole outbreak (17^th April–8^th May 2009).

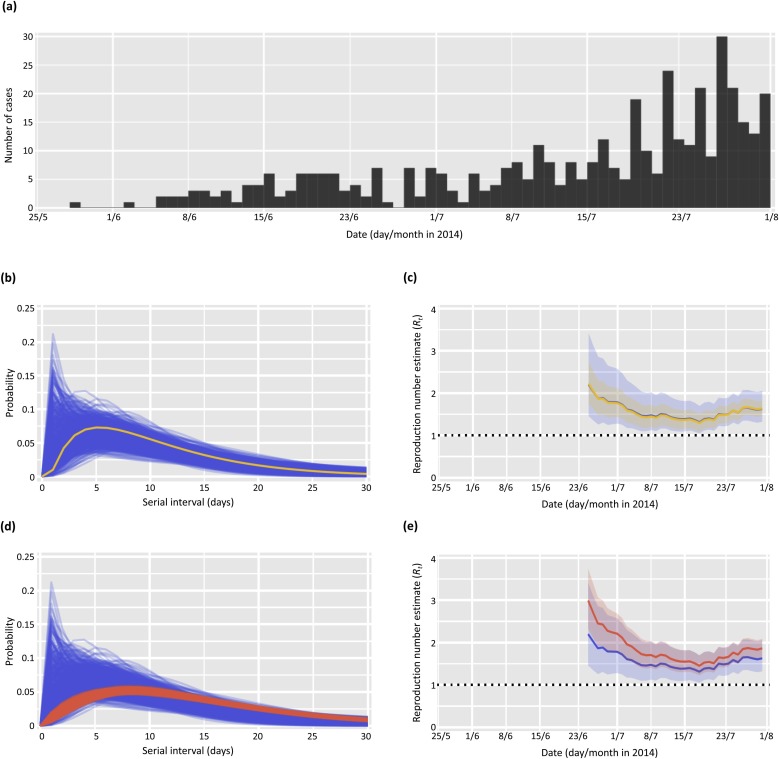
2.3.3. Ebola virus disease in Liberia (2014) – Fig. 4

We also analysed data from the West African 2013–2016 Ebola outbreak. We considered the daily incidence of confirmed and probable cases in Liberia between 28^th May and 31^st July 2014, computed from the World Health Organization line-list data as described by the International Ebola Response Team (International Ebola Response Team, 2016) and shown in Fig. 4a. In this time interval, 418 symptomatic confirmed and probable cases were reported. There were 16 confirmed and probable cases reported before this time, but these occurred sporadically and hence we conducted our analysis using data from 28^th May 2014 onwards.

Line-list serial interval data were available from the World Health Organization (International Ebola Response Team, 2016). Infected individuals were asked who their potential infectors might have been. Up to 31^st July 2014, nine such cases (‘early serial interval data’) were available for which information on exposure to a confirmed, probable or suspected case could be retrieved in this way. Data from 295 further pairs of cases up until 4^th December 2014 were also available and used in our analyses (‘all serial interval data’).

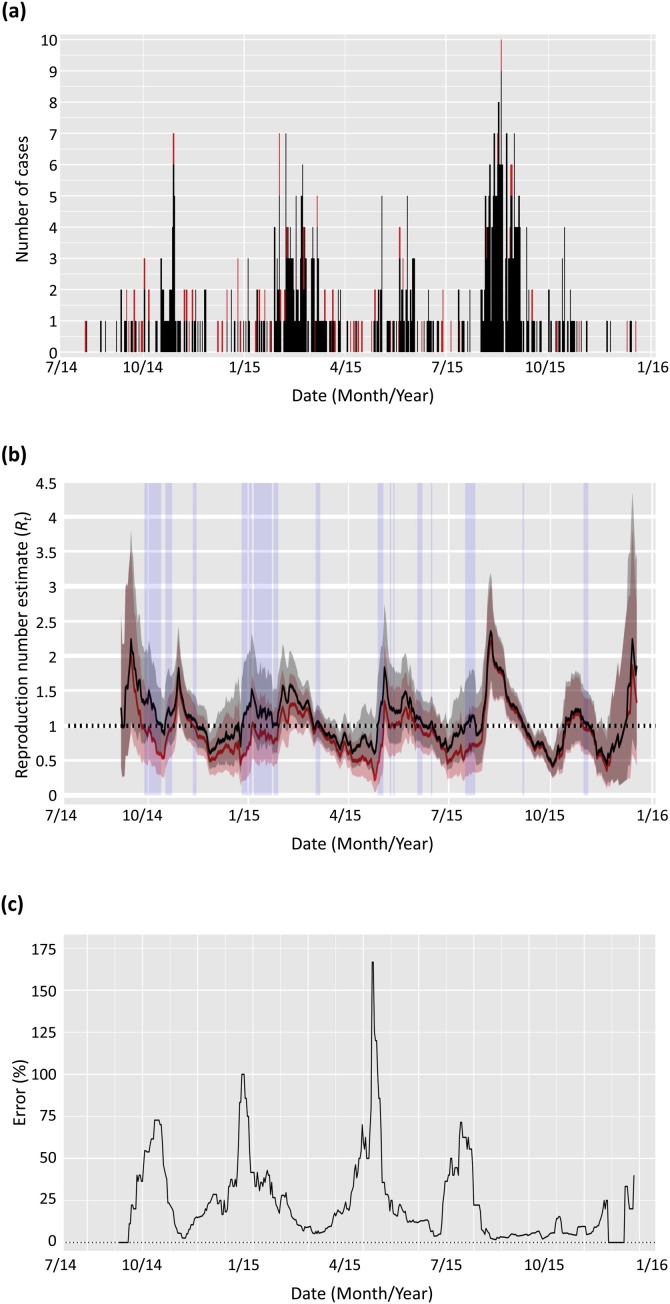
2.3.4. MERS in Saudi Arabia (2014–2015) – Fig. 5

Fig. 5.

Estimated reproduction number, R_t, for MERS in Saudi Arabia from August 2014 to December 2015. (a) MERS incidence over time, with cases imported from the animal reservoir shown in red and other cases in black (Food and Agriculture Organization of the United Nations, 2017). (b) Estimates of R_t obtained from the incidence data shown in (a), assuming an offset Gamma distribution with mean 6.8 days and standard deviation 4.1 days for the serial interval (Cauchemez et al., 2016). Solid lines show the mean estimates and the shaded areas show the 95% credible intervals. Results shown in black ignore the information on proximity to the animal reservoir and assume all infections arose from other human cases in the dataset. Results shown in red account for the cases known to be infected from the animal reservoir. Reproduction number estimates were generated using four-weekly sliding windows (τ = 27 days). The time periods shown with shaded blue rectangles correspond to those during which the mean estimated R_t ignoring importations is above the threshold 1, whilst the mean estimated R_t accounting for importations is below 1. (c) Relative error in the estimated mean R_t when ignoring importations. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article).

A dataset consisting of the daily numbers of laboratory confirmed human cases of MERS in Saudi Arabia between 11^th August 2014 and the 18^th December 2015 was extracted from the EMPRES-I system from FAO (Global Animal Disease Information System - Food and Agriculture Organization of the United Nations, 2017). The dataset indicates which cases were in humans who have regular (potentially infective) contacts with animals, particularly camels. Since the dromedary camel is considered as a reservoir species of the MERS-coronavirus (Haagmans et al., 2014), we interpreted reported regular contact with animals as an indication of infection from the reservoir. This allowed us to distinguish between cases arising from human-human transmission, for example transmission in households or hospitals (Al-Tawfiq and Perl, 2015), and human cases derived directly from the animal reservoir.

For the serial interval, we assumed an offset gamma distribution with mean 6.8 days and standard deviation 4.1 days, as estimated by Cauchemez et al. (2016).

3. Results

3.1. Estimating the reproduction number

We first applied our method to estimate the time-dependent reproduction number R _t throughout an outbreak of H1N1 influenza in a New York School, for which both incidence and serial interval data were available. We fitted a gamma distributed serial interval offset by one day. Results are shown in Fig. 2.

The median reproduction number estimate for the first seven days of the outbreak (April 18^th–April 24^th 2009) was 3.3 – with 95% credible interval (95% CrI) given by (2.1,5.6) – and the mean estimate for this period was 3.4. These estimates are consistent with a previous estimate of the reproduction number over this time period of 3.3 from a study by Lessler et al. (2009). Those authors used a similar approach to quantify the serial interval distribution to the method used here, but estimated the reproduction number based on the initial exponential growth rate of the outbreak.

3.2. Uncertainty in estimates of R_t

The method for estimating the time-dependent reproduction number, R _t, by Cori et al. (2013) previously relied on a pre-existing estimate of the serial interval distribution. In practical applications of that method, typically single serial interval distributions, estimated from previous outbreaks or based on early data from the ongoing outbreak, have been used to estimate R _t throughout an epidemic. In our approach, we propose to integrate the estimation of the serial interval distribution within the estimation of R _t. This allows R _t to be estimated directly not only from the most up-to-date incidence data, but also from up-to-date serial interval data.

As more serial interval data become available during an outbreak, the uncertainty surrounding the serial interval distribution estimates, and in turn the reproduction number estimates, typically reduces. To illustrate this principle, we estimated the changes in the reproduction number for an outbreak of H1N1 influenza in a school in Pennsylvania in 2009 (Cauchemez et al., 2011; Donnelly et al., 2011; Cori et al., 2013). We used serial interval data collected in a household study undertaken early in the 2009 influenza pandemic in San Antonio, Texas (Morgan et al., 2010). We estimated the reproduction number using two subsets of these serial interval data: first, only the data that were available early in the study (for which the primary cases occurred between 17^th–24^th April 2009), and; second, all the data from the study (17^th April–8^th May 2009). Results are shown in Fig. 3.

The mean R _t estimates using only the early serial interval data were mostly greater than those using all serial interval data. Moreover, using only the early serial interval data led to larger uncertainty in the serial interval distribution estimates, and in turn in the R _t estimates. In particular, the upper bound of the 95% credible interval obtained using the early serial interval data was much higher (up to 41% higher) than when all serial interval data were used. If control strategies were designed based on a pessimistic scenario corresponding to this upper bound, the R _t estimates based on the early serial interval data could have led to designing unnecessarily intense interventions. Of course, intense interventions when based on all available data are justifiable, but it is important for interventions to continue to be re-evaluated as new data become available during an outbreak (Merl et al., 2009; Shea et al., 2014; Thompson et al., 2018).

We also analysed data from the West African 2013–2016 Ebola outbreak (see Data section in Methods). The incidence data are shown in Fig. 4a. We computed three estimates of the time-dependent reproduction number using three different assumptions on the serial interval: (i) using a single distribution for the serial interval (yellow line in Fig. 4b); (ii) using the full posterior distribution of serial intervals estimated from the nine pairs of cases observed up to 31^st July 2014 (blue lines in Fig. 4b and d); and (iii) using the full posterior distribution of serial intervals estimated from all 304 pairs of cases observed up to 4^th December 2014 (red lines in Fig. 4d). In all analyses of the Ebola data, we used an offset gamma serial interval distribution. For (i), the serial interval distribution was constructed to match the mean and standard deviation of the observed nine pairs of early cases.

Using a single distribution for the serial interval rather than the full posterior distribution of serial intervals led to similar central estimates but a large underestimation of the uncertainty in the reproduction number (Fig. 4c). Furthermore, using the early serial interval data led to underestimating the mean reproduction number by as much as 26% compared to using all the serial interval data that were available (Fig. 4e).

3.3. Imported cases

We used incidence data of MERS cases in Saudi Arabia from 2014 to 2015 (Food and Agriculture Organization of the United Nations, 2017) – shown in Fig. 5a – to estimate the reproduction number throughout that outbreak. Data were available describing some cases as being likely importations from the animal reservoir. We assumed all other cases were due to local human-human transmission. We compared estimates of the reproduction number obtained when using (results in red in Fig. 5b) and not using (results in black in Fig. 5b) this information. As expected, disregarding the information on the imported cases and instead assuming that those cases arose from local human-human transmission led to overestimation of the reproduction number. The blue shaded time-windows in Fig. 5b highlight times at which the mean reproduction number estimated assuming only local transmission is greater than one (so that the epidemic would not be estimated to be under control) when in fact the reproduction number estimated using information on imported cases is below one. Fig. 5c shows that the relative error in the mean R _t estimates when ignoring imported cases varies over time but is sometimes very large, with relative errors of over 50% in October 2014, and January, May and July 2015.

4. Discussion

Quantifying disease transmissibility during outbreaks is crucial for designing effective control measures and assessing their effectiveness once implemented. This assessment forms a critical part of real-time situational awareness (Cauchemez et al., 2006a; Cowling et al., 2010; Christaki, 2015; Cori et al., 2017; Polonsky et al., 2019). Indeed, in circumstances in which the incidence of cases is still increasing, but the time-dependent reproduction number is dropping, there might be a very different outlook compared to if the incidence of cases and the reproduction number are both increasing. Assessment of the reproduction number can also be used for planning future interventions (Lipsitch and Bergstrom, 2004; Fraser et al., 2009).

We have developed a framework for estimating time-dependent reproduction numbers in real-time during outbreaks. Our approach builds on a well-established method (Cori et al., 2013) and addresses two important limitations of the approach as proposed in that study. The first important feature of our framework is that data on pairs of infector/infected individuals can be included in the estimation procedure, so that the serial interval distribution and the time-dependent reproduction number can be estimated jointly from the latest available data. This leads to more precise estimates of transmissibility, as well as accurate quantification of the uncertainty associated with these estimates. Second, our method allows datasets that distinguish between locally transmitted and imported cases to be analysed appropriately. We describe these limitations of the previous method in more detail below. We have shown that these key features lead to improved inference of pathogen transmissibility, with illustrations using datasets from epidemics of H1N1 influenza (Fig. 2, Fig. 3), Ebola virus disease (Fig. 4) and MERS (Fig. 5). We have also implemented our modelling framework in an online tool, allowing it to be used easily in outbreak response settings by stakeholders.

Various methods exist for estimating the values of reproduction numbers, particularly the basic reproduction number, from epidemic data (see Obadia et al. (2012) for an in-depth review). The most commonly used approach for estimating time-dependent reproduction numbers, other than the approach of Cori et al. (2013), is that of Wallinga and Teunis (2004). As described in the introduction, one caveat of the Wallinga and Teunis method is that it estimates the case reproduction number, which is not a measure of instantaneous transmissibility. If a policy-maker wishes to understand the impacts of control interventions in real-time, then an estimate of the case reproduction number is less useful than an estimate of the instantaneous reproduction number because the case reproduction number does not change immediately after interventions are altered; instead, it changes more smoothly and in a delayed manner (Fraser, 2007; Cori et al., 2013). In contrast, the instantaneous reproduction number changes straight away and is therefore a useful quantity for understanding the impacts of control strategies in real-time. Furthermore, estimation of the case reproduction number at any time usually requires incidence data from later times, although we note that extensions to the Wallinga and Teunis approach have been developed to relax this assumption of the original method (Cauchemez et al., 2006b).

Some approaches have been proposed to estimate the serial interval and reproduction numbers jointly from time series data on the numbers of new cases (Wallinga and Teunis, 2004; Forsberg White and Pagano, 2008), but it has been shown that it may not be possible to estimate both these quantities precisely from those data alone in the early stages of an outbreak (Fraser, 2007; Griffin et al., 2011). Our approach instead extends the framework of Cori et al. (2013), and relies on observations of transmission pairs in addition to the time series data to estimate the serial interval and the time-varying reproduction number in a two-step estimation process (Fig. 1).

As described above, the first limitation of the approach of Cori et al. (2013) is that it makes use of pre-existing estimates of the serial interval distribution as an input. This potentially leads to delays between studies inferring the serial interval and subsequent analyses estimating transmissibility, or means that estimates of transmissibility are based on estimates of the serial interval from earlier outbreaks. Here, we used data from the 2013–2016 Ebola outbreak in Liberia to show that failing to account for full uncertainty in the serial interval distribution may lead to underestimating the uncertainty surrounding reproduction number estimates (Fig. 4c). Moreover, ignoring recent data on the serial interval can dramatically impact estimates of the reproduction number and the uncertainty associated with those estimates (Figs. 3d, 4e). This is of practical importance – as an example, a number of studies conducted during and after the 2013-16 West African Ebola outbreak (e.g. Wiratsudakul et al., 2016; Bakker and Wallinga, 2016; Dalziel et al., 2018) used the same single serial interval estimate obtained near the beginning of the outbreak (WHO Ebola Response Team, 2014). Our results suggest that using the latest available data on pairs of index and secondary cases, and fully accounting for the corresponding uncertainty in the serial interval estimates, may lead to very different, but more robust estimates of the reproduction number. It is worth noting that the pairs of index/secondary cases included in the estimation should be as representative as possible; in particular, if too recent index cases are considered, some of their secondary cases may not have been observed yet, leading to artificial underestimation of the serial interval.

Although some approaches for estimating reproduction numbers allow imported cases to be accounted for (Wallinga and Teunis, 2004; Forsberg White and Pagano, 2008), the second limitation of the approach of Cori et al. (2013) is that it assumes that all cases in an outbreak (other than those observed at the first timestep) occur from local transmission, which can be erroneous. For some diseases – e.g. MERS (Funk et al., 2016) and yellow fever (Wilder-Smith and Monath, 2017) – transmission from alternative hosts (e.g. camels for MERS and non-human primates for yellow fever) can be common. Continued importation of cases into a local population from other geographical locations can also occur. For example, a number of cases of H1N1 influenza in New Zealand in 2009 were known imports from other locations (Paine et al., 2010). Failing to properly account for such non-locally transmitted cases can lead to overestimating the reproduction number, as we illustrated in our application to data on MERS in Saudi Arabia from 2014 to 2015 (Fig. 5b,c). Epidemiological studies often collect data on exposure routes for each case (Cowling et al., 2008, 2009; Forsberg White et al., 2009; Paine et al., 2010; Cori et al., 2017), and this information on the local or non-local source of incident cases should be included, when available, in estimates of pathogen transmissibility. Of course, such information might not be available directly from epidemiological data. In this case, one option might be to use statistical methods along with genetic and epidemiological data to differentiate between local and imported cases (Ypma et al., 2013; Cori et al., 2018).

One of the aims of epidemic control is to reduce the reproduction number below one. Failing to account for full uncertainty in the serial interval, not including recently available serial interval data, and failing to differentiate between local and imported cases might lead to incorrect assessment of the effectiveness of current control measures. Throughout most of this article, we discussed disease control in the context of whether or not the mean estimate of the reproduction number was less than or greater than one. However, policy-makers may prefer to choose more risk-averse policies. When the goal of interventions has been to minimise a function describing the cost of an outbreak, the idea of intervening to ensure that percentile estimates of that cost are minimised has been proposed (Tildesley et al., 2012; Cunniffe et al., 2016). A similar idea here might be directing control strategies towards ensuring that a specific percentile estimate of the reproduction number falls below one. In this context, inadequate quantification of the uncertainty surrounding reproduction number estimates may be as important as biases in the central estimates.

As well as in response to interventions, the reproduction number may change over time due to other factors. Seasonal variations in the parameters governing disease spread play a significant role in transmission of a number of pathogens (Dietz, 1976; Grassly and Fraser, 2006; Fisman, 2007; van Gaalen et al., 2017). For example, transmission of vector-borne pathogens varies due to factors including seasonal temperature variation (Lord, 2004; Obolski et al., 2019), and outbreaks of childhood diseases such as measles are affected by school term dates (Earn et al., 2000). These, and indeed any factor resulting in changes in pathogen transmissibility (e.g. the depletion of the number of susceptible individuals in the population (Thompson et al., 2019a)), will be reflected in time-dependent reproduction number estimates generated using our approach, so these estimates need to be interpreted carefully when assessing the effectiveness of interventions.

As with most previous methods, we propose estimation of the reproduction number based on the incidence of symptomatic cases and the serial interval distribution, rather than the incidence of infections and the distribution of the generation time (time between infection of a case and infection of their infector (Wallinga and Lipsitch, 2007; Park et al., 2019)). In some circumstances, the serial interval distribution might not match the generation time distribution. As an extreme example, the generation time can only take positive values, however for diseases for which infectiousness occurs before the onset of symptoms, negative values of the serial interval might be possible (Vink et al., 2014; Thompson et al., 2016).

Since the onset of symptoms occurs after the time of infection, considering the incidence of symptomatic cases instead of the incidence of infection also leads to delays in estimates of the reproduction number. This is unavoidable in most cases as surveillance systems typically do not record the timings of new infections. However, for analyses carried out retrospectively, if the distribution of the incubation period (time between infection and onset of symptoms) is known, then it is possible to eliminate this time lag by back-calculating the likely infection times from the times at which symptoms were recorded (Fraser, 2007). The instantaneous reproduction number can then be inferred from these back-calculated data. We note that this might contribute uncertainty in reproduction number estimates if there is significant variability in the time between infection and detection of symptoms between individuals, as is the case for Ebola (WHO Ebola Response Team, 2014; Hart et al., 2019).

An important feature of our method, like previous ones, is that, if the proportion of cases that go unreported remains constant throughout an outbreak, estimates of the reproduction number are unaffected by underreporting. However, reporting can vary over time within an outbreak. An interesting future extension of our approach might be accounting for uncertainty in the precise numbers of incident cases at each timestep. If information is available to quantify changes in reporting over time, this would permit correction to allow for temporal variation in underreporting, which might otherwise be interpreted as variation in the reproduction number. Underreporting has hindered estimation of disease burden for a number of diseases including dengue (Shepard et al., 2013), yellow fever (Garske et al., 2014) and Ebola (Dalziel et al., 2018; Thompson et al., 2019b). Other additions to our work might involve allowing for reporting delays (Cowling et al., 2010; van de Kassteele et al., 2019).

In conclusion, we have extended the commonly used approach of Cori et al. (2013) for estimating the time-dependent reproduction number to include important new features. We hope that our improved modelling framework is sufficiently flexible that it will be used by epidemiologists and policy-makers in a wide range of future outbreak response scenarios. This should be facilitated by our R package (EpiEstim 2.2) and our online interactive user-friendly interface (EpiEstim App - https://shiny.dide.imperial.ac.uk/epiestim).

Authors’ contributions

All authors except JES, ZNK, EM and TJ contributed to extending and linking the CoarseDataTools and EpiEstim R packages during the Hackout 3 meeting; JES, RNT and AC developed the software application; RNT and AC wrote the manuscript; All authors revised the manuscript; All authors discussed the research and approved the final version of the manuscript.

Funding

The Hackout 3 meeting at the Institute for Data Science (University of California Berkeley) was funded by the NIHR Modelling Methodology Health Protection Research Unit (Imperial College London) and the MRC Centre for Outbreak Analysis and Modelling (Imperial College London). Additional funding for JES was obtained through the RECON project at the NIHR Modelling Methodology Health Protection Research Unit (Imperial College London). RNT thanks Christ Church (University of Oxford) for funding his research via a Junior Research Fellowship. SC acknowledges financial support from the AXA Research Fund, the Investissement d’Avenir program, the Laboratoire d’Excellence Integrative Biology of Emerging Infectious Diseases program (Grant ANR-10-LABX-62-IBEID), the Models of Infectious Disease Agent Study of the National Institute of General Medical Sciences and the INCEPTION project (PIA/ANR-16-CONV-0005). AC acknowledges joint centre funding from the UK Medical Research Council and Department for International Development, as well as funding from the United States Agency for International Development (USAID). The results of this work do not necessarily reflect the views of USAID or any other funding body.

Declaration of Competing Interest

We have no competing interests.

Appendix A. Supplementary data

The following are Supplementary data to this article: