Abstract
Wall shear stress (WSS) has been shown to be associated with myocardial infarction (MI) and progression of atherosclerosis. Wall elasticity is an important feature of hemodynamic modeling affecting WSS calculations. The objective of this study was to investigate the role of wall elasticity on WSS, and justify use of either rigid or elastic models in future studies. Digital anatomic models of the aorta and coronaries were created based on coronary computed tomography angiography (CCTA) in four patients. Hemodynamics was computed in rigid and elastic models using a finite element flow solver. WSS in five timepoints in the cardiac cycle and time averaged wall shear stress (TAWSS) were compared between the models at each 3 mm subsegment and 4 arcs in cross sections along the centerlines of coronaries. In the left main (LM), proximal left anterior descending (LAD), left circumflex (LCX), and proximal right coronary artery (RCA) of the elastic model, the mean percent radial increase 5.95 ± 1.25, 4.02 ± 0.97, 4.08 ± 0.94, and 4.84 ± 1.05%, respectively. WSS at each timepoint in the cardiac cycle had slightly different values; however, when averaged over the cardiac cycle, there were negligible differences between the models. In both the subsegments (n = 704) and subarc analysis, TAWSS in the two models were highly correlated (r = 0.99). In investigation on the effect of coronary wall elasticity on WSS in CCTA-based models, the results of this study show no significant differences in TAWSS justifying using rigid wall models for future larger studies.
1 Introduction
Coronary artery disease is the leading cause of myocardial infarction (MI) in both men and women [1], accounting for nearly one-third of deaths in U.S. [2] Prevention of MI is challenging as over 50% of patients who suffer from acute MI do so without prior symptoms. [3] Anatomic features such as coronary plaque volume and high-risk plaque features are predictive of MI [4,5]. However, adding physiological information such as the ratio of distal to proximal blood pressure across a coronary segment (fractional flow reserve) [6,7] or tangential hemodynamic stress acting on the endothelial cells in coronary arteries (wall shear stress (WSS)) [8–10] has been shown to improve prediction of patients risk of MI.
Measurements of physiological pressure and flow conditions in coronary arteries are usually performed invasively through catheterization and intravascular imaging. Advancement of coronary computed tomography angiography (CCTA) imaging as well as high-performance computing now allows for noninvasive image-based patient-specific modeling and simulation of coronary blood flow and calculation of physiological condition. Recent trials have demonstrated the utility and promise of simulation-based assessment of fractional flow reserve in the coronary arteries as an alternative to invasive assessment [11,12].
Accurate patient-specific computational fluid dynamics (CFD) modeling requires accurate boundary condition (BC) specification. Therefore, it is of critical importance that BC selection for these models represents the patient's physiology as close as possible. There has been considerable recent attention paid to appropriate BC specification to capture unique features of coronary physiology, including lumped parameter models that appropriately mimics diastolic dominant flow, in which flow and pressure waveforms are out of phase due to cardiac contraction. Other recent work has proposed automated tuning methods for patient-specific BC determination [13–15].
Coronary arteries are also characterized by dynamic vessel motion, wall elasticity, and high vessel curvature, though fewer studies have evaluated the impact of these on computational hemodynamics predictions. In larger vessels, comparisons of wall shear stress in elastic versus rigid walls have shown up to 25% [16], 17% [17], and 4–15% [17,18] difference in the aorta, femoral, and carotid arteries, respectively. Elastic wall modeling has also been used to study hemodynamics in aortic [19], cerebral [20,21], and coronary aneurysms [22] as well as bypass grafts [13]. However, few studies have quantified the impact of wall elasticity in the coronary arteries. They mainly focused on single patient-specific models of either the right [23,24] or left coronary artery [20,25] (with no branches) or idealized models [26,27]. Modeling coronary arteries with elastic walls is computationally expensive, more time-consuming, and may not be readily implemented in clinical practice. Therefore, to get around this difficulty in computational studies with larger participant populations, all coronary walls were assumed to be rigid [10,28,29].
In addition to predicting myocardial infarction, WSS is associated with development and progression of coronary atherosclerotic plaque in invasive intravascular ultrasound imaging as revealed by two large clinical trails [10,30]. Reacting to local WSS, endothelial cells regulate vascular tone, thrombogenisis, inflammation, and vascular growth and remodeling [31,32]. Disruption of blood flow patterns in regions such as bifurcations or highly curved vessels causes endothelial cell response, initiating a cascade leading to atherosclerosis formation, and vessel remodeling [33,34]. To gain insight into the links between these processes and patient outcomes, it will require future studies with large patient cohorts. In support of those efforts, our intent here is to provide justification for the future choice of either rigid or elastic models of the coronary artery wall in simulations.
Therefore, the overall goal of this study is to quantify differences in WSS predictions in simulations with rigid versus elastic walls, in complete three-dimensional (3D) networks of multiple patient-specific coronary models based on noninvasive coronary CTA.
2 Methods
2.1 Clinical Data, Coronary Computed Tomography Angiography Acquisition, and Image Segmentation.
Coronary CTA images of four participants were selected from a completed randomized controlled trial in participants living with human immunodeficiency virus with 12 months of atorvastatin to improve coronary atherosclerosis as measured on CTA [35]. The selected participants all had moderate stenosis in at least one artery and the analyses performed in this study were all based on the coronary CTA images at baseline. electrocardiogram-gated coronary CTA imaging was performed using a dual source 128-slice CT scanner (Somatom Definition Flash, Siemens Medical Solutions, Forchheim, Germany) [36]. All had 600 μg sublingual nitroglycerin for vasodilation and up to 15 mg IV metoprolol to achieve a heart rate <65 bpm. 60–100 ml nonionic iodinated IV contrast (iopamidol 370 g/cm3, Isovue 370) was injected to ensure homogeneous enhancement of the entire coronary artery tree, followed by injection of saline. Each visible coronary artery was segmented to extract the luminal surfaces for hemodynamics calculation using a semi-automated segmentation software (QAngio CT RE, Medis, Leiden, The Netherlands). Participants' heart rate, diastolic, systolic, and mean aortic blood pressure were collected at the time of imaging, and participants' cardiac output were calculated retrospectively using syngo.via—Siemens Medical Solutions, Erlangen, Germany (Table 1).
Table 1.
Participant information at the time of scan
| Systolic blood pressure (mmHg) | Diastolic blood pressure (mmHg) | Stroke volume (ml) | Heart rate (bpm) | |
|---|---|---|---|---|
| Participant 1 | 142 | 88 | 82.9 | 51 |
| Participant 2 | 129 | 73 | 95.0 | 55 |
| Participant 3 | 102 | 68 | 99.9 | 56 |
| Participant 4 | 132 | 78 | 97.0 | 77 |
2.2 Model Construction and Mesh Generation.
Participant-specific models of the ascending aorta and coronary arteries were constructed from the segmentations described earlier and combined to form a full 3D anatomic model in simvascular, an open-source package for cardiovascular anatomic modeling, and finite element simulation.2 [37] An unstructured tetrahedral mesh was constructed for each using the open source Tetgen package included in simvascular. Branch points and areas of constriction were assigned to have a finer mesh resolution to capture the flow details, and the approximate total mesh size for each model was 1.3–2.0 × 106 elements. A mesh convergence study was performed for one model starting from 800k elements and went up to 1.3 × 106. Time averaged wall shear stress (TAWSS) along the centerline changed only by 3.2%.
2.3 Physiologic Boundary Conditions
Inlet BC: A custom aortic flowrate waveform for each model was generated by scaling a generic physiologic waveform obtained from the vascular model repository [38] to match the participant's cardiac output and heart rate provided by the clinical data.
Outlet aortic BC: A Windkessel RCR (R: resistance, C: capacitance) boundary condition was prescribed at the aortic outlet. The three elements of the Windkessel model consist of a proximal resistance (R) accounting for the viscous resistance of the downstream aorta, a capacitor (C) modeling the vessel compliance of the downstream vasculature, and a distal resistance (R) accounting the capillaries and venous circulation resistance.
Outlet coronary BC: A modified lumped parameter model was used to model the out of phase nature of coronary flow and pressure waveforms, which was previously described [15]. This model includes the intramyocardial pressure, which enforces the coronary circulation to be out of phase with the systemic circulation.
In all models, the coronary and aortic resistances were tuned such that the total coronary flow was approximately 4% of total cardiac output [39]. Resistances of the individual coronary outlets were weighted to be inversely proportional to their outlet area. In addition, the capacitance values were assigned to match previously reported ratios for the coronary arteries on the left and right side [15,40]. All resistance and capacitance values were iteratively tuned by running successive simulations until target participant physiological measurements listed in Table 1 and coronary flow ratios were well matched to be within 4.40 ± 1.30% of the total inlet flowrate. The resulting models successfully captured typical physiological flow features of the coronary circulation (Fig. 1).
Fig. 1.
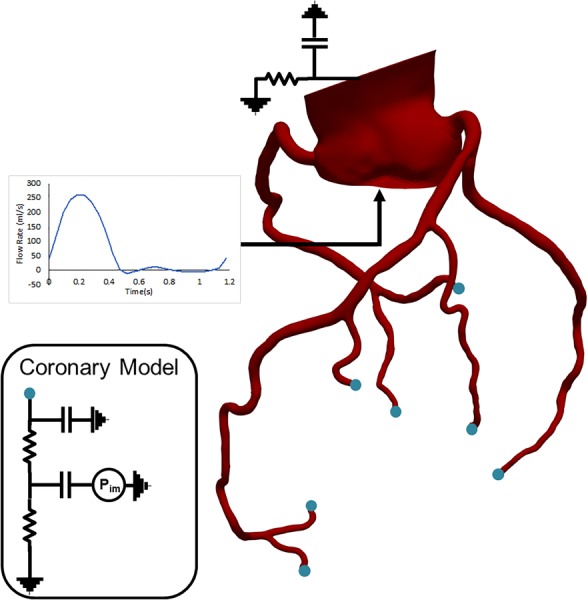
Coronary model with lump parameter network boundary conditions at the outlets and an inflow waveform at the inlet
2.4 Numerical Methods.
Blood was modeled to be a non-Newtonian fluid with dynamic viscosity of 0.04 g/(cm s) and density of 1.06 g/cm3. Simulations were performed for six full cardiac cycles to ensure independence from initial conditions. All the analyses were performed over the last cardiac cycle.
Rigid wall modeling: The incompressible weak form of the Navier–Stokes equations (Eq. (1)) were solved in the fluid domain for rigid wall models to find such that
| (1) |
where is fluid density, f is the body force, superscript denotes the fluid domain, is the trial solution space, is the trial weighing space, is the shear tensor, and w and are the weighting function for the momentum and continuity equations, respectively.
The numerical solution was performed using the svSolver finite element solver from the simvascular project, which uses the generalized-alpha method [41] for second-order time discretization, linear tetrahedral elements in space, and SUPG stabilization [42]. Backflow stabilization [43] was used to prevent divergence due to flow reversal at the outlets, and the bipartition method [44] with resistance-based preconditioning was employed for solution of the linear system resulting from finite element discretization. Implicit 0D/3D [45] coupling was used at the outlet boundaries.
Fluid–structure interaction (FSI)-wall modeling with the coupled momentum method (CMM-FSI): The elastic walls were modeled using CMM-FSI designed for modeling deformation of blood vessels in response to hemodynamic forces described in details in Figueroa et al. [46]. Briefly, this method couples the equation of deformation of the vessel wall at the variational level as boundary condition for the fluid domain replacing the no-slip boundary condition by a traction (i.e., Neuman) condition (Eq. (2)). represents the wall boundary, and the traction force is represented by tf
| (2) |
Therefore, expression for the unknown traction will be derived through the linear elastodynamic vessel wall equations. The wall stress is considered to be uniform through the thickness, assuming the vessel wall is thin and hence, the hemodynamic forces from the blood are then imposed as a body force in the linear elastodynamics equations of the wall. Using the same Eulerian frame, the degrees-of-freedom of the wall displacement are strongly coupled with the degrees-of-freedom of fluid, resulting in a monolithic formulation for the FSI problem on a fixed mesh. The resulting weak form of the CMM-FSI formulation is given as
| (3) |
where represents the fraction of the boundary where the given velocity field is represented by g as Dirichlet condition and is prescribed. represents Neuman boundary typically an outflow boundary, and the traction can be calculated. represents the lateral boundary of the fluid domain which represents the interface with the vessel wall. The wall material properties were considered to be uniform along all coronary 3D model with the following values which are in the range of previously reported values in the literature [47,48]: uniform wall thickness of , a Young's modulus of Pa, wall density of g/cm2, and Poison's ratio of and a shear constant of .
2.5 Shear Stress Calculation.
Instantaneous shear stress was calculated by and TAWSS by: where T is the cardiac cycle. Here, we calculate TAWSS because the time scales of some pathophysiological response to local hemodynamics such as vascular remodeling or changes in wall composition require many cardiac cycles. Time-averaged over cardiac cycles mimics this phenomenon.
2.6 Statistical Analysis.
To compare the shear stress calculated at each vessel and to perform a point by point and accurate comparison between the rigid and FSI wall models, each vessel was divided into 3 mm subsegments, where area-averaged TAWSS was calculated (Fig. S1A available in the Supplemental Materials on the ASME Digital Collection). In addition, we calculated TAWSS for each quadrant in the arterial cross section to investigate the role of wall elasticity at curved arteries in computed TAWSS calculation (Fig. S1B available in the Supplemental Materials on the ASME Digital Collection). A linear regression model was fit to assess the correlation between TAWSS calculated in rigid and FSI models, and a two-sample student t-test was used to report significance of this correlation. A two-sided p-value < 0.05 was considered to be significant.
3 Results
3.1 Wall Displacement Patterns in Fluid–Structure Interaction Models.
Wall deformation patterns were examined in the FSI models, as shown in a representative case in Fig. 2(a)–2(f), where the displacement (defined as total elastic motion of the vessel wall in response to blood flow) in the whole coronary artery network is presented at peak left coronary flow, midsystole, peak systole, early diastole, and mid-diastole, and time-averaged over the last cardiac cycle. The maximum over all displacement (accounting for transversal motion) was 0.97 cm in the aorta and 0.57 cm in the left main (LM) among all the branches including the left anterior descending (LAD), left circumflex (LCX), and right coronary artery (RCA) branches. It is important to note that the displacement reported here does not account for the coronary motion associated with the cardiac contraction. Hence, the total displacement in the coronaries is due to rigid body motion of the coronary ostium from radial expansion of the ascending aorta as well as the radial change of coronary arteries. The calculated maximum percent radial change (defined as the percent change between the CMM-FSI radius and the reference geometry) at LM, proximal RCA, LAD, and LCX did not exceed 5.72 ± 0.92% during the cardiac cycle (Figs. 3(a)–3(d)). Larger coronary arteries demonstrated higher displacement values.
Fig. 2.
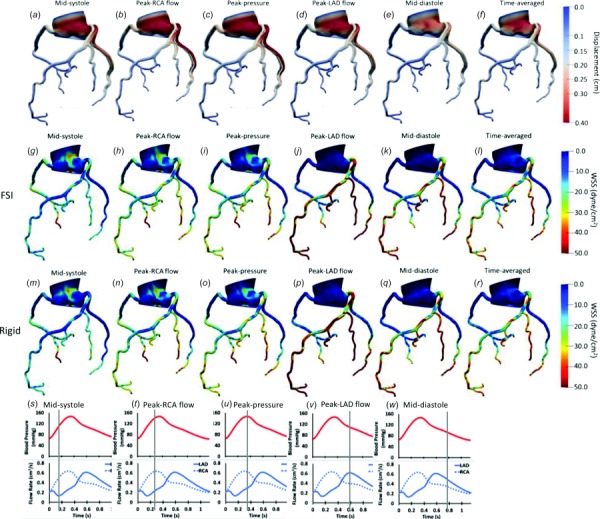
Displacement ((a)–(f)), wall shear stress contours in the FSI model ((g)–(l)), and rigid model ((m)–(r)) in 3D for a representative case. The contours are shown for participant 1 at midsystole (s), peak RCA flow (t), peak aortic pressure (u), peak LAD flow (v), and mid-diastole (w) in the cardiac cycle and time averaged through one cardiac cycle. Displacement of each coronary network is shown with respect to the original form (shown in gray). LAD: left anterior descending, RCA: right coronary artery.
Fig. 3.
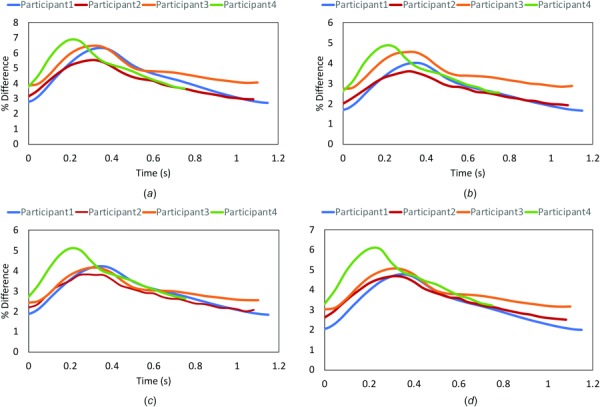
Percent radial displacement differences in the left main (a), proximal left anterior descending (pLAD) (b), proximal left circumflex (c), and proximal right coronary artery (d). The values of % radial change in a cardiac cycle in pLAD matches the literature value reported in Numao et al. [52] and Cho et al. [53]. The maximum percent difference (6.9%) does not exceed the 10% limitation of CMM methodology.
3.2 Wall Shear Stress Pattern.
Wall shear stress at five different time points (as explained above) as well as TAWSS are displayed for FSI (Figs. 2(g)–2(l)) and rigid (Figs. 2(m)–2(r)) models for a representative case. TAWSS values were relatively higher in the coronary arteries compared to the aorta in both rigid and FSI models (Fig. 4). In the coronary arteries, sections where the lumen narrows experienced higher TAWSS whereas low shear stress was observed before and after the narrowing due to disruption of laminar flow and formation of recirculatory regions. Similarly, low shear stress was observed at the outer walls of branch points. Larger vessels had higher WSS difference between the two models due to the higher displacement in larger arteries.
Fig. 4.
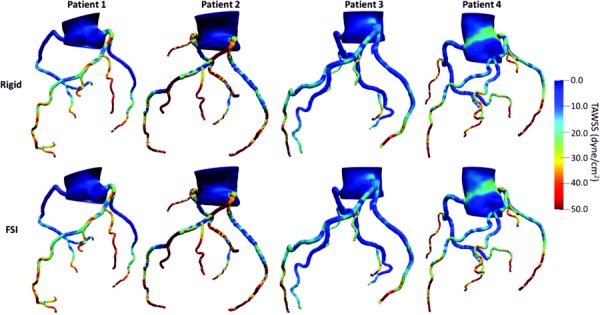
TAWSS in complete coronary network of four participants for rigid (upper panel) and FSI (lower panel) models
3.3 Comparison of Rigid Versus Fluid–Structure Interaction.
To better view the 3D shear stress distribution in all vessels circumferentially, an unwrapped WSS contour from the vessel surface are mapped onto a two-dimensional (2D) rectangle along the vessel centerline. WSS was generally higher at each time point at the cardiac cycle in the FSI models compared to the rigid wall models when viewed in an unwrapped configuration (Figs. 5 (pLAD) and 6 (pRCA)). However, TAWSS had similar spatial patterns and values in both models. A similar profile was observed in the 3D models of coronary arteries (Fig. 2). In pLAD where the luminal narrowing and plaque was present proximally, shear stress was higher compared to the regions without luminal narrowing (Fig. 5). With the lumen growing back to its natural diameter, the higher TAWSS (≥ 50 dynes/cm2) regions was replaced by low TAWSS (≤ 10.5 dynes/cm2). This is due to regions of recirculation immediately after the stenosis creating flow reversal and low wall shear stress. Within high WSS region in the luminal narrowing, the outer wall experienced higher WSS relative to the inner wall.
Fig. 5.
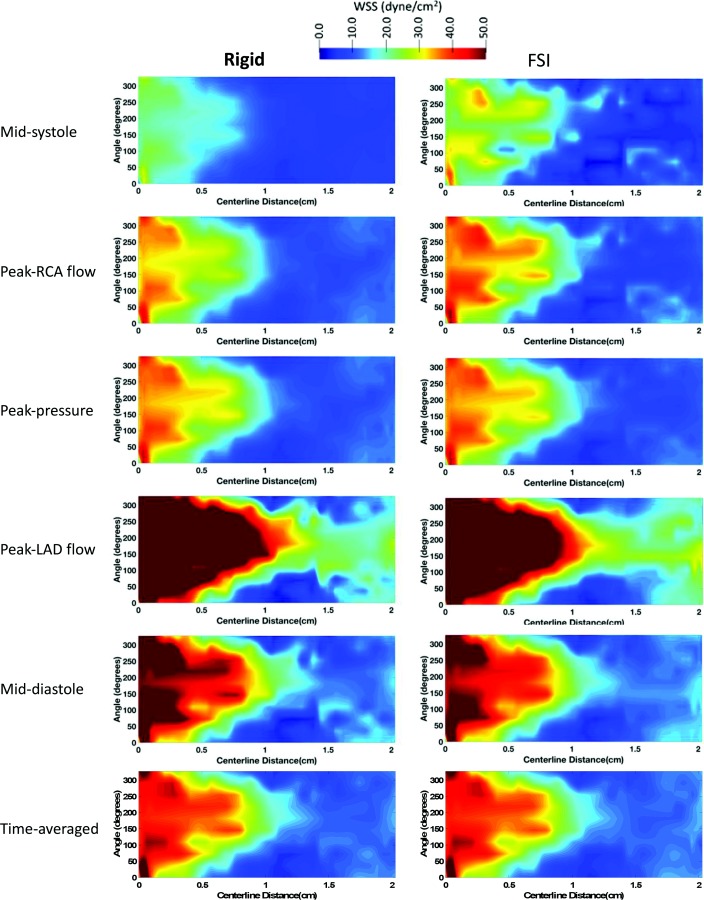
2D unwrapped map of WSS in pLAD of a representative case (participant 1) at midsystole, peak RCA flow, peak pressure, peak LAD flow, mid-diastole, and averaged through the last cardiac cycle for the rigid (left column) and FSI (right column) models. Time points along the cardiac are shown in Figs. 2(s)–2(w). LAD: left anterior descending, RCA: right coronary artery.
Fig. 6.
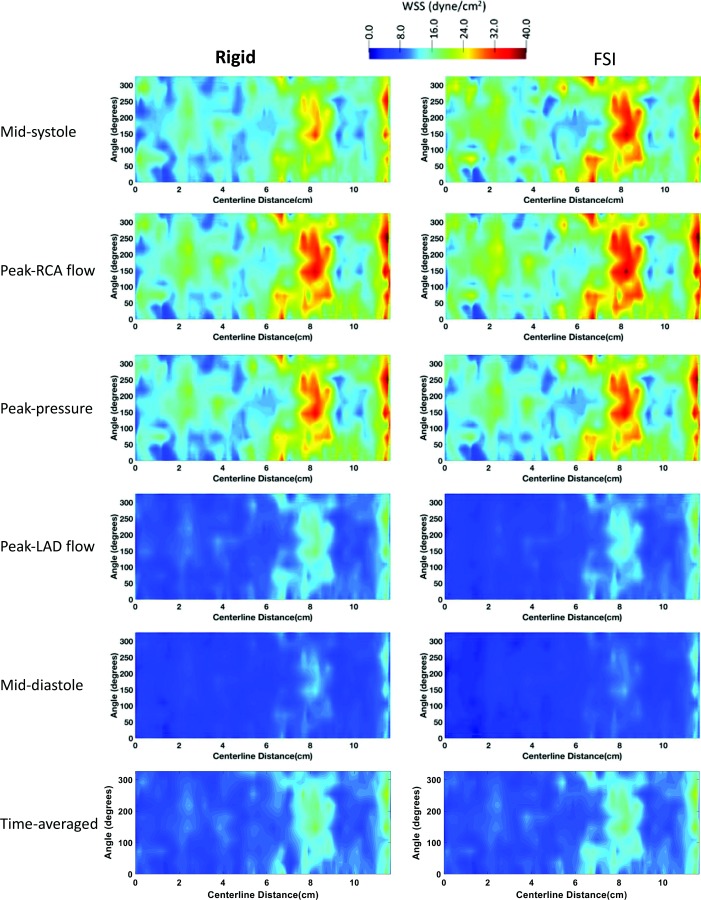
2D unwrapped map of WSS in pRCA of a representative case (participant 1) at midsystole, peak RCA flow, peak pressure, peak LAD flow, mid-diastole, and averaged through the last cardiac cycle for the rigid (left column) and FSI (right column) models. Time points along the cardiac are shown in Figs. 2(s)–2(w). LAD: left anterior descending, RCA: right coronary artery.
When divided into 3 mm subsegments (SB), a total of 704 coronary SB was analyzed to perform a head to head comparison of TAWSS in rigid and FSI models (Fig. 7(a)), there was excellent Pearson correlation of (r = 0.99) and the p-value between the two TAWSS calculation was found to be nonsignificant (p = 0.5). The mean values of TAWSS were found to be 15.6 ± 10.6 and 16 ± 10.5 dyne/cm2 in the rigid and FSI models, respectively.
Fig. 7.
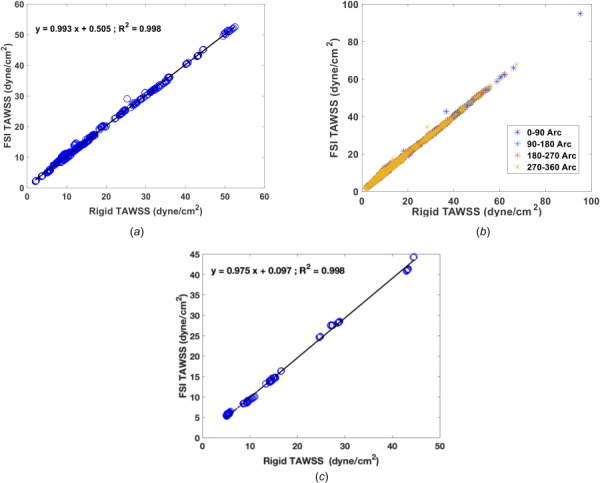
(a) Correlation of TAWSS at each 3 mm subsegment in all four participants with a total of 704 subsegments between the rigid and FSI models. (b) Correlation of TAWSS for four quadrant at each cross section in the rigid and FSI model. TAWSS had an excellent correlation of r = 0.99 in both subsegment and subarc analysis. (c) TAWSS comparison between the rigid wall model and an FSI model with Young's modulus of E = 105 Pa. In total of 170 3 mm subsegments, the Pearson correlation between the calculated TAWSS in the rigid and FSI models was r = 0.99.
When divided into 90 deg arcs, in the total of 704 SB, the mean TAWSS values were (16.3 ± 11.7, 16.6 ± 11.6; p = 0.56), (15.7 ± 10.6, 16.1 ± 10.5; p = 0.51), (15.4 ± 10.4, 15.8 ± 10.4; p = 0.50), and (15.7 ± 10.9, 16.1 ± 10.9; p = 0.53) dynes/cm2 for (rigid, FSI; p-value) models at 0–90, 90–180, 180–270, and 270–360 arc angles. Similar to the SB analysis, there was excellent agreement with Pearson correlations of r = 0.99 in all quadrants, with no significant differences when comparing the arch specific values in the rigid and FSI models (Fig. 7(b)).
4 Discussion
In this study, we investigated the role of wall elasticity on hemodynamics in patient-specific simulations based on coronary CTA imaging in four patients. CFD patient-specific modeling was implemented, in which boundary conditions were tuned to match each participants' clinical measurements taken at the time of imaging. The effect of wall elasticity was systematically compared in complete coronary artery networks with branches and in multiple participants. Wall shear stress patterns matched to what previous intravascular ultrasound imaging-based studies [9,10,33] observed where high WSS was present at the luminal narrowing regions and low WSS was observed immediately after relatively mild to high stenosis.
The instantaneous values of WSS (at each point of cardiac cycle) were slightly different when comparing the FSI and rigid wall models. This can be explained by the presence of wall deformation, which produces flow and pressure waves which propagate at a finite speed through the arteries, in contrast to the rigid cases which produces instantaneous wave propagation. For example, we saw slightly higher WSS values in the FSI model at midsystole when the LAD flow is at its minimum (Fig. 5), at which time the FSI wall reacts to the lack of blood supply and recoils, resulting in higher WSS values. On the contrary, the rigid wall catches up with the flow acceleration at peak LAD flow and the higher WSS propagates faster along the vessel. However, when looking at the TAWSS, the wave propagation speed effect dissipates and results in nearly identical TAWSS values along the vessel in the rigid and FSI models. This is evident in Fig. 7(a), where a subsegment analysis of TAWSS along the coronary arteries were compared, resulting an almost perfect match (r = 0.99 and a y intercept of 0.99). The findings are consistent with observations of prior studies [20,23–25] focusing on single vessels (i.e., RCA and LAD with no branches) in which TAWSS values had similar values with slight differences at select points in the cardiac cycle. In a further analysis, we studied the WSS at each quadrant in the cross section to test if wall FSI has an effect in highly curved vessels. Although WSS was higher at the outer walls (Fig. 7(b)) and lower at the inner walls, this trend persisted in both rigid and FSI models. Therefore, there was no significant difference in the arc-averaged TAWSS values in the two models implying that wall elasticity has a negligible effect in TAWSS calculation in highly curved arteries. This is also consistent with previous studies comparing WSS values at the inner and outer wall investigating the effect of wall deformation on WSS [20,26].
Limitations: In this study, we assumed blood to be a Newtonian fluid; this is a valid assumption in arteries larger than capillaries where the shear rate is relatively low for blood to behave as a Newtonian fluid.
Another limitation is the selection of CMM-FSI to model the fluid–structure interaction. The arbitrary Lagrangian–Eulerian (ALE) models are considered to be the “gold standard” models for deformable wall simulations. These models are significantly more computationally expensive, however, the CMM-FSI has been shown to be reliable and with comparable accuracy of ALE-FSI models for modest membrane-mode displacements (<10% of vessel radius) [49]. The percent radial displacement does not exceed 6.9% (in LM) through the cardiac cycle in all the vessels which is consistent with the CMM-FSI modeling assumption (Fig. 3). In addition, CMM-FSI modeling has been used in other studies to model deformable walls in coronary arteries [13,50,51]. Furthermore, with this CMM model we were able to capture the radial change in proximal arteries (i.e., pLAD, pRCA, and pLCX) within the range reported in literature [52,53] (Fig. 3(b)). Selection of uniform wall thickness and material properties (homogeneous isotropic) in both the aorta and coronary arteries is another limitation of this study. Studies in aortic aneurysms [54] and atherosclerotic coronary arteries [55] have shown that including anisotropic material models predicted higher wall stress compared to isotropic materials. This suggests that incorporation of anisotropic material models is likely to make the artery less deformable and would further accentuate the insignificance of FSI on coronary hemodynamics. To test how Young's elastic modulus effect TAWSS, an additional sensitivity analysis was performed in participant 1. We repeated the FSI simulation with the elastic modulus one order of magnitude lower than what is selected in all simulations (i.e., E = 105 Pa versus E = 106). In total of 170 3 mm subsegments (Fig. 7(c)), the Pearson correlation between the calculated TAWSS in the rigid and FSI models were r = 0.99 (slope of 0.97 and y-intercept of 0.097). The later analysis shows that reducing the Young's modulus by ten times does not change TAWSS values, significantly. In addition, we chose a wall thickness of 0.05 cm for coronary arteries, which is consistent with reported values in literature [56]. However, although the ascending aorta has about double the wall thickness than the coronaries [57], we assumed the aorta to have the same thickness since the target vessels were coronary arteries and we only included a small portion of the aorta in our model. Adding variable wall thickness and material property may be implemented in future studies. In addition, the material model was considered to be a linear elastic model; however, other more realistic nonlinear models in coronary arteries have been previously [58]. Furthermore, as mentioned in the Results section, the wall displacement reported in all FSI models include the rigid body motion to the aortic contraction and does not account for cardiac contraction motion. Finally, fixed boundary condition may have an effect of adding artificial wave propagation effects, though this effect would be larger with larger deformations. However, from inspection, the effects of clamping the outlets are limited to a fairly small region near the outlets. Future work may be done to inspect on the effect of fixed boundary condition on calculation of TAWSS.
In conclusion, the focus of this study was to investigate on the effect of coronary wall deformability in calculation of wall shear stress in coronary CTA-based participant specific CFD modeling. Our models show no significant differences in time-averaged wall shear stress justifying using rigid wall models for future larger population studies.
Supplementary Material
Supplementary PDF
Footnotes
References
- [1]. Benjamin, E. J. , Blaha, M. J. , Chiuve, S. E. , and Cushman, M. , 2017, “ Heart Disease and Stroke Statistics—2017 Update,” Circulation, 135(10), e146–e603. 10.1161/CIR.0000000000000485 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2]. Mozaffarian, D. , Benjamin, E. J. , Go, A. S. , Arnett, D. K. , Blaha, M. J. , Cushman, M. , Das, S. R. , de Ferranti, S. , Després, J.-P. , Fullerton, H. J. , Howard, V. J. , Huffman, M. D. , Isasi, C. R. , Jiménez, M. C. , Judd, S. E. , Kissela, B. M. , Lichtman, J. H. , Lisabeth, L. D. , Liu, S. , Mackey, R. H. , Magid, D. J. , McGuire, D. K. , Mohler, E. R. , Moy, C. S. , Muntner, P. , Mussolino, M. E. , Nasir, K. , Neumar, R. W. , Nichol, G. , Palaniappan, L. , Pandey, D. K. , Reeves, M. J. , Rodriguez, C. J. , Rosamond, W. , Sorlie, P. D. , Stein, J. , Towfighi, A. , Turan, T. N. , Virani, S. S. , Woo, D. , Yeh, R. W. , and Turner, M. B. , 2016, “ Executive Summary: Heart Disease and Stroke Statistics-2016 Update: A Report From the American Heart Association,” Circulation, 133(4), pp. 447–454. 10.1161/CIR.0000000000000366 [DOI] [PubMed] [Google Scholar]
- [3]. Parikh, N. I. , Gona, P., Larson, M. G., Fox, C. S., Benjamin, E. J., Murabito, J. M., O'Donnell, C. J., Vasan, R. S., and Levy, D. 2010, “ Long-Term Trends in Myocardial Infarction Incidence and Case-Fatality in the National Heart, Lung, and Blood Institute's Framingham Heart Study,” Circulation, 119(9), pp. 1203–1210. 10.1161/CIRCULATIONAHA.108.825364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Bittencourt, M. S. , Hulten, E. , Ghoshhajra, B. , O'Leary, D. , Christman, M. P. , Montana, P. , Truong, Q. A. , Steigner, M. , Murthy, V. L. , Rybicki, F. J. , Nasir, K. , Gowdak, L. H. W. , Hainer, J. , Brady, T. J. , Di Carli, M. F. , Hoffmann, U. , Abbara, S. , and Blankstein, R. , 2014, “ Prognostic Value of Nonobstructive and Obstructive Coronary Artery Disease Detected by Coronary Computed Tomography Angiography to Identify Cardiovascular Events,” Circ. Cardiovasc. Imaging, 7(2), pp. 282–291. 10.1161/CIRCIMAGING.113.001047 [DOI] [PubMed] [Google Scholar]
- [5]. Hadamitzky, M. , Achenbach, S. , Al-Mallah, M. , Berman, D. , Budoff, M. , Cademartiri, F. , Callister, T. , Chang, H.-J. , Cheng, V. , Chinnaiyan, K. , Chow, B. J. W. , Cury, R. , Delago, A. , Dunning, A. , Feuchtner, G. , Gomez, M. , Kaufmann, P. , Kim, Y.-J. , Leipsic, J. , Lin, F. Y. , Maffei, E. , Min, J. K. , Raff, G. , Shaw, L. J. , Villines, T. C. , and Hausleiter, J. ,. 2013, “ Optimized Prognostic Score for Coronary Computed Tomographic Angiography: Results From the CONFIRM Registry (COronary CT Angiography Evaluation for Clinical Outcomes: An International Multicenter Registry,” J. Am. Coll. Cardiol., 62(5), pp. 468–476. 10.1016/j.jacc.2013.04.064 [DOI] [PubMed] [Google Scholar]
- [6]. Melikian, N. , De Bondt, P. , Tonino, P. , De Winter, O. , Wyffels, E. , Bartunek, J. , Heyndrickx, G. R. , Fearon, W. F. , Pijls, N. H. J. , Wijns, W. , and De Bruyne, B. , 2010, “ Fractional Flow Reserve and Myocardial Perfusion Imaging in Patients With Angiographic Multivessel Coronary Artery Disease,” JACC Cardiovasc. Interventions, 3(3), pp. 307–314. 10.1016/j.jcin.2009.12.010 [DOI] [PubMed] [Google Scholar]
- [7]. Koo, B.-K. , Erglis, A. , Doh, J.-H. , Daniels, D. V. , Jegere, S. , Kim, H.-S. , Dunning, A. , DeFrance, T. , Lansky, A. , Leipsic, J. , and Min, J. K. , 2011, “ Diagnosis of Ischemia-Causing Coronary Stenoses by Noninvasive Fractional Flow Reserve Computed From Coronary Computed Tomographic Angiograms: Results From the Prospective Multicenter Discover-Flow (Diagnosis of Ischemia-Causing Stenoses Obtained Via Noni,” J. Am. Coll. Cardiol., 58(19), pp. 1989–1997. 10.1016/j.jacc.2011.06.066 [DOI] [PubMed] [Google Scholar]
- [8]. Choi, G. , Lee, J. M. , Kim, H.-J. , Park, J.-B. , Sankaran, S. , Otake, H. , Doh, J.-H. , Nam, C.-W. , Shin, E.-S. , Taylor, C. A. , and Koo, B.-K. , 2015, “ Coronary Artery Axial Plaque Stress and Its Relationship With Lesion Geometry Application of Computational Fluid Dynamics to Coronary CT Angiography,” JACC Cardiovasc. Imaging, 8(10), pp. 1156–1166. 10.1016/j.jcmg.2015.04.024 [DOI] [PubMed] [Google Scholar]
- [9]. Eshtehardi, P. , McDaniel, M. C. , Suo, J. , Dhawan, S. S. , Timmins, L. H. , Binongo, J. N. G. , Golub, L. J. , Corban, M. T. , Finn, A. V. , Oshinski, J. N. , Quyyumi, A. A. , Giddens, D. P. , and Samady, H. , 2012, “ Association of Coronary Wall Shear Stress With Atherosclerotic Plaque Burden, Composition, and Distribution in Patients With Coronary Artery Disease,” J. Am. Heart Assoc., 1(4), p. e002543. 10.1161/JAHA.112.002543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Stone, P. H. , Maehara, A. , Coskun, A. U. , Maynard, C. C. , Zaromytidou, M. , Siasos, G. , Andreou, I. , Fotiadis, D. , Stefanou, K. , Papafaklis, M. , Michalis, L. , Lansky, A. J. , Mintz, G. S. , Serruys, P. W. , Feldman, C. L. , and Stone, G. W. , 2018, “ Role of Low Endothelial Shear Stress and Plaque Characteristics in the Prediction of Nonculprit Major Adverse Cardiac Events: The PROSPECT Study,” JACC Cardiovasc. Imaging, 11(3), pp. 462–471. 10.1016/j.jcmg.2017.01.031 [DOI] [PubMed] [Google Scholar]
- [11]. Lu, M. T. , Ferencik, M., Roberts, R. S., Lee, K. L., Ivanov, A., Adami, E., Mark, D. B, Jaffer, F. A., Leipsic, J. A, Douglas, P. S., and Hoffmann, U., 2016, “ Noninvasive FFR Derived From Coronary CT Angiography. Management and Outcomes in the PROMISE Trial,” JACC Cardiovasc. Imaging, 10(11), pp. 1350–1358. 10.1016/j.jcmg.2016.11.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12]. Nørgaard, B. L. , Leipsic, J. , Gaur, S. , Seneviratne, S. , Ko, B. S. , Ito, H. , Jensen, J. M. , Mauri, L. , De Bruyne, B. , Bezerra, H. , Osawa, K. , Marwan, M. , Naber, C. , Erglis, A. , Park, S.-J. , Christiansen, E. H. , Kaltoft, A. , Lassen, J. F. , Bøtker, H. E. , and Achenbach, S. , 2014, “ Diagnostic Performance of Noninvasive Fractional Flow Reserve Derived From Coronary Computed Tomography Angiography in Suspected Coronary Artery Disease: The NXT Trial (Analysis of Coronary Blood Flow Using CT Angiography: Next Steps,” J. Am. Coll. Cardiol., 63(12), pp. 1145–1155. 10.1016/j.jacc.2013.11.043 [DOI] [PubMed] [Google Scholar]
- [13]. Tran, J. S. , Schiavazzi, D. E. , Ramachandra, A. B. , Kahn, A. M. , and Marsden, A. L. , 2016, “ Automated Tuning for Parameter Identification and Uncertainty Quantification in Multi-Scale Coronary Simulations,” Comput. Fluids, 27(5), pp. 128–138. 10.1016/j.compfluid.2016.05.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Sankaran, S. , Esmaily Moghadam, M. , Kahn, A. M. , Tseng, E. E. , Guccione, J. M. , and Marsden, A. L. , 2012, “ Patient-Specific Multiscale Modeling of Blood Flow for Coronary Artery Bypass Graft Surgery,” Ann. Biomed. Eng., 40(10), pp. 2228–2242. 10.1007/s10439-012-0579-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Kim, H. J. , Vignon-Clementel, I. E. , Coogan, J. S. , Figueroa, C. A. , Jansen, K. E. , and Taylor, C. A. , 2010, “ Patient-Specific Modeling of Blood Flow and Pressure in Human Coronary Arteries,” Ann. Biomed. Eng., 38(10), pp. 3195–3209. 10.1007/s10439-010-0083-6 [DOI] [PubMed] [Google Scholar]
- [16]. Lantz, J. , Renner, J. , and Karlsson, M. , 2011, “ Wall Shear Stress in a Subject Specific Human Aorta—Influence of Fluid-Structure Interaction,” Int. J. Appl. Mech., 3(4), pp. 759–778. 10.1142/S1758825111001226 [DOI] [Google Scholar]
- [17]. Liu, Y. , Lai, Y. , Nagaraj, A. , Kane, B. , Hamilton, A. , Greene, R. , McPherson, D. D. , and Chandran, K. B. , 2001, “ Pulsatile Flow Simulation in Arterial Vascular Segments With Intravascular Ultrasound Images,” Med. Eng. Phys., 23(8), pp. 583–595. 10.1016/S1350-4533(01)00088-1 [DOI] [PubMed] [Google Scholar]
- [18]. Zhao, S. Z. , Xu, X. Y. , Hughes, A. D. , Thom, S. A. , Stanton, A. V. , Ariff, B. , and Long, Q. , 2000, “ Blood Flow and Vessel Mechanics in a Physiologically Realistic Model of a Human Carotid Arterial Bifurcation,” J. Biomech., 33(8), pp. 975–984. 10.1016/S0021-9290(00)00043-9 [DOI] [PubMed] [Google Scholar]
- [19]. Xenos, M. , Labropoulos, N. , Rambhia, S. , Alemu, Y. , Einav, S. , Tassiopoulos, A. , Sakalihasan, N. , and Bluestein, D. , 2015, “ Progression of Abdominal Aortic Aneurysm Towards Rupture: Refining Clinical Risk Assessment Using a Fully Coupled Fluid–Structure Interaction Method,” Ann. Biomed. Eng., 43(1), pp. 139–153. 10.1007/s10439-014-1224-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Torii, R. , Oshima, M. , Kobayashi, T. , Takagi, K. , and Tezduyar, T. E. , 2008, “ Fluid-Structure Interaction Modeling of a Patient-Specific Cerebral Aneurysm: Influence of Structural Modeling,” Comput. Mech., 43(1), pp. 151–159. 10.1007/s00466-008-0325-8 [DOI] [Google Scholar]
- [21]. Bazilevs, Y. , Hsu, M.-C. , Zhang, Y. , Wang, W. , Liang, X. , Kvamsdal, T. , Brekken, R. , and Isaksen, J. G. , 2010, “ A Fully-Coupled Fluid-Structure Interaction Simulation of Cerebral Aneurysms,” Comput. Mech., 46(1), pp. 3–16. 10.1007/s00466-009-0421-4 [DOI] [Google Scholar]
- [22]. Gutierrez, N. G. , Kahn, A. , Burns, J. C. , and Marsden, A. L. , 2018, “ Computational Blood Flow Simulations in Kawasaki Disease Patients: Insight Into Coronary Artery Aneurysm Hemodynamics,” Global Cardiol. Sci. Pract., 2017(3), e201729. 10.21542/gcsp.2017.29 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23]. Zeng, D. , Ding, Z. , Friedman, M. H. , and Ross Ethier, C. , 2003, “ Effects of Cardiac Motion on Right Coronary Artery Hemodynamics,” Ann. Biomed. Eng., 31(4), pp. 420–429. 10.1114/1.1560631 [DOI] [PubMed] [Google Scholar]
- [24]. Torii, R. , Torii, R., Keegan, J., Wood, N. B., Dowsey, A. W., Hughes, A. D., Yang, G. Z., Firmin, D. N., McG Thom, S. A., and Xu, X. Y., 2009, “ The Effect of Dynamic Vessel Motion on Haemodynamic Parameters in the Right Coronary Artery: A Combined MR and CFD Study,” Br. J. Radiol., 82, pp. S24–S32. 10.1259/bjr/62450556 [DOI] [PubMed] [Google Scholar]
- [25]. Meza, D. , Rubenstein, D. A. , and Yin, W. A. , 2018, “ Fluid–Structure Interaction Model of the Left Coronary Artery,” ASME J. Biomech. Eng., 140(12), p. 121006. 10.1115/1.4040776 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26]. Qiu, Y. , and Tarbell, J. M. , 2000, “ Numerical Simulation of Pulsatile Flow in a Compliant Curved Tube,” ASME J. Biomech. Eng., 122(1), pp. 77–85. 10.1115/1.429629 [DOI] [PubMed] [Google Scholar]
- [27]. Malvè, M. , García, A. , Ohayon, J. , and Martínez, M. A. , 2012, “ Unsteady Blood Flow and Mass Transfer of a Human Left Coronary Artery Bifurcation: FSI vs. CFD,” Int. Commun. Heat Mass Transfer, 39(6), pp. 745–751. 10.1016/j.icheatmasstransfer.2012.04.009 [DOI] [Google Scholar]
- [28]. Vergallo, R. , Papafaklis, M. I. , Yonetsu, T. , Bourantas, C. V. , Andreou, I. , Wang, Z. , Fujimoto, J. G. , McNulty, I. , Lee, H. , Biasucci, L. M. , Crea, F. , Feldman, C. L. , Michalis, L. K. , Stone, P. H. , and Jang, I.-K. , 2014, “ Endothelial Shear Stress and Coronary Plaque Characteristics in Humans Combined Frequency-Domain Optical Coherence Tomography and Computational Fluid Dynamics Study,” Circ. Cardiovasc. Imaging, 7(6), pp. 905–911. 10.1161/CIRCIMAGING.114.001932 [DOI] [PubMed] [Google Scholar]
- [29]. Lee, J. M. , Choi, G., Koo, B.-K., Hwang, D., Park, J., Zhang, J., Kim, K.,-J., Tong, Y., Kim, H. J., Grady, L., Hyung, J., Nam, C., W., Shin, E., S., Cho, Y. S., Choi, S., Y., Chun, E. J., Choi, J., H., Nørgaard, B., L., and Kim, H. S., 2018, “ Identification of High-Risk Plaques Destined to Cause Acute Coronary Syndrome Using Coronary Computed Tomographic Angiography and Computational Fluid Dynamics,” JACC Cardiovasc. Imaging. (in press). 10.1016/j.jcmg.2018.01.023 [DOI] [PubMed] [Google Scholar]
- [30]. Chatzizisis, Y. S. , Jonas, M. , Coskun, A. U. , Beigel, R. , Stone, B. V. , Maynard, C. , Gerrity, R. G. , Daley, W. , Rogers, C. , Edelman, E. R. , Feldman, C. L. , and Stone, P. H. , 2008, “ Prediction of the Localization of High-Risk Coronary Atherosclerotic Plaques on the Basis of Low Endothelial Shear Stress-an Intravascular Ultrasound and Histopathology Natural History Study,” Circulation, 117(8), pp. 993–1002. 10.1161/CIRCULATIONAHA.107.695254 [DOI] [PubMed] [Google Scholar]
- [31]. Chatzizisis, Y. S. , Coskun, A. U. , Jonas, M. , Edelman, E. R. , Feldman, C. L. , and Stone, P. H. , 2007, “ Role of Endothelial Shear Stress in the Natural History of Coronary Atherosclerosis and Vascular Remodeling. Molecular, Cellular, and Vascular Behavior,” J. Am. Coll. Cardiol., 49(25), pp. 2379–2393. 10.1016/j.jacc.2007.02.059 [DOI] [PubMed] [Google Scholar]
- [32]. Wootton, D. M. , and Ku, D. N. , 1999, “ Fluid Mechanics of Vascular Systems, Diseases, and Thrombosis,” Annu. Rev. Biomed. Eng., 1, pp. 299–329. 10.1146/annurev.bioeng.1.1.299 [DOI] [PubMed] [Google Scholar]
- [33]. Stone, P. H. , Coskun, A. U. , Kinlay, S. , Clark, M. E. , Sonka, M. , Wahle, A. , Ilegbusi, O. J. , Yeghiazarians, Y. , Popma, J. J. , Orav, J. , Kuntz, R. E. , and Feldman, C. L. , 2003, “ Effect of Endothelial Shear Stress on the Progression of Coronary Artery Disease, Vascular Remodeling, and In-Stent Restenosis in Humans: In Vivo 6-Month Follow-Up Study,” Circulation, 108(4), pp. 438–444. 10.1161/01.CIR.0000080882.35274.AD [DOI] [PubMed] [Google Scholar]
- [34]. Maurovich-Horvat, P. , Ferencik, M. , Voros, S. , Merkely, B. , and Hoffmann, U. , 2014, “ Comprehensive Plaque Assessment by Coronary CT Angiography,” Nat. Rev. Cardiol., 11(7), pp. 390–402. 10.1038/nrcardio.2014.60 [DOI] [PubMed] [Google Scholar]
- [35]. Lo, J. , Lu, M. T., Ihenachor, E. J., Wei, J., Looby, S. E., Fitch, K. V., Oh, J., Zimmerman, C. O., Hwang, J., Abbara, S., Plutzky, J., Robbins, G., Tawakol, A., Hoffmann, U., and Grinspoon, S. K., 2015, “ Effects of Statin Therapy on Coronary Artery Plaque Volume and High-Risk Plaque Morphology in HIV-Infected Patients With Subclinical Atherosclerosis: A Randomised, Double-Blind, Placebo-Controlled Trial,” Lancet HIV, 2(2), pp. 52–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Abbara, S. , Arbab-Zadeh, A. , Callister, T. Q. , Desai, M. Y. , Mamuya, W. , Thomson, L. , and Weigold, W. G. , 2009, “ SCCT Guidelines for Performance of Coronary Computed Tomographic Angiography: A Report of the Society of Cardiovascular Computed Tomography Guidelines Committee,” J. Cardiovasc. Comput. Tomogr., 3(3), pp. 190–204. 10.1016/j.jcct.2009.03.004 [DOI] [PubMed] [Google Scholar]
- [37]. Updegrove, A. , Wilson, N. M. , Merkow, J. , Lan, H. , Marsden, A. L. , and Shadden, S. C. , 2017, “ SimVascular: An Open Source Pipeline for Cardiovascular Simulation,” Ann. Biomed. Eng., 45(3), pp. 525–541. 10.1007/s10439-016-1762-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38]. Wilson, N. M. , Ortiz, A. K. , and Johnson, A. B. , 2013, “ The Vascular Model Repository: A Public Resource of Medical Imaging Data and Blood Flow Simulation Results,” ASME J. Med. Device, 7(4), p. 040923. 10.1115/1.4025983 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Johnson, K. , Sharma, P. , and Oshinski, J. , 2008, “ Coronary Artery Flow Measurement Using Navigator Echo Gated Phase Contrast Magnetic Resonance Velocity Mapping at 3.0 T,” ASME J. Biomech. Eng., 41(3), pp. 595–602. 10.1016/j.jbiomech.2007.10.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40]. Burattini, R. , Sipkema, P. , van Huis, G. A. , and Westerhof, N. , 1985, “ Identification of Canine Coronary Resistance and Intramyocardial Compliance on the Basis of the Waterfall Model,” Ann. Biomed. Eng., 13(5), pp. 385–404. 10.1007/BF02407768 [DOI] [PubMed] [Google Scholar]
- [41]. Chung, J. , and Hulbert, G. M. , 1993, “ A Time Integration Algorithm for Structural Dynamics With Improved Numerical Dissipation: The Generalized-Alpha Method,” ASME J. Appl. Mech., 60(2), pp. 371–375. 10.1115/1.2900803 [DOI] [Google Scholar]
- [42]. Brooks, A. N. , and Hughes, T. J. R. , 1982, “ Streamline Upwind/Petrov-Galerkin Formulations for Convection Dominated Flows With Particular Emphasis on the Incompressible Navier-Stokes Equations,” Comput. Methods Appl. Mech. Eng., 32(1–3), pp. 199–259. 10.1016/0045-7825(82)90071-8 [DOI] [Google Scholar]
- [43]. Esmaily Moghadam, M. , Bazilevs, Y. , Hsia, T. Y. , Vignon-Clementel, I. E. , and Marsden, A. L. , 2011, “ A Comparison of Outlet Boundary Treatments for Prevention of Backflow Divergence With Relevance to Blood Flow Simulations,” Comput. Mech., 48(3), pp. 277–291. 10.1007/s00466-011-0599-0 [DOI] [Google Scholar]
- [44]. Esmaily-Moghadam, M. , Bazilevs, Y. , and Marsden, A. L. , 2013, “ A New Preconditioning Technique for Implicitly Coupled Multidomain Simulations With Applications to Hemodynamics,” Comput. Mech., 52(5), pp. 1141–1152. 10.1007/s00466-013-0868-1 [DOI] [Google Scholar]
- [45]. Esmaily Moghadam, M. , Vignon-Clementel, I. E. , Figliola, R. , and Marsden, A. L. , 2013, “ A Modular Numerical Method for Implicit 0D/3D Coupling in Cardiovascular Finite Element Simulations,” J. Comput. Phys., 244, pp. 63–79. 10.1016/j.jcp.2012.07.035 [DOI] [Google Scholar]
- [46]. Figueroa, C. A. , Vignon-Clementel, I. E. , Jansen, K. E. , Hughes, T. J. R. , and Taylor, C. A. , 2006, “ A Coupled Momentum Method for Modeling Blood Flow in Three-Dimensional Deformable Arteries,” Comput. Methods Appl. Mech. Eng., 195(41–43), pp. 5685–5706. 10.1016/j.cma.2005.11.011 [DOI] [Google Scholar]
- [47]. Lu, X. , Pandit, A. , and Kassab, G. S. , 2004, “ Biaxial Incremental Homeostatic Elastic Moduli of Coronary Artery: Two-Layer Model,” Am. J. Physiol.: Heart Circ. Physiol., 287(4), pp. H1663–H1669. 10.1152/ajpheart.00226.2004 [DOI] [PubMed] [Google Scholar]
- [48]. Hozapfel, G. A. , Sommer, G. , Gasser, C. T. , and Regitnig, P. , 2005, “ Determination of Layer-Specific Mechanical Properties of Human Coronary Arteries With Nonatherosclerotic Intimal Thickening and Related Constitutive Modeling,” Am. J. Physiol.: Heart Circ. Physiol., 289, pp. 2048–2058. 10.1152/ajpheart.00934.2004 [DOI] [PubMed] [Google Scholar]
- [49]. Tran, J. , Vedula, V. , Baeumler, K. , and Marsden, A. L. , 2018, “ A Comparison of Fluid-Structure-Interaction Approaches to Blood Flow Modeling With Vessel Prestress,” World Congress on Computational Mechanics, New York. [Google Scholar]
- [50].GBD 2015 Disease and Injury Incidence and Prevalence Collaborators, 2016, “ Global, Regional, and National Incidence, Prevalence, and Years Lived With Disability for 310 Diseases and Injuries, 1990–2015: A Systematic Analysis for the Global Burden of Disease Study 2015,” Lancet, 388, pp. 1545–1602. 10.1016/S0140-6736(16)31678-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51]. Tran, J. S. , Schiavazzi, D. E. , Kahn, A. M. , and Marsden, A. L. , 2019, “ Uncertainty Quantification of Simulated Biomechanical Stimuli in Coronary Artery Bypass Grafts,” Comput. Methods Appl. Mech. Eng., 345, pp. 402–428. 10.1016/j.cma.2018.10.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52]. Numao, T. , Ogawa, K. , Fujinuma, H. , and Furuya, N. , 1997, “ Pulsatile Diameter Change of Coronary Artery Lumen Estimated by Intravascular Ultrasound,” J. Cardiol., 30(1), pp. 1–8.https://www.ncbi.nlm.nih.gov/pubmed/?term=Pulsatile+Diame-+ter+Change+of+Coronary+Artery+Lumen+Estimated+by+Intravascular+Ultrasound [PubMed] [Google Scholar]
- [53]. Cho, K. I. , Park, J. H. , Park, J. R. , Kim, S. , Ahn, J. M. , Lee, J. H. , Jang, H. J. , and Kim, T. I. , 2006, “ Assessment of Left Ventricular Function in Symptomatic Patients With Myocardial Bridge Using Two-Dimensional Strain,” Korean Circ. J., 36(9), p. 617. 10.4070/kcj.2006.36.9.617 [DOI] [Google Scholar]
- [54]. Vorp, D. A. , 2007, “ Biomechanics of Abdominal Aortic Aneurysm,” J. Biomech., 40(9), pp. 1887–1902. 10.1016/j.jbiomech.2006.09.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55]. Williamson, S. D. , Lam, Y. , Younis, H. F. , Huang, H. , Patel, S. , Kaazempur-Mofrad, M. R. , and Kamm, R. D. , 2003, “ On the Sensitivity of Wall Stresses in Diseased Arteries to Variable Material Properties,” ASME J. Biomech. Eng., 125(1), p. 147. 10.1115/1.1537736 [DOI] [PubMed] [Google Scholar]
- [56]. Fayad, Z. A. , Fuster, V. , Fallon, J. T. , Jayasundera, T. , Worthley, S. G. , Helft, G. , Aguinaldo, J. G. , Badimon, J. J. , and Sharma, S. K. , 2000, “ Noninvasive In Vivo Human Coronary Artery Lumen and Wall Imaging Using Black-Blood Magnetic Resonance Imaging,” Circulation, 102(5), pp. 506–510. 10.1161/01.CIR.102.5.506 [DOI] [PubMed] [Google Scholar]
- [57]. Mensel, B. , Kühn, J. P. , Schneider, T. , Quadrat, A. , and Hegenscheid, K. , 2013, “ Mean Thoracic Aortic Wall Thickness Determination by Cine MRI With Steady-State Free Precession: Validation With Dark Blood Imaging,” Acad. Radiol., 20(8), pp. 1004–1008. 10.1016/j.acra.2013.03.014 [DOI] [PubMed] [Google Scholar]
- [58].Lemaitre, J., 2001, Handbook of Materials Behavior Models, Academic Press, Cambridge, MA [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary PDF


