Graphical abstract
Keywords: Network inference, Multimodal data, Bayesian inference, Infectious disease, Transmission
Highlights
-
•
Using multiple linked data sources for network inference is common in many domains.
-
•
Infectious disease transmission is a key area for multimodal network models.
-
•
We identify challenges in existing multimodal network inference methods.
-
•
Bayesian methods are the focus; they can concurrently infer networks & parameters.
-
•
This review identifies approaches for integrating new biomedical data types.
Abstract
Networks inference problems are commonly found in multiple biomedical subfields such as genomics, metagenomics, neuroscience, and epidemiology. Networks are useful for representing a wide range of complex interactions ranging from those between molecular biomarkers, neurons, and microbial communities, to those found in human or animal populations. Recent technological advances have resulted in an increasing amount of healthcare data in multiple modalities, increasing the preponderance of network inference problems. Multi-domain data can now be used to improve the robustness and reliability of recovered networks from unimodal data. For infectious diseases in particular, there is a body of knowledge that has been focused on combining multiple pieces of linked information. Combining or analyzing disparate modalities in concert has demonstrated greater insight into disease transmission than could be obtained from any single modality in isolation. This has been particularly helpful in understanding incidence and transmission at early stages of infections that have pandemic potential. Novel pieces of linked information in the form of spatial, temporal, and other covariates including high-throughput sequence data, clinical visits, social network information, pharmaceutical prescriptions, and clinical symptoms (reported as free-text data) also encourage further investigation of these methods. The purpose of this review is to provide an in-depth analysis of multimodal infectious disease transmission network inference methods with a specific focus on Bayesian inference. We focus on analytical Bayesian inference-based methods as this enables recovering multiple parameters simultaneously, for example, not just the disease transmission network, but also parameters of epidemic dynamics. Our review studies their assumptions, key inference parameters and limitations, and ultimately provides insights about improving future network inference methods in multiple applications.
1. Introduction
Dynamical systems and their interactions are common across many areas of systems biology, neuroscience, healthcare, and medicine. Identifying these interactions is important because they can broaden our understanding of problems ranging from regulatory interactions in biomarkers, to functional connectivity in neurons, to how infectious agents transmit and cause disease in large populations. Several methods have been developed to reverse engineer or, identify cause and effect pathways of target variables in these interaction networks from observational data [1], [2], [3]. In genomics, regulatory interactions such as disease phenotype-genotype pairs can be identified by network reverse engineering [1], [4]. Molecular biomarkers or key drivers identified can then be used as targets for therapeutic drugs and directly benefit patient outcomes. In microbiome studies, network inference is utilized to uncover associations amongst microbes and between microbes and ecosystems or hosts [2], [5], [6]. This can include insights about taxa associations, phylogeny, and evolution of ecosystems. In neuroscience, there is an effort towards recovering brain-connectivity networks from functional magnetic resonance imaging (FMRI) and calcium fluorescence time series data [3], [7]. Identifying structural or functional neuronal pairs illuminates understanding of the structure of the brain, can help better understand animal and human intelligence, and inform treatment of neuronal diseases. Infectious disease transmission networks are widely studied in public health. Understanding disease transmission in large populations is an important modeling challenge because a better understanding of transmission can help predict who will be affected, and where or when they will be. Network interactions can be further refined by considering multiple circulating pathogenic strains in a population along with strain-specific interventions, such as during influenza and cold seasons. Thus, network interactions can be used to inform interventional measures in the form of antiviral drugs, vaccinations, quarantine, prophylactic drugs, and workplace or school closings to contain infections in affected areas [8], [9], [10], [11]. Developing robust network inference methods to accurately and coherently map interactions is, therefore, fundamentally important and useful for several biomedical fields.
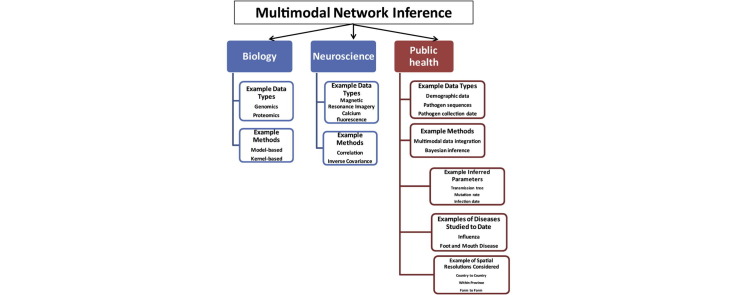
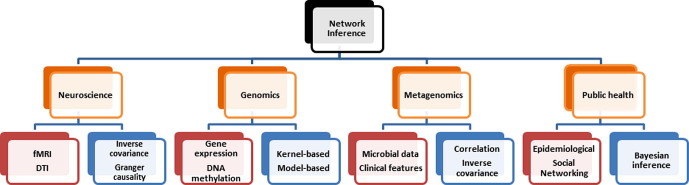
As summarized in Fig. 1 , many methods have been used to identify pairwise interactions in genomics, neuroscience [12], [13] and microbiome research [14] including correlation and information gain-based metrics for association, inverse covariance for conditional independence testing, and Granger causality for causation from temporal data. Further, multimodal data integration methods such as horizontal integration, model-based integration, kernel-based integration, and non-negative matrix factorization have been used to combine information from multiple modalities of ‘omics’ data such as gene expression, protein expression, somatic mutations, and DNA methylation with demographic, diagnoses, and phenotypical clinical data. Bayesian inference has been used to analyze changes in gene expression from microarray data as DNA measurements can have several unmeasured confounders and thereby incorporate noise and uncertainty [15]. Multi-modal integration can be used for classification tasks, to predict clinical phenotypes such as tumor stage or lymph node status, for clustering of patients into subgroups, and to identify important regulatory modules [16], [17], [18], [19], [20]. In neuroscience, not just data integration, but multimodal data fusion has been performed by various methods such as linear regression, structural equation modeling, independent component analysis, principal component analysis, and partial least squares [21]. Multiple modalities such as FMRI, electroencephalography, and diffusion tensor imaging (DTI) have been jointly analyzed to uncover more details than could be captured by a single imaging technique [21]. In metagenomics, network inference from microbial data has been performed using methods such as inverse covariance and correlation [2]. In evolutionary biology, the massive generation of molecular data has enabled Bayesian inference of phylogenetic trees using Markov Chain Monte Carlo chain (MCMC) techniques [22], [23]. In infectious disease transmission network inference, Bayesian inference frameworks have been primarily used to integrate data such as dates of pathogen sample collection and symptom report date, pathogen genome sequences, and locations of patients [24], [25], [26]. This problem remains challenging as the data generative processes and scales of heterogeneous modalities may be widely different, transformations applied to separate modalities may not preserve the interactions between modalities, and separately integrated models may not capture interaction effects between modalities [27].
Fig. 1.
Examples of multimodal network inference methods in different applications. Different modalities of data have been integrated in several applications for inferring specific networks. Most network inference methods focus on recovering network topology.
As evidence mounts regarding the complex combination of biological, environmental, and social factors behind disease, emphasis on the development of advanced modeling and inference methods that incorporate multimodal data into singular frameworks has increased. These methods are becoming more important to consider given that the types of healthcare data available for understanding disease pathology, evolution, and transmission are numerous and growing. For example, Internet and mobile connectivity has enabled mobile sensors, point-of-care diagnostics, web logs, and participatory social media data which can provide complementary health information to traditional sources [28], [29]. In the era of precision medicine, it becomes especially important to combine clinical information with biomarker and environmental information to recover complex genotype-phenotype maps [30], [31], [32], [33]. Infectious disease networks are one area where the need to bring together data types has long been recognized, specifically to better understand disease transmission. Data sources including high-throughput sequencing technologies have enabled genomic data to become more cost effective, offering support for studying transmission by revealing pathways of pathogen introduction and evolution in a population. Yet, genomic data in isolation is insufficient to obtain a comprehensive picture of disease in the population. While these data can provide information about pathogen evolution, genetic diversity, and molecular interaction, they do not capture other environmental, spatial, and clinical factors that can affect transmission. For infectious disease surveillance, this information is usually conveyed through epidemiological data, which can be collected in various ways such as in clinical settings from the medical record, or in more recent efforts through Web search logs, or participatory surveillance. Participatory surveillance data types typically include age, sex, date of symptom onset, and diagnostic information such as severity of symptoms. In clinical settings, epidemiological data are generally collected from patients reporting illness. This can include, for example, age at diagnosis, sex, race, family history, diagnostic information such as severity of symptoms, and phenotypical information such as presence or absence of disease which may not be standardized. High-throughput sequencing of pathogen genomes, along with linked spatial and temporal information, can advance surveillance by increasing granularity and leading to a better understanding of the spread of an infectious disease [37]. Considerable efforts have been made to unify genomic and epidemiologic information from traditional clinical forms into singular statistical frameworks to refine understanding of disease transmission [24], [25], [26], [34], [35], [36].
One approach to design and improve disease transmission models has been to analytically combine multiple, individually weak predictive signals in the form of sparse epidemiological, spatial, pathogen genomic, and temporal data [24], [25], [34], [35], [38]. Molecular epidemiology is the evolving field wherein the above data types are considered together; epidemiological models are used in concert with pathogen phylogeny and immunodynamics to uncover disease transmission patterns [39]. Pathogen genomic data can capture within-host pathogen diversity (the product of effective population size in a generation and the average pathogen replication time [25], [26]) and dynamics or provide information critical to understanding disease transmission such as evidence of new transmission pathways that cannot be inferred from epidemiological data alone [40], [41]. In addition, the remaining possibilities can then be examined using any available epidemiological data.
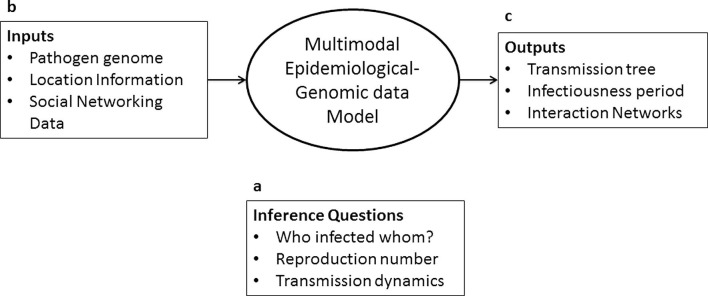
As molecular epidemiology and infectious disease transmission are areas in which network inference methods have been developed for bringing together multimodal data we use this review to investigate the foundational work in this specific field. A summary of data types, relevant questions and purpose of such studies is summarized in Fig. 2 , and we further articulate the approaches below. In molecular epidemiology, several approaches have been used to overlay pathogen genomic information on traditionally collected epidemiologic information to recover transmission networks. Additional modeling structure is needed in these problems because infectious disease transmission occurs through contact networks of heterogeneous individuals, which may not be captured by compartmental models such as Susceptible–Infectious–Recovered (SIR) and Susceptible–Latent–Infectious–Recovered (SLIR) models [42]. As well, for increased utility in epidemiology, there is a necessity to estimate epidemic parameters in addition to the transmission network. Unlike other fields wherein recovery of just the topology of the networks is desired, in molecular epidemiology Bayesian inference is commonly used to reverse engineer infectious disease transmission networks in addition to estimating epidemic parameters (Fig. 2).
Fig. 2.
Modeling transmission of infectious diseases, an area in which use of multiple modalities of data has been developed. (a) Several key questions can be answered such as who infected whom or how did the infection transmit through the population or region. (b) Possible inputs to the model include pathogen genomic sequences, spatial and temporal information, point-of-care diagnostic information, and mobile health information. The data are brought together in multimodal network inference frameworks. (c) Some possible outputs are the transmission tree, latency period, epidemic reproduction number, phylogenetic tree, and proportion of infected hosts sampled.
While precise features can be extracted from observed data, there are latent variables not directly measured which must simultaneously be considered to provide a complete picture. Thus, Bayesian inference methods have been used to simultaneously infer epidemic parameters and structure of the transmission network in a single framework. Instead of capturing pairwise interactions, such as correlations or inverse covariance, Bayesian inference is capable of considering all nodes and inferring a global network and transmission parameters [7]. Moreover, Bayesian inference is capable of modeling noisy, partially sampled realistic outbreak data while incorporating prior information.
While this review focuses on infectious disease transmission, network inference methods have implications in many areas. Modeling network diffusion and influence, identifying important nodes, link prediction, influence probabilities and community topology and parameter detection are key questions in several fields ranging from genomics to social network analysis [43]. Analogous frameworks can be developed with different modalities of observational genomics or clinical data to model information propagation and capture the influences of nodes, nodes that are more influential than others, and the temporal dynamics of information diffusion. For modeling information spread in such networks, influence and susceptibility of nodes can serve to be analogous to epidemic transmission parameters. However, these modified methods should also account for differences in the method of information propagation in such networks from infectious disease transmission by incorporating constraints in the form of temporal decay of infection, strengths of ties measured from biological domain knowledge, and multiple pathways of information spread.
1.1. Selection criteria
To identify the studies most relevant for this focused review, we queried PubMed. For practicality and relevance, our search, summarized in Fig. 3 , was limited to papers from the last ten years. As our review is focused on infectious disease transmission network inference, we started with the keywords ‘transmission’ and ‘epidemiological’. To ensure that we captured studies that incorporate pathogen genomic data, we added the keywords ‘genetic’, ‘genomic’ and ‘phylogenetic’ giving 5557 articles total. Next, to narrow the results to those that are comprised of a study of multi-modal data, we found that the keywords ‘combining’ or ‘integrating’ alongside ‘Bayesian inference’ or ‘inference’ were comprehensive. These filters yielded 73 and 61 articles in total. We found that some resulting articles focused on outbreak detection, sexually transmitted diseases, laboratory methods, and phylogenetic analysis. Also, the focus of several articles was to either overlay information from different modalities or to sequentially analyze them to eliminate unlikely transmission pathways. After a full-text review to exclude these and focus on methodological approaches, 8 articles resulted which use Bayesian inference to recover transmission networks from multimodal data for infectious diseases, and which represent the topic of this review. This included Bayesian likelihood-based methods for integrating pathogen genomic information with temporal, spatial, and epidemiological characteristics for infectious diseases such as foot and mouth disease (FMD), and respiratory illnesses, including influenza. As incorporating genomic data simultaneously in analytical multimodal frameworks is a relatively novel idea, the literature on this is limited. Recent unified platforms have been made available to the community for analysis of outbreaks and storing of outbreak data [44]. Thus, it is essential to review available literature on this novel and burgeoning topic. For validation, we repeated our queries on Google Scholar. Although Google Scholar generated a much broader range of papers, based on the types of papers indexed, we verified that it also yielded the articles selected from PubMed. We are confident in our choice of articles for review as we have used two separate publications databases. Below we summarize the theoretical underpinnings of the likelihood-based framework approaches, inference parameters, and assumptions about each of these studies and articulate the limitations, which can motivate future research.
Fig. 3.
Study design and inclusion-exclusion criteria. This is a decision tree showing our searches and selection criteria for both PubMed and Google Scholar. We focused only on genomic epidemiology methods utilizing Bayesian inference for infectious disease transmission.
2. Review of multimodal integration methods for transmission network inference
Infectious disease transmission study is a rapidly developing field given the recent advent of widely available epidemiological, social contact, social networking and pathogen genomic data. In this section we briefly review multimodal integration methods for combining pathogen genomic data and epidemiological data in a single analysis, for inferring infection transmission trees and epidemic dynamic parameters.
Advances in genomic technology such as sequences of whole genomes of RNA viruses and identifying Single Nucleotide Variations using sensitive mass spectrometry have enabled the tracing of transmission patterns and mutational parameters of the Severe Acute Respiratory Syndrome (SARS) virus [45]. In this study, phylogenetic trees were inferred based on Phylogenetic Analysis Using Parsimony (PAUP∗) using a maximum likelihood criterion [46]. Mutation rate was then inferred based on a model which assumes that the number of mutations observed between an isolate and its ancestor is proportional to the mutation rate and their temporal difference [47]. Their estimated mutation rate was similar to existing literature on mutation rates of other viral pathogens. Phylogenetic reconstruction revealed three major branches in Taiwan, Hong Kong, and China.
Gardy et al. [29] analyzed a tuberculosis outbreak in British Columbia in 2007 using whole-genome pathogen sequences and contact tracing using social network information. Epidemiological information collection included completing a social network questionnaire to identify contact patterns, high-risk behaviors such as cocaine and alcohol usage, and possible geographical regions of spread. Pathogen genomic data consisted of restriction-fragment-length polymorphism analysis of tuberculosis isolates. Phylogenetic inference of genetic lineage based on Single Nucleotide Polymorphisms from the genomic data was performed. Their method demonstrated that transmission information inference such as identifying a possible source patient from contact tracing by epidemiological investigation can be refined by adding ancestral and diversity information from genomic data.
In one of the earliest attempts to study genetic sequence data, as well as dates and locations of samples in concert, Jombart et al. [38] proposed a maximal spanning tree graph-based approach that went beyond existing phylogenetic methods. This method was utilized to uncover the spatiotemporal dynamics of the influenza A (H1N1) from 2009 and to study its worldwide spread. A total of 433 gene sequences of hemagglutinin (HA) and of neuraminidase (NA) were obtained from GenBank. Classical phylogenetic approaches fail to capture the hierarchical relationship between both ancestors and descendants sampled at the same time. Using their algorithm called SeqTrack [48], the authors constructed ancestries in samples based on a maximal-spanning tree. SeqTrack [38] utilizes the fact that in the absence of recombination and reverse mutations, strains will have unique ancestors characterized by the fewest possible mutations, no sample can be the ancestor of a sample which temporally preceded it, and the likelihood of ancestry can be estimated from the genomic differentiation between samples. SeqTrack was successful in reconstructing the transmission trees in both completely and incompletely sampled outbreaks unlike phylogenetic approaches, which failed to capture ancestral relationships between the tips of trees. However, this method cannot capture the underlying within-host virus genetic parameters. Moreover, mutations generated once can be present in different samples and transmission likelihood based on genetic distance may not be reliable.
The above methods exploit information from different modalities separately. Recent methodological advancements have seen simultaneous integration of multiple modalities of data in singular Bayesian inference frameworks. In the following section we discuss state-of-the-art approaches based on Bayesian inference, to reconstruct partially-observed transmission trees and multiple origins of pathogen introduction in a host population [25], [34], [35], [49], [50]. We specifically focus on Bayesian likelihood-based methods as the methods consider heterogeneous modalities in a single framework and simultaneously infer the transmission network and epidemic parameters such as rate of infection transmission and rate of recovery.
3. Bayesian inference-based approaches for transmission network inference
Infectious disease transmission network inference is one problem area wherein there is a foundational literature of Bayesian inference methods; reviewing them together allows understanding and comparison of specific related features across models. Methods are summarized in Table 1 .
Table 1.
Summary of network inference methods to-date used in infectious disease modeling.
| Literature source | Location | Time span | Pathogen | Sample size | Assumptions | Inferred Parameters |
|---|---|---|---|---|---|---|
| Cottam et al. (2008) [40] | Durham area | 2001 | FMD | 22 |
|
|
| Ypma et al. (2012) [25] | The Netherlands | 2003 | Avian influenza A (H7N7) | 185 |
|
|
| Morelli et al. (2012) [24] |
|
|
FMD |
|
|
|
| Ypma et al. (2013) [34] | Durham County, England | 2001 | FMD | 12 premises |
|
|
| Teunis et al. (2013) [56] | Netherlands | December 2002 –December 2007 | Norovirus | 160 |
|
|
| Didelot et al. (2014) [26] | British Columbia | 2004–2011 | Tuberculosis | 40 |
|
|
| Mollentze et al. (2014) [49] | KwaZulu Natal province, South Africa | 1 March 2010–8 June 2011 | Rabies virus | 195 |
|
|
| Jombart et al. (2014) [35] | Singapore | 2003 | SARS | 15 |
|
|
In Bayesian inference, information recorded before the study is included as a prior in the hypothesis. Based on Bayes theorem as shown below, this method incorporates prior information and likelihoods from the sample data to compute a posterior probability distribution or, . The denominator is a normalization constant or, the marginal probability density of the sample data computed over all hypotheses [51]. The hypothesis for this problem can be expressed in the form of a transmission network over individuals, locations, or farms, parameters such as rate of infectiousness and recovery, or mutation probability of pathogens. The posterior probability distribution can then be estimated as in the equation below.
The posterior probability is then a measure that the inferred transmission tree and parameters are correct.
It can be extremely difficult to analytically compute the posterior probability distribution as it involves iterating over all possible combinations of branches of such a transmission tree and parameter values. However, it is possible to approximate the posterior probability distribution using MCMC [52] techniques. In MCMC, a Markov chain is constructed which is described by the state space of the parameters of the model and which has the posterior probability distribution as its stationary distribution. For an iteration of the MCMC, a new tree is proposed by stochastically altering the previous tree. The new tree is accepted or rejected based on a probability computed from a Metropolis-Hastings or Gibbs update. The quality of the results from the MCMC approximation can depend on the number of iterations that it is run for, the convergence criterion and the accuracy of the update function [22].
Cottam et al. [40] developed one of the earliest methods to address this problem studying foot-and-mouth disease (FMD) in twenty farms in the UK. In this study, FMD virus genomes (the FMD virus has a positive strand RNA genome and it is a member of the genus Aphthovirus in the family Picornaviridae) were collected from clinical samples from the infected farms. The samples were chosen so that they could be used to study variation within the outbreak and the time required for accumulation of genetic change, and to study transmission events. Total RNA was extracted directly from epithelial suspensions, blood, or esophageal suspensions. Sanger sequencing was performed on 42 overlapping amplicons covering the genome [53]. As the RNA virus has a high substitution rate, the number of mutations was sufficient to distinguish between different farms. They designed a maximum likelihood-based method incorporating complete genome sequences, date at which infection in a farm was identified, and the date of culling of the animals. The goal was to trace the transmission of FMD in Durham County, UK during the 2001 outbreak to infer the date of infection of animals and most likely period of their infectiousness. In their approach, they first generated the phylogenies of the viral genomes [54], [55]. Once the tip of the trees were generated, they constructed possible transmission trees by recursively working backwards to identify a most recent common ancestor (MRCA) in the form of a farm and assigned each haplotype to a farm. The likelihood of each tree was then estimated using epidemiological data. Their study included assumptions of the mean incubation time prior to being infectious to be five days, the distribution of incubation times to follow a discrete gamma distribution, the most likely date of infection to be the date of reporting minus the date of the oldest reported lesion of the farm minus the mean incubation time, and the farms to be a source of infection immediately after being identified as infected up to the day of culling. Spatial dependence in the transmission events was determined from the transmission tree by studying mean transmission distance. Their study indicated possible intermediate infected farms not inferred by the method and multiple introductions of pathogens in the area.
Ypma et al. [25] developed a Bayesian likelihood-based framework integrating genetic and epidemiological data. This method was tested on an epidemic dataset of 241 poultry farms in an epidemic of avian influenza A (H7N7) in The Netherlands in 2003 consisting of geographical, genomic, and date of culling data. Consensus sequences of the HA, NA and polymerase PB2 genes were derived by pooling sequence data from five infected animals for 185 out of the 241 farms analyzed. The likelihood of one farm infecting another increased if the former was not culled at the time of infection of the latter, if they were in geographical proximity, or if the sampled pathogen genomic sequences were related. Their model included several assumptions such as non-correlation of genetic distance, time of infection, and geographical distance between host and target farms. The likelihood function was generated as follows: for the temporal component, a farm could infect another if its infection time was before the infection time of the target farm or if the infection time of the latter was between the infection and culling time of the former. If a farm was already culled, its infectiousness decayed exponentially. For the geographical component, two farms could infect each other with likelihood equal to the inverse of the distance between them. This likelihood varied according to a spatial kernel. For the genomic component, probabilities of transitions and transversions, and the presence or absence of a deletion was considered. If there was no missing data, the likelihood function was just a product of independent geographical, genomic, and temporal components. This method also allowed missing data by assuming that all the links to a specific missing data type are in one subtree. MCMC [52] was performed to sample all possible transmission trees and parameters. Marginalizing over a large number of subtrees over all possible values can also prove computationally expensive. Mutations were assumed to be fixed in the population before or after an infection, ignoring a molecular clock.
In the method by Morelli et al. [24], the authors developed a likelihood-based function that inferred the transmission trees and infection times of the hosts. The authors assumed that a premise or farm can be infected at a certain time followed by a latency period, a time period from infectiousness to detection, and a time of pathogen collection. This method utilized the FMD dataset from the study by Cottam et al. In order to simplify the posterior distribution further, latent variables denoting unobserved pathogens were removed and a pseudo-distribution incorporating the genetic distance between the observed and measured consensus sequences was generated. The posterior distribution corresponded to a pseudo-posterior distribution because the pathogens were sampled at observation time and not infection time. The genetic distance was measured by Hamming distance between sequences in isolation without considering the entire genetic network. Several assumptions including independence of latency time and infectiousness period were made. In determining the interval from the end-of-latency period to detection, the informative prior was centered on lesion age. This made this inference technique sensitive to veterinary estimates of lesion age. This study considered a single source of viral introduction in the population, which is feasible if the population size considered is small. This technique did not incorporate unobserved sources of infection and assumed all hosts were sampled. The authors also assumed that each host had the same probability of being infected.
Teunis et al. [56] developed a Bayesian inference framework to infer transmission probability matrices. The authors assumed that likelihood of infection transmission over all observed individuals would be equal to the product of conditional probability distributions between each pair of individuals i and j, and the corresponding entry from the transition probability matrix representing any possible transmissions from ancestors to i. The inferred matrices could be utilized to identify network metrics such as number of cases infected by each infected source and transmission patterns could be detected by analyzing pairwise observed cases during an outbreak. The likelihood function could be generated by observed times of onset, genetic distance, and geographical locations. Their inferred parameters were the transmission tree and reproductive number. Their method was applied to a norovirus outbreak in a university hospital in Netherlands.
In a method developed by Ypma et al. [34], the statistical framework for inferring the transmission tree simultaneously generated the phylogenetic tree. This method also utilized the FMD dataset from the study by Cottam et al. Their approach for generating the joint posterior probability of the transmission tree differed from existing methods in including the simultaneous estimation of the phylogenetic tree and within-host dynamics. The posterior probability distribution defined a sampling space consisting of the transmission tree, epidemiological parameters, and within-host dynamics which were inferred from the measured epidemiological data and the phylogenetic tree and mutation parameters which were inferred from the pathogen genomic data. The posterior probability distribution was estimated using the MCMC technique. The performance of the method was evaluated by measuring the probability assigned to actual transmission events. The assumptions made were that all infected hosts were observed, time of onset was known, sequences were sampled from a subpopulation of the infected hosts, and a single source/host introduced the infection in the population. In going beyond existing methods, the authors did not assume that events in the phylogenetic tree coincide with actual transmission events. A huge sampling fraction would be necessary to capture such microscale genetic diversity. This method works best when all infected hosts are observed and sampled.
Mollentze et al. [49] have used multimodal data in the form of genomic, spatial and temporal information to address the problem of unobserved cases, an existing disease well established in a population, and multiple introductions of pathogens. Their method estimated the effective size of the infected population thus being able to provide insight into number of unobserved cases. The authors modified Morelli et al.’s method described above by replacing the spatial kernel with a spatial power transmission kernel to accommodate wider variety of transmission. In addition, the substitution model used by Morelli et al. was modified by a Kimura three parameter model [57]. This method was applied to a partially-sampled rabies virus dataset from South Africa. The separate transmission trees from partially-observed data could be grouped into separate clusters with most transmissions in the under-sampled dataset being indirect transmissions. Reconstructions were sensitive to choice of priors for incubation and infectious periods.
In a more recent approach to study outbreaks and possible transmission routes, Jombart et al. [35], in addition to reconstructing the transmission tree, addressed important issues such as inferring possible infection dates, secondary infections, mutation rates, multiple pathways of pathogen introduction, foreign imports, unobserved cases, proportion of infected hosts sampled, and superspreading in a Bayesian framework. Jombart tested their algorithm outbreaker on the 2003 SARS outbreak in Singapore using 13 known cases of primary and secondary infection [35], [45], [58]. In this study, 13 genome sequences of Severe Acute Respiratory Syndrome (SARS) were downloaded from GenBank and analyzed. Their method relies on pathogen genetic sequences and collection dates. Similar to their previous approach [50], their method assumed mutations to be parameters of transmission events. Epidemiological pseudo-likelihood was based on collection dates. Genomic pseudo-likelihood was computed based on genetic distances between isolates. This method would benefit from known transmission pathways and mutation rates and is specifically suitable for densely sampled outbreaks. Their method assumed generation time—time from primary to secondary infections—and time from infection to collection were available. Their method ignored within-host diversity of pathogens. Instead of using a strict molecular clock, this method used a generational clock.
Didelot et al. [26] developed a framework to examine if whole-genome sequences were enough to capture transmission events. Unlike other existing studies, the authors took into account within-host evolution and did not assume that branches in phylogenetic trees correspond to actual transmission events. The generation time corresponds to the time between a host being infected and infecting others. For pathogens with short generation times, genetic diversity may not accrue to a very high degree and one can ignore within-host diversity. However, for diseases with high latency times and ones in which the host remains asymptomatic, there is scope for accumulation of considerable within-host genetic diversity. Their method used a timed phylogenetic tree from which a transmission tree is inferred on its own or can be combined with any available epidemiological support. Their simulations revealed that considering within-host pathogen generation intervals resulted in more realistic phylogenies between infector and infected. The method was tested on simulated datasets and with a real-world tuberculosis dataset with a known outbreak source with only genomic data and then modified using any available epidemiological data. The latter modified network resembled more the actual transmission activity in having a web-like layout and fewer bidirectional links. Their approach would work well for densely sampled outbreaks.
Some of the most common parameters inferred for infectious disease transmission in these Bayesian approaches are the transmission tree between infected individuals or animals, the mutation rates of different pathogens, phylogenetic tree, within-host diversity, latency period, and infection dates [24], [34], [40], [26]. Additional parameters in recent work are reproductive number [26], foreign imports, superspreaders, and proportion of infected hosts sampled [35].
4. Limitations of existing methods
Several simplifying assumptions have been made in the reviewed Bayesian studies, limiting their applicability across different epidemic situations. In Cottam’s [40] approach, the phylogenetic trees generated from the genomic data are weighed by epidemiological factors to limit analysis to possible transmission trees. However, sequential approaches may not be ideal to reconstruct transmission trees and a method that combines all modalities in a single likelihood function may be necessary. Ypma et al. [25] assumed that pathogen mutations emerge in the host population immediately before or following infections. Moreover, the approach weighed each data type via their likelihood functions and considers each data type independent of the others, which may not be a realistic assumption. Jombart et al. [38] also inferred ancestral relationships to the most closely sampled ancestor as all ancestors may not be sampled. Morelli et al. [24] assumed flat priors for all model parameters. However, the method was estimated with the prior for the duration from latency to infection centered on the lesion age making the method sensitive to it and to veterinary assessment of infection age. The method developed by Mollentze et al. [49] required knowledge of epidemiology for infection and incubation periods. Identifying parents of infected nodes, as proposed by Teunis et al., [56] assumes that all infectious cases were observed which may not be true in realistic, partially-observed outbreaks. Didelot et al. [26] developed a framework based on a timed phylogenetic tree, which infers within-host evolutionary dynamics with a constant population size and densely-sampled outbreaks.
Several of these approaches rely on assumptions of densely-sampled outbreaks, a single pathogen introduction in the population, single infected index cases, samples capturing the entire outbreak, that all cases comprising the outbreak are observed, existence of single pathogen strains, and all nodes in the transmission network having constant infectiousness and the same rate of transmission. However, in real situations the nodes will have different infectiousness and rate of spreading from animal to animal, or human to human. Moreover, the use of clinical data only is non-representative of how infection transmits to a population as it generally only captures the most severely affected cases. Our literature review is summarized in Table 1.
5. Future work
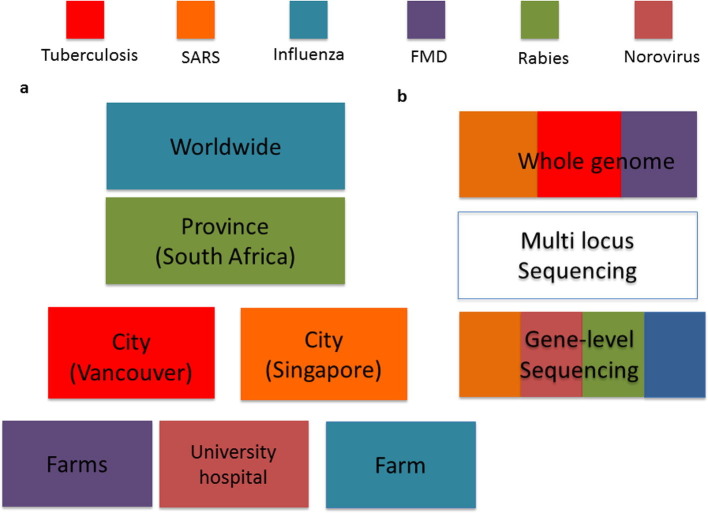
As large-scale and detailed genomic data becomes more available, analyses of existing Bayesian inference methods described in our review will inform their integration in epidemiological and other biomedical research. As more and more quantities of diverse data becomes available, developing Bayesian inference frameworks will be the favored tool to integrate information and draw inference about transmission and epidemic parameters simultaneously. The specific focus in this review on the application of network inference in infectious disease transmission enables us to consider and comment on common parameters, data types and assumptions (summarized in Table 1). Novel data sources have increased the resolution of information as well as enabled a closer monitoring and study of interactions; spatial and genomic resolution of the Bayesian network-inference studies reviewed are summarized in Fig. 4 to illustrate the scope of current methods. Further, we have added suggestions for addressing identified challenges in these methods regarding their common assumptions and parameters in Table 2 . Given the increasing number and types of biomedical data available, we also discuss how models can be augmented to harness added value from these multiple and higher-granularity modalities such as minor variant identification from deep sequencing data or community-generated epidemiological data.
Fig. 4.
Different spatial and genomic resolutions utilized to study disease spread. (a) Regions of interest considered for different studies. Influenza studies considered world-wide spread, SARS was studied in Singapore, Tuberculosis (TB) dataset was from British Columbia, Norovirus in a university hospital in the Netherlands, and Foot and Mouth Disease (FMD) in 12 farms in Durham. (b) Different genomic sequencing platforms utilized in studies. For the TB study, Whole genome sequencing was performed on Illumina HiSeq platform with M. tuberculosis CDC1551 reference sequence and aligned using Burrows-Wheeler Aligner algorithm. SARS DNA sequences were obtained from GenBank and aligned using MUSCLE. For avian influenza, RNA consensus sequences of the haemagglutinin, neuriminidase and polymerase PB2 genes were sequenced. For H1N1 influenza, isolates were typed for hemagglutinin (HA) and neuraminidase (NA) genes.
Table 2.
Summary of gaps in existing inference techniques and suggestions for future research.
| Presently available data and methods | Suggestions for future research | |
|---|---|---|
| Genomic |
|
|
| Spatial |
|
|
| Methods |
|
|
| Data Generation |
|
|
| Parameters |
|
|
Existing methods are based on pathogen genome sequences which may largely be consensus in nature where the nucleotide or amino acid residue at any given site is the most common residue found at each position of the sequence. Other recent approaches have reconstructed epidemic transmission using whole genome sequencing. Detailed viral genomic sequence data can help distinguish pathogen variants and thus augment analysis of transmission pathways and host-infectee relationships in the population. Highly parallel sequencing technology is now available to study RNA and DNA genomes at greater depth than was previously possible. Using advanced deep sequencing methods, minor variations that describe transmission events can be captured and must also then be represented in models [59], [60].
Models can also be encumbered with considerable selection bias by being based on clinical or veterinary data representative of a subsample of only the most severely infected hosts who access clinics. Existing multi-modal frameworks are designed based on clinical data such as sequences collected from cases of influenza [35], [38] or veterinary assessment of FMD [24], [53], which generally represent the most severe cases with access to traditional healthcare institutions and automatically inherit considerable selection bias. Models to-date do not consider participatory surveillance data that has become increasingly available via mobile and Internet accessibility (e.g. data from web logs, search queries, Web survey-based participatory efforts such as GoViral with linked symptomatic, immunization, and molecular information [61] and online social networks and social network questionnaires). Another approach to improve the granularity of collected data could be community-generated data. These data can be fine-grained and can capture information on a wide range of cases from asymptomatic to mildly infectious to severe. This data can be utilized to incorporate additional transmission parameters of a community which can be more representative of disease transmission. As exemplified in Fig. 4a, community-generated data can be collected at the fine-grained spatial level of households, schools, workplaces, or zip codes and models must then also accommodate these spatial resolutions.
Studies to-date have also generally depended on available small sample sizes and some are specifically tailored to a specific disease or pathogen such as SARS, avian influenza, or FMD [34], [35], [40]. Methods will have to handle missing data and unobserved and unsampled hosts to be applicable to realistic scenarios. In simpler cases, assumptions of single introductions of infection with single strains being passed between hosts may be adequate. However, robust frameworks will have to consider multiple introductions of pathogens in the host population with multiple circulating strains and co-infections in hosts. In order to be truly useful, frameworks have to address questions regarding rapid mutations of certain pathogens, phylogenetic uncertainty, recombination and reassortment, population stochastics, super spreading, exported cases, multiple introductions of pathogens in a population, within and between-host pathogen evolution, and phenotypic information. Methods will also need to scale up to advances in next-generation sequencing technology capable of producing large amounts of genomic data inexpensively [62], [63].
In the study of infectious diseases, the challenge remains to develop robust statistical frameworks that will take into account the relationship between epidemiological data and phylogeny and utilize that to infer pathogen transmission while taking into account realistic evolutionary times and accumulation of within-host diversity. Moreover, to benefit public health inference methods need to uncover generic transmission patterns, wider range of infections and risks including asymptomatic to mildly infectious cases, clusters and specific environments, and host types.
Network inference frameworks from the study of infectious diseases can be analogously modified to incorporate diverse forms of multimodal data and model information propagation and interactions in diverse applications such as drug-target pairs and neuronal connectivity or social network analysis. The detailed examination of models, data sources and parameters performed here can inform inference methods in different fields, and bring to light the way that new data sources can augment the approaches. In general, this will enable understanding and interpretation of influence and information propagation by mapping relationships between nodes in other applications.
Conflict of interest
The authors declare no conflict of interest.
References
- 1.Narendra V., Lytkin N.I., Aliferis C.F., Statnikov A. A comprehensive assessment of methods for de-novo reverse-engineering of genome-scale regulatory networks. Genomics. 2011;97(1):7–18. doi: 10.1016/j.ygeno.2010.10.003. PubMed PMID: WOS:000286367200002. English. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kurtz Z.D., Müller C.L., Miraldi E.R., Littman D.R., Blaser M.J., Bonneau R.A. Sparse and compositionally robust inference of microbial ecological networks. PLoS Comput. Biol. 2015;11(5):e1004226. doi: 10.1371/journal.pcbi.1004226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Stetter O., Battaglia D., Soriano J., Geisel T. Model-free reconstruction of excitatory neuronal connectivity from calcium imaging signals. PLoS Comput. Biol. 2012;8(8):e1002653. doi: 10.1371/journal.pcbi.1002653. PubMed PMID: Medline:22927808. English. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Stolovitzky G., Monroe D., Califano A. Dialogue on reverse-engineering assessment and methods. Ann. N.Y. Acad. Sci. 2007;1115(1):1–22. doi: 10.1196/annals.1407.021. [DOI] [PubMed] [Google Scholar]
- 5.Deng Y., Jiang Y.-H., Yang Y., He Z., Luo F., Zhou J. Molecular ecological network analyses. BMC Bioinform. 2012;13(1):1. doi: 10.1186/1471-2105-13-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Steele J.A., Countway P.D., Xia L., Vigil P.D., Beman J.M., Kim D.Y. Marine bacterial, archaeal and protistan association networks reveal ecological linkages. ISME J. 2011;5(9):1414–1425. doi: 10.1038/ismej.2011.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Smith S.M., Miller K.L., Salimi-Khorshidi G., Webster M., Beckmann C.F., Nichols T.E. Network modelling methods for FMRI. Neuroimage. 2011;54(2):875–891. doi: 10.1016/j.neuroimage.2010.08.063. [DOI] [PubMed] [Google Scholar]
- 8.Colizza V., Barrat A., Barthelemy M., Valleron A.J., Vespignani A. Modeling the worldwide spread of pandemic influenza: baseline case and containment interventions. PLoS Med. 2007;4(1):e13. doi: 10.1371/journal.pmed.0040013. PubMed PMID: 17253899. Pubmed Central PMCID: 1779816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Carrat F., Luong J., Lao H., Sallé A.-V., Lajaunie C., Wackernagel H. A ‘small-world-like’ model for comparing interventions aimed at preventing and controlling influenza pandemics. BMC Med. 2006;4(1):26. doi: 10.1186/1741-7015-4-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wu J.T., Riley S., Fraser C., Leung G.M. Reducing the impact of the next influenza pandemic using household-based public health interventions. PLoS Med. 2006;3(9):e361. doi: 10.1371/journal.pmed.0030361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cauchemez S., Valleron A.-J., Boelle P.-Y., Flahault A., Ferguson N.M. Estimating the impact of school closure on influenza transmission from Sentinel data. Nature. 2008;452(7188):750–754. doi: 10.1038/nature06732. [DOI] [PubMed] [Google Scholar]
- 12.Stetter O., Battaglia D., Soriano J., Geisel T. Model-free reconstruction of excitatory neuronal connectivity from calcium imaging signals. PLoS Comput. Biol. 2012;8(8):e1002653. doi: 10.1371/journal.pcbi.1002653. PubMed PMID: 22927808. Pubmed Central PMCID: 3426566. Epub 2012/08/29.eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Smith S.M., Miller K.L., Salimi-Khorshidi G., Webster M., Beckmann C.F., Nichols T.E. Network modelling methods for FMRI. Neuroimage. 2011;54(2):875–891. doi: 10.1016/j.neuroimage.2010.08.063. PubMed PMID: 20817103. Epub 2010/09/08.eng. [DOI] [PubMed] [Google Scholar]
- 14.Kurtz Z.D., Muller C.L., Miraldi E.R., Littman D.R., Blaser M.J., Bonneau R.A. Sparse and compositionally robust inference of microbial ecological networks. PLoS Comput. Biol. 2015;11(5):e1004226. doi: 10.1371/journal.pcbi.1004226. PubMed PMID: 25950956. Pubmed Central PMCID: 4423992. Epub 2015/05/08.eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Baldi P., Long A.D. A Bayesian framework for the analysis of microarray expression data: regularized t-test and statistical inferences of gene changes. Bioinformatics. 2001;17(6):509–519. doi: 10.1093/bioinformatics/17.6.509. PubMed PMID: 11395427. [DOI] [PubMed] [Google Scholar]
- 16.Serra A., Fratello M., Fortino V., Raiconi G., Tagliaferri R., Greco D. MVDA: a multi-view genomic data integration methodology. BMC Bioinform. 2015;16:261. doi: 10.1186/s12859-015-0680-3. PubMed PMID: 26283178. Pubmed Central PMCID: 4539887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ray B., Henaff M., Ma S., Efstathiadis E., Peskin E.R., Picone M. Information content and analysis methods for multi-modal high-throughput biomedical data. Sci. Rep. 2014;4 doi: 10.1038/srep04411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang S., Li Q., Liu J., Zhou X.J. A novel computational framework for simultaneous integration of multiple types of genomic data to identify microRNA-gene regulatory modules. Bioinformatics. 2011;27(13):i401–i409. doi: 10.1093/bioinformatics/btr206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Daemen A., Gevaert O., Ojeda F., Debucquoy A., Suykens J.A., Sempoux C. A kernel-based integration of genome-wide data for clinical decision support. Genome Med. 2009;1(4):39. doi: 10.1186/gm39. PubMed PMID: 19356222. Pubmed Central PMCID: 2684660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gevaert O., De Smet F., Timmerman D., Moreau Y., De Moor B. Predicting the prognosis of breast cancer by integrating clinical and microarray data with Bayesian networks. Bioinformatics. 2006;22(14):e184–e190. doi: 10.1093/bioinformatics/btl230. PubMed PMID: 16873470. [DOI] [PubMed] [Google Scholar]
- 21.Sui J., Adali T., Yu Q., Chen J., Calhoun V.D. A review of multivariate methods for multimodal fusion of brain imaging data. J. Neurosci. Methods. 2012;204(1):68–81. doi: 10.1016/j.jneumeth.2011.10.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Huelsenbeck J.P., Ronquist F., Nielsen R., Bollback J.P. Bayesian inference of phylogeny and its impact on evolutionary biology. Science. 2001;294(5550):2310–2314. doi: 10.1126/science.1065889. [DOI] [PubMed] [Google Scholar]
- 23.Ronquist F., Teslenko M., van der Mark P., Ayres D.L., Darling A., Hohna S. MrBayes 3.2: efficient Bayesian phylogenetic inference and model choice across a large model space. Syst. Biol. 2012;61(3):539–542. doi: 10.1093/sysbio/sys029. PubMed PMID: 22357727. Pubmed Central PMCID: 3329765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Morelli M.J., Thébaud G., Chadœuf J., King D.P., Haydon D.T., Soubeyrand S. A Bayesian inference framework to reconstruct transmission trees using epidemiological and genetic data. PLoS Comput. Biol. 2012;8(11):e1002768. doi: 10.1371/journal.pcbi.1002768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ypma R.J., Bataille A.M., Stegeman A., Koch G., Wallinga J., van Ballegooijen W.M. Unravelling transmission trees of infectious diseases by combining genetic and epidemiological data. Proc. Biol. Sci./R. Soc. 2012;279(1728):444–450. doi: 10.1098/rspb.2011.0913. PubMed PMID: 21733899. Pubmed Central PMCID: 3234549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Didelot X., Gardy J., Colijn C. Bayesian inference of infectious disease transmission from whole-genome sequence data. Mol. Biol. Evol. 2014;31(7):1869–1879. doi: 10.1093/molbev/msu121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ritchie M.D., Holzinger E.R., Li R., Pendergrass S.A., Kim D. Methods of integrating data to uncover genotype-phenotype interactions. Nat. Rev. Genet. 2015;16(2):85–97. doi: 10.1038/nrg3868. [DOI] [PubMed] [Google Scholar]
- 28.Chunara R., Smolinski M.S., Brownstein J.S. Why we need crowdsourced data in infectious disease surveillance. Curr. Infect. Dis. Rep. 2013;15(4):316–319. doi: 10.1007/s11908-013-0341-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gardy J.L., Johnston J.C., Sui S.J.H., Cook V.J., Shah L., Brodkin E. Whole-genome sequencing and social-network analysis of a tuberculosis outbreak. N. Engl. J. Med. 2011;364(8):730–739. doi: 10.1056/NEJMoa1003176. [DOI] [PubMed] [Google Scholar]
- 30.Roukos D.H. Novel clinico–genome network modeling for revolutionizing genotype–phenotype-based personalized cancer care. Expert. Rev. Mol. Diagn. 2010;10(1):33–48. doi: 10.1586/erm.09.69. [DOI] [PubMed] [Google Scholar]
- 31.Kong J., Cooper L.A., Wang F., Gutman D.A., Gao J., Chisolm C. Integrative, multimodal analysis of glioblastoma using TCGA molecular data, pathology images, and clinical outcomes. IEEE Trans. Bio-med. Eng. 2011;58(12):3469–3474. doi: 10.1109/TBME.2011.2169256. PubMed PMID: 21947516. Pubmed Central PMCID: 3292263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tenenbaum J.D., Avillach P., Benham-Hutchins M., Breitenstein M.K., Crowgey E.L., Hoffman M.A., Jiang X., Madhavan S., Mattison J.E., Nagarajan R., Ray B. An informatics research agenda to support precision medicine: seven key areas. J. Am. Med. Inform. Assoc. 2016:791–795. doi: 10.1093/jamia/ocv213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ritchie M.D., de Andrade M., Kuivaniemi H. The foundation of precision medicine: integration of electronic health records with genomics through basic, clinical, and translational research. Front. Genet. 2015;6 doi: 10.3389/fgene.2015.00104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ypma R.J., van Ballegooijen W.M., Wallinga J. Relating phylogenetic trees to transmission trees of infectious disease outbreaks. Genetics. 2013;195(3):1055–1062. doi: 10.1534/genetics.113.154856. PubMed PMID: 24037268. Pubmed Central PMCID: 3813836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jombart T., Cori A., Didelot X., Cauchemez S., Fraser C., Ferguson N. Bayesian reconstruction of disease outbreaks by combining epidemiologic and genomic data. PLoS Comput. Biol. 2014;10(1) doi: 10.1371/journal.pcbi.1003457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Famulare M., Hu H. Extracting transmission networks from phylogeographic data for epidemic and endemic diseases: Ebola virus in Sierra Leone, 2009 H1N1 pandemic influenza and polio in Nigeria. Int. Health. 2015;7(2):130–138. doi: 10.1093/inthealth/ihv012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sintchenko V., Holmes E.C. The role of pathogen genomics in assessing disease transmission. BMJ. 2015;350:h1314. doi: 10.1136/bmj.h1314. PubMed PMID: 25964672. [DOI] [PubMed] [Google Scholar]
- 38.Jombart T., Eggo R., Dodd P., Balloux F. Reconstructing disease outbreaks from genetic data: a graph approach. Heredity. 2011;106(2):383–390. doi: 10.1038/hdy.2010.78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Maslow J.N., Mulligan M.E., Arbeit R.D. Molecular epidemiology: application of contemporary techniques to the typing of microorganisms. Clin. Infect. Dis. 1993:153–162. doi: 10.1093/clinids/17.2.153. [DOI] [PubMed] [Google Scholar]
- 40.Cottam E.M., Thébaud G., Wadsworth J., Gloster J., Mansley L., Paton D.J. Integrating genetic and epidemiological data to determine transmission pathways of foot-and-mouth disease virus. Proc. R. Soc. Lond. B: Biol. Sci. 2008;275(1637):887–895. doi: 10.1098/rspb.2007.1442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Worby C.J., Chang H.-H., Hanage W.P., Lipsitch M. The distribution of pairwise genetic distances: a tool for investigating disease transmission. Genetics. 2014;198(4):1395–1404. doi: 10.1534/genetics.114.171538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hethcote H.W. The mathematics of infectious diseases. SIAM Rev. 2000;42(4):599–653. [Google Scholar]
- 43.Salathe M., Jones J.H. Dynamics and control of diseases in networks with community structure. PLoS Comput. Biol. 2010;6(4):e1000736. doi: 10.1371/journal.pcbi.1000736. PubMed PMID: 20386735. Pubmed Central PMCID: 2851561. Epub 2010/04/14.eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jombart T., Aanensen D.M., Baguelin M., Birrell P., Cauchemez S., Camacho A. OutbreakTools: a new platform for disease outbreak analysis using the R software. Epidemics. 2014;7:28–34. doi: 10.1016/j.epidem.2014.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Vega V.B., Ruan Y., Liu J., Lee W.H., Wei L.C., Se-Thoe S.Y. Mutational dynamics of the SARS coronavirus in cell culture and human populations isolated in 2003. BMC Infect. Dis. 2004;4(1):1. doi: 10.1186/1471-2334-4-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.D.L. Swofford. PAUP. Phylogenetic analysis using parsimony (and other methods). Version 4, Sinauer Associates, Sunderland, Massachusetts, 2003.
- 47.Nei M., Kumar S. Oxford University Press; 2000. Molecular Evolution and Phylogenetics. [Google Scholar]
- 48.Jombart T. Adegenet: a R package for the multivariate analysis of genetic markers. Bioinformatics. 2008;24(11):1403–1405. doi: 10.1093/bioinformatics/btn129. PubMed PMID: 18397895. [DOI] [PubMed] [Google Scholar]
- 49.Mollentze N., Nel L.H., Townsend S., Le Roux K., Hampson K., Haydon D.T. A Bayesian approach for inferring the dynamics of partially observed endemic infectious diseases from space-time-genetic data. Proc. R. Soc. Lond. B: Biol. Sci. 2014;281(1782):20133251. doi: 10.1098/rspb.2013.3251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jombart T., Cori A., Didelot X., Cauchemez S., Fraser C., Ferguson N. Bayesian reconstruction of disease outbreaks by combining epidemiologic and genomic data. PLoS Comput. Biol. 2014;10(1):e1003457. doi: 10.1371/journal.pcbi.1003457. PubMed PMID: 24465202. Pubmed Central PMCID: 3900386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ellison A.M. Bayesian inference in ecology. Ecol. Lett. 2004;7(6):509–520. [Google Scholar]
- 52.Andrieu C., De Freitas N., Doucet A., Jordan M.I. An introduction to MCMC for machine learning. Mach. Learn. 2003;50(1–2):5–43. [Google Scholar]
- 53.Cottam E.M., Haydon D.T., Paton D.J., Gloster J., Wilesmith J.W., Ferris N.P. Molecular epidemiology of the foot-and-mouth disease virus outbreak in the United Kingdom in 2001. J. Virol. 2006;80(22):11274–11282. doi: 10.1128/JVI.01236-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Clement M., Posada D., Crandall K.A. TCS: a computer program to estimate gene genealogies. Mol. Ecol. 2000;9(10):1657–1659. doi: 10.1046/j.1365-294x.2000.01020.x. [DOI] [PubMed] [Google Scholar]
- 55.Templeton A.R., Crandall K.A., Sing C.F. A cladistic analysis of phenotypic associations with haplotypes inferred from restriction endonuclease mapping and DNA sequence data. III. Cladogram estimation. Genetics. 1992;132(2):619–633. doi: 10.1093/genetics/132.2.619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Teunis P., Heijne J.C., Sukhrie F., van Eijkeren J., Koopmans M., Kretzschmar M. Infectious disease transmission as a forensic problem: who infected whom? J. R. Soc. Interface. 2013;10(81):20120955. doi: 10.1098/rsif.2012.0955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kimura M. Estimation of evolutionary distances between homologous nucleotide-sequences. Proc. Natl. Acad. Sci.-Biol. 1981;78(1):454–458. doi: 10.1073/pnas.78.1.454. PubMed PMID: WOS:A1981LA96300088. English. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Ruan Y., Wei C.L., Ling A.E., Vega V.B., Thoreau H., Thoe S.Y.S. Comparative full-length genome sequence analysis of 14 SARS coronavirus isolates and common mutations associated with putative origins of infection. The Lancet. 2003;361(9371):1779–1785. doi: 10.1016/S0140-6736(03)13414-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Holmes E.C., Ghedin E., Halpin R.A., Stockwell T.B., Zhang X.Q., Fleming R. Extensive geographical mixing of 2009 human H1N1 influenza A virus in a single university community. J. Virol. 2011;85(14):6923–6929. doi: 10.1128/JVI.00438-11. PubMed PMID: 21593168. Pubmed Central PMCID: 3126550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Poon L.L., Song T., Rosenfeld R., Lin X., Rogers M.B., Zhou B. Quantifying influenza virus diversity and transmission in humans. Nat. Genet. 2016;48(2):195–200. doi: 10.1038/ng.3479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Goff J., Rowe A., Brownstein J.S., Chunara R. Surveillance of acute respiratory infections using community-submitted symptoms and specimens for molecular diagnostic testing. PLoS Curr. 2014;7 doi: 10.1371/currents.outbreaks.0371243baa7f3810ba1279e30b96d3b6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Frost S.D., Pybus O.G., Gog J.R., Viboud C., Bonhoeffer S., Bedford T. Eight challenges in phylodynamic inference. Epidemics. 2015;10:88–92. doi: 10.1016/j.epidem.2014.09.001. PubMed PMID: 25843391. Pubmed Central PMCID: 4383806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Metzker M.L. Sequencing technologies—the next generation. Nat. Rev. Genet. 2010;11(1):31–46. doi: 10.1038/nrg2626. [DOI] [PubMed] [Google Scholar]