How Modelling Can Enhance the Analysis of Imperfect Epidemic Data

Abstract

Mathematical models play an increasingly important role in our understanding of the transmission and control of infectious diseases. Here, we present concrete examples illustrating how mathematical models, paired with rigorous statistical methods, are used to parse data of different levels of detail and breadth and estimate key epidemiological parameters (e.g., transmission and its determinants, severity, impact of interventions, drivers of epidemic dynamics) even when these parameters are not directly measurable, when data are limited, and when the epidemic process is only partially observed. Finally, we assess the hurdles to be taken to increase availability and applicability of these approaches in an effort to ultimately enhance their public health impact.

Highlights

Many data can be used to estimate the transmission potential of a pathogen, including descriptions of the transmission chains, human cluster sizes, sources of infection, and epidemic curves.

An important agenda in public health is understanding the impact of control methods. However, the dynamic nature of epidemics makes this task challenging. Models can disentangle the natural course of outbreaks from the effect of external factors.

In the absence of reliable surveillance data, models can reconstruct epidemic history by combining age-specific seroprevalence data with an understanding of the natural history of infection.

Mechanisms of immunity are hard to observe at an individual level, yet they affect population-level dynamics. Models can tease out such signatures.

Morbidity and mortality can be difficult to estimate when many infections are unobserved and severe infections are reported more often. Models can be used to correct for under-reporting and selection bias.

The Multiple Contributions of Modelling to the Study of Infectious Disease

Over the past 30 years, mathematical modelling has become an essential tool for the study of epidemics of infectious disease [1]. Such an approach is complementary to traditional methods in that, contrary to classical epidemiological methods common to both communicable and noncommunicable diseases, modelling explicitly accounts for the interactions between individuals in an effort to explain the complex transmission dynamics inherent in the spread of infectious diseases in populations. Mathematical models are now commonly used to address a variety of questions that can inform policy making, for example, the optimal allocation of intervention measures 2, 3, the planning and evaluation of vaccination programmes 4, 5, nowcasting and forecasting 6, 7, the design and evaluation of vaccine efficacy in clinical trials 8, 9, 10, and real-time risk assessment during epidemics 11, 12. A number of reviews have already covered different aspects of this quickly expanding field. For example, Grassly and Fraser explained basic principles [13], while Heesterbeek et al. [14] and Metcalf and Lessler [15] discussed their use and impact on policy making in the context of the complex landscape of global health and major emerging infectious disease outbreaks.

Here, we focus on yet another contribution of modelling and show how the use of these techniques can considerably strengthen the analyses of epidemiological data collected during an epidemic. We take the perspective of an epidemiologist who collected data during an epidemic and is now at the difficult stage of trying to estimate key epidemiological parameters (e.g., transmissibility, severity, proportion of asymptomatic infections, impact of interventions, drivers of spread and control) from these data, in a context where data collection may be affected by selection bias (e.g., severe cases are more likely to be detected), under-reporting or missing data issues (e.g., the source of infection of a case is unknown), and where the parameters of interest may therefore not be directly measurable. We highlight, with concrete examples, how modelling techniques have proved instrumental in tackling challenges associated with the analysis of such imperfect data, estimating key epidemiological parameters, and gaining essential insight into the underlying epidemic process.

Estimating Transmissibility and Transmission Risk Factors

The reproduction number R (see Glossary; also called the effective reproduction number) characterizes the level of transmission at a given time during an epidemic and is defined as the mean number of secondary infections caused by a case at that time. The epidemic can affect a substantial proportion of the population only if R  > 1 [1].

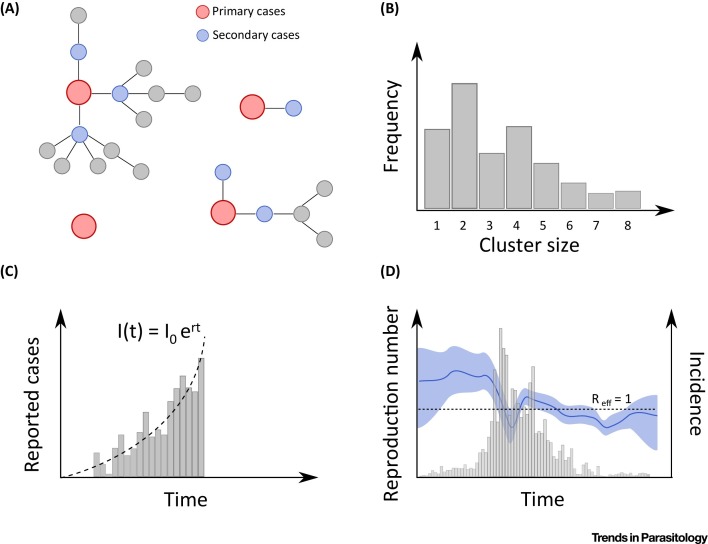
The most natural way to estimate reproduction numbers is to rely on data documenting chains of transmission (Figure 1 A). For example, during the large epidemic of Ebola in West Africa, major efforts were implemented to identify and reconstruct these chains. Faye et al. analysed such data for Conakry, the capital city of Guinea, during the first part of the epidemic (February–August, 2014) [16]. When the information about who was infected by whom is available, estimating reproduction numbers is straightforward and just a matter of counting secondary infections for each individual case. From these data, Faye et al. estimated that, at the start of the epidemic, an Ebola case infected on average 1.4, 0.4, and 0.5 contacts in the community, the hospital, and funeral settings, respectively, and that there was an important reduction of transmission in hospitals and funerals once controls were in place. They also demonstrated that hospitalization of cases halved their transmission potential in the community, highlighting the critical role of prompt case isolation to reduce community transmission; and that healthcare workers, who were at high risk of infection, contributed little to transmission.

Figure 1.

Approaches to Estimate the Reproduction Number. (A) When chains of transmission are available, the reproduction number is obtained by counting directly the number of secondary infections. (B) The reproduction number can also be estimated from the distribution of the sizes of clusters of human cases. (C) Epidemic time series are also informative. At the start of an epidemic, the number of cases grows exponentially, and the growth rate r can be used to estimate of the reproduction number. (D) During the course of an epidemic, variations of the reproduction number can also be estimated.

While data on chains of transmission are highly valuable, they are difficult or impossible to collect for many pathogens and are thus extremely rare. Modellers have therefore developed alternative approaches to characterize transmission from more partial and incomplete data. For example, upon the emergence of the highly pathogenic avian influenza strain H5N1, the prospect of a major severe influenza pandemic was raised if the virus were to increase its potential for interhuman transmission. In such situations, where we are confronted with stuttering chains of transmission in humans, Ferguson et al. argued that it would be possible to detect any such increase from the examination of the size of clusters of human cases (i.e., the number of human infections generated from a spillover from the reservoir) (Figure 1B) [17]. This is because the average size C of a cluster is expected to increase with the reproduction number R, with the simple relationship $C=1/\left(1-R\right)$. However, a potential difficulty in using cluster size to evaluate transmissibility is that selection biases (e.g., larger clusters are more likely to be detected) or under-reporting (i.e., a proportion of cases are missed during investigations) may bias inference in different directions. Methods have therefore been proposed to correct for such effects [18]. It is also well acknowledged that case-to-case heterogeneity in infectivity that can cause superspreading events must be accounted for 19, 20.

These approaches may sometimes prove impractical if it is not possible to measure the size of human clusters. For example, in 2012, human cases of swine-origin influenza A H3N2v infections were detected in the USA, in particular among people attending animal fairs [21]. The large volume of visitors at these fairs prevented the implementation of thorough epidemiological investigations required to identify all infected persons and determine cluster sizes. How then to interpret the observation that 50% of cases detected by viral surveillance had not been exposed to swines? Was that the sign of a starting pandemic? When we observe a set of independent cases for whom the likely source of infection (human vs reservoir) has been identified, the reproduction number R can be estimated from the proportion F of cases linked to the reservoir, with the simple formula: R  = 1 − F  = 0.5 [21]. While the transmission potential of the H3N2v strain was higher than that of other swine strains, it was therefore still substantially smaller than what is required to generate a pandemic (i.e., R  < 1). Estimation methods based on the size of human clusters or the proportion of cases linked to the reservoir are most relevant for situations where stuttering chains of transmission are observed (i.e., there is not yet strong evidence for high interhuman transmission potential) since a point estimate for R is available with these methods only when R  < 1. These methods can be used to test the hypothesis that R  > 1; but if the hypothesis cannot be rejected, other approaches and types of data will be required to derive a point estimate of R.

Data collected during detailed outbreak investigations can provide critical insights into transmission patterns. For example, if two members of the same household become sick – with the delay between symptom onsets roughly equal to the serial interval of the disease – this may suggest that the first case infected the second. However, other sources of infection (e.g., from outside the household or from other household members) cannot be excluded. Statistical methods have been developed to probabilistically reconstruct chains of transmission and infer transmission risk factors from data gathered during outbreak investigations where all members of a social structure (e.g., household, school, village) are investigated and times of symptom onset are recorded. These methods were used extensively to characterize the transmission of influenza in households from a powerful study design where household contacts of confirmed influenza cases are followed-up for a few weeks after symptom onset of the first case. These analyses provided key insights about the determinants of influenza transmission – such as estimates of the risk of household transmission, and how this varies with household size, the infectivity and susceptibility of children relative to adults, the serial interval of influenza (which is important to determine for how long cases should be isolated, to assess the impact of treatment delays on transmission or estimate other parameters such as the reproduction number), the relationship between viral shedding and infectivity, and the protective effect of baseline antibody titres 2, 22, 23, 24, 25, 26, 27, 28. These methods have also been used to investigate transmission in more complex social settings such as a school [29] or a small village [30]. In the latter example, Salje et al. were able to estimate that chikungunya transmission occurred on average at about 100 m from the household location, based on a detailed investigation of a chikungunya outbreak in a village in Bangladesh where each household was geotagged [30].

Epidemic time series, which are often available through routine surveillance, can also be used to decipher fundamental aspects of spread and estimate parameters such as the reproduction number. The number of cases at the start of an epidemic usually grows exponentially, which means that the number of cases at time t can be modelled as $I\left(t\right)=I_0{e}^{rt},$ where I ₀ is the number of cases at time 0, and r is the exponential growth rate. During exponential growth, the logarithm of the number of cases grows linearly $\{\text{ln}\left[I\left(t\right)\right]=ln\left(I_0\right)+rt\}$ so that the exponential growth rate parameter r can be estimated with a simple linear regression of the log-incidence. The reproduction number R can then be derived from the exponential growth rate estimate and the distribution of the generation time of the disease (Figure 1C) [31]. For a simple model like the susceptible–infectious–recovered (SIR) model (Box 1 ), the reproduction number can be estimated as R  = 1 +   r  . GT, where GT is the mean generation time. Mills et al. used such an approach to estimate the reproduction number of the 1918 influenza pandemic from the analysis of weekly mortality records in 45 US cities, and to inform efforts to prepare for a severe influenza pandemic [32].

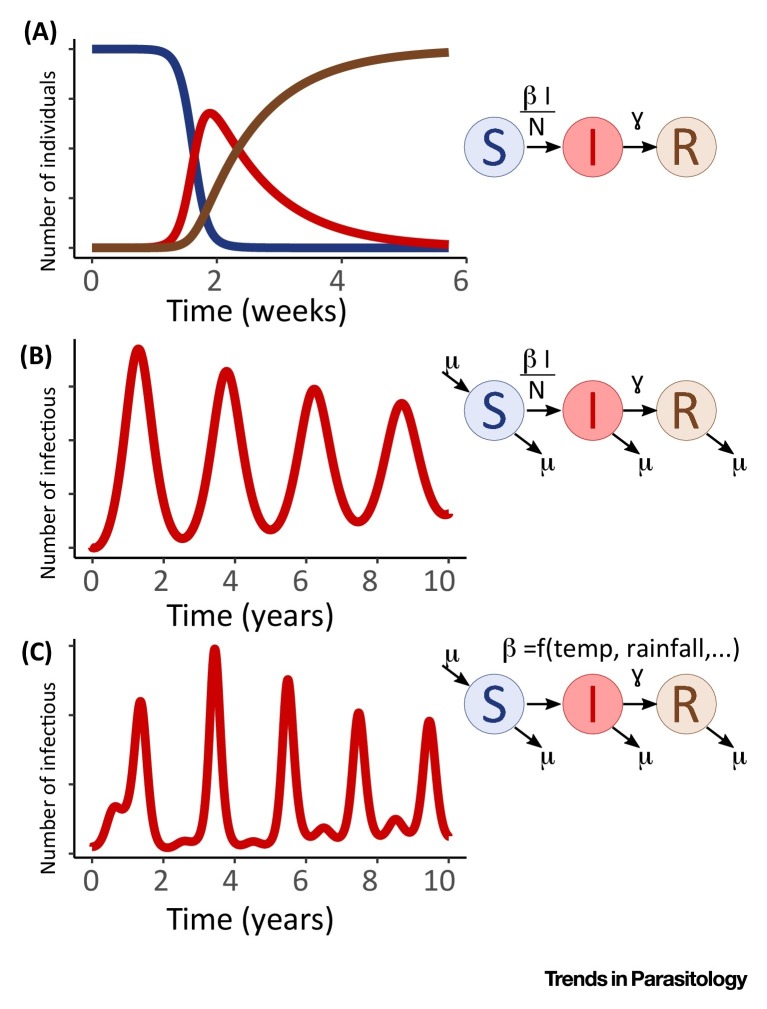
Figure I.

Schematics of Compartmental Models and Population Dynamics.

Box 1. Compartmental Models – The Susceptible–Infectious–Recovered (SIR) Model.

Compartmental models are some of the most established models in the field of infectious disease epidemiology. In one of the simplest versions, the susceptible–infectious–recovered (SIR) model, the population is divided up into susceptible (S), infectious (I), and recovered (R; i.e., immune) individuals and can transit between these compartments over time. A susceptible individual becomes infected at a rate of β I/N and remains infectious for a duration of 1/γ before recovering and acquiring immunity. At the beginning of an epidemic, the number of infectious individuals increases exponentially. As the number of susceptible individuals start to deplete, and infectious individuals recover, transmission diminishes, and the outbreak reaches its peak before dying out completely (Figure IA). This model is valid for the time scale of a typical epidemic, yet does not capture replenishment of susceptible populations through, for example, birth and migration processes. This is an important underlying driver of recurrence of epidemics and may, in particular in childhood diseases, result in periodic outbreaks (Figure IB), although at an even longer time scale the model may result in a positive steady state of the number of infected. While the simplest versions of the SIR model assume the transmission parameter β to be constant over the course of an epidemic, periodic changes thereof could be another explanation for observed periodicity in infection dynamics. In Figure IC we show the impact of a seasonally forced β (for instance as a result of climatic variations) on transmission dynamics. Interventions, for instance aimed at reducing contact rates between people (i.e., social isolation), could further reduce the transmission parameter and stop epidemics from following their natural course. Depending on the characteristics of the pathogen and its transmission, other compartments can be added to the model, such as an ‘exposed’ compartment (SEIR model) to account for an incubation period that determines the time individuals are infected but not yet infectious. Further, departures from simplifying assumptions, such as homogeneous mixing (i.e., each individual has an equal probability of being in contact with any other individual in a population), can be implemented depending on the context and transmission system.

Statistical methods for estimating the parameters of these models have greatly improved in the past 20 years. While earlier approaches such as the time-series SIR (TSIR) model imposed some relatively strong constraints about the structure of the data and the underlying transmission model (e.g., the time step of the data had to be equal to the generation time of the pathogen) [40], these constraints were relaxed in subsequent developments, allowing more flexibility and model complexity 65, 66, 67.

Alt-text: Box 1

It is important to note that a number of extrinsic factors, such as interventions, climate, entomological, or social factors, may impact the reproduction number over time. Methods have therefore been developed to track trends in the reproduction number during the course of an epidemic, again from the analysis of the epidemic curve and prior knowledge about the generation time (Figure 1D) [33]. These approaches, for example, showed that, during the SARS epidemic in Hong Kong in 2001, the reproduction number dropped from 3.6 to 0.7 following the implementation of control measures [33]. Extensions have since been proposed to ensure that estimates can be provided in near real-time, even when some of the secondary infections have not yet been detected 34, 35, 36.

Similarly, changes in the reproduction number over time can indicate whether a disease system is nearing elimination, such as in response to mass drug administration campaigns against parasitic worm diseases, including schistosomiasis, onchocerciasis, and lymphatic filariasis. Assessing whether a disease system has reached its breakpoint, that is, a state below which parasite densities are too low for the population to sustain, is critically important to determine whether it is warranted to end a campaign. Typically, such questions are addressed by fitting complex transmission models to epidemiological data (e.g., annual microfilaria prevalence levels) and examining whether the system, under the fitted parameters, indeed approaches elimination and with what level of certainty 37, 38. Recent efforts have focused on more general, ‘model-free’ approaches that are based on the idea that parasite populations below the breakpoint exhibit dynamics that can be distinguished in epidemiological data of parasite burden or prevalence [39]. Specifically, the authors demonstrate a direct relationship between the reproduction number (for macroparasites the mean number of parasites produced by a single reproductive parasite) and the rate of change of the empirically measured mean worm burden, as captured by the elimination feasibility coefficient. Such efforts critically rely on measurements of infection intensity both prior to and during campaigns, as well as reliable data on treatment coverage.

Unravelling Drivers of Epidemic Dynamics

When the disease starts to affect a substantial proportion of a population, evaluating the impact of extrinsic factors on transmission is complicated by the fact that the reproduction number $R\left(t\right)$ at time t also depends on the level of immunity in the population at that time: $R\left(t\right)=R_0\left(t\right).S\left(t\right)$ where $R_0\left(t\right)$ is the basic reproduction number (i.e., the expected number of secondary infections caused by a case if the whole population were susceptible, under conditions equal to those observed at time t) and $S\left(t\right)$ is the proportion of susceptible individuals in the population. As immunity builds up in the population, the effective reproduction number is therefore expected to decline, even if there is no change in conditions (e.g., climatic conditions, control efforts, behaviour change). To ensure that estimates of the impact of extrinsic factors are not biased, it is therefore important to correctly account for the depletion of susceptible individuals in the population. To this end, a suite of compartmental, SIR-type models were developed to track the build-up of immunity along with other key quantities such as the number of infections (Box 1).

These models have proved extremely useful for understanding the complex interplay between transmission factors and immunity in the shaping of epidemics. Consider measles, which caused important cyclical outbreaks in industrialized countries before vaccine introduction. Fitting such models to biweekly measles notifications from England and Wales during 1944–1964, Finkenstädt and Grenfell demonstrated that fluctuations of the susceptible population (driven by infections and births) and seasonal variations in the transmission rate (driven by school holidays) were necessary to explain the observed cyclical patterns of outbreaks during that time period [40]. Moreover, the study showed that the shift from annual to biannual cycles after 1950 was explained by a reduction in birth rates, resulting in a slower replenishment of the susceptible population, and that only about 50% of measles cases were reported.

The framework also helped to decipher the drivers of epidemic seasonality or the impact of interventions. For example, from influenza-related mortality data in the USA, Shaman et al. demonstrated that the transmission of influenza was strongly modulated by absolute humidity [41], while Perkins et al. analysed chikungunya surveillance data from 50 countries to describe how chikungunya transmission was impacted by temperature and precipitation [42]. During the 1918 pandemic influenza, Bootsma and Ferguson observed stark heterogeneity in the presence and size of a second wave (the autumn wave) across cities in the USA – more than seen in European cities, where only one city experienced a second wave [43]. The authors posited the hypothesis that autumn waves resulted from imperfect, short-lived efforts that controlled transmission during the first wave, yet, when lifted, facilitated a second wave due to a susceptible population larger than would be expected in the absence of control. To test this hypothesis and estimate the impact of social distancing (e.g., school closures, banning of mass gatherings, case isolation, and hygiene measures), the authors fitted Susceptible-Exposed-Infectious-Recovered (SEIR)-type models (Box 1) to observed time series of pneumonic and influenza mortality. They found that (i) including both a time-limited effect of social distancing (as informed by onset and end dates of control) and changes in contact rates in response to increasing mortality best explained the observed time series, and that (ii) the impact of control efforts was limited (reduction in mortality 10–30%) yet could have been improved if they were implemented earlier and left in place for longer.

Models have also been used to parse epidemiological data and assess the presence, strength, and duration of cross-immunity (i.e., where infection by one strain or serotype results in immunity against others) and other complex mechanisms of immunity. SIR-type models (Box 1) can be expanded to account for the circulation of multiple strains with cross-immunity and the waning of immunity. By comparing the fit of models with and without cross-immunity to enterovirus surveillance data in Japan, Takahashi et al. demonstrated that, following infection by enterovirus serotype A16, individuals are immune to infection by closely related enterovirus serotype A71 for 2 months [44]. Similarly, Reich et al. estimated that individuals infected by one of the four dengue serotypes remained immune to the other serotypes for 1–3 years, based on 30 years of serotyped monthly dengue notification data from Thailand 45, 46, 47.

Reconstructing Transmission History from Serological Data

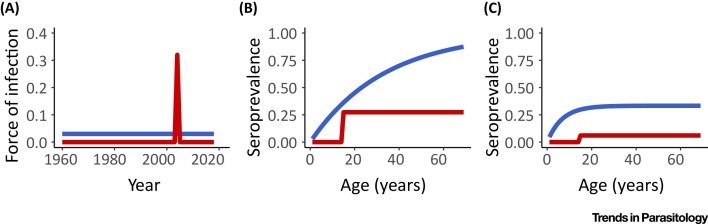
While time-series of cases have proven helpful to disentangle a multitude of epidemiological processes, for infectious diseases with limited surveillance capacities and a high risk of misdiagnosis, alternative data types and associated methods are needed to answer questions about the history of pathogen circulation. In such a situation, age-stratified serological surveys, which assess immunological markers of previous infections, can be used to reconstruct the history of circulation of a pathogen in the population. Consider a disease system where infection causes lifelong immunity. In a scenario where a single epidemic of the pathogen occurred 15 years ago (i.e. in 2003) and infected 30% of the population, we would expect that 30% of those aged 15 years or older in 2018 are seropositive, while none of those aged <15 years should be (Figure 2 A,B, red line). By contrast, if there was constant low-level circulation of the pathogen, we would expect seroprevalence to increase gradually with age (Figure 2A,B, blue line). The age-stratified seroprevalence therefore contains a strong signature of the long-term history of pathogen circulation. Serocatalytic models have been developed to formally reconstruct year-to-year variations in the force of infection from such data [48]. Based on two age-stratified serological studies, Salje et al. used these approaches to show that, over the past 60 years, four distinct chikungunya outbreaks occurred in the Philippines, each affecting about a quarter of the population [49]. Similarly, combining age-stratified data from over 100 serosurveys, Cucunubá et al. used catalytic models to quantify the impact of the Chagas’ disease control and elimination programme in Colombia during the past three decades [50]. The study showed that, while the force of infection dropped by up to 90% in urban settings, it remained constant in remote areas, highlighting major geographic variations in the impact of the programme.

Figure 2.

Estimating Historical Patterns of Infection from Age-stratified Serological Surveys. The panels show how the history of circulation of a pathogen (A) is expected to impact age-stratified seroprevalence when immunity is life-long (B) or temporary (C). In the red scenario, an epidemic infecting 30% of the population occurred 15 years ago. If immunity is life-long, the seroprevalence is expected to be 30% among those aged ≥15 years but null among younger individuals (B). In the blue scenario, low-level continuous circulation of the pathogen (A) is expected to lead to a slow increase of seroprevalence with age (B). In the case of waning immunity, a plateau in seroprevalence for older individuals may be expected (C). Catalytic models were developed to reconstruct the history of circulation of the pathogen from serological surveys. The force of infection is the annual probability a susceptible individual will become infected.

The classical catalytic models can be modified to relax the hypothesis of lifelong immunity. Reversible catalytic models were used particularly for malaria, where each individual is born susceptible, can become seropositive upon exposure to malaria, but later revert to the susceptible state. Seroreversion leads to a plateau in the age-profile of seroprevalence that accounts for the switching of individuals between immune and susceptible states (Figure 2C). Using these methods, Drakeley et al. investigated the prevalence of IgG antibodies of Plasmodium falciparum antigens in several locations of Tanzania, and estimated a half-life of 50 years for MSP-1₁₉ antibody as well as the rates of seroconversion [51]. Reversible catalytic models were used in other settings, for instance in Northern Ghana [52], where the authors established the wide heterogeneity in seroconversion and seroreversion rates between the antibodies to antigens specific to various stages of the parasite life cycle.

Quantifying Asymptomatic Infections and Disease Severity

The clinical presentation for many diseases can vary from fully asymptomatic to severe symptoms requiring hospitalization and death. Quantifying the proportion of subclinical infections, or measures of severity such as the case fatality ratio (CFR), is crucial to understanding epidemic dynamics and disease burden. This is, however, a challenging task. For example, in 2009, when the swine-origin influenza pandemic H1N1pdm09 started in Mexico, the first estimates of the CFR obtained from Mexican surveillance data by dividing the number of reported deaths by the number of reported cases overestimated the CFR by two orders of magnitude. This is because, while deaths (i.e., the numerator of the CFR) were relatively well reported, only very severe cases were picked up by surveillance and so the total number of infections (i.e., the denominator of the CFR) was completely underestimated. To estimate this denominator, Fraser et al. decided that, instead of using data from Mexican surveillance that was getting saturated and missed a lot of mild cases, they would rely on surveillance implemented by developed countries around the world to detect sick travellers returning from Mexico as it was likely to have better sensitivity [12]. From the number of influenza cases detected among returning travellers, and air-passenger data documenting the total number of travellers returning from Mexico and the average duration of stay in Mexico, they were able to back-calculate the size of the Mexican epidemic and derive the CFR. This was done under the assumption that visitors mixed perfectly with the Mexican population. Their estimate of the CFR was lower than the one obtained from the Mexican surveillance; but it still overestimated the CFR, possibly because travellers were actually less likely to be exposed to influenza than Mexican inhabitants due to inhomogeneous mixing.

By contrast, to estimate the total number of MERS-CoV infections in Saudi Arabia, Lessler et al. relied on a detailed comparison of cases detected by passive surveillance (e.g., cases identified because they seek care with MERS-like symptoms) and active surveillance (e.g., investigation of the contacts of confirmed cases) [53]. The two surveillance systems each present their own strengths and weaknesses: passive surveillance is expected to detect most severe cases but will overestimate severity; while active surveillance is far from exhaustive but should provide more accurate estimates of the proportion of infections that become symptomatic. By combining data from the two systems, Lessler et al. were able to derive from the number of severe cases (passive surveillance data) and the severity profile of cases (active surveillance data) the total number of MERS-CoV infections. They estimated that about half of MERS-CoV infections had been missed by surveillance in 2012–2014 with the probability of developing symptoms ranging from 11% in persons under 10 years of age to 88% in those aged >70 years.

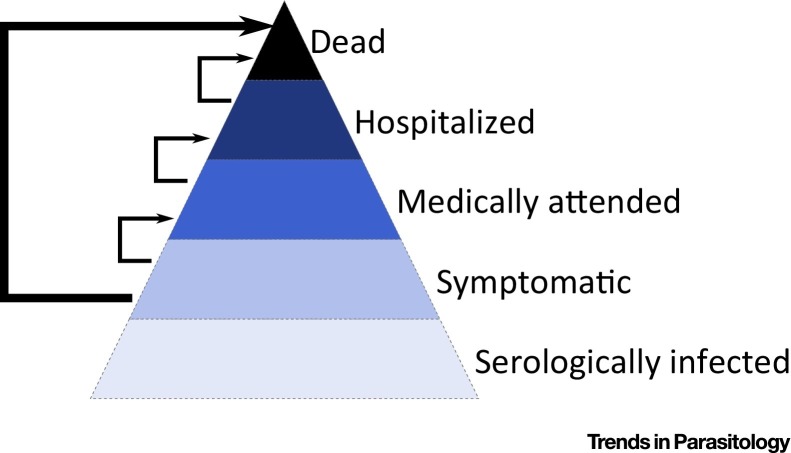
For a pathogen with low severity, such as the H1N1pdm09 pandemic influenza strain, it may prove difficult to estimate the CFR from a single cohort of infected individuals as this would require very large numbers of participants [54]. Instead, Presanis et al. derived ‘pyramidal’ estimates of severity [55]. To estimate the symptomatic CFR, that is, the proportion of symptomatic cases who died, they considered the conditional probabilities of the different steps a symptomatic case has to go through before dying: the probability of medical attendance among symptomatic cases, the probability of hospitalization among medically attended cases, and the probability of death after hospitalization (Figure 3 ). Each probability was estimated using different datasets: a CDC survey on health-seeking behaviours following influenza-like illnesses, a study among medically attended infection in Milwaukee, and another study among hospitalized cases in New York. The symptomatic case fatality ratio was estimated at 0.048%.

Figure 3.

Pyramide of Severity. The proportion of symptomatic individuals that die can be estimated from the conditional probabilities of the different steps that a symptomatic case has to go through before dying (e.g., probability of a symptomatic case being medically attended, medical attendance to hospitalization, hospitalization to death) that can be derived from different data sources [55].

Finally, even when asymptomatic or inapparent infections are not observed at all, the impact they have on the epidemic dynamics may be observed on apparently unrelated statistics, providing a pathway to characterize them. For example, Fraser et al. used reporting of symptoms during the 1918 influenza outbreak in a large sample of households in Baltimore to estimate the proportion of asymptomatic infections [56]. The main idea behind their approach is that, if a large proportion of household members report symptoms, this indicates that the proportion of asymptomatic infections cannot be very high. The authors used a chain-binomial model [57] which describes the expected distribution of households according to their size and the number of infected members given two parameters: the probability of contracting the infection from the community (i.e., from outside the household) and the probability of transmission from an infected member of the household to a susceptible one. This classical model was expanded to include a probability of asymptomatic infection, and thus to describe the expected distribution of households according to their size and the number of members reporting symptoms. The authors concluded that, during the 1918 influenza pandemic, the probability of asymptomatic infection was very low (<6%).

Concluding Remarks

In conclusion, modelling has become an important tool to enhance the analysis of imperfect epidemic data and estimate key epidemiological parameters even when they are not directly measurable or when data are limited and imperfect. There are, however, important hurdles to overcome before the methods discussed here can be used by all (see Outstanding Questions). First, a lot of infectious disease epidemiologists may simply be unaware of these developments, and it is important to better communicate these approaches to this audience – for example, in reviews, such as this one, and with concrete examples. Interested epidemiologists are encouraged to receive training in epidemic modelling, for example by attending one of the few dedicated short courses. While short-course participants are unlikely to become expert modellers after 1 or 2 weeks training, these courses can prove extremely helpful to build a deeper understanding of the field and what can and cannot be achieved with modelling [58]. Another important challenge to make these approaches available to all is the persisting lack of user-friendly software designed for nonexperts [34], although important efforts are being made to address this gap (see e.g., the RECON initiativei or increasingly common code-sharing efforts [59]). While a lot of simple tasks can be automated in generic and user-friendly tools, the analysis of more complex datasets with relatively atypical structures is likely to benefit from the investment of expert modellers, which can best be achieved through collaboration. These collaborations are particularly important during epidemic crises where it is essential to develop an efficient flow to quickly collect, process, and analyse data and report results back to the public health community [11]. Finally, while we focused this paper on the analyses of epidemiological data gathered during infectious disease epidemics, major developments are ongoing to better integrate other types of data (e.g., social media [60], viral genetic sequences 61, 62, contact and behavioural data 63, 64) into these analyses as well.

Outstanding Questions.

How can we reduce the gap between methods of development and implementation in the field, to make tools more accessible for the wider public health community?

How can we minimize delays between data collection, analysis, and communication of findings to inform outbreak responses in time?

How can we integrate data from different sources (social media data, viral genetic sequences) to take advantage of their complementarity?

Glossary

Case fatality ratio

the proportion of deaths among infected individuals.

Force of infection

the per capita rate of infection in susceptible individuals.

Generation time

the time delay between infection in a particular case and infection in people infected by that case.

Reproduction number

the mean number of persons infected by a case.

Serial interval

the time delay between symptom onset in a given case and in persons infected by that case.

Serocatalytic models

a class of model used to estimate the annual rate of seroconversion from the age-profile of seroprevalence.

Resources

ⁱ www.repidemicsconsortium.org/