Intelligent Metamaterials Based on Nonlinearity for Magnetic Resonance Imaging

Graphical Abstract

Coupled nonlinear metamaterials, featuring the self-adaptive, or intelligent, response that selectively amplifies the magnetic field, are harnessed to enhance the magnetic field for lower radiofrequency energy excitation and suppress its resonance for higher energy excitation. The intelligent metamaterials serve to enhance the signal-to-noise ratio of magnetic resonance imaging in excess of 10-fold.

Metamaterials provide a powerful platform to probe and enhance nonlinear responses in physical systems towards myriad applications. Herein, we report the development of a coupled nonlinear metamaterial (NLMM) featuring a self-adaptive response that selectively amplifies the magnetic field. The resonance of the NLMM is suppressed in response to higher degrees of radiofrequency excitation strength and recovers during a subsequent low excitation strength phase, thereby exhibiting an intelligent, or nonlinear, behavior by passively sensing excitation signal strength and responding accordingly. The nonlinear response of the NLMM enables us to boost the signal-to-noise ratio during magnetic resonance imaging to an unprecedented degree. Our results provide insights into a new paradigm to construct NLMMs consisting of coupled resonators and pave the way towards the utilization of NLMMs to address a host of practical technological applications.

Metamaterials represent a major class of rationally designed composites, the range of possible effective material properties of which is unparalleled in naturally occurring materials. Electromagnetic metamaterials feature unit cell designs intended to tailor the effective electric and magnetic properties of the artificial materials, such as the effective permittivity, permeability,^{[1, 2]} and chirality,^{[3, 4]} from the microwave to the optical regimes. Myriad unique phenomena and functionalities, including invisibility cloaking,^[5] subwavelength resolution imaging,^[6] transformation optics,^[7] hyperbolic responses,^[8] and perfect absorption,^[9] among others, have been achieved by leveraging the on-demand material properties of electromagnetic metamaterials. Another notable feature of metamaterials is the strong electromagnetic near-field confinement effect in the vicinity of their unit cells. Through the incorporation of quantum materials in the metamaterial unit cells, significant nonlinear responses have been demonstrated from the microwave and terahertz to the optical regime. ^[10,11] The capacity of metamaterials for electric field confinement has enabled the realization of a range of physical phenomena in metamaterials, such as electron emission^[12] and phase transition in quantum materials.^[13] In turn, the electric field enhancement resulting from the near-field confinement leads to nonlinear responses in metamaterials that have been harnessed to enable high harmonic generation,^[14] saturable absorption,^[15], phase-conjugation,^[16] and optical electrifying effects,^[17] among other features.

In addition to confining the electric field, metamaterials also are capable of interacting with and efficiently tailoring the magnetic field. The ability of metamaterials to manipulate the magnetic field has enabled their applications to inductive wireless power transfer^[18], enhancement of the magneto-optic effect,^[19], high-quality sensing,^[20,21] plasmonic black absorber,^[22] and magnetic field confinement,^[23,24] among others. Another important application of the capacity for magnetic field manipulation is magnetic resonance imaging (MRI), which is the focus herein. For example, negative permeability metamaterials have been employed as waveguides^[25] and lenses^[26] to image deep tissues using 1.5 Tesla (T) MRI systems and a cylindrical meta-atom has been developed to mitigate the field inhomogeneity in 7 T MRI systems based on the Kerker effect.^[27] Recently, judiciously designed metamaterials, consisting of wire^[28] or helical resonator arrays,^[29] have been utilized to enhance the signal-to-noise ratio (SNR) of the MRI by amplifying the RF magnetic field strength due to their capacity for magnetic field enhancement. However, an ongoing limitation of currently-available linear metamaterials (LMMs) for enhancing SNR in MRI systems reported to date is their linear nature, resulting in an amplification of the magnetic field during both radiofrequency (RF) transmission and reception phases in MRI, as shown in Figure 1a. The adoption of a linear metamaterial in MRI therefore requires modification of the RF excitation pulses during the transmission phase,^[28,29] resulting in undue complications, suboptimal performance, potential safety concerns, and a substantial impediment to clinical adoption.

Figure 1.

Concept of the nonlinear metamaterial (NLMM). a). Illustrative comparison of the linear metamaterial (LMM) and the NLMM. The LMM enhances the magnetic field during both the RF transmission and reception phases, while the NLMM remains silent during RF transmission and magnifies the magnetic field during RF reception. b) Schematic and e) theoretical oscillation amplitude of the linear metamaterial. c) Schematic and f) theoretical analysis results of the varactor-loaded spit ring resonator (VLSRR). d) Schematic of the nonlinear metamaterial consisting of a coupled liner helical array and VLSRR and g) its theoretical response when k = 0.2 and Δω = 0.3. h) - j) Calculated frequency response of the NLMM at different excitation strengths for varied conditions, e.g. k = 0.05, Δω = 0.3; k = 0.2, Δω = 0.3; and k = 0.2, Δω = 0; respectively.

Nonlinear metamaterials (NLMMs) yield an opportunity to construct intelligent and self-adaptive metamaterials in order to selectively enhance the magnetic field during MRI. By leveraging the voltage-dependent capacitance of a varactor diode induced by a reverse-biased p–n junction^{[30, 31]}, we developed an NLMM operating at RF frequencies. As opposed to the addition of a varactor in each unit cell of the metamaterial array, we herein introduce an NLMM featuring a single nonlinear resonator coupled to a linear metamaterial in order to selectively control the resonance as a function of excitation strength. Notably, we demonstrate that this newly-developed NLMM remains silent during the transmission phase of MRI, allowing for the uniform and optimal excitation of the subject, and becomes active during the reception phase, leading to enhancement of the magnetic field and amplification of the SNR, as shown in Figure 1a.

We firstly consider the nonlinear resonance response of the NLMMs’ oscillation mode amplitude using the lumped coupled-mode theory (CMT), which is widely employed to describe the resonance response of electromagnetic metamaterials.^{[32, 33]} To this end, we begin with the response of linear metamaterials (LMMs), expressed by:^[34]

$$\frac{d{a}_1}{dt}=\left[j{\omega }_{o1}-\frac{1}{{\tau }_{e1}}-\frac{1}{{\tau }_{01}}\right]a_1+\sqrt{\frac{2}{{\tau }_{e1}}}{s}_{+}$$ (1)

in which a₁ represents the mode amplitude of the resonator, 1/τ_e1 and 1/τ₀₁ are the decay rates due to the radiation loss and ohmic loss, respectively, and s₊ represents the excitation signal. The equation is solved in the frequency domain as is described in detail in Section 1 of the Supporting Information. For an LMM consisting of an array of helices, as shown in Figure 1b, the response of its collective mode may be simply modeled using Eq. (1), with the oscillation strength of a resonator array maximized at the resonance frequency.^[29] The response of the resonator (|a₁|/|s₊|) is independent of the excitation strength, as illustrated by the results shown in Figure 1e. The resonance of the metamaterial array induces a magnetic field enhancement in the near field of the array. Of note, the CMT provides a lumped parameter description of the response but neglects design details, therefore, this approach to modeling the coupled resonators remains valid for LMMs consisting of arbitrary numbers of unit cells, such as single unit cells, 2 × 1, or 4 × 4 unit cell configurations, among others.

In contradistinction to the response of the LMMs described above, in cases in which there is an existing nonlinear component within a resonator, such as a varactor in a split-ring resonator (SRR, as shown in Figure 1c), the response of the resonator is dependent upon the excitation strength. In the case of a varactor-loaded split ring resonator (VLSRR), its resonance frequency varies as a function of the oscillation strength in the resonator. When the oscillation strength in the VLSRR is relatively low, the varactor maintains its original capacitance. However, when the oscillation strength in the VLSRR is relatively high, the rectifying effect in the varactor acts as driving voltage to the varactor and increases its capacitance,^[30,31] which in turn decreases the resonance frequency of the VLSRR. The excitation power-dependent response of the VLSRR is modeled by:

$$\frac{d{a}_2}{dt}=\left[j({\omega }_{o2}-{\lambda }_0\left|a_2\right|)-\frac{1}{{\tau }_{e2}}-\frac{1}{{\tau }_{02}}\right]a_2+\sqrt{\frac{2}{{\tau }_{e2}}}{s}_{+}$$ (2)

where a₂ is the mode amplitude of the VLSRR, ω_o2 is the original resonance frequency of the VLSRR, 1/τ_e2 and 1/τ₀₂ are the decay rates due to radiation and ohmic loss, respectively, and λ₀ is the nonlinear coefficient determined by the properties of the varactor. The derivation and solution of Equation 2 may be found in Section 1 of the Supporting Information. When the excitation strength is low (e.g. |s₊| = 0.001), the VLSRR behaves in a linear fashion with its peak amplitude at the designated resonance frequency (ω_o2), as shown in Figure 1f. As the excitation strength increases, the resonance frequency of the VLSRR shifts to lower frequencies. When the excitation strength is sufficiently high, we observe an abrupt transition in the spectrum as the frequency increases. This is due to the bi-stable nonlinear behavior in the amplitude response of the VLSRR (please see Section 1 and Figure S1 in the Supporting Information). Along with the frequency shift, the peak oscillation amplitude in the resonator decreases. The resonance frequency difference between the LMM and VLSRR (Δω = (ω_o2 - ω_o1) / ω_o1) may be any arbitrary value for general cases.

When an LMM composed of a helical resonator array and a VLSRR are proximate to one another, a nonlinear metamaterial (NLMM) is formed, as shown in Figure 1d. A coupling factor (k) is introduced into the system to describe the interaction between the LMM and the VLSRR as follows:^[35]

$$\left[\begin{array}{c}\frac{d{a}_1}{dt}\\ \frac{d{a}_2}{dt}\end{array}\right]=\left[\begin{array}{cc}j{\omega }_{o1}-\frac{1}{{\tau }_{e1}}-\frac{1}{{\tau }_{o1}}& jk\\ jk& j\left[(1+\mathrm{\Delta }\omega ){\omega }_{o1}-{\lambda }_0\left|a_2\right|\right]-\frac{1}{{\tau }_{e2}}-\frac{1}{{\tau }_{02}}\end{array}\right]\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]+\left[\begin{array}{c}\sqrt{\frac{2}{{\tau }_{e1}}}\\ \sqrt{\frac{2}{{\tau }_{e2}}}\end{array}\right]s_{+}$$ (3)

In this system, two parameters, Δω and k, are variables, while all other parameters may be determined by the material properties and structural design. In Figure 1g, we assume an arbitrary coupling factor of k = 0.2, which indicates a moderate degree of coupling between the helical resonator and the nonlinear coil, and Δω = 0.3 as an arbitrary resonance frequency difference. The calculated oscillation mode amplitudes for different excitation strengths are shown in Figure 1g. Due to the coupling effect between the LMM and the VLSRR, two resonance peaks appear in the spectra of the low excitation condition. In the first mode, the resonance of the LMM and the VLSRR are in phase, while they are out of phase in the second mode. Qualitatively, the strong oscillation amplitude in the first mode yields a strong magnetic field enhancement in the vicinity of the NLMM when the excitation is low. As the excitation power increases, both resonance modes shift to lower frequencies and a bi-stable response appears when the excitation surpasses a critical excitation strength. The peak oscillation amplitude decreases dramatically, which yields a decrease in the magnetic field enhancement. Using the CMT model, we investigated the effect of the coupling factor (k) and resonance frequency difference (Δω) on the resonance frequency and amplitude. As shown in Figures 1h-1j, we calculated the spectra for different combinations of k and Δω, and conclude that the excitation-dependent response is valid for a wide range of parameters. Furthermore, the degree of modulation of the oscillation strength may also be tailored through the frequency difference (k) and coupling factor (Δω).

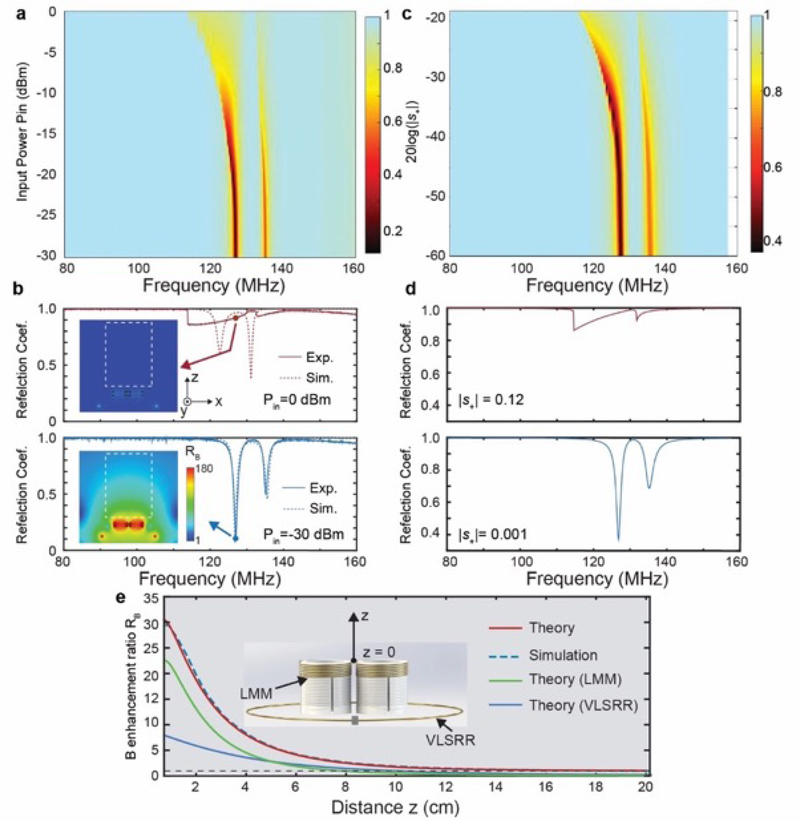
In order to experimentally validate the nonlinear response of the NLMMs (coupled LMM and VLSRR), we fabricated the LMM using 3D printing and coil winding technology; the dimensions of its composite helical unit cells may be found in the Methods section and Section 2 of the Supporting Information. The VLSRR was fabricated by welding a varactor to the gap of a split-ring resonator. We employed a vector network analyzer (VNA, E5071C Keysight Inc.) coupled to a loop antenna to characterize the resonance response of the LMM, VLSRR, and the combined NLMM.^[30] Details of the experiments may be found in the Methods section and Section 3 of the Supporting Information. In the discussion herein, the LMM consists of two helical resonator unit cells for the sake of simplicity, however, this component may include increasing numbers of unit cells in an array fashion, such as a 4 × 4 square array, for example. The resonance frequency of the LMM was ~ 130.9 MHz and the resonance frequency of the VLSRR was ~ 132.5 MHz when the incident power was −30 dBm. For the NLMM consisting of the coupled LMM and VLSRR, two resonance modes, which correspond to the dips in the reflection spectrum, are observed and the resonance modes shift to lower frequency as the excitation power increases, as shown in Figure 2a. The reflection spectrum for the highest and lowest incident powers are shown in Figure 2b. For the low incident power (P_in = −30 dBm), a strong resonance is observed at 127 MHz, indicating that the NLMM is operating as a linear resonator, i.e. operating in the linear region. Numerical simulations using CST Microwave Studio accurately match the measured spectrum; details of the simulation may be found in the Methods section. The field distribution derived from the simulation indicates a significant magnetic field enhancement in the vicinity of the NLMMs. When the incident power is high (P_in = 0 dBm), the reflection spectrum features two bi-stable response transitions at 114 MHz and 133 MHz, and the reflection at 127 MHz is high, indicating a weak oscillation strength in the NLMM. In the numerical simulation, it is challenging to model a dynamic nonlinear response. Therefore, in order to estimate the field distribution for the high incident power condition, we used the static response by assuming an increase in capacitance of the varactor from 3.2 pF to 4.7 pF. The simulated reflection amplitude at 127 MHz derived in this fashion approximates the experimental results. There is little magnetic field enhancement in the region about the NLMM in the high incident power condition, manifesting as effective silencing of this system in this regime.

Figure 2.

Demonstration and analysis of the NLMM response. a) Experimentally measured reflection coefficient of the NLMM as a function of input power. b) The measured reflection coefficient and simulation results for the highest (top) and lowest (bottom) input powers. Insets: magnetic enhancement ratio maps at 127 MHz where the dashed square labels the region of interest. c) and d) Calculated reflection coefficients based on the CMT model for the NLMMs at different excitation strengths. e) Calculated and simulated magnetic field enhancement ratio (R_B) along the central line of the NLMM. Inset: schematic of the NLMM.

Using the CMT model, the reflection coefficient is derived by solving Equation 3, as detailed in the Section 1 of the Supporting Information. During this calculation, we swept the incident amplitude |s₊| from 0.001 to 0.12, and obtained the derived spectra shown in Figure 2c, which agreed well with the aforementioned experimental results. At |s₊| = 0.001, the resonance reflection response matches well with the measured spectrum. In the case of the high incident amplitude, the resonance is suppressed and a bi-stable response is observed. The agreement between the theoretical calculation and experimental results serves to validate the lumped parameter CMT model.

Next, we employed the Biot-Savart law to study the magnetic field enhancement ratio of the NLMM in the linear region.^[29] When a low power RF magnetic field is incident on the NLMM at its resonance frequency, strong oscillating currents are induced in the LMM and the VLSRR, which induce localized magnetic enhancement. The magnetic field at an arbitrary position may be calculated by the curve integral of the current in the LMM and the VLSRR. Thus, the magnetic enhancement ratio R_B is defined as the ratio between the overall magnetic field induced by the NLMM and the incident magnetic field (this calculation is detailed in Section 4 of the Supporting Information). The magnetic field enhancement ratio peaks at a distance of 7 mm from the top of the NLMMs and decays following an inverse function along the central line of the NLMM. The accuracy of the theoretically calculated magnetic field enhancement is supported by its close match to the numerical simulation results (dashed line in Figure 2e). We studied the contribution of the LMM and the VLSRR to the magnetic field enhancement using the Biot-Savart law. The magnetic field at a given location is the sum of the magnetic field induced by the LMM and VLSRR, in addition to the incident field. The contribution to the total magnetic field from the LMM is larger than VLSRR at locations in close proximity to the surface of the NMM. However, when the distance is larger than 5 cm, the contribution from the VLSRR is larger than the LMM. The sum of the magnetic field induced by the LMM and the VLSRR approaches zero for further distances (i.e. z > 16 cm) where the magnetic field enhancement effect is negligible and the overall magnetic field is less than 1.1 times of the incident field. Ultimately, the overall magnetic field strength decays to the strength of the incident field. The calculated magnetic field is employed to assess the SNR enhancement in MRI imaging as discussed below.

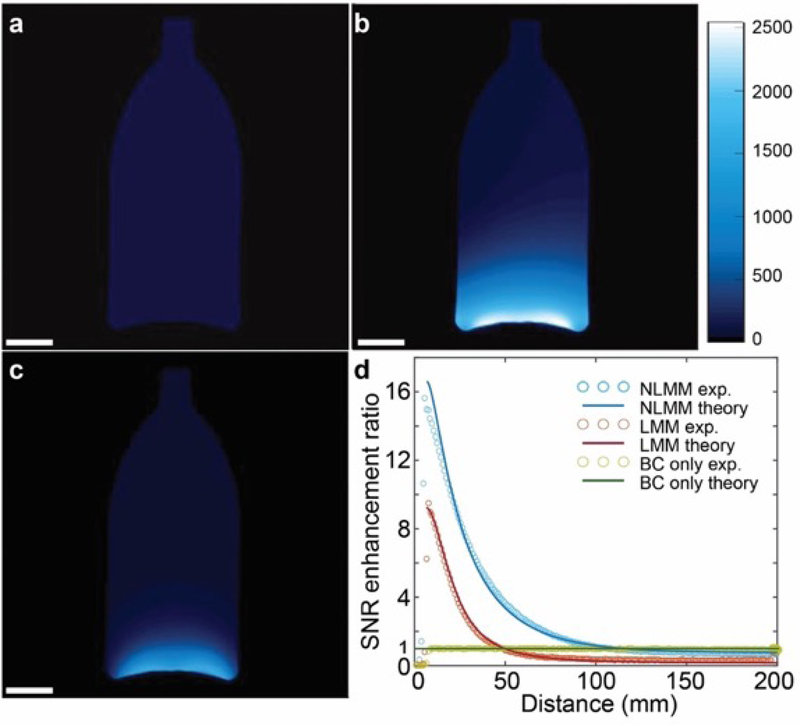
Experimental validation of the MRI SNR enhancement was performed using a conventional bottle-shaped phantom filled with mineral oil in order to evaluate the performance of the NLMMs operating with the body coil (BC) in a 3T clinical MRI system (Philips Healthcare). For comparison, we also imaged the phantom with the BC alone as a reference standard and with an LMM (without the coupled VLSRR). In the experiments using the NLMMs and the LMMs, the bottom of the phantom was ~ 5 mm away from the top surface of the metamaterials. The two-image method was employed to evaluate the SNR,^[36] as detailed in the Methods section and Section 5 of the Supporting Information. During the imaging sequence, an image of the phantom was acquired using gradient echo imaging, followed by capturing a noise image by setting the transmission RF energy to 0, as shown in Figure S7 in the Supporting Information. The SNR in the region of interest (ROI) was evaluated as the ratio between the signal and the standard deviation of the noise image. As shown in Figure 3a, the SNR of the image captured by BC control group was uniform throughout the phantom. In the presence of the NLMM, the SNR was markedly increased particularly in proximity to the NLMM, and decayed gradually along the vertical axis, as shown in Figure 3b. In the presence of the LMM (Figure 3c), the SNR was also enhanced in proximity to the metamaterial, but decayed more rapidly than the NLMM, ultimately becoming smaller than the reference standard using the BC coil alone at the superior portion of the phantom. Figure 3d demonstrates the comparison of the SNR along the central line of the phantom imaged using the NLMM, LMM, and the BC coil alone. The peak SNR enhancement ratio (SNR_NLMM/SNR_BC) is ~ 15.9 for the NLMM and decays to 1 at the distance of 11.4 cm, saturating at 0.75 for the locations further away. Therefore, the decay length at which the SNR enhancement diminishes below the reference standard in the case of the NLMMs consisting of two helical resonators and a coupled VLSRR approximates 11 cm. However, the LMM exhibits a peak SNR enhancement of 9.5 and decays to 1 at a distance of 6 cm, further decreasing to 0.3 at the top of the phantom. The peak SNR enhancement ratio and decay profile in the case of the LMM is similar to previous reports of linear MMs applied for MRI SNR enhancement.^[28,29,37] The larger peak SNR enhancement in the case of the NLMM is partially attributed to the additional magnetic field enhancement resulting from the VLSRR component, which is absent in the LMM. The more gradual decay rate is mainly due to the uniform excitation in the NLMM, while the excitation is non-uniform in the LMM. We mapped the excitation magnetic field ($B_1^{+}$) for the LMM (Figure S8 in the Supporting Information) and observed that the magnetic field at greater distances from the LMM is much weaker than in proximity to the metamaterial. The gradient in the excitation magnetic field superimposes with the signal gradient during the RF reception phase, resulting in rapid decay in the SNR enhancement. In the case of the NLMM, the excitation RF energy is maintained, similar to the BC only experiment, thereby yielding a uniform excitation magnetic field as the NLMM remains effectively silenced during the RF transmission phase. The SNR enhancement ratio of the NLMM exhibits only the gradient induced during the RF reception phase. Of note, the uniform RF transmission magnetic field (Figure S8c in the Supporting Information) provides further evidence of the inactivity of the NLMM during the RF transmission phase.

Figure 3.

3T MRI imaging of mineral oil phantom. Gradient echo imaging employed. a) Image captured by the body coil in absence of metamaterials. b) Image captured by the body coil in presence of NLMMs. c) Image captured by the body coil in presence of LMMs. d) Comparison of the SNR enhancement ratio for the nonlinear and linear MMs at the center of the phantom. Scale bars in a), b) and c) are 3 cm.

The mechanism of SNR enhancement was explored by deriving the theoretical SNR enhancement and comparing the above MRI experimental results. The theoretical SNR for the BC only and NLMM experiments, in which the excitation RF field yields a uniform 90° flip angle, may be estimated by^[38]

$$SNR\propto \frac{{\omega }_o^2{B}_1^{-}}{\sqrt{R_s+R_c}}$$ (4)

in which ω₀ is the MRI RF frequency, $B_1^{-}$ is the magnetic field that the receiving coil generates if it operates like a transmission coil, R_s is the equivalent resistance of the sample, and R_c is the resistance of the coil. Compared with the BC only imaging, the NLMMs enhance $B_1^{-}$ according to Figure 2e. In addition, the noise induced by the sample is also increased due to the magnetic field enhancement effect. This increase in noise is linear to the integral of the magnetic field enhancement, as discussed in Section 4 of the Supporting Information. In the case of the NLMMs, the noise is amplified 1.8-fold according to our calculations and, therefore, the SNR enhancement ratio is smaller than the magnetic field enhancement ratio. As shown in Figure 3d, the theoretical SNR enhancement agrees well with the experimental results. At locations of greater distance from the NLMM, the magnetic field enhancement is ~ 1 and the signal is not improved while the noise remains increased, leading to an overall reduction in SNR at these locations. We also theoretically calculated the SNR enhancement ratio of the LMM by considering the gradient in the excitation field^[28] combined with the lack of the VLSRR, as well as the BC only condition, both of which also match well with the experimental results (Figure 3d).

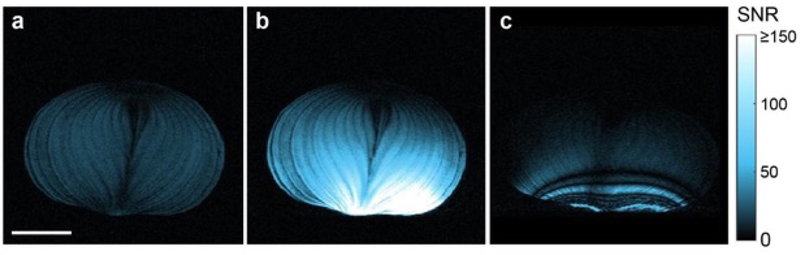
Finally, in addition to the experimental MRI validation using the mineral oil phantom, we also imaged an onion to demonstrate the performance of the NLMMs. During these experiments, as opposed to the gradient echo imaging employed above, we used turbo spin echo (TSE) imaging, which features a series of RF transmission pulses for both excitation and refocusing of the spin excitation and is also a mainstay in clinical imaging. Importantly, since the NLMM remains silent during the transmission phase, both the excitation and refocusing RF pulses are not disturbed and do not require any specific modifications. As shown in Figure 4a and 4b, the SNR was increased significantly at the bottom of the sample with the NLMMs, while the SNR along the top of the sample remained similar to the BC only experiment. However, in the case of LMMs (Figure 4c), there are artifacts in the image due to the interaction between the RF pulses and the LMMs in the transmission phase. The LMM enhanced the excitation and refocusing pulses and induced distortions in the image, precluding its use in spin echo-based imaging. This result demonstrates that the intelligent functionality of the NLMMs may also readily operate with a variety of RF transmission pulses, which is beyond the capabilities of LMMs. Additional images of a larger biological sample, a sweet melon, are shown in Figure S9 in the Supporting Information.

Figure 4.

3 T MRI of an onion by employing spin echo imaging. a) Image captured in the absence of metamaterials. b) Image captured in the presence of NLMMs. c) Image captured in presence of the LMMs. NLMMs enhance the SNR by ≈15-fold along the bottom of the onion, as shown in (b). LMMs distort and induce artifacts, as shown in (c) due to the interaction between the LMM and the excitation and refocusing pulses in spin echo imaging. Scale bar is 5 cm.

The observed phenomena, including a uniform excitation magnetic field and improved SNR in MRI, validate the predicted behavior of the NLMMs, consisting of an LMM resonator and a VLSRR. In the RF transmission phase, the strong excitation RF magnetic field induces a nonlinear response in the NLMM, effectively turning off its magnetic field enhancement performance due to its resonance shift. During the RF reception phase stage, the NLMM becomes active, operating at the resonance frequency of the MRI and enhancing the received RF signal. In sharp contrast to the LMM, the NLMM does not require any modification in the RF pulse sequences. In other words, the NLMM may be readily integrated into MRI in order to enhance performance without modifying the existing and optimized MRI RF transmission pulse sequence configurations. Importantly, the NLMM yields a negligible increase in specific absorption rate (SAR) since the NLMM is not serving to enhance the transmission RF magnetic field, thereby mitigating the safety concerns of predecessor LMM-based approaches. The NLMMs consisting of 4 × 4 array of helical resonators in combination with VLSRR also operates well with the MRI as detailed in Section 7 of the Supporting Information. With further technical development, coupled NLMMs composed of arbitrary numbers and configurations of helical resonators may be realized and optimized for specific imaging applications.

This work demonstrates an intelligent and nonlinear metamaterial, capable of adaptively varying its resonance response according to the excitation strength. The NLMM consists of an array of linear helical resonators and a coupled varactor-loaded split ring resonator, featuring a bi-stable nonlinear response under high power RF excitation. We employed the NLMM to enhance the SNR of MRI, achieving marked improvements in performance. Our findings provide insight into a deeper understanding of the nonlinear behavior of metamaterials and open opportunities for using nonlinear physics in artificial materials to realize revolutionary improvements in clinical imaging tools. Furthermore, the readily distinguishable responses of the strong and weak excitation conditions may enable self-adaptive tailoring of the electromagnetic field to achieve functionalities beyond those validated herein, such as unidirectional wireless inductive coupling and phase conjugation.