Sample size considerations for comparing dynamic treatment regimens in a sequential multiple-assignment randomized trial with a continuous longitudinal outcome

Abstract

Clinicians and researchers alike are increasingly interested in how best to personalize interventions. A dynamic treatment regimen (DTR) is a sequence of pre-specified decision rules which can be used to guide the delivery of a sequence of treatments or interventions that are tailored to the changing needs of the individual. The sequential multiple-assignment randomized trial (SMART) is a research tool which allows for the construction of effective DTRs. We derive easy-to-use formulae for computing the total sample size for three common two-stage SMART designs in which the primary aim is to compare mean end-of-study outcomes for two embedded DTRs which recommend different first-stage treatments. The formulae are derived in the context of a regression model which leverages information from a longitudinal outcome collected over the entire study. We show that the sample size formula for a SMART can be written as the product of the sample size formula for a standard two-arm randomized trial, a deflation factor that accounts for the increased statistical efficiency resulting from a longitudinal analysis, and an inflation factor that accounts for the design of a SMART. The SMART design inflation factor is typically a function of the anticipated probability of response to first-stage treatment. We review modeling and estimation for DTR effect analyses using a longitudinal outcome from a SMART, as well as the estimation of standard errors. We also present estimators for the covariance matrix for a variety of common working correlation structures. Methods are motivated using the ENGAGE study, a SMART aimed at developing a DTR for increasing motivation to attend treatments among alcohol- and cocaine-dependent patients.

1. Introduction

Dynamic treatment regimens (DTRs) are sequences of pre-specified decision rules leading to courses of treatment which adapt to a patient’s changing needs.¹ DTRs operationalize clinical decision-making by recommending particular treatments or intervention components to certain subsets of patients at specific times.² Consider the following example DTR which was designed to increase engagement with an intensive outpatient rehabilitation program (IOP) for patients with alcohol and/or cocaine dependence: “Within a week of the participant becoming non-engaged in the IOP, provide a phone-based session focusing on helping the patient re-engage in the IOP. At week 8, look back at the participant’s engagement pattern over the past eight weeks. If the participant continued to not engage, provide a second phone-based session, this time focusing on facilitating personal choice (i.e., highlighting various treatment options the patient can choose from in addition to IOP). Otherwise, provide no further contact.”³ Notice that the DTR recommends intervention strategies for both engaged and non-engaged participants at week 8. Alternative names for DTRs include adaptive treatment strategies^4,5 and adaptive interventions,^6,7 among others.

Scientists often have questions about how best to sequence and individualize interventions in the context of a DTR. Sequential, multiple-assignment, randomized trials (SMARTs) are one type of randomized trial design that can be used to answer questions at multiple stages of the development of high-quality DTRs.^8,9,10 The characteristic feature of a SMART is that some or all participants are randomized more than once, often based on previously-observed covariates. Each randomization corresponds to a critical question regarding the development of a high-quality DTR, typically related to the type, timing, or intensity of treatment. SMARTs have been employed in a variety of fields, including oncology,^11,12,13 surgery,^14,15 substance abuse,¹⁶ and autism¹⁷.

Most SMARTs contain an embedded “tailoring variable”, a pre-defined covariate observed during treatment which determines whether or how a participant will be randomized in the next stage of the SMART. For example, participants who “respond” to treatment may be re-randomized between different treatment options than participants who do not respond. SMARTs with embedded tailoring variables also contain embedded DTRs; that is, by design, participants in the SMART receive sequences of treatments which are consistent with the recommendations made by one or more DTRs. Note that SMARTs need not contain an embedded tailoring variable; however, we restrict our focus in this manuscript to those that do. We discuss this in more detail in section 2.

The comparison of two embedded DTRs which recommend different first-stage treatments is a common primary aim for a SMART.⁷ There exist data analytic methods for addressing this aim when the outcome is continuous,⁷ survival,¹⁸ binary,¹⁹ cluster-level²⁰ and longitudinal.^21,22 A key step in designing a SMART, as with any randomized trial, is determining the sample size needed to be able detect a desired effect with given power. However, there is no existing method for determining sample size for such a comparison when the outcome is continuous and longitudinal.

Our primary contribution is tractable sample size formulae for SMARTs with a continuous longitudinal outcome in which the primary aim is an end-of-study comparison of two DTRs which recommend different first-stage treatments. Additionally, we present estimators for parameters in the working covariance matrix used in the analysis methods developed by Lu et al.²¹

In section 2, we provide a brief overview of three common SMART designs and introduce a motivating example. Section 3 reviews the estimation procedure introduced by Lu et al., and extends it by developing estimators for various working covariance structures.²¹ In section 4, we develop and present sample size formulae for SMARTs in which the primary aim is a comparison of two embedded DTRs which recommend different first-stage treatments using a continuous longitudinal outcome. The sample size formulae are evaluated via simulation in section 5.

2. Dynamic Treatment Regimens and Sequential Multiple-Assignment Randomized Trials

A DTR is a sequence of functions (“decision rules”), each of which takes as inputs a person’s history up to the time of the current decision (including baseline covariates, adherence, responses to previous treatments, etc.) and outputs a recommendation for the next treatment.¹⁰ Consider the example DTR in section 1. The recommended first-stage treatment is a phone-based session with a focus on re-engagement with the IOP. At week 8, each participant’s history of engagement is assessed, and an appropriate second-stage treatment is recommended. For participants who have shown a pattern of continued non-engagement, the recommended second-stage treatment is a second phone-based session focusing on personal choice. For all other participants, the DTR recommends no further contact. The tailoring variable is an indicator as to whether or not the participant demonstrated a pattern of continued non-engagement prior to week 8.

We consider two-stage SMARTs in which the primary outcome is continuous and repeatedly measured in participants over the course of the study. Our examples refer to trials in which at least one observation of the outcome is made in each stage, though that is not required for the estimation method presented in section 3. For simplicity, we refer to the tailoring variable as response status to first-stage treatment, and, in the second stage, we describe participants as “responders” or “non-responders”. We denote a DTR embedded in a SMART with a triple of the form (a₁, a_2R, a_2NR), where a₁ is an indicator for the recommended first-stage treatment, a_2R an indicator for the second-stage treatment recommended for responders, and a_2NR the second-stage treatment recommended for non-responders. Throughout, (a₁, a_2R, a_2NR) is non-random and is used to index the DTRs embedded in a SMART.

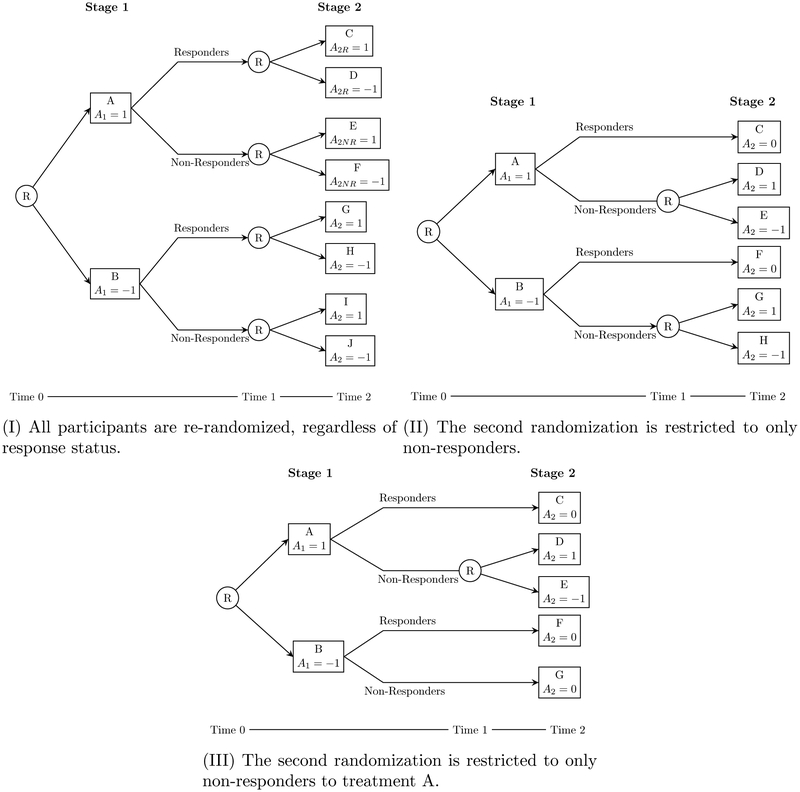
We introduce three common two-stage SMART designs in figure 1 which vary in the subsets of participants who are re-randomized after the first stage. Each of these designs contains an embedded tailoring variable, and thus, for the purposes of this manuscript, contains embedded DTRs.

Figure 1:

Three commonly-used two-stage SMART designs. Each design varies in choice of which subsets of participants are re-randomized. Circled R indicates randomization, capital letters indicate (potentially non-unique) treatments, and a_– provides a coding system used to index embedded DTRs.

In design I, all participants are re-randomized. There are eight DTRs embedded in this design: for example, the DTR which starts by recommending A, then recommends C for responders and F for non-responders. Using the notation in figure 1, this DTR would be written (1, 1, −1). SMARTs of this form have been run in the fields of drug dependence,^23,24 smoking cessation,²⁵ and childhood depression,²⁶ among others.

SMARTs using design II restrict the second randomization to only non-responders; that is, only participants who have a certain value of the tailoring variable (here, “non-response”) are re-randomized. This is perhaps the most common SMART design, and it has been utilized in the study of ADHD,²⁷ adolescent marijuana use,²⁸ alcohol and cocaine dependence³, and more. There are four embedded DTRs in this design. Because responders are not re-randomized, a_2R is set to zero for all embedded DTRs.

In design III, re-randomization is restricted to only non-responders who receive a particular first-stage treatment. SMARTs of this type have been used to investigate cognition in children with autism spectrum disorder^17,29 and implementation of a re-engagement program for patients with mental illness.³⁰ There are three DTRs embedded in this design. Note that, as in design II, responders are not re-randomized, so a_2R is set to zero for all embedded DTRs. Furthermore, a_2NR is set to zero when a₁ = −1, as non-responders to treatment B are not re-randomized.

For more information on various SMART designs and case studies for each type, see Lei, et al.³¹

To illustrate our ideas, we use ENGAGE, a SMART designed to study the effects of offering cocaine- and/or alcohol-dependent patients who did not engage in an IOP phone-based sessions either geared toward re-engaging them in an IOP or offering a choice of treatment options.³ The study recruited 500 cocaine- and/or alcohol-dependent adults who were enrolled in an IOP and failed to attend two or more sessions in the first two weeks. ENGAGE is modeled on design II. In the context of figure 1, treatment A was two phone-based motivational interviews focused on reen-gaging the participant with the IOP (“MI-IOP”); treatment B was two phone-based motivational interviews geared towards helping the participant choose and engage with an intervention of their choice (“MI-PC”). Participants who exhibited a pattern of continued non-engagement after eight weeks were considered non-responders, and re-randomized to receive either MI-PC (treatments D and G) or no further contact (treatments E and H). Responders were provided no further contact (treatments C and F). Following the coding in figure 1, the example DTR from section 1 is labeled (1, 0, 1).

An important continuous outcome in ENGAGE is “treatment readiness”. This is a measure of a patient’s willingness and ability to commit to active participation in a substance abuse treatment program. The score ranges from 8–40 and is coded so that higher scores indicate greater treatment readiness. Measurements are taken at baseline, and 4, 8, 12, and 24 weeks after program entry.

3. Estimation

We extend the work of Lu and colleagues by offering more detailed guidance on the estimation of model parameters used in computing quantities of interest on which to compare two embedded DTRs.²¹ We first review the method below.

3.1. Marginal Mean Model

Consider a SMART design with embedded DTRs labeled by (a₁, a_2R, a_2NR). Suppose we have a longitudinal outcome $Y_i=\left(Y_{t_1,i},\dots ,Y_{t_T,i}\right)$, i = 1,…, n, observed such that Y_t,i is measured for each of n participants at each of T timepoints {t_j : j = 1,…, T; t₁ <…< t_T}. We do not require that these timepoints be equally-spaced, though they must be common to all participants in the study. Define t* ∈{t_j} to be the time of the measurement taken immediately before the assessment of response status and second randomization. In ENGAGE, for example, T = 5,{t_j} = {0, 4, 8, 12, 24}, and t* = t₃ = 8. Let X_i be a vector of mean-centered baseline covariates, such as age at baseline, sex, etc., for the ith individual.

We are interested in $\text{E}\left[Y_t^{\left(a_1,a_{2R},a_{2NR}\right)}|X\right]$, the marginal mean outcome at time t under DTR (a₁, a_2R, a_2NR) conditional on X. This is the mean outcome at time t had all individuals with characteristics X been offered DTR (a₁, a_2R, a_2NR). Recall that a DTR recommends treatments for both responders and non-responders; therefore, $\text{E}\left[Y_t^{\left(a_1,a_{2R},a_{2NR}\right)}|X\right]$ is marginal over response status. Note that $Y_{t,i}^{\left(a_1,a_{2R},a_{2NR}\right)}$ is a potential outcome: the value of the outcome Y_t,i that would be observed had participant i been treated according to the DTR (a₁, a_2R, a_2NR).

We impose a modeling assumption on $\text{E}\left[Y_t^{\left(a_1,a_{2R},a_{2NR}\right)}|X\right]$ namely, that $\text{E}\left[Y_t^{\left(a_1,a_{2R},a_{2NR}\right)}|X\right]={\mu }_t^{\left(a_1,a_{2R},a_{2NR}\right)}(X;\theta )$, where ${\mu }_t^{\left(a_1,a_{2R},a_{2NR}\right)}(X;\theta )$ is a marginal structural mean model with unknown parameters θ =(η^⊤,γ^⊤)^⊤. We use η to represent a column vector of parameters indexing baseline covariates, and γ is a column vector of coefficients on terms involving treatment effects; we discuss in more detail below. As noted by Lu and colleagues, the sequential nature of treatment delivery in SMARTs may suggest constraints on the form of ${\mu }_t^{\left(a_1,a_{2R},a_{2NR}\right)}(X;\theta )$ which depend, in part, on the design of the SMART.²¹ For instance, in ENGAGE, at time t = 0, no treatments have been assigned, so all DTRs share a common mean. At times t = 4 and t = 8, the four embedded DTRs differ only by recommended first-stage treatment; thus there are two means of $Y_t^{\left(a_1,a_{2}R,a_{2}NR\right)}$ at each timepoint. Finally, for times t > t*= 8, each DTR has a different mean $Y_t^{\left(a_1,a_{2}R,a_{2}NR\right)}$.

An example marginal structural mean model for ENGAGE (and, more generally, design II) is

$${\mu }_t^{\left(a_1,a_{2R},a_{2NR}\right)}\left(X_1;\theta \right)={\eta }_1{X}_1+{\gamma }_0+\mathbb{1}\left\{t\le t^{*}\right\}\left({\gamma }_{1}t+{\gamma }_2{a}_{1}t\right)+\mathbb{1}\left\{t>t^{*}\right\}({\gamma }_1{t}^{*}+{\gamma }_2{t}^{*}{a}_1+{\gamma }_3\left(t-t^{*}\right)+{\gamma }_4\left(t-t^{*}\right)a_1+{\gamma }_5\left(t-t^{*}\right)a_{2NR}+{\gamma }_6\left(t-t^{*}\right)a_1{a}_{2NR}),$$ (1)

where $\mathbb{1}\left\{E\right\}$ is the indicator function for the event E.

Using contrast coding, i.e., {a₁,a_2NR}∈ {−1, 1}², we can write

$$2{\gamma }_2=E\left[\frac{Y_{t_j}^{(1,0,\cdot )}-Y_{t_k}^{(1,0,\cdot )}}{t_j-t_k}-\frac{Y_{t_j}^{(-1,0,\cdot )}-Y_{t_k}^{(-1,0,\cdot )}}{t_j-t_k}|X\right],t_j,t_k\le t^{*}.$$ (2)

This represents the difference in slopes of expected treatment readiness in the first stage of the SMART between DTRs starting with different first-stage treatments (second-stage treatment is arbitrary, as t < t*). Also, we can interpret η₁ as the difference in expected outcome $Y_t^{\left(a_1,a_{2R},a_{2NR}\right)}$ associated with a one-unit difference in baseline covariate X₁, marginal over all embedded DTRs.

We present example models for designs I and III in the online supplement. For more on modeling considerations for longitudinal outcomes in SMARTs, see Lu et al.²¹

3.2. Observed Data

Suppose we have data arising from a SMART with n participants. Let A_1,i ∈{−1,1} be a random variable which indicates first-stage treatment randomly assigned to participant i (i = 1,…, n), and let R_i ∈ {0, 1} indicate whether the ith participant responded to A_1,i, in which case R_i = 1, or not, so R_i = 0. Define A_2,i ∈ {−1, 1}to be the randomly-assigned second-stage treatment. Throughout, we use uppercase A to denote random treatment assignments; lowercase a’s are non-random indices used to denote embedded DTRs.

In design II, since only non-responders are re-randomized, we set A_2,i = 0 for responders; similarly for design III. We observe a continuous outcome Y_t,i for each participant at each of T timepoints. In general, the data collected on the ith individual over the course of the study are of the form

$$\left(X_i,Y_0,A_{1,i},Y_{\left[0<t\le t^{*}\right],i},R_i,A_{2,i},Y_{\left[t>t^{*}\right],i}\right),$$

where Y_[u<t≤v],i is a vector consisting of all values of the outcome observed for the i^th participant between times u and v.

3.3. Estimating Equations

Our goal is to estimate and make inferences on θ, the length-p column vector of mean parameters in the marginal structural mean model of interest. For notational convenience, let $\mathcal{D}$ be the set of DTRs embedded in the SMART under study; for instance, in design II,

$$\mathcal{D}=\left\{\left(a_1,a_{2R},a_{2NR}\right):a_1\in \{-1,1\},a_{2R}=0,a_{2NR}\in \{-1,1\}\right\}.$$

This creates, which can be corrected using inverse-probability weighting.^7,32,2

Let W^(d)(A_1,i, R_i, A_2,i) be a weight associated with participant i and DTR $d\in \mathcal{D}$ defined as

$$W^{(d)}\left(A_{1,i},R_i,A_{2,i}\right)=\frac{I^{(d)}\left(A_{1,i},R_i,A_{2,i}\right)}{P\left(A_{1,i}=a_1\right)P\left(A_{2,i}=a_2|A_{1,i}=a_1,R_i\right)},$$ (3)

where I^(d)(A_1,i, R_i, A_2,i) is an indicator of whether participant i is consistent with DTR d. The form of I^(d)(A_1,i, R_i, A_2,i) depends on the particular SMART design under study; for each of the designs in figure 1, these expressions are shown in table 1.

Table 1:

Design-specific indicators for consistency with a given DTR $d\in \mathcal{D}$.

Design	I(d)(A1,i, Ri, A2,i)
I	$\mathbb{1}\left\{A_{1,i}=a_1\right\}\left(\mathbb{1}\left\{A_{2,i}=a_{2R}\right\}{R}_i+\mathbb{1}\left\{A_{2,i}=a_{2NR}\right\}\left(1-R_i\right)\right)$
II	$\mathbb{1}\left\{A_{1,i}=a_1\right\}\left(R_i+\mathbb{1}\left\{A_{2,i}=a_{2NR}\right\}\left(1-R_i\right)\right)$
III	$\mathbb{1}\left\{A_{1,i}=a_1\right\}\left(\mathbb{1}\left\{a_1=-1\right\}+\mathbb{1}\left\{a_1=1\right\}\left(R_i+\mathbb{1}\left\{A_{2,i}=a_{2NR}\right\}\left(1-R_i\right)\right)\right)$

We use W^(d)(A_1,i, R_i, A_2,i) to account for the facts that, in some SMARTs (e.g., designs II and III) there is known imbalance in the proportion of responders and non-responders consistent with each DTR, and that that some (or all) participants are consistent with more than one embedded DTR.

In design II, for example, only non-responders to first-stage treatment are re-randomized; if all randomizations are with probability 0.5, W^(1,0,1)(1, 1, 0) = (.5 × 1)⁻¹ = 2 and W^(1,0,1)(1, 0, 1) = (.5 × .5)⁻¹ = 4. Note that in design I, all participants are re-randomized; hence, all participants receive a weight of 4. The analyst may freely substitute W^(d)(A_1,i, R_i, A_2,i) = I^(d)(A_1,i, R_i, A_2,i) in this case.

Define $D^{(d)}\left(X_i\right)\in {ℝ}^{T\times p}$ to be the Jacobian of μ^(d)(X_i;θ) with respect to θ; i.e., D^(d) (X_i) = ∂μ^(d)(X_i;θ)/∂θ^T. Let $V^{(d)}\left(X_i;\tau \right)\in {ℝ}^{T\times T}$ be a working covariance matrix for Y^(d), conditional on baseline covariates X, under DTR $d\in \mathcal{D}$. Here, τ = (σ^⊤, ρ^⊤)^⊤ is a vector of parameters indexing variance (σ) and correlation (ρ) components of the working covariance structure. We discuss V^(d)(X_i;τ) in detail in section 3.4. We estimate θ by solving the estimating equations

$$0=\frac{1}{n}\sum _{i=1}^n\sum _{d\in \mathcal{D}}\left[W^{(d)}\left(A_{1,i},R_i,A_{2,i}\right)\cdot D^{(d)}{\left(X_i\right)}^{\top }{V}^{(d)}{\left(X_i;\tau \right)}^{-1}\left(Y_i-{\mu }^{(d)}\left(X_i;\theta \right)\right)\right].$$ (4)

We call the solution to equation (4) $\widehat{\theta }$.

Under usual regularity conditions for M-estimators (see, e.g., van der Vaart, theorem 5.4.1)³³ and given data from a SMART (see appendix A), $\widehat{\theta }$ is consistent for θ. Furthermore, $\sqrt{n}(\widehat{\theta }-\theta )$ has an asymptotic multivariate normal distribution:

$$\sqrt{n}(\widehat{\theta }-\theta )\Rightarrow \mathcal{N}\left(0,B^{-1}M{B}^{-1}\right),$$

where

$$B:=\text{E}\left[\sum _{d\in \mathcal{D}}{W}^{(d)}\left(A_{1,i},R_i,A_{2,i}\right)D^{(d)}{\left(X_i\right)}^{\top }{V}^{(d)}{\left(X_i;\tau \right)}^{-1}{D}^{(d)}\left(X_i\right)\right]\in {ℝ}^{p\times p}$$ (5)

and

$$M:=\text{E}\left[{\left(\sum _{d\in \mathcal{D}}{W}^{(d)}\left(A_{1,i},R_i,A_{2,i}\right)D^{(d)}{\left(X_i\right)}^{\top }{V}^{(d)}{\left(X_i;\tau \right)}^{-1}\left(Y_i-{\mu }^{(d)}\left(X_i;\theta \right)\right)\right)}^{\otimes 2}\right]\in {ℝ}^{p\times p},$$ (6)

with Z^⊗2 = ZZ^⊤. Proofs of these claims are available in the supplement. Note that $\widehat{\theta }$ is consistent for θ regardless of the chosen structure of V^(d)(X;τ); however, we conjecture that choices of V^(d)(X;τ) closer to the true covariance matrix Var(Y^(d)) will yield more efficient estimates.

3.4. Estimation of the Working Covariance Matrix

Decisions regarding the structure of V^(d)(X; τ) should be made by the scientist according to existing knowledge regarding the within-person covariance structure of Y^(d). In general, for an embedded DTR $d\in \mathcal{D},V^{(d)}(X;\tau )$ takes the form

$$V^{(d)}(X;\sigma ,\rho )=S^{(d)}{(\sigma )}^{1/2}{R}^{(d)}(\rho )S^{(d)}{(\sigma )}^{1/2},$$

where $S^{(d)}{(\sigma )}^{1/2}\in {ℝ}^{T\times T}$ is a diagonal matrix with diagonal entries ${\sigma }_{t_1}^{(d)},\dots ,{\sigma }_{t_T}^{(d)}$, where ${\sigma }_{t_j}^{(d)}=\text{Var}\left(Y_{t_j}^{(d)}\right)$, and $R^{(d)}(\rho )\in {ℝ}^{T\times T}$ is working correlation matrix for Y^(d). Note that this notation allows for different working covariance structures for each DTR, as well as non-constant variances of the longitudinal outcome across time.

We propose the following procedure to estimate V^(d)(X;τ). First, estimate θ by solving equation (4) using the T × T identity matrix as V^(d)(X;τ) for all $d\in \mathcal{D}$. Call the solution ${\widehat{\theta }}_{(0)}$. Next, use ${\widehat{\theta }}_{(0)}$ to estimate ${\sigma }_t^{(d)}$ as follows

$${\left({\widehat{\sigma }}_t^{(d)}\right)}^2=\frac{{\sum }_{i=1}^n{W}^{(d)}\left(A_{1,i},R_i,A_{2,i}\right){\left(Y_{i,t}-{\mu }_t^{(d)}\left(X_i;{\widehat{\theta }}_{(0)}\right)\right)}^2}{{\sum }_{i=1}^n{W}^{(d)}\left(A_{1,i},R_i,A_{2,i}\right)-p}$$ (7)

where p is the dimension of θ. If the scientist believes that this variance is constant over time for each DTR, the estimator in equation (7) can be averaged over time; one can also average over DTR if one believes the variance is constant across all embedded DTRs. Estimators for ρ^(d) vary with choice of correlation structure R^(d)(ρ); we present estimators for selected structures in table 2.

Table 2:

Correlation estimators for selected working correlation structures, assuming constant within-person variance over time. $d\in \mathcal{D}$ is an embedded DTR, $W_i^{(d)}$ is shorthand for W^(d)(A_1,i, R_i,A_2,i) and ${\widehat{e}}_{i,t}^{(d)}(\widehat{\theta })$ is the estimated residual $Y_{i,t}-{\mu }_t^{(d)}\left(X_i;\widehat{\theta }\right)$.

Cor. structure	$\text{Cor}\left(Y_{t_j}^{(d)},Y_{t_k}^{(d)}\right)$	Estimator
AR(1)	$\{\begin{array}{ll}1\hfill & t_j=t_k\hfill \\ {\left({\rho }^{(d)}\right)}^{|j-k|}\hfill & t_j\ne t_k\hfill \end{array}$	${\widehat{\rho }}^{(d)}=\frac{{\sum }_{i=1}^n{W}_i^{(d)}{\sum }_{m=1}^{T-1}{\widehat{e}}_{i,t_m}^{(d)}(\widehat{\theta }){\widehat{e}}_{i,t_{m+1}}^{(d)}(\widehat{\theta })}{{\left({\widehat{\sigma }}^{(d)}\right)}^2\cdot n\cdot (T-1)}$
Exchangeable	$\{\begin{array}{ll}1\hfill & t_j=t_k\hfill \\ {\rho }^{(d)}\hfill & t_j\ne t_k\hfill \end{array}$	${\widehat{\rho }}^{(d)}=\frac{{\sum }_{i=1}^n{W}_i^{(d)}{\sum }_{l<m}{\widehat{e}}_{i,t_l}^{(d)}(\widehat{\theta }){\widehat{e}}_{i,tm}^{(d)}(\widehat{\theta })}{{\left({\widehat{\sigma }}^{(d)}\right)}^2\cdot n\cdot T(T-1)/2}$
Unstructured	$\{\begin{array}{cc}1& t_j=t_k\\ {\rho }_{t_j,t_k}^{(d)}& t_j\ne t_k\end{array}$	${\widehat{\rho }}_{t_j,t_k}^{(d)}=\frac{{\sum }_{i=1}^n{W}_i^{(d)}{\widehat{e}}_{i,t_j}^{(d)}(\widehat{\theta }){\widehat{e}}_{i,t_k}^{(d)}(\widehat{\theta })}{{\left({\widehat{\sigma }}^{(d)}\right)}^2\cdot n}$

Note that the denominator in equation (7) must be positive. For a fixed DTR $d\in \mathcal{D}$, the sum of the weights is, in expectation, the total sample size n (see supplement). Therefore, the denominator is approximately n − p, as in the usual mean squared error in multiple regression, for example. We recommend that analysts choose appropriately parsimonious marginal structural mean models (i.e., p < n) to ensure that equation (7) is positive.

To complete the estimation procedure, we again solve equation (4), this time using ${\widehat{V}}^{(d)}(X;\widehat{\tau })=S^{(d)}{(\widehat{\sigma })}^{1/2}{R}^{(d)}(\widehat{\rho })S^{(d)}{(\widehat{\sigma })}^{1/2}$ as the working covariance matrix. This process can be further iterated, as suggested by Liang and Zeger;³⁴ we call the final estimate of the model parameters $\widehat{\theta }$.

4. Sample Size Formulae for End-of-Study Comparisons

Often, longitudinal outcomes are collected in trials to improve the efficiency of the primary aim analysis, even when comparing two treatment groups on the mean of some summary measure such as the end-of-study observation.³⁵ Fitting a longitudinal regression model and using the result to estimate the difference in mean summary measure improves efficiency of the comparison by leveraging within-person correlation (see, e.g. Fitzmaurice et al., section 2.5).³⁶ Furthermore, this approach allows investigators to simultaneously address secondary aims using the same regression model.

As with standard randomized clinical trials, a common primary aim of a SMART is the comparison of mean end-of-study outcomes for two embedded DTRs which recommend different first-stage treatments^12,18,31,37. We now present sample size formulae for SMARTs with longitudinal outcomes in which this is the primary aim, addressed using the general estimation procedure of section 3; that is, using a regression approach which includes all observed outcome data. We restrict our focus to two-stage SMARTs in which the outcome is observed at three timepoints – baseline, just prior to the second randomization, and at the end of the study – and in which all randomizations occur with probability 0.5. Additionally, we consider a saturated, piecewise-linear mean structure μ^(d)(θ) similar to model (1).

Recall from section 3.1 that θ is a p-vector of parameters which indexes a marginal structural mean model for the treatment effects in a SMART. Let c be a length-p contrast vector so that the null hypothesis of interest takes the form

$$H_0:c^{\top }\theta =0,$$

which we will test against an alternative of the form H₁: c^⊤θ = Δ. To compare mean end-of-study outcomes between two embedded DTRs which recommend different first-stage treatments, the estimand of interest is

$$c^{\top }\theta =\text{E}\left[Y_{t_T}^{\left(1,a_{2R},a_{2NR}\right)}-Y_{t_T}^{\left(-1,a_{2R}^{\prime },a_{2NR}^{\prime }\right)}\right],$$ (8)

for some choice of a_2R, $a_{2R}^{\prime }$, a_2NR, and $a_{2NR}^{\prime }$. For example, to test equality of mean end-of-study outcomes for DTRs (1, 0, 1) and (−1, 0, −1) in design II under model (1) (assuming no X,{t_j} = {0, 1, 2}, t* = 1), the estimand is the linear combination c^⊤γ, where c^⊤ = (0, 0, 2, 0, 2, 2, 0).

We employ a 1-degree of freedom Wald test. The test statistic is

$$Z=\frac{\sqrt{n}{c}^{\top }\widehat{\theta }}{{\sigma }_c},$$

where ${\sigma }_c=\sqrt{c^{\top }{B}^{-1}M{B}^{-1}c}$. Under the null hypothesis, by asymptotic normality of $\sqrt{n}(\widehat{\theta }-\theta )$, the test statistic follows a standard normal distribution.

Define δ to be the standardized effect size as described by Cohen for an end-of-study comparison, i.e.,

$$\delta =\frac{\mathrm{\Delta }}{\sigma },$$ (9)

where $\sigma =\text{Var}\left(Y_t^{(d)}\right)$ (see working assumption A2 below).³⁸

In order to simplify the form of σ_c and obtain tractable sample size formulae, we make the following working assumptions (A1 and A2):

• A1Constrained conditional covariance matrices for DTRs under comparison.
  1. The variability of $Y_t^{(d)}$ around the DTR mean ${\mu }_t^{(d)}(\theta )$ among non-responders is no more than the variance of $Y_t^{(d)}$ unconditional on response; i.e.,

     $$\text{E}\left[{\left(Y_t^{(d)}-{\mu }_t^{(d)}(\theta )\right)}^2|R^{\left(a_1\right)}=0\right]\le \text{E}\left[{\left(Y_t^{(d)}-{\mu }_t^{(d)}(\theta )\right)}^2\right],$$

     for all t > t* and DTRs $d\in \mathcal{D}$ under study.
  2. For times t_i ≤ t_j ≤ t*, response status is uncorrelated with products of residuals; i.e,

     $$\text{Cov}\left(R^{\left(a_1\right)},\left(Y_{t_i}^{(d)}-{\mu }_{t_i}^{(d)}(\theta )\right)\left(Y_{t_j}^{(d)}-{\mu }_{t_j}^{(d)}(\theta )\right)\right)=0.$$

     for DTRs $d\in \mathcal{D}$ under study.
  3. The covariance between the end-of-study measurement and the measurements prior to the second stage among responders is less than or equal to the same quantity among non-responders:

     $$\text{Cov}\left(Y_t^{(d)},Y_{t_T}^{(d)}|R^{\left(a_1\right)}=1\right)\le \text{Cov}\left(Y_t^{(d)},Y_{t_T}^{(d)}|R^{\left(a_1\right)}=0\right)$$

     for DTRs $d\in \mathcal{D}$ under study and t ≤ t*.
• A2Exchangeable marginal covariance structure.
  The marginal variance of Y^(d) is constant across time and DTR, and has an exchangeable correlation structure with correlation ρ, i.e.,

  $$\text{Var}\left(Y^{(d)}\right)=\Sigma ={\sigma }^2{\left[\begin{array}{cccc}1& \rho & \cdots & \rho \\ \rho & 1& \cdots & \rho \\ ⋮& ⋮& \ddots & ⋮\\ \rho & \rho & \cdots & 1\end{array}\right]}_{T\times T}$$

  for all $d\in \mathcal{D}$.

Note that the above are working assumptions which we do not believe hold in general. We will see in sections 5 and 6 that sample size formula (10) (given below) is robust to moderate violations of working assumption A1 and that inputs to the formula can be adjusted in a way to accommodate violations of working assumption A2. A working assumption similar to A1(a) is commonly made in developing sample-size formulae for SMARTs with outcomes collected once at the end of the study.^39,19,20 Working assumptions A1(b) and A1(c) impose further constraints on the covariance of the outcome conditional on response and allow for tractable sample size formulae. We believe working assumption A1(b) is approximately satisfied in most common definitions of response (see the supplement). Working assumption A2 is not strictly necessary, but is used to simplify the sample size formulae and facilitate easier elicitation of parameters. See section 6 for more discussion.

Working assumption A1 arises specifically as a consequence of unequal weights in equation (4) (i.e., when there exists imbalance between responders and non-responders, by design); therefore, the assumption is not necessary in design I, and can be relaxed to apply to only the two DTRs in which non-responders are re-randomized in design III. See appendix B for more details on how this assumption is used. Furthermore, working assumption A2 cannot be satisfied in design I if all eight embedded DTRs have unique means.

Under working assumptions A1 and A2, the minimum-required sample size to detect a standardized effect size δ with power at least 1 – β and two-sided type-I error α is

$$n\ge \frac{4{\left(z_{1-\alpha /2}+z_{1-\beta }\right)}^2}{{\delta }^2}\cdot \left(1-{\rho }^2\right)\cdot \text{DE,}$$ (10)

where DE is a SMART-specific “design effect” for an end-of-study comparison (see table 3). These design effects are functions of response rates $P\left(R^{\left(a_1\right)}=1\right)=r_{a_1}$; if researchers do not have well-informed estimates of these probabilities, they may use a conservative design effect in which $r_{a_1}=0$ for a₁ ∈ {−1, 1}.

Table 3:

Design effects for sample size formula (10). $r_{a_1}=P\left(R^{\left(a_1\right)}=1\right)$ is the response rate to first-stage treatment a₁.

Design	Design effect	Conservative design effect
I	2	2
II	$\frac{1}{2}\left(2-r_1\right)+\frac{1}{2}\left(2-r_{-1}\right)$	2
III	$\frac{1}{2}\left(3-r_1\right)$	$\frac{3}{2}$

Note that the first term in formula (10) is the typical sample size formula for a traditional two-arm randomized trial with a continuous end-of-study outcome and equal randomization probability. The middle term is due to the within-person correlation in the outcome, and is identical to the corresponding correction term for GEE analyses sized to detect a group-by-time interaction when there is no baseline group effect (see, e.g., Fitzmaurice et al., ch. 20³⁶).

5. Simulations

We conducted a variety of simulations to assess the performance of sample size formula (10). We are interested in the empirical power for a comparison of the DTR which recommends only treatments indicated by 1 and the DTR which recommends only treatments indicated by −1 when the study is sized to detect an effect size of δ. In ENGAGE, this might correspond to a comparison of mean end-of-study outcomes under the DTR which recommends MI-IOP in the first stage, no further contact for engagers, and MI-PC in the second stage for continued non-engagers versus the mean end-of-study outcomes under the regimen which recommends MI-PC in the first-stage, then no further contact for both engagers and non-engagers.

We consider four types of scenarios: first, when no assumptions are violated; second, when each of working assumptions A1(a) to A1(c) are violated; finally, when the working correlation structure is misspecified, in violation of working assumption A2. In each scenario, sample sizes are computed based on nominal power 1 − β = 0.8 and two-sided type-I error α = 0.05.

We believe sample sizes from formula (10) will be slightly conservative when all assumptions are satisfied, as formula (10) is an interpretable upper bound on a sharper formula given in appendix B and the supplement. For design I, we do not expect power to be affected by violations of working assumption A1, as the assumption arises as a consequence of over- or under-representation of responders and non-responders consistent with a particular DTR (see appendix B). Since there is no such imbalance in design I, working assumption A1 is not applicable. Similarly, in design III, only non-responders to one first-stage treatment are re-randomized, so we expect that empirical power will decrease slightly, but not seriously, when violating working assumption A1. We expect empirical power to suffer most severely when violating this working assumption in design II.

We further conjecture that scenarios in which the true within-person correlation structure of Y^(d) is autoregressive, sample sizes from formula (10) will be very anti-conservative. Under an AR(1) correlation structure, less information about the end-of-study outcome is provided by the baseline measure than would be under an exchangeable correlation structure. Since, by using formula (10), we have assumed more information is available from earlier measurements than is actually the case, we will be underpowered. Similarly, we expect over-estimation of ρ in formula (10) to lead to anti-conservative sample sizes.

5.1. Data Generative Process

For each simulation, the true marginal mean model is as in model (1) for design II; analogous models are used for designs I and III – see the supplement for examples. We do not include baseline covariates X; this is a conservative approach, as we believe that adjustment for prognostic covariates typically will increase power (see, eg., Kahan et al.⁴⁰). Estimates of marginal means from ENGAGE were used to inform a reasonable range of “true” means from which to simulate, though the scenarios presented here are not designed to mimic ENGAGE exactly. All simulations take T = 3 and values of γ and σ are chosen to achieve δ= 0.3 or δ = 0.5 (“small” and “moderate” effect sizes, respectively).

Data were generated according to a conditional mean model which, when averaged over response, yields the marginal model of interest. Potential outcomes $Y_{t,i}^{(d)}$ were simulated from appropriately-parameterized normal distributions (see appendix C for details); data were “observed” by selecting the potential outcome corresponding to treatment assignment as generated from a Bernoulli(0.5) distribution.

We consider three mechanisms for generating response status. In the first, “R_⫫”, response is) generated from a Bernoulli ($r_{a_1}$) distribution, where $r_{a_1}=P\left(R^{\left(a_1\right)}=1\right)$, independently of all previously-observed data. In the second and third scenarios (“R₊” and “R₋”, respectively), response status is still generated from a Bernoulli distribution, but each individual is assigned a probability of response correlated with their observed value of Y₁. These correlations are either positive or negative, depending on the response model. This is intended to mimic different coding choices for Y, in the sense of responders tending to have higher or lower values of Y₁ than non-responders. For details of how these are generated, see appendix C, which also contains additional details regarding the data generative models used. In the supplement, we present simulation results under additional models for response.

For each simulation scenario, we compute upper and lower bounds on allowable values of $\text{Var}\left(Y_2^{(d)}|R^{\left(a_1^{(d)}\right)}=1\right)$, beyond which it is not possible to either achieve the desired marginal variance, or which induces violation of working assumption A1(a). The results shown in the corresponding column of table 4 were generated when responders’ variances were set to 75% of the lower bound beyond which the fixed marginal variance forces $\text{E}\left[{\left(Y_t^{(d)}-{\mu }_t^{(d)}(\theta )\right)}^2|R^{\left(a_1\right)}=0\right]\ge {\sigma }^2$.

Table 4:

Sample sizes and empirical power results for an end-of-study comparison of the DTR recommending only treatments indexed by 1 and that which recommends only treatments indicated by −1. δ is the true standardized effect size as defined in equation (9), r is the common probability of response to first-stage treatment, and ρ is the true exchangeable within-person correlation. n is computed using formula (10) with α= 0.05 and β= 0.2. R_⫫ refers to a generative model in which response status is independent of all prior outcomes; R₊ and R₋ refer to generative models in which response is positively or negatively correlated with Y₁, respectively. All violation scenarios assume the R₊ generative model, except working assumption A1(c). Results are the proportion of 3000 Monte Carlo simulations in which we reject H₀ : c^⊤θ = 0 at the 5% level.

					Empirical power
					A1 and A2 satisfied			Violation of A1			Violation of A2
Design	δ	r	ρ	n	R⫫	R+	R−	A1(a)	A1(b)	A1(c)	True AR(1)
I	0.3	0.4	0.0	698	0.798	0.807	0.803	0.798	0.796	‡	‡
			0.3	635	0.819	0.817	0.800	0.820	0.804	0.815	0.780*
			0.6	447	0.815	0.862	0.773*	0.865	0.817	0.827	0.728*
			0.8	252	0.835	0.925	0.733*	†	†	0.840	0.721*
		0.6	0.0	698	0.796	0.799	0.806	0.800	0.791	‡	‡
			0.3	635	0.808	0.813	0.792	0.824	0.805	0.807	0.775*
			0.6	447	0.833	0.856	0.798	0.859	0.831	0.838	0.727*
			0.8	252	0.827	0.901	0.758*	†	†	0.835	†
	0.5	0.4	0.0	252	0.799	0.801	0.798	0.798	0.801	‡	‡
			0.3	229	0.813	0.815	0.797	0.814	0.811	0.814	0.771*
			0.6	161	0.824	0.872	0.789	0.868	0.833	0.843	0.742*
			0.8	91	0.843	0.931	0.734*§	0.926	†	0.839§	0.725*
		0.6	0.0	252	0.796	0.797	0.810	0.792	0.802	‡	‡
			0.3	229	0.817	0.815	0.808	0.811	0.823	0.823	0.771*
			0.6	161	0.838	0.859	0.790	0.861	0.832	0.837	0.749*
			0.8	91	0.835§	0.896	0.765*§	0.896	†	0.859	†
II	0.3	0.4	0.0	559	0.801	0.801	0.808	0.778*	0.803	‡	‡
			0.3	508	0.804	0.813	0.831	0.800	0.797	0.798	0.795
			0.6	358	0.817	0.819	0.834	0.807	0.759*	0.788	0.811
			0.8	201	0.836	0.814	0.836	0.809	†	0.792	0.806
		0.6	0.0	489	0.804	0.796	0.793	0.736*	0.810	‡	‡
			0.3	445	0.797	0.804	0.818	0.758*	0.795	0.780*	0.804
			0.6	313	0.824	0.831	0.844	0.793	0.752*	0.770*	0.824
			0.8	176	0.845	†	†	0.754*	†	0.776*	0.842
	0.5	0.4	0.0	201	0.801	0.800	0.802	0.768*	0.794	‡	‡
			0.3	183	0.813	0.800	0.819	0.790	0.813	0.796	0.803
			0.6	129	0.814	0.828	0.833	0.810	0.763*	0.799	0.815
			0.8	73	0.839	0.841	0.852	0.829	†	0.795	0.804
		0.6	0.0	176	0.807	0.799	0.796	0.733*	0.808	‡	‡
			0.3	160	0.816	0.815	0.821	0.767*	0.808	0.802	0.812
			0.6	113	0.829	0.830	0.837	0.792	0.765*	0.770*	0.817
			0.8	64	0.845§	†	†	0.783*§	†	0.789§	†
III	0.3	0.4	0.0	454	0.806	0.813	0.806	0.782*	0.794	‡	‡
			0.3	413	0.815	0.809	0.814	0.789	0.800	0.800	0.775*
			0.6	291	0.821	0.811	0.818	0.794	0.783*	0.787*	0.687*
			0.8	164	0.824	0.812	0.839	0.812	†	0.802	0.637*
		0.6	0.0	419	0.813	0.814	0.817	0.781*	0.769*	‡	‡
			0.3	381	0.823	0.812	0.808	0.776*	0.791	0.795	0.771*
			0.6	268	0.823	0.817	0.844	0.807	0.750*	0.754*	0.709*
			0.8	151	0.820	†	†	0.803	†	0.784*	†
	0.5	0.4	0.0	164	0.808	0.804	0.795	0.776*	0.802	‡	‡
			0.3	149	0.822	0.815	0.827	0.811	0.791	0.805	0.789
			0.6	105	0.811	0.810	0.812	0.810	0.798	0.785*	0.698*
			0.8	59	0.838	†	0.823	0.845	†	0.817§	0.684*
		0.6	0.0	151	0.798	0.809	0.803	0.778*	0.772*	‡	‡
			0.3	138	0.812	0.809	0.814	0.800	0.782*	0.799	0.778*
			0.6	97	0.803§	0.812	0.826§	0.826§	0.762*	0.774*§	0.705*§
			0.8	55	0.826§	†	†	0.837§	†	0.797§	†

^*Statistically significantly less than 0.8 at the 5% level.

^†Our data generative model could not accommodate this scenario (see appendix C).

^‡Violation of this working assumption is not applicable when ρ = 0.

^§Fewer than 3000 simulations generated data in which all treatment sequences were observed.

Violation of working assumption A1(b) was induced by defining response status as

$$R^{\left(a_1\right)}=\mathbb{1}\left\{Y_1^{(d)}\in \left(-\infty ,{\kappa }_{a_1}^{\text{low }}\right]\cup \left[{\kappa }_{a_1}^{\text{high }},\infty \right)\right\},$$ (11)

where κ^low and κ^high are chosen to be the r/2 and (1 – r/2)th quantiles of the $\mathcal{N}\left({\mu }_1^{(d)},{\sigma }^2\right)$ distribution, respectively. This ensures control on response probability while also inducing large positive correlation between $R^{\left(a_1\right)}$ and ${\left(Y_1^{(d)}-{\mu }_1^{(d)}\right)}^2$.

Violation of working assumption A1(c) was induced by choosing $\text{Cor}\left(Y_t^{(d)},Y_2^{(d)}|R^{\left(a_1\right)}=1\right)>\text{Cor}\left(Y_t^{(d)},Y_2^{(d)}|R=0\right)$ while keeping respective variances fixed. In our generative model, it was difficult to exert precise control over these quantities when response was related to prior outcomes; as such, these violations were induced under the R_⫫ response model.

There exist natural constraints on how much larger than $\text{cov}\left(Y_t^{(d)},Y_2^{(d)}|R=0\right)$ the responders’ covariance can be while ensuring that (1) all conditional covariance matrices are positive definite and (2) $\text{cov}\left(Y_t^{(d)},Y_2^{(d)}|R=0\right)\ge 0$ for t = 0, 1. These constraints vary with ρ. We choose $\text{Cor}\left(Y_t^{(d)},Y_2^{(d)}|R^{\left(a_1\right)}=1\right)$ such that $\text{cov}\left(Y_t^{(d)},Y_2^{(d)}|R^{\left(a_1\right)}=1\right)$ is the midpoint between the minimum covariance for which the assumption is violated and the maximum covariance allowed by the aforementioned constraints.

5.2. Simulation Results

Simulation results based on 3,000 simulated data sets are compiled in table 4. We find that sample size formula (10) performs as expected when all assumptions are satisfied. Empirical power is not significantly less than the target power of 0.8, per a one-sided binomial test with level 0.05. The sample size is, as expected, often conservative, particularly when within-person correlation is high.

There may be some concern that, for high within-person correlation, formula (10) is overly conservative; should this concern arise, we recommend use of the sharper formulae presented in the supplement. The difference between the sharper formulae and formula (10) is maximized when $\rho =(1+\sqrt{5})/2\approx 0.62$, so we expect to see the largest differences in power between formula (10) and the sharp formula when we set ρ = 0.6.

When all working assumptions are satisfied, we see that empirical power for R₊ and R₋ scenarios are similar or slightly higher than under the R_⫫ model. In general, there do not appear to be practical differences in empirical power between the response models.

As conjectured, violating working assumption A1(a) does not impact empirical power in design I (compare the results to column “R₊”). For design II, empirical power is consistently less than the nominal value when working assumption A1(a) is violated. However, while the empirical power is often statistically significantly less than 0.8, for practical purposes the loss of power is relatively small. For design III, we notice small reductions in power relative to scenarios in which both working assumptions A1 and A2 are satisfied, though the conservative nature of formula (10) appears to protect against more severe loss of power. This suggests that our sample size formula is moderately robust to reasonable violations of A1(a).

For small ρ, we see no meaningful change in empirical power when violating working assumption A1(b). However, as ρ increases, this also leads to increased correlation between response and the other products of first-stage residuals, which increases the severity of the violation. For ρ = 0.6, we see noticeable, but not extreme, departures from nominal power. When ρ = 0.8, our generative model was not able to violate working assumption A1(b) without also violating working assumption A1(a); as such, we omit those results.

Interestingly, as can be seen in the supplement, defining non-response as in equation (11) (i.e., replacing $R^{\left(a_1\right)}$ with $1-R^{\left(a_1\right)}$) leads to higher-than-nominal power. When there exists negative correlation between response and products of squared first-stage residuals, the form of ${\sigma }_c^2$ derived in appendix B is more conservative, leading to increased power.

Simulation results show that our sample size formula is quite robust to violations of working assumption A1(c) for low-to-moderate within-person correlations; at high correlations, the empirical power is statistically significantly less than 0.8. However, as with working assumption A1(a), the practical reduction in power is relatively small.

The final column of table 4 suggests that formula (10) is highly sensitive to violations of working assumption A2 in regards to the true correlation structure. In particular, when the true correlation structure is not exchangeable with correlation ρ and is instead AR(1) with correlation ρ, empirical power is substantially lower than the target of 0.8, particularly as ρ increases. This is unsurprising: as our assumed exchangeable ρ increases, the difference between the assumed and actual correlation between the end-of-study measurement and earlier measurements increases, leading to more severe loss of power.

Note that when within-person correlation is high, sample size becomes rather small. Since the method presented here is based on asymptotic normality, we caution the reader that small sample sizes (e.g., n < 100) provided by formula (10) may be quite sensitive to violation of the working assumptions.

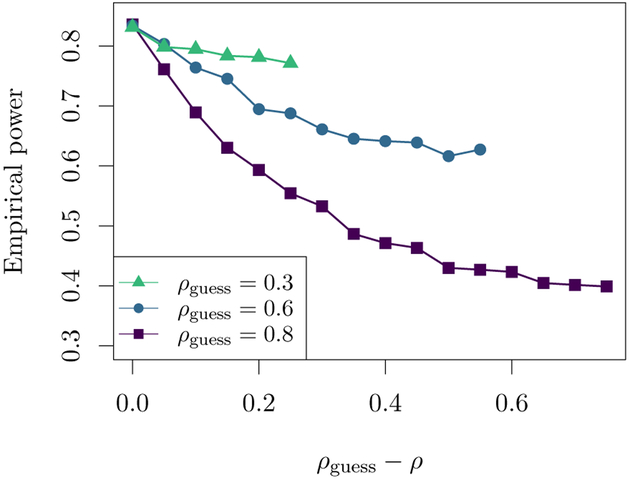
In figure 2, we examine the effect on empirical power of misspecifying the within-person correlation. Analytically, we see from formula (10) that if the assumed ρ is smaller than the true within-person correlation, the sample size will be conservative. On the other hand, when the assumed ρ in formula (10) is larger than the true correlation, the sample size will be anti-conservative. Figure 2 shows plots of empirical power against the difference between the assumed within-person correlation ρ_guess and the true ρ. For small ρ_guess, formula (10) appears to be quite robust to misspecification of ρ; however, as ρ_guess increases, the formula becomes highly sensitive to such a violation of working assumption A2. This is supported analytically, since formula (10) is a function of ${\rho }_{\text{guess}}^2$.

Figure 2:

Empirical power versus the difference between the true within-person correlation ρ and hypothesized correlation ρ_guess used to compute sample size. Results are shown for design II with a hypothesized response rate of 0.4, and sample size was chosen to detect standardized effect size δ= 0.3 for the comparison of DTRs (1, 0, 1) and (−1, 0, −1). Each point is based on 3000 simulations with target power 0.8 and significance level 0.05. Results are similar for designs I and III and different values of δand r.

6. Discussion

We have derived sample size formulae for SMART designs in which the primary aim is a comparsion of two embedded DTRs that begin with different first-stage treatments on a continuous, longitudinal outcome. We derived the formulae for three common SMART designs.

The sample size formula is the product of three components: (1) the formula for the minimum sample size for the comparison of two means in a standard two-arm trial (see, e.g., Friedman et al.,⁴¹ page 147), (2) a deflation factor of 1 – ρ² that accounts for the use of a longitudinal outcome, and (3) a SMART-specific “design effect”, an inflation factor that accounts for the SMART design.

The SMART design effect can be interpreted as the cost of conducting the SMART relative to conducting a standard two-arm randomized trial of the two DTRs which comprise the primary aim. The benefit of conducting a SMART (relative to the standard two-arm randomized trial) is the ability to answer additional, secondary questions that are useful for constructing effective DTRs. For example, such questions may focus on one or more of the other pairwise comparisons between DTRs, on whether the first- and second-stage treatments work synergistically to impact outcomes (e.g., a test of the null that γ₆ = 0 in model (1)), or may focus on hypothesis-generating analyses that seek to estimate more deeply-tailored DTRs.^42,43,44

The formulae are expected to be easy-to-use for both applied statistical workers and clinicians. Indeed, inputs α, β, and Δ are as in the sample size formula for a standard z-test. Furthermore, estimates of ρ, $r_{a_1}$, and σ are often readily available from the literature or can be estimated using data from prior studies (e.g., prior randomized trials, or external pilot studies).

We make a number of recommendations concerning the use of the formulae; in particular, how best to use the formulae conservatively in the absence of certainty concerning prior estimates of ρ, $r_{a_1}$, and/or the structure of the variance of the repeated measures outcome. First, in designs II and III, if there is uncertainty concerning the response rate (e.g., response rate estimates are based on data from smaller prior studies), one approach is to err conservatively by assuming a smaller-than-estimated response rate. In both designs, the most conservative approach is to assume a response rate of zero.

Second, as in standard randomized trials in which the primary aim is a pre-post comparison, the required sample size decreases as the hypothesized within-person correlation increases.⁴⁵ Therefore, if the hypothesized ρ is larger than the true ρ, the computed sample size will be anti-conservative, resulting in an under-powered study. Indeed, we see this in the results of the simulation experiment (see figure 2). Here, again, one approach is to err conservatively towards smaller values of ρ.

Finally, working assumption A2 (concerning the variance of the repeated measures outcome) may be seen as overly restrictive in the imposition of an exchangeable correlation structure. For example, studies with a continuous repeated measures outcome may observe an autoregressive correlation structure. However, the exchangeable working assumption can be employed conservatively in the following way: if the hypothesized structure is not exchangeable, one approach is to set ρ in formula (10) to the smallest plausible value (e.g., the within-person correlation between the baseline and end-of-study measurements for an autoregressive structure). Because this approach utilizes a lower bound on the value of the true within-person correlations, it is expected to yield a larger than needed (more conservative) sample size. Similarly, if the true within-person correlation is expected to differ by DTR, one approach is to employ the smallest plausible ρ. As with the third recommendation, these recommendations are not unique to SMARTs; indeed, these strategies may also be used to size standard two-arm randomized trials with repeated measures outcome.

In the case where $\text{Var}\left(Y_t^{(d)}\right)$ varies with time and/or DTR, we conjecture that power will suffer if a pooled estimate of σ² is used when the variance decreases with time. To see this, consider that the standardized effect size δ defined in equation (9) has as a denominator the pooled standard deviation of $Y_2^{(d)}$ across the groups under comparison. Should the estimate of pooled standard deviation be larger than the true value, the variance of $c^{\top }\widehat{\theta }$ will increase; since the estimate will be less efficient than hypothesized, power will be lower than expected. Conversely, we also conjecture that when $\text{Var}\left(Y_t^{(d)}\right)$ increases with t, the sample size will be conservative using similar reasoning.

The main contribution of this manuscript is the development of sample size formulae for SMARTs in which the primary aim is an end-of-study comparison of two embedded DTRs which recommend different first-stage treatments (so-called “separate-path” DTRs).⁴⁶ It is possible, though, that some trialists may have interest in sizing a SMART for an end-of-study comparison of “shared-path” DTRs; that is, two DTRs which recommend the same first-stage treatment. We believe that, for the comparison of shared-path DTRs, investigators are better set to use a standard sample size calculation to compare the second-stage treatments which differ between the DTRs, then upweighting the result by the proportion of participants expected to be in these groups.

There are a number of interesting ways to build on this manucript in future methodological work. First, some scientists may be interested in a primary aim comparison that involves other features of the marginal mean trajectory, such as the area under the curve (AUC). Future work could develop formulae for these other primary aim comparisons. An important challenge here is in whether and how to define the standardized effect size δ. Second, an interesting extension of this work is to better understand the cost-benefit trade-off between adding additional sample size versus adding additional measurement occasions to the SMART design. The formulae presented here employ the rather simplistic working assumption that there are T = 3 measurement occasions (at baseline, the end of the first stage, and the end of the second stage). Based on limited simulation experiments, sample sizes based on our formulae are expected to perform conservatively when T > 3. Future work could develop rules of thumb for how best to allocate additional sample size versus additional measurement occasions given budget constraints (e.g., a fixed total study cost and fixed costs for an additional participant and additional measurement occasion). Third, as the field moves toward simulation-based approaches for sample size calculation, there is a clear need for the development of software that would allow applied statistical workers and clinicians to make fewer (or more flexible) assumptions concerning many of the features of the SMART, or to be more flexible with respect to the design of the SMART. An important challenge here is to make the software general enough to be used across a number of different types of SMART designs (e.g., three stages of randomization), yet not so flexible that it is difficult to use. The benefits of this is the ability to examine the power for various different scientific questions given a single data generative model and for many other types of SMARTs.

A. Identifiability Assumptions

We make the following assumptions in order to show that equation (4) has mean zero.

• I1Positivity.

  The probabilities P (A₁ = 1) and P (A₂ = 1 { A₁, R) are non-zero.

• I2Consistency with potential outcomes.⁴⁷
  A participant’s observed responder status is “consistent” with the participant’s corresponding potential responder status under the assigned first-stage treatment; i.e.,

  $$R_i=\mathbb{1}\left\{A_{1,i}=1\right\}{R}_i^{(1)}+\mathbb{1}\left\{A_{1,i}=-1\right\}{R}_i^{(-1)}.$$

  Furthermore, a participant’s observed repeated measures outcomes are consistent with the participant’s corresponding potential repeated measures outcomes under the assigned treatment sequence; see table A1.

Table A1:

Design-specific consistency assumptions. $d\in \mathcal{D}$ indexes embedded DTRs (a₁, a_2R, a_2NR).

Design	Y2,i
I	${\sum }_{d\in \mathcal{D}}\frac{1}{2}\mathbb{1}\left\{A_{1,i}=a_1\right\}\left(R_i\mathbb{1}\left\{A_{2,i}=a_{2R}\right\}+\left(1-R_i\right)\mathbb{1}\left\{A_{2,i}=a_{2NR}\right\}\right)Y_{2,i}^{(d)}$
II	${\sum }_{d\in \mathcal{D}}\mathbb{1}\left\{A_{1,i}=a_1\right\}\left(\frac{1}{2}{R}_i+\left(1-R_i\right)\mathbb{1}\left\{A_{2,i}=a_2\right\}\right)Y_{2,i}^{(d)}$
III	${\sum }_{d\in \mathcal{D}}\mathbb{1}\left\{A_{1,i}=a_1\right\}\left(\mathbb{1}\left\{a_1=-1\right\}+\mathbb{1}\left\{a_1=1\right\}\left(\frac{1}{2}{R}_i+\left(1-R_i\right)\mathbb{1}\left\{A_{2,i}=a_2\right\}\right)\right)Y_{2,i}^{(d)}$

The factor of 1/2 for responders in designs II and III accounts for the fact that these participants are consistent with two DTRs. For example in design II, if R_j = 1 for some j, $Y_j^{\left(a_1,0,1\right)}=Y_j^{\left(a_1,0,-1\right)}:=Y_j^{\left(a_1,0,\cdot \right)}$.

• I3Sequential randomization.
  At each stage in the SMART, observed treatments A₁ and A₂ are assigned independently of future potential outcomes, given the participant’s history up to that point. That is,

  $$\begin{gathered} \left\{Y_i^{(d)},R_i^{\left(a_1\right)}\right\}⫫A_{1,i} \\ \left\{Y_i^{(d)}\right\}⫫A_{2,i}|A_{1,i},R_i \end{gathered}$$

Identifiability assumptions I1 and I3 are satisfied by design in a SMART (see, e.g., Lavori and Dawson⁴⁸); identifiability assumption I2 is connects the potential outcomes and observed data, and is typically accepted in the analysis of randomized trials.

B. Derivation of Sample Size Formulae

We derive the sample size formulae for comparing two DTRs which recommend different first-stage treatments that are embedded in a SMART in which a continuous longitudinal outcome is collected throughout the study. These formulae are based on the regression analyses described in section 3 and a Wald test.

We consider a SMART in which the outcome is collected at three timepoints: at baseline (t₁ = 0), immediately before assessing response/non-response (t₂ = 1), and at the end of the study (t₃ = 2). We ignore the presence of baseline covariates X and assume μ^(d)(θ) is piecewise-linear in θ (see, for example, model (1)). Recall that $\theta \in {ℝ}^p$.

Recall from section 4 that we wish to the null hypothesis H₀ : c^⊤θ= 0, where $c\in {ℝ}^p$ is a contrast vector specifying a linear combination of θ. In particular, we are interested in contrasts c which yield an end-of-study comparison between two embedded DTRs which recommend different first-stage treatments. For example, in design II, the end-of-study comparison of DTRs (1, 0, 1) vs. (−1, 0, −1) is given by c = (0, 0, 2, 0, 2, 2, 0)^⊤. Since, here, c is a vector, this yields a 1-degree of freedom Wald test for which we can use a Z statistic:

$$Z=\frac{\sqrt{n}{c}^{\top }\widehat{\theta }}{{\sigma }_c},$$

where ${\sigma }_c=\sqrt{c^{\top }{B}^{-1}M{B}^{-1}c}$. Under H₀, by asymptotic normality of $\sqrt{n}(\widehat{\theta }-\theta )$, the test statistic follows an asymptotic standard normal distribution. Suppose we wish to test H₀ against the alternative hypothesis c^⊤θ = Δ. The minimum-required sample size is

$$n\ge {\left(z_{1-\alpha /2}+z_{1-\beta }\right)}^2\frac{{\sigma }_c^2}{{\mathrm{\Delta }}^2},$$ (B1)

where z_p is the pth quantile of the standard normal distribution. Formula (B1) is a standard result in the clinical trials literature;^41,49 however, because of the dependence on σ_c, the formula is not useful as written. The goal of the remainder of this appendix is to derive a closed-form upper bound on σ_c so as to obtain a sample size formula in terms of marginal quantities which can be more easily elicited from clinicians, or estimated from the literature. In particular, we want this upper bound to be a multiple of σ², the assumed common marginal variance across time and DTR, so that the final formula will involve Cohen’s effect size δ = Δ/σ˙.

Recall the definitions of $B\in {ℝ}^{p\times p}$ and $M\in {ℝ}^{p\times p}$ in equations (5) and (6), respectively. These quantities depend on $D^{(d)}\in {ℝ}^{T\times p}$, the jacobian of μ^(d)(θ), and $V^{(d)}(\tau )\in {ℝ}^{T\times T}$, the working covariance matrix for Y^(d). By assumed linearity of μ^(d)(θ), D^(d) is a fixed, constant matrix for all d. Furthermore, we assume that the working covariance matrix V^(d)(τ) is correctly specified and satisfies working assumption A2 so that V^(d)(τ) = Σ for all $d\in \mathcal{D}$. Note that Σ is non-random.

The estimand in equation (8) is a function of potential outcomes; as written in equations (5) and (6), B and M are functions of observed data. We begin by expressing B in terms of potential outcomes. Under the positivity, consistency, and sequential ignorability conditions (identifiability assumptions I1 to I3), we can apply lemma 4.1 of Murphy et al.¹⁰ so that

$$\begin{gathered} B=\sum _{d\in \mathcal{D}}\underset{A_1,R,A_2}{\text{E}}\left[W^{(d)}\left(A_1,R,A_2\right)D^{(d)}{\left(V^{(d)}(\tau )\right)}^{-1}{\left({\mathit{D}}^{(d)}\right)}^{\top }\right] \\ =\sum _{d\in \mathcal{D}}{D}^{(d)}{\Sigma }^{-1}{\left(D^{(d)}\right)}^{\top }. \end{gathered}$$ (B2)

We now turn our attention to M. Expanding the outer product inside the expectation, we have

$$\begin{gathered} \mathit{M}=\underset{A_1,R,A_2,\mathit{Y}}{\text{E}}\left[{\left(\sum _{d\in \mathcal{D}}{W}^{(d)}\left(A_1,R,A_2\right)D^{(d)}{\left(V^{(d)}(\tau )\right)}^{-1}\left(Y-{\mu }^{(d)}(\theta )\right)\right)}^{\otimes 2}\right] \\ =\sum _{d\in \mathcal{D}}\underset{A_1,R,A_2,Y}{\text{E}}\left[{\left(W^{(d)}\left(A_1,R,A_2\right)\right)}^2{\left(D^{(d)}{\Sigma }^{-1}\left(Y-{\mu }^{(d)}(\theta )\right)\right)}^{\otimes 2}\right]+\sum _{d\ne d^{\prime }}\underset{A_1,R,A_2,Y}{\text{E}}\left[W^{(d)}\left(A_1,R,A_2\right)W^{\left(d^{\prime }\right)}\left(A_1,R,A_2\right)D^{(d)}{\Sigma }^{-1}\left(Y-{\mu }^{(d)}(\theta )\right){\left(Y-{\mu }^{(d^{\prime })}(\theta )\right)}^{\top }{\Sigma }^{-1}{\left(D^{\left(d^{\prime }\right)}\right)}^{\top }\right]. \end{gathered}$$ (B3)

Consider a single summand of the first term in equation (B3). We can write this as

$$D^{(d)}{\Sigma }^{-1}\underset{A_1,R,A_2,Y}{\mathrm{E}}\left[W^{(d)}{\left(A_1,R,A_2\right)}^2{\left(Y-{\mu }^{(d)}(\theta )\right)}^{\otimes 2}\right]{\Sigma }^{-1}{\left(D^{(d)}\right)}^{\top },$$ (B4)

where, as before, Z^⊗2 = ZZ^⊤. The inner expectation is a T × T matrix, the (i, j)th element of which is

$$\underset{A_1,R,A_2,Y}{\text{E}}\left[W^{(d)}{\left(A_1,R,A_2\right)}^2\left(Y_{t_i}-{\mu }_{t_i}^{(d)}(\theta )\right)\left(Y_{t_j}-{\mu }_{t_j}^{(d)}(\theta )\right)\right].$$ (B5)

Notice that the work above is design-independent: B and M have the same form as equations (B2) and (B3), respectively, for all designs. Below, we proceed only for design II, but derivations for designs I and III are analogous, substituting appropriate definitions of W^(d)(A₁, R, A₂). Recall that, for design II, when all randomization probabilities are 0.5, $W^{(d)}\left(A_1,R,A_2\right)=2\mathbb{1}\left\{A_1=a_1^{(d)}\right\}(R+2(1-R)\mathbb{1}\left\{A_2=a_2^{(d)}\right\})$.

It can be shown that we can achieve an upper bound on σ_c which involves σ and ρ by imposing working assumption A1 on the inner expectation in equation (B4) such that all diagonal terms are at least 2 · DE · σ² and all off-diagonal terms are at most 2 · DE · ρσ², where DE is the design effect as in table 3.

Consider, for example, t = 1. By repeated use of iterated expectation and application of identifiability assumptions I2 and I3, equation (B5) becomes

$$\begin{gathered} \underset{Y_{t_0},A_1,Y_{t_1},R,A_2,Y_{t_2}}{\text{E}}\left[W^{(d)}{\left(A_1,R,A_2\right)}^2{\left(Y_{t_1}-{\mu }_{t_1}^{(d)}(\theta )\right)}^2\right] \\ =\underset{Y_{t_0},A_1,Y_{t_1},R,A_2}{\text{E}}\left[4\mathbb{1}\left\{A_1=a_1^{(d)}\right\}\left(R+4(1-R)\mathbb{1}\left\{A_2=a_2^{(d)}\right\}\right){\left(Y_{t_1}-{\mu }_{t_1}^{(d)}(\theta )\right)}^2\right] \\ =\underset{Y_{t_0}^{(d)},A_1,Y_{t_1},R^{\left(a_1\right)},A_2^{(d)}}{\text{E}}\left[4\mathbb{1}\left\{A_1=a_1^{(d)}\right\}\left(R^{\left(a_1\right)}+4\left(1-R^{\left(a_1\right)}\right)\mathbb{1}\left\{A_2=a_2^{(d)}\right\}\right){\left(Y_{t_1}^{(d)}-{\mu }_{t_1}^{(d)}(\theta )\right)}^2\right] \\ =\underset{S_2\left({\overline{A}}_1\right)}{\text{E}}\left[4\mathbb{1}\left\{A_1=a_1^{(d)}\right\}\left(R^{\left(a_1\right)}+4\left(1-R^{\left(a_1\right)}\right)\underset{A_2|S_2\left({\overline{A}}_1\right)}{\text{E}}\left[\mathbb{1}\left\{A_2=a_2^{(d)}\right\}\right]\right){\left(Y_{t_1}^{(d)}-{\mu }_{t_1}^{(d)}(\theta )\right)}^2\right] \\ =\underset{Y_{t_0}^{(d)},A_1,Y_{t_1}^{(d)},R^{\left(a_1\right)}}{\text{E}}\left[4\mathbb{1}\left\{A_1=a_1^{(d)}\right\}\left(2-R^{\left(a_1\right)}\right){\left(Y_{t_1}^{(d)}-{\mu }_{t_1}^{(d)}(\theta )\right)}^2\right]. \end{gathered}$$ (B6)

$$=4\underset{Y_1^{(d)}}{\text{E}}\left[{\left(Y_1-{\mu }_1^{(d)}\right)}^2\right]-2\underset{Y_1^{(d)},R^{\left(a_1\right)}}{\text{E}}\left[{\left(Y_1-{\mu }_1^{(d)}\right)}^2{R}^{\left(a_1\right)}\right]$$ (B7)

$$=4{\sigma }^2-2\text{Cov}\left({\left(Y_1-{\mu }_1^{(d)}\right)}^2,R^{\left(a_1\right)}\right)-2\text{E}\left[R^{\left(a_1\right)}\right]\text{E}\left[{\left(Y_1-{\mu }_1^{(d)}\right)}^2\right]$$ (B8)

$$=2\left(2-r_{a_1}\right){\sigma }^2.$$ (B9)

Equation (B7) follows from equation (B6) by identifiability assumption I3 and smoothing over $Y_{t_0}^{(d)}$, equation (B8) arises from the definition of covariance, and equation (B9) is a consequence of working assumption A1(b).

Similar derivations can be performed for the remaining combinations (i, j). Under working assumptions A1 and A2, equation (B5) is exactly equal to $2\left(2-r_{a_1}\right){\Sigma }_{i,j}$ for i, j ∈ {1, 2}. For the last diagonal element (i = j = 3), equation (B5) is at least $2\left(2-r_{a_1}\right){\Sigma }_{3,3}$; the remaining off-diagonal quantities are bounded above by $2\left(2-r_{a_1}\right){\Sigma }_{i,j}$. This allows us to bound c^⊤B⁻¹MB⁻¹c above by

$$\begin{gathered} c^{\top }{B}^{-1}M{B}^{-1}c\le 2\cdot \frac{1}{2}\left(\left(2-r_1\right)+\left(2-r_{-1}\right)\right)c^{\top }{B}^{-1}{\left(\sum _{d\in \mathcal{D}}{D}^{(d)}{\Sigma }^{-1}\right)}^{\otimes 2}{B}^{-1}c \\ =\frac{4{\sigma }^2(1-\rho )\left({\rho }^2+4\rho -\frac{1}{2}\left(r_1+r_{-1}\right)(2\rho +1)+2\right)}{1+\rho }. \end{gathered}$$ (B10)

Plugging equation (B10) into formula (B1) leads to the aforementioned “sharp” sample size formula for design II. Some algebra shows that

$${\sigma }_c^2\le 4{\sigma }^2\cdot \left(1-{\rho }^2\right)\cdot \frac{1}{2}\left(\left(2-r_1\right)+\left(2-r_{-1}\right)\right),$$ (B11)

which allows for an easy-to-understand sample size formula. Plugging this result into formula (B1), we arrive at formula (10).

C. Details Concerning the Data-Generative Process for Simulations

To construct table 4, we employ two data-generative models. Here, we describe the first, which we believe to be more realistic and which is used to simulate under all scenarios in table 4 except for those in which working assumption A1(c) is violated. A description of the second model, used to violate working assumption A1(c), is available in the supplement.

In general, generating realistic longitudinal data from a SMART is difficult when precise control must be exerted over the marginal covariance structure of the outcomes. As such, the generative model described here is rather complex. We attempt to distill the details in this appendix and provide further details about response status and variance generation in the supplement.

For each scenario described in table 4, we compute the sample size for the trial using formula (10) and the appropriate design effect from table 3. We then, for each “participant” i, generate potential outcomes under each embedded DTR as follows:

$$\begin{gathered} Y_{0,i}^{(d)}={\gamma }_0+{ϵ}_{0,i} \\ {Y}_{1,i}^{(d)}|Y_{0,i}^{(d)}={\gamma }_0+\rho Y_{0,i}^{(d)}+{\gamma }_1+{\gamma }_2{a}_1+{ϵ}_{1,i}^{\left(a_1\right)} \\ {R}_i^{\left(a_1\right)}|Y_{0,i}^{(d)},Y_{1,i}^{(d)}=g_{a_1}\left(Y_{1,i}^{\left(a_1\right)}\right) \\ {Y}_{2,i}^{(d)}|Y_{0,i}^{(d)},Y_{1,i}^{(d)},R_i^{\left(a_1\right)}=\left(1-c_0(\rho )-c_1(\rho )\right){\gamma }_0+c_0(\rho )Y_{0,i}^{(d)}+c_1(\rho )Y_{1,i}^{(d)}+\left(1-c_1(\rho )\right)\left({\gamma }_1+{\gamma }_2{a}_1^{(d)}\right)+{\gamma }_3+{\gamma }_4{a}_1^{(d)}+{\xi }^{(d)}\left(R_i^{\left(a_1\right)}\right)+\left(R^{\left(a_1\right)}-r_{a_1,i}\right)\left({\lambda }_1+{\lambda }_2{a}_1^{(d)}\right)+{ϵ}_{2,i}^{(d)}\left(R_i^{\left(a_1\right)}\right), \end{gathered}$$ (C1)

where ${ϵ}_0~\mathcal{N}\left(0,{\sigma }^2\right)$, ${ϵ}_1^{(d)}~\mathcal{N}\left(0,\left(1-{\rho }^2\right){\sigma }^2\right)$, and ${ϵ}_2^{(d)}\left(R_i^{\left(a_1\right)}\right)~\mathcal{N}\left(0,v^{(d)}\left(R_i^{\left(a_1\right)}\right)\right)$. ${\sigma }^2=\text{Var}\left(Y_t^{(d)}\right)$ is the assumed constant marginal variance of the outcome as in working assumption A2. Here, $a_j^{(d)}$ is the jth-stage treatment recommended by DTR d.

Table C1:

Design-specific conditional mean components ${\xi }^{(d)}\left(R^{\left(a_1\right)}\right)$ for model (C1). $r_{a_1,i}$ is the probability of response to first-stage treatment for participant i. Dashes indicate that the corresponding parameter is not used in the model for that design; variances in the lower part of the table span across multiple rows when (non-)responders to the corresponding first-stage treatment are not re-randomized.

Design	${\xi }^{(d)}\left(R^{\left(a_1\right)}\right)$
I	$\frac{R^{\left(a_1\right)}}{r_{a_1,i}}\left({\gamma }_5+{\gamma }_7{a}_1^{(d)}\right)a_{2R}^{(d)}+\frac{1-R^{\left(a_1\right)}}{1-r_{a_1,i}}\left({\gamma }_6+{\gamma }_8{a}_1^{(d)}\right)a_{2NR}^{(d)}$
II	$\frac{1-R^{\left(a_1\right)}}{1-r_{a_1,i}}\left({\gamma }_5+{\gamma }_6{a}_1^{(d)}\right)a_{2NR}^{(d)}$
III	$\frac{1-R^{\left(a_1\right)}}{1-r_{a_1,i}}\mathbb{1}\left\{a_1^{(d)}=1\right\}\cdot {\gamma }_5{a}_{2NR}^{(d)}$

The error terms ϵ_t add the “additional” variance to $Y_j^{(d)}$ which is needed to achieve marginal variance σ². Outcomes $Y_{t,i}^{(d)}$ are generated as functions of an individual’s outcomes at previous timepoints, which induces variance in, say, $Y_2^{(d)}$ when marginalizing over $Y_1^{(d)}$ and $Y_0^{(d)}$. Hence, $v^{(d)}\left(R^{\left(a_1\right)}\right)$ is the additional variance added to the response-conditional end-of-study outcome beyond that which is induced by defining $Y_{2,i}^{(d)}|R_i^{\left(a_1\right)}$ as a function of $Y_{0,i}^{(d)}$ and $Y_{1,i}^{(d)}$. This is required to ensure that the marginal variance of $Y_2^{(d)}$ is σ². All errors ϵ are generated independently of one another.

The parameters γ_j are interpreted exactly as in, say, model (1) (see section 3.3 and equation (2)), and index the generative marginal structural mean model. The functions c_t(ρ) control within-person correlation between $Y_{2,i}^{(d)}$ and previously-observed outcomes $Y_{t,i}^{(d)}$, t < t*. For an exchangeable correlation structure, we use c₀(ρ) = c₁(ρ) = ρ/(1 + ρ); for AR(1), c₀(ρ) = 0 and c₁(ρ) = ρ.

Note that the second-stage outcome $Y_{2,i}^{(d)}$ is generated conditionally on response status, since participants in a SMART can only be a responder or a non-responder to first-stage treatment. Since second-stage treatments in a SMART are often restricted based on response, these treatment effects can typically only be estimated using either responders or non-responders. ${\xi }^{(d)}\left(R^{\left(a_1\right)}\right)$ is a design-specific function of response which involves marginal parameters γ_j for second-stage treatment effects and their interactions with first-stage treatment effects. Our choices of ${\xi }^{(d)}\left(R^{\left(a_1\right)}\right)$ are given in table C1. For example, in design II, only non-responders are re-randomized, and so the effect of a_2NR should only be simulated among non-responders, and upweighted appropriately to reflect this (see table C1).

The final component of the generative mean structure for $Y_{2,i}^{(d)}|R_i^{\left(a_1\right)}$ is $\left(R_i^{\left(a_1\right)}-r_{a_1,i}\right)\left({\lambda }_1+{\lambda }_2{a}_1^{(d)}\right)$, where ${\tau }_{a_1,i}$ is the probability of response to first-stage treatment for participant i. The parameters λ₁ and λ₂ control how responders and non-responders differ from the marginal mean at time 2, and cancels to zero when averaged over response status.

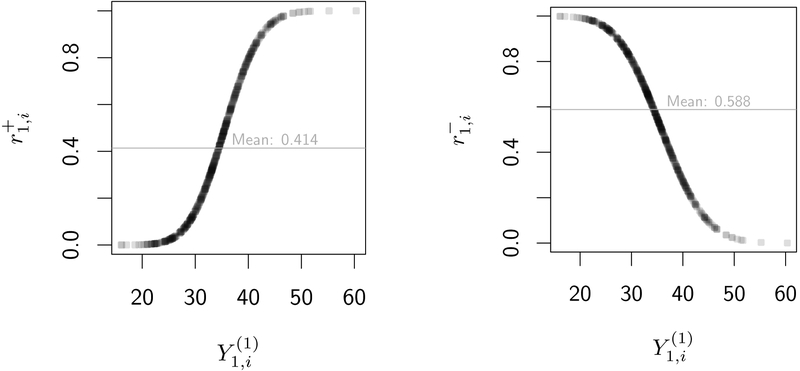
In order to design a realistic generative model, we define response as a function of $Y_{1,i}^{\left(a_1\right)}$. In table 4, we consider three possible response models: “R_⫫”, in which response status is independent of $Y_{1,i}^{\left(a_1\right)}$, “R₊”, in which $P\left(R_i^{\left(a_1\right)}=1\right)$ increases with $Y_{1,i}^{\left(a_1\right)}$, and “R₋”, in which $P\left(R_i^{\left(a_1\right)}=1\right)$ is decreasing in $Y_{1,i}^{\left(a_1\right)}$. In figure C1, we plot probabilities of response versus $Y_{1,i}^{(d)}$ under both R₊ and R₋ response models. We consider both R₊ and R₋ to ensure that power is not affected by the choice of coding for Y (e.g., “higher-is-better” vs. “lower-is-better”). More details are provided in the supplement.

Table C2:

Example choices of parameters in data generative model to achieve δ= 0.3 and ρ = 0.3 when r₁ = r₋₁ = 0.4 under R₊ and working assumptions A1 and A2 are satisfied for each of designs I to III.

Parameter	Design I	Design II	Design III
γ0	35.0	33.5	35.0
γ1	−4.0	−0.8	−0.5
γ2	2.7	0.9	1.0
γ3	−1.6	−0.8	0.2
γ4	−1.5	0.4	−0.2
γ5	0.4	−0.4	0.8
γ6	−0.4	0.1	-
γ7	0.4	-	-
γ8	0.4	-	-
λ1	0.3	0.1	0.8
λ2	0.4	−0.5	0.0
σ2	64	36	64
$v^{\left(1,1,a_{2NR}\right)}(1)$	57.62	21.12	56.56
$v^{\left(1,-1,a_{2NR}\right)}(1)$	57.62
$v^{\left(1,a_{2R},1\right)}(0)$	53.07	18.48	55.27
$v^{\left(1,a_{2R},-1\right)}(0)$	53.07	21.64	43.37
$v^{\left(-1,1,a_{2NR}\right)}(1)$	57.89	19.39	53.68
$v^{\left(-1,-1,a_{2NR}\right)}(1)$	57.89
$v^{\left(-1,a_{2R},1\right)}(0)$	49.80	14.20	53.97
$v^{\left(-1,a_{2R},-1\right)}(0)$	55.78	20.80

Figure C1:

Individual probabilities of response versus potential outcomes at the end of the first stage of a SMART under response models R₊ and R₋. Based on a simulated SMART with n = 500 individuals; a₁ = 1 was chosen arbitrarily and without loss of generality. Empirical average response rate is plotted as a horizontal line in gray. Darker regions of the curve contain more observations.

(I) Response probabilities in the R₊ model versus (II) Response probabilities in the R₋ model versus $Y_{1,i}^{(1)}$ with average response rate r₁ = 0.4. Higher val- $Y_{1,i}^{(1)}$ with average response rate r₁ = 0.6. Higher values of $Y_{1,i}^{(1)}$ are associated with higher response prob- ues of $Y_{1,i}^{(1)}$ are associated with lower response prob- ues of $Y_{1,i}^{(1)}$ are associated with lower response probabilities.

The above models are used to generate potential outcomes $Y_i^{(d)}$ and potential response status $R_i^{\left(a_1\right)}$ for each “participant” under each DTR d = (a₁, a_2R, a_2NR). This is done to ensure the generative model satisfies identifiability assumption I2; identifiability assumptions I1 and I3 are satisfied by design. From these potential data, we “observe” data as follows:

1. Choose $Y_{0,i}=Y_{0,i}^{(d)}$. Note that since no treatment has been assigned at time 0, there is only one possible value of Y₀, so the potential and observed outcomes coincide.

2. Generate A_1,i ~ Bernoulli(0.5).

3. Choose $Y_{1,i}=Y_{1,i}^{\left(A_{1,i},\cdot ,\cdot \right)}$, the potential outcome at time 1 corresponding to the DTR(s) which recommend first-stage treatment A_1,i.

4. Choose $R_i=R^{\left(A_{1,i}\right)}$, the potential response status of the participant under first-stage treatment A_1,i.

5. Generate A_2,i | R_i ~ Bernoulli(p_i), where p_i is either 0.5 or 0 depending on the value of R_i and the SMART design under consideration. (For example, in design II, p_i = 0 for all i such that R_i = 1 since responders are not re-randomized.)

6. Choose $Y_{2,i}|R^{\left(A_{1,i}\right)}=Y_{2,i}^{\left(A_{1,i},R^{\left(A_{1,i}\right)}{A}_{2,i}\right),\left(1-R^{\left(A_{1,i}\right)}\right)A_{2,i})}$, the potential outcome at time 2 had the participant had response status R_i and been treated according to a DTR which recommends A_1,i in the first stage and A_2,i in the second.

Table C3:

Target and estimated marginal variance matrices V^(d)(τ) from the data generative model described in appendix C. The “unstructured estimate” is produced by estimating the variance at each timepoint and for each DTR, and correlation for each DTR using the unstructured estimate in table 2, then averaging over DTRs. The “exchangeable estimate” is computed by assuming variance is constant over time and DTR, and using the exchangeable estimate of ρ from table 2, averaged over DTRs. The exchangeable estimate is used in simulations assuming working assumption A2 is satisifed.

Design	Target Structure	Unstructured Estimate	Exchangeable Estimate
I	$\left(\begin{array}{ccc}64& 19.2& 19.2\\ 19.2& 64& 19.2\\ 19.2& 19.2& 64\end{array}\right)$	$\left(\begin{array}{ccc}63.9& 19.3& 19.1\\ 19.3& 63.8& 18.7\\ 19.1& 18.7& 62.5\end{array}\right)$	$\left(\begin{array}{ccc}63.4& 18.9& 18.9\\ 18.9& 63.4& 18.9\\ 18.9& 18.9& 63.4\end{array}\right)$
II	$\left(\begin{array}{ccc}36& 10.8& 10.8\\ 10.8& 36& 10.8\\ 10.8& 10.8& 36\end{array}\right)$	$\left(\begin{array}{ccc}35.9& 10.9& 11.0\\ 10.9& 35.9& 11.1\\ 11.0& 11.1& 35.8\end{array}\right)$	$\left(\begin{array}{ccc}35.9& 10.9& 10.9\\ 10.9& 35.9& 10.9\\ 10.9& 10.9& 35.9\end{array}\right)$
III	$\left(\begin{array}{ccc}64& 19.2& 19.2\\ 19.2& 64& 19.2\\ 19.2& 19.2& 64\end{array}\right)$	$\left(\begin{array}{ccc}63.9& 19.4& 19.9\\ 19.4& 63.7& 21.3\\ 19.9& 21.3& 63.6\end{array}\right)$	$\left(\begin{array}{ccc}63.8& 20.0& 20.0\\ 20.0& 63.8& 20.0\\ 20.0& 20.0& 63.8\end{array}\right)$

In table C2 we provide values of the parameters chosen for simulations to achieve a standardized effect size δ= 0.3 for the end-of-study comparison of interest. The values of $v^{(d)}\left(R^{\left(a_1\right)}\right)$ are specific to the scenario in which all working assumptions are satisfied, ρ = 0.3, average response probabilities are r₁ = r₋₁ = 0.4, and when response is computed under the R₊ model. In table C3, we show that the target marginal variance structures are achieved using this data generative model.