Simultaneous tracers and a unified model of positional and mass isotopomers for quantification of metabolic flux in liver

Abstract

Computational models based on the metabolism of stable isotope tracers can yield valuable insight into the metabolic basis of disease. The complexity of these models is limited by the number of tracers and the ability to characterize tracer labeling in downstream metabolites. NMR spectroscopy is ideal for multiple tracer experiments since it precisely detects the position of tracer nuclei in molecules, but it lacks sensitivity for detecting low-concentration metabolites. GC-MS detects stable isotope mass enrichment in low-concentration metabolites, but lacks nuclei and positional specificity. We performed liver perfusions and in vivo infusions of ²H and ¹³C tracers, yielding complex glucose isotopomers that were assigned by NMR and fit to a newly developed metabolic model. Fluxes regressed from ²H and ¹³C NMR positional isotopomer enrichments served to validate GC-MS-based flux estimates obtained from the same experimental samples. NMR-derived fluxes were largely recapitulated by modeling the mass isotopomer distributions of six glucose fragment ions measured by GC-MS. Modest differences related to limited fragmentation coverage of glucose C1–C3 were identified, but fluxes such as gluconeogenesis, glycogenolysis, cataplerosis and TCA cycle flux were tightly correlated between the methods. Most importantly, modeling of GC-MS data could assign fluxes in primary mouse hepatocytes, an experiment that is impractical with ²H or ¹³C NMR.

1. INTRODUCTION

The cellular mechanisms of most disease states impact complex metabolic networks that may be targets for therapy if they can be identified (Cappel et al., 2019; Kim et al., 2017). A general approach to characterizing metabolism is to estimate metabolic flux using isotopically labeled substrates (e.g., tracers containing ¹³C, ²H, ¹⁵N, etc.) that incorporate into downstream metabolites (tracees) (Antoniewicz, 2018; Buescher et al., 2015; Cobelli et al., 1992). Information about the pathways that convert the tracer to the tracee is encoded in the number and position of the isotopic nuclei that appear in the tracee (Des Rosiers et al., 2004). If these labeling patterns can be detected, mathematical models that relate metabolic activity to the formation of these labeling patterns can be used to decode flux through complex networks of metabolism (Antoniewicz et al., 2007). In practice, a single tracer may be insufficient to accurately delineate fluxes of intersecting pathways (Crown and Antoniewicz, 2013; Crown et al., 2016). A simple approach is to use multiple tracers in separate parallel experiments (Figure 1A) (Crown and Antoniewicz, 2013). Tracee detection is simplified, but the approach is impractical in humans and many preclinical models of disease. The use of multiple tracers in a single experiment is ideal (Figure 1B), but this approach generates complicated metabolite labeling patterns that are difficult to interpret (Brunengraber et al., 1997). The challenge is to pair analytical chemistry tools, that rigorously define labeling patterns, with computational tools that relate these patterns to metabolic flux. The reward is novel insight into metabolic changes that underpin diseases such as cancer, obesity, diabetes and cardiovascular disease.

Figure 1. Application of multiple stable isotope tracers.

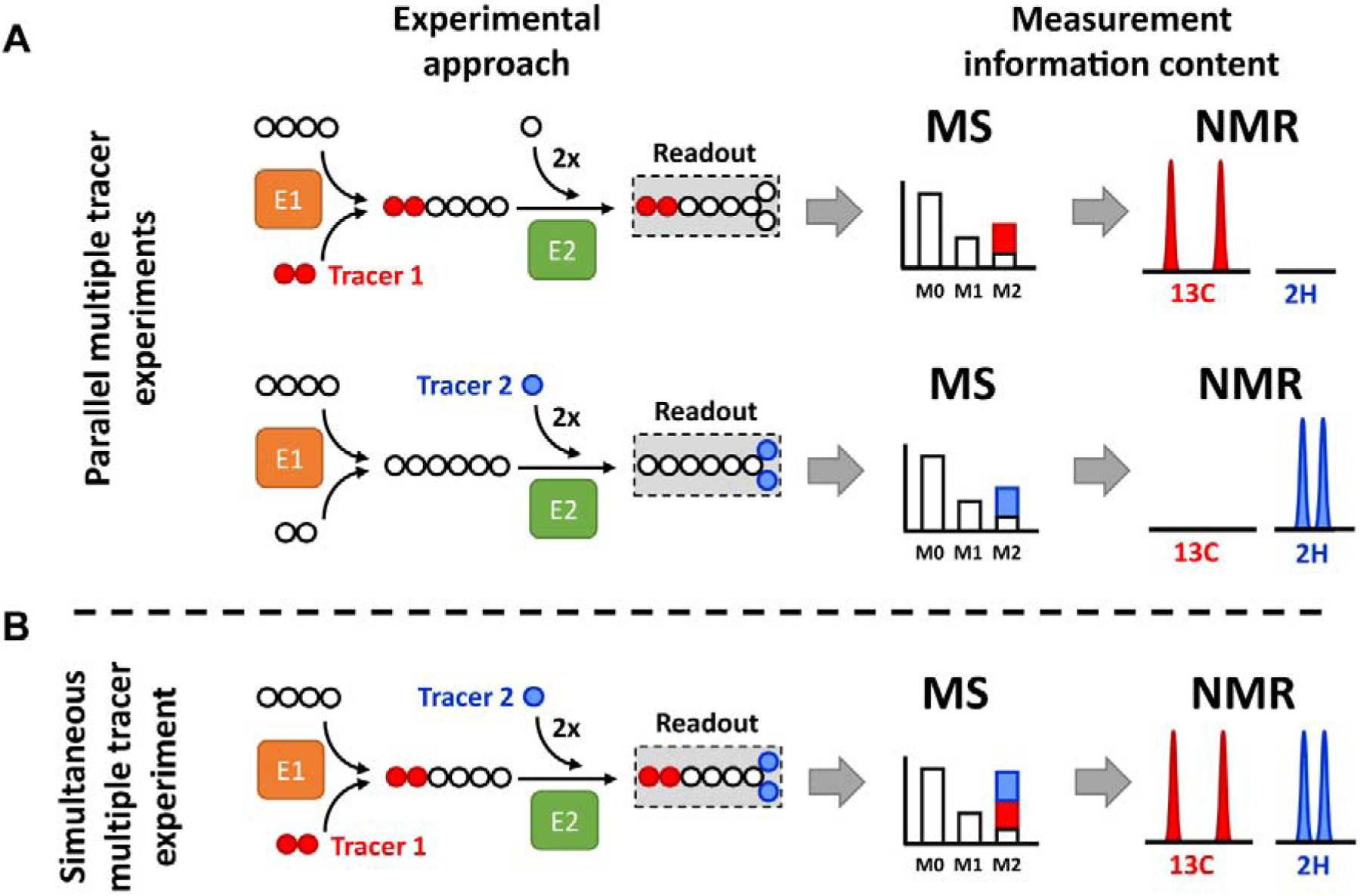
Example metabolic network consisting of two enzymatic reactions (E1 and E2). Tracer 1 provides two ¹³C atoms, while tracer 2 provides two ²H atoms. (A) Parallel experimental setup: tracer 1 and 2 are administered in two separate biological experiments generating two separate datasets. Therefore, individual MIDs and NMR spectra contain labeling information originating from each single tracer. (B) Simultaneous experimental setup: both tracers are administered in the single biological experiment and generate a single dataset. Labeling from tracer 1 and 2 becomes convoluted in the MID and is difficult to interpret without mathematical modeling. In contrast, NMR detection is nucleus-sensitive and can distinguish between signals originating from ²H and ¹³C atoms.

Nuclear magnetic resonance (NMR) and mass spectrometry (MS) are powerful tools for characterizing isotope enrichment patterns in metabolites (Des Rosiers et al., 2004). NMR detects every chemically-unique position of a molecule at a different frequency (chemical shift), and these resonances are characteristically split into multiplets when neighboring atoms in the same molecule are also labeled with an NMR active nuclei (spin-spin coupling). For example, detection of [1,2-¹³C₂]glucose by ¹³C NMR yields doublets at frequencies corresponding to carbons 1 and 2, while [2,3-¹³C₂]glucose yields doublets at frequencies corresponding to carbons 2 and 3. The ability to detect nucleus- and position-specific labeling is the most notable strength of NMR.

In contrast, MS detects a shift in the mass of a tracee when tracer nuclei are incorporated (Figure 1). The relative abundance of isotope-labeled nuclei incorporated into a metabolite forms a mass isotopomer distribution (MID) (M+0, M+1, M+2, etc.). Each of these mass isotopomers represents a distinct class of positional isotopomers. For example, the combined abundances of [1,2-¹³C₂]glucose and [2,3-¹³C₂]glucose would be detected as M+2 glucose, although the two positional isotopomers would not be distinguished by MS. Positional information could be obtained through chemical degradation of glucose into distinct carbon units (Chandramouli et al., 1999; Landau et al., 1995; Schumann et al., 2001), or by collision-induced or in-source fragmentation to isolate MIDs of fragment ions that contain different subsets of atoms from the target analyte (Choi et al., 2012; Dauner and Sauer, 2000). Antoniewicz and colleagues mathematically reconstructed the positional isotopomers of ²H-glucose from GC-MS analysis of several glucose derivatives that produce discrete fragment ions of the parent glucose molecule (Antoniewicz et al., 2011). Although the labeling information is less specific than NMR, the notable advantage of MS is that it is several orders-of-magnitude more sensitive, enabling microscale experiments with limited sample volumes.

Liver contains overlapping pathways of glucose, lipid and mitochondrial metabolism that cannot be measured with a single tracer (Jones et al., 2001b) (Figure 2). These pathways have direct roles in liver diseases like nonalcoholic fatty liver disease, cirrhosis and hepatocellular carcinoma, and also influence the systemic pathologies of obesity, diabetes and cardiovascular disease. Thus, characterizing metabolic flux in liver is an important priority because of its potential as a target against many different diseases. Hepatic glucose production can be determined by the dilution of an infused glucose tracer (e.g., [3,4-¹³C₂]glucose or [6,6-²H₂]glucose) (Jin et al., 2005), but the experiment provides no insight into the metabolic pathways that produced the glucose. A deuterated water (²H₂O) tracer incorporates deuterium nuclei into glucose at specific positions that reflect the activities of glucose-6-phosphate isomerase (C2 hydrogen), triosphosphate isomerase (C5 hydrogen) and phosphoenolpyruvate carboxykinase (C6 hydrogens) (Jones et al., 2000; Landau et al., 1995). Carbon-13 labeled gluconeogenic substrates (e.g., [U-¹³C₃]propionate or [U-¹³C₃]lactate) incorporate ¹³C into glucose after traversing the TCA cycle. The rearrangement of those carbons indicates anaplerosis and oxidative metabolism in liver mitochondria (Jones et al., 1997; Landau et al., 1993; Magnusson et al., 1991). Simultaneous application of all three tracers can elucidate flux through numerous cytosolic and mitochondrial pathways in liver if the appropriate ²H and ¹³C glucose labeling patterns can be distinguished (Jones et al., 1998) (Figure 2).

Figure 2. Simultaneous utilization of ²H and ¹³C tracers provides insights into distinct pathways of hepatic metabolism.

The diagram on the right summarizes positions that are typically monitored by NMR to estimate hepatic fluxes. (Note that all H and C positions are potentially labeled with this combination of tracers.) Glucose labeling from heavy water (²H₂O) allows discrimination between contributions of glycogen, glycerol and TCA cycle intermediates towards endogenous glucose production (EGP). By introduction of ¹³C labeled gluconeogenic precursors such as [U-¹³C₃]propionate (or [U-¹³C₃]lactate), the TCA cycle intermediates become labeled, and subsequently, distinct ¹³C labeling patterns are transferred into glucose molecules by means of the gluconeogenic pathway (only carbons 1,2,3 of glucose were considered here for simplicity). These isotopomers indicate contributions from anaplerotic, cataplerotic and TCA cycle fluxes. Finally, infusion of [3,4-¹³C₂]glucose at a known rate followed by measurement of tracer dilution allows estimation of endogenous glucose rate of appearance (EndoRa) and therefore conversion of relative to absolute fluxes in vivo. This final step is unnecessary for ex vivo and in vitro experiments where total glucose output can be measured without tracers.

Hasenour et al. combined GC-MS analysis of multiple glucose fragment ions with mathematical modeling of the convoluted ²H/¹³C MIDs to estimate liver metabolic fluxes in vivo using microliter quantities of blood (Hasenour et al., 2015). We expand this concept to model the ²H and ¹³C NMR data and GC-MS-based MIDs using a unified metabolic network. First, a least-squares regression of ²H labeling in glucose fragments (Antoniewicz et al., 2011) following ²H₂O administration to rats was recapitulated by direct measurement of positional enrichments using ²H NMR. Second, simultaneous ²H and ¹³C labeling in isolated perfused mouse liver and in vivo rats was detected by ²H and ¹³C NMR and by GC-MS. However, the additional position-specific information provided by NMR supported an expanded metabolic model of liver metabolism that included reactions to more accurately account for ²H enrichment on C1, C3, and C4 carbons of glucose. A unified MFA model demonstrated flux solutions for GC-MS data that were strongly correlated with NMR solutions. Finally, we demonstrate that modeling of GC-MS mass isotopomer data provides flux measurements in primary mouse hepatocytes cultured with ²H and ¹³C tracers, an experimental model that cannot be addressed using less sensitive NMR approaches.

2. MATERIALS AND METHODS

2.1. Animals

Animal protocols were approved by the Institutional Animal Care and Use Committee at the University of Texas Southwestern Medical Center. Male C57BL6/J mice and Sprague Dawley rats were maintained on 12-hr/12-hr dark/light cycle, with unrestricted access to food and water unless otherwise noted. Animals were fed a standard chow (NCD; Teklad Diet 2016, Harlan Laboratories).

2.2. Materials

[U-¹³C₃]Propionate (99%) (CLM-1865-PK), [3,4-¹³C₂]D-glucose (99%) (CLM-6750-PK), and ²H₂O (99.9%) (DLM-4-PK) were purchased from Cambridge Isotope Laboratories (Andover, MA). Other common chemicals were obtained from Sigma (St. Louis, MO) unless otherwise noted.

2.3. Primary hepatocyte isolation

Primary mouse hepatocytes were isolated using the two-step collagenase method (Akie and Cooper, 2015) with some modifications. Briefly, mice were anesthetized with isofluorane and their portal veins were cannulated. Livers were then infused with 50 mL of liver perfusion medium (LPM) at 8 mL/min and then 50 mL of liver digestion medium (LDM) at 5 mL/min followed by careful excision and clearance from gall bladder and other tissues. Hepatic tissue was then scraped into a tissue culture dish containing isolation medium (IM) using forceps and scalpel. The hepatocyte suspension was filtered using a 100 μm cell strainer and centrifuged (4°C, 50 × g, 5 min). Cell pellets were resuspended in 10 mL of Percoll solution (Percoll:10×PBS 9:1 v/v) and centrifuged again (4°C, 350 × g, 5 min) to separate dead cells. Hepatocytes were washed once more with 40 mL of IM and plated on collagen-coated 60 mm dishes (1 million cells per dish). Cell viability was confirmed using trypan blue staining and was above 90%. Cells were allowed to attach and recover after isolation for 4 h, and the medium was then changed to maintenance medium (MM) (Figure S6). Hepatocytes were cultured overnight in 5% CO₂ atmosphere at 37°C. All experiments were performed one day after isolation.

2.4. Liver perfusion

Livers from 12–13 week old male C57BL6/J mice were isolated as previously described (Burgess et al., 2004). Briefly, each mouse was injected with heparin, liver was exposed by laparotomy, and the portal vein was cannulated. Perfusion was initiated simultaneous with hepatic vein dissection. The liver was isolated and perfused at 8 mL/min with a non-recirculating system in a double-jacketed vessel maintained at 37°C for 60 minutes. Perfusate consisted of a well-oxygenated Krebs-Henseleit bicarbonate buffer containing lactate, pyruvate and a mixture of non-esterified fatty acids (NEFA) bound to fatty acid-free BSA. Two compositions of perfusate were utilized in this study containing high substrate (1.5 mM lactate, 0.15 mM pyruvate, 0.25 mM glycerol, 0.8 mM NEFA) and low substrate (0.5 mM lactate, 0.05 mM pyruvate, 0.25 mM glycerol, 0.1 mM NEFA). Both conditions contained 0.1 mM [U-¹³C₃]propionate and 3% v/v ²H₂O as tracers.

2.5. In vivo ²H₂O injections

Rats were either fed ad libitum or fasted for 24 hours. Animals received an intraperitoneal injection of 0.9% NaCl ²H₂O solution (35 μL/g body weight) and after 2 hours, were anesthetized with isoflurane and blood was collected by cardiac puncture into EDTA coated tubes. Blood was centrifuged at 4°C for 10 min at 1100 × g. Plasma was aliquoted and stored at −80°C until analysis.

2.6. Stable isotope tracer in vivo infusions

Rats were surgically implanted with indwelling jugular vein catheters and allowed to recover for 4 days. Body weight was monitored daily and loss never exceeded 10% of weight prior to surgery. Experiments were carried out in either ad libitum fed or 24h fasted rats. Prior to tracer infusion, rats received an intraperitoneal injection of 0.9% NaCl in ²H₂O solution (27 μL/g body weight). Tracers [U-¹³C₃]propionate and [3,4-¹³C₂]glucose were administered as a 10-min prime (88.35 and 3.6 μmol/kg/hr, respectively) followed by an 80-min continuous infusion (17.67 and 0.72 μmol/kg/hr, respectively). At the end of the infusion, rats were anesthetized using isofluorane, blood was collected by cardiac puncture into tubes containing EDTA, plasma was separated by centrifugation (4°C, 1100 × g, 10 min), aliquoted and stored at −80°C until analysis.

2.7. Glucose derivatives preparation for NMR

Plasma glucose was converted to monoacetone glucose (MAG) using a previously described procedure (Burgess et al., 2004; Satapati et al., 2012). First, 2–5 mL of plasma was deproteinized by addition of 70% perchloric acid (ratio 10:1 v/v) and centrifugation (4°C, 21000 × g, 10 min). The supernatant was collected and the extraction was repeated by reconstituting the pellet in a water volume equivalent to the original plasma volume. Extracts were neutralized to pH 7–8 by the addition of KOH and then lyophilized. Next, samples were reconstituted in 3 mL of water and passed through a column containing Dowex (50WX8–200) and Amberlite exchange resin (IRA-67) in 2.5:2 v/v ratio (Dowex on top). Glucose was eluted using 120 mL of deionized water and the eluent was adjusted to pH 7 and freeze-dried. Combined dried glucose was suspended in 3 mL of acetone-containing concentrated H₂SO₄ solution (ratio 1:46 v/v) and stirred for 4 h at room temperature. Following addition of 3 mL of H₂O and adjusting to pH 2 (using Na₂CO₃ solution) the reaction was carried out for an additional 24 h. Finally, the reaction was stopped by adjusting to pH=7.5–8.0 (using 1.5 M Na₂CO₃) and the samples were lyophilized again. The MAG was extracted using boiling ethyl acetate (5×5mL). After being dried down, samples were purified using an SPE column (DSC-18 SPE Tube, Sigma 52603-U) and stored at room temperature until further analysis. MAG samples were reconstituted in 7 μL of H₂O and 193 μL of acetonitrile and transferred into 3 mm NMR tubes.

2.8. Glucose derivatives preparation for GC-MS

For GC-MS analysis, 50–100 μL of plasma was deproteinized using an excess of cold acetone (8:1 v/v), vortexed and centrifuged (4°C, 21000 × g, 5 min). The decanted supernatant was then dried under air. For methyloxime pentapropionate (MOX) derivatives, 50 μL of 2% methoxylamine hydrochloride in pyridine was added, and samples were incubated at 90°C for 60 min. Next, 100 μL of propionic anhydride was added, and samples were incubated at 60°C for 30 min. Samples were then evaporated under air, dissolved in 100 μL of ethyl acetate, centrifuged (4°C, 21000 × g, 10 min) and transferred into GC vials containing a glass insert. Aldonitrile pentapropionate (ALDO) derivatives were prepared similarly, but 2% hydroxylamine was used instead of methoxylamine. Finally, di-O-isopropylidine propionate (DIO) derivatives were prepared by adding 500 μL of fresh 0.38 M H₂SO₄/acetone solution (1:46 v/v), incubating the samples at room temperature for 60 min, followed by addition of 400 μL of 0.44 M Na₂CO₃. Samples were then extracted using 1 mL of saturated NaCl solution and 1 mL of ethyl acetate. The top layer was collected, evaporated under air, re-suspended in propionic anhydride/pyridine solution (2:1 v/v), and incubated at 60°C for 30 min. Samples were evaporated under air, dissolved in 100 μL of ethyl acetate, centrifuged (4°C, 21000 × g, 10 min), and transferred into GC vials containing a glass insert.

2.9. Organic acids derivatives preparation for GC-MS

Primary mouse hepatocytes were washed with ice-cold PBS and scraped from the dish in cold MeOH. The cell suspension was centrifuged and supernatant was stored in −80°C prior to analysis. Organic acids were measured by GC-MS as described previously (Des Rosiers et al., 1994; Fu et al., 2019). Briefly, 300 μL of cell extract was mixed with 10 μL of internal standard mixture, and samples were dried under air flow. Next, 350 μL of 0.8% sulfosalicylic acid and 50 μL of fresh 5 M hydroxylamine-HCl solution were added to each sample, and the solution was neutralized with 80 μL of 2 M KOH to pH 6–7. Samples were sonicated for 15 min and then incubated at 65°C for 60 min. The reaction mixture was acidified to pH 1–2 using 80 μL of 2 M HCl, and ~200 mg NaCl was added. Samples were extracted with ethyl acetate. The dried extract was added to acetonitrile-containing MTBSTFA as a silylation reagent and reacted at 60°C for 60 min.

2.10. NMR spectroscopy

NMR spectra were recorded on a 14.1 T Varian Inova spectrometer (Varian Instruments, Palo Alto, CA) equipped with a 3 mm broadband probe tuned to 92 or 150 MHz for ²H and ¹³C measurements, respectively. Proton decoupled ²H NMR spectra were acquired without lock at 50°C with 1 s acquisition time and 1 s relaxation delay. Manual shimming adjustment was performed on ¹H signal by monitoring response of the line width of selected resonances. Partially relaxed proton decoupled ¹³C spectra were acquired at 25°C using 50° pulse angle, 1.5 s acquisition time, 0.05 s relaxation delay, and a spectral width of 200 ppm. Resonance areas were quantified using ACD/Labs 12.0 software (Advanced Chemistry Development, Toronto, ON, Canada) using line broadening of 0.5 Hz and 0.1 Hz for ²H and ¹³C resonances, respectively.

2.11. GC-MS

Analysis was performed using an Agilent 7890-A GC-MS system equipped with an HP-5ms column (30m×0.25mm I.D., 0.25μm film thickness; Agilent J&W) combined with an Agilent 5975-C mass spectrometer (70eV, electron ionization source). For all samples, a 1 μL injection volume was used and split mode was adjusted for optimal signal-to-noise ratio. For analysis of DIO and ALDO derivatives, the following temperature gradient was used: 80°C for 1 min, ramped at 20°C/min to 280°C, held for 4 min and ramped at 40°C/min to 325°C. For MOX derivatives, the program remained the same with exception of the ramp to 280°C, which was set at 10°C/min. After a 5 min solvent delay, MS data collection was initiated. Scan range was set to 144–150 m/z for MOX derivatives, 170–380 m/z for ALDO derivatives and 300–320 m/z for DIO derivatives. Each sample was injected three times. For analysis of organic acid enrichment, the following temperature gradient was used: 150°C for 3 min, ramped at 5°C/min to 205°C, next ramped at 50°C/min to 250°C, held for 1 min, next ramped at 25°C/min to 275°C and held for 3 min. Scan range was set to 261.1–264.1 m/z for lactate, 274.1–277.1 m/z for pyruvate, 289.1–293.1 m/z for succinate, 287.2–291.2 m/z for fumarate, 419.2–423.2 m/z for malate, 432.2–436.2 for OAA, 446.2–451.2 for AKG and 459.2–465.2 for citrate. Measurement uncertainty was estimated by root-mean-square error calculated for unlabeled glucose samples and theoretical MID values obtained from known abundances of naturally occurring isotopes.

2.12. Flux calculations using NMR isotopomer analytical equations

The relative flux contributions of glycogenolysis and gluconeogenesis to endogenous glucose production (EGP) and TCA cycle related fluxes can be assessed by the ²H and ¹³C isotopomer abundances of glucose, as proposed by Landau and others (Jin et al., 2004; Landau, 1999; Landau et al., 1993):

Glycogenolysis (hexose units):

$$V_{\mathit{\text{Glycogen}}}=V_{\mathit{\text{EGP}}}*\frac{(H2-H5)}{H2}$$

Glycerol contribution to gluconeogenesis (hexose units):

$$V_{\mathit{\text{Glycerol}}}=V_{\mathit{\text{EGP}}}*\frac{(H5-H6S)}{H2}$$

Phosphoenolpyruvate (PEP) contribution to gluconeogenesis (hexose units):

$$V_{\mathit{\text{PEP}}}=V_{\mathit{\text{EGP}}}*\frac{H6S}{H2}$$

where variables H2, H5 and H6S refer to signal areas of the ²H NMR spectrum of MAG. Cataplerosis = flux through Phosphoenolpyruvate carboxykinase (PEPCK) (triose units):

$$V_{\mathit{\text{PEPCK}}}=2*V_{\mathit{\text{PEP}}}*\frac{(D12-D23)}{(Q2-D23)}$$

TCA cycle turnover = flux through citrate synthase (CS):

$$V_{\mathit{\text{CS}}}=2*V_{\mathit{\text{PEP}}}*\frac{D23}{(Q2-D23)}$$

Label recycling = combined flux through pyruvate kinase, malic enzyme and the Cori cycle (triose units):

$$V_{\mathit{\text{PK}}+\mathit{\text{ME}}}=2*V_{\mathit{\text{PEP}}}*\frac{(D12-Q2)}{(Q2-D23)}$$

where variables D12, D23 and Q2 refer to ¹³C-¹³C spin-coupled multiplets of C2 of MAG. In vivo [3,4-¹³C₂]glucose fractional enrichment in blood plasma (e_plasma):

$$e_{\mathit{\text{plasma}}}=m*\frac{(C3D34+C4D34)}{(M1+M2)}+b$$

where m is a slope and b is an intercept of the calibration curve, C3D34 and C4D34 are doublet areas at C3 and C4 of MAG, while M1 and M2 are singlet areas of unlabeled methyl groups of MAG. In vivo endogenous glucose production (EGP):

$$V_{\mathit{\text{EGP}}}=V_{\mathit{\text{inf}}}*\frac{\left(e_{\mathit{\text{inf}}}-e_{\mathit{\text{plasma}}}\right)}{e_{\mathit{\text{plasma}}}}$$

where V_inf is tracer infusion rate and e_inf is fractional enrichment of [3,4-¹³C₂]glucose in the infusate.

2.13. Metabolic network and flux modeling

Metabolic flux analysis was performed using a modified version of the INCA software, which is based on the elementary metabolite unit (EMU) method. INCA was previously developed for analysis of MS datasets, but the software was adapted to simulate ¹³C NMR multiplet ratios and ²H NMR spectra using linear transformations of EMU mass isotopomer abundances, as first described by Antoniewicz et al. (2007). For example, the C2 multiplet areas of MAG were calculated from the transformation,

$$\left[\begin{array}{c}S\\ D12\\ D23\\ Q\end{array}\right]={\left[\begin{array}{cccc}1& 1& 1& 1\\ 0& 0& 1& 1\\ 0& 1& 0& 1\\ 0& 0& 0& 1\end{array}\right]}^{-1}\left[\begin{array}{c}{A}_2^{M+1}\\ A_{23}^{M+2}\\ A_{12}^{M+2}\\ A_{123}^{M+3}\end{array}\right]$$

where $A_2^{M+1}$ is the M+1 abundance of the EMU comprising C2 of glucose, $A_{23}^{M+2}$ is the M+2 abundance of the EMU comprising C2 and C3, $A_{12}^{M+2}$ is the M+2 abundance of the EMU comprising C1 and C2, and $A_{123}^{M+3}$ is the M+3 abundance of the EMU comprising C1−C3. The ²H NMR signals of MAG were calculated from the transformation,

$$\left[\begin{array}{c}H1\\ H2\\ H3\\ H4\\ H5\\ H6R\\ H6S\end{array}\right]=\left[\begin{array}{c}{A}_{H1}^{M+1}\\ A_{H2}^{M+1}\\ A_{H3}^{M+1}\\ A_{H4}^{M+1}\\ A_{H5}^{M+1}\\ A_{H6R}^{M+1}\\ A_{H6S}^{M+1}\end{array}\right]$$

where $A_{Hj}^{M+1}$ represents the M+1 abundance of the EMU comprising the j^th hydrogen atom of glucose.

A base metabolic network model representing liver metabolism was developed in INCA based on previously published models (Hasenour et al., 2015; Jones et al., 2001b; Landau et al., 1993). The model consisted of 19 reactions and 18 metabolites. Four additional reactions were tested at the validation stage (Table S1). Fluxes were estimated by minimizing the sum of squared residuals (SSRs) between simulated and experimentally derived MIDs (from MS datasets) or positional isotopomer ratios (from NMR datasets). All GC-MS data were weighted by the standard errors of measurements while all NMR fractional abundance measurements were weighted by the default error of 0.01. Best-fit flux estimates were obtained from least-squares regression starting from at least 50 random initial values. Error-weighted residuals were checked for normality, and goodness-of-fit was assessed by a chi-square test (Antoniewicz et al., 2006). The SSRs of all best-fit solutions fell within the expected range, unless otherwise noted.

2.14. Accuracy score

We applied a novel scoring metric, modified from similar approach (Crown et al., 2016), to assess the accuracy of fluxes estimated using different tracers or modeling methods:

$$A=\frac{1}{n}\sum _{i=1}^n{a}_i$$

with

$$a_i=\frac{\sqrt{{\left(J_{i,\mathit{\text{exp}}}-J_{i,\mathit{\text{ref}}}\right)}^2}}{J_{i,\mathit{\text{ref}}}}$$

The accuracy score (A) for a given tracer method is calculated as the average of individual flux accuracy scores (a_i) for n fluxes of interest. An individual flux accuracy score is calculated as the absolute difference between a flux value obtained in an experiment (J_i,exp) and a reference experiment (J_i,ref), divided by the reference flux value. This is an extension of the standard formula for calculating accuracy. An individual flux accuracy score of 0 indicates that the flux value for a particular experiment is identical with the flux value from the reference experiment. The lower the value of accuracy score, the closer the values of J_i,exp are to the reference flux values on average.

3. RESULTS

3.1. In vivo glucose labeling from ²H₂O can be partially reconstructed using GC-MS

GC-MS measurement of six distinct fragment ions of glucose was previously shown to be sufficient for computational reconstruction of ²H labeling in all 6 positions of deuterated glucose standards (Antoniewicz et al., 2011). Therefore, we tested whether the same computational approach could be applied to complex mixtures of labeled glucose generated in vivo following exposure to ²H₂O. Ad libitum fed and 24-h fasted rats were injected with ²H₂O and blood was collected after 2 hours (Figure S1A). Plasma glucose samples were converted into three derivatives (MOX, DIO, ALDO, see Materials and Methods) that yield six distinct fragment ions (m/z = 145, m/z = 173, m/z = 259, m/z = 284, m/z = 301, m/z = 370) when analyzed by GC-MS (Figure 3A). The accuracy and precision of the GC-MS MIDs obtained from unlabeled blood glucose samples were in excellent agreement with theoretical values calculated from the natural abundance of stable isotopes (Table S2), similar to previous reports (Antoniewicz et al., 2011). Following ²H₂O administration, samples from the fasted group exhibited a MID shift toward higher mass isotopomers compared to the fed group (Figure 3B). Likewise, when these MIDs were used to mathematically reconstruct the positional labeling of glucose using the least-squares regression method of Antoniewicz et al. (Antoniewicz et al., 2011) and MATLAB’s quadratic programming solver (quadprog, with active set algorithm), ²H enrichment was increased in all hydrogen positions (relative to H2 enrichment) by fasting (Figure S1B).

Figure 3. Glucose labeling from ²H₂O – single tracer experiment.

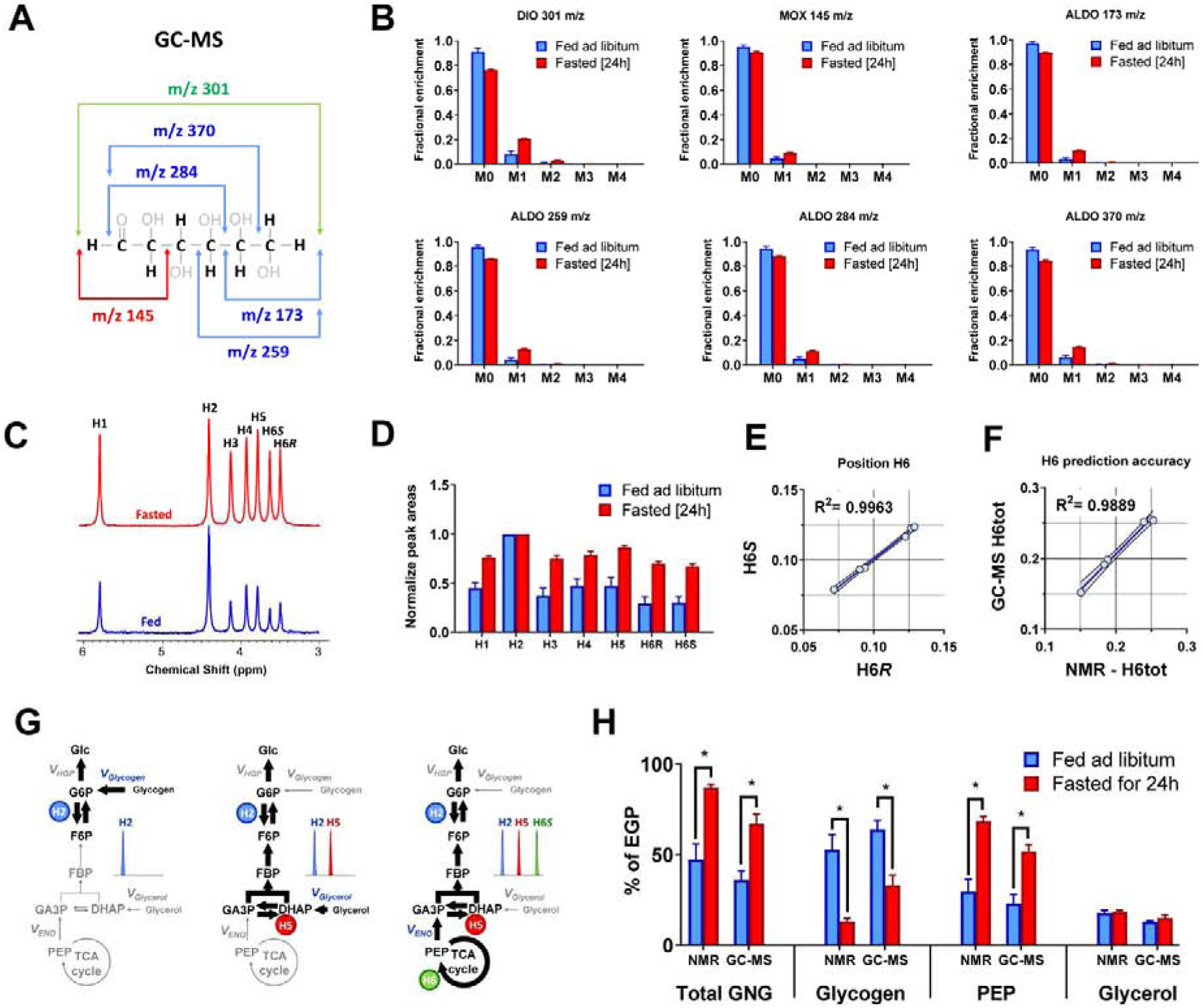
(A) In order to partially decipher positional labeling of glucose, different m/z fragment ions can be monitored by GC-MS, each of which contains a different set of atoms from the parent molecule. (B) Natural abundance corrected MIDs of different glucose fragments analyzed using GC-MS, (C) ²H NMR spectrum of MAG signals normalized to resonance at position H2, (D) integrals of ²H NMR resonances normalized to signal at position H2, (E) Correlation between H6R and H6S position in ²H NMR spectra of rats injected with ²H₂O, (F) Correlation between total H6 signal (H6tot) measured using NMR and estimated using least-squares regression from GC-MS data are shown. (G) Schematic representation of ²H labeling of glucose in positions H2, H5 and H6. All newly synthesized glucose molecules become labeled at position H2. Glucose derived from all sources of gluconeogenesis (glycerol or PEP) will be additionally labeled at position H5. Finally, if PEP (but not glycerol) was a precursor for gluconeogenesis, glucose molecules will be simultaneously labeled at positions H2, H5 and H6 (for simplicity other positions are not discussed here, as they are not used for flux calculations using the analytical equations). (H) Comparison of flux contributions to gluconeogenesis obtained using ²H NMR and GC-MS based prediction of glucose positional enrichment.

To test the accuracy of the predicted positional enrichments we directly measured the relative ²H enrichment of each position using ²H NMR (Figure 3C). As expected, there was an overall increase in deuteron incorporation at all glucose positions in fasted animals compared to the fed animals (Figure 3D). The two chiral hydrogens (H6S and H6R) on carbon 6 (C6) of glucose can be differentiated by NMR but not GC-MS. NMR data demonstrated that H6S and H6R exhibited near perfect correlation with each other (Figure 3E). Hence, the total enrichment at position H6 (H6_tot) was used for comparisons between GC-MS and NMR measurements of ²H incorporation, and the values were found to strongly correlate with each other (Figure 3F). Positions H4, H5 and H6_tot of glucose were predicted with a high level of accuracy from GC-MS data, but positions H1 and H3 were underestimated, and position H2 was overestimated relative to NMR (Figure S1C–F and Table S3). We tested the quality of positional ²H predictions by implementing four different MATLAB optimizing algorithms for the same GC-MS dataset. Surprisingly, the optimal solution and best-fit SSR values varied significantly depending on which optimizer was used (Figure S2A–C). Furthermore, the predicted enrichments at H2 were strongly anti-correlated with enrichments at H1 and H3, while predicted enrichments at H5 and H6 were also strongly anti-correlated with each other (Figure S2D). These observations indicate that the regression of positional ²H enrichments of glucose from these six fragment MIDs is difficult for complex labeling patterns generated by liver metabolism, and the best-fit solutions can vary depending on the optimization algorithm chosen.

Nonetheless, since only glucose H2, H5 and H6 are used to estimate sources of glucose production (Landau et al., 1996) (Figure 3G), we examined whether these ratios recapitulated the known effects of fasting on fractional rates of gluconeogenesis and glycogenolysis. As expected, glycogenolysis (V_Glycogen) was high in fed animals but low in fasted animals, while the opposite was observed for gluconeogenesis from precursors passing through the TCA cycle (V_PEP), regardless of whether ²H enrichment was calculated from GC-MS MIDs or measured by ²H NMR (Figure 3H). Although the techniques reported modestly different values by direct comparison (Figure S1G), their V_Glycogen and V_PEP estimates were strongly correlated (Figure S1H). Measurements of gluconeogenesis from glycerol (V_Glycerol) by the two techniques were not correlated, though their average values were similar and the range of this flux was quite narrow compared to the other pathways (Figure S1H). Thus, reconstruction of positional glucose labeling from GC-MS fragment ions provides flux estimates in reasonable agreement with direct deuterium measurements by ²H NMR and detects the known effects of fasting on liver glucose metabolism.

3.2. MFA of simultaneous ²H and ¹³C NMR isotopomers

Carbon-13 tracers, such as [U-¹³C₃]propionate or [U-¹³C₃]lactate which traverse the hepatic TCA cycle and incorporate into glucose, provide information that complements ²H incorporation through redundant measures of V_PEP flux (Figure 2). Many ¹³C positional isotopomers of glucose are formed by this process, and can be directly detected by ¹³C NMR via chemical shift and spin-spin coupling, but only a few ([1,2-¹³C]glucose, [2,3-¹³C]glucose and [1,2,3-¹³C]glucose) are required to exactly solve steady-state nonlinear equations that describe ¹³C isotopomer formation by TCA cycle metabolism (Jones et al., 1997; Sherry et al., 2004). These solutions have been integrated into analytical equations that describe glucose production and TCA cycle metabolism as a function of ²H and ¹³C glucose isotopomers (Jin et al., 2004). In contrast, the MFA model of Hasenour et al. (Hasenour et al., 2015) must regress these solutions from mass isotopomers of glucose comprised of labeling at all possible positions. To provide a unified platform to compare NMR and MS-based approaches for flux quantification, we developed a MFA model that simultaneously regresses all ²H and ¹³C NMR data from glucose to determine fluxes of glucose production and TCA cycle metabolism. The key advantages of this approach are that it provides estimates of goodness-of-fit, confidence intervals, the ability to test a variety of modeling assumptions, and most importantly, allows NMR and MS data to be directly compared or combined in a unified model.

First, we modified the INCA modeling platform (Young, 2014) to accept ²H and ¹³C NMR data as inputs for an MFA model based on previous descriptions of hepatic metabolism (Hasenour et al., 2015; Jones et al., 2001b; Landau et al., 1993) (Table S1). We examined a broad range of metabolic fluxes, using tracer doses of [U-¹³C₃]propionate, ²H₂O and [3,4-¹³C₂]glucose (the latter only for in vivo experiments) by using the following experimental conditions: 1) fasted mouse livers perfused with high substrate concentrations; 2) fed mouse livers perfused with low substrate concentrations; 3) in vivo tracer infusion in ad libitum fed rats and; 4) in vivo tracer infusion in 24-hour fasted rats (Figure S3A, B). Regressing the data to the base metabolic model (Hasenour et al., 2015) (Table S1) resulted in good agreement to the directly measured ¹³C labeling data (carbons C1, C2, C5, C6) but not ²H data (examples of fitting results for ¹³C and ²H are presented in Figure 4A and 4B, respectively). More importantly, the poorly fit data resulted in flux estimates that were not in agreement with flux estimates obtained from previously reported analytical equations (Jin et al., 2004) that use specific glucose ²H and ¹³C NMR signals as variables (Figure 4C).

Figure 4. NMR based metabolic flux analysis - model development and validation.

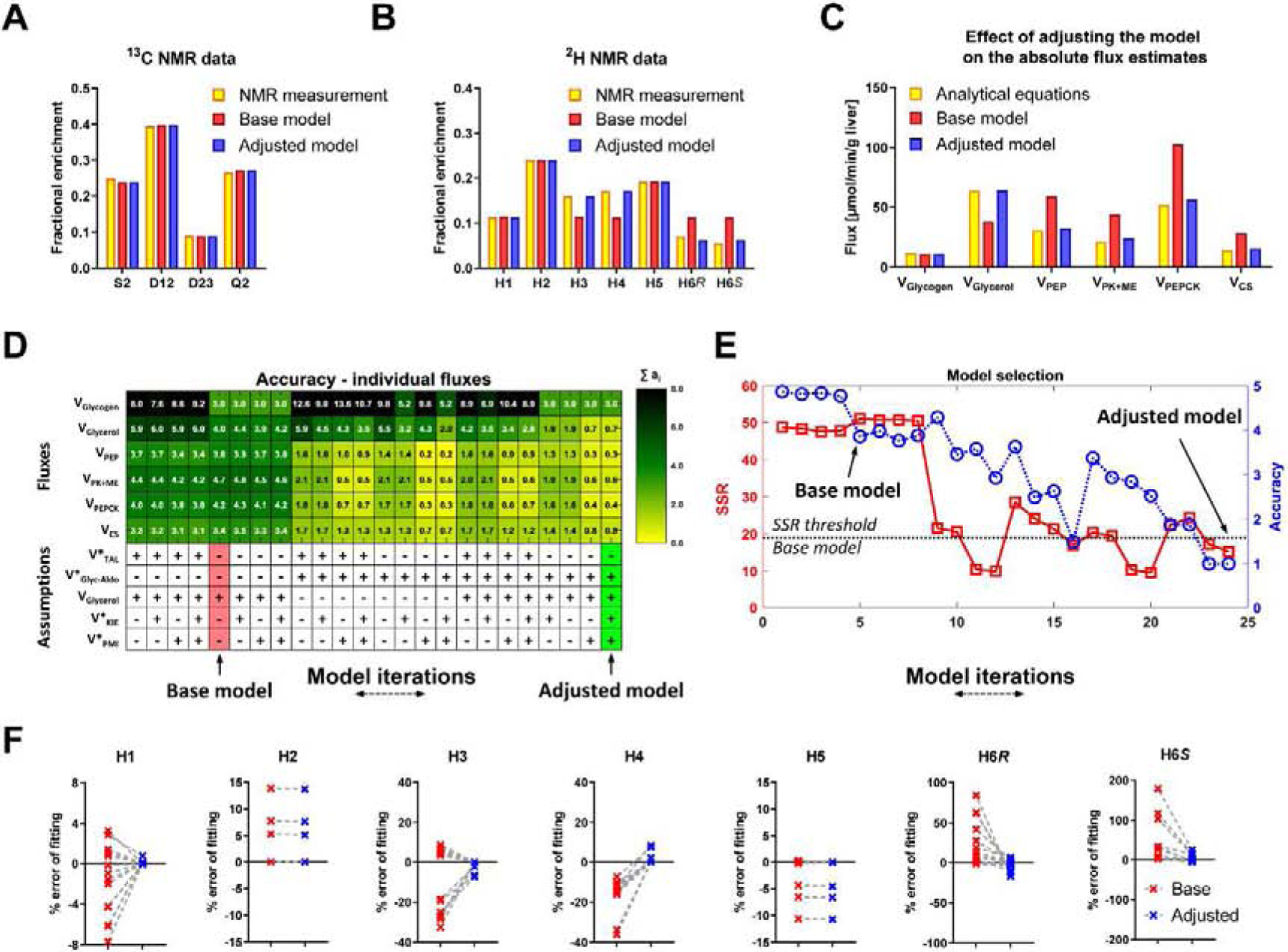
(A,B) An example of NMR measurements and their fits to the base and adjusted model (A) ¹³C NMR carbon-2 isotopomers of MAG, (B) ²H NMR isotopomers of MAG. (C) An example of changes in absolute fluxes between analytical equations before and after adjusting the MFA model. (D) Heatmap showing contributions of individual flux accuracy scores (a_i). Additional reactions (see Table S1) were used in different combinations to create 25 model iterations. Base model (red), Adjusted model (green). V_Glycerol is included in the base model but, since V_Glyc-Aldo affect the same flux, different combinations of these two reactions were investigated. (E) Accuracy score (A) (blue) and SSR (red). Subsequent model iterations organized in the same order as in panel D, (F) Percent errors of fitting ²H NMR data to base and adjusted model, calculated as follows: (predicted enrichment − measured enrichment)/measured enrichment × 100%.

The poor agreement between flux estimates likely arose because the analytical equations require only ²H enrichment in positions H2, H5 and H6 (Jin et al., 2004), but the MFA model attempts to fit ²H NMR data at all positions of glucose (including H1, H3, H4 and various ¹³C multiplets of glucose that are not utilized by the analytical model) without the mechanisms necessary to accurately describe those data. Inasmuch as the assumptions of the analytical model have been validated, and can be exactly solved by the measurement of a small subset of positional isotopomers (Jin et al., 2004), we presumed that an MFA model that regresses the full NMR data set should approximate the flux solutions of the analytical model (i.e., not perturb ²H2:²H5:²H6 or ¹³C multiplet ratios fundamental to the analytical solutions). Hence, additional metabolic mechanisms that affect ancillary positions were included in modified MFA models to test for flux estimates that approximated the analytical model (Table S1). These models included: 1) the presence of a ²H kinetic isotope effect at triose-phosphate isomerase (TPI) that results in lower than expected deuterium labeling of glucose at position H3 (Browning and Burgess, 2012; Leadlay et al., 1976); 2) equilibrium exchange at aldolase that introduces ²H labeling of trioses and eventual enrichment at position H4 of glucose (Rognstad et al., 1974); 3) additional H1 labeling by phosphomannose isomerase (PMI) (Chandramouli et al., 1999) and; 4) exchange of ²H labeling in the front (C1–C3) and back (C4–C5) halves of glucose due to transaldolase activity (Browning and Burgess, 2012).

We tested these modifications in multiple combinations using an accuracy scoring metric (A) for six fluxes in pathways of hepatic glucose and TCA cycle metabolism: V_Glycogen, V_Glycerol, V_PEP, V_PK+ME, V_PEPCK and V_CS (Figure 4D). Smaller A values indicate better agreement between the modified regression model and the analytical solutions. In general, the sum of squared residuals (SSR) improved as the MFA model converged to solutions that better matched the analytical equations (Figure 4E) (base model DOF = 9, expected SSR range [2.7 – 19.0], adjusted model DOF = 6, expected SSR range [1.2–14.4]). The MFA model that was closest (based on A score) to the overall flux estimates obtained using the analytical equations consisted of all the reactions present in the base model and the added assumptions of 1) a kinetic isotope effect at TPI; 2) equilibrium exchange at aldolase; and 3) additional labeling by PMI (Figure 4D,E). This adjusted model demonstrated significant improvements in the model fit for glucose ²H enrichment (Figure 4F) and provided flux estimates that were in agreement with those directly calculated from analytical equations and NMR data (Figure 4C). Interestingly, the model adjustments were ²H specific and did not affect the ¹³C fits (Figure S3C). In summary, the adjusted MFA model delivers the same information as the isotopomer ratios used in the analytical flux equations, but accounts for ²H and ¹³C labeling of all atom positions in glucose.

3.3. Positional isotopomer information detected by NMR is conserved in six glucose fragments detected by GC-MS

Since NMR analysis provides highly specific ²H and ¹³C positional isotopomer information that can be used to solve analytical equations or regressed to a more sophisticated MFA model with similar results (see above), we used this data to test the accuracy of MFA based on glucose fragment MIDs obtained from GC-MS. To control for factors unrelated to isotopomer enrichments, we used matched samples for NMR and GC-MS analysis, identical MFA models and ²H body water enrichments determined from GC-MS data to constrain the NMR data regression (Figure S4) (for details see supplementary data).

To control for substrate concentration, inter-organ tracer recycling, hormone action and to enable direct measurement of glucose production, we first examined a simple system consisting of isolated mouse liver perfused with tracers (²H₂O and [U-¹³C₃]propionate) and variable substrate concentrations (low and high) to manipulate flux. Fasted livers perfused with high concentrations of substrates produced glucose that was significantly more labeled with ²H in all positions compared to fed livers perfused with low concentrations of substrates (data not shown), similar to the effect of fasting in rats in vivo (Figure 3C). [U-¹³C₃]propionate was incorporated into TCA cycle intermediates and formed isotopomers detected as ¹³C NMR multiplets in glucose resonances (Figure 5A). When the C2 multiplet was normalized to the singlet, there was a substantial increase in labeling of all isotopomer populations: D12, D23 and Q2 were elevated by high substrate conditions (Figure 5B), indicating changes in rates of TCA cycle turnover and cataplerotic/anaplerotic flow of carbon (Figure 5C). The same was true for the glucose C5 multiplets (data not shown), which is the triose equivalent of C2. An overall increase in isotope enrichment from livers perfused with high substrates was also evident by GC-MS analysis (Figure 5D), though distinctions between ²H and ¹³C enrichment could not be inferred by direct inspection of the six glucose fragment MIDs. However, when the absolute glucose output measurements and MS datasets were regressed (Figure 5E) to the same metabolic network model that had been previously adjusted to describe NMR data (Table S1), both MS- and NMR-based regressions provided similar results. Fasted livers perfused with high substrate concentrations exhibited a complete loss of glycogenolysis and an increase in gluconeogenesis (Figure 5F). Anaplerosis and TCA cycle flux were also increased by perfusion with higher levels of free fatty acids and gluconeogenic substrates (Figure 5G). The only quantitative disagreement occurred when estimating the balance between glycerol and glycogen contributions to total glucose production under low-substrate conditions (Figure 5F).

Figure 5. Glucose labeling using a double tracer method - mouse liver perfusions.

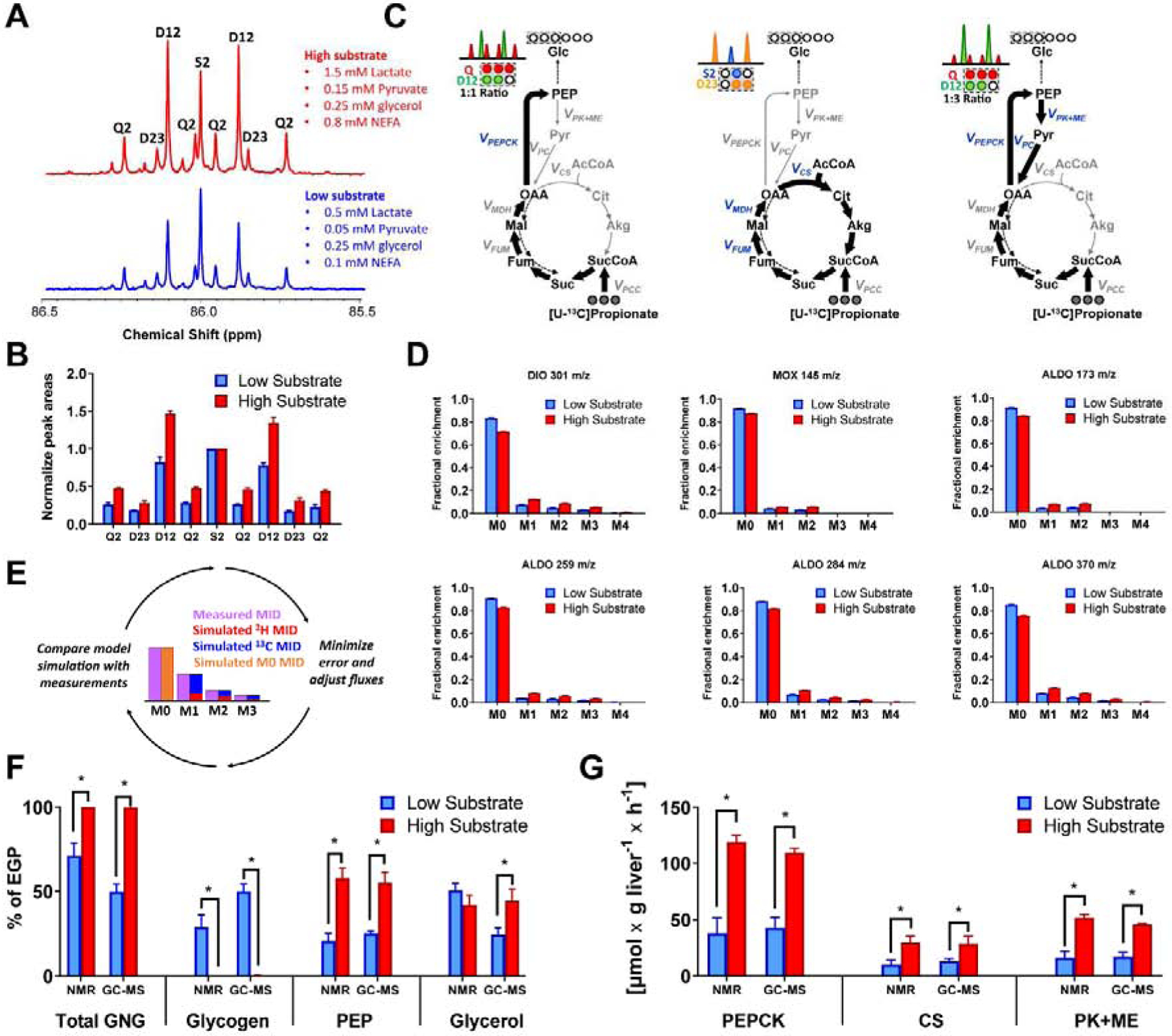
(A) ¹³C NMR spectrum of carbon 2 resonance (C2) of MAG - signals normalized to the C2 singlet, (B) ¹³C NMR integrals of C2 MAG - signals normalized to C2 singlet, (C) Schematic representation of ¹³C labeling of glucose from [U-¹³C₃]propionate by rapidly labeling TCA cycle intermediates. Labeling of the front half of glucose will give a 50% Q2 signal (C1–C3 carbons labeled) and a 50% D12 (only C1–C2 carbons labeled). The latter arises because half of TCA cycle intermediates lose the carbon destined for C3 following symmetrization at fumarate and succinate, and subsequent decarboxylation of OAA to yield PEP. A D12 to Q ratio above 0.5 reflects label recycling, as 50% of every C1–C3 labeled pyruvate that reenters the TCA cycle is further converted to C1–C2 glucose. In addition, oxidative turns of the TCA cycle will generate a D23 signal because the carbon destined for C1 is lost during condensation of OAA with unlabeled acetyl-CoA and subsequent oxidative decarboxylation steps. (D) Natural abundance corrected (for unlabeled atoms) MIDs of different glucose fragments analyzed using GC-MS. Note that contributions of ²H and ¹³C are impossible to resolve by direct inspection of the MIDs. (E) Diagram illustrating individual contributions of ²H and ¹³C estimated by model-based regression of MIDs. (F) Comparison of flux contributions to gluconeogenesis (GNG) (G) Comparison of TCA cycle related fluxes. Fluxes obtained by modeling either ²H/¹³C NMR or GC-MS data using the same metabolic network.

Since in vivo experiments require infusion of a glucose tracer and detection of an additional glucose isotopomer to measure hepatic glucose production, we tested NMR and GC-MS datasets obtained from ad libitum fed and 24-h fasted rats (Figure S3B). In this triple-tracer experiment, the MFA model must not only fit MIDs of glucose fragments to ²H enrichment and ¹³C isotopomers originating from the TCA cycle and glucose synthesis, it must also specifically distinguish the contribution of M+2 glucose originating from infused [3,4-¹³C₂]glucose. In contrast, ¹³C NMR selectively detects the distinct positional isotopomers of [3,4-¹³C₂]glucose as spin-spin coupling between C3 and C4 (C3D34 and C4D34) at enrichments as low as 0.1% (Figure 6A,B). There was excellent agreement between [3,4-¹³C₂]glucose enrichment directly measured by ¹³C NMR and enrichment predicted from MFA modeling of GC-MS data (Figure 6C), which translated to similar absolute estimations of EGP values (Figure 6D). When glucose fragment MIDs from GC-MS analysis or NMR isotopomers were regressed using the same MFA model, both data sets produced similar flux estimates in pathways of hepatic glucose production and TCA cycle metabolism (Figure 6E–G). Despite modest differences in the absolute values of some fluxes, there was an excellent correlation between most NMR and GC-MS estimations Figure 7. Only V_Glycerol (gluconeogenesis from glycerol) did not correlate across all conditions, but even this flux retained correlation under fasted conditions (Figure 7C). Examination of these relationships by Passing-Bablok regression (Passing and Bablok, 1983) and Bland-Altman analysis (Bland and Altman, 1986; Giavarina, 2015) suggested slight positive mean bias of NMR relative to MS for V_PEP (+9.4%), V_PEPCK (+16.7%) and V_PK+ME (+24.1%), but a negative bias for V_Glycogen (−45.8%) (Figure S5, Table S4). V_CS showed no statistical bias while V_Glycerol could not be analyzed since it did not meet the requirement of linearity (for more details see supplementary data). Thus, mass isotopomers of glucose fragments determined by GC-MS can be modeled using MFA to provide metabolic fluxes that are largely consistent with positional isotopomers detected by NMR, with most differences being related to the contribution of glycogen to EGP.

Figure 6. Glucose labeling from 3 simultaneous tracers – in vivo tracer infusions in rats.

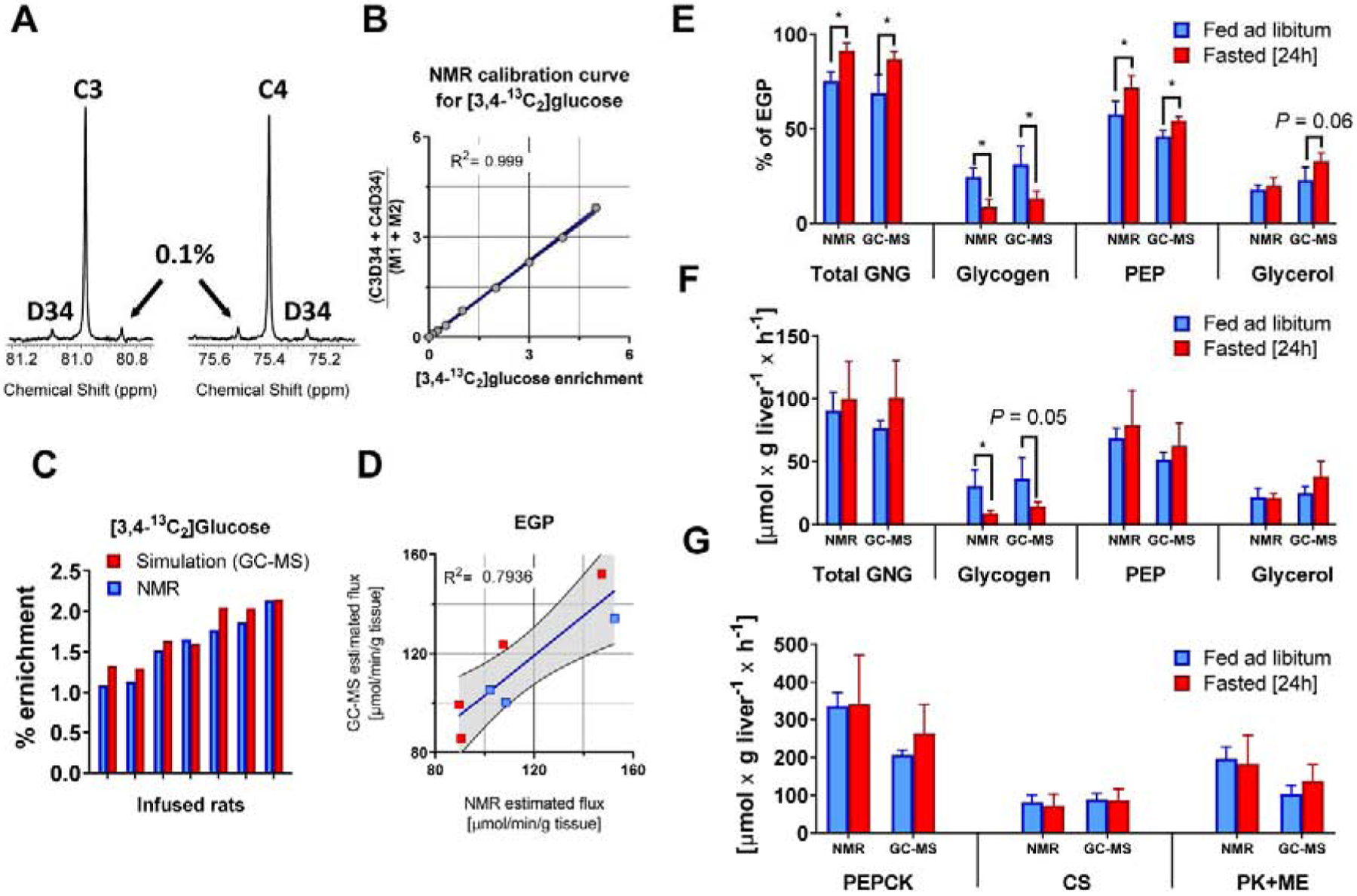
(A) ¹³C NMR spectrum of carbons 3 and 4 of MAG from 0.1% [3,4-¹³C₂]glucose standard (B) calibration curve for relationship between [3,4-¹³C₂]glucose enrichment and the ratio of NMR signals (C3D34 + C4D34)/(M1+M2), (C) comparison of [3,4-¹³C₂]glucose enrichment measured using ¹³C NMR and simulated using best-fit solution obtained from model regression of GC-MS data, (D) correlation between EGP values obtained using NMR and GC-MS methods, (E) Comparison of flux contribution to gluconeogenesis (GNG) and (F) absolute flux values of gluconeogenic and (G) TCA cycle related pathways. Fluxes obtained by modeling either ²H/¹³C NMR or GC-MS data using same metabolic network.

Figure 7. Correlation between NMR and GC-MS based flux estimates.

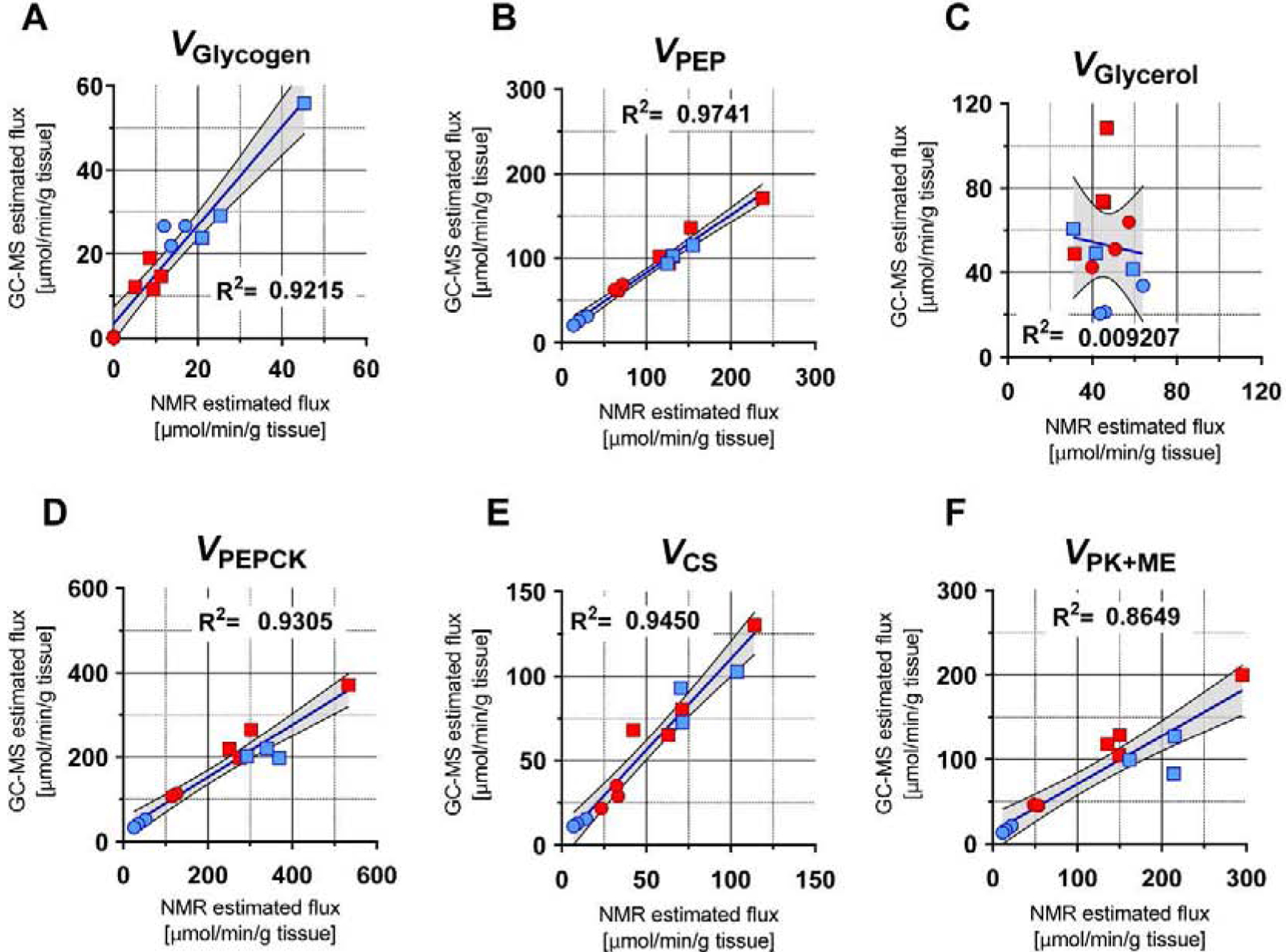
Squares - tracer infusions in rats, circles – perfused mouse livers, blue – fed condition, red – fasted condition. All fluxes are reported in μmol/g liver/hr. (A) V_Glycogen, (B) V_PEP, (C) V_Glycerol, (D) V_PEPCK, (E) V_CS, (F) V_PK+ME.

3.4. In vitro applications of MFA in primary mouse hepatocytes

The validated MFA approach was tested on primary mouse hepatocytes, a common model system used to examine molecular physiology, cell signaling and pharmacological mechanisms, which provides a mass of sample too small to be interrogated by ²H and ¹³C NMR. Hepatocytes were cultured in 60 mm dishes in DMEM supplemented with 0.1 mM [U-¹³C₃]propionate, and cells were sampled over 4 h to test TCA cycle intermediates for ¹³C enrichment. Cells reached isotopic steady state within 60 minutes (Figure 8A). Thus, double tracer hepatocyte experiments (²H₂O and [U-¹³C₃]propionate) were carried out on glucose accumulating in fresh media following a 60 minute steady state phase (Figure S6). To test whether the GC-MS method could detect metabolic changes in vitro, we cultured hepatocytes under two extreme nutritional conditions. Control hepatocytes were precultured with 25 mM glucose and 10 nM insulin to induce glycogen storage, while starved hepatocytes were precultured without addition of glucose and insulin to deplete glycogen (Figure S6). Following the steady state phase, media samples were collected after 9 h of incubation with tracer media, and glucose labeling was analyzed by GC-MS. Glucose produced by starved hepatocytes produced higher levels of enrichment compared to control hepatocytes (data not shown). MFA demonstrated that starved hepatocytes had metabolic characteristics that were similar to perfused livers from fasted mice or in vivo tracer infusions in fasted rats. Hence, the contribution of glycogen to EGP was almost negligible, while gluconeogenesis was significantly higher in starved hepatocytes (Figure 8B). Similar trends were observed for pathways related to the TCA cycle, such as V_PEPCK, V_PK+ME, and V_CS (Figure 8C). Thus, GC-MS measurement of glucose MIDs combined with simultaneous ²H and ¹³C MFA detected physiological changes in response to fasting, under conditions that could not be examined using standard NMR techniques due to the small sample volumes inherent in cell culture experiments.

Figure 8. GC-MS analysis of in vitro glucose labeling - primary mouse hepatocytes.

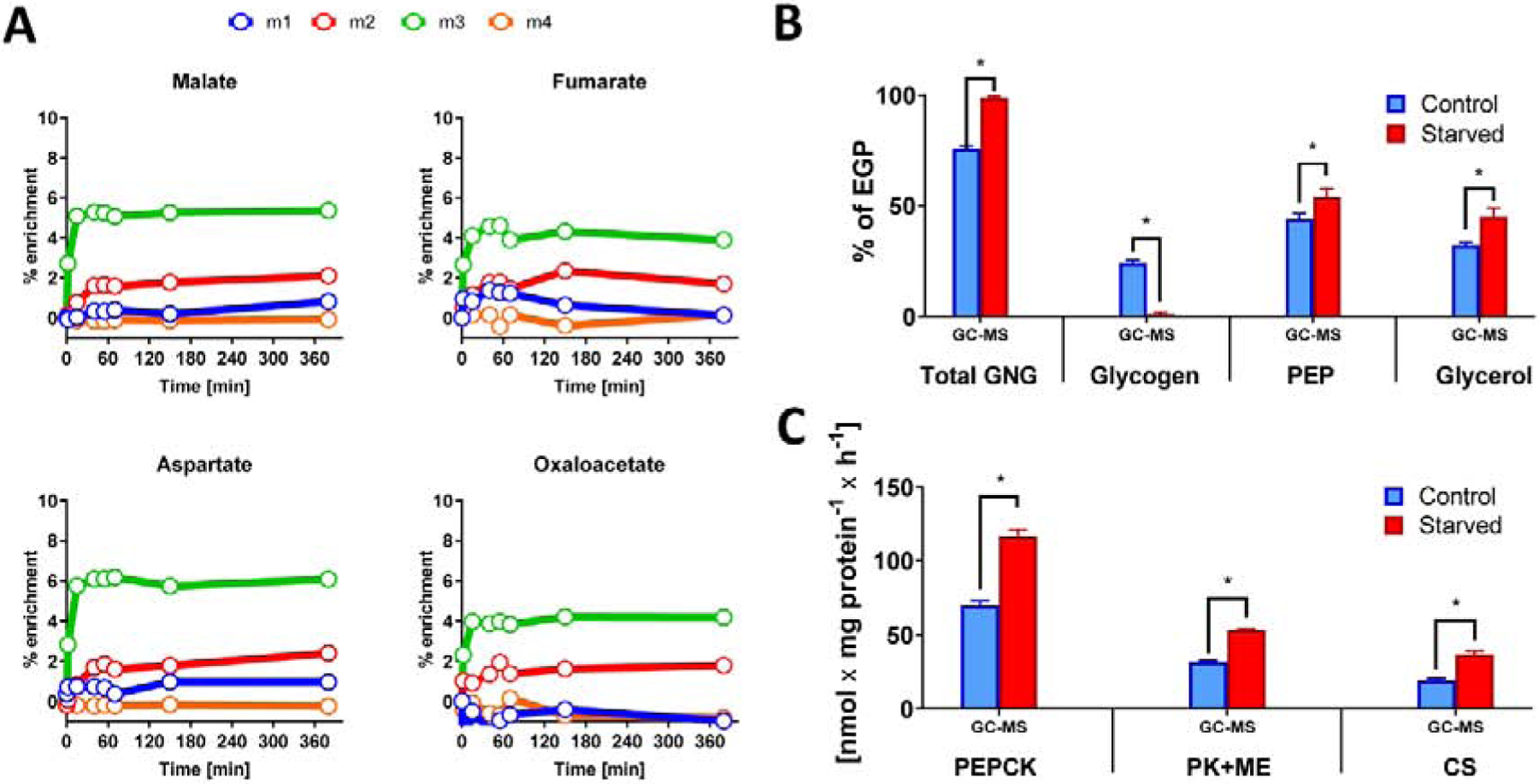
(A) Labeling of TCA cycle intermediates from [U-¹³C₃]propionate over time. Primary hepatocytes reach isotopic steady state within the first 60 minutes of labeling. (B) Comparison of sources of glucose production and (C) TCA cycle related fluxes between fasted and fed primary mouse hepatocytes.

4. DISCUSSION

The use of multiple stable isotope tracers greatly improves the precision and accuracy of flux calculations in large metabolic networks (Leighty and Antoniewicz, 2013), but presents a challenge for detecting and modeling the resulting enrichment data. NMR analysis of tracee metabolites provides highly specific information about which isotope (e.g. ²H, ¹³C or ¹⁵N) and where in the metabolite the isotope was incorporated. Therefore, it is relatively straightforward to determine multiple fluxes in a single experiment, sometimes by direct inspection of the NMR spectra (Burgess et al., 2003; Jones et al., 1997). However, NMR does not directly provide the absolute enrichment of ²H and ¹³C positional isotopomers because ¹H and ²H are not visible in the same spectra, and ¹²C is not NMR visible at all. Therefore, internal standards and/or calibration curves are frequently implemented with use of ²H and ¹³C NMR (e.g. Figure 6B). In contrast, the ability of MS to detect unlabeled molecules (M0) relative to other mass enrichments provides a modeling advantage, particularly when the absolute enrichment of a specific isotopomer directly relates to an absolute flux, such as is the case with plasma glucose enrichment and glucose turnover. But the strongest advantage of MS is that the analysis can be performed on much smaller sample sizes than NMR, and is hence amenable to cell culture, tissue biopsies and microliter blood collection. The principle limitation of MS, the lack of positional enrichment data, can be overcome by fragmentation approaches, if fragment data can be interpreted. Advances in metabolic modeling capabilities (Antoniewicz et al., 2007; Young, 2014) provide a potential solution for analysis of fragment MIDs through mathematical deconvolution of complex labeling patterns by application of isotopomer balances and least-squares regression. In this study, we show that using this approach to model MS-derived MIDs from double tracer (²H₂O and [U-¹³C₃]propionate) or triple tracer (²H₂O, [U-¹³C₃]propionate and [3,4-¹³C₂]glucose) experiments provides flux estimates that are comparable with those obtained using direct characterization of positional isotopomers by ²H and ¹³C NMR spectroscopy, and reflect expected physiological changes in metabolic pathways during fasting. Furthermore, the exceptional sensitivity of the GC-MS method allowed examination of flux in primary hepatocytes, an experiment that is impractical by ²H and ¹³C NMR analysis.

Reconstruction of the complete glucose ²H labeling patterns based on the MIDs of specific glucose fragments was previously demonstrated using individually labeled glucose standards (Antoniewicz et al., 2011). These experiments nicely demonstrated the potential of mathematical modeling to infer positional labeling information from combinations of fragment MIDs. By isolating the individual MIDs of C1–C2, C1–C4, C1–C5, C1–C6, C4–C6 and C5–C6 fragments of glucose, the ²H enrichment of each carbon position could be regressed. When we performed a similar analysis on glucose samples obtained in vivo following ²H₂O administration in rats, positions H4, H5 and H6 were accurately modeled but positions H1 and H3 were underestimated, and position H2 was overestimated. The inaccuracy likely arises due to strong anti-correlation between predicted enrichments at H2 with those at positions H1 and H3, leading to variable results at these positions when using different numerical solvers (Figure S2). The normalized parameter covariance matrices indicate that the information content of the GC-MS fragments is insufficient to completely deconvolute enrichments at positions H1–H3 when glucose is enriched in all possible positions and typical experimental errors are present. However, the discrepancies between ²H NMR and GC-MS were largely systematic, inasmuch as the flux estimates obtained for PEP-derived gluconeogenesis and glycogenolysis correlated well with each other.

Glucose fragment MIDs were also sufficient for MFA based modeling of fluxes related to the TCA cycle. The primary data required to solve the model is contained in either C1–C3 or C4–C6, since the front and back halves of glucose are assumed to represent symmetric inputs from the triose pool (C1–C3 = C4–C6), which is enriched by ¹³C labeled TCA cycle intermediates. These three carbon units have 8 potential ¹³C isotopomers, but only 3 (1,2-¹³C₂, 2,3-¹³C₂ and U-¹³C₃) are formed within a single pass of the TCA cycle and are sufficient to solve an isotopomer model of the TCA cycle, anaplerosis and gluconeogenesis (Jin et al., 2004; Jones et al., 1997; Landau et al., 1993; Previs and Kelley, 2015). These isotopomers are specifically detected in the ¹³C NMR spectrum of glucose (Figure 2, and 5A) at the C2 resonance as spin-spin coupling between C2–C1, or C2D12 (1,2-¹³C₂); C2–C3 or C2D23 (2,3-¹³C₂); and C1-C2-C3 or C2Q (U-¹³C₃) (Jones et al., 1997). The MIDs of glucose fragments capture similar information, though no specific isotopomer can be evaluated by any single fragment. Rather, fluxes are regressed by modeling the contributions of all possible glucose isotopomers to the formation of the six measured glucose fragment MIDs.

When both ²H and ¹³C tracers are present, an isotopomer model must be used to estimate fluxes through regression of convoluted ¹³C and ²H MIDs, since their mass shifts cannot be distinguished by nominal resolution GC-MS. Although only glucose H2, H5 and H6 ²H NMR peak areas are necessary to model V_Glycogen, V_Glycerol and V_PEP using analytical equations (Burgess et al., 2003), the GC-MS fragment MIDs are regressed simultaneously by fitting ²H enrichments at all positions. Thus, direct comparison was made by also regressing all peak areas from NMR data, which required an adjusted model that accurately accounts for H1, H3 and H4 enrichment, namely by accounting for a kinetic isotope effect at TPI, equilibrium exchange at aldolase and additional labeling by PMI. There was good agreement between GC-MS-based and NMR-derived flux estimates obtained from simultaneous ²H and ¹³C labeling experiments once the MFA model was adjusted. An exception was glycerol-derived gluconeogenesis (V_Glycerol), which was similar between GC-MS and NMR on average, but sample-to-sample flux variations did not always correlate between the two methods. When liver glycogen was depleted (fasting), V_glycerol was correlated between the two methods, but when V_Glycogen was high (ad libitum fed), the two methods lost correlation. Thus, a precise measurement of V_Glycerol may be challenging for GC-MS-based MFA in the fed state because 1) ²H and ¹³C enrichments are lower under these conditions and 2) the model must infer differences in ²H enrichment at positions H2 and H5 (Landau, 1999), that were difficult to assign even when ²H labeling alone was present (Figure S1).

A general, but underappreciated, feature of NMR is its ability to detect isotopomers comprised of ¹³C in adjacent positions at low enrichment. Spin-spin coupling by adjacent ¹³C nuclei induces distinctive multiplets that are well separated from naturally abundant ¹³C found in the singlet signal. Hence, as long as there is sufficient material for detection, positional isotopomers can be discriminated at vanishingly small enrichments. For example, [3,4-¹³C₂]glucose was detected at 0.1% enrichment as the C3D34 (or C4D34) by ¹³C NMR, below the practical detection limit of an M+2 signal by MS. This specificity is likely the reason why correlations were slightly better in liver perfusions compared to in vivo infusions (Figure 7). Liver perfusions eliminate inter-organ tracer recycling and, most importantly, do not require a glucose tracer (e.g., [3,4-¹³C₂]glucose) to measure hepatic glucose production since it is measured directly. Additional glucose fragments may improve position isotopomer characterization by GC-MS, though the six fragments used here already provide excellent positional coverage (Antoniewicz et al., 2011), and additional fragments would potentially lower the throughput of the method. The use of [6,6-²H₂]glucose, as originally implemented by Hasenour et al. (Hasenour et al., 2015), provides a distinct M+2 signal originating from the back half of glucose, where fragment coverage is highest, and may yield better precision for GC-MS analysis. However, this could not be tested against NMR since [6,6-²H₂]glucose obscures the H6 signal from ²H₂O in the ²H NMR spectra (Jin et al., 2005).

The specific strength of the GC-MS approach is in the analysis of low quantity/high enrichment analytes, while the strength of the NMR approach is in the analysis of high quantity/low enrichment analytes. For example, [U-¹³C₃]tracers in humans (analogous to the experiments described here) generate plasma glucose ¹³C isotopomers of less than 0.5% enrichment. The necessary labeling information can easily be detected as multiplets in the ¹³C NMR spectra, but the analysis requires ~20 mL of blood (Browning and Burgess, 2012). The >1000-fold higher sensitivity of MS detection compared to NMR is difficult to take advantage of under this condition because the analysis cannot distinguish the relevant isotopomers from the other 99.5% of the analyte. However, the sensitivity advantage of MS is highly relevant when detecting isotopomers that are unambiguously distinguished from natural abundance (e.g., at fractional enrichments well above background, or for high-mass isotopologues where natural abundance is negligible). Under these conditions, GC-MS analysis provides an enormous advantage for certain experimental protocols, such as those utilizing primary cells, that generate pg quantities of analyte. As proof of principle, we modeled glucose fragment MIDs obtained from primary mouse hepatocytes cultured with simultaneous ²H and ¹³C tracers. Hepatocytes generated far too little glucose for NMR analysis but fluxes were easily characterized using the GC-MS fragment MIDs of glucose. Thus, the decision to use NMR or MS for isotopomer analysis should take into account limitations in analyte mass and/or enrichment.

We note that the general approach of using simultaneous tracers and positional enrichment monitoring is applicable to the analysis of any metabolic pathway that incorporates tracer nuclei through independent biochemical mechanisms. For example, we previously demonstrated that pathways leading to triglyceride synthesis—including de novo lipogenesis, elongation, desaturation and esterification—can be monitored by ²H NMR resonances of appropriate positions within the triglyceride of liver extracts (Duarte et al., 2014). Others have demonstrated that using this approach with the addition of ¹³C labeled glucose/fructose and ¹³C NMR further elucidated the substrates that fed these synthetic pathways (Silva et al., 2019). Appropriate fragmentation and/or sufficient mass resolution will eventually allow pathways such as these to be examined by modeling the mass isotopomers on small-scale samples (e.g., plasma VLDL or plasma membrane).

In conclusion, the MIDs of glucose fragments provide compatible, but not quantitatively identical predictions of glucose isotopomers when validated by ²H and ¹³C NMR. However, NMR data and glucose fragment MIDs provide fluxes that are, in most cases, highly correlated and responsive to physiological interventions when regressed with an equivalent EMU-based MFA model. Importantly, the GC-MS approach could easily model fluxes from glucose labeled by primary hepatocytes, well below the detection limits of NMR. Thus, this approach will provide valuable insight into metabolic mechanisms of normal physiology, disease and pharmacological action on a scale that is small enough to be applied in mouse models and primary cells.

Highlights.

• Multiple tracers can solve large metabolic models yet generate complex isotopomers

• ²H and ¹³C isotopomers are specifically detected by NMR but must be deduced from MS

• Positional NMR isotopomers revealed pathways required for accurate model solutions

• The resulting model regressed both NMR and MS data to similar flux solutions

• MS data was modeled in cell culture where NMR was impractical