Megakaryocyte volume modulates bone marrow niche properties and cell migration dynamics

Abstract

All hematopoietic cells that develop in the bone marrow must cross the endothelial barrier to enter the blood circulation. Blood platelets, however, are released by bigger protrusions of huge progenitor cells, named megakaryocytes, and enter the blood stream as so-called proplatelets before fragmenting into mature platelets. Recently, a second function of megakaryocytes has been identified, as they modulate the quiescence of hematopoietic stem cells, mostly via different soluble factors. We know from light sheet fluorescence microscopy images that megakaryocytes are distributed throughout the bone marrow facing a dense vascular network. Here, we used such three-dimensional images to provide a realistic simulation template reflecting the in vivo cell-vessel distributions resulting in reliable whole-bone analysis in silico. Combining this approach with an automated image analysis pipeline, we found that megakaryocytes influence migration of neutrophils and hematopoietic stem cells, and thus act as biomechanical restrainers modulating cell mobility and extravasation. Indeed, as a consequence of increased megakaryocyte volumes in platelet-depleted mice neutrophil mobility was reduced in these animals.

Introduction

Hematopoiesis is the process of forming blood cells, which occurs predominantly in the bone marrow (BM). During this process, hematopoietic stem cells (HSC) undergo lineage restriction and differentiate into restricted hematopoietic progenitors, which then give rise to blood cells by proliferation and further differentiation.

During the last decade, the identification of new HSC markers, development of genetically modified mouse strains and microscopy techniques enabled the identification and intensive investigation of the perivascular niche as the major site of HSC localization and activity, where 80% of HSC were found to be associated with sinusoids, 10% with arterioles and a further 10% with transition zone vessels.^1–4 The perivascular niche has been determined to be a microenvironment containing different cell types and signaling molecules, together regulating HSC maintenance, quiescence, proliferation, differentiation and migration.^5–8

Blood cells differentiated from HSC leave the BM by migrating towards the sinusoids to enter the circulation.⁹ In general, many of these migratory processes are chemotactic, i.e. driven by chemoattractants.⁹ One of the most prominent cell types of the BM are neutrophils, which are the most abundant subpopulation of leukocytes; neutrophils have a short lifespan (6-12 h) in the circulation, after which they quickly migrate to tissues where they perform their functions.¹⁰ Neutrophil homeostasis is orchestrated through a balance of neutrophil production and release from BM into the blood and migration back into the BM for elimination.¹¹ The neutrophil reserve within the BM is estimated to be 6×10¹¹ in humans and 12×10⁷ in mice.^10,12

Megakaryocytes are derived from multipotent HSC and belong to the myeloid cell lineage.¹³ Megakaryocytes mainly reside in the BM, mostly in close proximity to the vasculature,^14,15 and have a diameter of up to 50 µm in mice and 50-100 µm in humans.¹³ Mature megakaryocytes produce platelets and release them into the blood circulation in order to maintain constant platelet counts. In addition, they actively regulate HSC proliferation in both positive and negative manners.^16–19 Recent studies revealed that most HSC are in close proximity to sinusoidal blood vessels.^1,4,20 Likewise, more than 70% of megakaryocytes were found to be in contact with the BM vasculature.¹⁵ Besides this indirect correlation, at least a subset of megakaryocytes was found to be in close proximity to HSC.^16,18,19 Moreover, megakaryocytes were shown to influence HSC quiescence via different cytokines, such as CXCL4,¹⁶ transforming growth factor β1 (TGFβ1)¹⁷ and thrombopoietin.^18,21 However, very recently it was shown that liver-derived, and not megakaryocyte-derived, thrombopoietin is required for HSC maintenance in the BM.²²

Nevertheless, megakaryocyte activity in the intact medullary space and its interplay with other BM cells has gained great attention in the last decade; numerous in vitro investigations, based on two-dimensional (2D) cryosections, and in vivo (two-photon) imaging studies have been reported.²³ Intrinsic limitations of these methods such as loss of volume information, cutting artifacts or small field of view impair scientific models¹⁵ and treatment of patients.²⁴ Recently, whole bone optical clearing and imaging have been established to overcome these limitations. Despite the significant advances in imaging technology, tools for correct quantitative analysis of the geometry and localization of megakaryocytes, HSC and other BM components are still in their infancy. As image segmentation is a complex and error-prone method, exact definition of the image-processing pipeline is of great importance. The recently developed machine learning toolkits^25,26 are powerful complements to the portfolio, and allow for more comprehensive data analysis, and access to previously masked information. Successful segmented objects derived from complex microscopy data can be used for in silico analysis of cell distributions within the BM architecture as recently demonstrated.^15,16,20

Modular toolkits in particular have been proven to be powerful, not only for image analysis, but also for structure reconstruction as well as simulations of growth and organization.^27,28 Unfortunately, these tools are not yet universally applicable. Here, we developed and compared different image processing pipelines and simulation scenarios for precise identification of megakaryocytes in three-dimensional (3D) light sheet fluorescence microscopy (LSFM) image stacks of uncut murine bones. Megakaryocytes have been described to have an impact, based on biochemical processes, on cell migration in the BM. However, the impact of increases in their number and size is unclear. To date, the only available technique for investigating cell migration in the BM is intravital imaging, which is hampered by the limited time during which measurements can be made because of the need for anesthesia of the animals and accumulating phototoxicity,²⁹ limited penetration depth³⁰ and a relatively small field of view of typically 300-500 μm² that does not allow observation of the whole bone simultaneously. Here, computational simulations represent an important complementing and well-controllable tool for elucidating underlying cell mechanisms.^31–33 Typically, simulation studies use artificial meshes as templates due to the lack of experimental data or to minimize the computational effort. Unfortunately, such simplified artificial templates for megakaryocytes and the vasculature can bias simulations and lead to misinterpretations as we show in this study. Here, we demonstrate that using the segmented cell and vessel objects of true 3D images can overcome those limitations, providing a simulation framework that has the prerequisites to reflect the physiological situation optimally.

Methods

More methodological details are present in the Online Supplementary Material.

Mice

All animal experiments were approved by the district government of Lower Frankonia (Bezirksregierung Unterfranken). We used 8- to 12-week old C57BL/6JRj (Janvier Labs) or Lyz2^GFP mice.³⁴

Thrombocytopenia was induced by intravenous injection of rat anti-GPIbα³⁵ (CD42b; 2.0 μg/g body weight Emfret Analytics, Eibelstadt, Germany;).

Two-photon intravital imaging

Lyz2^GFP mice³⁴ were anesthetized by intraperitoneal injection of medetomidine 0.5 mg/g, midazolam 5 mg/g and fentanyl 0.05 mg/g body weight. A 1-cm midline incision was made to expose the frontoparietal skull, while carefully avoiding damage to the bone tissue. The mouse was placed on a custom-designed metal stand equipped with a stereotactic holder to immobilize the head. BM vasculature was visualized by injection of bovine serum albumin-Alexa546 (8 μg/g body weight) and anti-CD105 Alexa546 (0.6 μg/g body weight). Neutrophils were visualized by the endogenously expressed green fluorescent protein. Stacks were acquired at a frame rate of 1/min on an upright two-photon fluorescence microscope (TCS SP8 MP, Leica Microsystems, Wetzlar, Germany) equipped with a 25× water objective with a numerical aperture of 1.0. A tunable broad-band Ti:Sa laser (Chameleon, Coherent, Dieburg, Germany) was used at 780 nm to capture green fluorescent protein and Alexa546 fluorescence. For each mouse, three time series of z-stacks were recorded (20 min each, 1 z-stack/min) with a voxel size of 0.87 x 0.87 x 1 μm³. Details on image analysis are provided in the Online Supplementary Material.

Light sheet fluorescence microscopy image processing and segmentation

Image stacks were processed, visualized, and analyzed using FIJI,³⁶ Ilastik 1.2.²⁵ and Imaris^® 8.4 (Bitplane AG, Zurich, Switzerland). The four different analysis pipelines (I-IV), shared the same image-preprocessing steps performed in FIJI and Imaris. In the first pipeline (I), the membrane algorithm was directly applied on megakaryocytes. The second, simple one-pass pipeline (II) utilized the Imaris cell soma algorithm with one seeding step, whereas the extended two-pass pipeline (III) employed two subsequent seeding steps for large and small megakaryocytes. Our customized pipeline (IV) corrected for fake invaginations by creating virtual cell somata before applying two-step seeding. Bone and BM were identified using the pixel classification algorithm of Ilastik software, with results transferred to Imaris 8.4 for segmentation and further analysis. Details are provided in the Online Supplementary Material.

Static and dynamic computational simulations

Simulations of megakaryocyte distribution (static) and cell migration (dynamic) in the BM were performed by custom-written algorithms (Online Supplementary Figures S4 and S6) in Matlab (Mathworks, Natick, MA, USA) which virtually reconstruct the BM space using 3D images at a voxel level and simulate cell distribution and/or migration depending on various adjustable parameters (cell type, BM crowdedness, cell velocity, chemotaxis and vessel stickiness) as indicated in the Results section. All migrating cells (HSC or neutrophils) are placed into the template (Online Supplementary Figure S5) so that spatial overlap with the vasculature or other cells is avoided. Megakaryocytes are preset in the template according to the vessel-biased distributions identified by Stegner et al.¹⁵ Details are provided in the Online Supplementary Material.

Statistical analysis

Data exported from Imaris were processed with Microsoft Excel 2016 (Microsoft Corporation, Redmond, WA, USA) and statistics were analyzed using OriginPro 2016 (OriginLab Corporation, Northampton, MA, USA) or SigmaPlot (Systat Software, San Jose, CA, USA). We tested datasets for variance homogeneity (Levene test). The Mann-Whitney test, two-parameter t-test and one-way analysis of variance (with the Tukey post-hoc test) were applied where appropriate. P-values ≥0.05 were considered as not significant (ns), while P-values <0.05 were considered statistically significant (*P< 0.05; **P<0.01; ***P<0.001).

Results

A full three-dimensional dataset is crucial for unbiased quantification of megakaryocyte-vasculature characteristics and interplay

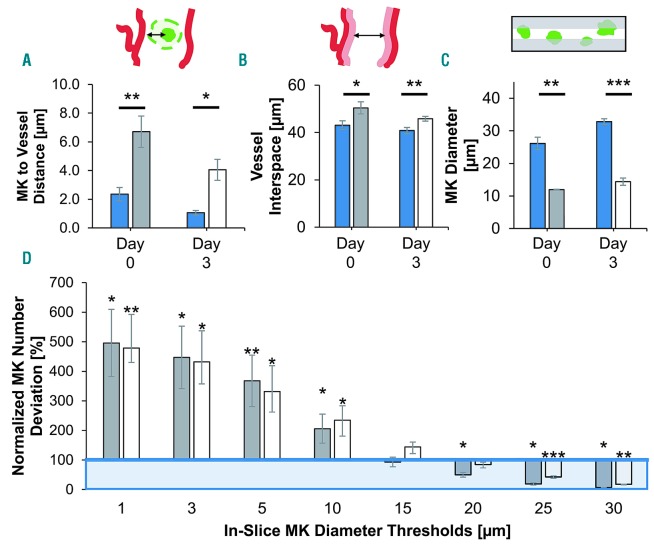
First, we assessed the potential benefits of whole stack imaging compared to sectioning. To do this, we virtually sliced existing image stacks (10 slices per stack each with a thickness of 10 μm), and compared exemplified slices (mimicking a typical experimental setting) to the complete 3D image. We compared key parameters such as megakaryocyte-to-vessel distance, vessel interspace, and mean megakaryocyte diameter. It should be noted that this is not an assessment of the bias of cutting artifacts, but purely the impact of the intrinsically 2D-limited information in exemplified slices. Due to the elaborate and complex sample preparation, including critical chemicals to acquire 3D BM images, it is not possible to subsequently process the same bones for 2D analysis, so virtual slices are used. For completeness, we evaluated datasets for steady-state conditions (day 0) and 3 days after complete platelet depletion (day 3) individually.

We first measured the mean megakaryocyte-to-vessel distance (edge-to-edge). Our data revealed fundamentally increased distances in virtual slices compared to the distances in full stacks. While megakaryocytes in stacks were generally located in closest proximity of vessels ≈ 1.1 - 2.4 μm, we observed a roughly 3- to 4-fold increase in virtual slices for both measurement time points. Day 3 megakaryocytes, usually larger than day 0 megakaryocytes, were generally situated closer to blood vessels than day 0 megakaryocytes in 3D stacks and virtual slices alike (Figure 1A, Online Supplementary Table S1). Second, we assessed the available interspace between vessels in BM. In stacks, the distances we measured were the same at both time points. In slices, distances were significantly increased at both time points compared to the respective ground truth values, being roughly 17% higher at day 0 and 12% at day 3 (Figure 1B, Online Supplementary Table S1). Third, we determined the mean megakaryocyte diameter. In stacks, megakaryocyte diameters on day 3 were about 26% larger than on day 0 (Ø_day0=26.1 ± 1.9 μm vs. Ø_day3=32.8 ± 0.9 μm). In contrast, the average diameters we measured in slices were almost half at both time points, being 46% and 44% of the stack megakaryocyte diameters on day 0 and 3, respectively (Figure 1C, Online Supplementary Table S1).

Figure 1.

Comparison of data derived from full image stacks and virtual slices. Data displayed for two time points: before induced thrombopoiesis with generally smaller megakaryocytes (day 0, dark gray bars) and after with very large megakaryocytes (day 3, white bars) in comparison to three-dimensional stack ground truth (blue bars/box). Virtual slices extracted from full image stacks. Binary mask of stack megakaryocytes (=ground truth) was used for in-slice megakaryocyte segmentation (see inset 1C). Bar graphs represent the mean ± standard deviation (SD). Two-parameter t-test: stack vs. virtual slice data for day 0 and day 3, respectively. *P<0.05; **P<0.01; ***P<0.001. (A) Mean megakaryocyte-to-vessel distance is increased in slices compared to full stack analysis. (B) Measured vessel interspace is significantly greater in virtual slices than in full stacks. (C) Mean megakaryocytes diameter is massively underestimated in virtual slices. (D) Megakaryocyte numbers in slices deviate significantly from stack ground truth depending on diameter threshold of the megakaryocytes. Megakaryocyte numbers normalized to equal marrow volume; percentage relative to stack ground truth. Mk: megakaryocyte.

As we measured clear bias by analysis of the sliced stack, we wondered whether there was a megakaryocyte number bias in slices. Here, we first determined the ground truth of intact stacks by counting megakaryocytes, and normalizing the number to a defined volume of BM: n_{MK_day0} = 20801 ± 4223 megakaryocytes/mm³ and n_{MK_day3} = 15992 ± 1700 megakaryocytes/mm³ in stacks and exemplified slices alike. We set a threshold megakaryocyte size to discard artifacts and cell fragments. In stacks, we defined 525 μm³ (equivalent to 10 μm sphere diameter) as the minimum megakaryocyte volume. In slices we applied a range of increasing minimum diameter thresholds (1 μm to 30 μm), and compared the deviation to stack megakaryocyte numbers. Lower thresholds resulted in massive overestimation of megakaryocyte numbers, from roughly 500% with the 1 μm threshold to around 200% with the 10 μm threshold. We measured stack-comparable megakaryocyte numbers at 15 μm and 15/20 μm on day 0 and 3, respectively. Higher diameter thresholds led to significant underestimation of in-slice megakaryocyte numbers at both time points (Figure 1D).

An iterative multi-step image processing pipeline is essential for reliable segmentation of megakaryocytes

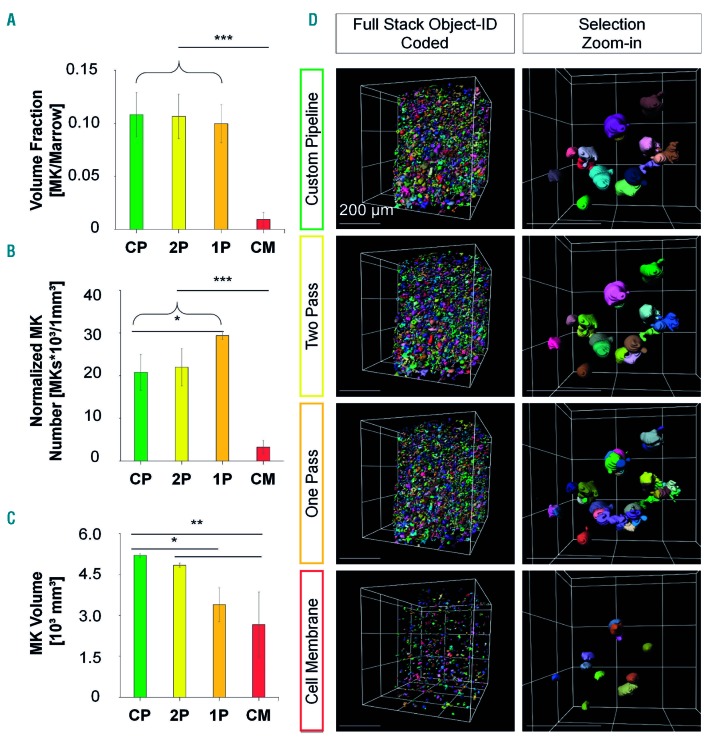
Megakaryocyte segmentation was challenging because of the considerable variability in cell shape and size, ranging over several orders of magnitude, hampering pre- and post-segmentation artifact removal. To optimize the analysis, we tested four different analysis pipelines, using both FIJI and Imaris for different tasks, and compared their segmentation performance: (i) Imaris cell membrane, (ii) one-pass, (iii) two-pass, and (iv) custom-designed. A manual side-by-side comparison of their relative performance (Figure 2, Online Supplementary Figures S1 and S2, Table 1) revealed a severe amount of fake invaginations and false seeding points for (i)-(iii), although the effect was least severe for (iii). Thus, we successfully extended the two-pass pipeline into a (iv) customized pipeline by one additional step of correction (Figure 2D, Online Supplementary Figure S2D), achieving a superior performance and minimizing artifacts compared to the previous algorithms. The Imaris cell membrane tool showed the most severe underperformance: megakaryocyte-to-marrow volume fraction, normalized mean megakaryocyte numbers, and mean megakaryocyte volume were greatly underestimated. Overall, only a few megakaryocytes were recognized and only the unstained innermost lumen was segmented. The one-pass pipeline delivered megakaryocytes to the same marrow fractions as our customized pipeline. However, the strong increase of normalized mean megakaryocyte numbers and the decrease in mean megakaryocyte volumes indicated high over-segmentation of megakaryocytes. The two-pass pipeline, as the direct progenitor of our customized pipeline, performed better in the comparison of (i) and (iii). We found comparable values for total megakaryocyte volume fraction (normalized to marrow volume) and mean megakaryocyte numbers. However, for the much larger megakaryocytes on day 3 after platelet depletion, the mean megakaryocyte volume was underestimated by 16% while no deviation was observed for the smaller megakaryocytes on day 0.

Figure 2.

Segmentation performance of the customized pipeline compared with the one-/two-pass pipelines and the Imaris cell membrane algorithm on day 0. (A-C) Data depicted for the customized pipeline (CP; green bars), two-pass pipeline (2P; yellow bars), one-pass pipeline (1P; orange bars), and Imaris cell membrane algorithm (CM; red bars) before induced thrombopoiesis (day 0). (A) Megakaryocyte-to-marrow volume fraction is comparable between the customized and one-/two-pass pipelines with a massive decrease when the Imaris cell membrane algorithm is used. (B) Normalized mean megakaryocyte numbers are comparable with the customized and two-pass pipelines, whereas they are significantly increased with the one-pass pipeline and massively decreased with the Imaris cell membrane algorithm. (C) Customized and two-pass pipelines deliver comparable mean megakaryocyte volumes, whereas those yielded by the one-pass pipeline or the Imaris cell membrane algorithm are significantly decreased. Bar graphs represent the mean ± standard deviation. *P<0.05; **P<0.01; ***P<0.001 (one-way analysis of variance, Tukey post-hoc test). (D) Exemplified segmentation results. Left column: full stack with segmented megakaryocytes, object ID color-coded. Sparsely located megakaryocytes with cell membrane algorithm opposed to other pipelines. Right column: zoom-in to selection. Megakaryocyte fragmentation is higher in the one-and two-pass pipelines compared to the customized pipeline. Cell membrane algorithm with sparse and small megakaryocytes. Grid size and scale bar = 200 µm. Mk: megakaryocyte.

The results suggest that the suitability and performance of pipelines (i)-(iii) depend on the volume of the megakaryocytes. To pinpoint this correlation, we sorted our data by megakaryocyte volume, and compared deviations of megakaryocyte numbers and volumes systematically to our optimized custom pipeline (Online Supplementary Figure S1): the greatest deviation was shown by (i) which underestimated megakaryocyte numbers throughout all volume classes. Large megakaryocytes were widely neglected, while the volume of small megakaryocytes was overrepresented due to over-fragmentation. The same tendency, albeit less pronounced, was observed for (ii) (Online Supplementary Figure S1). Pipeline (iii) performed more comparably to (iv). However, the numbers of very small megakaryocytes were still slightly overestimated on both day 0 and day 3, and we found significantly underestimated numbers of mid-to-larger megakaryocytes on day 3. Volumes of the largest megakaryocytes were significantly underestimated on both days (Online Supplementary Figure S1).

Experimental three-dimensional image stacks serve as templates for realistic simulation of cell distribution in the bone marrow

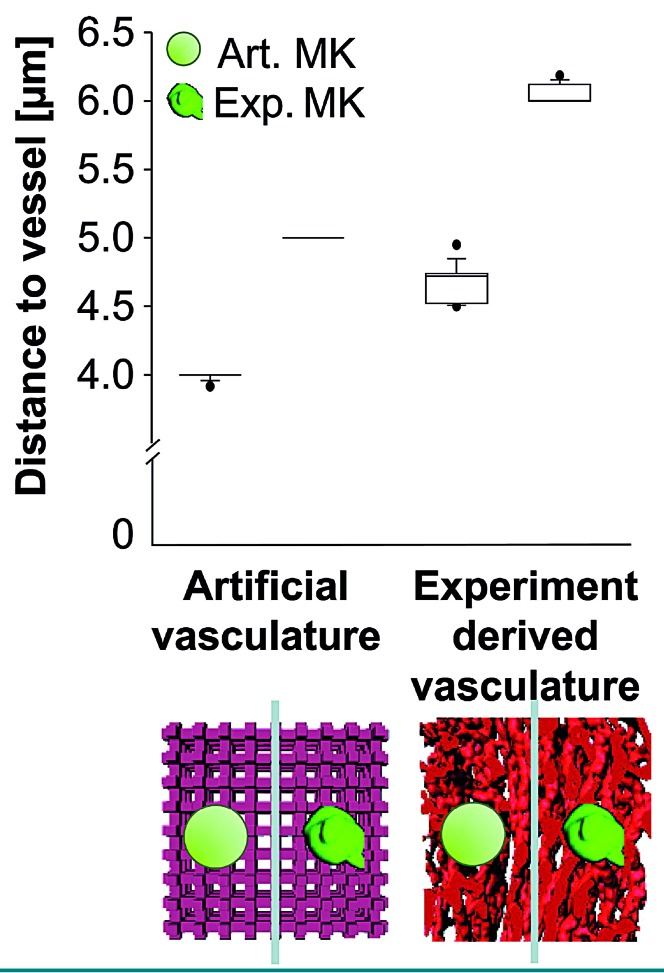
We recently showed that segmented 3D LSFM images can be used as templates for static simulation of megakaryocyte distribution in the BM.¹⁵ Here, we systematically compared this approach to conventional simulation methods. To do this, we used experimentally derived structures of megakaryocytes (MK^exp) and vessels (V^exp) on the one hand, and simplified artificial structures (MK^art, V^art) on the other hand. To acknowledge the complexity of the in vivo system we employed a voxel-based simulation model using a Brownian walk with obstacles (Online Supplementary Figure S4). The artificial vasculature was constructed as a 3D lattice with correct intervascular distances and megakaryocytes were spherical objects of proper size (Online Supplementary Figure S3). We combined all four possible pairs (MK^artV^art, MK^expV^exp, MK^artV^exp, MK^expV^art) for in silico modeling (Figure 3).

Figure 3.

Vessel and megakaryocyte shape changes the outcome of simulated megakaryocyte distribution in the bone marrow. Megakaryocyte distribution in the bone marrow was simulated and the edge-to-edge distance between the cells and the vasculature was calculated. Simulations were performed either with a simplified artificial vessel lattice (light red) or with real bone marrow vasculature imaged by light sheet fluorescence microscopy (red). In both vessel templates, artificial (non-hatched) or real megakaryocytes (hatched) were placed randomly. For the artificial megakaryocyte simulations only one spherical megakaryocyte type was used, while real megakaryocyte simulations were performed with a pool of different megakaryocytes with a representative distribution of diameters. In total, ten simulations of each type were performed with 700 or 1100 megakaryocytes per simulation for artificial and real vasculature, respectively. Differences between all groups were significant at P<0.001 (one-way analysis of variance and pairwise comparison procedures with the Dunn method) Mk: megakaryocyte.

For the simulation megakaryocytes were randomly placed in the intervascular space without overlaps with vessels or other megakaryocytes (Online Supplementary Figure S4). It should be noted that we used randomly distributed objects of the same average diameter for all four possible megakaryocyte-vessel pairings, so that the resulting megakaryocyte-to-vessel distances would be comparable, if the approaches were comparable. However, for MK^art the cells were found to be closer to the vessels than for MK^exp no matter whether the vessels were artificial (3.99 ± 0.03 μm vs. 5.00 ± 0.00 μm) or had been experimentally derived (4.67 ± 0.14 μm vs. 6.04 ± 0.07 μm) (Figure 3). For all cases with V^art, the cell-vessel distance for both MK^art and MK^exp appeared to be decreased. Thus, the cell distribution in the BM looks significantly different when simplified artificial 3D objects are chosen.

Megakaryocytes hamper simulated cell migration in the bone marrow

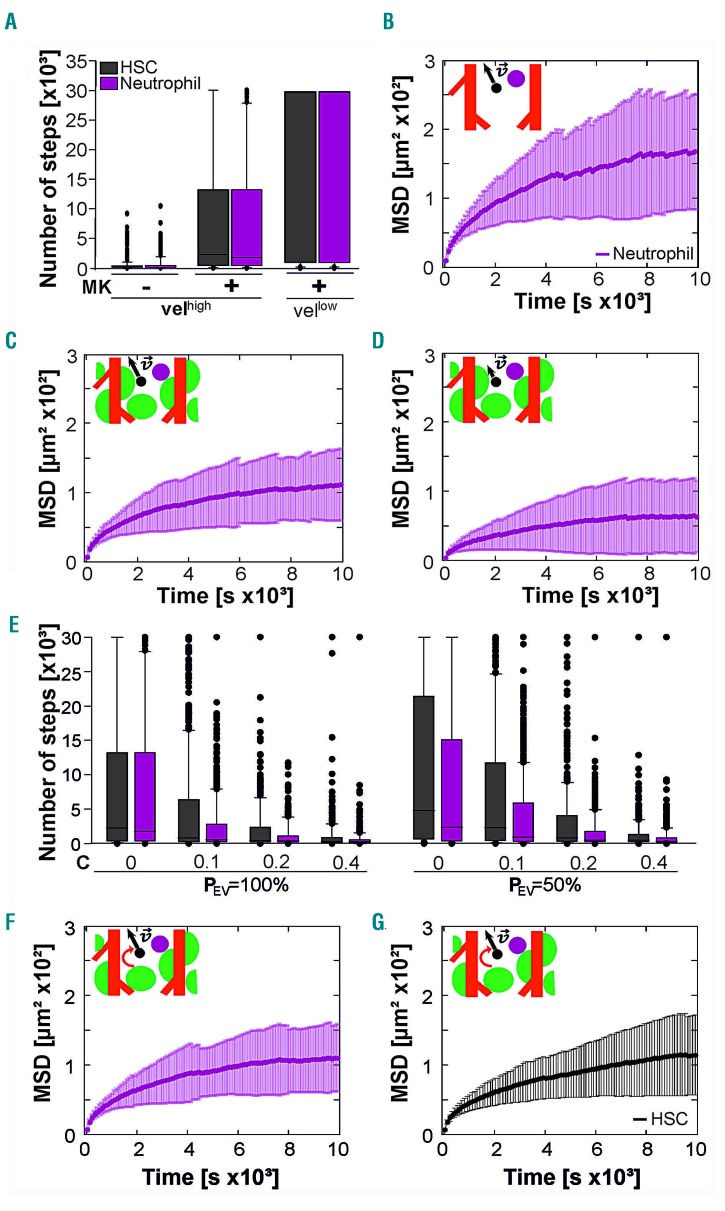
Next, we used the 3D LSFM templates for simulations of cell migration (Online Supplementary Figure S5). Physiologically, HSC and neutrophils are recruited to the peripheral blood during stem cell mobilization or inflammatory processes, respectively. In this context, we aimed to learn more about the recruitment process and the role of megakaryocytes, cell velocity and cell size in HSC and neutrophil migration to BM vasculature in silico. To simulate migration of small HSC and bigger neutrophils in the BM, we designed artificial cells considering the real diameter and sphericity of these types of cells.^37,38 The HSC and neutrophils were set to migrate randomly in the intervascular space with a predefined step size of 3 ± 2 μm (mean ± standard deviation). The time between two steps was set at 20 s. To analyze migration towards the vasculature, the number of steps until first contact with a BM vessel was assessed, assuming that the cell would subsequently migrate into the intraluminal space. To further characterize the migration, the mean squared displacement (MSD) of cell trajectories was determined for different time scales. Simulations were performed with and without megakaryocytes in the BM to assess the influence of BM crowdedness on cell migration (Figure 4A-C; Online Supplementary Figure S7). We found that megakaryocytes dramatically reduced the motility of HSC and neutrophils. The number of steps (n^steps) to reach the vasculature increased in the presence of megakaryocytes (HSC: from n_steps = 513 ± 1107 to n_steps = 8057 ± 10310, neutrophils: from n_steps = 628 ± 1270 to n_steps = 7869 ± 10175) (Figure 4A) and the trajectories exhibited lower MSD values (HSC: from MSD_20s = 9.52 ± 5.95 μm² to MSD_20s = 6.85 ± 1.27 μm², neutrophils: from MSD20_s =10.57 ± 5.06 μm² to MSD_20s = 6.96 ± 1.26 μm²) (Figure 4B, C; Online Supplementary Figure S7). Fitting the first 25% of the MSD trajectories to determine the apparent diffusion coefficient (D_app)³⁹ revealed reduced D_app in the presence of megakaryocytes (Online Supplementary Table S3). Likewise, saturation limits of the MSD curves were reduced in the presence of megakaryocytes (HSC: from 171 ± 1.3 μm² to 133 ± 0.8 μm²; neutrophils: from 182 ± 1.8 μm² to 116 ± 0.5 μm²) (Online Supplementary Table S4). Collectively, these data suggest that megakaryocytes represent passive obstacles, and significantly hamper cell migration in the BM. Lowering cell velocity (step size of 2 ± 1 µm) further suppressed migration for both HSC and neutrophils (HSC: n_steps = 8100 ± 13162 and MSD_20s = 3.73 ± 1.13 μm², neutrophil: n_steps = 19694 ± 13924 and MSD_20s = 3.91 ± 1.02 μm²) (Figure 4A, D). Interestingly, there were no significant differences between the investigated cell types, despite their different size and shape.

Figure 4.

Adjustable biophysical parameters influence simulated cell migration in the bone marrow. Simulation of cell migration in bone marrow was performed with adjustable parameters: cell type, bone marrow crowdedness, cell velocity, chemotaxis and vessel stickiness. (A) Number of steps until entering the vessel lumen for artificial hematopoietic stem cells (HSC; black) and neutrophils (magenta) migrating in the bone marrow with or without increased crowdedness resulting from the presence of megakaryocytes at high and low instantaneous velocities of V_high = 3 ± 2 μm/step and V_low = 2 ± 1 μm/step, respectively. The probability of entering the vessel lumen after contact (P_EV) was set at P_EV = 100% and chemotaxis was absent (C = 0). (B-D) Mean squared displacement (MSD) and neutrophil trajectories for the megakaryocyte-free template at high velocities (B) and a megakaryocyte-containing simulation environment at high (C) and low (D) velocities. P_EV = 100% and C = 0. (E) Number of steps until entering the vessel lumen for P_EV = 100% and P_EV = 50% for increasing chemotaxis (C = 0; 0.1; 0.2; 0.4) in the presence of megakaryocytes. (F-G) MSD analysis of neutrophil and HSC migration data from (E) for P_EV = 50% and C = 0. Six hundred simulations were performed for each simulation type. Plots for HSC migration are shown in Online Supplementary Figure S7.

Chemotaxis and weak cell-to-vessel adhesion reveal the impact of cell size on migration in silico

Cell migration in the BM can be guided by chemotactic processes. Thus, we introduced chemotaxis into our cell migration algorithm, with the vessel walls being assumed to be the source of the chemoattractant (Online Supplementary Figure S6). Furthermore, we extended the algorithm with an adjustable probability for entering the vessel (P_EV) to reflect a highly physiological cell migration process. We found that the number of required steps to reach and enter the vessels decreased (Online Supplementary Table S2) as the chemotaxis increased with a stronger gradient guiding the cells towards nearby vessels (Figure 4E). At the same time the corresponding MSD values for both investigated P_EV of 100% and 50% significantly increased (Online Supplementary Table S2 and S3, Figure 4F). Here, neutrophils appeared to enter the vasculature faster than HSC, which is in contrast to the simulations without chemotaxis. As expected, reducing P_EV from 100% to 50% increased the time until entering the vasculature (Online Supplementary Table S2, Figure 4E), but did not change the MSD values (Online Supplementary Table S2, Figure 4C, G). Interestingly, for probability P_EV=50% neutrophils reached the vasculature significantly faster than HSC even in the absence of chemoattractants. In other words, cell size matters for migration to the vasculature, and this size effect can even be augmented by biophysical parameters such as chemotaxis and cell-to-vessel adhesion probability.

Treatment known to deplete circulating platelets and increase megakaryocyte volume is associated with a reduction in neutrophil mobility in the bone marrow

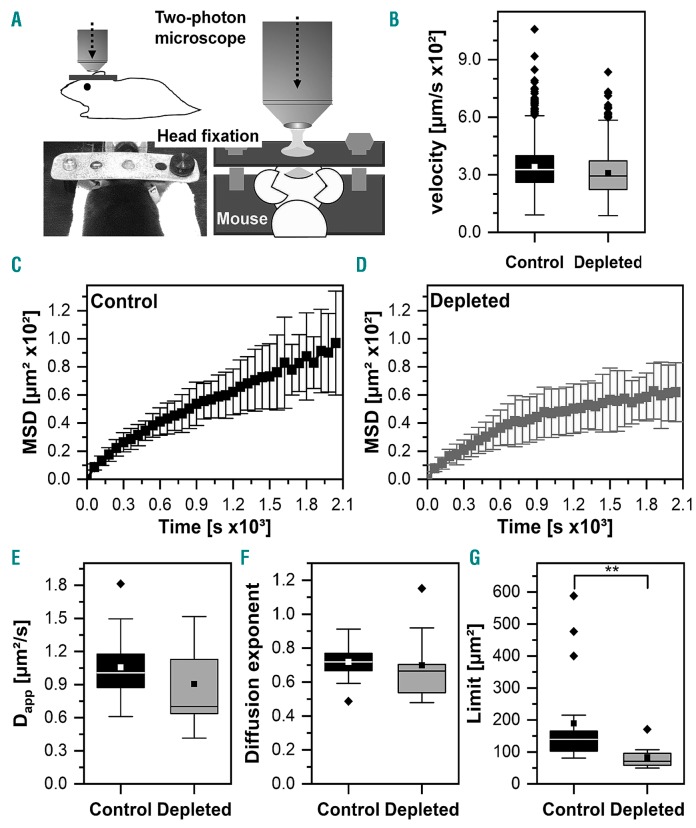
Next, we assessed whether the data obtained from the computational simulations could be validated in vivo (Figure 5; Online Movies 1 and 2). A depletion of megakaryocytes would inevitably also remove the biochemical factors derived from megakaryocytes. Factors such as platelet factor-4 (PF4) and TGFβ1 have been shown to modulate HSC quiescence^16,17 so it would be impossible to discriminate between the biochemical and biomechanical effects of megakaryocyte depletion. As an alternative approach we treated platelets with anti-GPIbα antibodies, which do not deplete megakaryocytes, but result in increased megakaryocyte volume of vessel-associated megakaryocytes on day 3 after platelet depletion.¹⁵ In our computational simulations the larger megakaryocytes had a greater impact than steady-state megakaryocytes on neutrophil mobility (not shown). Thus, we compared neutrophil mobility in naïve mice and mice on day 3 following platelet-depletion (Figure 5) with the parameters detailed in the Online Supplementary Material (Online Supplementary Tables S3 and S4). As expected from our simulations neutrophil mobility was decreased in platelet-depleted mice (saturation limit from 120 ± 5.58 μm² to 66.7 μm² in platelet-depleted mice), supporting our hypothesis that megakaryocytes restrain the mobility of neutrophils.

Figure 5.

Intravital imaging reveals decreased mobility of neutrophils in platelet-depleted mice. (A) Scheme of two-photon microscopy of the bone marrow 72 h after the induction of platelet depletion (or mock injection) through a 1 cm open cranial window (thinned skull) using a head-fixation in a stereotactic holder as illustrated. (B) Instantaneous velocities of neutrophils (62-149 per mouse) tracked in mice depleted of platelets (n=3 mice, 0.034 ± 0.011 μm/s) and the control group (n=5, 0.031 ± 0.011 μm/s). (C, D) Mean and standard deviation of the time-dependent mean squared displacement of the control group and the megakaryocyte-depleted mice. (E-F) The apparent diffusion coefficient, D_app, and diffusion exponent, α, for the control group (D_app= 106 ± 32 μm², α = 0.72 ± 0.10) and megakaryocyte-depleted mice (D_app = 90.5 ± 38.4 μm², α = 0.70 ± 0.21) as obtained from equation 3. P=0.129 for D_app and P=0.092 for α (Mann-Whitney test). (E) Saturation limit, L, for the control group (L = 189 ± 150 μm²) and megakaryocyte-depleted mice (L = 82.7 ± 38.0 μm², P=0.0018) as obtained from equation 2. MSD: mean squared displacement.

Supporting information

We have uploaded two supporting videos - one exemplary dataset of naïve and megakaryocyte-depleted mice – as well as the MatLab scripts used in the simulation and the Ilastik training file used in bone and BM segmentation on Zenodo under DOI: 10.5281/zenodo.3144732.

Discussion

Here, we provide a profound 3D image reconstruction and segmentation pipeline for different BM components and use these data for computational simulations by complex tailored cell localization and migration algorithms. Realistic simulation templates were deployed for migration simulations of HSC and neutrophils. Our data clearly show that volumetric analysis of the number and localization of megakaryocytes provides additional information.

Furthermore, we performed computational 3D simulations of megakaryocyte distribution and BM cell migration using the 3D segmented LSFM data. These simulations suggest that megakaryocytes play an important role in cell migration even if not migrating themselves. Instead, they represent passive obstacles, and thus significantly influence migration of other cells, such as HSC and neutrophils, in the BM. We discovered this from realistic simulations using templates with high physiological relevance derived from segmented cell and vessel objects in 3D LSFM images.

The image analysis pipeline is clearly superior to commonly used strategies, and minimizes bias of crucial parameters such as cell number and volume. Our data emphasize the need for (customized) multistage segmentation pipelines with active artifact removal when studying complex specimens. While both common pipelines failed significantly, the two-pass algorithm performed closest to our custom pipeline, albeit with some flaws. Besides the risk of over-segmentation, further manual assessment confirmed incomplete segmentation of larger megakaryocyte somata with weak and irregular staining as often found in typical samples. Unfortunately, this results in invaginations and consequently volume underestimation. During segmentation, seeding points were often not set properly. They were preferentially placed on high intensity membrane or cell-cell touching areas and often missed cell centers, which leads to inaccurate determination of cell volumes, but similar cell numbers (Figure 2D, Online Supplementary Figure S2D).

Previous studies often utilized Ilastik pixel classification for discrimination of distinct objects such as co-cultured cells.⁴⁰ In line with recent work,²⁵ we demonstrated successful segmentation of challenging tissue structures. Although the best results were achieved here with the full feature set for pixel classification, these sets could be reduced and optimized to smaller structure/pattern sizes that also suit memory-limited scenarios.

The segmented objects of the LSFM images are not only important for proper quantitative imaging, but are also very advantageous when it comes to realistic simulations of cellular distributions, dynamics and interactions of cells within the BM. Thus, we found that real sample templates were highly advantageous, in terms of accuracy, compared to simplified artificial 3D objects. Of course, the conventional method using periodic and other simple structures would minimize computational time, but could lead to biased results, masking important features of a given distribution.

Previous studies have shown that the deletion of megakaryocytes activates quiescent HSC and expands the HSC pool as well as increasing HSC mobilization and proliferation.^16–18 These effects could be partially reproduced by ablation of cytokines, such as TGFβ1¹⁷ and CXCL4¹⁶ in megakaryocytes and platelets. However, as megakaryocytes, despite their relatively low number (accounting for less than 0.1% of all BM cells), make up a significant volume within the BM and are distributed along the blood vessels, we hypothesized that megakaryocytes might serve as passive obstacles hindering the egress of other cells from the BM. As the biomechanical barrier function of megakaryocytes cannot be technically uncoupled from the potential chemical effects (e.g. cytokine release) of megakaryocytes, which are also abolished if these cells are depleted, in vivo, we took advantage of mathematical modeling approaches using LSFM-derived objects. These simulations based on 3D Brownian dynamics clearly demonstrate that megakaryocytes might act as a biomechanical restraint hindering BM egress of HSC or neutrophils (Figure 4). Importantly, this effect comes into play even under circumstances such as chemotactic cues or high cell velocities, indicating that it is an important factor modulating the egress of cells from the BM. Other cell features, such as deformability have also been shown to be important when it comes to extravasation and tumor growth⁴¹ or immune responses.⁴² Extravasation conditions and prerequisites have been modeled previously e.g. by Xiao and colleagues⁴³ with the interesting result that cell shape rather than elasticity may play an important role when squeezing through a narrow gap. This knowledge may guide more complex simulations in the future. However, to date it exceeds the computational power of common laboratories and facilities. In contrast, the simulations presented here can be run on a single workstation in a few hours, still being sufficient to describe a typical large-tissue scenario observed in animal experiments. One limitation of using platelet depletion is that this treatment might potentially affect other features of the BM environment that could influence the migration of BM cells. On the other hand, the use of anti-GPIbα antibodies to deplete platelets is the ‘gold standard’ in the field and has no obvious effects on immune cells.³⁵ Moreover, our first in vivo data on neutrophil mobility in naïve and platelet-depleted mice (Figure 5; Online Supplementary Tables S3 and S4) support the hypotheses derived from our mathematical modeling approach, as the saturation limit of the neutrophil MSD trajectories in platelet depletion was significantly reduced compared to steady-state conditions (Figure 5G; Online Supplementary Table S3). Consequently, this study points to the importance of biomechanical properties of the BM environment in regulating cell motility, a factor which has so far not been appreciated sufficiently. Moreover, our study showcases how the combination of advanced imaging approaches in combination with computational simulations can refine hypotheses.