Methods for Estimating the Case Fatality Ratio for a Novel, Emerging Infectious Disease

Abstract

During the course of an epidemic of a potentially fatal disease, it is important that the case fatality ratio be well estimated. The authors propose a novel method for doing so based on the Kaplan-Meier survival procedure, jointly considering two outcomes (death and recovery), and evaluate its performance by using data from the 2003 epidemic of severe acute respiratory syndrome in Hong Kong, People's Republic of China. They compare this estimate obtained at various points in the epidemic with the case fatality ratio eventually observed; with two commonly quoted, naïve estimates derived from cumulative incidence and mortality statistics at single time points; and with estimates in which a parametric mixture model is used. They demonstrate the importance of patient characteristics regarding outcome by analyzing subgroups defined by age at admission to the hospital.

The epidemic of severe acute respiratory syndrome (SARS) in 2003 showed how rapidly new infectious diseases can spread. Within a month of its recognition, SARS had spread worldwide, with epidemics occurring in China, Hong Kong, Taiwan, Vietnam, Singapore, and Canada (1). Although the worldwide case incidence remained relatively low (8,098 cases), relatively high mortality (774 deaths) resulted in widespread concern and alarm, sometimes to the point of panic, in the populations affected (2, 3). Coupled with the economic costs resulting from restriction of movement placed on the affected countries (4), the epidemic highlighted the need for a rapid international response to disease control. More recently, the outbreak of H5N1 influenza in birds in southeast Asia has again reinforced the potential for pandemic spread of newly emerging or evolving infectious agents.

During an outbreak of a novel or emerging infectious agent such as SARS, one of the most important epidemiologic quantities to be determined is the case fatality ratio—the proportion of cases who eventually die from the disease. This ratio is often estimated by using aggregate numbers of cases and deaths at a single time point, such as those compiled daily by the World Health Organization during the course of the SARS epidemic (5). However, simple estimates of the case fatality ratio obtained from these reports can be misleading if, at the time of analysis, the outcome is unknown for a nonnegligible proportion of patients. The estimates obtained during the SARS epidemic by dividing the number of deaths by the total number of reported cases were much lower (3–5 percent during the first few weeks of the global outbreak) than those obtained when appropriate statistical techniques were used and varied significantly between countries (6–8). Furthermore, as the epidemic progressed, these statistically naïve estimates falsely suggested a rise in the case fatality ratio (9), fueling the already high levels of public alarm in the affected populations.

In this paper, we show how to estimate the case fatality ratio during the course of an epidemic by adapting the Kaplan-Meier method for use with two outcomes—death and recovery. We illustrate this procedure with the complete SARS data from Hong Kong (all 1,755 cases) and compare the results with estimates computed from aggregate or cumulative numbers of cases and deaths at different stages of the epidemic and by using parametric mixture models (10, 11).

STATISTICAL METHODS FOR ESTIMATING THE CASE FATALITY RATIO

Simple estimators

Two simple estimators can be obtained for the case fatality ratio from aggregate case reports. If, at any given time point s, D(s), R(s), and C(s) denote the cumulative number of deaths, recoveries, and cases, respectively, then these estimators are

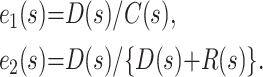The first estimator ignores the censoring that arises when patients remain ill in the hospital. The second implicitly assumes that the case fatality ratio for those who remain in the hospital will be similar to that for those whose outcome is known. Furthermore, for the second estimator to work reasonably well, the hazards of death and recovery at any time t measured from admission to the hospital, conditional on an event occurring at time t, should be proportional. Binomial confidence intervals for the underlying probability of death can be calculated from either estimate by using exact methods or a normal approximation, as appropriate.

Parametric mixture models

Parametric mixture models (or cure models) are commonly used to study situations in which a proportion of individuals never develops the primary outcome of interest (11, 12). In this setting, these individuals are those who recover from infection. Suppose that we have two terminal states (death and recovery) that occur with probability θ₀ and θ₁, respectively (where θ₀ + θ₁ = 1). We denote the conditional density that an individual will reach terminal state i time t after being admitted to the hospital by f(t|i) for i = 0,1. This conditional density can be modeled in a parametric form, for example, the gamma distribution. The parameters can be estimated by using maximum likelihood methods. An individual who dies at time t after admission contributes

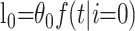to the likelihood. Similarly, an individual who recovers at time t after admission contributes

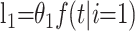to the likelihood. Finally, an individual who remains in the hospital at time t after admission contributes

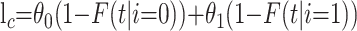to the likelihood, where 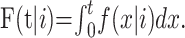Confidence bounds for the parameter estimates (including the estimate of the case fatality ratio 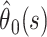made at time s in the epidemic) can be calculated by using likelihood ratio statistics.

Extension of the Kaplan-Meier method for two outcomes

We have two terminal states (death and recovery) whose hazard functions are denoted by h₀(t) and h₁(t), respectively, where t is measured from time of admission to the hospital, with associated (possibly incomplete) survivor functions

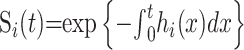and corresponding density functions 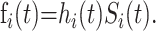If we let t_max(s) denote the maximum observed time from hospital admission to death or recovery that has occurred by time s in the epidemic, the probability of death (θ₀(s)) or discharge (θ₁(s)) at or before time s can be obtained from

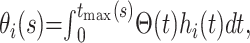where Θ(t) is the survival function if both endpoints are treated as a single composite endpoint. When the epidemic is complete, 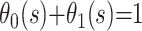and 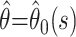is an estimate of the case fatality ratio. During the epidemic, however, the survivor functions for death and recovery, S_i(t), are incomplete; hence, 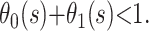It follows that our estimate of the case fatality ratio at time s should lie between 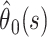and 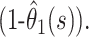To obtain an estimate, we must make an assumption about the pattern of deaths and discharges beyond the point of observation. A sensible assumption is that the remaining outcomes occur with the same relative probabilities as observed up to the time of analysis, so that our estimate of the case fatality ratio at time s is

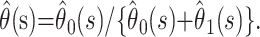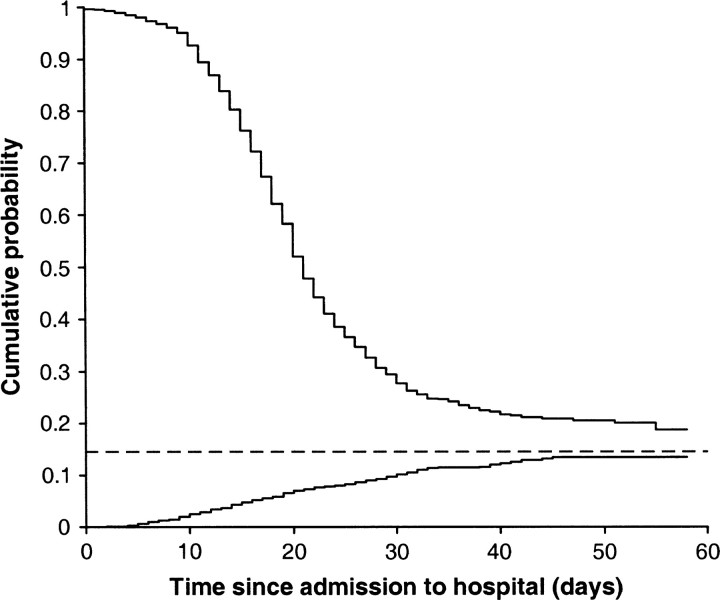
Figure 1 illustrates this approach.

FIGURE 1.

Illustration of the adapted Kaplan-Meier method for an epidemic showing 1 minus the estimated survivorship function for the time from hospital admission to death (bottom line) and the estimated survivorship function for the time from hospital admission to recovery (top line). When the epidemic is complete, these two curves meet. Before this time, they do not meet, and the case fatality ratio is estimated on the basis of the past pattern of deaths/recovery (dotted line).

At any time point s in the epidemic, the hazard function can be estimated by discretizing time into days and using the simple estimator 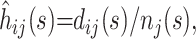where d_ij(s) is the number of events of type i on day j (where j is measured from time of admission to the hospital) and n_j(s) is the number remaining at risk j days after admission to the hospital.

To calculate confidence bounds at time s in the epidemic, we take the asymptotic variance of 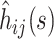to be 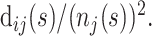To obtain a working approximation, we ignore the correlation between 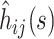and the 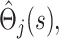treat the different 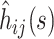as independent, and treat the 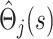as estimates of a single uncensored survival distribution (in which both states are treated as a single composite endpoint). Thus, the variance-covariance matrix of the vector 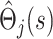is Ω(s), say, with elements

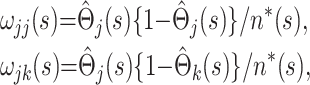where j>k and n*(s) is an effective total sample size, taken to be halfway between the total sample size and the total uncensored sample size at time point s in the epidemic. Alternatively, using Greenwood's formula (13),

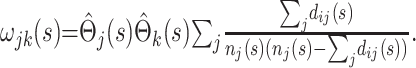Then, approximately by local linearization (the delta method),

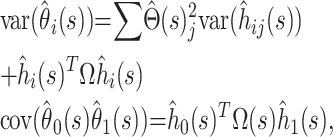where 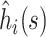is the column vector of the 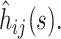When the delta method is used again, the variance of the estimator 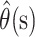is given by

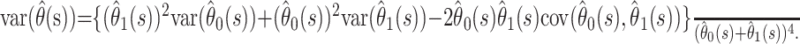Confidence bounds for 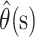can be calculated by using a normal approximation. However, when the case fatality ratio is low, it is better to calculate bounds by using a normal approximation on the logit scale. Thus,

DATA: HONG KONG SARS CASES

Our analyses were based on the complete record of the 1,755 cases of SARS in Hong Kong in 2003 defined according to the World Health Organization clinical case definition. Detailed epidemiologic descriptions of these cases are presented elsewhere (14, 15).

Patients are considered at risk from the date on which they are admitted to the hospital because this date is known at the time of analysis. An alternative would be to define time since onset of infection. However, using this definition could potentially bias results; those who have not yet been admitted to the hospital could not be included in the analysis. We therefore excluded from our analysis 124 cases admitted to the hospital prior to onset of infection (that is, nosocomial infection acquired after being admitted for other conditions), three cases whose discharge date was not known, and 22 cases whose final outcome was not known, reducing the number of cases to 1,606. In earlier analyses, we used the date of final discharge from a health-care facility as the date on which an individual was considered to have recovered (14, 15). However, some patients, particularly the elderly, were discharged earlier than this date from the acute care hospital to rehabilitation care facilities (mostly as a precautionary measure because the natural history of SARS was unknown at the time of the 2003 outbreak, particularly the infectiousness of those who had recovered). In the analyses presented here, we consider these individuals to have recovered (at the date on which they were discharged from the acute care hospital) since no additional individuals later died of SARS-related causes.

To compare the different estimators, we analyzed the data as they would have been observed at seven different time points in the epidemic (table 1). Prior to April 2, 2003, there was insufficient outcome data (on death and recovery) to estimate the case fatality ratio.

TABLE 1.

Summary of the number of cases and the degree of censoring at different time points for the epidemic of severe acute respiratory syndrome in Hong Kong, 2003

	Date
	April 2	April 9	April 16	April 23	April 30	May 7	May 14
No. of cases	925	1,201	1,367	1,489	1,547	1,582	1,607
% of observations censored	85.9	81.2	71.5	51.6	35.1	25.2	17.3

RESULTS

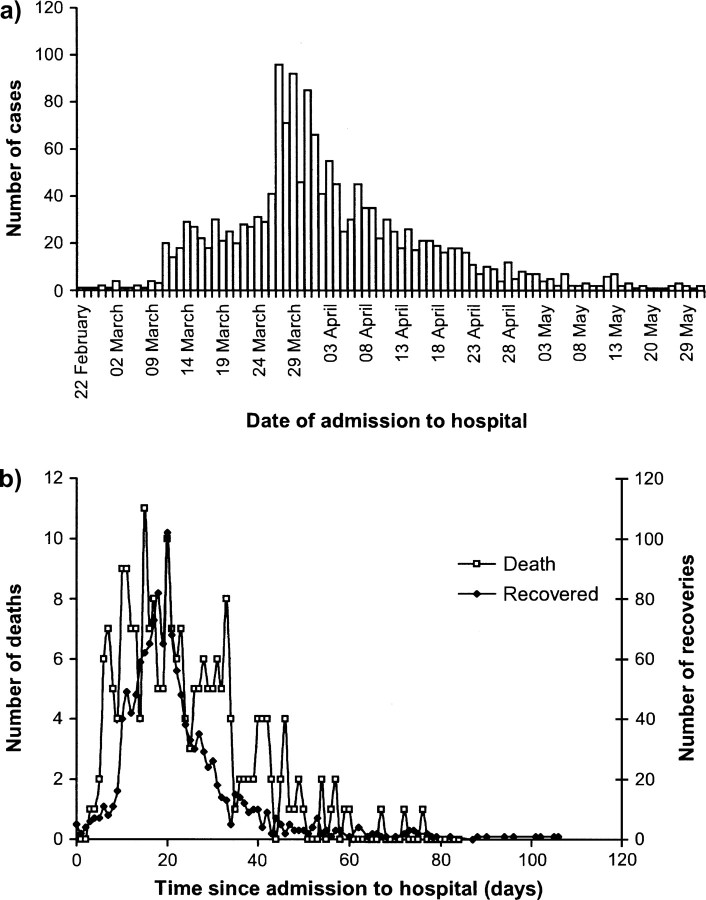
Figure 2a shows the time course of the epidemic in Hong Kong. The first case was reported on February 15, 2003, and the epidemic peaked 6 weeks later, on March 27, 2003. The mean duration of stay in the hospital over the course of the epidemic was 23 days for those who died and 23 days for those discharged from acute care hospitals (in most instances to a rehabilitation care facility). The latter duration was in part decided by clinical guidelines that determined the length of stay in the hospital prior to discharge and may not reflect the natural course of infection. Therefore, the final outcome for patients lagged behind their identification by approximately 3 weeks (figure 2b). Thus, when the case fatality ratio was estimated, the degree of censoring was heavy even at the peak of the epidemic. Table 1 illustrates this, with 86 percent of case outcomes remaining unknown even in the first week of April, when the epidemic had started to decline. Our analyses focus on estimating the case fatality ratio from this point onward; at earlier time points, there were too few deaths or recoveries to obtain reliable estimates.

FIGURE 2.

a) Incidence of cases of severe acute respiratory syndrome (SARS) in Hong Kong in 2003 by date of hospital admission; b) time from admission to the hospital to death/ discharge for the Hong Kong SARS cases.

The final case fatality ratio based on this sample was 14.2 percent, which is lower than the officially reported figure of 17.2 percent (302/1,755) for the full data set. This difference was due mainly to exclusion of the 124 patients infected after they had been admitted to the hospital for other conditions (that is, nosocomial infections), many of whom had multiple comorbidities and an older age distribution, thus leading to a much higher proportion of case fatalities than in the general sample.

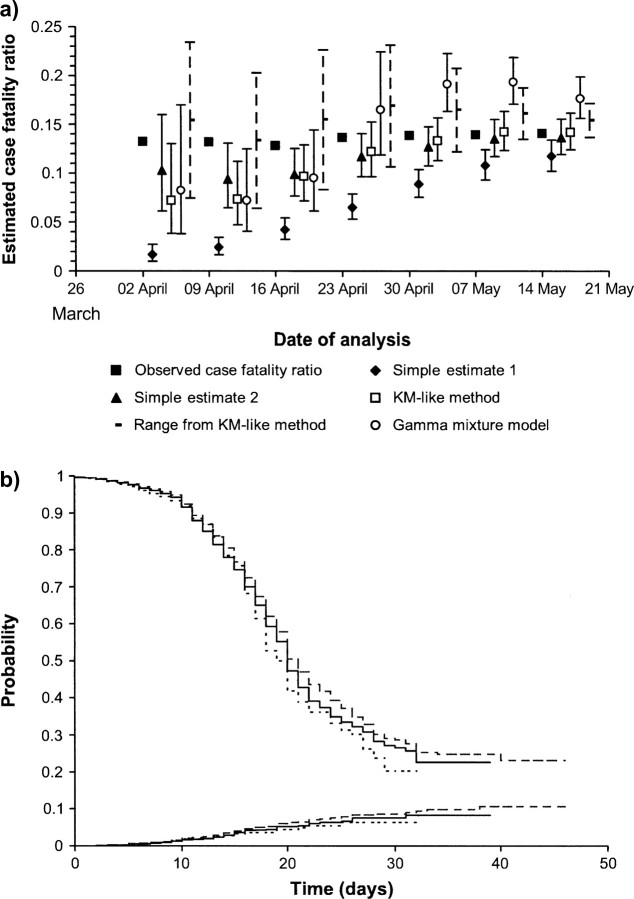
Figure 3a shows the estimates obtained by using the four methods and the case fatality ratio (eventually) observed for those individuals who had been admitted to the hospital by these time points. The observed case fatality ratio increased slightly over this time period, reflecting a change in the age distribution of the cases. Early in the epidemic, the first simple estimator based on the ratio of deaths to cases, e₁, underestimates the case fatality ratio because many cases remain in the hospital; hence, the numerator underestimates the total number of SARS-related deaths that will eventually occur in the sample.

FIGURE 3.

a) Estimates of the case fatality ratio and 95 percent confidence intervals over the course of the epidemic of severe acute respiratory syndrome in Hong Kong in 2003. Black square, case fatality ratio eventually observed for patients admitted to the hospital by the time denoted on the x-axis; black diamond, first simple estimate (deaths/cases); black triangle, second simple estimate (deaths/(deaths + recovered)); white square, adapted Kaplan-Meier (KM) method; black dotted line, range obtained from the adapted KM method; white circle, gamma mixture model. b) KM curves for the nonparametric survival (bottom lines) and discharge probabilities (top lines) obtained from the data sets on April 9 (short dashed line), April 16 (continuous line), and April 23 (long dashed line).

The second simple estimate based on the ratio of deaths of those for whom the outcome is known, e₂, is reasonable at most points in the epidemic. However, at one time point in the epidemic (April 16), the estimate is lower than that eventually observed, and the confidence intervals do not contain the observed case fatality ratio.

The parametric mixture model provides reasonable estimates of the case fatality ratio early in the epidemic (up to April 30). However, late in the epidemic, the estimates become higher that those eventually observed. This shift to higher estimates is due to a change in parameters and reflects the poor fit of the parametric distribution (in this example, the gamma distribution, but similarly poor fits are obtained with the Weibull and lognormal distributions).

The nonparametric Kaplan-Meier–based method provides reasonable estimates of the case fatality ratio when the degree of censoring is moderate (from April 30 onward, when the proportion of observations censored is less than 40 percent). However, early in the epidemic, the estimates are lower, and, at one of the time points analyzed (April 9), the confidence intervals do not contain the (eventually) observed case fatality ratio. By inspecting the Kaplan-Meier curves for the nonparametric survival and discharge probabilities obtained from the data sets between April 9 and April 23 (figure 3b), it appears that the estimated survivor functions changed between these dates. This unusual pattern in the data reduces estimates of the case fatality ratio obtained before April 23.

A conservative alternative to presenting estimates and associated confidence intervals early in the epidemic, when the degree of censoring is high and precision is low, could be to present the range 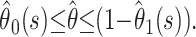Figure 3a shows that the observed case fatality ratio lies in this range. However, the precision of the range is low until very late in the epidemic.

In many situations, subgroup-specific estimates of the case fatality ratio are desired. For SARS, one of the most important factors determining the case fatality ratio is age (14, 15). Table 2 shows estimates of the case fatality ratio obtained for different age groups. The estimates obtained based on the data observed by two time points—April 23 and May 7—are given, along with the case fatality ratios eventually observed for all patients. The estimates obtained at the two time points during the epidemic demonstrate the same trend with age as for the final case fatality ratios.

TABLE 2.

Estimates of the case fatality ratio by age for the epidemic of severe acute respiratory syndrome in Hong Kong, 2003

Age group (years)	Final case fatality ratio	April 23			May 7
				Estimate	95% confidence interval	Estimate	95% confidence interval
≤30	0.4	0		0.5	0.0, 1.3
31–44	8.2	8.7	4.3, 13.1	8.2	5.4, 11.0
45–59	14.7	13.7	6.1, 21.2	15.1	9.7, 20.4
60–74	40.4	37.8	23.5, 52.1	43.1	33.3, 52.9
≥75	66.3	66.1	51.9, 80.3	74.9	64.3, 85.5

DISCUSSION

Our analyses show that two methods—the simple estimate of the case fatality ratio calculated for those whose outcome is known and the modified Kaplan-Meier method—adequately estimated the case fatality ratio during the SARS epidemic. The first method is appealing because of its simplicity and the ease with which it can be calculated. As case data accrue, particularly toward the end of the epidemic, the estimates will be close to those finally observed once the epidemic is complete. However, throughout the early and middle stages of the epidemic, this estimator ignored much of the available data. In contrast, the modified Kaplan-Meier estimator uses these censored data and hence will more rapidly detect changes in the case fatality ratio (for example, due to changes in treatment). However, when the degree of censoring is high (greater than 60 percent), as was true very early in the epidemic, it is more appropriate to present a range rather than a single point estimate. The parametric mixture model performed well early in the epidemic. However, toward the end of the epidemic, the estimates obtained were overly pessimistic because of a poor fit of the parametric model to the data.

Our findings demonstrated the considerable bias in the naïve estimate of the case fatality ratio calculated for all diagnosed patients. Although such methods are clearly easier to describe to policy makers and the public, important biases mean that the drawbacks will always outweigh the benefits and should not be used. The dangers of the naïve approach were evident in the SARS epidemic, where changes over time in the naïve estimates led some to conclude that the SARS infectious agent was evolving to be more lethal (8, 9) when in fact the changes in estimates were simply an artifact due to the estimation method. The public health impact of inaccurate estimates, resulting in misinformation, conflicting messages, or inconsistent intelligence, can and does exacerbate public alarm and even induce panic, which almost always accompany major outbreaks of infectious diseases such as SARS (2, 3).

One of the major challenges encountered during the SARS epidemic was understanding the reasons underlying the variation in case fatality ratios reported for different countries. A large part of this variation could in retrospect be attributed to difficulties in standardizing the definition of a SARS case and in assigning cause of death. In particular, it is clear that comorbidities such as diabetes mellitus, coronary artery disease, hypertension, and chronic obstructive pulmonary disease significantly increased the case fatality ratio, particularly in the elderly (16–21). In addition, a change in the case mix over time (for example, in the age distribution of patients) could be misinterpreted as a change in virulence of the pathogen. Furthermore, using data on hospitalized cases, as presented here, could potentially overestimate the underlying case fatality of infection if individuals with less severe or no symptoms of disease do not present at the hospital. Sensitive and specific serologic tests used among contacts of SARS cases (22), as well as in the wider community (23), have found very few previously unidentified SARS infections, suggesting that the case fatality ratio per hospital admission, as estimated here, was essentially equivalent to the case fatality ratio per case of infection. However, this may not be true, in fact usually is not, for other epidemics.

The methods presented here are applicable to any disease for which the final outcome is not known for a proportion of patients. The underlying assumptions for the different methods may determine which method is appropriate in different settings. For the SARS epidemic, the nonparametric, modified Kaplan-Meier method provided the most reasonable estimates over the course of the epidemic. With this method, one important assumption is that the relative probability of death and discharge after the time of analysis is similar to that up to the time of analysis. This assumption could be violated if the mean duration from hospital admission to death is substantially shorter than the mean duration from hospital admission to discharge and results in biased estimates of the case fatality ratio. In such settings, parametric or semiparametric cure models may be more appropriate.

Several other factors can complicate estimation of the case fatality ratio, even for a well-known disease. These factors include uncertainty about case definition, case ascertainment (particularly if some cases are asymptomatic or in difficult-to-reach populations), and the impact of treatment on identification of cases. In addition to using appropriate statistical methods, analyses should therefore be undertaken to determine the sensitivity of estimates to these factors.

Finally, one of the most important factors to evaluate in an epidemic is the effectiveness of treatments. With the emergence of a previously unknown pathogen or illness, particularly if the case fatality ratio is high, it is not often possible to conduct randomized trials of new treatments. Without such trials, evaluation of treatment must rely on evaluation of any decrease in the case fatality ratio as treatment evolves (16, 19, 20, 24–27). Inaccurate estimates of the case fatality ratio will therefore adversely affect clinical practice and therapeutic decisions. For example, clinicians, when faced with a novel, unfamiliar disease, are likely to experiment with different management interventions based on evolving estimates of case fatality as the definitive clinical outcome of interest.

In future epidemics, careful estimation and analysis of any trends in the case fatality ratio could be used to evaluate the effectiveness of new treatments as they are introduced. In such a situation, we recommend that the case fatality ratio initially be defined by the range from the modified Kaplan-Meier method as shown here. As data accrue, the case fatality ratio can be obtained more precisely by using the point estimate and associated 95 percent confidence interval and compared with estimates obtained from parametric cure models (14). Throughout the epidemic, analyses should be undertaken to test the sensitivity of estimates to variations in case definition and ascertainment as well as to test for the significance of case mix (for example, by age). To help readers and public health practitioners apply this method, the Appendix provides information about a macro file using Stata statistical software (Stata Corporation, College Station, Texas) that calculates all four estimates for a given data set.

APPENDIX

A Stata macro that calculates all four estimates for any given data set can be downloaded from the Statistical Software Components archive (hosted by the Department of Economics at Boston College (http://econpapers.repec.org/software/bocbocode/)) by typing the command ssc install casefat from within Stata when connected to the Internet. The macro requires indicator variables for death and recovery and the event time. It also includes options to set the time at which a person becomes at risk, to set a time at which the analysis is undertaken, to calculate the variance-covariance matrix using Greenwood's formula (11), and to construct confidence intervals on the logit scale. Further details are provided in the help file associated with the macro.