Information theory applications for biological sequence analysis

Abstract

Information theory (IT) addresses the analysis of communication systems and has been widely applied in molecular biology. In particular, alignment-free sequence analysis and comparison greatly benefited from concepts derived from IT, such as entropy and mutual information.

This review covers several aspects of IT applications, ranging from genome global analysis and comparison, including block-entropy estimation and resolution-free metrics based on iterative maps, to local analysis, comprising the classification of motifs, prediction of transcription factor binding sites and sequence characterization based on linguistic complexity and entropic profiles. IT has also been applied to high-level correlations that combine DNA, RNA or protein features with sequence-independent properties, such as gene mapping and phenotype analysis, and has also provided models based on communication systems theory to describe information transmission channels at the cell level and also during evolutionary processes.

While not exhaustive, this review attempts to categorize existing methods and to indicate their relation with broader transversal topics such as genomic signatures, data compression and complexity, time series analysis and phylogenetic classification, providing a resource for future developments in this promising area.

INTRODUCTION

Information theory (IT) addresses the analysis of communication systems, which are usually defined as connected blocks representing a source of messages, an encoder, a (noisy) channel, a decoder and a receiver. IT, generally regarded as having been founded by Claude Shannon (1948) [1, 2], attempts to construct mathematical models for each of the components of these systems.

IT has answered two essential questions about the ultimate data compression, related with the entropy of a source, and also the maximum possible transmission rate through a channel, associated with its capacity, computed by its statistical noise characteristics. The fundamental theorem of IT states that it is possible to transmit information through a noisy channel (at any rate less than channel capacity) with an arbitrary small probability of error. This was a surprising and counter-intuitive result. The key idea to achieve such transmission is to wait for several blocks of information and use code words, adding redundancy to the transmitted information [3, 4].

Although IT was first developed to study transmission of messages over channels for communication engineering applications, it was later applied to many other fields of research. Nowadays, IT is not a mere subset of communication theory and is playing a key role in disciplines such as physics and thermodynamics, computer science (through the connections with Kolmogorov complexity), probability and statistics [5, 6] and also in the life sciences. In fact, living organisms are able to process and transmit information at many levels, from genetic to ecological inheritance mechanisms [7], which frames IT as a broad research ground that crosses many disciplines.

Over three decades ago, in a seminal book [8], Lila Gatlin explored the relation between IT and biology and the applicability of entropy concepts to DNA sequence analysis, following previous work in the 1960’s [9, 10]. This was one of the first attempts to analyze DNA from an IT point of view, further pursued during that decade. Interestingly, Claude Shannon’s PhD thesis, ‘An Algebra for Theoretical Genetics’ in 1940, precedes his IT founding articles.

Following Gatlins’ work, other authors have proposed methods based on IT to address problems related with data coming from molecular biology, ranging form the analysis of mitochondrial sequences [11] to the relation between information content with evolutionary classification [12]. In 1996, Román-Roldán and colleagues reviewed methods for DNA sequence analysis through IT ([13] and reference therein), highlighting the renewed interest in the area, owing to the increase of data generated from genome projects.

Recently, other reviews have provided a broader view of the area, setting the ground for new developments. In particular, excellent surveys by Adami [14], Hanus [15] and Battail [16] describe topics in molecular biology where IT has provided valuable solutions. More recently, an IEEE special issue was fully dedicated to IT in molecular biology and neurosciences [17], which illustrates the growing interest in these cross-disciplinary efforts.

Sequence analysis has greatly benefited from methods and concepts derived from IT. For example, the notion of entropy, which was first used to study the thermodynamics of gases, was later defined as a measure of the uncertainty associated with a probabilistic experiment and applied to estimating sequence randomness. In [18], entropy and information definitions across disciplines were explored, comparing their meaning in thermodynamics (Boltzmann’ principle) and statistics (Fisher information matrix).

The notion of complexity is also transversal and connected with the entropy of a source. The concept of physical complexity of a sequence, as proposed in [14, 19], refers to the amount of information that is stored in that particular sequence about a given environment, i.e. for genomes, this ‘niche’ is the one in which the sequence replicates.

Compression is also related with Shannon’s entropy definitions and was also applied to biological sequences. There is a clear association between these concepts: a sequence with low entropy (high redundancy) will, in principle, be more compressible and the length of the compressed sequence gives an estimate of its complexity, and consequently, of its entropy [20]. The drawback of this method is its dependency on the compression procedures, which might fail to recognize complex organization levels in the sequences. Although data compression is closely related with IT applications, a complete review of this topic is out of the scope of this work; see other surveys on average mutual information (AMI) applications [21], Kolmogorov complexity-based features [22] and a comprehensive review by Giancarlo et al. [23] for more details.

The relation with Linguistics and Semiotics is also explored elsewhere [24, 25], and aspects related with coevolution and phylogenetic analysis are descried in [26].

Interestingly, a significant set of these methods comprises an alignment-free feature. These methodologies have grown in the past decades as powerful approaches to compare and analyze biological sequences, constituting alternatives to alignment-based techniques (see [27, 28] for general reviews). For example, several dissimilarity measures can be derived from IT concepts (such as Kullback-Leibler discrepancy (K-LD), mutual information and complexity) leading to alignment-free methods for genome classification.

In this context, this survey is focused on IT applications for biological sequences analysis concentrating on those that simultaneously encompass an alignment-free feature. It also tries to establish common points and highlight similar characteristics so to bridge both methodologies and explore its synergy.

The structure of this review reflects the interconnectivity between the subjects and, to some extent, corresponds to a personal view of the area. The concepts of Rényi and Shannon’ entropy, Kolmogorov complexity, time-delayed mutual information and autocorrelation functions are clearly interconnected. Another difficulty encountered was to categorize the methods and their applications in a logical way, giving the clear intersection and overlap between methods and application. This is reflected in the final structure of the review, which attempts to take an application-driven goal-dependent approach. Therefore, the sections are organized in global analysis and comparison (block-entropy estimation and resolution-free metrics based on iterative maps), local analysis (classification of motifs, prediction of transcription factor binding sites and sequence characterization based on linguistic complexity and entropic profiles), high-level associations merging DNA, RNA or proteins with sequence-independent properties. Finally, communication systems theory models for the description of information channels are also briefly mentioned.

METHODS

Biological sequences representation

A sequence X can be represented as a succession of N symbols from a given alphabet A, of length r, X = s₁ , … ,s_N, s_i ∈ A, i = 1, … ,N. For DNA, the alphabet A is composed by the nucleotide symbols representing the 4 bases A = {A,C,G,T}, and for proteins, each symbol of this alphabet represents one of the amino acids. For natural language texts, A is the set of all possible characters in each idiom. A segment of L symbols, with L ≤ N, is designated an L-tuple (or L-word, L-plet, L-mer or L-gram). The set 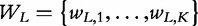consisting of all possible L-tuples obtained from the alphabet A has K = r^L elements.

The identification of L-tuples in the sequence X can then be object of counting occurrences with overlapping 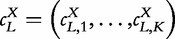, which can be further normalized by the total number of strings. The obtained vector of L-tuple frequencies is thus defined by 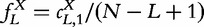and will be pervasively used. For convenience, the frequency vector f is sometimes indexed by the L-tuple it represents .

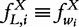Several other sequence representations exist [29], mapping strings into vectorial spaces. See [30] for a comprehensive review on sequence representation, covering DNA, RNA and proteins.

It is also common to model sequences using time series framework, in particular, borrowing concepts from the field of stochastic processes, e.g. Markov Chain models, and dynamic systems. This has been a ubiquitous representation in the biophysicists’ literature, namely to study long- and short-range correlations in DNA and unraveling periodic properties and correlation structure of biosequences. Comprehensive reviews of the field include [31, 32], where a review of information-theoretical aspects from Shannon and Rényi entropy to Kolmogorov complexity are revisited, along with DNA sequence periodicity evaluations, and [33], which provides a general introduction to spectral methods for genome analysis. DNA spectra based on maximizing Shannon’s entropy are shown to be effective in characterizing sequence periodicities [34], illustrating the connection between these topics.

DNA representation through iterated function systems, namely chaos game representation (CGR) [35], was proposed as alternative mappings and later extended to higher-order alphabets [36] or alternative geometries [37]. Formally, each symbol mapping x_i ∈ ℜ² of an N-length DNA sequence X is given as follows:

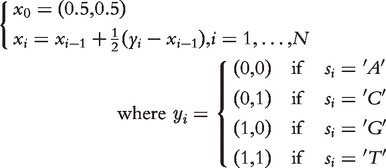(1)

Besides its appealing graphical support and generalizations, CGR was recently proven to be an efficient representation for string algorithms [38] such as longest common extension queries, solved in constant time.

CGR properties and generalizations have been extensively applied as a consequence to the natural development of alignment-free techniques for sequence comparison [27, 28] and will be reviewed here only in the context of its IT-framework application.

Entropy definitions and properties

Entropy is a measure of the uncertainty associated with a probabilistic experiment. For a discrete random variable X taking values in {x₁, x₂, … , x_M} with probabilities {p₁, p₂, … , p_M}, represented as P(X = x_i) = p_i, the Shannon’s entropy H_Sh of this experiment is a functional of the distribution of X, and is given as follows:

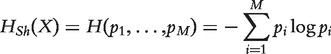(2)

Shannon’s entropy formulation can be interpreted as the minimum number of binary (yes/no) questions necessary, on ‘average’, to determine the output of one observation of X. This formulation can also be interpreted in terms of expected values, i.e. . The Shannon’s entropy is a nonnegative quantity and its definition can be axiomatically derived [3]. It can be shown that 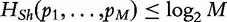with equality if and only if all p_i = 1/M, which means that the situation with the most uncertainty or with the highest entropy occurs when all possibilities are equally likely, thus ascertaining a maximum value for H_Sh(X).

Other important notions related to the entropy definition include joint, conditional and relative entropy of two discrete random variables X and Y, with joint probability function p(x_i,y_j) = P(X = x_i, Y = y_j) = p_ij, i = 1, … ,M and j = 1, … ,L. These measures further deepen the former definition and extended it to the multivariate case, thus permitting the application of new techniques to distribution function comparison.

The relative entropy or K-LD of the probability mass function p(X) with respect to the mass function q(X) is defined as follows:

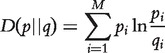(3)

The Mutual Information between two random variables X and Y—or the information conveyed about X by Y—is defined as follows:

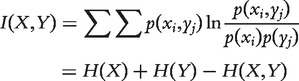(4)

Mutual information is a special case of the relative entropy because 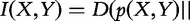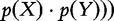. Following the properties of D(p||q), the mutual information is 0 if and only if p(X,Y) = p(X)ċp(Y), which is the definition of independence between variables X and Y. Therefore, I(X,Y) is measuring the ‘dissimilarity’ between those variables as assessed by their ‘dependence’. Additional results relating these measures are proven elsewhere [3, 4].

The Rényi formulation appeared as a generalization of the Shannon’s measures [39, 40]. The Rényi entropy of order 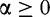, , 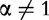H_α is defined both for discrete p and continuous f(x) probability functions:

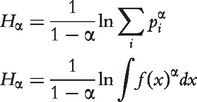(5)

Shannon’s entropy is a special case of Rényi’s when . When α is 0, Renyi entropy corresponds to logarithm of the size of the support of set and converges to the min-entropy H∞ when a→∞. Properties of Rényi-derived functionals for different probability distributions are further described [41].

The notions of complexity and entropy are extensively presented elsewhere [4, 42] and only briefly exemplified in the reviewed applications.

APPLICATIONS AND RESULTS

Global analysis and comparison

The first approach to measuring sequence entropy was through calculating the entropy of L-tuple distributions across the target sequences. This corresponds to estimating the probabilities of each L-tuple using all the frequencies 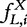and applying directly Shannon’s equation [Equation (2)]. These ‘block entropies’ (or L-gram entropies) can be interpreted as the degree of variability of L-tuples across the whole sequence, thus representing a global overall measure of randomness.

This section will briefly describe some methods that use L-tuple distributions to estimate a global entropic measure for the sequence, which is related with its randomness, complexity and compressibility.

There is a strong rational for using these features because the introduction of the ‘genomic signature’ concept in the 90s [43], following previous analysis on oligonucleotide over- and underrepresentation [44]. The key finding was that dinucleotide vectors constituted a signature of an organism, i.e. there are significant differences between intra- and interspecies odds ratio based on normalized 2-tuple frequencies. The odds ratios 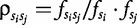represent the dinucleotide bias of 2-tuples. Interestingly, this is closely related with probabilistic independence and mutual information between the distributions. Extensions to these odds ratios may serve for better understanding of different properties of genomes through evolution [45].

Block entropy and divergence

Gatlin’s pioneer work [8] proposed to use L-tuple frequencies to estimate a sequence feature named divergence. The first divergence D₁ is defined as 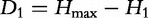, corresponding to the difference between the maximum nucleotide (1-tuple) entropy H_max = 2 bits and the observed 1-tuple or nucleotide entropy. This was used in several assessments on GenBank data [13, 46].

Another evaluation aimed at estimating block entropies H_L, which measure the average amount of uncertainty of words of length L, or their normalized values H_L/L. The conditional entropies 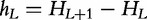were also proposed as a genomic characteristic that gives the uncertainty of the L + 1 symbol given the preceding L symbols. One result that was obtained through these definitions was that proteins are fairly close to random sequences, with entropy reductions in the order of just 1% [47, 48]. Similar results were obtained for bacterial DNA, which may be associated with the subtle balance between error and fidelity because higher entropy translates into more information holding capacity.

To evaluate the distribution of this divergence as to assess hypothesis concerning randomness, surrogate sequences were simulated and their corresponding values calculated. These artificial DNA sequences were obtained through random shuffles of the original L-tuple frequencies and allowed their comparison, showing that up to triple shuffling the values of h_L were statistically different [49].

High-order divergences based on block entropies can be estimated directly from L-spectra [50, 51]. These spectra correspond to histograms of L-mer occurrences, for which statistical approximations for random sequences can be derived, along with the evaluation of relative spectral widths and reduced Shannon information. The application of these measures to Pyrobaculum aerophilum and Escherichia coli (which have entropies closed to the maximum value) were able to distinguish them from random surrogates.

Extensions to Shannon’ entropy were also tested, namely using Rényi and Tsallis definitions [52], and applied to >400 chromosomes of 24 species, leading to reasonable clusters.

Block entropies can also be used for comparisons of different features such as coding versus noncoding regions, represented as a sequence of binary values (0 and 1) for each distinct region of the genome [53]. The authors used nonoverlapped or lumped L-grams and compared artificially generated sequences with human chromosomes and several organisms. The results obtained are compatible with previously proposed evolutionary mechanisms.

Estimation problems

In practice, one of the major problems faced when calculating high-order block entropies is the finite size sample effect [54], due to estimation bias [55], which causes a systematic underestimation for increasing L. For example, if L = 16, the total number of possible 16-mers is 4¹⁶ ≈ 4.2ċ10⁹, exceeding the size of the human genome and hampering the accurate estimation of this quantity.

Several correction and estimation methodologies were proposed to address this problem, [56–61], although it is expected that the main sample effect always persists for some higher word length. The theoretical limits of this measure and impact on this measure of existing repeated structures were also analyzed [62].

The evaluation of these quantities on genomes for several organisms such as E. coli and Saccharomyces cerevisiae was addressed [63]. Multispecies gene block entropies can also be estimated using Self-Organizing Maps [64], based on feature selection.

Many compression techniques have also been developed to estimate sequence entropy and complexity [60, 65]. Some applications include [66–68].

More theoretical approaches based on compression were also proposed, to cope with undersampled regimes when the alphabet and sample sizes are comparable ([69] and references therein). Alternative methods based on thorough descriptions of the statistical and convergence properties of different estimators [70] might also support future applications in DNA and proteins.

CGR-based entropies

Departing from the key idea of using L-tuple frequencies, several analyses were also conducted using directly CGR. In fact, these maps, besides providing a visually appealing description of the sequences, generalize all L-tuple characteristics and are therefore adequate to be applied to whole genomes.

The close relation between CGR and genomic signatures previously presented was strongly highlighted by Deschavanne and colleagues [71]. The pictures representing whole genomes were qualitatively the same as those obtained for short segments, which supports the idea of genomic signatures as pervasive, species-specific features and qualify CGR maps as a powerful tool to unveil it.

One option was to use histograms of the frequencies [72, 73] where, instead of using the frequencies directly, the authors proposed to estimate histograms of the number of CGR sub-quadrants m that have a given density. Therefore, what it is being assessed is a measure of the distribution homogeneity. The comparison of human beta globin genes with random sequences presented significant differences independent of the number of sub-quadrants used. The authors defined entropic profiles in this article as the function of the entropy versus m.

Using CGR sub-quadrant frequencies, although appealing, translates in practice into calculating block entropies depending on a fixed resolution L. To overcome this fact and aiming at defining a resolution-free estimate of the entropy, Parzen’s window method with Gaussian kernels was applied to CGR [74]. In this work, the genome entropy is defined as the Rényi quadratic entropy (α = 2) of the probability density estimation of the CGR map. The results have shown that this measure is in accordance with expected values, for example, sequence ATCG … ATCG (repetition of the motif ATCG) has the same entropy of a random sequence of length 4. Other results on Markov Chain derived sequences of different orders and random surrogates are also consistent.

Sequence comparison

Measures based on information-theoretical concepts have been applied widely to compare sequences in an alignment-free context [27, 28]. Often, these applications seek to define dissimilarities to classify and/or cluster genomic strings, a fundamental aspect in phylogenetic reconstruction studies. In this regard, mutual information and compression-based approaches have provided solid results that match most of the known molecular evolutionary events.

The measures include dissimilarity estimations via compression ratios [75] Kolmogorov [76] and Lempel-Ziv–based complexities [77], compared in [78].

Entropy concepts such as mutual information are a key feature to comparison tasks. In particular K-LD is a popular choice as an alignment-free technique [79]. Extensions to K-LD were also applied to classify DNA from E. coli and Shigella flexneri threonine operons and search sequence databases [80]. A symmetrized K-LD version (SK-LD) proposed in [81] was tested for the classification of shuffled open reading frames sequences, demonstrating its higher performance in the presence of genome rearrangements when compared with BLAST.

A mixed approach combining L-mer ranks and entropy concepts was proposed by [82]. The key idea of the information-based similarity index is to compare L-mer ranks of two sequences weighted by the relative Shannon entropy, which corresponds to a weighted city-block dissimilarity on the rank-order. Zipf and redundancy analysis using rank distributions had already discriminated between coding and noncoding regions [83]. Zipf’s approach is based on calculating the histograms of word occurrences in linguistic texts and ranking them from most to less frequent. One remarkable feature in natural languages is the Zipf’s law, where a linear relation of this function in double logarithmic scale is found. The results obtained by Mantegna and colleagues [83] show that, by applying Zipf’s regression, noncoding regions are closer to natural languages in terms of regression parameters and exhibit more redundancy than coding regions, as measured by block entropies. The application to SARS coronavirus illustrates the potential of combining IT and rank-order statistics for genomic analysis.

Local analysis, time series and entropic profiles

In this section, the aspects related with local features of sequences will be reviewed, i.e. related with the information and properties of specific positions, motifs and regions (e.g. splicing, transcription factors binding sites (TFBSs), coding versus noncoding, respectively). Overall properties such as time series correlations and sequence profiles (linguistic and entropic) will also be reviewed.

TFBS and motifs

The analysis and comparison of TFBS is probably the most successful application of IT in molecular biology [84, 85]. A TFBS motif is usually represented as a matrix such as Position Frequency Matrix (PFM), which can represent a probabilistic model for the binding site. These sites can be thus interpreted as sources of symbols (nucleotides) whose emission probabilities are usually estimated through alignment.

In the pioneer work by Schneider [86], the relative entropy and information content of the binding site were derived, as a conservation measurement of the TFBS. If a nucleotide is highly conserved across several promoters, its relative entropy will be higher. Likewise, for nonconserved sites, this value will be close to zero. This can be visualized through sequence logos [87]. In practice, these inputs can be multiple sequence alignments of promoter sequences [88], from which per site redundancies are calculated as to characterize and analyze the TFBS.

The literature on TFBS identification and characterization through IT methodologies is now vast [89, 90] and will not be fully covered here—see [84] for a recent comprehensive review on this topic. A brief overview is warranted, covering alignment-free methods.

Several methods based on IT have been applied to model TFBS, such as using the proposed minimum transferred information between the site and the transcription factor during the binding process [91], incorporating position interdependencies. Also the motif characterization going beyond Information Content and Maximum a posteriori estimations were explored [92] to infer regulatory motifs in promoter sequences. IT models allowed extracting E. coli Fur binding sequences [93]. By also including in the mutual information estimation structural properties of DNA and amino acids, the prediction of their interaction can be improved [94].

Rényi entropy was also applied in this context, to create models accounting for nucleotide binding sites transition in E. coli, T7 and λ-organism [95, 96], to compare Rényi- and Shannon-based redundancies in LexA Lambda Cro/CrI, T7, ribosome, HincII and T7 binding sites [97] and evaluate TFBS through its differential counterpart [98].

Several alignment-free methods for TFBS can be found in the literature. For example, conservation-based motif discovery algorithms were shown to be competitive in speed and accuracy [99]. Other methods for TFBS prediction that neither require pre-aligned sequences nor the construction of a position weight matrices (PWMs) exist, for example the SiTaR tool [100]. Alignment-free methods for comparing TFBS motifs were also proposed recently [101], where Kullback-Leibler dissimilarities based on L-mer frequency vectors allowed to retrieve significant motifs and compare TFBS and PFM, illustrating the advantages of using hybrid techniques. Potential recognition sites for replication initiation in 3′UTRs and 5′UTRs of classical swine fever virus strains were obtained through iteratively maximizing the information content of unaligned sequences [102].

Other relevant applications of IT for motifs/regions characterization beyond the TFBS scope exist. For example, ab initio exon recognition can be performed through the minimization of Shannon entropy over a set of unaligned human sequences containing a structured motif [103]. Splicing recognition and the effect of mutations can also be predicted through the sequence information content [104].

The analysis of motifs for genome characterization and fragment classification also benefits from IT methodologies. The mutual information between an L-tuple distribution and a set of genomes can be used as a feature selection method for support vector machine classification [105]. By maximizing the conditional entropy it is possible to find the best L-tuples in terms of discriminative power in fragment classification for taxonomy in metagenomics studies. The authors show that this criterion performs well on the phyla level for a significant set of bacterial genomes.

The entropy of genomes is also closely related to word statistics and coverage [106], which can be used for the detection of nonhuman DNA samples. In fact, specific, substrings or motifs and their distribution strongly characterize a genome, which has clear connections with IT concepts, as illustrated.

Time series and correlation properties

Time series analysis methodologies have a long tradition of applications to the study of biological sequences. This allowed to estimate long- and short-range correlations in sequences, to analyze internucleotide distances and to evaluate the correlations when specific gaps of length k are considered. The key idea is to estimate high-level periodicities, which may have relevant biological significance.

Internucleotide distances d_i are vectors that collect the gap lengths between two consecutive occurrences of nucleotide i [107]. Their distributions univocally characterize a given DNA sequence and are shown to be species-specific, thus constituting a genomic signature. Extension to L-tuple internucleotide distances, coupled with Shannon’s entropy, can provide dissimilarity measures for gene clustering [108].

Other type of k-gap correlation was proposed, based on discrete autoregressive processes of order p, DAR(p) [109]. The profiles of the estimated parameters, representing autocorrelations, are shown to be species-specific, thus also conveying a genomic signature concept, that can be further used for classification purposes [110]. In fact, the clustering tree obtained for 125 chromosomes of eight eukaryotic species reveals good agreement with phylogenetic relationships.

Profiting from gap-based distributions, new definitions have been proposed. The mutual information function I(k) quantifies the amount of information that can be obtained from one nucleotide s about another nucleotide t that is located k nucleotides downstream from s [111]. To filter for period-3 oscillations in coding regions, AMI values can be computed. AMI distributions are shown to be different in coding and noncoding DNA without prior training on species-specific genomes.

AMI was later applied to bacteriophage-λ genome in [112], where the authors compare linear and nonlinear model approximations for the prediction of nucleotide position t + τ based on previous lagged symbols. AMI was also successfully used to classify Oryza sativa coding sequence (CDS), complementing hidden Markov models and Neural Networks methods [113].

Interestingly, AMI is shown to be a species-specific feature and also is pervasive for short segments [114], which is in close connection with the genomic signature concept previously defined [115]. In fact, the estimation of AMI profiles (obtained for different gap values k) of genomic sequences of eukaryotic and prokaryotic chromosomes, as well as viruses subtypes, allowed to extract and classify DNA fragments and also cluster genomes in a consistent way, which supports AMI as a key feature for species characterization [114].

Linguistic complexity and entropic profiles

Another type of analysis related with entropy and complexity concepts for local analysis was developed. In these studies, the characterization of the ‘linguistic complexity’ of genomes is related with the notion of self-repetitiveness [48, 116–118]. Linguistic complexity is estimated by using a sliding window and assessing the ratio of the number of all present L-tuples over the total number of possible words. In highly repetitive regions, the fraction will be low because a small percentage of all possible substrings form the dictionary is used. Likewise, regions with more distinct L-tuples have high variability and, therefore, higher entropy.

This alignment-free methodology was shown to be useful to determine new biological features in S. cerevisiae yeast chromosomes and to filter regular regions [116]. In [117], linguistic complexity was calculated for Haemophilus influenzae complete genome in linear time using suffix trees, illustrating its efficient implementation.

Linguistic complexity was later compared with Pearson’s chi-square tests, complexity estimation by Wootton–Federhen and symbol Shannon entropy [119] giving rise to different profiles for genes and pseudogenes and showing that the regions around the start codon have the most significant discriminant power.

The analysis of vocabulary use can support the comparison between genome regions. The notion of topological entropy H_top [120] is based on analyzing, for a given sequence with length N, what is the proportion of L-tuples that appear, with a maximum of N − L + 1. If all the possible sub-words are present, H_top = 1; H_top is approximate zero if the sequence is highly repetitive, i.e. contains few sub-words. The authors apply this measure to human exon–intron comparison, namely for chromosomes X and Y, obtaining larger topological entropies for introns than for exons, which contradicts previous studies [83]. The discrepancies observed might be related with the distinct definitions used: topological entropies are based on truncated words set space to avoid finite sample effects and, therefore, the results may not be directly comparable and should be further elucidated.

The number of shared L-tuples between two genomes (relative to the smaller L-gram set) and spectral rearrangements of the corresponding matrixes can be used to define clusters of positions [121]. These measures also define profiles of conserved regions in whole genomes in an alignment-free way.

Another option to analyze the homogeneity of the frequency vectors along the genome is to partition the sequence in blocks of length B, calculate the entropy of each block and then estimate the entropy of all these entropies, what the authors called ‘superinformation’ [122]. By spanning different nonoverlapping window lengths B, the authors where able to distinguish between coding and noncoding regions in human chromosomes, namely TTC34 gene (chr1).

Another measure of sequence homogeneity across CDS of the yeast genome was also assessed [123], based on partitioning the sequence into blocks and estimating all their codon probabilities, which were further used to calculate its Shannon’s entropy. Codons that are distributed uniformly will have entropies close to one. The analysis of 16 S. cereviseae chromosomes was able to cluster amino acids in terms of structural properties.

The presented measures have subjacent a resolution or parameter indicating the specific block/window length. By using CGR maps and previous work on Rényi entropies, local estimation of the probability density function were used as a proxy for the local complexity of the sequence. In fact, highly populated CGR quadrants correspond to overexpression of a given suffix. Previous work on CGR (local) genomic signature characteristics allowed to correctly detect horizontal transfer in bacterial genomes [124].

To overcome domain problems when using Gaussian kernels in CGR maps (which extend beyond the unit square), new functions based on cuboids were proposed [125], which later allowed the estimation of ‘Entropic Profiles’ (EP) [126]. These EP are defined for each position in the sequence and, although conveying local information, take into account, by definition, global features. This property can be explored for data mining procedures and motif finding. By spanning the parameter space, one can also estimate the local scale of each position, i.e. the suffix length for which that position is most statistically significant. New efficient implementations are now available [127, 128], allowing the study of whole genomes.

High-level correlations

Biological sequences can be interpreted in a broader sense by defining possible transformations of the original DNA, RNA or protein sequences. This section will describe some work on these high-level mappings, where new recoding and alphabets are used or partial information, such as single nucleotide polymorphisms (SNPs), are the basis for the analysis and comparison. This section will also address topics where sequence features are connected with nonstring characteristics, such as phenotypes and protein–protein interaction (PPI) network connectivity.

The relation between the decrease of structural entropy associated to component compartmentalization in eukaryotic cells was analyzed recently [129]. In this work, thermodynamical entropy of molecules is normalized by the Shannon’s entropy loss associated to the presence of a specific DNA sequence with length n, ΔS_DNA = −2n bits, thus trying to bridge the two concepts.

The analysis of molecular structures and binding can also be recoded as strings, where each atom is translated onto a symbol related to its structure in the molecule. From this representation, molecular descriptors based on Shannon’s [130] and Rényi Entropy can be derived [131], useful for virtual chemical screening and drug discovery.

The goal of gene mapping is to identify DNA regions that are responsible for particular observed traits or phenotypes. The application of IT to estimate these relationships is typically based on identifying sets of SNPs or markers, coded as strings, and a set of phenotypes (e.g. case versus control individuals) and then calculate the mutual information between both distributions, in a given sample or population. If the two are independent, the mutual information is zero and no information is conveyed by a given SNP for that condition. The method allowed estimation of positions (locus) with the highest mutual information for parkinsonism and schizophrenia [132], and also identification of regions associated with Graves autoimmune disease [133] by correcting finite sample problems and estimating statistical significance through Gamma distribution approximations. Further applications include the detection of gene–gene and gene–environmental interactions in complex diseases, a method with promising results in evaluating bladder cancer data [134].

Linguistic complexity based on maximum vocabulary of amino acid sequences and protein entropy was used as a key feature to compare nodes in PPI networks in yeast [135]. Interestingly, statistically significant differences were found between hub and nonhub proteins, but also between bottleneck nodes for some PPI data sets. Overall, complexities of hubs and/or bottleneck proteins were shown to have lower complexity, which seems to have relevant evolutionary explanations. This fact also illustrates the cross analysis between the global entropic properties of biological sequences and their correlation with their node function in the PPI network.

Communication systems and error-correcting codes

The relation between Communication Engineering and Molecular Biology has been highlighted in a number of reports [15, 136]. In fact, several models for information transmission have appeared in the literature. Briefly, these are constituted by a source, an encoder, a message that goes through a (noisy) channel, a decoder and a receiver. Gatlin proposed a simple model where a given source transmits DNA sequences, the channel corresponds to transcription and translation and the received message is the amino acid protein sequence [8]. Since then, several other models have been proposed by Yockey [137], Roman-Roldan [13] and May, who reviewed this area [138, 139]. Other proposed channels including mutations (substitutions, insertions and deletions) were also analyzed in terms of their capacities [140].

The analysis of the protein communication channel, which considers an organism’s proteome as the message transmitted in the evolution process, was conducted for archaea, bacteria and eukaryotes [141]. The authors take into account mutation and crossovers and estimate, for each domain of life, the capacities and rate distortion functions.

Coding theory [142], the evolution of the genetic code [143] and models for DNA to protein information transfer [144, 145] were also object of several studies.

Error-correcting codes, in particular, convolution code models, were also applied do DNA with the goal of extracting features for sequence comparison and analysis [146]. By coding the first exon of beta-globin genes of different species, a possible method for similarity definitions based on coding was proposed.

DISCUSSION AND CONCLUSIONS

In a recent article [16], Battail addressed the urgent need of IT in biology, as an essential step to understand the living world. He argues that, despite the tremendous progress of communication engineering in the past decades, communication theory remains completely neglected by biosemiotics and biology. One of the possible reasons might be the focus on semantic aspects and meaning of the former, while IT scope is on literal communication, leading to the irony that both areas ‘have not been able to communicate with each other’. It is expected that the role of IT in molecular biology and sequence analysis, will indeed increase. DNA assembly problems [147] and metagenomic analysis [148] are just recent examples of this trend.

The present review addresses IT applications for sequence analysis, focusing on alignment-free methods. One of its main contributions is to categorize the applications according to its ultimate goal, reflected in the overall structure of this work, while offering a vast reference list to complement topics outside the scope of this survey.

Key Points.

• Information Theory, widely applied in molecular biology, has provided successful methods for alignment-free sequence analysis and comparison.

• Current applications include global and local characterization of DNA, RNA and proteins, from estimating genome entropy to motif and region classification.

• Promising results are expected in gene mapping and next-generation sequencing projects, metagenomics- and communication theory-based models of information transmission in organisms.

FUNDING

This work was partially supported by national funds through Fundação para a Ciência e a Tecnologia (FCT, Portugal) under contracts PEst-OE/EEI/LA0021/2013 and PEst-OE/EME/LA0022/2011 (under the Unit IDMEC - Pole IST, Research Group IDMEC/LAETA/CSI), as well as projects InteleGen (PTDC/DTP-FTO/1747/2012) and BacHBerry (FP7). SV acknowledges support by Program Investigador FCT (IF/00653/2012) from FCT, co-funded by the European Social Fund (ESF) through the Operational Program Human Potential (POPH).