Predicting Super Spreading Events during the 2003 Severe Acute Respiratory Syndrome Epidemics in Hong Kong and Singapore

Abstract

One of the intriguing characteristics of the 2003 severe acute respiratory syndrome (SARS) epidemics was the occurrence of super spreading events (SSEs). Here, the authors report the results of identifying the occurrence of SSEs in the Hong Kong and Singapore epidemics using mathematical and statistical analysis. Their predicted occurrence of SSEs agreed well with the reported occurrence of all seven super spreaders in the two cities. Additional unidentified SSEs were also found to exist. It was found that 71.1% and 74.8% of the infections were attributable to SSEs in Hong Kong and Singapore, respectively. There also seemed to be “synchronized” occurrences of infection peaks in both the community and the hospitals in Hong Kong. The results strongly suggested that the infection did not depend on the total number of symptomatic cases, with only a very small proportion of symptomatic individuals being shown to be infectious (i.e., able to infect other individuals). The authors found that the daily infection rate did not correlate with the daily total number of symptomatic cases but with the daily number of symptomatic cases who were not admitted to a hospital within 4 days of the onset of symptoms.

As of August 7, 2003, the severe acute respiratory syndrome (SARS) epidemic had been reported in 34 countries and regions with 8,422 reported probable cases and 916 deaths (1), and the epidemic transmission had ceased. One of the most intriguing characteristics of the epidemic was the occurrence of super spreading events (SSEs). An SSE is a large cluster of infection in which one or more individuals infect many more other individuals than an average SARS patient does. The World Health Organization attributed the super spreading phenomenon to the lack of stringent infection control measures in hospitals during the early days of the epidemic (2), but this does not explain some of the SSEs identified so far, for example, the Amoy Gardens outbreak (3, 4). At least two separate SSEs have been identified in the Hong Kong epidemic (3, 5), and five have been identified in the Singapore epidemic (6). Unless there is an understanding of the factors leading to SSEs, preventable SSE-based transmission might recur and may be more explosive the next time.

The occurrence of SSEs has made it difficult to determine key parameters of epidemic SARS, especially the case reproduction number. The effective reproduction number, R_t, is defined as the number of infections caused by each new case occurring at time t. Epidemic decay results when the effective reproduction number is maintained below one (7). Riley et al. (8) and Lipsitch et al. (9) concluded that a single infectious case of SARS would infect 2.7 or three secondary cases without any control measures, based on the Hong Kong and Singapore data, respectively. The SSE phenomena were also reported for other diseases, such as measles (10), rubella, laryngeal tuberculosis, and Ebola hemorrhagic fever (11). Austin and Anderson (12) suggested that, for methicillin-resistant Staphylococcus aureus in England and Wales, super spreaders might increase R₀ by 39–132 percent over and above that expected without heterogeneity.

Capturing the occurrence of SSEs during the SARS epidemic by examining the date of infection for all cases and finding out the number and proportion of subjects infected by SSEs would provide important information to improve our understanding of the epidemiology of SARS and the roles played by SSEs. A better understanding of factors associated with the occurrence of SSEs should contribute to more effective prevention and control in the future.

MATERIALS AND METHODS

General approach

The actual date of exposure (infection) was unclear for most cases of SARS. We tried to estimate the daily number of exposed individuals who received a sufficient dose of SARS coronavirus to develop the disease (defined as “infected cases” here). This was done using the information on daily admission or daily onset of symptoms, the distribution of the incubation period, and the distribution of the time from the onset of symptoms to hospital admission. We used mathematical and statistical models to build on the relations among the various parameters. Analyzing the daily number of infected cases would allow us to capture the occurrence of SSEs in an epidemic. In an SSE, the number of infected cases would exceed the expected numbers derived from the number of infectious individuals in the community and the infection rate. We estimated the number of infected cases due to the SSEs by subtracting the expected number of infected cases if no SSE occurred from the estimated total number of infected cases. We further explored the relations between the daily number of symptomatic cases and the daily number of infected cases and tried to identify the group(s) of symptomatic individuals who were most likely to be infectious. The implications for control of future SARS epidemics or other epidemics involving SSEs are discussed.

Estimating the daily number of infected cases

Detailed statistics on daily admissions of SARS cases in Hong Kong were obtained from the Clinical Trials Centre of the University of Hong Kong (13), and the distribution of the daily onset of SARS cases in Singapore was obtained from the Morbidity and Mortality Weekly Report (6). The data available for Hong Kong allowed us to do separate estimations for three subgroups: residents of Amoy Gardens, health-care workers, and the general community (excluding the former two groups). The daily numbers of individuals who were exposed to the SARS coronavirus and who subsequently developed the disease (i.e., the infected cases) were predicted from the distribution of the daily number of hospital admissions for the Hong Kong data and from the distribution of the daily number of symptom onsets for the Singapore data.

Let E_n be the number of infected cases on day n, O_n be the daily number of individuals with the onset of symptoms (who were assumed to become infectious), and I_n be the daily number of individuals who were admitted to a hospital. We considered the relation among the daily number of infected cases, the daily number with onset of symptoms, and the daily number of admissions to a hospital using a simple statistical model:

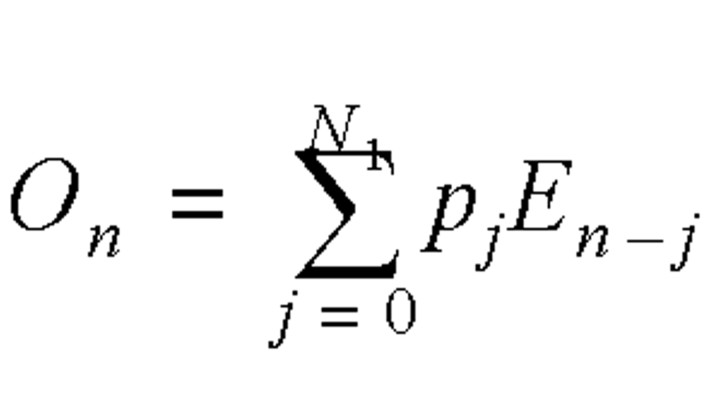
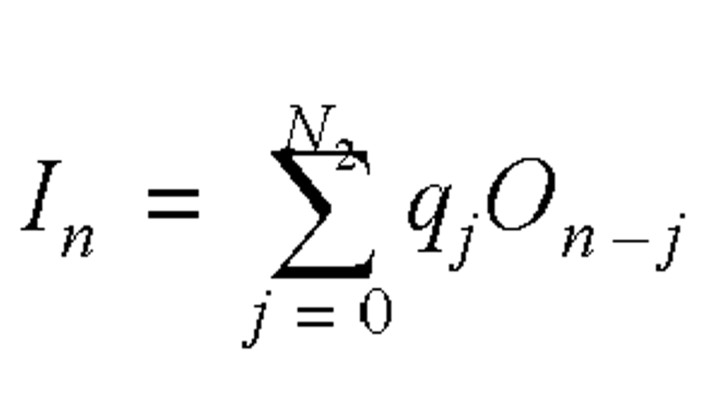
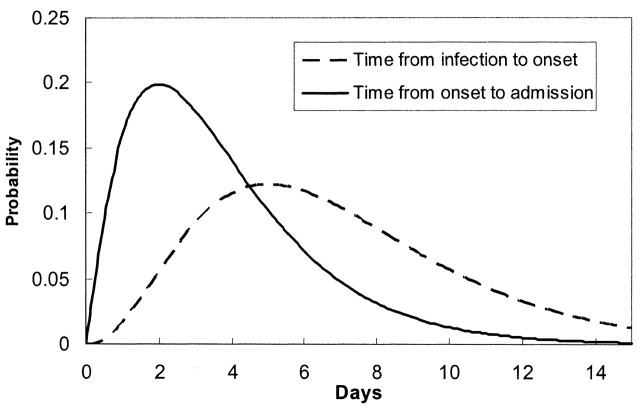
where N₁ was the longest incubation period from infection to symptom onset (N₁ = 15) and N₂ was the longest infectious period, which was assumed to be from symptom onset to admission (N₂ = 15). The incubation period distribution, p_j, was the probability of the onset of symptoms on the jth day after exposure if an individual received a sufficient dose of the SARS virus to cause the disease. The daily admission distribution, q_j, was the probability of admission on the jth day after becoming symptomatic. The most reliable data on the reported daily probability of incubation, p_j, and the daily probability of admission, q_j, were probably those from Donnelly et al. (14), which were based on 57 well-defined cases in Hong Kong. It was expected that errors would be introduced when applying these data to other regions or countries, in particular the distribution of waiting time from symptom onset to hospital admission, which might be affected significantly by local conditions. Fortunately, both equation 2 and the daily probability of admission were not used for analyzing the Singapore data, as the daily distribution of individuals with onset of symptoms was available (6). The incubation period was 2–15 days, and the onset probability satisfied a γ distribution, while the time from onset to admission was about 0–15 days, and the admission probability satisfied another γ distribution (figure 1).

FIGURE 1. Distributions of the incubation period and the lag time from symptom onset to hospital admission for severe acute respiratory syndrome cases in Hong Kong, People’s Republic of China, during 2003. (From C. A. Donnelly et al. Lancet 2003;361:1761–6 (14)).

Rewriting equation 2 in a matrix form, we have

I = QO ,

where I = [I₁, I₂ … I_N]^–1, and O = [O_–14, O_–13 … O_N]^–1. Q = {θ_i,j} is an N × (N + 15) matrix with θ_i,i+j = q_15–j for 1 ≤ i ≤ N, 0 ≤ j ≤ 15, and otherwise θ_i,j = 0. The daily number of symptom onsets could then be obtained by solving the following nonlinear programming problem:

min₀ F(O) = (I – QO)^T(I – QO),

where O_n ≥ 0.

The trust region method (15–17) was used here to solve the nonlinear problem. Similarly, the daily number of infected cases could be estimated from the daily cases of symptom onset using equation 1. Equation 1 has also been applied to study other diseases, such as acquired immune deficiency syndrome (AIDS) (18), anthrax (19), and bovine spongiform encephalopathy (20). It is known that the deconvolution problem obtained from equations 1 and 2 is ill posed (18). Our numerical method was shown to be stable and to satisfy the positivity constraints.

Estimating the number of infected cases due to SSEs

We used a simple model to explore the underlying relations among the daily number of infected cases, the daily number of infectious cases (symptomatic but not hospitalized), the infection rate, λ_G, of general spreaders per day, and the number of infected cases due to SSEs. The daily number of infected cases was composed of those who were infected by general spreaders, E_Gn, and those infected by SSEs, E_Sn. The number of infected cases on day n due to general spreaders should be proportional to the total number of individuals on day n with symptoms but not yet admitted to a hospital, 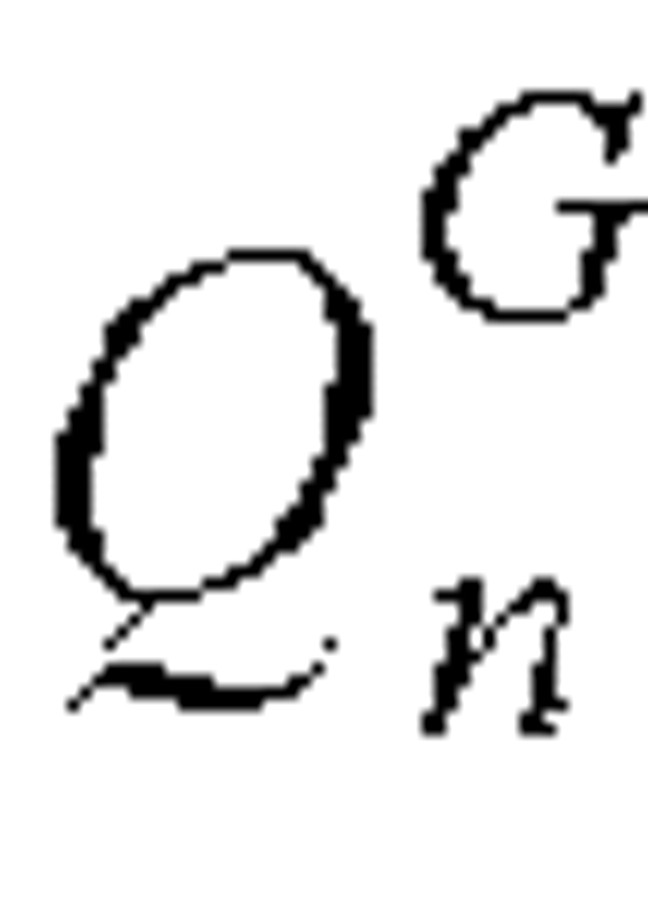. 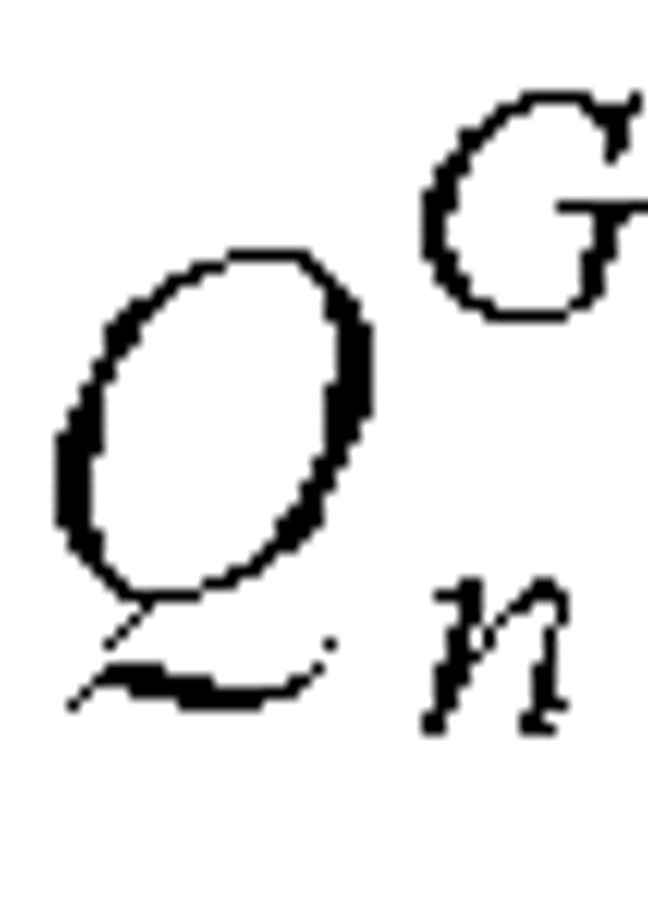was calculated as the sum of the residual individuals with onset of symptoms in each of the previous 15 days (longest lag time before admission) who were not yet admitted to a hospital. The number of residual individuals with symptoms on day n who had an onset of symptoms dated n – J, where 0 ≤ J ≤ 15, was as follows:

.

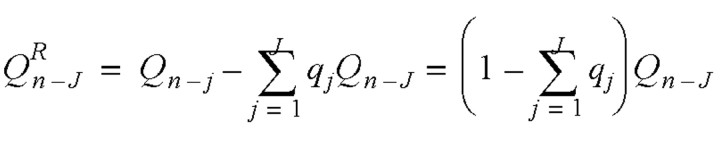We define 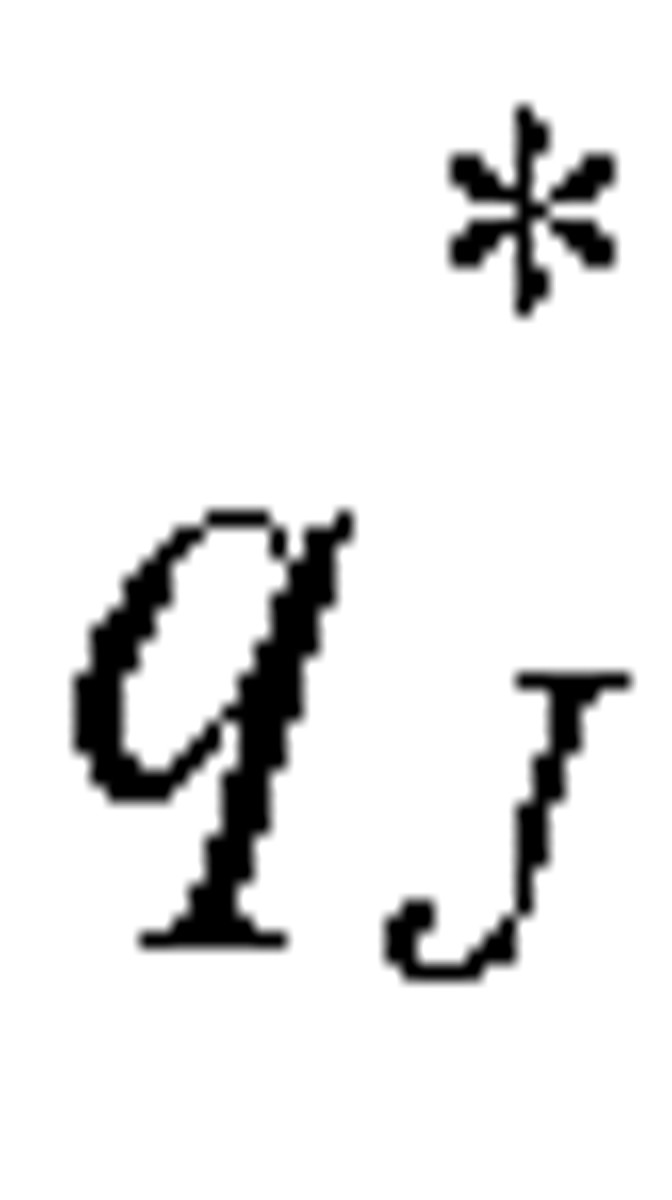as the residual probability of being symptomatic without hospital admission:

.

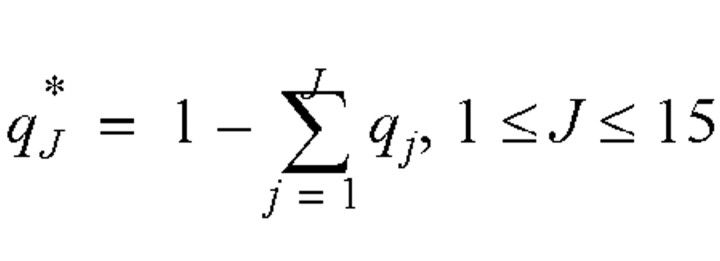Thus, the total number of individuals on day n with symptoms but not yet admitted to hospitals could be calculated as follows:

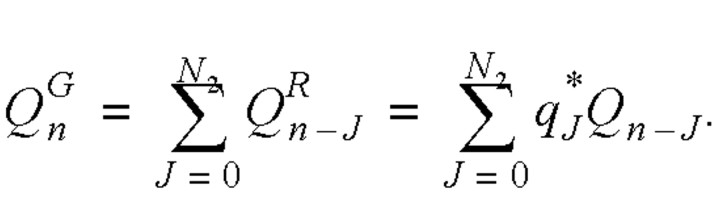
Thus, the daily number of infected cases satisfied the following equation:

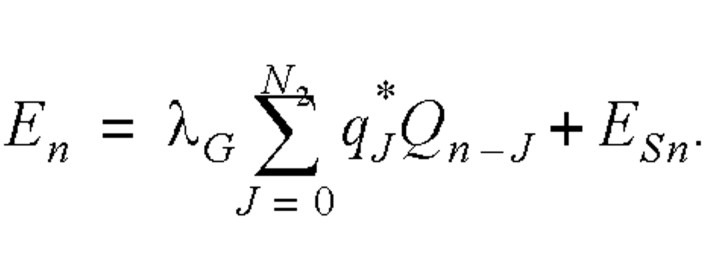
We assume that the infection rate λ_G was constant during the entire infectious period for a general spreader (8).

Distinguishing the infection between the two types of spreaders was not easy. We adopted a simple approach and assumed that the infection rate of the general spreaders was no higher than those obtained by Riley et al. (8) and Lipsitch et al. (9); that is, the number infected by each general spreader was assumed to be not greater than three. As the mean infectious period (from symptom onset to admission) determined by the γ distribution was 3.18 days, the average infection rate per day for an infectious individual was 0.94 (3/3.18). This infection rate value was not applicable after the public health control measures were instituted. An average daily infection rate for the entire duration of the epidemics in Hong Kong and Singapore could also be calculated by the reported total number of infected cases (1), excluding those due to reported SSEs (table 1), divided by the total number of cases daily that were symptomatic but not yet admitted to a hospital over the entire period of the epidemic (obtained by summing the daily number of symptomatic cases that were not yet admitted to a hospital (equation 6) over the entire duration of the epidemics). With this method, the average infection rate per day of general spreaders for the entire epidemic was found to be 0.23 and 0.14 for Hong Kong and Singapore, respectively. Once the infection rate of the general spreaders was known, the number of infected cases due to SSEs on the same day could be calculated as follows:

TABLE 1.

Comparison of reported and predicted numbers of infected cases due to super spreading events during the 2003 epidemics of severe acute respiratory syndrome in Singapore and Hong Kong, People’s Republic of China

	Reported events										Predicted events
	Super spreader’s age			Date of symptom onset	Date of hospitalization	Date of isolation	Infected cases linked to SSEs*				Peak	Predicted no. of infected cases	Predicted no. of infected cases due to SSEs, by rate†
	No. of years	Reference					Reported (no.)	Suspected (additional no.)	Reference				Rate A	Rate B
Singapore
	22	Leo et al., 2003 (6)		February 25	March 1–5	March 6	21	3	Leo et al., 2003 (6)		March 1–4	29	25	29
	27	Leo et al., 2003 (6))		March 7	March 10–12	March 13	23	5	Leo et al., 2003 (6)		March 10–11	68	50	66
	53	Leo et al., 2003 (6)		March 12	March 12–19	March 20	23	18	Leo et al., 2003 (6)		March 21	21	5	19
	60	Leo et al., 2003 (6)		March 24	March 24– April 3	April 4	40	22	Leo et al., 2003 (6)		March 28–30	60	26	47
	64	Leo et al., 2003 (6)		April 5	April 5–8	April 9	15		Leo et al., 2003 (6)		April 7–8	21	0	10
	Unidentified										April 16	8	0	7
Hong Kong
	26	Tomlinson and Cockram, 2003 (5); Lee et al., 2003 (22)		February 24	March 4	March 12	138		Lee et al., 2003 (22)		March 9–10	276	271	275
	33	DoH,* 2003 (3)		March 14	March 15–19, 22	March 22	329		DoH, 2003 (3)		March 20–21	567	334	502
	Unidentified										March 31–April 1	360	60	273
	Unidentified										April 4–7	178	0	75
	Unidentified										April 12–16	211	0	91
	Unidentified										April 23–24	65	0	31

* SSEs, super spreading events; DoH, Department of Health, Hong Kong Special Administrative Region of the People’s Republic of China.

† Rate A, an average infection rate of 0.94 per day for an infectious individual; rate B, an average infection rate of 0.23 (Hong Kong) and 0.14 (Singapore) per day for an infectious individual.

.

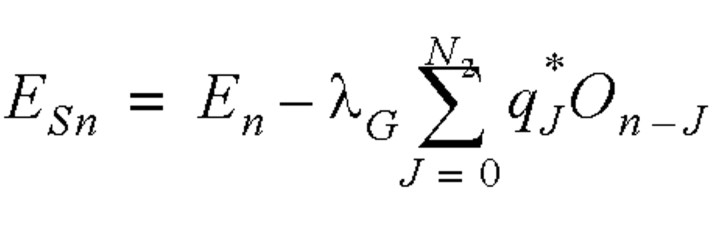Verifying predicted SSEs against reported SSEs

Relevant information on major reported SSEs was obtained from Morbidity and Mortality Weekly Reports (6, 21). In addition, Lee et al. (22) describe the March 2003 outbreak at the Prince of Wales Hospital in Hong Kong, and the Hong Kong government (3) and the World Health Organization investigation team (4) report on the epidemiologic and environmental investigations of the Amoy Gardens outbreak in Hong Kong. The SSEs captured by the predicted daily number of infected cases and the estimated numbers of infected cases due to SSEs would be compared against the features (dates, numbers infected) of the reported SSEs.

Exploring the relations between daily number of symptomatic cases and daily number of infected cases

We explored the relations between the daily number of symptomatic cases who were not hospitalized and the daily number of infected cases, by calculating Pearson’s correlation coefficient. The correlation between the daily number of infected cases and the different subgroups of symptomatic cases was also explored to identify the group(s) of symptomatic individuals who were most likely to be infectious.

RESULTS

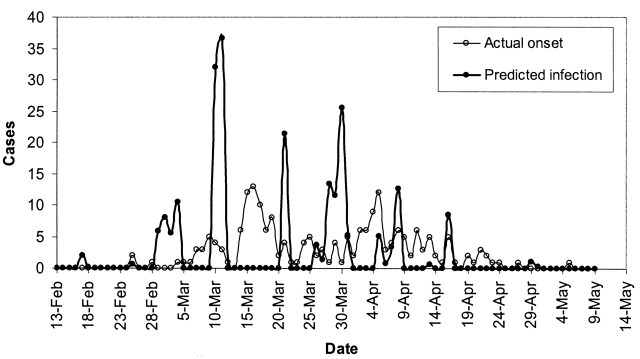
Figures 2 and 3 show the predicted daily number of infected cases and the daily numbers of hospital admissions for SARS in Hong Kong among the total population, the health-care workers, the Amoy Gardens’ residents, and the general community. Each peak or aggregate of cases in time could be interpreted as reflecting an SSE in which one or more infectious subjects could be involved. The curves for infected cases in figure 2, parts A and B, and figure 3, part B, were characterized by three obvious high peaks on March 9–10, March 20–21, and March 31–April 2, respectively. The first peak (March 9–10) corresponded to the outbreak of SARS at the Prince of Wales Hospital (5). The second peak (March 20–21) corresponded to the outbreak of SARS in the Amoy Gardens (figure 3, part A). The third peak coincided with the peak in hospital admission of cases in Hong Kong (figure 2, part A). There appeared to be synchronized occurrences of infection peaks in both the general community and among health-care workers in Hong Kong (visible only in the derived time series of infections and not in the observed series of admissions), and there were certain days with no predicted infected cases. Another 3–4 smaller aggregates of cases were discerned following the three major peaks. For Amoy Gardens, a single peak stood out around March 20 (figure 3, part A), with another aggregate of infected cases around April 4. Our estimated daily number of infected cases in Singapore revealed six peaks occurring around March 4, March 11, March 21, March 30, April 8, and April 16 (figure 4).

FIGURE 2. The predicted daily number of infected cases and the daily number of hospital admissions for severe acute respiratory syndrome in Hong Kong, People’s Republic of China, during the 2003 epidemic among the total population (A) and the health-care workers (B). Mar, March; Apr, April.

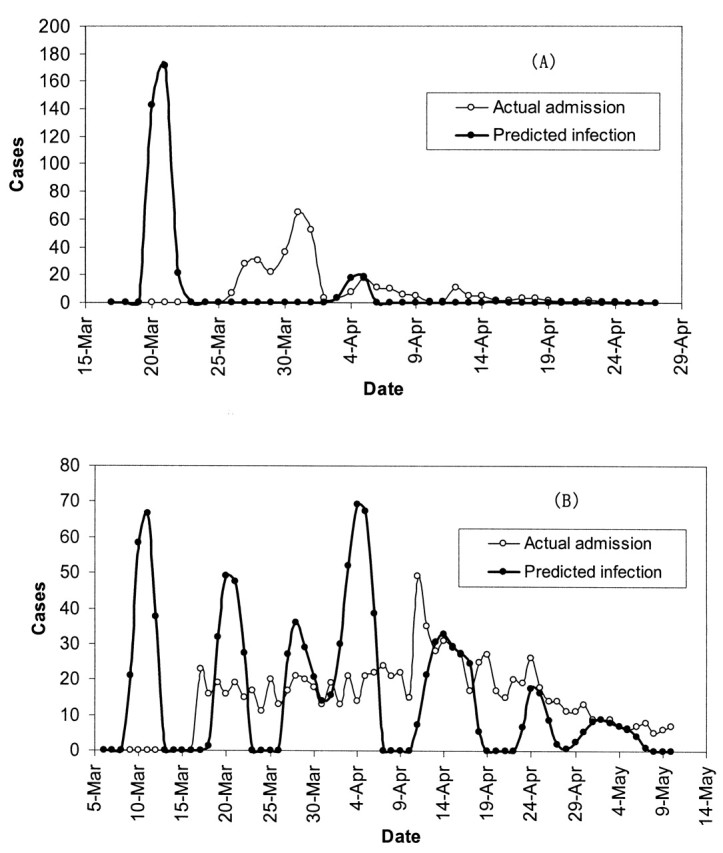
FIGURE 3. The predicted daily number of infected cases and the daily number of hospital admissions for severe acute respiratory syndrome in Hong Kong, People’s Republic of China, during the 2003 epidemic among the Amoy Gardens’ residents (A) and the general community (B). Mar, March; Apr, April.

FIGURE 4. The predicted daily number of infected cases and the daily number of persons with symptom onset for severe acute respiratory syndrome in Singapore during the 2003 epidemic. Feb, February; Mar, March; Apr, April.

The reported super spreaders in Hong Kong and Singapore summarized in table 1 correspond fairly well with the peaks or aggregates of predicted infected cases captured in figures 2, 3, and 4. All reported SSEs in Singapore and that of the patient aged 26 years in Hong Kong occurred in hospitals, while the index patients were hospitalized before isolation (6, 22). The predicted period of peaks in table 1 agreed well with the dates of hospitalization (the suspected infection period as derived from the date of isolation) for all super spreaders, except the patient aged 53 years who was reported to be isolated on March 20. The index case in the outbreak at Amoy Gardens (patient aged 33 years) (table 1) was known to have stayed overnight on March 14 and 19 at a flat in Amoy Gardens. Our predicted infection peak was March 20–21.

There was good agreement between the predicted number of infected cases due to SSEs and the reported number of infected cases traced back to the identified super spreaders (table 1). In general, each SSE in Hong Kong caused more infections than in Singapore. On the other hand, SSEs in Hong Kong accounted for 71.1 percent (1,247 of 1,755 cases) of all SARS infections, whereas in Singapore they were responsible for 74.8 percent (178 of 238 cases) of all cases. Our prediction also revealed four unidentified SSEs in Hong Kong and one in Singapore.

No correlation was found between the daily number of newly infected cases and the daily total number of symptomatic cases who were not yet hospitalized (potentially infectious cases), and Pearson’s linear correlation coefficient r was less than 0.1 for both Singapore and Hong Kong. There was better correlation between the number of infected cases and the number of symptomatic cases with 4 or more days after the onset of symptoms but not yet admitted to a hospital, with r = 0.128 (p = 0.26, two tailed) for Singapore and 0.292 (p = 0.03, two tailed) for Hong Kong (figure 5). The correlation coefficients between the number of infected cases and the number of symptomatic cases with 10 or more days after the onset of symptoms, but not yet admitted to hospitals, are 0.152 (p = 0.18, two tailed) for Singapore and 0.518 (p < 0.001, two tailed) for Hong Kong. On the other hand, subgroups of potentially infectious cases with different incubation periods did not show any correlation with the daily number of infected cases.

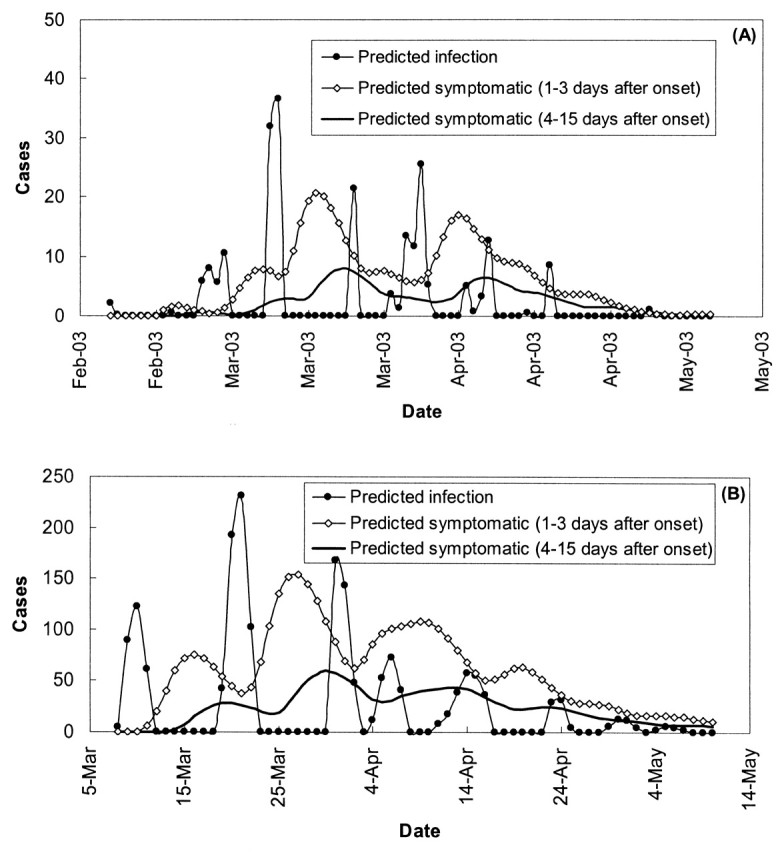
FIGURE 5. The relation between the predicted daily number of infected cases and the predicted daily number of symptomatic cases of severe acute respiratory syndrome grouped according to days between symptom onset and hospital admission for Singapore (A) and Hong Kong, People’s Republic of China (B), during the 2003 epidemic. Feb, February; Mar, March; Apr, April.

DISCUSSION

By making use of the probability distributions of the incubation period and the time from the onset of symptoms to hospital admission, as well as the relations between the daily number of infected cases or between the daily number with symptom onset and the daily number of hospital admissions, we were able to estimate the daily numbers of newly infected cases, which were usually not known during the epidemics. Plotting the daily number of newly infected cases allowed us to identify peaks or aggregates of infections that would suggest SSEs. The good agreement between our predicted infection peaks and the reported occurrence of all seven SSEs in Hong Kong and Singapore suggested some underlying but not yet fully understood mechanisms of disease transmission. The possibility of predicting the likely exposure time also helps in environmental studies to identify the environmental conditions at the time of infection. We predicted several additional SSEs that had not been identified and reported. It might be worthwhile to document and investigate these unidentified SSEs retrospectively by reviewing relevant medical records and epidemiologic investigation reports.

It is not known whether the larger number of infected cases per SSE in Hong Kong when compared with Singapore (table 1) was due to differences in the effectiveness of or variations in the choice of disease control measures or due to other factors, such as a higher population density in Hong Kong and other environmental factors. Interestingly, the average infection rate per day of general spreaders for the entire epidemic period in Hong Kong was also significantly greater than that in Singapore (0.23 compared with 0.14). According to our estimations, SSEs played a very important role in the SARS epidemic, being responsible for nearly three fourths of the infections in Hong Kong and Singapore. This has important public health implications. If our model is valid, the control of SARS epidemics would be directly governed by the ability to prevent/control the SSEs. One super spreader or SSE could ignite a whole new outbreak if the mechanisms of an SSE or effective control strategies are not identified.

In Singapore and Hong Kong, not all patients with SARS were infectious. In fact, the majority of them had very low, if any, infectivity. This supports the findings of a hospital study in Vietnam that most SARS patients do not transmit the virus (23). In Singapore, 81 percent of the first 205 reported probable SARS patients had no evidence of transmission to other persons (6). It is not known whether there were differences of many orders of magnitude in the viral shedding rate in time or between infected individuals. There was also no evidence to show whether a super spreader could remain infectious during the entire symptomatic period prior to admission. However, our results seemed to suggest that each super spreader had a relatively short period of strong infectivity, with the peaks in predicted numbers of new infections indicating SSEs being quite narrow.

Why SSEs occurred has remained a mystery, and the identification of potential super spreaders could be difficult. Our results strongly suggest that the daily number of new infections did not depend on the total number of symptomatic cases, as only a very small proportion of the symptomatic individuals were infectious. We do not know exactly what makes a super spreader different from other infected individuals, but our results suggested that late admission to a hospital (more than 4 days) after symptom onset could be partly responsible for the occurrence of SSEs, especially during the early phase of the epidemic, since patients admitted late would have developed a high viral load. This agrees with the results of a study of SSEs in Beijing, where the efficiency of SARS transmission increases at a later stage of the illness (24). Peiris et al. (25) found that the viral load increased after the onset of symptoms and peaked at around day 10. The World Health Organization’s consensus document on the SARS epidemiology (23) noted that, in the data from Singapore, few secondary cases occurred when symptomatic cases were isolated within 5 days of illness onset. The importance of early detection/diagnosis and early admission/isolation cannot be overemphasized.

The mechanisms for the high-frequency transmission of most super spreaders remain largely unknown. The super spreading phenomena of Ebola were suspected to be due to a larger number of “contacts” of the super spreaders or some inherent differences in the virus-host relations, such as, perhaps, a more virulent virus strain or higher levels of viral shedding (11). The great variability in the numbers of infected cases among the seven identified super spreaders in SARS epidemics in Singapore and Hong Kong suggested that some epidemiologic and environmental factors could have contributed to the infection. For the outbreak at Amoy Gardens in Hong Kong, it has been suggested that the environmental control systems (drainage system and aerosol flows) were responsible for amplifying the virus sources and for transmitting the virus to a large number of people (3). In the case of the Prince of Wales Hospital, the use of a nebulized bronchodilator was believed to be an important factor that increased the droplet loading surrounding the index patient (5). However, new studies suggest the possible roles of airborne virus-laden aerosols and the ventilation system design (26). These two examples suggest the possible roles of the environment in amplifying viral sources in SSEs and further support our hypothesis that an SSE is also determined by environmental factors. Hence, proper environmental and ventilation design would be very important in controlling future SSE-based SARS coronavirus transmissions.

SSEs need to be properly investigated to identify the common underlying factors for the effective prevention of SARS in the future. These factors may be associated with the agent, the environment, and/or the host. Factors related to the agent would include the strain (infectivity, virulence), virus load and source, and survival in different media. Environmental factors such as proximity of contacts, temperature, humidity, aerosolization processes, airflows, and ventilation can be important. Host factors would include age, sex, nutritional status, immune defense, comorbidity, personal habits, and drug use.

It is obviously important to critically evaluate the assumptions and the numerical procedure in the simple model. For example, the estimates of infection numbers and dates are sensitive to the incubation period distribution. Donnelly et al. (14) reported that the mean incubation period was 6.37 (95 percent confidence interval: 5.29, 7.75) days. The World Health Organization consensus document (23) also summarized that the mean incubation periods were 4–7.2 days. We performed a sensitivity study by considering three different incubation probability distributions with a mean of 5.3, 6.37, and 7.3 days, with both a small and a large variance (8 and 16.69 days²). The predicted general intermittent behavior of the infection patterns is very similar, but the infection peaks can be advanced or delayed by about 1 day.

There are a number of limitations to our mathematical analyses. We used data on reported cases from governments, which might include only those SARS cases with more severe clinical symptoms. It is still unclear whether a subclinical form of the disease exists in the community. Our chosen mathematical model was also a simple one and did not include the spatial relations of disease transmission (8). The assumption of the infectious period from symptom onset to hospital admission did not consider the fact that some patients were still infectious after hospitalization but were not under effective isolation during the early days of the epidemic. After the strict isolation measures were implemented in Hong Kong and Singapore, the reported date of admission would be equivalent to the date of isolation, although some limited hospital-acquired infection might still occur. In Hong Kong, the community infection constituted a much higher proportion of the total number of cases than in Singapore. The impact of the infectivity period assumption on the analyses for Hong Kong might be smaller than the impact on those for Singapore.

The simple mathematical model for determining the occurrence of SSEs can be used to determine the key parameters of SSEs during any potential future SARS epidemics. In practice, such a simple model needs to be combined with studies on transmission dynamics, which provide essential data on the infection rate of the general spreaders. The accuracy of the prediction of SSE occurrence depends on the accuracy of the input data, that is, the distribution of the daily number of individuals admitted to hospitals (or becoming symptomatic), the daily probability of symptom onset after being infected, and the daily probability of being admitted to hospitals after developing symptoms. This means that various hypotheses derived from our analyses remain to be confirmed by further epidemiologic and clinical studies.

ACKNOWLEDGMENTS

This study was supported by Hong Kong University SARS Research Fund 2003.

Received for publication February 6, 2004; accepted for publication April 20, 2004.