Accurate prediction of human essential genes using only nucleotide composition and association information

Abstract

Motivation

Previously constructed classifiers in predicting eukaryotic essential genes integrated a variety of features including experimental ones. If we can obtain satisfactory prediction using only nucleotide (sequence) information, it would be more promising. Three groups recently identified essential genes in human cancer cell lines using wet experiments and it provided wonderful opportunity to accomplish our idea. Here we improved the Z curve method into the λ-interval form to denote nucleotide composition and association information and used it to construct the SVM classifying model.

Results

Our model accurately predicted human gene essentiality with an AUC higher than 0.88 both for 5-fold cross-validation and jackknife tests. These results demonstrated that the essentiality of human genes could be reliably reflected by only sequence information. We re-predicted the negative dataset by our Pheg server and 118 genes were additionally predicted as essential. Among them, 20 were found to be homologues in mouse essential genes, indicating that some of the 118 genes were indeed essential, however previous experiments overlooked them. As the first available server, Pheg could predict essentiality for anonymous gene sequences of human. It is also hoped the λ-interval Z curve method could be effectively extended to classification issues of other DNA elements.

Availability and Implementation

http://cefg.uestc.edu.cn/Pheg

Supplementary information

Supplementary data are available at Bioinformatics online.

Introduction

Catalogs of essential genes on a whole-genome scale, determined using wet-lab methods, are available for a large number of prokaryotic and eukaryotic organisms which are provided in DEG and OGEE databases (Chen et al., 2012; Luo et al., 2014). Computational methods with high accuracy offer an appealing alternative method for identifying essential genes. Computational methods are broadly divided into three types: machine learning-based methods combining intrinsic and context-dependent features (Cheng et al., 2013; Deng et al., 2011), flux balance analysis-based methods (del Rio et al., 2009; Gatto et al., 2015; Kuepfer et al., 2005) and homology search and evolutionary analysis-based methods (Peng et al., 2012; Wei et al., 2013). With respect to essential gene prediction in bacteria, we integrated the orthology and phylogenetic information and subsequently developed a universal tool named Geptop (Wei et al., 2013), which has shown the highest accuracy among all state-of-the-art algorithms.

Some studies have focused on essential gene prediction in eukaryotic genomes. In 2005, Chen and Xu investigated protein dispensability in Saccharomyces cerevisiae by combining high-throughput data and machine learning-based methods (Chen and Xu, 2005). In 2006, Seringhaus et al. reported a machine learning-based method that integrated various intrinsic and predicted features to identify essential genes in yeast S.cerevisiae genomes (Seringhaus et al., 2006). Yuan et al. integrated informative genomic features to perform knockout lethality predictions in mice using three machine learning-based methods (Yuan et al., 2012). Lloyd et al. analyzed the characteristics of essential genes in the Arabidopsis thaliana genome and used A.thaliana as a machine learning-based model to transform the essentiality annotations to Oryza sativa and S.cerevisiae (Lloyd et al., 2015).

Recently, three research teams approximately identified 2000 essential genes in human cancer cell lines using CRISPR-Cas9 and gene-trap technology (Blomen et al., 2015; Hart et al., 2015; Wang et al., 2015). Their results showed high consistency, which further confirmed the accuracy and robustness of the essential gene sets (Fraser, 2015). These studies provided an in-depth analysis of tumor-specific essential genes and feasible methods to screen tumor-specific essential genes (Fraser, 2015; Hart and Moffat, 2016). The essential genes screened by these three teams provided a clear definition of the requirements for sustaining the basic cell activities of individual human tumor cell types. Practically, these genes can be regarded as targets for cancer treatment (Fraser, 2015). The data from these three groups provided a rare opportunity to theoretically study the function, sequence composition, evolution and network topology of human essential genes. One of the most important and interesting theoretical issues in modern biology is whether essential genes and non-essential genes can be accurately classified using computational methods. The models established in the aforementioned three eukaryotic organisms, S.cerevisiae (Chen and Xu, 2005; Seringhaus et al., 2006), Mus musculus (Yuan et al., 2012) and A.thaliana (Lloyd et al., 2015), involved intrinsic features, or intrinsic and context-dependent features. These context-dependent features included those features extracted from experimental omics data. However, the features derived from experimental data are frequently unavailable; consequently, this type of machine learning model cannot be extended to a wide range of genomes. In the present study, we addressed this problem in humans by using only intrinsic features derived from sequences, from which certain features can be characterized using a λ-interval Z curve. The λ-interval Z curve considered information of both adjacent nucleotide compositions and internal nucleotide associations. To facilitate the use of interested researchers, we have provided a user-friendly online web server, Pheg, which can be freely accessed without registration at http://cefg.uestc.edu.cn/Pheg.

2 Materials and methods

2.1 Data collection

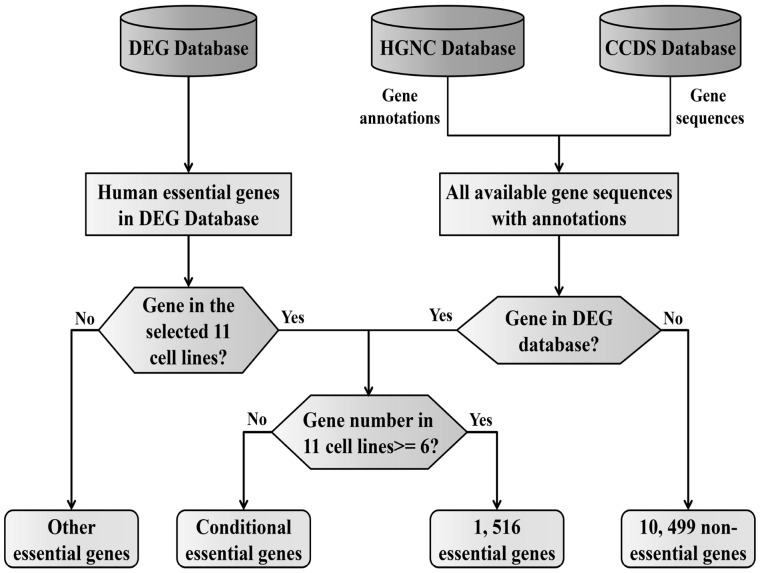
We extracted the gene essentiality data from the DEG database (http://tubic.tju.edu.cn/deg/), the updated version of which contained human gene essentiality information from three recent works (Blomen et al., 2015; Hart et al., 2015; Wang et al., 2015). These essentiality annotations serve as the basis for constructing our benchmark dataset. The flowchart shown in Figure 1 illustrates the construction of the positive and negative datasets.

Fig. 1.

Description of the construction of the human essential and non-essential gene datasets

In the three studies, 13 datasets were provided. Due to lines HCT116 and KBM7 are represented by two datasets each, 11 cancer cell lines (KBM7, K562, Raji, Jiyoye, A375, HAP1, DLD1, GBM, HCT116, Hela, rpel) are involved in total. Blomen et al. and Wang et al. identified the essential genes in the KBM7 cell line. We combined these two datasets into one gene set, KBM7. A total of 2073 and 386 essential genes were contained in the two datasets for HCT116. The 386 genes in this dataset were markedly different from those in the datasets for the other cell lines, so this dataset was excluded. Ultimately, 11 essential gene sets were obtained, corresponding to a single cell line. Essential genes, by definition, are indispensable for the survival of organisms under optimized growth conditions. Those genes are considered the foundation of life (Juhas et al., 2011), and they should be persistent in a wide range of cell lines and species. Therefore, we only retained genes that were identified as lethal genes in more than half of the investigated cell lines. When a gene appeared as essential in more than six cell lines (11/2 ≈ 6), it was selected as one sample in the positive dataset. According to this principle, we obtained a total of 1518 essential genes. We downloaded all of the protein coding gene sequences from the CCDS database (Harte et al., 2012) (https://www.ncbi.nlm.nih.gov/CCDS/CcdsBrowse.cgi), and the annotations of protein coding genes were obtained from the HGNC database (http://www.genenames.org/cgi-bin/statistics, March 1, 2016), which contained 19 003 annotation entries. The essential gene sequences were extracted according to the annotations, and genes with no counterpart in the CCDS database were excluded. According to this criterion, we excluded 2 genes and obtained 1516 essential genes. We used the essential gene annotation in the DEG dataset, and the gene sequences were extracted from the CCDS because the former did not contain the information for non-essential genes. For human essentiality annotations in the DEG database, a number of scattered annotated essential genes aside from those in the 11 cell lines were identified. A total of 28 166 essential gene annotated entries (including conditional essential gene annotated entries) were obtained. Among these annotations, there were many repeated annotation entries; therefore, there were considerably fewer unique entries. To obtain a more reliable negative dataset, i.e. absolutely non-essential genes, we excluded all of the human essential genes annotated in the DEG database (Luo et al., 2014) from the list of the protein coding genes. The remaining genes were regarded as the negative dataset, and their gene sequences were extracted from the CCDS database. Genes with no counterpart in the CCDS database were also excluded. A total of 10 499 non-essential genes were obtained using this method. Ultimately, a total of 12 015 gene entries were obtained in the benchmark dataset: 1516 essential genes and 10 499 non-essential genes. The protein coding gene annotations are provided in Supplementary Material S1, and information for the benchmark dataset is provided in Supplementary Material S2.

2.2 λ-Interval Z curve

The originally proposed Z curve variables might reflect the composition of a single nucleotide considering the features derived from phase heterogeneity of a single nucleotide (Zhang, 1997; Zhang and Chou, 1994; Zhang and Zhang, 1991, 1994). Herein, we provided a summary of the Z curve method used for gene identification (Zhang and Wang, 2000). Let us suppose that the frequencies of bases A, C, G and T occurring in an ORF or a gene fragment at positions 1, 4, 7, …, 2, 5, 8, … and 3, 6, 9, …, are represented by a₁, c₁, g₁, t₁; a₂, c₂, g₂, t₂; a₃ and c₃, g₃, t₃, respectively. Those 12 symbols represent the frequencies of the bases at the 1st, 2nd and 3rd codon positions, respectively. According to the symbols defined above, the universal Z curve mathematical expression is as follows (Zhang and Wang, 2000):

$$\begin{array}{c}\{\begin{array}{c}{x}_i=(a_i+g_i)-(c_i+t_i)\\ y_i=(a_i+c_i)-(g_i+t_i)\\ z_i=(a_i+t_i)-(g_i+c_i)\end{array}\\ x_i,y_i,z_i\in [-1,1],i=1,2,3\end{array}$$ (1)

Because composition bias for oligonucleotides in coding DNA sequence (CDS) regions or open reading frames (ORFs) exists, the adjacent w-nucleotides Z curve method was proposed (Gao and Zhang, 2004; Guo et al., 2003). Let us suppose that w represents the length of the adjacent nucleotide sequence. The Z curve variables for the phase-specific adjacent w-nucleotides can be calculated as follows:

$$\{\begin{array}{l}{x}_{S_w}^k=[p^k(S_{w}A)+p^k(S_{w}G)]-[p^k(S_{w}C)+p^k(S_{w}T)]\\ y_{S_w}^k=[p^k(S_{w}A)+p^k(S_{w}C)]-[p^k(S_{w}G)+p^k(S_{w}T)],k=1,2,3\\ Z_{S_w}^k=[p^k(S_{w}A)+p^k(S_{w}T)]-[p^k(S_{w}G)+p^k(S_{w}C)]\end{array}$$ (2)

where k equals 1, 2, or 3 to indicate that the first oligonucleotide bases are situated at the 1st, 2nd and 3rd codon positions, respectively.

Recent studies demonstrated the existence of long-range associations in chromosomes and showed that these associations are crucial for gene regulation (Fullwood et al., 2009). Although the two adjacent nucleotides in the primary structure have no association in some cases, strong associations in terms of tertiary structure might exist. Therefore, we introduced the λ-interval Z curve to virtually represent the interval range association. The details of this method are described as follows. Let us used p_k(S_wX) to represent the frequency of oligonucleotides S_wX in genes or ORFs, where X is one of the four basic bases A, T, G and C. To facilitate this presentation, the length of the oligonucleotide S_w is represented as w. According to the predetermined characters, we generated the universal equation for the λ-interval Z curve based on Z curve theory as follows:

$$\{\begin{array}{l}{x}_{S_w}^k=[p^k(S_{w}A)+p^k(S_{w}G)]-[p^k(S_{w}C)+p^k(S_{w}T)]\\ y_{S_w}^k=[p^k(S_{w}A)+p^k(S_{w}C)]-[p^k(S_{w}G)+p^k(S_{w}T)],\\ k=1:\lambda +1,2:\lambda +2,3:\lambda +3\\ Z_{S_w}^k=[p^k(S_{w}A)+p^k(S_{w}T)]-[p^k(S_{w}G)+p^k(S_{w}C)]\end{array}$$ (3)

where x, y and z represent the accumulation of the three base groups classified according to chemical bond properties. Variable k denotes the phase-specific index of the first base in the nucleotide sequence S_w, and λ represents the intervals between S_w and X. The first base in the oligonucleotide S_w was located at position k. The core part of λ-interval Z curve forms oligonucleotide S_wX. A schematic diagram of the formation of these oligonucleotides is shown in Figure 2. The oligonucleotide window S_w slides along a DNA molecule sequence according to phase, forming oligonucleotide sets with base X, which is λ intervals away from the last base of S_w. The periodicity derived from three codons is denoted as S_wX.

Fig. 2.

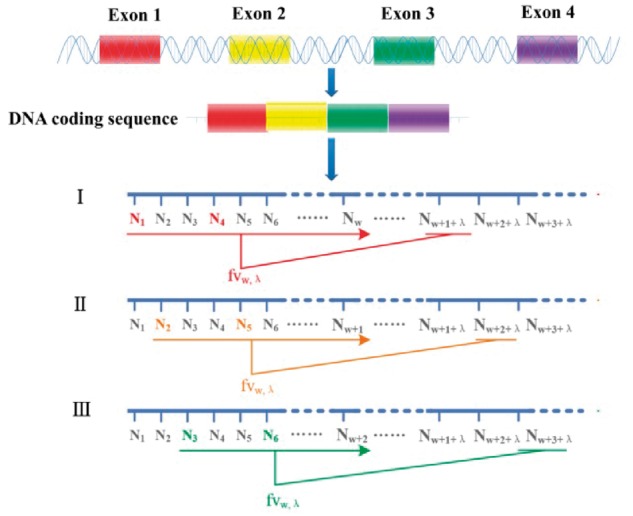
Description of the process of constructing the oligonucleotides using the λ-interval Z curve method. A gene or an ORF has three phases (I, II, III represent first, second and third phase, respectively) denoted with different colors (Color version of this figure is available at Bioinformatics online.)

When w is equal to 1 and λ is equal to 0, Equation (3) can be transformed into Equation (1). When w is more than 1 and λ is equal to 0, Equation (3) can be transformed into Equation (2). Thus, the phase-specific single nucleotide Z curve and phase-specific adjacent w-nucleotide Z curve are incorporated into the λ-interval Z curve. Using the λ-interval Z curve, we can extract more features to characterize DNA sequences. According to Equations (1) and (2), when w is greater than 0 and λ is equal to 0 we can obtain 3 × 3 × 4^w−1 variables to characterize DNA sequences. When w and λ are greater than 0, we can obtain 3 × 3 × 4^w variables. For convenience, we used fv_w,λ to represent the variables with the length of w for oligonucleotides S_w, and the highest interval length between oligonucleotides S_w and base X is λ. To obtain more information from a DNA sequence, the final variable is described as FV_{w, λ}, where w represents the longest oligonucleotides and λ is the highest interval. This variable can be represented as follows:

$$F{V}_{w,\lambda }=[\underset{i=1,j=0}{\overset{i=w-1,j=\lambda }{\cup }}f{v}_{i,j},f{v}_{w,0}{]}^T$$ (4)

where the symbol ‘U’ represents the union set of fv_w,λ, i.e. FV_2,0 = [fv_1,0, fv_2,0]^T, FV_2,1 = [fv_1,0∪ fv_1,1, fv_2,0]^T, FV_2,2 = [fv_1,0∪ fv_1,1 ∪ fv_1,2, fv_2,0]^T, …, FV_3,0= [fv_1,0∪fv_2,0, fv_3,0], …. FV_2,0 and FV_3,0 are the combination of adjacent phase-specific w-nucleotide Z curve variables. We performed this prediction with w ranging from 2 to 4 and λ ranging from 0 to 5. According to the discussion above, we obtained 4 545 variables for FV_{4, 5}.

2.3 Support vector machine

Linear SVMs play a key role in solving ultra-large-scale data, reflecting the effectiveness, rapid speed and splendid generalization of this method in training and prediction. LIBLINEAR, designed by Fan et al. (2008), is an easy-to-use, freely available software tool to manage large sparse data. The new version of LIBLINEAR (version 2.1-4) supports not only classification, such as L2-loss and L1-loss linear support vector machine, but also regression, such as L2-regularized logistic regression. Given the ultra-high-dimensional feature vectors and large samples contained in the benchmark dataset in the present study, we used the LIBLINEAR software package for prediction. The new version of LIBLINEAR can be downloaded from https://www.csie.ntu.edu.tw/∼cjlin/liblinear/. In the present study, we used the 5-fold cross-validation test to determine the best penalty parameter c with the penalty parameter from 2⁻¹⁸ to 2¹⁰. We further adopted the jackknife test to assess the predictive power of our classifier. The area under the ROC (Receiver Operating Characteristic), curve, the AUC, is often used to measure the performance quality of a binary classifier. An AUC of 0.5 is equivalent to random prediction, whereas an AUC of 1 represents a perfect prediction. There is no bias for evaluating the performance of the unbalanced dataset through AUC. Therefore, we adopted the AUC as a cross-validation criterion in the present study.

2.4 Feature extraction technology

First, the predictive power of a classifier can be influenced by the relevance and noise in the original features. Second, additional time for training and predicting tasks can be increased due to the high-dimensional features. Feature selection (FS) technology is a powerful method for the removal of noise and redundant features from the original features. Hence, the dimension of the features can be reduced. Recursive feature extraction through SVM linear kernels is a powerful FS algorithm (Guyon et al., 2002), but the correlation bias was not considered using this method. Yan and Zhang (2015) proposed an improved method, called SVM-recursive feature extraction (RFE)+correlation bias reduction (CBR), which incorporates the CBR. The main concept is that the ranking criterion can be directly derived from the SVM-based model. The feature with the smallest weight is excluded for each run time. The training process was repeated by incorporating CBR until the ranks of all features are obtained. We used SVM-RFE + CBR FS technology to perform feature selection and improve the performance of the classifier.

3 Results

3.1 Cross-validation results

The final features of this method were described by FVw_,λ., a value that contains information on the composition of the adjacent w-nucleotides (Gao and Zhang, 2004) and λ-interval nucleotides. The association information was also captured by FVw,_λ. Therefore, this method achieves improved performance compared with using the original Z curve. The following results solidly confirmed this point.

We performed a 5-fold cross-validation test with w ranging from 2 to 4 and λ ranging from 0 to 5. The detailed results are provided in Table 1, showing that area under the curve (AUC) values gradually increased with increasing λ when w was fixed. An examination of the performance under variable values for w and fixed values for λ revealed that the performance for the classifier improved with increasing values for w. As shown in Table 1, we obtained an AUC value of 0.8002 under FV_2,0.

Table 1.

AUC values at different w, λ and penalty parameters c

Variablesa	c	AUC
FV2,0	256	0.8002
FV2,1	64	0.8198
FV2,2	16	0.8256
FV2,3	128	0.8275
FV2,4	64	0.8293
FV2,5	64	0.8365
FV3,0	32	0.8276
FV3,1	1	0.8333
FV3,2	0.5	0.8347
FV3,3	0.25	0.8356
FV3,4	0.5	0.8408
FV3,5	0.25	0.8429
FV4,0	1	0.8344
FV4,1	0.5	0.8369
FV4,2	0.5	0.8386
FV4,3	0.25	0.8413
FV4,4	0.25	0.8436
FV4,5	0.25	0.8449

^aThe subscript of the variables correspond to w and λ.

However, after utilizing the λ-interval nucleotide composition, the performance was improved, for example, the best AUC achieved for this model was 0.8449 through the 5-fold cross-validation test under variable FV_4,5. The AUC was improved 4.47% compared with FV_2,0. The information redundancy and noise in the original features can influence the predictive power of a classifier, and high-dimensional features also increase the time costs for training and prediction. FS technology can mitigate these disadvantages. The SVM-RFE + CBR method was adopted to rank these features in descending order based on the contribution of each feature. Subsequently, the top 100 features were used to constitute the initial feature subset to train and test the model, and the next 100 features were added into the feature subset, followed by prediction using the same methods. This process was repeated until the top 4500 features had been added according to the rank order. The test results of each model were evaluated according to the AUC scores via a 5-fold cross-validation test. The AUC values for different top features are shown in Figure 3A. Among all 4545 features examined, the best AUC of 0.8814 was achieved for the top 800 selective features. The final AUC value was 8.12% higher than that for FV_2,0. To conduct an objective evaluation of this method, we performed a rigorous jackknife test based on the top 800 selected features using the parameters determined via a 5-fold cross-validation test. We obtained an AUC value of 0.8854. As expected, excellent performance was obtained after adopting the λ-interval nucleotide composition and feature selection technology. Those results illustrated that the essentiality of human genes could be well reflected by only sequence information.

Fig. 3.

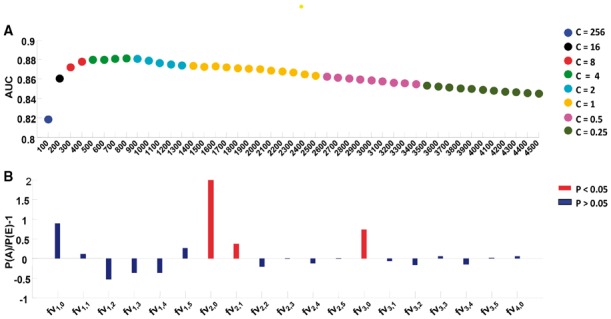
AUC values obtained under different top n features and the contribution of each group. (A) The AUC scores under different top features. Dots with different colors denote different c values. (B) The selective tendentiousness for every variable type. The red bars denote that the selective tendentiousness is statistically significant in hypergeometric distribution test (Color version of this figure is available at Bioinformatics online.)

As we are extremely interested in the actual essential genes in the predicted results, we used the positive predictive value (PPV) to further refine. This evaluation index can be calculated using the formula TP/(TP + FP), where TP (true positive) and FP (false positive) represent the number of real essential and non-essential genes among the positive predictions. Therefore, the PPV reflects the proportion of actual essential genes among the predicted essential genes. We obtained a PPV of 73.05% (TP = 515, FP = 190) using the jackknife test based on the top 800 features. Sn (sensitivity), Sp (specificity) can reflect the correctly predicted percentage of positive and negative samples, respectively. To give a comprehensive evaluation, we additionally calculated Sn, Sp. We obtained Sp with value of 98.19% and Sn with value of 33.97% under the default threshold of LIBLINEAR. Note that the Sn is much lower than Sp and this case is cause by the unbalanced dataset (the size of non-essential genes is much larger than essential genes). One of the simplest cross validation tests is the holdout method. In this procedure, the dataset is separated into two subsets, namely, training and testing datasets. We randomly sampled one-fifth of the positive and negative samples from the benchmark dataset for the training model, and the remaining samples were used as the testing dataset. To comprehensively assess the method used in the present study, we repeated the holdout method 100 times. The composition of our training and testing samples has differences in every holdout process. The mean AUC score was used as the final evaluator. A mean AUC score of 0.8537 with a variance of 1.67e-005 was obtained. Additionally, the proportions of samples in the training and predicting datasets were changed for further investigation. One-tenth of the positive and negative samples were randomly sampled as the training dataset, and the remaining samples were used as the testing dataset. This procedure was repeated 100 times. We obtained a mean AUC score of 0.8347 with a variance of 2.77e-005. These results further confirmed that this method was robust and accurate.

3.2 Different contributions of each group of variables to the classification ability

Features with fixed w and λ values correspond to a specific group of variables. A total of 19 special groups were obtained, namely, fv_1,0, fv_1,1, fv_1,2 …. fv_1,5; fv_2,0, fv_2,1 …. fv_2,5; fv_3,0, fv_3,1 …. fv_3,5 and fv_4,0. We calculated the percentage of features in these groups, and the results are provided in Table 2.

Table 2.

Feature details for every variable type in the top 800 selective features

Variables	No. (A)	No. (E)	P(A)	P(E)	P(A)/P(E) - 1	P value	AUC	C
fv1,0	3	9	0.0038	0.0020	0.8938	0.200495	–	–
fv1,1	7	36	0.0088	0.0079	0.1047	0.452683	0.7220	1024
fv1,2	3	36	0.0038	0.0079	−0.5266	0.965324	0.6216	64
fv1,3	4	36	0.0050	0.0079	−0.3688	0.900314	0.6028	1024
fv1,4	4	36	0.0050	0.0079	−0.3688	0.900314	0.6018	128
fv1,5	8	36	0.0100	0.0079	0.2625	0.292801	0.6302	256
fv2,0	19	36	0.0238	0.0079	1.9984	1.60E-06	0.7902	64
fv2,1	35	144	0.0438	0.0317	0.3809	0.024077	0.7551	1024
fv2,2	20	144	0.0250	0.0317	−0.2109	0.906339	0.6841	1024
fv2,3	25	144	0.0313	0.0317	−0.0137	0.566007	0.6633	512
fv2,4	22	144	0.0275	0.0317	−0.1320	0.802176	0.6856	1024
fv2,5	25	144	0.0313	0.0317	−0.0137	0.566007	0.6816	1024
fv3,0	44	144	0.0550	0.0317	0.7359	7.89E-05	0.8236	2
fv3,1	94	576	0.1175	0.1267	−0.0729	0.821727	0.7652	8
fv3,2	84	576	0.1050	0.1267	−0.1715	0.983389	0.7125	32
fv3,3	107	576	0.1338	0.1267	0.0554	0.272681	0.7168	1024
fv3,4	86	576	0.1075	0.1267	−0.1518	0.970308	0.7027	64
fv3,5	103	576	0.1288	0.1267	0.0159	0.44446	0.6983	1024
fv4,0	107	576	0.1338	0.1267	0.0554	0.272681	–	–

Notes: The feature groups statistically significant in hypergeometric distribution test are indicated bold font.

No. (A): feature numbers in the top 800 features; No. (E): feature numbers in the original variable FV_{4, 5}.

P(A): actual frequency that variables in the top 800 features, P(A) = No.(A)/800; P(E): expected frequency that variables in FV_4,5, P(E) = No.(E)/4545.

P value: hypergeometric distribution test.

For each group, there were two frequencies: P(A), which denotes the actual frequency of features in each group appearing in the top 800 selected features, and P(E), which denotes the expected frequency of the features in each group appearing in the original 4545 features. Therefore, P(A) was obtained based on the number of selected features in each group divided by 800, and P(E) was calculated by dividing the number of total features in each group by 4545. P(A) and P(E) are listed in columns 4 and 5, respectively. If P(A) is higher than P(E), then the group makes a higher-than-average contribution to the identification of essential genes. We calculated the selected tendentiousness using the formula P(A)/P(E)-1, and the results are listed in column 6 of Table 2. We further conducted a hypergeometric distribution test for each group, and the p values are listed in column 7. Figure 3B and Table 2 show that fv_2,0 (p = 1.60E-06), fv_2,1 (p = 0.024077) and fv_3,0(p = 7.89E-05) are preferentially selected and are statistically significant. These results demonstrated that there are strong signals for classifying essential and non-essential genes when the character interval is equal to zero or one, but the other groups did not show these strong signals. To further confirm this result, the variables fv_2,0, fv_2,1, fv_2,2, fv_2,3, fv_2,4, fv_2,5 and fv_3,0, fv_3,1, fv_3,2, fv_3,3, fv_3,4 and fv_3,5 were used as input features. Improved performance was obtained under fv_2,0, fv_2,1 and fv_3,0 compared with the other groups (Table 2, column 8). Those results demonstrated that the shorter interval association provides more information. However, longer interval association can still play an independent role. Hence, integrating the interval information into adjacent ones could significantly improve our classifier’s capacity of discernment (Table 1).

3.3 A web server for predicting essential genes in human

To facilitate the use of interested researchers, we constructed a user-friendly online web server named Pheg (Predictor of human essential genes), which is freely accessible at http://cefg.uestc.edu.cn/Pheg. Pheg’s algorithm is based on the λ-interval Z curve. Additional parameters are not necessary, making this server convenient to use. Pheg can predict whether a query gene (or multi query genes) with FASTA format is (are) essential using only the CDS region of a gene (or multi genes) as input. We integrated logistic regression into the Pheg server to estimate the reliability of the predicted results. Hence, this server can output a probabilistic estimated value as a measurement of gene essentiality for the inputted coding region. This is the first available server for predicting human gene essentiality. Comparatively, some computational models have been proposed for the other eukaryotes however all of them did not provide online prediction service. We re-predicted the genes in the benchmark dataset via Pheg and obtained an AUC = 0.9249 and PPV = 83.84%. A total of 612 genes were identified as essential genes among the 1516 positive samples. This means the number of false negative samples is 904 and tends to be a quite large number. However, this case is pervasive in the issue of essential gene prediction because the researchers try to keep a high TN proportion in order to correctively deal with a very high number of negative samples. Among the 10 499 negative samples in our benchmark, 118 ones were predicted as essential genes by Pheg. To estimate how many genes among those predictions are real essential genes, we calculated precisions using 5-fold, 10-fold, 15-fold and 20-fold cross-validation tests, and we obtained precisions with values of 70.43%, 71.63%, 72.48%, 72.22%, which were approximately 70%. Hence, we expect that 82 (118 × 70%) are correctly predicted essential genes. The information for these 118 genes is provided in Supplementary Material S3.

Addtionally, we used these 118 gene sequences to conduct a BLAST (Basic Local Alignment Search Tool) search against essential genes in the genome of Mus musculus (mouse). The current mouse essential gene set is accessible in the OGEE database (Chen et al., 2012). Considering that no BLAST program is embedded in OGEE, we downloaded the essential gene annotations (gene_essentiality) at (http://ogee.medgenius.info/downloads/) and extracted the essential gene annotation of M. musculus. We obtained the essential gene sequences according to the annotations (http://ogee.medgenius.info/downloads/). A BLAST search was performed via ncbi-blast-2.2.30+-win64.exe (Shiryev et al., 2007) using the data from OGEE, and homologs for 20 genes were identified (e value < 1e-100) among the 118 predicted essential genes. The details for these 20 genes are provided in Supplementary Material S4. The Exome Aggregation Consortium (ExAC) incorporates high-quality exome sequencing data, and it provides rare opportunity to investigate loss-of-function (LoF) intolerance of a gene via quantitative index pLI (Lek et al., 2016). Herein, The 20 genes identified as essential were further investigated using ExAC Browser (http://exac.broadinstitute.org/). Two-sample t-test illustrated that the mean pLI values between those 20 predicted essential genes and those remained non-essential genes in our negative dataset is significantly different (P < 0.05), indicating functions of the 20 predicted genes are more vital. These results illustrated that at least a part of these 118 genes have higher probability to be factually essential genes and have been overlooked in the essential gene screening in previous experimental studies. Hence, Pheg sever could be used to predict essentiality for anonymous gene sequences of human and closely related species, and identifying novel essential genes using Pheg may supplement the essential gene list of human.

4 Discussion

The Z curve has been widely used in the field of bioinformatics for tasks such as protein coding gene identification (Chen et al., 2003; Guo et al., 2003; Guo and Zhang, 2006; Hua et al., 2015; Zhang and Wang, 2000), promoter recognition (Yang et al., 2008), translation start recognition (Ou et al., 2004), recombination spots recognition (Dong et al., 2016), and nucleosome position mapping (Wu et al., 2013). However, correlation and λ-interval nucleotide composition have not been incorporated into the Z curve method. In the present study, we present a λ-interval Z curve based on Z curve theory. The DNA sequence can be understood as an ordinary character sequence; therefore, the method proposed in the present study has the potential for applications in mining characteristics from other character sequences and can be used as a universal feature extraction method for DNA sequences.

Based on the λ-interval Z curve, we obtained excellent performance in human essential gene identification. This excellent performance might be attributable to the following points: First, we introduced the concept of intervals, reflecting association information and the λ-interval nucleotide composition. Second, we used feature selection technology in the present study. Thus, noisy and redundant features could be removed from the original features. Table 2 shows the improved performance obtained under fv_2,0, fv_2,1 and fv_3,0 compared with the other variable groups. Further comparison of these results with other feature groups shown in Table 2, and this comparison shows that the AUC values obtained with λ-interval variables are smaller than those obtained with adjacent variables. However, the performance can be improved after adding λ-interval oligonucleotide association information (see Table 1). Hence, the λ-interval Z curve should reflect additional important information for essential genes that cannot be contained in adjacent nucleotide association information.

In 2005, Chen and Xu used a neural network and SVM to predict the dispensability of proteins in the yeast S. cerevisiae based on the protein evolution rate, protein-interaction connectivity, gene-expression cooperativity and gene-duplication data (Chen and Xu, 2005). The next year, Seringhaus et al. only used 14 features to predict essential genes in S. cerevisiae and obtained a PPV = 0.69 (Seringhaus et al., 2006). Yuan et al. assembled a comprehensive list of 491 candidate genomic features to predict a lethal phenotype in a knockout mouse using three machine learning methods (Yuan et al., 2012), and the best AUC value was 0.782. In 2015, Lloyd et al. investigated the relationship between phenotype lethality and gene function, copy number, duplication, expression levels and patterns, rate of evolution, cross-species conservation, and network connectivity, and the random forest-based model used in this study achieved an AUC of 0.81, which is significantly better than that obtained by random guessing (Lloyd et al., 2015). Those previous researches in three eukaryotes illustrated classifiers can gave satisfactory prediction through combining sequence information with other features. For human essential gene identification, we only used the sequence composition and interval association information in the present study and still obtained an AUC of 0.8854. Considering that this result is better than the results obtained in previous studies using integrated features, the gene essentiality of the human genome can be accurately reflected based on only the sequence information.

We also surveyed two other properties related to gene essentiality. Homologous genes between human and other 17 species were downloaded from HCOP (http://www.genenames.org/cgi-bin/hcop). These data were used for calculating how many species maintain homologous genes compared with human. Results of two-sample t-test illustrated that there is significant difference for persistence value between essential and non-essential genes (P = 4.9493e-214). The mean persistence for essential genes was 12.7, whereas the mean persistence for non-essential genes was 8.3. We also downloaded the human protein-protein interaction data (BIOGRID-ORGANISM-3.4.139.mitab.zip) from the BioGRID database (Stark et al., 2006). Results of network topology analysis revealed there is significant difference in the degree of connectivity between essential and non-essential genes via the two-sample t-test (P = 1.6160e-229). The mean connectivity degree for essential genes was 76, whereas the mean connectivity degree for non-essential genes was 19. Thus, essential genes tend to maintain persistence in more species and have more neighbors in protein-protein interaction networks than non-essential genes. If the two types of features are integrated in the future we think the classifier of essentiality could be further improved.