Different Epidemic Curves for Severe Acute Respiratory Syndrome Reveal Similar Impacts of Control Measures

Abstract

Severe acute respiratory syndrome (SARS) has been the first severe contagious disease to emerge in the 21st century. The available epidemic curves for SARS show marked differences between the affected regions with respect to the total number of cases and epidemic duration, even for those regions in which outbreaks started almost simultaneously and similar control measures were implemented at the same time. The authors developed a likelihood-based estimation procedure that infers the temporal pattern of effective reproduction numbers from an observed epidemic curve. Precise estimates for the effective reproduction numbers were obtained by applying this estimation procedure to available data for SARS outbreaks that occurred in Hong Kong, Vietnam, Singapore, and Canada in 2003. The effective reproduction numbers revealed that epidemics in the various affected regions were characterized by markedly similar disease transmission potentials and similar levels of effectiveness of control measures. In controlling SARS outbreaks, timely alerts have been essential: Delaying the institution of control measures by 1 week would have nearly tripled the epidemic size and would have increased the expected epidemic duration by 4 weeks.

Editor’s note: An invited commentary on this article appears on page 517, and the authors’ response appears on page 520.

On November 16, 2002, the first known case of atypical pneumonia occurred in Guangdong Province in southern China (1). In late February 2003, the infection spread from Guangdong to Hong Kong. From there it spread by airline throughout the world and seeded outbreaks in Vietnam, Singapore, and Canada (2–4). On March 12, 2003, the World Health Organization issued a global alert. On March 15, the World Health Organization issued a second global alert and provided a case definition and a name, severe acute respiratory syndrome (SARS), for the new disease (1). By this time, Hong Kong, Vietnam, Singapore, and Canada had instituted general infectious disease control measures, such as quarantine, isolation, and strict hygiene measures in hospitals (1). The etiologic agent of the disease, a coronavirus, was identified on April 16, 2003 (5). Estimates of important epidemiologic measures such as the case-fatality rate and the incubation period were reported in May 2003 (6–8).

Despite the rapid progression of understanding of the new disease, differences between the epidemic curves (numbers of probable SARS cases by date of symptom onset) have been awaiting further explanation. For the affected regions, these epidemic curves have been publicly available from the end of March 2003 onwards (9), and they reveal distinct temporal patterns in numbers of SARS cases. This is especially remarkable for the epidemics in Hong Kong, Vietnam, Singapore, and Canada, since these epidemics started almost simultaneously in late February 2003 and similar control measures were put in place at almost the same time in March 2003 (figure 1, parts a–d). The question arises as to whether the affected regions differed in terms of transmission potential for SARS or effectiveness of control measures. In this paper, we interpret the observed epidemic curves with regard to disease transmission potential and effectiveness of control measures, and we compare the epidemiologic profiles of SARS outbreaks in Hong Kong, Vietnam, Singapore, and Canada.

FIGURE 1. Epidemic curves (numbers of cases by date of symptom onset) for severe acute respiratory syndrome (SARS) outbreaks in a) Hong Kong, b) Vietnam, c) Singapore, and d) Canada and the corresponding effective reproduction numbers (R) (numbers of secondary infections generated per case, by date of symptom onset) for e) Hong Kong, f) Vietnam, g) Singapore, and h) Canada, 2003. Markers (white spaces) show mean values; accompanying vertical lines show 95% confidence intervals. The vertical dashed line indicates the issuance of the first global alert against SARS on March 12, 2003; the horizontal solid line indicates the threshold value R = 1, above which an epidemic will spread and below which the epidemic is controlled. Days are counted from January 1, 2003, onwards.

DATA

Observed epidemic curves

The epidemic curve is the number of reported cases by date of symptom onset. For each reported case i, we denote the symptom onset date by t_i. For the SARS epidemics in Hong Kong, Vietnam, and Singapore, we derived the dates of symptom onset from epidemic curves provided by the World Health Organization (9). For Canada, we used the epidemic curve provided by Health Canada (10).

Observed distribution of generation intervals

The generation interval, denoted by τ, is the time from symptom onset in a primary case to symptom onset in a secondary case. Sometimes this generation interval is called the serial interval (8) or generation time (11). The generation intervals observed during the SARS outbreak in Singapore are well described by a Weibull distribution with a shape parameter α and a scale parameter β, with values corresponding to a mean generation interval of 8.4 days and a standard deviation of 3.8 days (8). We denote this distribution by τ ∼ w(τ|α,β).

ESTIMATION OF REPRODUCTION NUMBERS

Reproduction numbers

The key epidemiologic variable that characterizes the transmission potential of a disease is the basic reproduction number, R₀, which is defined as the expected number of secondary cases produced by a typical primary case in an entirely susceptible population (12–15). When infection is spreading through a population, it is often more convenient to work with the effective reproduction number, R, which is defined as the actual average number of secondary cases per primary case. The value of R is typically smaller than the value of R₀, and it reflects the impact of control measures and depletion of susceptible persons during the epidemic. If R exceeds 1, the number of cases will inevitably increase over time, and a large epidemic is possible. To stop an epidemic, R needs to be persistently reduced to a level below 1. Estimation of R is a simple affair if there is information about who infected whom. Then it is possible to construct an infection network (11), wherein cases are connected if one person infected the other. Estimation of R involves simply counting the number of secondary infections per case.

A likelihood-based estimation procedure

Often, estimation of the effective reproduction number is a complicated affair, because only the epidemic curve is observed and there is no information about who infected whom. Recent analyses of closely monitored epidemics have shown that it is possible to estimate the probability that one person has infected another if the spatial locations of the infected persons are available (11, 16). However, when only times of symptom onset are available, most investigators resort to approximating R by assuming an exponential increase in the number of cases over time (8, 17) or by fitting a specific model that summarizes assumptions about the epidemiology of the disease (7, 18, 19). Such assumptions can be avoided by using a likelihood-based estimation procedure that infers “who infected whom” from the observed dates of symptom onset as provided by the epidemic curve. However, the computational burden of a straightforward numerical evaluation of the likelihood appears to be enormous, since it requires consideration of all possible infection networks, and even for a small outbreak of 50 cases there are almost 7 × 10⁸² possible infection networks (see Appendix 1).

Here we show that it is possible to obtain likelihood-based estimates of R while avoiding the computational problems if we use pairs of cases rather than the entire infection network. The relative likelihood p_ij that case i has been infected by case j, given their difference in time of symptom onset t_i– t_j, can be expressed in terms of the probability distribution for the generation interval. This distribution for the generation interval is available for many infectious diseases, and we denote it by w(τ). The relative likelihood that case i has been infected by case j is then the likelihood that case i has been infected by case j, normalized by the likelihood that case i has been infected by any other case k:

The effective reproduction number for case j is the sum over all cases i, weighted by the relative likelihood that case i has been infected by case j:

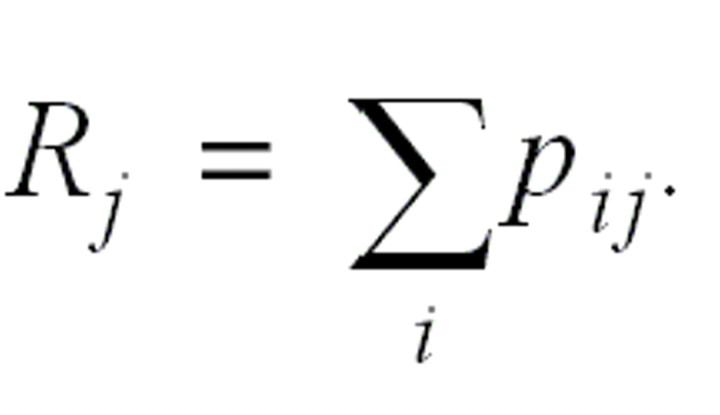
Note that we are not making any assumption regarding the distribution of numbers of secondary infections per case (i.e., the p_ij are independent in j). Additional detail on the derivation of these equations is provided in Appendix 1. The estimation algorithm allows estimation of the effective reproduction numbers for infectious diseases at a finer temporal resolution under more general assumptions than was previously possible.

Testing the estimation procedure with simulated data

To test how well the estimation procedure approximates the underlying value of an effective reproduction number during a typical SARS outbreak, we estimate the effective reproduction numbers from simulated epidemic curves. We have constructed a stochastic, individual-based model that simulates epidemic processes with exactly specified properties. The model allows for a variable effective reproduction number R_t as a function of symptom onset data t, and the model parameters are estimated from observations on the SARS epidemic in Singapore (see Appendix 2). Applying the estimation procedure to simulated epidemic curves shows that most of the estimates are close to the actual reproduction numbers and that a few estimates based on small outbreak sizes are below the actual values that are used in the simulation model. On average, the estimates tend to be lower than the actual values but deviate less than 5 percent from the actual reproduction numbers. If we account for the effects of incomplete reporting and temporal change in generation interval, the estimates become only slightly less accurate, and on average they deviate less than 15 percent from the actual reproduction numbers (see Appendix 2).

RESULTS

For Hong Kong, Vietnam, Singapore, and Canada, we have converted the epidemic curves into the time course of effective reproduction numbers. The results are shown in figure 1, parts e–h. These four large outbreaks were sparked almost simultaneously by the same index patient. All regions have faced erratic “super-spread events” wherein cases produced more than 10 secondary infections. These “super-spread events” show up in parts e–h of figure 1 as temporary increases in effective reproduction numbers around the symptom onset date of the index case for the “super-spread event.” In Hong Kong, Vietnam, and Singapore, there were “super-spread events” marking the start of the outbreak. In Hong Kong, Singapore, and Canada, there were “super-spread events” after control measures were implemented.

During the early phase of the SARS epidemic, before the first World Health Organization global alert was issued on March 12, 2003, the average effective reproduction numbers were markedly similar across the regions: Each case produced approximately three secondary infections (table 1). A value of R slightly higher than 3 is consistent with the observed epidemics in all four regions. Around mid-March, control measures were implemented in all regions, and during this period the effective reproduction numbers decreased sharply. For some regions, the effective reproduction numbers continued to decrease at a slow pace, suggesting improvement of control measures while the epidemic was going on. After the first World Health Organization global alert, each case produced approximately 0.7 secondary infections (table 1). A value of R = 0.7 is consistent with all four regions, except Canada. By the beginning of July 2003, transmission of the SARS virus had been stopped in all regions where the infection was introduced in late February 2003 (1).

TABLE 1.

Average daily effective reproduction number (R) for cases of severe acute respiratory syndrome (SARS) with a symptom onset date before or after the issuance of the first global alert against SARS on March 12, 2003, for regions where infection was introduced in late February 2003

Symptom onset	Hong Kong			Vietnam			Singapore			Canada
	R	95% CI*		R	95% CI		R	95% CI		R	95% CI
Before alert	3.6	3.1, 4.2		2.4	1.8, 3.1		3.1	2.3, 4.0		2.7	1.8, 3.6
After alert	0.7	0.7, 0.8		0.3	0.1, 0.7		0.7	0.6, 0.9		1.0	0.9, 1.2

* CI, confidence interval.

To explore the range of epidemic curves that can result from the same epidemic process, we performed extensive computer simulations using a model of epidemics with characteristics similar to those of SARS (see Appendix 2). The outcome of 10,000 simulations shows a highly variable epidemic size and epidemic duration: The mean epidemic size is 685 cases (95 percent confidence interval (CI): 27, 2,446), and the mean epidemic duration is 98 days (95 percent CI: 32, 187). All observed sizes and durations of SARS epidemics are within this very wide range of possible outcomes resulting from chance alone. Additionally, we used computer simulations to explore the effect of the timing of implementation of control measures on the epidemic size and duration, in a setting that is typical for the SARS outbreaks. The simulation results show a high sensitivity to the timing of implementation of control. On average, a 1-week delay in implementation of control measures results in a 2.6-fold increase in mean epidemic size and a 4-week extension of the mean epidemic duration.

DISCUSSION

This study showed that there exists a direct relation between the epidemic curve and the time course of the reproduction number R. This relation is determined by the distribution of the generation intervals. The relation can be used to monitor the combined effects of transmission potential and control measures during an epidemic. We have shown that the epidemic curves for SARS in Hong Kong, Vietnam, Singapore, and Canada, though apparently different, are all consistent with a single time course of the effective reproduction numbers for SARS. This apparent difference in epidemic curves arises because chance effects, such as the occurrence of a rare “super-spread event,” leave a lasting trace on the epidemic curve. In contrast, chance events manifest only as temporary increases in the reproduction number. Our analysis of the epidemic curves for SARS shows that one should be cautious in taking a smaller epidemic size and a shorter epidemic duration as proof of better infection control.

We have presented the relation between observed epidemic curves and inferred reproduction numbers from an infection-network perspective. We are certainly not the first researchers to do so: Infection networks have been used extensively in the area of sexually transmitted diseases (20), and an infection-network perspective was adopted to analyze a closely observed foot-and-mouth epidemic in Great Britain (11). Our contribution is the derivation of likelihood-based estimates of effective reproduction numbers, requiring only the observed time of symptom onset for the observed cases. The use of a likelihood framework provides a set of powerful tools for inference, uncertainty analysis, and model selection (20); the use of only time of symptom onset allows us to apply this method to routinely collected epidemic-curve data. However, estimation of effective reproduction numbers from epidemic curves has an intrinsic limitation that should be kept in mind: The effective reproduction number contains entangled information about the transmission potential (i.e., the basic reproduction number) and the effectiveness of control measures. These two components can be disentangled only when we obtain additional information—for example, about the time of implementation of control measures. Moreover, individual contributions to the effective reproduction number are entangled if their date of symptom onset is smaller than the generation interval. This limitation can be overcome if more detailed information on who infected whom is available (see Appendix 1).

For the SARS outbreak in Hong Kong, it is possible to compare our results with previously published estimates. Our estimate of the average effective reproduction number prior to the first global alert (R = 3.6, 95 percent CI: 3.1, 4.2) is more precise than the estimate obtained by assuming an exponential increase in the number of cases (R = 3.5, 95 percent CI: 1.5, 7.7) (8) and more precise than the estimated lower bound excluding “super-spreading events” (R > 2.7) (7). Our estimate of the average effective reproduction number after the first global alert (R = 0.7, 95 percent CI: 0.7, 0.8) is much higher than the previously estimated lower bound excluding “super-spread events” (R > 0.14) (7). This comparison illustrates that the estimation algorithm presented here allows more precise estimation of the effective reproduction numbers for infectious diseases under more general assumptions than was previously possible.

The effectiveness of control measures against SARS can be estimated if it is assumed that the sudden decrease in the effective reproduction number for SARS around the time of the first global alert was indeed caused by the implementation of control measures. The decrease in the reproduction number from 3 to 0.7 then suggests that the control measures taken around this time prevented approximately 77 percent (100 × (3 – 0.7)/3 percent ≈ 77 percent) of all potential secondary infections. This effectiveness suffices for eventually stopping infections in situations where each case causes up to 4.3 (1/(1 – 0.77) ≈ 4.3) secondary infections. Recalling that before implementation of control measures, each SARS case produced, on average, approximately three secondary infections, this effectiveness has been barely sufficient for the eventual interruption of the chain of human-to-human transmission of the SARS virus.

As the direct threat of a worldwide SARS epidemic has waned, the question arises as to how we can use the experience with SARS to improve infection control against new infectious diseases. Our analysis of the epidemic curves for SARS, as reported for Hong Kong, Vietnam, Singapore, and Canada, shows how crucial the rapid implementation of control measures has been in limiting the impact of the epidemics, both in terms of preventing more casualties and in terms of shortening the period during which stringent infection control measures were in place. A first lesson from the several SARS epidemics is that a timely alert against a new infectious disease is most essential. Our analysis suggests that the control measures implemented prevented approximately three quarters of all potential secondary infections; this may be insufficient to stop another new infectious disease. A second lesson, then, is that it is crucial to estimate the transmission potential of a new emerging disease as soon as possible and to establish whether additional, more stringent control measures are required.

ACKNOWLEDGMENTS

This article benefited greatly from discussions with members of the World Health Organization-SARS modeling working group (Drs. Roy Anderson, Kari Auranen, Neil Ferguson, Nigel Gay, Marc Lipsitch, Mick Roberts, and Ping Yan) and from comments by Drs. Hans Heesterbeek, Nico Nagelkerke, and Siem Heisterkamp.

APPENDIX 1

Estimation Procedure

Infection networks

An outbreak of an infectious disease can be described as a directed network in which the nodes represent cases and the directed edges between the nodes represent transmission of infection between cases. We consider an outbreak of n reported cases, of which q cases have contracted infection from outside the population. This leaves n – q persons whose primary case is among the reported cases. We label the cases by an index i ϵ{1, º, n}. Because each case has exactly one primary case, each node in the infection network must have exactly one incoming edge. Because a case patient cannot have infected himself or herself, there cannot be any edges from a node to itself. The structure of a network that satisfies these constraints can be uniquely represented by a vector v, of which the ith element v(i) denotes the label of the primary case that has infected the case with label i. We use v(i) = 0 to refer to sources of infection outside the population. We denote the entire set of all infection networks that satisfy the above constraints by V. The number of different network structures in V is (n – q)^n–1, since, for any of the n – q nonimported cases, there are n – 1 possible primary cases. Note that the set V includes network structures with cycles and that such structures cannot represent transmission between cases.

Likelihood inference for infection networks

We use a probability model to infer the likelihood that a specific infection network v underlies the observed epidemic curve t. The probability model is built on the assumption that transmission of infection occurred only among the reported n cases. A key element in this model is the probability density function for the generation interval, w(τ|θ). Here, τ is the generation interval and θ is a vector of parameters that specify the probability distribution. We require w(τ|θ) = 0 for τ < 0. All infection networks with cycles have at least one negative generation interval, and these networks are assigned zero probability by this requirement. In the absence of an observed epidemic curve, each infection network is considered equally likely. This is equivalent to requiring independence between unobserved transmission events from case j to case i and from case j to any other case k. Henceforth we will refer to this requirement as the “independence condition.” In Appendix 2, we simulate epidemic processes that do not meet the above-mentioned technical conditions, and we use these simulations to test for the robustness of the likelihood-based estimation procedure.

Likelihood functions

The probability of observing epidemic curve t, given the parameters θ for the generation interval and v for the infection network, is

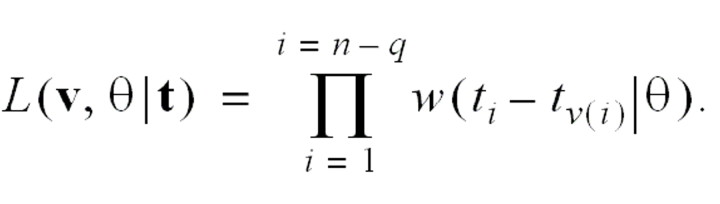
Because we are interested in the likelihood of sets of infection networks, we sum the likelihood over networks in a set. This requires a “weight function” c(v|θ) for each infection network. The independence condition implies that c(v|θ) is a constant, denoted c. The integrated likelihood over the set of all networks is therefore

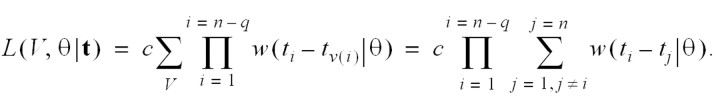
The integrated likelihood over the set of all infection networks in which case k has been infected by case l is

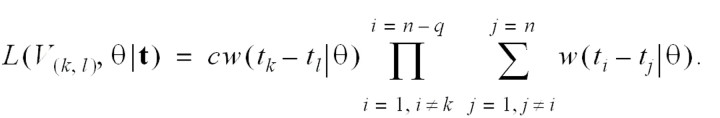
Estimation

The relative likelihood that case k has been infected by case l is

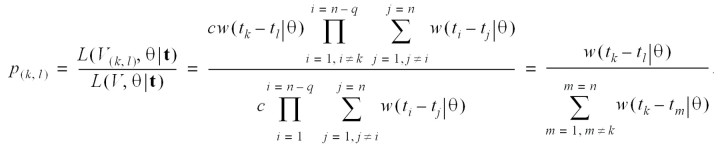
The relative likelihood of case l’s infecting case m is independent of the relative likelihood of case l’s infecting any other case k (by the independence condition). The distribution of the effective reproduction number for case l is

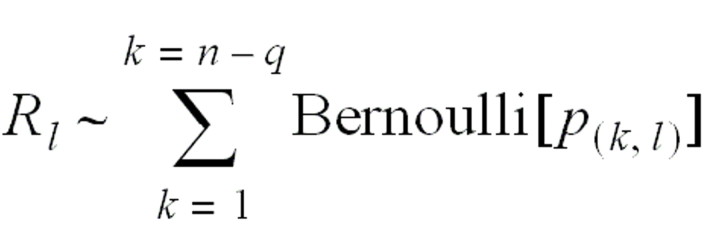
with an expected value

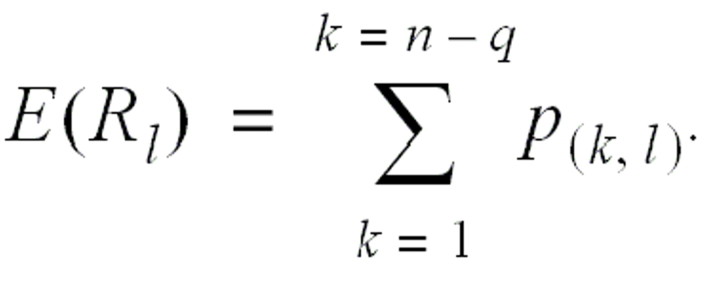
The average daily reproduction number R_t is calculated as the arithmetic mean over R_lfor all of those cases l who show the first symptoms of illness on day t.

Simultaneous estimation of parameters v and θ

When we have observed transmission of infection between some pairs of cases, it is possible to infer both infection network (v) and generation interval (θ) simultaneously. We must consider the likelihood

where (k,l) denotes all pairs of cases for which any case k is known to have been infected by another case l. Estimates for both generation interval (θ) and infection network (v) are obtained by maximizing this equation using the expectation-maximization algorithm (21). Note that the independence condition applies only to the unobserved transmission events.

APPENDIX 2

Testing the Estimation Procedure with Simulated Data

A stochastic simulation model

We have constructed a stochastic, individual-based model to generate infection networks that result from epidemic processes with exactly specified properties. We use such simulated infection networks for testing the estimation procedure and for exploring the expected distribution of epidemic size and epidemic duration. The model allows for a variable effective reproduction number R_t as a function of symptom onset date t. In the simulations described here, we set the effective reproduction number to a value of R_t = 3 for cases with a symptom onset date before the issuance of the first global alert on March 12, 2003, and to a value of R_t = 0.7 for cases with a symptom onset date on or after March 12, 2003. The model draws for each case the number of secondary infections from a negative binomial distribution, which is determined by the mean R and the shape parameter k_t = (R_t + R_t²)/σ_t². The model uses values of k_t = 0.18 for cases with a symptom onset date before March 12, 2003, and k_t = 0.08 for cases with a symptom onset date on or after March 12, 2003; these values correspond to the distribution of the number of secondary infections per case as observed during the severe acute respiratory syndrome (SARS) outbreak in Singapore (4). The model draws for each new infection the generation interval from a Weibull distribution with a mean and standard deviation of 8.4 days and 3.8 days, respectively (8). Each simulation is started by one index case that produces at least 10 secondary cases, which corresponds to a SARS outbreak that is started by a so-called “super-spread event,” to ensure that the epidemic takes off.

Accuracy of the estimation procedure

We test for accuracy of the proposed estimation procedure by first generating 20 epidemic curves using the stochastic simulation model and then estimating the time course of the reproduction number for the simulated epidemic curves using the proposed method. The estimated reproduction numbers tend to be close to the actual values used in the simulation model, except for simulated epidemic curves with a small number of cases in which the estimated reproduction numbers are well below the actual values (the actual values of the reproduction numbers for the simulated epidemic curves were 3 and 0.7 for cases with symptom onset data before and after March 12, 2003, respectively; the average estimated values were 3.09 and 0.68).

The effect of incomplete reporting

The estimation procedure supposes that all infected persons will show overt clinical symptoms and that all cases will be reported, an assumption that might not be correct for an infectious disease like SARS. To test for the impact of incomplete reporting on the estimated effective reproduction number, we modified the model such that each infected individual would have a probability of his or her case’s being reported of 0.5. The resulting estimates were only slightly less accurate than they were with complete reporting (the actual values of the reproduction numbers for the simulated epidemic curves were 3 and 0.7 for cases with symptom onset data before and after March 12, 2003, respectively; the average estimated values were 2.69 and 0.70).

The effect of changes in generation interval

The estimation procedure presented here supposes that the distribution of generation intervals does not change over time. However, for the SARS epidemic in Singapore, there was a tendency for the generation interval to decrease after control was implemented (8). Cases with a symptom onset date before March 12, 2003, had a mean generation interval of 10.0 days and a standard deviation of 2.8 days, whereas cases with a symptom onset date on or after March 12, 2003, must have had a mean generation interval of 8.2 days and a standard deviation of 3.9 days (8). To test for the impact of this temporal change in the duration of the generation interval, we modified the model by using two different Weibull distributions, one before March 12 and the other one on or after March 12, each parameterized according to the Singapore data. The estimates were, on average, slightly lower than they were with use of the same generation interval throughout the epidemic (the actual values of the reproduction numbers of the simulated epidemic curves were 3 and 0.7 for cases with symptom onset data before and after March 12, 2003, respectively; the average estimated values were 2.60 and 0.66 over 20 simulations).

Received for publication October 27, 2003; accepted for publication March 29, 2004.