Abstract
Many mechanical properties of cortical bone are largely governed by the underlying microarchitecture; however, the influence of microarchitecture on the fatigue life of bone is poorly understood. Furthermore, imaging-based studies investigating intracortical microarchitecture may expose bone samples to large doses of radiation that may compromise fatigue resistance. The purpose of this pilot study was to 1) investigate the relationship between intracortical microarchitecture and the fatigue life of human bone in compression and 2) examine the effects of synchrotron irradiation on fatigue life measurements. Cortical samples were prepared from the femoral and tibial shafts of three cadaveric donors. A subset of samples was imaged using synchrotron X-ray microCT to quantify microarchitecture, including porosity, canal diameter, lacunar density, lacunar volume, and lacunar orientation. A second group of control samples was not imaged and used only for mechanical testing. Fatigue life was quantified by cyclically loading both groups in zero-compression until failure. Increased porosity and larger canal diameter were both logarithmically related to a shorter fatigue life, whereas lacunar density demonstrated a positive linear relationship with fatigue life (r2 = 45–73%, depending on measure). Irradiation from microCT scanning reduced fatigue life measurements by 91%, but relationships with microarchitecture measurements remained. Additional research is needed to support the findings of this pilot study and fully establish the relationship between intracortical microarchitecture and the compressive fatigue life of bone.
Keywords: Synchrotron radiation imaging, Mechanical fatigue, Irradiation, Porosity, Canal diameter, Lacunar density
Graphical abstract
Highlights
-
•
Increased porosity and larger canal diameters were associated with a shorter compressive fatigue life.
-
•
A higher lacunar density was related to a longer compressive fatigue life.
-
•
Irradiation from synchrotron X-ray microCT scanning reduced fatigue life by 91%.
-
•
The influence of microarchitecture on fatigue life exhibited similar trends for both irradiated and non-irradiated bone.
1. Introduction
Strength is perhaps the most commonly reported mechanical measure of bone quality, which describes the maximum load carrying capacity of bone prior to failure (i.e., permanent damage or fracture) (Hernandez and van der Meulen, 2017). Although impaired bone strength is strongly associated with an increased risk of fracture (Faulkner et al., 2006; Crabtree et al., 2002), not all fractures result from inadequate strength in response to a sudden overload. Some fractures are associated with a mechanical fatigue phenomenon, defined as the accumulation of microdamage in response to repetitive loading and cumulative activity. This microdamage has been associated with material property degradation (Carter and Hayes, 1977a), and may eventually lead to failure at submaximal loads (Burr et al., 1990; Burr et al., 1998) in the absence of adequate bone repair (i.e., remodeling). Mechanical fatigue is believed to be the predominant etiology of stress fractures in active individuals (Edwards, 2018) and may play an important role in insufficiency fractures, such as atypical femoral fractures in patients on long-term bisphosphonate therapy (Lenart et al., 2009; Shane et al., 2010).
The mechanical fatigue behavior of a material is frequently quantified in terms of its fatigue life, i.e., the number of repetitive loading cycles it can endure before failure. Fatigue life measurements are heavily influenced by specific details of the loading regime, such as the magnitude, frequency, loading ratio, and mode of loading (Zioupos et al., 2007; Carter and Hayes, 1976; Zioupos et al., 2001; Caler and Carter, 1989); however, even when these parameters are held constant, a large degree of scatter in fatigue life is inevitably observed. In fact, two seemingly identical samples subjected to the same loading regime may exhibit fatigue life measurements that vary up to two orders of magnitude (Taylor, 1998). In cortical bone, the apparent density or elastic modulus may account for a portion of this scatter (Taylor et al., 1999; Carter et al., 1981); however, the remaining variance is likely explained by other inherent characteristics, such as intracortical microarchitecture.
The intracortical microarchitecture of secondary bone is made up of transverse Volkmann's canals, longitudinally-oriented osteons that encompass Haversian canals, and the osteocyte lacunar-canalicular network. Monotonic tests of cortical bone have shown that elevated vascular porosity and increased pore size are associated with corresponding reductions in bone stiffness, strength, and fracture toughness (McCladen et al., 1993; Dickerson et al., 1981; Schaffler and Burr, 1988; Yeni et al., 1997). Previous studies utilizing a fracture mechanics approach may partially explain these diminished mechanical properties, suggesting that certain microarchitectural features act as voids causing stress/strain concentrations within the bony matrix (Currey, 1962; Yeni et al., 2001; Nicolella et al., 2006), thereby facilitating the initiation of microcracks and directing further crack propagation (Reilly, 2000; Carter and Hayes, 1977b). On the other hand, there is research to suggest that intracortical microarchitecture may provide beneficial toughening mechanisms, as Haversian systems and cellular networks may act as barriers to microcrack growth by deflecting or arresting propagating cracks (Nalla et al., 2003; O'Brien et al., 2005). Although the influence of intracortical microarchitecture on quasi-static mechanical properties has been investigated extensively, there is limited knowledge regarding the relationship between microarchitecture and the fatigue behavior of cortical bone. Zioupos et al. demonstrated the negative effects of increased porosity, which may account for a 49% reduction in the fatigue strength of bone (Zioupos et al., 2007), but the influence of more specific microarchitectural features such as the morphology of lacunar and vascular pores is unknown.
The primary objective of this pilot study was to investigate the relationship between intracortical microarchitecture and the compressive fatigue life of human bone. We focused this initial investigation on compression, because the majority of stress fractures in athletic populations manifest on the ‘compressive’ surfaces of long bones (i.e., the medial surface of the femur (Johnson et al., 1994) and posteromedial surface of the tibia (Boden et al., 2001)). We hypothesized that increased porosity, due to larger vascular canals and more abundant lacunae would be associated with a reduced fatigue life. Intracortical microarchitecture is frequently quantified using high-flux X-ray sources such as synchrotron radiation microCT and desktop X-ray microscopy. Although it is known that radiation doses from common imaging modalities can drastically reduce the strength and fracture toughness of cortical bone (Barth et al., 2010) this issue is rarely addressed. Therefore, a secondary objective of this study was to report the effects of irradiation on the compressive fatigue life or cortical bone.
2. Methods
2.1. Sample preparation
Fresh-frozen cadaveric femoral and tibial bones from three donors (Table 1) with no known history of bone-related diseases were obtained from the University of Calgary's Body Donation Program following institutional approval from the Conjoint Health Research Ethics Board. A total of 56 cylindrical bone cores were extracted from the cortex of the mid-diaphysis with a drill press and subsequently turned down to a ‘dog-bone’ geometry using a mini lathe. The cores were approximately 35 mm in length and 5 mm in diameter; they were oriented along the longitudinal axis of the bone and extracted arbitrarily from all regions around the cortical cross section. The exact dimensions and weight of each core was recorded to calculate the apparent density. The central gauge length, gauge diameter, and transitional radius of the samples were 7, 2.5, and 5.5 mm, respectively. Samples were visually inspected to ensure a smooth surface finish with no obvious machining defects. The samples were then hydrated with phosphate buffered saline (PBS) and stored in a −30 °C freezer.
Table 1.
Demographic information and cause of death for the three donors.
| Donor |
|||
|---|---|---|---|
| 1 | 2 | 3 | |
| Age | 77 | 71 | 99 |
| Sex | Male | Female | Female |
| Height (cm) | 173 | 165 | 157 |
| Weight (kg) | 67.7 | 58.9 | 51 |
| Cause of death | Chronic obstructive pulmonary disease | Chronic renal failure | Congestive heart failure |
2.2. Synchrotron X-ray micro-computed tomography imaging
To address the effects of irradiation on fatigue life measurements, bone samples were split into two groups; 41 samples were allocated to the ‘irradiated group’ (IRR) and imaged using synchrotron X-ray microCT (Biomedical Imaging and Therapy, Canadian Light Source), while 15 samples were not imaged and reserved as non-irradiated controls (CTRL). In the irradiated samples, a 3.6 × 2.4 mm region in the center of the waisted geometry was scanned with a photon energy of 40 keV and a voxel size of 0.9 μm. Scans were performed over 180° of rotation with a rotation step of 0.2° and five-frame averaging for each of the 900 frames. An exposure time of 400 ms per frame and the time required to move between each rotation angle resulted in a total scan duration of 1 h. A PinPoint ion chamber was used to quantify radiation exposure. For the described experimental conditions, the total absorbed dose was 7.9 kGy. The synchrotron scanning protocol was approved by the University of Saskatchewan Research Ethics Board.
2.3. Image processing
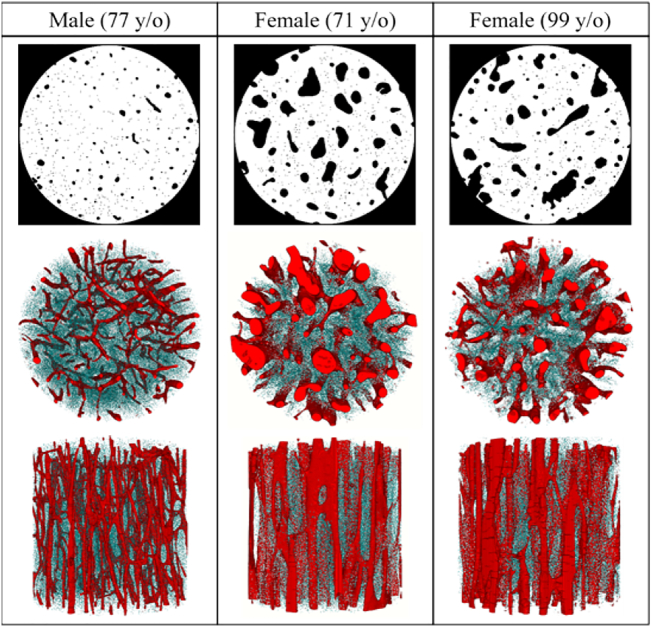
The projections were reconstructed using NRecon software (V 1.4.4, Skyscan-Bruker, Kontich, Belgium) and binned 2 × 2 to create a stack of 1250 slices (1332 × 1332 pixels) with an effective voxel size of 1.8 μm. A series of filters and thresholds were used to segment canals and osteocyte lacunae, creating three separate stacks of binary images containing: 1) only canals, 2) only lacunae, or 3) both canals and lacunae (Fig. 1). The binary volume of canals was obtained using a Gaussian low-pass filter, which effectively ‘smoothed out’ and removed all lacunae. The binary volume of lacunae was obtained using hysteresis thresholding (Dong et al., 2014). First, the canal mask was subtracted from the original image. Then, an initial low threshold was used to select pixels that undoubtedly belonged to lacunae. Finally, a higher secondary threshold was applied to select voxels of a higher intensity but only if it was connected to a voxel previously identified by the initial lower threshold. The binary volumes containing both canal and lacunae were combined to create a mask with both sources of intracortical porosity.
Fig. 1.
A 2D binary mask of the intracortical porosity (top row) and 3D reconstruction of a representative sample from each donor. The transverse (middle row) and longitudinal views (bottom row) illustrate the vast morphological differences in vascular canals (red) and osteocyte lacunae (blue) between the three donors. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
2.4. Quantifying intracortical microarchitecture
The binary volumes of intracortical porosity and canals were used to determine porosity and canal diameter, respectively, using the BoneJ plugin included in the FIJI software package (v1.51, NIH, USA) (Schindelin et al., 2012; Doube et al., 2010). Porosity was quantified as the percentage of void volume (Vo.V) to total volume (TV) within a rectangular region of interest 1.5 mm × 1.5 mm × 2 mm (4.5 mm3). Due to computational demands, lacunar volume, orientation and the total number of lacunae (N.Lc) were measured within a smaller region of interest, 1.12 mm × 1.12 mm × 2 mm (2.5 mm3) using the particle analysis tool included in the BoneJ plugin. Only particles with a volume >10 μm3 were considered, consistent with confocal microscopy measurements of lacunae (McCreadie et al., 2004) and volume limits used in previous synchrotron-based studies (Carter et al., 2013). Lacunar density (N.Lc/BV) was calculated as the N.Lc per cubic millimeter of bone, where bone volume (BV) was defined as TV − Vo.V. Lacunar volume was calculated as the sum of voxels within each lacuna. Lacunar orientation was determined using a best-fit ellipsoid for each lacuna and calculated as the absolute angle (0 to 90°) between the longest axis relative to the loading axis (i.e. the longitudinal axis of the sample).
Measures of lacunar volume and orientation were initially verified using binary images of idealized geometries (i.e., spheres and ellipsoids) with known dimensions and orientations. The fabricated shapes were scaled to have a voxel size equivalent to the processed images (1.8 μm) and analyzed using methods identical to those described above. The relative error between the measured and expected volume was <9% for all the idealized geometries, while orientation demonstrated errors up to 5%, corresponding to an absolute difference of 2.2°. We also examined the accuracy of lacunar shape measurements (i.e., elliptical axes and aspect ratios), but these measures demonstrated relative errors >70%. Thus, although lacunar shape is thought to effect the strain distribution in the bony matrix (Hemmatian, 2017), the resolution of this system was not able to accurately capture these measures and was therefore not included in our analyses.
2.5. Mechanical testing
Mechanical testing was performed at room temperature on a subset of irradiated samples (n = 15) and all control samples (n = 15). Samples were rehydrated in PBS for a minimum of 6 h before being secured with wedge grips in an Instron Electropuls E3000 test frame (Instron, Norwood, MA). This method of sample fixation was shown to provide fatigue life measurements in compression (Loundagin et al., 2018) in line with values reported when compressive platens with machined depressions were used to secure samples (Taylor et al., 1999). Prior to fatigue testing, the initial elastic modulus was quantified with a bone-mounted extensometer (632.29F-30, MTS, Eden Praire, MN). The bone samples were preloaded in compression (100 N) followed by a compressive ramp load to 200 N, corresponding to a stress of approximately 40 MPa. The elastic modulus was calculated from the linear stress-strain curve for the entirety of the ramp load. Samples were then wrapped in PBS-soaked gauze and a custom drip system provided continuous hydration throughout the fatigue tests. Fatigue life was assessed by cyclically loading samples in zero-compression under load control at a frequency of 2 Hz. The stress range of the sinusoidal waveform was 88 MPa with a stress ratio R = 0. Fatigue life was defined as the number of loading cycles until failure, which corresponded to complete fracture in all samples. The peak loading magnitude of 88 MPa corresponds to approximately 5000 μɛ and was chosen as 50% of the ultimate compressive strength (177 MPa). The ultimate compressive strength was previously determined in our lab by monotonically loading cadaveric samples to failure and is comparable to previously reported values for human cortical bone (Reilly and Burstein, 1975; Evans and Vincentelli, 1974; Öhman et al., 2011). Furthermore, a compressive load of 88 MPa has previously elicited fatigue failure within 104 cycles (Zioupos et al., 2007) which would provide a reasonable testing duration to avoid sample degradation.
2.6. Statistical analysis and interpretation
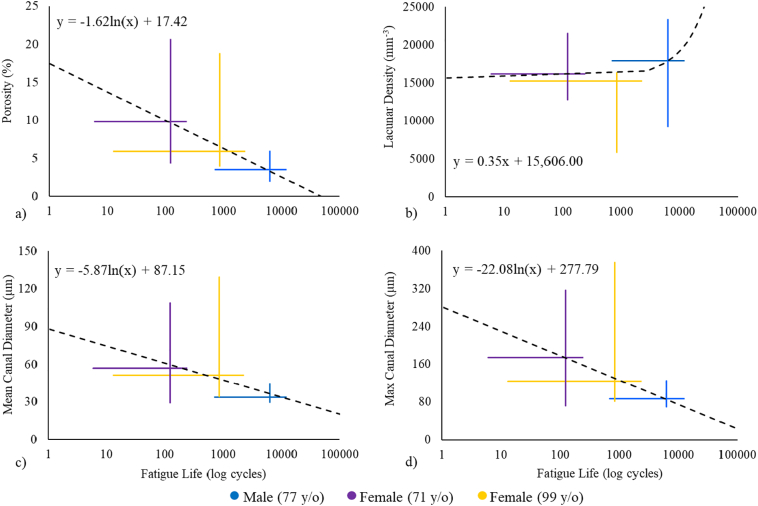
All 41 irradiated samples were used to calculate the means and standard deviations for each microarchitectural parameter to best describe the wide variation of microarchitecture in the donors. The distribution of all experimental variables was assessed using the Shapiro-Wilk test of normality. Apparent density, lacunar density, lacunar volume and lacunar orientation were normally distributed (p ≥ 0.215), while porosity, mean canal diameter, max canal diameter, elastic modulus and fatigue life were not (p ≤ 0.000). Statistical differences between anatomical locations (i.e., tibia and femur) and amongst donors were examined using independent t-tests or univariate ANOVAs, respectively, for the normally distributed variables and Mann-Whitney U or Kruskal-Wallis non-parametric tests for the non-normally distributed variables. When necessary, statistical analyses were followed with post-hoc pairwise comparisons adjusted for Bonferroni correction. Each sample was treated as an independent measure which may be justified given that microarchitectural parameters illustrate considerable variation within the cross-section of a single bone (Cooper et al., 2003). Statistical differences in elastic modulus and fatigue life measurements between irradiated and control samples were examined using non-parametric Mann-Whitney U tests. The relationship between microarchitectural parameters and fatigue life measurements for the irradiated bone were examined using Pearson product-moment correlations with both a linear and logarithmic model. Because the microarchitecture of the control samples was unknown, it was not possible to make direct correlations between microarchitectural parameters and the fatigue life of the control samples. Instead, this relationship was investigated by plotting the range of each microarchitectural parameter obtained from the irradiated samples against the range of fatigue life measurements from the control samples (Fig. 3). All statistical analyses were performed in SPSS (SPSS Inc., Chicago, IL, USA) with α = 0.05.
Fig. 3.
The relationship between the microarchitecture of irradiated samples and the fatigue life of control samples. For each donor the vertical and horizontal crosshairs demonstrate the range microarchitectural parameters from the irradiated samples and fatigue life measurements from the control samples, respectively.
3. Results
3.1. Intracortical microarchitecture
There were no significant differences in apparent density or any microarchitectural measurements between samples obtained from the tibia (n = 13) and femur (n = 28). Table 2 illustrates the individual donor and combined average data pooled across anatomical location. The male donor demonstrated a significantly lower porosity, mean canal diameter, max canal diameter, and lacunar volume than the two female donors. Lacunar density was significantly lower for the 99-year-old female compared to the other two donors (p ≤ 0.045). The 71-year-old female had lower apparent density than the male (p = 0.001) but was not significantly different from the other female donor (p = 0.166). This initial investigation only included three donors, therefore drawing conclusions regarding donor-dependent differences in relation to age or sex is inappropriate. However, and more importantly for the purpose of this study, using samples from three donors was sufficient to obtain significant variation in all microarchitectural features such that correlations between microarchitecture and fatigue life could be investigated.
Table 2.
The median (range: max–min) apparent density and intracortical microarchitectural measures for each donor and combined. Statistical differences between the 3 donors was assessed using a one-way ANOVA.
| Male (77 y/o) | Female (71 y/o) | Female (99 y/o) | Combined | |
|---|---|---|---|---|
| N | 15 | 13 | 13 | 41 |
| Density (g/cm3) |
1.95 (1.88–2.06) |
1.85a (1.76–1.93) |
1.91 (1.72–2.07) |
1.91 (1.72–2.07) |
| Porosity (%) |
3.50 (1.90–6.00) |
9.90a (4.30–20.70) |
5.90a, b (3.90–18.87) |
5.60 (1.90–20.7) |
| Mean canal diameter (μm) |
33.87 (29.79–44.22) |
56.95a (29.17–108.85) |
51.33a (34.35–129.25) |
43.56 (29.17–129.25) |
| Max canal diameter (μm) |
87.07 (69.99–124.97) |
174.14a (72.09–316) |
123.70a (81.86–374.92) |
107.40 (69.99–374.92) |
| Lacunar density (mm−3) |
17,916.40 (9168.40–23,373.20) |
16,218.80 (12,788.80–21,516.00) |
15,261.6a, b (5757.20–16,424.40) |
16,032.40 (5757.20–23,373.20) |
| Lacunar volume (mm3) |
123.36 (93.87–173.23) |
138.10a (119.82–176.73) |
141.90a (133.27–170.77) |
136.77 (93.87–176.73) |
| Lacunar orientation (°) |
42.62 (37.92–72.29) |
50.49 (36.01–59.14) |
47.27 (33.43–53.65) |
47.16 (33.43–72.29) |
Statistically different from the 77-year old male.
Statistically different from both the 71-year-old female and 77-year-old male, p ≤ 0.05.
3.2. Mechanical testing and irradiation
Of the 15 irradiated samples used for mechanical testing, five broke during either set-up or modulus testing, which was an early indicator of the severe material property degradation associated with the imaging protocol. One sample from the control group fractured outside the gauge length during fatigue testing and was removed from the analysis. This left 10 samples from the irradiated group and 14 samples from the control group that could be analyzed following mechanical testing. The median fatigue life for the irradiated group was 43 cycles (range: 2–114 cycles), whereas that for the control group was 468 cycles (range: 6–12,433 cycles; Table 3). This represented a 91% reduction in the fatigue life associated with our synchrotron X-ray microCT scanning protocol. Although the fatigue life was significantly different between the irradiated and control groups (p = 0.004), the elastic modulus was not significantly different between groups (p = 0.322).
Table 3.
The median (range: max–min) elastic modulus and fatigue life of the irradiated (IRR) and control (CTRL) samples. Statistical differences between the irradiated and control samples were only calculated using the pooled sample set (i.e., combined) and examined using non-parametric Mann-Whitney U tests.
| Male (77 y/o) | Female (71 y/o) | Female (99 y/o) | Combined | ||
|---|---|---|---|---|---|
| Irradiated | n (IRR) | 4 | 4 | 2 | 10 |
| Modulus (GPa) | 16.31 (14.76–17.87) |
13.29 (9.11–16.34) |
16.76 (16.62–16.89) |
16.02 (9.11–17.87) |
|
| Fatigue life (cycles) | 44 (25–114) |
32.5 (2–82) |
29 (25–33) |
43a (2–114) |
|
| Control | n (CTRL) | 5 | 6 | 3 | 14 |
| Modulus (GPa) | 17.88 (16.66–18.91) |
14.21 (10.00–15.68) |
19.29 (13.40–21.66) |
16.17 (10.00–21.66) |
|
| Fatigue life (cycles) | 6327 (699–12,433) |
123 (6–237) |
854 (13–2282) |
468 (6–12,433) |
Statistically different from the control group, p ≤ 0.05.
3.3. Relationship between intracortical microarchitecture and fatigue life
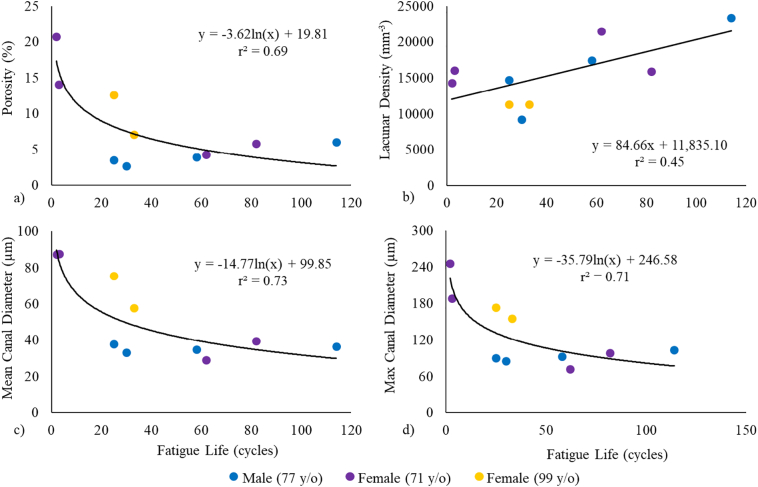
The linear and logarithmic relationships between each microarchitectural parameter and fatigue life measurements of the irradiated samples are summarized in Table 4. Relationships with porosity as well as mean and max canal diameter were better described with a logarithmic model, while lacunar density was better described with a linear relationship (Fig. 2). Separately, these parameters explained 45% to 73% of the variance in fatigue life measurements. Lacunar volume and lacunar orientation did not explain a significant amount of the variance in fatigue life using either model.
Table 4.
Linear (y = m ∗ x + b) and logarithmic (y = m ∗ ln(x) + b) relationships between microarchitectural parameters and fatigue life measurements of irradiated samples. Pearson product-moment correlations (r2) are italicized if the relationship was significant, p ≤ 0.05.
| Porosity (%) | Mean canal diameter (μm) | Max canal diameter (μm) | Lacunar density (mm−3) | Lacunar volume (μm3) | Lacunar orientation (°) | |
|---|---|---|---|---|---|---|
| Linear | m = −0.09 b = 12.08 r2 = 0.32 p = 0.092 |
m = −0.45 b = 71.48 r2 = 0.48 p = 0.027 |
m = −1.03 b = 174.93 r2 = 0.41 p = 0.048 |
m = 84.66 b = 11,835.1 r2 = 0.45 p = 0.033 |
m = 0.16 b = 127.19 r2 = 0.05 p = 0.55 |
m = −0.07 b = 54.23 r2 = 0.05 p = 0.53 |
| Log | m = −3.62 b = 19.81 r2 = 0.69 p = 0.003 |
m = −14.77 b = 99.85 r2 = 0.73 p = 0.002 |
m = −35.79 b = 246.58 r2 = 0.71 p = 0.002 |
m = 1177.97 b = 11,685.87 r2 = 0.13 p = 0.316 |
m = 0.08 b = 133.73 r2 = 0.00 p = 0.991 |
m = −1.49 b = 56.03 r2 = 0.03 p = 0.62 |
Fig. 2.
The relationship between the irradiated fatigue life and a) porosity, b) lacunar density, c) mean canal diameter and d) maximum canal diameter.
The relationships between the microarchitectural parameters for all irradiated samples and fatigue life measurements of the control samples are illustrated in Fig. 3. The crosshairs represent the data for each subject; the vertical line illustrates the range of the microarchitecture from irradiated samples while the horizontal line shows the range of fatigue life measurements of control samples from the corresponding subject. The intersection of the crosshairs is at the median of the variables and these points were used to generate the reported trend lines. Comparing these trend lines to those obtained with the fatigue life of the irradiated samples (Fig. 2), it is apparent that porosity, mean canal diameter, and max canal diameter showed similar negative logarithmic trends in both irradiated and control groups. However, the positive linear relationship between lacunar density and fatigue life was less evident in the control samples (Fig. 3b). Although the effect of microarchitecture on fatigue life demonstrated similar trends in both groups, radiation exposure modified the magnitude of this effect.
4. Discussion
There is an abundance of research detailing the effects of intracortical microarchitecture on the monotonic material properties of bone, as well as potential toughening mechanisms; however, the influence of microarchitecture on the fatigue behavior of bone is not well described. The purpose of this pilot study was to investigate the relationship between intracortical microarchitecture and the compressive fatigue life of human bone. The current results suggest that increased porosity and larger vascular canals are associated with a reduced fatigue life, whereas increased lacunar density was related to a longer fatigue life. The findings from this study also demonstrate the profound effects that synchrotron radiation microCT scanning can have on compressive fatigue life measurements. In addition, this initial investigation helped identify several methodological shortcomings that will serve to inform our future investigations into the potential relationship between intracortical microarchitecture and mechanical fatigue behavior.
Intracortical porosity has previously been reported to explain 76% of the variance in bone strength (McCladen et al., 1993), illustrating the dramatic effects that microarchitecture may have on the monotonic mechanical properties of bone. In fact, Hernandez et al. reported a strong power-law relationship between bone volume fraction (Vf = 1 − porosity) and the ultimate compressive strength (UCS) of bone (Hernandez et al., 2001):
In the current study, porosity values ranged from 1.9% to 20.7%, for which this equation would predict a 33% reduction in ultimate strength. However, the logarithmic relationship between porosity and fatigue life (Table 4) observed in this study would predict a 99.4% reduction in fatigue life for the same change in porosity. Increased porosity would, of course, reduce the effective cross-sectional area of the bone, and consequently its load carrying capacity. While this fact may explain the observed reductions in monotonic strength, additional factors closely related to porosity, such as canal diameter, may be able to account for the additional decline in fatigue resistance.
Vascular canals are the primary contributors to intracortical porosity, so it is not surprising that canal diameter had a similar effect on fatigue life measurements. However, a sample with a single large canal may produce the same porosity as a sample with many small canals. Yeni et al. suggested that an abundance of smaller canals may increase the fracture toughness of cortical bone (Yeni et al., 1997). As a pore in the bony matrix, vascular canals are often thought of as stress concentrations, the magnitude of which (i.e., maximum stress) is theoretically independent of pore size. However, pore size will determine the size of the stress gradient radiating from the canal edge, dictating the volume of highly stressed bone within the matrix (Kasiri and Taylor, 2008). In other words, smaller canals would produce a smaller volume of highly stressed matrix in which microcracks may initiate but will likely not propagate as they quickly reach the boundary of the stress gradient. This concept is well explained by the Critical Distance Theory, which evaluates the sensitivity of material failure to various stress concentrating features (Taylor, 2008). Despite the fact that circular pores of various sizes will produce stress concentrations of equal magnitude, according to the Critical Distance Theory, failure will only take place when the stress at a critical distance from the feature is equal to some critical stress magnitude. In this way canal diameter may be a more specific determinant of bone fatigue behavior than porosity alone, but additional confirmatory data are required to support this hypothesis.
Alternative explanations related to the strong relationship observed between canal diameter and fatigue life may be that our measurements of canal diameter are correlated to other aspects of bone quality not accounted for herein, such as osteon geometry or matrix mineralization. An age-dependent increase in canal diameter has been associated with a concurrent reduction in both osteon area and osteon wall thickness (Bernhard et al., 2013). Bernhard et al. calculated geometric indices of osteon cross-sections to estimate the mechanical capacity of an individual osteon. It was suggested that thinner osteon walls (likely due to by the presence of a larger canal) would reduce an osteon's compressive and bending strength (Bernhard et al., 2013). Furthermore, Yeni et al. hypothesized that the stress concentrating effects of a canal may be mitigated by the surrounding osteon's ability to dissipate energy through various toughening mechanisms, but a large enough canal would eventually negate an osteon's contribution to fracture toughness (Yeni and Norman, 2000). The size of osteons and canals are a reflection of bone remodeling dynamics; larger osteons indicate increased bone resorption while larger canals are indicative of decreased bone deposition (Busse et al., 2010; Qiu et al., 2010). Without new bone formation the matrix will have a higher and more homogeneous mineral content (Roschger et al., 2008). Increased mineral content may improve the fatigue strength of cortical bone (Zioupos et al., 2007); however, a more heterogeneous distribution throughout the bone matrix is an essential component of bone toughness by facilitating crack deflection, ultimately increasing the crack length and fatigue resistance of bone (Katsamenis et al., 2015).
The effect of osteocyte lacunar density on the mechanical fatigue behavior of bone observed herein is somewhat contradictory. Histomorphometric examinations of human cortical bone have demonstrated that microdamage is more likely located in lacunae-deficient regions (Qiu et al., 2005; Vashishth et al., 2000), suggesting that lacunae do not promote the development of microdamage. In contrast, studies investigating the presence of damage caused by monotonic and cyclic loading observed microcracks initiating adjacent to and touching osteocyte lacunae (Reilly, 2000). If more abundant lacunae do act as nucleation sites for microdamage, the current results suggest that this damage would not impair the overall fatigue resistance of bone and may actually increase fatigue life. Measures of osteocyte lacunar density could simply be an indicator of overall bone quality. Lacunar measurements were found to be extremely sensitive to post-processing techniques, and previous research suggests considerable natural variation within bone (Carter et al., 2013). Although our segmentation methods were consistent amongst all samples, lacunar density demonstrated a large degree of variability within each donor and a larger sample size is needed to understand that true effects of osteocyte lacunae on the fatigue life of bone.
Radiation doses typical of synchrotron X-ray scattering and tomography experiments have been estimated to range between 0.04 and 6000 kGy (Barth et al., 2010). A dose of 210 kGy has previously been shown to lower the facture toughness of bone by a factor of five (Barth et al., 2010), and even a fraction of this radiation (34 kGy) may reduce the tensile fatigue life by two orders of magnitude (Akkus and Belaney, 2005). Our results are consistent with these findings as the average fatigue life of the irradiated group was 91% lower than the control group. Despite the considerably reduced fatigue life of the irradiated samples, similar logarithmic trends were observed between microarchitectural parameters and fatigue life of the control samples. The y-intercept of the logarithmic models describing the irradiated fatigue life (Fig. 2) were comparable to the y-intercept of the trend lines describing the fatigue life of the control group (Fig. 3); however, the slope of the irradiated model was steeper than that of the control trend line. Collectively this suggests that radiation exposure likely modifies the effects of microarchitecture but is not a confounding factor. Although the statistical comparison of these trend lines is inappropriate given the limited number of donors and our small sample size, this finding provides confidence that the general role of microarchitecture in the fatigue failure of bone is not significantly affected by exposure to radiation.
The effects of radiation observed in this study are also consistent with previous findings that report irradiation being more detrimental to the plastic properties of bone compared to the elastic properties (Currey et al., 1997). The elastic modulus did not differ between the irradiated and control groups, but fatigue life was significantly reduced, demonstrating considerable loss of plasticity. Irradiation causes the embrittlement of bone by increasing the degree of collagen cross-linking and reducing its ability to plastically deform (Barth et al., 2011). Intrinsic toughening mechanisms that control crack initiation are heavily dependent on the collagen network (Ritchie et al., 2009) and, thus, may be eradicated by irradiation. On the other hand, extrinsic toughening mechanisms that control crack growth rely on microarchitecture features such as osteons that will be less effected by irradiation (Ritchie et al., 2009). Therefore, the influence of microarchitecture on the fatigue life of both irradiated and non-irradiated bone should be similar, at least mechanistically, although irradiated microarchitecture may be less effective at resisting crack growth. Given the dramatic reductions in fatigue life measurements for irradiated bone, care should be taken when interpreting results from mechanical tests following microCT scanning.
It was expected that a loading magnitude of 88 MPa (approximately 50% ultimate compressive strength of non-irradiated bone) would cause fatigue failure within 103–104 cycles (Zioupos et al., 2007; Vashishth et al., 2001). While the average fatigue life of the control group was within this range (2640 cycles), the majority of the fatigue life measurements were on the order of 102 cycles and only two samples survive >104 cycles. These shorter fatigue lives may be due in part to the older age of the donors used in the current study (71–99 y/o) compared to the younger donors (52–79 y/o) tested in the referent study (Zioupos et al., 2007). Regardless, the chosen loading magnitude resulted in low-cycle fatigue. Future work should consider lower loading magnitudes to observe high-cycle fatigue failure which better describe physiological loading conditions and are more relevant for clinical applications. This pilot study should also serve as a warning of the detrimental effects that irradiation may have on the fatigue behavior of cortical bone in compression. Radiation doses of 25 and 35 kGy have been shown to drastically reduce both the bending and tensile fatigue life of bone, respectively (Akkus and Belaney, 2005; Islam et al., 2016). The present results demonstrate similar reductions in the compressive fatigue life of bone even when the radiation dose was reduced by >75% (7.9 kGy). Although some measures of bone quality seem to be unaltered by low radiation doses associated with desktop microCT <1 kGy (Lee and Jasiuk, 2014), a systematic study to determine a tolerable dose that does not affect the fatigue behavior of bone is needed.
This study was limited to morphological measures of intracortical microarchitecture and therefore we can only assess the association between these parameters and the fatigue life of bone. To gain a more mechanistic understanding of the fatigue failure process, the development and progression of fatigue damage should be quantified with respect to the spatial and morphological differences in microarchitecture. Furthermore, it was difficult for us to evaluate the influence of porosity and canal diameter separately because they were directly related (r2 = 0.87, p ≤ 0.001). Quantifying canal separation or canal density may help decipher the effects of vascular canals independent from porosity. Similar to previous findings (Wachter et al., 2002), canal diameter (r2 = 0.50, p = 0.022) and porosity (r2 = 0.57, p = 0.011) were strongly correlated with the elastic modulus and this may, in part, explain the strong relationships observed between intracortical microarchitecture and fatigue life measurements. In fact, elastic modulus accounted for more variation in the fatigue life than any of the microarchitectural measures in the irradiated group (r2 = 0.86, p ≤ 0.001) and was significantly associated with the fatigue life of the control group (r2 = 0.73, p ≤ 0.001; Fig. 4). Elastic modulus is a composite measure reflecting the cumulative influence of many bone characteristics such as microarchitecture and composition. While we cannot rule out that elastic modulus governs the fatigue behavior of bone, it does not explain how morphological differences in intracortical microarchitecture may directly impact the fatigue life. This study was also limited to tissue samples from three donors. Although theses samples illustrated considerable variation, which allowed us to assess the relationship between microarchitecture and fatigue life, the cause of death for two donors was chronic diseases known to affect bone quality (Misof et al., 2016; Nickolas et al., 2013). Therefore, a larger sample size is required to confirm the generalizability of the findings from this pilot study.
Fig. 4.
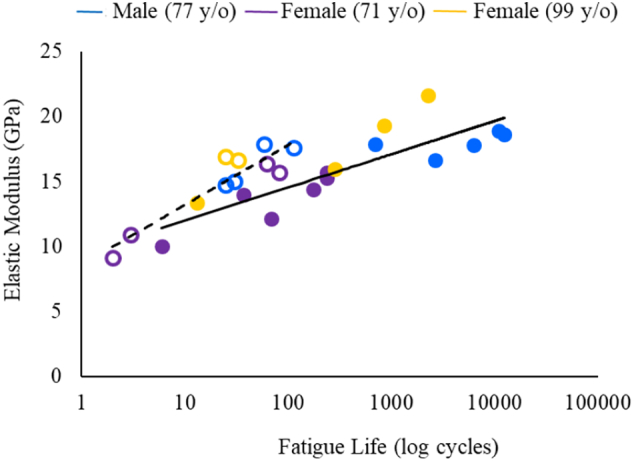
Fatigue life of irradiated samples (r2 = 0.86, open circles) and control samples (r2 = 0.73, closed circles) as a function of elastic modulus.
To summarize, a substantial amount of work has been done to quantify the fatigue behavior of cortical bone, yet there remains a large amount of scatter in fatigue life measurements that has not been previously explained. Considering that the toughening mechanisms of bone are derived from its microarchitecture and contribute to the bone's ability to withstand repetitive loading, the large differences observed in fatigue life are likely related to these inherent differences in intracortical microarchitecture. This pilot study attempted to establish, for the first time, the relationship between canal diameter, lacunar density and lacunar volume with the fatigue life of cortical bone in compression. Although both canal diameter and porosity explained a significant amount of the variance in fatigue life, canal diameter may be a better predictor of the overall fatigue behavior. We suspect that this is due to the volume of the stress concentration created by larger canals. However, future studies are needed to confirm the current results and explicitly investigate the mechanisms by which microarchitecture affects the fatigue behavior of cortical bone. Finally, radiation doses consistent with synchrotron X-ray microCT scanning eradicated the fatigue resistance of bone. Although microCT scanning modified the relationship between microarchitecture and fatigue life measurements, logarithmic trends remained suggesting that porosity and canal diameter may influence the fatigue life of irradiated and non-irradiated bone in a similar manner.
Transparency document
Transparency document.
CRediT authorship contribution statement
Lindsay L. Loundagin: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing - original draft, Writing - review & editing, Visualization. Ifaz T. Haider: Software, Validation, Formal analysis, Writing - review & editing. David M.L. Cooper: Resources, Formal analysis, Writing - review & editing, Supervision, Project administration, Funding acquisition. W. Brent Edwards: Conceptualization, Methodology, Formal analysis, Writing - review & editing, Supervision, Project administration, Funding acquisition.
Acknowledgements
This work was supported in part by a seed grant from the Faculty of Kinesiology at the University of Calgary as well as the Natural Science and Engineering Research Council of Canada (Grant Nos. NSERC; RGPIN 01029-2015 and RTI 00013-2016). The research described in this paper was performed at the BMIT facility at the Canadian Light Source, which is supported by the Canada Foundation for Innovation, Natural Sciences and Engineering Research Council of Canada, the University of Saskatchewan, the Government of Saskatchewan, Western Economic Diversification Canada, the National Research Council Canada, and the Canadian Institutes of Health Research.
Footnotes
The Transparency document associated with this article can be found, in online version.
Contributor Information
Lindsay L. Loundagin, Email: lindsay.loundagin@ucalgary.ca.
Ifaz T. Haider, Email: ifaz.haider@ucalgary.ca.
David M.L. Cooper, Email: david.cooper@usask.ca.
W. Brent Edwards, Email: wbedward@ucalgary.ca.
References
- Akkus O., Belaney R.M. Sterilization by gamma radiation impairs the tensile fatigue life of cortical bone by two orders of magnitude. J. Orthop. Res. 2005;23(5):1054–1058. doi: 10.1016/j.orthres.2005.03.003. [DOI] [PubMed] [Google Scholar]
- Barth H.D., Launey M.E., MacDowell A.A., Ager J.W., Ritchie R.O. On the effect of X-ray irradiation on the deformation and fracture behavior of human cortical bone. Bone. 2010;46(6):1475–1485. doi: 10.1016/j.bone.2010.02.025. [DOI] [PubMed] [Google Scholar]
- Barth H.D., Zimmermann E.A., Schaible E., Tang S.Y., Alliston T., Ritchie R.O. Characterization of the effects of X-ray irradiation on the hierarchical structure and mechanical properties of human cortical bone. Biomaterials. 2011;32(34):8892–8904. doi: 10.1016/j.biomaterials.2011.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernhard A., Milovanovic P., Zimmermann E.A. Micro-morphological properties of osteons reveal changes in cortical bone stability during aging, osteoporosis, and bisphosphonate treatment in women. Osteoporos. Int. 2013;24(10):2671–2680. doi: 10.1007/s00198-013-2374-x. [DOI] [PubMed] [Google Scholar]
- Boden B.P., Osbahr D.C., Jimenez C. Low-risk stress fractures. Am. J. Sports Med. 2001;29(1):100–111. doi: 10.1177/03635465010290010201. [DOI] [PubMed] [Google Scholar]
- Burr D., Milgrom C., Boyd R., Higgins W., Robin G., Radin E. Experimental stress fractures of the tibia. J Bone Jt Surgery, Br. 1990;72(3):370–375. doi: 10.1302/0301-620X.72B3.2341429. [DOI] [PubMed] [Google Scholar]
- Burr D.B., Turner C.H., Naick P. Does microdamage accumulation affect the mechanical properties of bone ? J. Biomech. 1998;31:337–345. doi: 10.1016/s0021-9290(98)00016-5. [DOI] [PubMed] [Google Scholar]
- Busse B., Hahn M., Schinke T., Püschel K., Duda G.N., Amling M. Reorganization of the femoral cortex due to age-, sex-, and endoprosthetic-related effects emphasized by osteonal dimensions and remodeling. J Biomed Mater Res - Part A. 2010;92(4):1440–1451. doi: 10.1002/jbm.a.32432. [DOI] [PubMed] [Google Scholar]
- Caler W.E., Carter D.R. Bone creep-fatigue damage accumulation. J. Biomech. 1989;22(6–7):625–635. doi: 10.1016/0021-9290(89)90013-4. [DOI] [PubMed] [Google Scholar]
- Carter D.R., Hayes W.C. Fatigue life of compact bone—I: effects of stress amplitude, temperature and density. J. Biomech. 1976;9(1):27–34. doi: 10.1016/0021-9290(76)90136-6. [DOI] [PubMed] [Google Scholar]
- Carter D.R., Hayes W.C. Compact bone fatigue damage. 1. Residual strength and stiffness. J. Biomech. 1977;10(1):325–337. doi: 10.1016/0021-9290(77)90005-7. [DOI] [PubMed] [Google Scholar]
- Carter D.R., Hayes W.C. Compact bone fatigue damage: a microscopic examination. Clin. Orthop. Relat. Res. 1977;127(1):265–274. [PubMed] [Google Scholar]
- Carter D.R., Caler W.E., Spengler D.M., Frankel V.H. Uniaxial fatigue of human cortical bone. The influence of tissue physical characteristics. J. Biomech. 1981;14(7):461–470. doi: 10.1016/0021-9290(81)90096-8. Jan. [DOI] [PubMed] [Google Scholar]
- Carter Y., Thomas C.D.L., Clement J.G., Peele A.G., Hannah K., Cooper D.M.L. Variation in osteocyte lacunar morphology and density in the human femur — a synchrotron radiation micro-CT study. Bone. 2013;52(1):126–132. doi: 10.1016/j.bone.2012.09.010. [DOI] [PubMed] [Google Scholar]
- Cooper D.M.L., Turinsky a L., Sensen C.W., Hallgrímsson B. Quantitative 3D analysis of the canal network in cortical bone by micro-computed tomography. Anat. Rec. 2003;274(1):169–179. doi: 10.1002/ar.b.10024. [DOI] [PubMed] [Google Scholar]
- Crabtree N., Kroger H., Martin A. Improving risk assessment: hip geometry, bone mineral distribution and bone strength in hip fracture cases and controls. The EPOS study. Osteoporos. Int. 2002;13(1):48–54. doi: 10.1007/s198-002-8337-y. [DOI] [PubMed] [Google Scholar]
- Currey J.D. Stress concentrations in bone. Q J Microsc Sci. 1962;103(1):111–133. [Google Scholar]
- Currey J.D., Foreman J., Laketic I., Mitchell J., Pegg D.E., Reilly G.C. Effects of ionizing radiation on the mechanical properties of human bone. J. Orthop. Res. 1997;15(1):111–117. doi: 10.1002/jor.1100150116. [DOI] [PubMed] [Google Scholar]
- Dickerson R., Hutton W., Stott J. The mechanical properties of bone in osteoporosis. J Bone Jt Surg Br. 1981;63(2):233–238. doi: 10.1302/0301-620X.63B2.7217148. [DOI] [PubMed] [Google Scholar]
- Dong P., Haupert S., Hesse B. 3D osteocyte lacunar morphometric properties and distributions in human femoral cortical bone using synchrotron radiation micro-CT images. Bone. 2014;60(3):172–185. doi: 10.1016/j.bone.2013.12.008. [DOI] [PubMed] [Google Scholar]
- Doube M., Kłosowski M.M., Arganda-carreras I., Fabrice P. BoneJ: free and extensible bone image analysis in ImageJ. Bone. 2010;47(6):1076–1079. doi: 10.1016/j.bone.2010.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards W.B. Modeling overuse injuries in sport as a mechanical fatigue phenomenon. Exerc. Sport Sci. Rev. 2018;46(4):224–231. doi: 10.1249/JES.0000000000000163. [DOI] [PubMed] [Google Scholar]
- Evans F.G., Vincentelli R. Relations of the compressive properties of human cortical bone to histological structure and calcification. J. Biomech. 1974;7(1):1–10. doi: 10.1016/0021-9290(74)90064-5. [DOI] [PubMed] [Google Scholar]
- Faulkner K.G., Wacker W.K., Barden H.S. Femur strength index predicts hip fracture independent of bone density and hip axis length. Osteoporos. Int. 2006;17(4):593–599. doi: 10.1007/s00198-005-0019-4. [DOI] [PubMed] [Google Scholar]
- Hemmatian H. Katholieke Universiteit Leuven; 2017. Does the Osteocyte Lacuna Affect Bone Adaptive Response in Aging? [Google Scholar]
- Hernandez C.J., van der Meulen M.C.H. Understanding bone strength is not enough. J. Bone Miner. Res. 2017;32(6):1157–1162. doi: 10.1002/jbmr.3078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernandez C.J., Beaupré G.S., Keller T.S., Carter D.R. The influence of bone volume fraction and ash fraction on bone strength and modulus. Bone. 2001;29(1):74–78. doi: 10.1016/s8756-3282(01)00467-7. [DOI] [PubMed] [Google Scholar]
- Islam A., Chapin K., Moore E., Ford J., Rimnac C., Akkus O. Gamma radiation sterilization reduces the high-cycle fatigue life of allograft bone. Clin. Orthop. Relat. Res. 2016;474(3):827–835. doi: 10.1007/s11999-015-4589-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson A.W., Weiss C.B., Wheeler D.L. Stress fractures of the femoral shaft in athletes: more common than expected a new clinical test. Am. J. Sports Med. 1994;22(2) doi: 10.1177/036354659402200216. [DOI] [PubMed] [Google Scholar]
- Kasiri S., Taylor D. A critical distance study of stress concentrations in bone. J. Biomech. 2008;41(3):603–609. doi: 10.1016/j.jbiomech.2007.10.003. [DOI] [PubMed] [Google Scholar]
- Katsamenis O.L., Jenkins T., Thurner P.J. Toughness and damage susceptibility in human cortical bone is proportional to mechanical inhomogeneity at the osteonal-level. Bone. 2015;76:158–168. doi: 10.1016/j.bone.2015.03.020. [DOI] [PubMed] [Google Scholar]
- Lee W., Jasiuk I. Effects of freeze–thaw and micro-computed tomography irradiation on structure–property relations of porcine trabecular bone. J. Biomech. 2014;47(6):1495–1498. doi: 10.1016/j.jbiomech.2014.02.022. [DOI] [PubMed] [Google Scholar]
- Lenart B.A., Neviaser A.S., Lyman S. Association of low-energy femoral fractures with prolonged bisphosphonate use: a case control study. Osteoporos. Int. 2009;20(8):1353–1362. doi: 10.1007/s00198-008-0805-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loundagin L.L., Schmidt T.A., Edwards W.B. Mechanical fatigue of bovine cortical bone using ground reaction force waveforms in running. J. Biomech. Eng. 2018;140(3) doi: 10.1115/1.4038288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCladen R., Mgeough J., Barker M. Age-related changes in the tensile properties of cortical bone. J Bone Jt Surg. 1993;75(8):1193–1205. doi: 10.2106/00004623-199308000-00009. [DOI] [PubMed] [Google Scholar]
- McCreadie B.R., Hollister S.J., Schaffler M.B., Goldstein S.A. Osteocyte lacuna size and shape in women with and without osteoporotic fracture. J. Biomech. 2004;37(4):563–572. doi: 10.1016/S0021-9290(03)00287-2. [DOI] [PubMed] [Google Scholar]
- Misof B.M., Moreira C.A., Klaushofer K., Roschger P. Skeletal implications of chronic obstructive pulmonary disease. Curr Osteoporos Rep. 2016;14(2):49–53. doi: 10.1007/s11914-016-0301-8. [DOI] [PubMed] [Google Scholar]
- Nalla R.K., Kinney J.H., Ritchie R.O. Mechanistic fracture criteria for the failure of human cortical bone. Nature. 2003;2(3):164–168. doi: 10.1038/nmat832. [DOI] [PubMed] [Google Scholar]
- Nickolas T.L., Stein E.M., Dworakowski E. Rapid cortical bone loss in patients with chronic kidney disease. J. Bone Miner. Res. 2013;28(8):1811–1820. doi: 10.1002/jbmr.1916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicolella D.P., Moravits D.E., Gale A.M., Bonewald L.F., Lankford J. Osteocyte lacunae tissue strain in cortical bone. J. Biomech. 2006;39(9):1735–1743. doi: 10.1016/j.jbiomech.2005.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Brien F.J., Taylor D., Lee T.C. The effect of bone microstructure on the initiation and growth of microcracks. J. Orthop. Res. 2005;23(2):475–480. doi: 10.1016/j.orthres.2004.08.005. [DOI] [PubMed] [Google Scholar]
- Öhman C., Baleani M., Pani C. Compressive behaviour of child and adult cortical bone. Bone. 2011;49(4):769–776. doi: 10.1016/j.bone.2011.06.035. [DOI] [PubMed] [Google Scholar]
- Qiu S., Rao S.D., Fyhrie D.P., Planitkar S., Parfitt M.A. The morphological association between microcracks and osteocyte lacunae in human cortical bone. Bone. 2005;37(1):10–15. doi: 10.1016/j.bone.2005.01.023. [DOI] [PubMed] [Google Scholar]
- Qiu S., Rao D.S., Palnitkar S., Parfitt A.M. Dependence of bone yield (volume of bone formed per unit of cement surface area) on resorption cavity size during osteonal remodeling in human rib: implications for osteoblast function and the pathogenesis of age-related bone loss. J. Bone Miner. Res. 2010;25(2):423–430. doi: 10.1359/jbmr.091003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reilly D.T., Burstein A.H. The elastic and ultimate properties of compact bone tissue. J. Biomech. 1975;8(6):393–405. doi: 10.1016/0021-9290(75)90075-5. Jan. [DOI] [PubMed] [Google Scholar]
- Reilly G.C. Observations of microdamage around osteocyte lacunae in bone. J. Biomech. 2000;33(9):1131–1134. doi: 10.1016/s0021-9290(00)00090-7. [DOI] [PubMed] [Google Scholar]
- Ritchie R.O., Buehler M.J., Hansma P. Plasticity and toughness in bone. Phys. Today. 2009;62(6):41–47. [Google Scholar]
- Roschger P., Paschalis E.P., Fratzl P., Klaushofer K. Bone mineralization density distribution in health and disease. 2008;42:456–466. doi: 10.1016/j.bone.2007.10.021. [DOI] [PubMed] [Google Scholar]
- Schaffler M.B., Burr D.B. Stiffness of compact-bone — effects of porosity and density. J. Biomech. 1988;21(I):13–16. doi: 10.1016/0021-9290(88)90186-8. [DOI] [PubMed] [Google Scholar]
- Schindelin J., Arganda-Carreras I., Frise E. Fiji - an open source platform for biological image analysis. Nat. Methods. 2012;9(7):676–682. doi: 10.1038/nmeth.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shane E., Burr D., Ebeling P.R. Atypical subtrochanteric and diaphyseal femoral fractures: report of a task force of the American Society for Bone and Mineral Research. J. Bone Miner. Res. 2010;25(11):2267–2294. doi: 10.1002/jbmr.253. [DOI] [PubMed] [Google Scholar]
- Taylor D. Fatigue of bone and bones: an analysis based on stressed volume. J. Orthop. Res. 1998;16(2):163–169. doi: 10.1002/jor.1100160203. [DOI] [PubMed] [Google Scholar]
- Taylor D. The theory of critical distances. Eng. Fract. Mech. 2008;75(7):1696–1705. [Google Scholar]
- Taylor D., Brien F.O., Prina-mello A., Ryan C., Reilly P.O., Lee T.C. Compression data on bovine bone confirms that a “stressed volume” principle explains the variability of fatigue strength results. J. Biomech. 1999;32(11):1199–1203. doi: 10.1016/s0021-9290(99)00112-8. [DOI] [PubMed] [Google Scholar]
- Vashishth D., Verborgt O., Divine G., Schaffler M.B., Fyhrie D.P. Decline in osteocyte lacunar density in human cortical bone is associated with accumulation of microcracks with age. Bone. 2000;26(4):375–380. doi: 10.1016/S8756-3282(00)00236-2. [DOI] [PubMed] [Google Scholar]
- Vashishth D., Tanner K.E., Bonfield W. Fatigue of cortical bone under combined axial-torsional loading. J. Orthop. Res. 2001;19(3):414–420. doi: 10.1016/S0736-0266(00)00036-X. [DOI] [PubMed] [Google Scholar]
- Wachter N.J., Krischak G.D., Mentzel M. Correlation of bone mineral density with strength and microstructural parameters of cortical bone in vitro. Bone. 2002;31(1):90–95. doi: 10.1016/s8756-3282(02)00779-2. [DOI] [PubMed] [Google Scholar]
- Yeni Y.N., Norman T.L. Calculation of porosity and osteonal cement line effects on the effective fracture toughness of cortical bone in longitudinal crack growth. J. Biomed. Mater. Res. 2000;51(3):504–509. doi: 10.1002/1097-4636(20000905)51:3<504::aid-jbm27>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- Yeni Y.N., Brown C.U., Wang Z., Norman T.L. The influence of bone morphology on fracture toughness of the human femur and tibia. Bone. 1997;21(5):453–459. doi: 10.1016/s8756-3282(97)00173-7. [DOI] [PubMed] [Google Scholar]
- Yeni Y.N., Vashishth D., Fyhrie D.P. Estimation of bone matrix apparent stiffness variation caused by osteocyte lacunar size and density. J. Biomech. Eng. 2001;123(1):10–17. doi: 10.1115/1.1338123. [DOI] [PubMed] [Google Scholar]
- Zioupos P., Currey J.D., Casinos A. Tensile fatigue in bone: are cycles-, or time to failure, or both, important? J. Theor. Biol. 2001;210(3):389–399. doi: 10.1006/jtbi.2001.2316. Jun. [DOI] [PubMed] [Google Scholar]
- Zioupos P., Gresle M., Winwood K. Fatigue strength of human cortical bone: age, physical, and material heterogeneity effects. J Biomed Mater Res - Part A. 2007;86(3):627–636. doi: 10.1002/jbm.a.31576. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Transparency document.