QM/QM studies for Michael reaction in coronavirus main protease (3CL^Pro)

Abstract

Severe acute respiratory syndrome (SARS) is an illness caused by a novel corona virus wherein the main proteinase called 3CL^Pro has been established as a target for drug design. The mechanism of action involves nucleophilic attack by Cys145 present in the active site on the carbonyl carbon of the scissile amide bond of the substrate and the intermediate product is stabilized by hydrogen bonds with the residues of the oxyanion hole. Based on the X-ray structure of 3CL^Pro co-crystallized with a trans-α,β-unsaturated ethyl ester (Michael acceptor), a set of QM/QM and QM/MM calculations were performed, yielding three models with increasingly higher the number of atoms. A previous validation step was performed using classical theoretical calculation and PROCHECK software. The Michael reaction studies show an exothermic process with −4.5 kcal/mol. During the reaction pathway, an intermediate is formed by hydrogen and water molecule migration from a histidine residue and solvent, respectively. In addition, similar with experimental results, the complex between N3 and 3CL^Pro is 578 kcal/mol more stable than N1-3CL^Pro using Own N-layer Integrated molecular Orbital molecular Mechanics (ONIOM) approach. We suggest 3CL^Pro inhibitors need small polar groups to decrease the energy barrier for alkylation reaction. These results can be useful for the development of new compounds against SARS.

1. Introduction

Human coronavirus (HCoV) is responsible for severe acute respiratory syndrome (SARS). This illness is characterized by high fever, malaise, rigor, headache, and may progress to generalized interstitial infiltration in the lung, requiring intubation and mechanical ventilation, with a fatality rate of 10–15% [1]. It was reported for the first time in China, in 2002, and has spread to other countries in Asia, North America and Europe. SARS now appears to have been contained. However, transmission occurs mainly by face-to-face contact and it is always possible that it may reemerge during cold seasons. In addition, there are no licensed vaccines or specific drugs available to prevent HCoV infection [2], [3].

HCoV, and other members of its family, can produce a single 250 kDa polyprotein, which can be cleaved by a specific proteinase, called 2A, resulting in two fragments, which are further processed by other proteinase, called 3C, forming proteins which are required for structural components of virus. 3C proteinase is crucial for viral maturation and infectivity. The interruption of the proteolytic processing prevents formation of new virions [4]. Cysteine proteinase is called the main proteinase (M^Pro) or the 3C-like proteinase (3CL^Pro or 3C^pro). The name 3C-like proteinase was introduced because of similar substrate specificities found between two virus genus, coronavirus and picornavirus, which HCoV and human rhinovirus (HRV, responsible for common cold) belong these genus respectively [5], [6]. This similarity makes it possible to develop inhibitors for both enzymes [7]. In addition, there is little sequence similarity between virus and mammalian enzymes. This characteristic makes this enzyme an attractive target for the development of new antiviral therapeutic agents [5], [6], [7].

The substrate specificity of 3CL^pro is determined mainly by the P1, P2 and P1′ positions, which are occupied preferentially by Leu, Gln, and (Ser, Ala or Gly) [6]. This enzyme employs a catalytic dyad of conserved His41 and Cys145 residues. However, further studies showed an interaction between a molecule of water with His41 Hδ in the place of the third member of the catalytic triad present in other proteolytic enzymes [8], [9]. The SARS-CoV exhibits the highest proteolytic activity at pH 7.3–8.5 [9], which implies that a thiolate-imidazolium ion pair is formed between the Cys145 and His41 in the active site. Thus, the cysteine thiol moiety possesses a thiolate form at physiological conditions [9]. After the substrate binds to the active site, the thiolate nucleophile attacks the carbonyl carbon of the scissile amide bond, leading to the formation of an oxyanion tetrahedral intermediate [7], [10]. This intermediate is stabilized by strong hydrogen bonds donated by amide groups of the enzyme. The so-called “oxyanion hole”, in the case of 3CL^pro, is formed by the backbone of Gly143 and Cys145 [7], [9].

Several inhibitors have been developed for HRV and HCoV virus [11], [12], [13], [14], [15]. The most successful of them is AG7088 (rupintrivir), which is undergoing testing for its efficiency in the treatment of common cold by HRV, and has advanced to phase II/III clinical trials [16], [17], [18]. This compound is a peptidomimetic with a trans-α,β-unsaturated ethyl ester moiety (Michael acceptor), which is able to form an irreversible covalent bond within the active site of 3CL^pro proteinase [16], [17], [18]. Similar strategy was used for the development of four wide-spectrum coronavirus inhibitors (N1, N3, N9 and I2) [19]. These inhibitors were designed based on the P4-P1 substrate for recognition of S1, S2 and S4 regions of the active site of M^Pro, and they have a trans-α,β-unsaturated ethyl ester moiety as well. High-resolution crystallographic studies identified 21 different amino acids residues located in the active site of M^Pro. These inhibitors have been shown to interact directly with the side chains of Gly143, Cys145, His163, His164, Glu166, Gln189, Thr190, and with the main chain of Ala191, Pro168, Arg188, Gln192, Asp187, Met165, Phe140, His41, Met49, Thr26, Thr25, Leu141, Asn142 and His172. These inhibitors, similar to AG7088, have the same kinetic mechanism. Initially, the enzyme forms a reversible complex with the inhibitor, and then undergoes nucleophilic attack by the thiolate cysteine [16], [19].

The increasing interest in search of a coronavirus inhibitor with higher biological activity has addressed the need of theoretical studies as suitable tool for the design of new compounds [20], [21]. In addition, the knowledge of inhibitors such as analogous fumarate, vinyl sulfones, and vinyl esters, which contain an active double bound, has shown activity for cysteine proteinase and papain-like enzymes [15], [22]. The active site of these enzymes undergoes an addition leading to an alkylated enzyme, as a classical Michael reaction [15], [23]. Initially, the reactivity of the Michael reaction with biological nucleophiles was studied using the semiempirical method AM1 [24]. In this study, the activation enthalpy of the reagents (methylamine, imidazole, both as Michael donors), acrylic acid (as Michael acceptor), and the products (corresponding anions) were characterized. The authors showed that the reaction occurs through an endothermic process, and the rate of the Michael reaction is a function of the rate constant (derived from energy of activation) and the concentration of acceptor and nucleophile [24]. In another study, AM1 was used to study the reactivity of salicylaldehyde acylhydrazone derivatives, acting as Michael acceptors. Conformational analysis, lowest unoccupied molecular orbital (LUMO), and molecular electrostatic potential (MEP) were performed to localize the most favorable atom for nucleophilic attack by the thiolate ion [25]. On the other hand, a set of semiempirical PM3 models using different nucleophilic agents and Michael acceptors were carried out. These models proposed a mechanism through an exothermic process, through tetrahedral intermediate which is more stable than the reagent. A correlation between second-order rate constant and the value of the exponential term in the Arrhenius equation was found, suggesting the use of semiempirical method PM3 for the calculation of the reaction pathways of this system [26]. Another study, Hartree-Fock with 6-31+G(d) and Monte Carlo with a hybrid method AM1/TIP3P calculation were used to study the nucleophilic addition reaction of methanethiolate to N-methylacetamide both gas phase and aqueous solution [27]. Differently from previous PM3 calculation [26], a stable tetrahedral intermediate were not formed, but these calculations suggested that this structure is a transition state, implying a concerted mechanism [27]. Finally, the reaction for the alkylation of methyl thiolate by electrophilic three-membered heterocycles was carried out by density-functional theory (DFT), using BLYP/TZV+P and COSMO approaches [28]. From this small model of cysteine proteinase, the authors concluded that improved inhibition potency was not resultant from influences on the alkylation step, but from a favorable ionic interaction between carboxylate and imidazolium ion which can stabilize the noncovalent enzyme inhibitor complex. Furthermore, a water molecule, available in the active site, could act as a proton donor to decrease the energy barrier in the ring-opening reactions [28].

Although several researches have been devoted to study the Michael reaction using models for cysteine proteinase with considerable potential, none of these calculations considered the complete active site, the oxyanion hole, with their respective amino acids (Cys145, His45 and Gly143), and specially the enzyme environment with reasonable theoretical level. Moreover, the cartesian coordinates of atoms in all models were generated randomically, and they did not take into account the enzymatic geometry [20], [21], [22], [23], [24], [25], [26], [27], [28]. Considering these observations, we carried out computational studies including force-field-based methods (molecular mechanics—MM), density-functional theory, and the hybrid approach (QM/QM and QM/MM) denoted by our own n-layered integrated molecular orbital and molecular mechanics (ONIOM). As M^Pro consists of two protomers, A and B [19], in our studies only protomer A will be evaluated. It has 309 amino acids with a total of 4.738 atoms (without water molecules) [19]. Consequently, it has higher computational cost for quantum calculations. Therefore, the enzyme needs to be described by an adequate model, combining accuracy with computational tractability. Combined quantum mechanical and molecular mechanical (QM/MM) methods have gained widespread use in the computational study of large molecular systems, including the enzyme reaction mechanism. The QM/MM approach was described for the first time by Warshel and Levitt [29]. These methods involve modeling a small region of the system that requires quantum mechanical formalism (QM), where occur break and formations of bonds for example, by semiempirical, ab initio or density-functional theory methods and treating the remainder of protein and solvent environment with a low cost molecular mechanics (MM) method. This hybrid approach has been developed because of higher computational cost of conventional QM methods when applied for large systems [30]. Following this guideline, QM/MM methods were applied to study Michael reactions in M^Pro enzyme as detailed below. Our attention was focused on the molecular level of the ligand and in the interaction between the ligand and the active site in the pseudo-active site model and protein. This approach can describe the interactions between the ligand and amino acids present in the active site of M^Pro. These calculations can be useful for the design of new inhibitors with non-peptidic structure. Peptidyl inhibitors are very susceptible to other proteases and they have low oral bioavailability [11], [15]. Proteinases are potentially important chemotherapeutic targets and have involvement in many others diseases such as viral and parasitic infections, arthritis, cancer, and osteoporosis [15]. One such example is the successful use of proteinase inhibitors in the treatment of acquired immune deficiency syndrome (AIDS) [31].

2. Computational methods

The publication of the X-ray structure of SARS M^Pro cyteine proteinase in the Research Collaboratory for Structural Bioinformatics Database (access code 1WOF) [19], [32] permitted that our studies were initiated. Three different models were constructed using the atomic coordinate from 1WOF, which they were systematically increased.

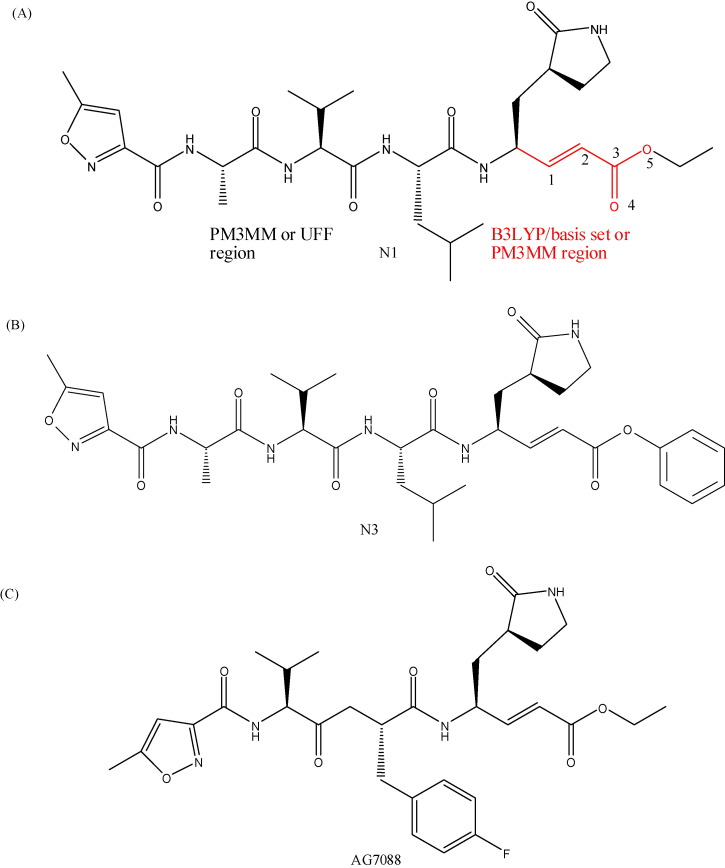
In the first model, only the ligand (N1) was fully optimized with tight self-consistent field (scf) routine implemented in Gaussian 03 software [33]. Becke's three-parameter hybrid functional [34], along with the nonlocal correlation functional of Lee, Yang and Parr (B3LYP-DFT) [35], [36] with 3-21G, 6-31G, 6-31G(d), 6-31G(d,p) and 6-31+G(d,p) basis set [37] and semiempirical Parametric Method 3 with MM correction for peptide bond (PM3MM) [38] methods were used in this study. Afterward, two models with two-layer hybrid were created by ONIOM approach [39], [40]. The first one, B3LYP/basis set and PM3MM were defined as higher and lower layer respectively. Similarly, the second ONIOM model was constructed using PM3MM and the universal force field (UFF) [41] as higher and lower respectively. The higher layer was defined by the double bond and ester group present in trans-α,β-unsaturated system, and whole ligand was defined as lower layer (Fig. 1A). The main goal is observe the effect in Mulliken net atomic charges and geometry in our ONIOM models. In this step, a validation between classical QM and ONIOM was performed. For this purpose, the tight keyword was used to ensure adequate convergence. Of course, the computational cost was increased. The orbital of N1, N3 and AG7088 (Fig. 1) were carried out using PM3MM and B3LYP/6-31G(d) as well.

Fig. 1.

(A) N1: In red the selected atoms with higher layer and in black atoms with lower layer, (B) N3 and (C) AG7088.

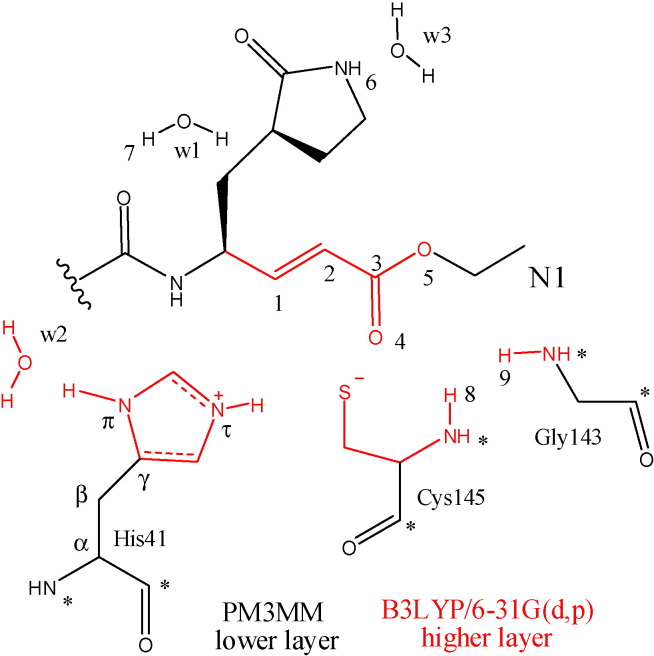
Afterward the validation result, another model was designed to study the additions reaction between N1 and the active site of SARS-CoV. The model was constructed through cartesian coordinates of N1 and the active site (including oxyanion pocket) obtained from protomer A of 1WOF, which was previously prepared by AMBER8 [42]. Different models were constructed with ONIOM in two and three-layers. However, only a small model with N1, His41, Cys145, Gly143, and three water molecules using B3LYP/6-31G(d,p):PM3MM approach was successfully minimized. In other words, this model considered the trans-α,β-unsaturated moiety, catalytic system, and oxyanion hole in higher layer with 32 atoms, and others parts of ligand, amino acids, and two water molecules in lower layer with 133 atoms. As the amino acids were dissected from protomer A, hydrogen atoms were added to occupy the free valence. The cartesian coordinate of α-carbons and hydrogens added were keep fix during the geometry optimization. Neutral charge was assumed for the whole model, but thiolate-imidazolium ion pair was considered in started geometry (Fig. 2 ). The first model of this set was called Reagent, the second of Inter1, which the C₁–S distance was fixed by 2.720 Å, and the last one was called by Hprod, which consists of an alkylated model. These structures described the nucleophilic attack from thiolate to trans-α,β-unsaturated moiety of N1. Mulliken net atomic charges, geometrical parameters and relative energies were evaluated in detail for this Michael reaction.

Fig. 2.

Model of N1 complexed with oxyanion and catalytic system. The colors red, black, and * symbol were used to assign atoms with higher layer, lower layer, and frozen respectively.

A third model was created, which consists in the whole protein. This model was constructed to demonstrate the influence of long-range electrostatic interactions in Michael adduct reactions, including all atoms of protein. Initially, the geometry of protomer A was obtained from PDB, as describe previously. This structure was prepared following the recommendation by AMBER software, and the three waters molecules were added using the coordinates of PDB file. The S–C₁ bond was broken, and a geometry optimization was carried out by classical force field UFF using Gaussian (default routines). After, ONIOM approaches was carried to build a model with two-layer (PM3MM:UFF and B3LYP/6-31G(d,p):UFF). The ligand, water molecules, His41, Gly143 and Cys145 were definite in higher layer and the others atoms were definite in lower layer, similar to previous model, but Cβ and respective hydrogens of His41 were included in QM part. The same ONIOM model was used to study the complexation between N3 and M^Pro as well. A validation of stereochemical quality of optimized structures was performed by Ramachandran plot [43] using PROCKECK software [44]. All calculations were performed using the Redwood machine present in Mississippi Center for Supercomputing Research—MCSR.

3. Results and discussion

3.1. ONIOM validation

In general, the lower layer environment directly influences the QM region in hybrid approaches. Consequently, it may be significant in an enzymatic system. As our system has several atoms, it was not possible to avoid a separation between higher and lower layer by a covalent bond. In the case of ONIOM approach, the separation between the regions introduces a link atom. Link atoms have the theoretical disadvantage of introducing extra degrees of freedom, and it is possible that interactions arising as a result of the presence of the link atom might be overcounted. Also, it has to be taken into consideration that hybrid approaches, in general, demand more time than classical calculations, thus it is necessary to limit the number of atoms in the higher layer. In addition, enlarging the higher layer does not necessarily result in a more accurate model [45]. However, it is suggested that QM part should be sufficiently large to incorporate the atoms where chemical and electronic changes occur, including charged QM group, and should not disrupt conjugated system. Considering all observations above, a validation of our system was carried out to check if ONIOM models can give results similar to those obtained by classical QM calculations.

Thus, selected Mulliken net atomic charges (Table 1 ) and geometrical parameters (Table 2 ) of trans-α,β-unsaturated system (atoms 1–5, Fig. 1) of N1 inhibitor were compared using classical QM and ONIOM models. Table 1 shows Mulliken net atomic charges for selected atoms (Fig. 1) calculated by PM3MM, B3LYP/basis set, B3LYP/basis set:PM3MM, B3LYP/6-31G(d,p):UFF and PM3MM:UFF. As it can be seen in all cases, the Mulliken net atomic charges changed according to the theoretical level, as expected. Mulliken net atomic population analysis is an arbitrary scheme for assigning charges. Indeed, all such schemes are ultimately arbitrary. Atomic charges, unlike the electron density, are not a quantum mechanical observable, and are not unambiguously predictable from first principle [46]. However, the most positively charged atom is C₃, except for B3LYP/6-31+G(d,p) that is C₂, and the most negative atom is O₄, except for B3LYP/3-21G, B3LYP/6-31G and B3LYP/6-31+G(d,p):PM3MM that is O₅. In general, a good correlation coefficient (r ²) was obtained between classical QM and ONIOM models, ranging from 0.97 to 0.99, except between B3LYP/6-31+G(d,p) and correspondent ONIOM model (B3LYP/6-31+G(d,p):PM3MM (r ²  = 0.517)). This difference can be explained. 6-31+G(d,p) basis set has diffuse functions that permit orbitals to occupy a large region of space only for heavy atoms. It is possible that orbitals between heavy atoms of quantum part and link atoms, which are hydrogens, are not interacting, maybe it is necessary a double plus of this basis set, 6-31++(d,p), which adds diffuse functions for hydrogen atoms as well. Although 6-31++(d,p) basis set calculations are necessary to answer this question, the size of our system, with 43 heavy atoms, makes this practically unviable.

Table 1.

Selected Mulliken net atomic charges of N1 from QM and ONIOM models

Atom	PM3MM	3-21G	6-31G	6-31G(d)	6-31G(d,p)	6-31+G(d,p)
C1	−0.072	−0.062	−0.016	−0.043	0.003	−0.024
C2	−0.169	−0.262	−0.115	−0.197	−0.143	0.250
C3	0.407	0.664	0.486	0.619	0.610	0.066
O4	−0.385	−0.508	−0.451	−0.498	−0.499	−0.502
O5	−0.265	−0.522	−0.526	−0.477	−0.485	−0.308

Atom	ONIOM						PM3MM:UFF	B3LYP/6-31G(d,p):UFF
	PM3MM	3-21G	6-31G	6-31G(d)	6-31G(d,p)	6-31+G(d,p)
C1	–	−0.100	−0.048	−0.0561	−0.056	0.111	−0.043	−0.024
C2	–	−0.227	−0.215	−0.218	−0.218	−0.079	−0.216	−0.114
C3	–	0.429	0.430	0.432	0.432	0.483	0.428	0.561
O4	–	−0.383	−0.387	−0.381	−0.382	−0.491	−0.395	−0.512
O5	–	−0.316	−0.320	−0.312	−0.312	−0.501	−0.315	−0.475
r2		0.987	0.934	0.986	0.969	0.517	0.991	0.997

ONIOM models were constructed with B3LYP/correspondent basis set:PM3MM, PM3MM:UFF, B3LYP/6-31G(d,p):UFF.

Table 2.

Select geometrical parameters of N1 from QM and ONIOM models

Geometry	PM3MM	3-21G	6-31G	6-31G(d)	6-31G(d,p)	6-31+G(d,p)	X-ray
C1 C2	1.335	1.334	1.342	1.337	1.337	1.338	1.545
C2–C3	1.481	1.481	1.472	1.482	1.482	1.483	1.523
C3 O4	1.218	1.231	1.241	1.216	1.216	1.218	1.209
C3–O5	1.364	1.380	1.378	1.354	1.354	1.354	1.360
C1 C2–C3	121.234	119.473	121.180	120.796	120.719	121.124	114.069
C2–C3 O4	128.166	126.643	126.327	125.751	125.745	125.840	124.773
C2–C3–O5	112.288	110.267	111.073	110.648	110.676	110.736	110.589
C1 C2–C3 O4	2.929	0.693	1.051	1.235	1.234	1.196	−0.401
C1 C2–C3–O5	−177.095	−179.423	−179.023	−178.819	−178.826	−178.880	−177.634

Geometry	ONIOM						PM3MM:UFF	B3LYP/6-31G(d,p):UFF
	PM3MM	3-21G	6-31G	6-31G(d)	6-31G(d,p)	6-31+G(d,p)
C1 C2	–	1.332	1.342	1.336	1.336	1.338	1.338	1.339
C2–C3	–	1.482	1.476	1.487	1.487	1.485	1.478	1.479
C3 O4	–	1.227	1.237	1.212	1.212	1.213	1.219	1.214
C3–O5	–	1.396	1.399	1.376	1.376	1.379	1.363	1.368
C1 C2–C3	–	119.339	120.904	120.397	120.397	120.743	120.240	119.100
C2–C3 O4	–	125.748	125.892	125.180	125.180	125.496	112.302	124.994
C2–C3–O5	–	108.618	109.733	109.286	109.286	109.427	111.004	110.075
C1 C2–C3 O4	–	0.064	0.216	0.311	0.311	0.404	0.563	0.180
C1 C2–C3–O5	–	−179.479	−179.272	−179.203	−179.203	−179.126	−178.689	−179.901
r2		1.000	1.000	1.000	1.000	1.000	1.000	1.000

ONIOM models were constructed with B3LYP/correspondent basis set:PM3MM, PM3MM:UFF, B3LYP/6-31G(d,p):UFF.

The same methodology to validate Mulliken net atomic charges was carried out to study geometrical parameters in ONIOM models. Table 2 shows the trans-α,β-unsaturated geometry of N1. Atomic distances, angles, and dihedral angles of classical QM calculations were compared with ONIOM and X-ray geometry. As shown in this table, a high correlation between classical QM and ONIOM geometry (r ²  = 1.00) was obtained. Only two atomic distances are different from the others, C₁ C₂ and C₂–C₃, in X-ray structure. This is a consequence of sp³ hybridization of C₁ and C₂ atoms that they have in protein structure, which is alkylated by Cys145 [19]. Although these differences exist, a good correlation among X-ray, classical QM and ONIOM geometry was obtained, with r ²  = 0.99 in all cases.

Molecular orbital (MO) HOMO (highest occupied molecular orbital) and LUMO were carried out for N1, N3, and AG7088 by PM3MM (N1 only) and B3LYP/6-31G(d). MO are expected to be responsible for the specificity of the interactions between protein and ligand. As it can be seen in Fig. 3 , HOMO is localized mainly on the γ-lactam ring, whereas LUMO is localized mainly on the isoxazole ring. Semiempirical and DFT methods have practically the same localization of molecular orbitals, even though DFT MO are more extended, as a result of inclusion of d orbitals from basis set. Only a small region of HOMO is localized in the trans-α,β-unsaturated system. These features suggest the most important part of these inhibitors, and indicating that heteroatoms of lactam and isoxazole ring have a nucleophilic and electrophilic character respectively, responsible for electronic interaction with receptor. In other words, lactam and isoxazole rings are important for the reversible complex formed with the enzyme, before the nucleophilic attack by the thiolate cysteine [16], [19]. In the case of inhibitors of 3CL^pro, previous SAR studies described that an amine in P1 and small hydrophobic groups in P2 positions are required to improve antiviral activity, which are the same positions of the MO found in our studies [16], [47], [48], [49].

Fig. 3.

Selected MO plots for N1 (A–D) and AG7088 (E and F) in vacuum system. All hydrogens were hidden for a best visualization. (A) N1: HOMO–PM3MM; (B) N1: LUMO–PM3MM ; (C) N1: HOMO–B3LYP/6-31G(d); (D) N1: LUMO–B3LYP/6-31G(d); (E) N3: HOMO–B3LYP/6-31G(d); (F) N3: LUMO–B3LYP/6-31G(d); (G) AG7088 HOMO–B3LYP/6-31G(d); (H) AG7088 LUMO–B3LYP/6-31G(d).

In this first validation, semiempirical PM3MM and ONIOM models demonstrated ability to reproduce results obtained by DFT, principally with B3LYP/6-31G(d) and B3LYP/6-31G(d,p). Furthermore, ONIOM models using MM as lower layer gave reasonable results. These ONIOM models can be used to study the mechanism of Michael reaction considering the whole enzyme.

As demonstrated earlier, validation of models is very important for the next steps, which Michael reaction will be performed. It can have a dramatic influence on the results that will be obtained from this. As can be seen, small region in higher layer can reproduce similar charge and geometrical when compared with classical QM calculations (except for B3LYP/6-31+G(d,p)). Moreover, semiempirical and DFT calculations had similar MO positions. These previous results permit the construction of ONIOM models with satisfactory assurance.

3.2. Michael reaction studies

As described previously, three models were constructed to study this Michael reaction. However, one of them called Oxyprod will be discussed differently from the others. Select geometrical parameters, Mulliken charges, and Reaction coordinates for all models are provided in Table 3, Table 4 , and Fig. 4 respectively. For a better analysis of these results, four groups were created using nine atomic distances and one dihedral angle. In the first group, the nucleophilic attack was described by C₁–S, C₁–C₂, and Hτ–C₂ distances. In the second group, the effect of catalytic system will be discussed analyzing the distances among Hτ, Nτ, and S atoms. The effect of the oxyanion pocket will be discussed comparing the distances among O₄, H₈ and H₉, as third group. Finally, conformational changes will be discussed by H₇(w1)–C₂, O(w2)-Hπ distances, and C–Cα–Cβ–Cγ(His41) dihedral angle.

Table 3.

Select geometric parameters of calculated models in Å

Geometry	Reagent	Inter1	HProd	Oxyprod
Nucleophilic attack
C1–S	3.827	2.720	1.873	1.810
C1–C2	1.336	1.347	1.542	1.511
Hτ–C2	3.955	3.559	1.097	3.199
Catalytic system
Hτ–Nτ	2.113	1.993	2.295	1.072
Hτ–S	1.361	1.368	2.884	4.267
Oxyanion pocket
O4–H8	2.374	2.872	2.522	2.893
O4–H9	4.105	3.529	4.197	4.508
Conformational change
H7(w1)–C2	3.435	3.590	4.035	2.288
O(w2)–Hπ	1.910	1.913	1.897	1.767

Table 4.

Selected Mulliken charge for all models

Atom	Reagent	Inter1	Hprod	Oxyprod
S	−0.140	−0.169	−0.071	−0.216
C1	−0.099	−0.039	−0.141	0.000
C2	−0.183	−0.234	−0.172	−0.687
Nτ	−0.125	−0.120	−0.115	0.462
O4	−0.402	−0.436	−0.402	−0.313

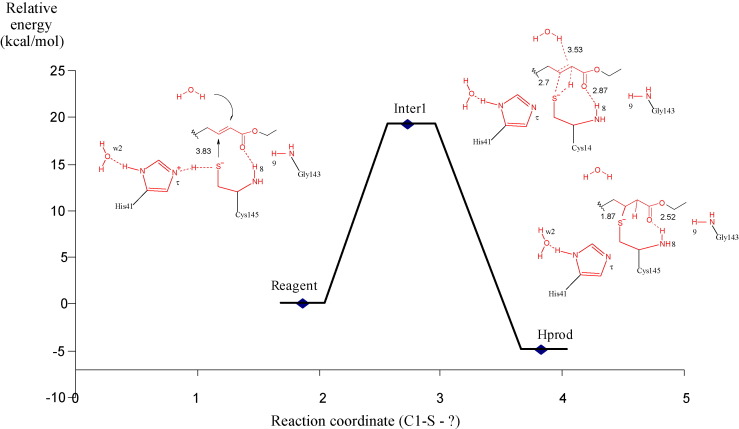
Fig. 4.

Minimum energy reaction path. The x-axis defines the nucleophilic attack coordinate (interatomic distance between C₁ and S(Cys145), and the y-axis defines relative energy. The distances are in angstroms. The colors red and black define atoms with higher and lower layer respectively.

As it can be seen by the first group of geometrical parameters (Table 3), the distance between C₁ and S(Cys145) decreased from 3.8 to 1.87 Å, while the C₁–C₂ distance (typical double bond) increased from 1.34 to 1.54 Å in Reagent and Hprod models. These results suggest that, while S(Cys145) attack C₁, a negative charge (−0.23) is formed on C₂ (Table 4, Inter1). This negatively charged atom can abstract a proton (Hτ) from Nτ(His41), as seen in Table 3 by the Hτ–C₂ distance that changed from 1.10 Å (Reagent) to 3.95 Å (Hprod). It shows that the hybridization of C₁ and C₂ changed from planar sp² to tetrahedral sp³ as well. The analysis of catalytic system (Hτ–Nτ and Hτ–S distances) showed that Hτ is located between S(Cys145) and Nτ(His41), 2.11 and 1.36 Å from Nτ and S atom respectively. S and Nτ atoms have charge density very close between each other (−0.14 and −0.12, respectively (Table 4)). It is implying that the energy barrier for catalysis process should be very low, and ionic and neutral form of His41 and Cys145 are very close in energy in studies performed in vacuum system. After nucleophilic attack, the distance between Hτ and Nτ increased from 2.11 to 2.95 Å, while the negative charge on Nτ decreased from −0.12 to −0.11, as seen in Table 3, Table 4 respectively. In addition, a negative charge is formed on S and C₂ atoms (−0.07 and −0.17 respectively). The oxyanion hole has been described as formed by backbone hydrogens of Cys145 and Gly143 [19]. In our model, it is formed by H₈ and H₉. However, Table 3 shows that only O₄–H₈ distance is a standard hydrogen bond (2.37–2.62 Å).

The minimum energy reaction path connecting Reagent and Hprod is depicted in the diagram coordinate shown in Fig. 4. Our calculations show that the product obtained has a relative energy of −4.85 kcal/mol. Although frequency calculation are not available in ONIOM approach, our calculations suggest that a transition state structure was obtained (Inter1) with a distance of 2.72 Å between S and C₁ atom, and it has 19.31 kcal/more less stable than Reagent model.

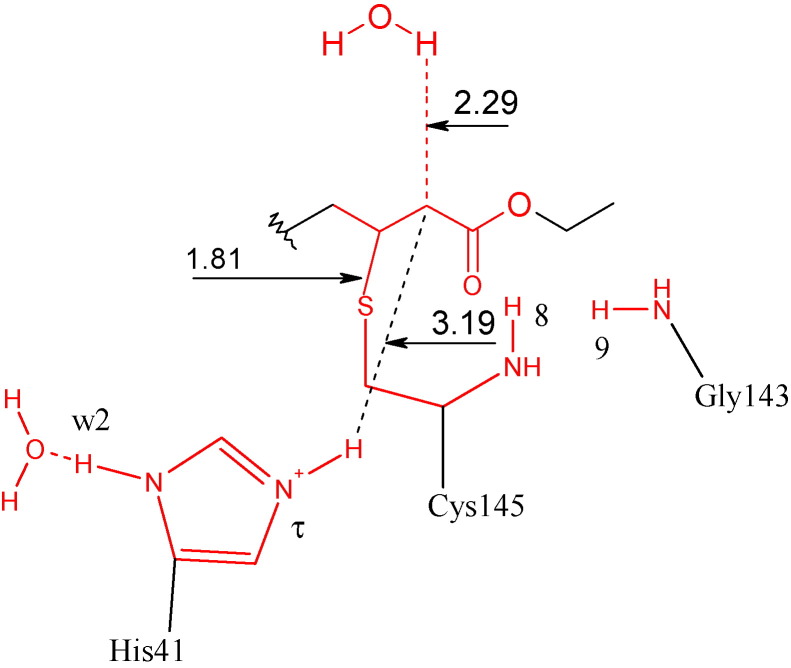
A search for a transition state found an unexpected saddle point structure, called Oxyprod (Fig. 5 ), which has C₁–S distance less than Hprod (1.81 Å, Table 3). Weak hydrogen bonds are formed between Hτ(His41) and O₅ (2.89 Å). In addition, a higher negative charge is formed in C₂ (−0.69), which is stabilized by Hτ(His41) and another proton from water molecule (w1) with distances of 2.89 and 2.41 Å respectively. This model has more 50.05 kcal/mol than Reagent model. Similar structure had described for papain inhibitors [28]. In this case, a favorable ionic interaction between imidazolium and ligand was observed, even though the cartesian coordinate of atoms was not fixed and the geometry of enzyme was not considered. As a result, the atoms could find favorable position in the PES.

Fig. 5.

Oxyprod: The distances are in angstroms. The colors red and black define atoms with higher and lower layer respectively.

In this study, a Michael reaction has investigated using QM/QM models of ligand (N1), oxyanion pocket (Cys145 and Gly143), and catalytic system (Cys145 and His41). Theses results indicate an exothermic mechanism, as described previously [26], [28]. In addition, a transition state can be described for the whole protein addressing for a concerned mechanism, because S and Hτ atoms are approximating of trans-α,β-unsaturated in the same time. Furthermore, an interaction between hydrogen from water molecule (H₇w1) and C₂ was obtained (2.29 Å) due the negative charge formed after nucleophilic attack. It is probably that this water molecule decreases the activation energy in transition state structure as well, very similar with Oxyprod (Fig. 5). Likewise with our results, QM/MM studies obtained by Byun and Gao showed that a tetrahedral intermediate does not exist for cysteine protease [27]. Another point, it is very probable that small polar groups of Michael acceptor can decrease the energy barrier for this reaction. It can be observed for inhibitors of papain [22]. Consequently, they should be more active than apolar groups. In addition, previous studies have revealed that all proteases have a His–Cys catalytic dyad [6], [9], [19]. However, our calculations have shown an interaction between a water molecule (w2) and Hπ(His41). Perhaps, the w2 has important role as a third member, similar with others proteases [15].

3.3. QM/MM studies of M^Pro

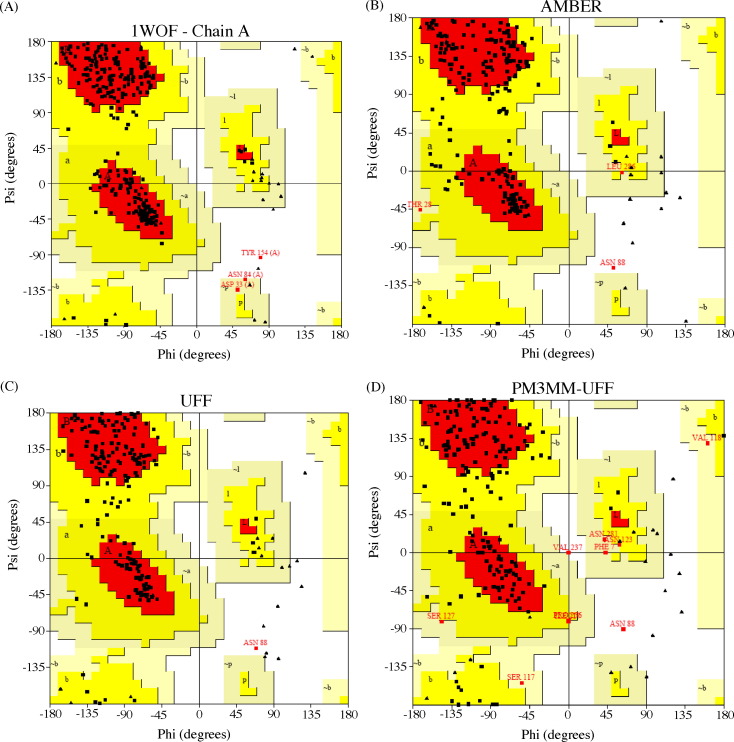
In this part of our studies, the whole protein was considered, which active site, oxyanion hole, and the trans-α,β-unsaturated moiety are in QM part. Initially, the stereochemical quality of PM3:UFF was compared with X-ray structure of 1WOF, AMBER force field and UFF (Fig. 6a-d). As can be seen by Ramanchandran plots, the quality of models depend of methodology used. In general, Asn88 was found in disallowed region for all models. Amber force field showed more than two amino acids in this region, Thr28 and Leu286 (Fig. 6b). In addition, the hybrid model showed Asn88 and Val237 in disallowed region, and Ser117, Val118, Asn123, Ser127, Ile217, Pro256, Asn281 in generously allowed region (Fig. 6c). Although the PROCHECK showed a set of amino acids which have geometrical distortion in Phi and Psi angles, none of them are present in active site. In other words, the hybrid model can be used to study the interaction between the ligand and M^Pro [16], [19].

Fig. 6.

Ramachandran plot for: (A) X-ray structure, (B) AMBER, (C) UFF, (D) PM3MM:UFF and (E) AM1:UFF. Amino acids found in disallowed region are in red.

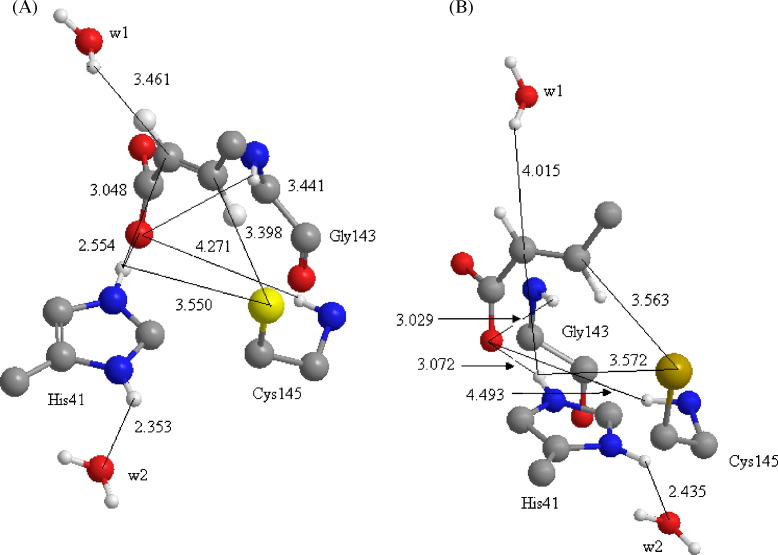
After this validation, which geometrical aspects were compared among different force field and the ONIOM model, the geometry of optimized active site, oxyanion hole, and the trans-α,β-unsaturated moiety were demonstrated by Fig. 7 . As can be seen, the water molecules (w1 and w2) are very close of trans-α,β-unsaturated and His41 respectively, for both N1 and N3. The distance between w1 and Cα is 3.46 and 4.01 Å; and the distance between w2 and His41 is 2.35 and 2.43 Å for N1 and N3 respectively, characterizing a typical hydrogen bond between w2 and His41. As described before, it is possible that these water molecules can contribute for decrease the active energy in the alkylation process. Before the nucleophilic attack by Cys145, a reversible complex is formed between inhibitor and protease. This complex is characterized by the distance among ligand and enzyme. First, the sulphur atom of Cys145 distance 3.40 and 3.56 Å from Cβ for N1 and N3 respectively. Second, the oxyanion hole is well characterized by distance among Gly143, Cys145 and ligand. The hydrogen of Gly143 and Cys145 distance 3.44 and 3.03 Å from oxygen of ligand for N1 and N3 respectively, characterizing a hydrogen bond. In the case of Cys145, this distance increases to 4.27 and 4.49 Å. Furthermore, a hydrogen bond was formatted between His41 and the oxygen of ligand, which distance 2.55 and 3.07 Å for N1 and N3. This result shows that His41 can contribute for complex stage stabilizing the oxyanion hole, and after to nucleophilic attack of sulphur atom of Cys145, which Hτ can approximate of Cα.

Fig. 7.

(A) Interaction between active site and N1; (B) select hydrogen bonds between ligand and N1 and N3 by PM3MM:UFF.

The binding energy between M^Pro and two inhibitors (N1 and N3) [9] is described in Table 5 . As can be seen, both inhibitors can complex with enzyme with favorable binding energy. N1 and N3 can stabilize the M^Pro by −340.997 and −918.992 kcal/mol respectively. In other words, N3 can stabilize the enzyme 577,995 kcal/mol more than N1. This difference of binding energy between N1 and N3 can be attributed by intermolecular interactions. In order to observe this with more details, the interactions between ligand and protein, the number of hydrophobic interactions, hydrogen bond (HB), and bad contact among atoms in active site were carried out by Rasmol and Swiss-PDBViewer softwares [50], [51]. Rasmol showed that ethyl group of N1 distance 6.25 and 5.08 Å, from Met49 and Leu27, respectively, while aromatic ring of N3 distance only 3.40 and 4.54 Å from the same amino acids. Following, Swiss-PDBViewer showed that N1 and N3 have 27 and 29 HB, and 7 and 5 atoms with undesirable contact between ligand and protein, respectively. According with observations, it seems that N3 fits better than N1 in active site, decreasing the binding energy. This result shows the first step of reaction, which the inhibitor initially forms a reversible complex with the protease. The evaluation of the ONIOM model addresses for N3 as more active than N1, similar to experimental results [9], which enzyme inhibition of 10.7 and 9.0 μM were obtained by N1 and N3 respectively.

Table 5.

Relative energy of complex between N1 and N3, M^PRO, and inhibitors (N1 and N3) by ONIOM (PM3MM:UFF) (kcal/mol)

Structure	N1 energy (kcal/mol)	N3 energy (kcal/mol)
Complex	−3248.628	−3491.021
Mpro	−2889.470	−2573.404
N1	−18.161	–
N3	–	1.375
Binding energya	−340.997	−918.992

^aBinding energy = Ecomplex − EM^pro − E(N1 or N3).

4. Conclusion

In this study, the models constructed were validated with classical quantum-mechanic calculation (DFT) and X-ray structure, which assured trustful models. As the whole system has 4.738 atoms, two strategies were adopted to decrease the complexity of the system. The first one, the number of atoms was decreased resulting in a small model which only the ligand, active site and oxyanion hole were studied by QM/QM, using B3LYP/6-31G(d,p):PM3MM model. On the other hand, the second strategy, the whole system was studied by PM3MM/UFF. The results of both models indicated the main conformational changes during complexation and alkylation reaction between M^Pro and N1 (and N3, in the case of QM/MM studies). These approaches allowed us to study the Michael reaction by QM/QM and QM/MM, which showed an exothermic and concerned mechanism. Furthermore, the results suggested that small polar groups and the water molecule (w1) can address the reaction decreasing the energy barrier for the second step of reaction, which it would be a good starting point for new leader compounds. In addition, the water molecule (w2) could have an important participation as a third member of the catalytic system. Another point, although only the binding energy of two compounds was performed, the QM/MM model was able to estimate the theoretical activity of them. Although further calculations are necessary to understand the whole process, these findings can provide information for development of new inhibitors against a future emerging SARS disease, and showed new perspectives about the proteolytic mechanism of Cys proteases.