Face and eyes localization algorithm in thermal images for temperature measurement of the inner canthus of the eyes

Highlights

• •We developed algorithm for detection and localization of face and eyes in thermal images.
• •The novelty is the modification of the RHT method.
• •The algorithm is highly accurate and fast.
• •The essential parameters of the IR camera were examined before experiments.

Abstract

In this paper, a novel algorithm for the detection and localization of the face and eyes in thermal images is presented, particularly the temperature measurement of the human body by measuring the eye corner (inner canthus) temperature. The algorithm uses a combination of the template-matching, knowledge-based and morphological methods, particularly the modified Randomized Hough Transform (RHT) in the localization process, also growing segmentation to increase accuracy of the localization algorithm. In many solutions, the localization of the face and/or eyes is made by manual selection of the regions of the face and eyes and then the average temperature in the region is measured. The paper also discusses experimental studies and the results, which allowed the evaluation of the effectiveness of the developed algorithm. The standardization of measurement, necessary for proper temperature measurement with the use of infrared thermal imaging, are also presented.

1. Introduction

Automated face localization is a concept, which has been actively researched form more than 35 years, while face localization in thermal images is a new concept. The developed algorithm of face and eye localization in thermal images is presented in this paper, as well as some major problems connected with face localization in thermal images. Processing facial images has a wide range of applications, such as biometric identity authentication, human–computer interaction, multimedia, access control to secure computer networks and manual or automatic screening at airports. In medicine, a face detection system with visual images, or thermal images when temperature is important, can be used to detect disease in humans and also for robust and accurate human body temperature measurement with temperature measurement of the inner canthus of the eyes. The inner canthus of the eyes are suggested for temperature measurement utilizing infrared thermal imagers [1], as it is the warmest area of the face. In Fig. 1 the face of the human with increased core temperature is presented. Many studies have proved that face detection in a thermal spectrum offers a few distinct advantages over the visible spectrum. Thermal imagery is independent of ambient lightning, because the Infrared Radiation (IR) sensors only measure the heat emitted by the object – the human body.

Fig. 1.

Thermal image of the face with increased core temperature.

Measurement of the human body core temperature with screening thermography is an alternative to traditional methods of the temperature measurement on the forehead or underarm. Face localization in thermal images is achieved by a few steps: pre-processing, acquisition, processing and temperature measurement. Pre-processing includes the standardization of the camera parameters, described later in this paper and local measurement conditions, such as ambient temperature and humidity. Also, the human body temperature must be stabilized if thermal images are acquired in a laboratory, for example, avoidance of activity and skin temperature stabilization after removing clothes. Acquisition includes only localization and taking thermal images or sets of thermal images of the examined face.

The processing step includes normalization of the face images, also localization of the face, eyes and inner canthi regions of the left and right eye using various methods. Temperature measurement includes determining the temperature in all localized and recognized regions on the face.

The developed face localization algorithm is based on local feature representation. The proposed algorithm is based on the modified Randomized Hough Transform (RHT), the face and eye verification procedure and finally, growing segmentation with morphological operations for localization of the inner canthi area.

2. Previous work

Human face localization is one of the identification methods in biometric systems, which are based on physiological characteristics, such as face, fingerprints and iris, and also on behavioral features, for example, voice, handwritten signature or gait. Face localization is one of the most effective and non-contact methods of human detection. A survey of the relevant literature can be found in [2] which shows the results of much research on visible-spectrum imagery. The main goal of the face localization research presented in this work is to determine the localization of the face in the image and the parameters of the face, such as position and dimensions of the eye, region of the inner canthi, and maximum, minimum and average temperature in the region.

An excellent classification of the localization methods is proposed by Yang, Kriegman and Ahuya in [3]. The methods can be classified into four categories: template-matching methods [4], knowledge-based methods [5], feature invariant approaches [6] and appearance-based methods [7]. Many algorithms use combinations of the above methods to increase the effectiveness of face localization. Template-matching methods are based on predefined criteria or are parameterized by a function of the face pattern. In this way, the template for the eyes, nose, mouth and face can be used. The template is compared with the test image and the correlation values between these two images are computed. This approach is simple to implement, but there are many problems with variation in scale or pose. In [8] a novel approach for face localization based on the difference vector plus kernel principal component analysis is proposed. The difference vector is the difference between the original image and the common vector which is obtained by the images processed by the Gram–Schmidt orthogonalization. The result is derived from finding the minimum distance between the test difference feature vectors and the training difference feature vectors. The morphological method for face localization using fiducial points is presented in [9]. This method is independent of facial expressions. In the localization process, the fiducial points are fed as inputs into a back propagation neural network for learning and identification of a person. The human face can be recognized also by morphological shape decomposition [10], [11], being the decomposition of an image object into a union of simple components using morphological operations, that is, erosion and dilation. In [12] a modification of the Hough transform can be found, which can deal with variations in scale or pose in a specified range. Next, are the knowledge-based methods based on the rules provided by the researcher. Put simply, a face often appears in an image with two eyes, a nose and a mouth. The distances and position are computed for selected components, for example, left and right eyes, and the relationship rule is examined. There are problems with defining the rules, because if the rule is too specific, than the face cannot pass the rule, otherwise if the rule is too general, it may give many results. Different approaches use feature-based methods, which are based on facial features and texture or skin color of the face. These algorithms are very sensitive to illumination and noise. Appearance methods are based on statistical analysis. One of the most effective methods is based on eigenfaces, in which the neural network computes a face description by approximating the eigenvectors of the image’s autocorrelation matrix. Other methods have applied principal component analysis to face localization. In this method, the eigenfaces are generated from a set of training faces. Then, the similarity between the input face and the eigenfaces is computed. The localization of human faces in visual images is related to certain problems, such as pose, occlusion by another object, imaging condition or facial expression.

Thermal imagery [13], [14] is independent of ambient illumination since the human face and body emit thermal energy. The energy is emitted by any object above zero absolute temperature. Thermal energy is then registered by a detector, such as an FPA (Focal Plane Array) microbolometer, also data, defining the conditions of measurement (emissivity, ambient temperature, humidity, distance from the object), are registered and available for analysis or for processing algorithms. Identifying faces from thermal images has become an area of growing interest. In general, in many applications, the methods used in the IR-spectrum are based on well-known visible-spectrum methods. The comparison of localization efficiency for thermal images and visible images was shown by Wilder et al. [15]. Among the statistical methods, the method of eigenfaces has been used successfully in the analysis of thermal images, increasing the efficiency of localization. Socolinsky and Selinger [16] compared the quality of face localization in video images and thermal images with the use of two basic statistical methods – PCA (Principle Component Analysis) and LDA (Linear Discriminant Analysis). Face localization issues in thermal images are discussed in [17] and Ring et al. discussed the problem of measuring human body temperature using thermal images [18]. The human body and the face are characterized by a specific average value of the temperature of about 30 °C. Hence, it becomes a feature for effective localization and identification of a human face, which, in combination with some knowledge-based or template-matching methods, can be an effective instrument for automatic measurement of the temperature of the inner canthi. However, some requirements must be met, for example, fixed metrological parameters of the infrared thermal imager and constant measurement conditions (ambient temperature, humidity). Examples of the common problems in thermal imaging are shown in Fig. 2 .

Fig. 2.

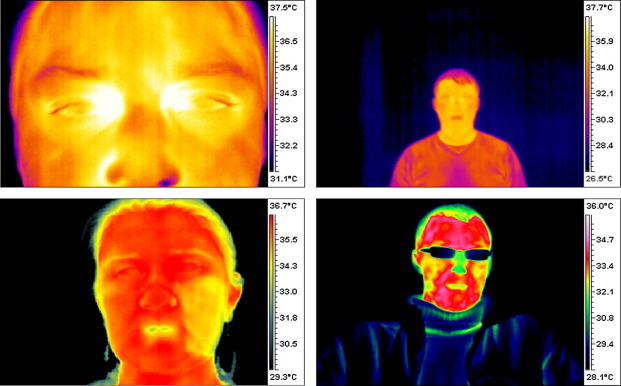
Examples of common problems: (a) thermal image is taken too close, (b) thermal image is taken too far away, (c) face is distorted by cream (right side of the face) and (d) wearing spectacles prevents correct temperature measurement.

3. Standardization of the measurement

The use of infrared thermal imaging for fever screening has grown in importance since the incidence of SARS (Severe Acute Respiratory Syndrome) infection, particularly the H1N1 (subtype of the influenza A virus) pandemic outbreak. One can find the application of infrared thermal imaging for fever detection in airports. Some references on this topic can be found in [19]. If the thermal imaging camera used for automated face localization is used also for fever screening, the importance of proper camera usage and camera quality rises. There are two standards concerning the application of screening thermographs for human febrile temperature screening: IEC 80601-2-59:2008, Medical electrical equipment – Part 2-59: Particular requirements for basic safety and essential performance of screening thermographs for human febrile temperature screening and ISO/TR 13154:2009, Medical electrical equipment – Deployment, implementation and operational guidelines for identifying febrile humans using a screening thermograph. In general, the standards provide information about proper camera mounting, subject preparation and thermal image acquisition. It is important that the temperature of the inner canthi should be measured with at least a 9 × 16 pixel region.

Most thermal imaging cameras available on the market are equipped with MEMS (Micro-Electro-Mechanical Systems) based uncooled microbolometer arrays and are designed for industrial application (e.g. predictive maintenance, thermal imaging for automation) or home energy audit. In many cases, there is no need for absolute temperature measurement so traceability to International Temperature Scale 1990 (ITS-90) is hardly ever required. In contrast, fever screening requires the thermal imager to have good thermal resolution, good medium/long-term stability and regular traceable calibration. In recent years, in-field-of-view fixed-point cells have been developing, especially for medical thermography applications [20].

Thermal images for the investigations presented in this work have been captured with a Wuhan-Guide TP8 thermal imaging camera. Some of the essential parameters of the camera were examined: stability, temperature error and the influence of the object in scene. The camera is equipped with a 384 × 288 pixel uncooled FPA microbolometer. Its spectral range is 8–14 μm, thermal sensitivity 0.08 °C and the intrinsic error is ±1 °C or ±1% of the reading in a −20 °C to + 250 °C range, whichever is greater.

The parameters were investigated based on a reference black body and a reference platinum resistance thermometer for precise temperature measurement of the black body cavity. The temperature range was restricted to ambient and human body temperature.

The set-up for the testing procedures is presented in Fig. 3 . The reference temperature source was the LAND P80P black body, together with the Kaye RTD500 platinum reference thermometer. The emissivity of the black body is 0.995 and the reference thermometer’s accuracy is ±0.01 °C.

Fig. 3.

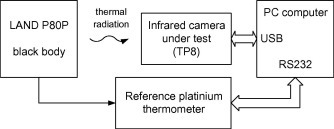
Scheme of the measuring stand for the investigation of the metrological properties of the ThermoPro TP8 thermal imaging camera.

3.1. Stability test

The stability test was performed for 0 °C of the black body cavity. Thermal images were registered during the 100 min period with a 5 min interval. From the registered images, the mean temperature of the cavity was calculated for a 35 × 35 and an 8 × 8 pixel area. The errors during the measurements were calculated as the difference between the mean temperature and that indicated by the reference platinum thermometer. The results are depicted in Fig. 4 a. After 75 min, the TP8 camera’s stability was better than ±0.2 °C.

Fig. 4.

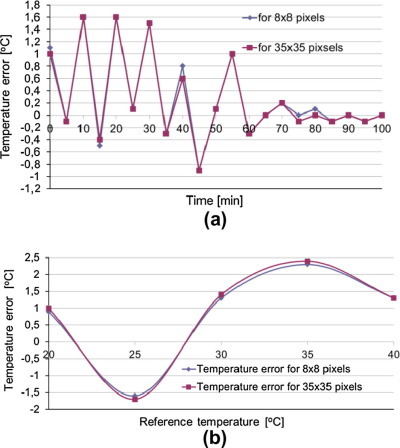
(a) Results of stability test for the TP8 thermal imaging camera, (b) results of temperature error in measured range.

3.2. Temperature error

The measured temperature range for temperature error determination was restricted from +20 °C to +40 °C. The camera was stabilized – powered on at least 90 min before the measurements – according to the results from the stability test. The error was calculated in the same way as for the stability test, and the results are presented in Fig. 4b. As can be seen, the error for the most interesting temperature range – around 36.6 °C (inner canthi temperature for a healthy person) – is significant (+2 °C) but can be treated as a systematic error for the tested camera, thus can be corrected during the measurements procedure. The important conclusion from this test is that the thermal imaging camera has to be calibrated before its first use in an application, for example face localization for fever screening. For the tested TP8 camera, the determined absolute temperature error is higher than that specified by the manufacturer.

3.3. Object in scene

The influence of the object in scene was tested in a simple way, described in [21]. A cup of hot water at 42 °C (object in scene) was placed between the camera and the black body cavity in such a way that the cup could influence the temperature inside the cavity. The temperature of the black body was set to 30 °C. The set-up is presented in Fig. 5 . The mean temperature was calculated from the same area of the black body cavity, 20 × 20 pixels, without and with the object in-scene. The mean temperature was higher, even up to +1 °C, than that without the object, which is significant for fever screening.

Fig. 5.

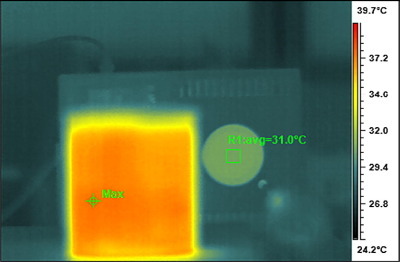
Influence of object in scene on measured temperature of the object (black body cavity in this case).

4. Proposed algorithm

The goal of the proposed algorithm is to achieve the most accurate temperature measurement of the inner canthi. Therefore, the most important step is the fast and accurate localization of the face, eyes and regions of the inner canthi, which give us information about human temperature. The scheme of the proposed method is presented in Fig. 6 .

Fig. 6.

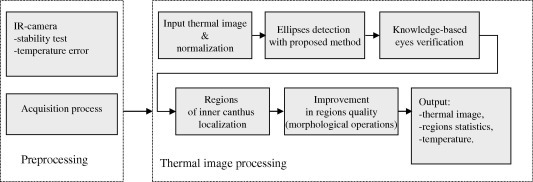
Scheme of the proposed algorithm.

In the first step called pre-processing, the metrological parameters of the infrared thermal imager and measurement condition were set or measured. The parameters fall into two categories. The first is connected with the infrared thermal imager, for example, temperature stability, temperature error, thermal resolution and geometric resolution. The method of determination of these parameters was described in the previous section. The second category is connected with the measurement conditions, for example, emissivity (for human skin ε  = 0.98), humidity, ambient temperature and distance from the object (in our case human face). The correct determination of these parameters reduces the number of possible errors and ensures that the measured temperature is correct.

In the next step, groups of thermal image processing methods for face and eye localization, inner canthi localization and temperature measurement are proposed. The thermal image is taken as an input of the algorithm. The normalization of the image is achieved by automatically setting the temperature range from 30 to a maximum of 40 °C. It is an effective method to reduce the processed data, also eliminating other objects from the image. Next the general part of the algorithm is described.

The previous experience of the authors suggests using template-matching methods in conjunction with knowledge-based methods, as used successfully for the localization process in the visual images. One of the methods which allows the accurate localization of objects is the Hough transform (HT) [22], which was designed as a method for detecting objects and shapes in 2D images, in particular, line detection [23], circles, as well ellipses, and other shapes described by the parametric equation (generalized Hough transform). Over the years, this has been adapted to create, for example, the adaptive HT, combinatorial HT or randomized HT. In the standard HT (SHT), an object model and image as the edge map are the input variables. In this work the object model is given by the ellipse model presented in Eq. (1), and the thermal image as a 2D temperature matrix represented by a 2D grayscale image.

$$\frac{{(x-x_s)}^2}{a^2}+\frac{{(y-y_s)}^2}{b^2}=1\text{,}$$ (1)

where x_s, y_s are the ellipse center, a, b are the ellipse axes.

In this case, to find the ellipse would require solving the four simultaneous non-linear equations; also, only the ellipses with a vertical or horizontal longer axis will be detected. The extension of Eq. (1) to all angles of the longer axis is presented below.

$$\frac{{((x-x_s)\cos \alpha +(y-y_s)\sin \alpha )}^2}{a^2}+\frac{{((x-x_s)\sin \alpha +(y-y_s)\cos \alpha )}^2}{b^2}=1$$ (2)

where x_s, y_s are the ellipse center, a, b are the ellipse axes, α is the angle of the longer axis.

In this case, we have five parameters which describe the ellipse and all of them must be calculated. In this case use of the HT to detect the ellipse is impractical.

In the HT all the pixels on the image are examined looking for parameters that correspond to the tested model. Each image pixel votes in the Hough space (parameters matrix) for a corresponding ellipse. The votes are summed and stored in the Hough space, also called the accumulator. By identifying the peaks of the parameter matrix, the object parameters are identified. For lines we have only two parameters, for ellipses five parameters (Eq. (2)).

The most useful property of the HT is its robustness to noise, while its disadvantage is computational complexity, which dramatically increases memory consumption by filling the Hough space. The HT also has other properties, for example a point in the image corresponds to a sinusoidal curve in the parameter space and points lying on the same curve in the parameter space correspond to lines through the same point in the image. All pixels in the SHT must be examined, which of course increases the memory consumption. In addition, the parameter space is discrete, generating problems with resolving Eq. (2).

A Randomized Hough Transform (RHT) [22] improves the accuracy and robustness of the SHT. The three points P ₁  = (x ₁,  y ₁), P ₂  = (x ₂,  y ₂), P ₃  = (x ₃,  y ₃), which belong to one ellipse (Fig. 7 ), are randomly selected from the image, then the tangents of an ellipse at three points are determined by using a method of minimum least squares and the points of intersection of the tangents and the bisectors of the angles are determined. The intersection is the center of the ellipse O.

Fig. 7.

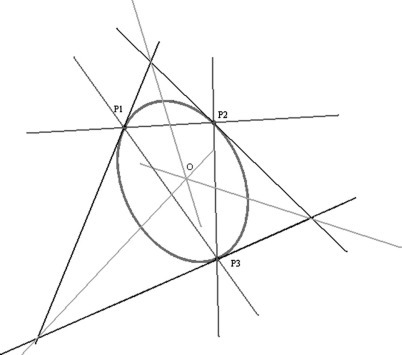
Estimate of ellipse center.

Next, the remaining parameters of the ellipse are calculated from Eq. (3). Then the inequality in Eq. (4) must be checked and if it is true, the parameters represent the valid ellipse and the votes are summed in the Hough space. The procedure is repeated for the next three points.

$$\begin{array}{c}\hfill a{(x_1-x_s)}^2+2b(x_1-x_s)(y_1-y_s)+c{(y_1-y_s)}^2=1\hfill \\ \hfill a{(x_2-x_s)}^2+2b(x_2-x_s)(y_2-y_s)+c{(y_2-y_s)}^2=1\hfill \\ \hfill a{(x_3-x_s)}^2+2b(x_3-x_s)(y_3-y_s)+c{(y_3-y_s)}^2=1\hfill \end{array}$$ (3)

$$\mathit{ac}-b^2>0$$ (4)

When all the pixels of the image are examined, the parameters of the ellipse can be taken from the parameter matrix as the parameters with the maximum votes.

The novelty is the modification of the RHT method, based on combination of two methods – template-matching and feature extraction (Fig. 8 ). The RHT and region growing segmentation [4] were used for this purpose. RHT combined with region growing segmentation decreases the time complexity and improves the accuracy of pixel localization. Region growing segmentation is used also for the detection of homogeneous regions of the inner canthi.

Fig. 8.

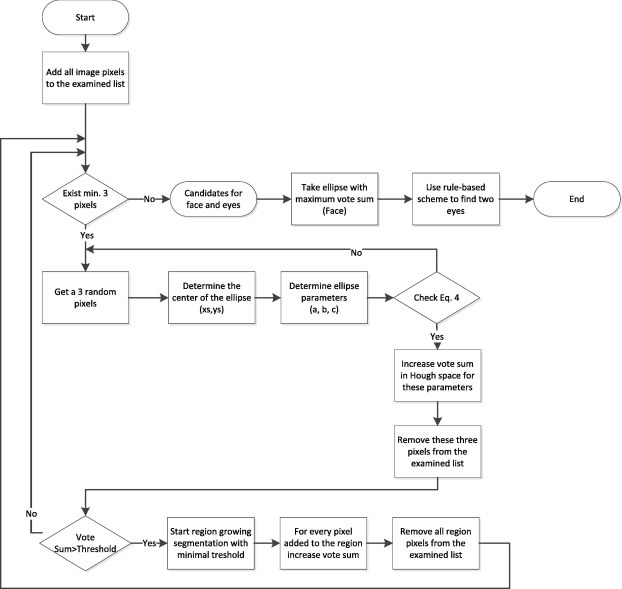
Scheme of the face and eye localization part of the proposed algorithm.

During the Hough space filling process, the modified algorithm checks the votes sum, if it is higher than, for example, 5 pixels, than the region growing segmentation is started. The starting point is the last examined and belongs to the ellipse pixel from the image. In our case it is a great solution, because region growing with, say, an homogenous step equal to 0.1 °C, is faster and more accurate than examination of the one pixel with all the parameters in the range. The pixels belonging to the homogenous region increase the votes sum in the parameter space, also they are deleted from the list of processed pixels.

After filling the Hough space, the maximum votes selection in the space describes the parameters of the largest ellipse on the image. Also the information about axes, angle of the slope of the larger axis and position of the ellipse center are obtained. If the information about the axes is allowed, the parameter space can be used for eye localization.

For the eye localization procedure, the knowledge-based scheme is proposed on the rule-base, such as the face usually contains two eyes located on the opposite side of the vertical axis and on one side of the horizontal axis. It is only a numerical procedure, requiring only review of the Hough space and finding similar ellipses.

After finishing the face and eye localization process, the inner canthi localization process is run. It is an important step, because the inner canthi will be used for human temperature calculations, thus every pixel is important. A morphological operation is used. We use segmentation with region growing with a minimum step of 0.1 °C and the open/close process to achieve the regions. Segmentation is started from the pixel with the maximum temperature. The pixel is taken from the eye region (left or right eye ellipse). After segmentation, the quality of the inner canthi region is applied by the open/close operation. At the end the minimum, maximum and average temperatures are computed from all the pixels belonging to the processed region.

5. Experiment and results

The experiment was conducted in the thermovision measurement laboratory in the Institute of Automatic Control at Silesian University of Technology, with a database of 125 thermal images of faces. The camera used was characterized by the parameters described in Section 3. In Fig. 9 the scheme of the examination room is presented and the measurement parameters are given. The ambient temperature was 23.3 °C, relative humidity 44.0%, distance between the camera and the examined human varied between 0.5 and 3 m with 0.5 m steps. After the acquisition of the images, normalization was performed to attenuate objects surrounding the face. An example of normalization is presented in Fig. 10 . The distance between the human and the camera lens was varied to test different space filling in the image by the face (see Fig. 11 ), the proportion of the face to the image and for different resolutions of the region of interest – face and eyes. The influences of the other objects, such as other persons and heat sources, were minimized before starting the experiment. Also the distance between the camera and the walls must be such as to provide minimal influence from the thermal energy reflected by the walls. The tested persons were in the room for a minimum of 15 min before the experiment started and they did not wear glasses. Thermal images of the humans were taken only in the upright position, deviations in the vertical axis was a maximum 15°. For reference, the axillary temperature was measured simultaneously with the image acquisition. The parameters in the algorithm were chosen to maximize the quality of the final result.

Fig. 9.

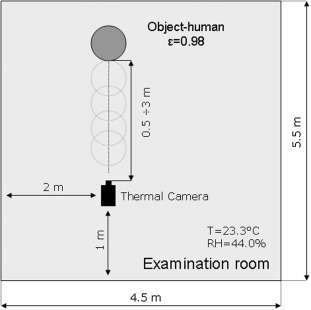
Scheme of the examination room.

Fig. 10.

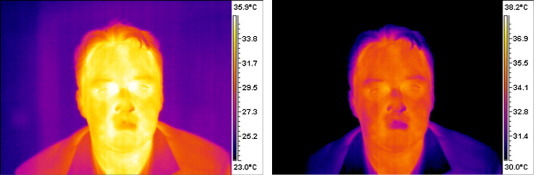
Examples of thermal face images. Raw thermal image (left). Normalized thermal image (right).

Fig. 11.

Thermal face image from different distances camera-face. 0.5 m, 1.5 m, 3 m (from left to right).

The first experiment was designed to determine the optimal distance between the examined human face and the thermal camera lens. The determinant of the optimal distance was the accuracy of the localization and the time complexity. The accuracy of localization for different regions of interest was made by comparing the set of pixels from the manual selection and the set of pixels identified by automatic region localization. Fifty per cent accuracy indicates that half of the pixels of the two sets of pixels are identical. For example, Table 1 shows that the average accuracy at a distance of 1.5 m for the region LE is equal to 97.1%, which means that 97.1% of the pixels in the left eye region localized by the proposed algorithm coincide with the same pixels in the left eye region localized manually. The accuracy of localization depends on the distance from the camera. It is presented in Table 1.

Table 1.

Average accuracy (%) of the localization regions of interests performed for all the tested thermal images, where Face – face region, LE – left eye region, RE – right eye region, LIC – left inner canthus of the eye region, RIC – right inner canthus of the eye region.

Region	Distance (m)
	0.5	1.5	2.5	3.0
Face	40.1	97.3	35.1	32.2
LE	45.2	97.1	27.9	27.1
LIC	37.2	97.5	14.2	11.7
RE	43.2	97.1	27.2	29.4
RIC	36.1	97.5	13.9	12.1

The same conclusion, regarding the dependency of localization on the distance from the camera, comes from the analysis of the average temperature of the eye region for the tested thermal images (Fig. 12 ). The difference between temperature obtained from the algorithm and axilla temperature is the smallest for the 1.5 m distance and is about 0.1 °C. Of course, this relationship will change once the infrared thermal imager is changed, particularly with different detector resolutions – when the resolution increases then the allowable distance also increases. This experiment shows that the best distance for temperature measurement is about 1.5 m. At distances greater than 1.5 m the number of pixels in the tested regions dramatically decreases; on the other hand, at distances of less than 1.5 m the field of view of the thermal camera should be considered.

Fig. 12.

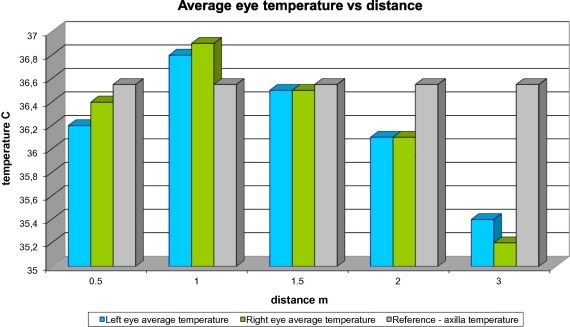
Relationship between average temperature of the eye region and the distance from the infrared thermal imager. Also the temperature of the human body measured by the contact method is presented on the chart.

Fig. 13 represents the decreasing trend of the number of pixels, which is qualified by the algorithm of the inner canthus of the eye region. In conjunction with information from Table 1, this shows the efficiency of the proposed algorithm. The thermal image has 110 592 pixels, the algorithm gives good results for a set of pixels representing about 0.1% of the total number of pixels.

Fig. 13.

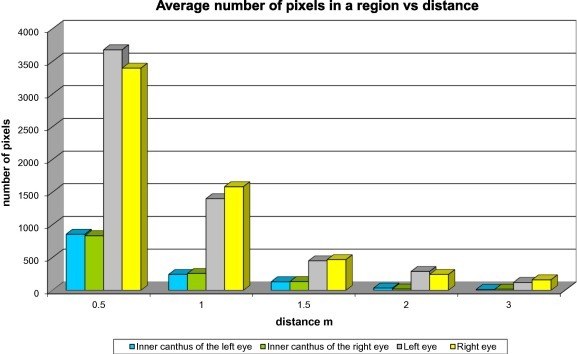
Comparison of the average number of pixels in regions using the proposed algorithm.

Next, experiments show the comparison between the proposed method, the SHT and RHT. The comparison was based on the average accuracy of the localization of the regions (see Table 2 ) and on the computational complexity (see Table 3 ). The experiment was performed on a PC class computer with a 2.8 GHz processor and 2 GB of RAM memory.

Table 2.

Average accuracy of the localization regions of interest performed for all the tested thermal images, where Face – face region, LE – left eye region, RE – right eye region, LIC – left inner canthus of the eye region, RIC – right inner canthus of the eye region, SHT – standard hough transform, RHT – Randomized Hough Transform, PA – proposed algorithm.

Region	Average accuracy (%)
	SHT	RHT	PA
Face	95.1	97.3	97.3
LE	93.2	96.6	97.1
LIC	92.7	96.4	97.5
RE	92.9	96.9	97.1
RIC	92.7	97.1	97.5

Table 3.

Time complexity of the algorithm, SHT – standard hough transform, RHT – Randomized Hough Transform, PA – proposed algorithm. Average time complexity was calculated from all of the sets.

Region	Time complexity (s)
	Average	Maximum	Minimum
SHT	4.431	4.829	3.935
RHT	0.821	0.877	0.752
PA	0.265	0.381	0.201

The SHT allows good results to be obtained, especially if average accuracy is to be taken into consideration. The result confirms the HT theory, it is a very accurate method, but, in the standard form, the time complexity is unacceptable. The average time complexity of about 4 s results from the method of image analysis – every pixel in the image must be examined in 5-dimensional space. The proposed method decreases the time complexity with accuracy on a similar level as the RHT method. Simple calculations, based on selected face area with different number of pixels, show that the time complexity decreases linear with number of pixels.

On the output of the proposed algorithm, we have a thermal image with marked regions, geometrical statistics and the temperature in the localized regions. For example, Fig. 14 shows an example of an output thermal image with marked regions of the face and the eyes. The calculated parameters are given. Ellipses of the face and eye regions are always models of the face, thus never perfectly matched to the shape of the real examined face. Geometric parameters of the face showed: O = (214, 150) pixels at the center of the ellipse and about 87° to be the angle of the vertical axis. Similar information is obtained for the left/right eye region and the left/right inner canthus of the eye.

Fig. 14.

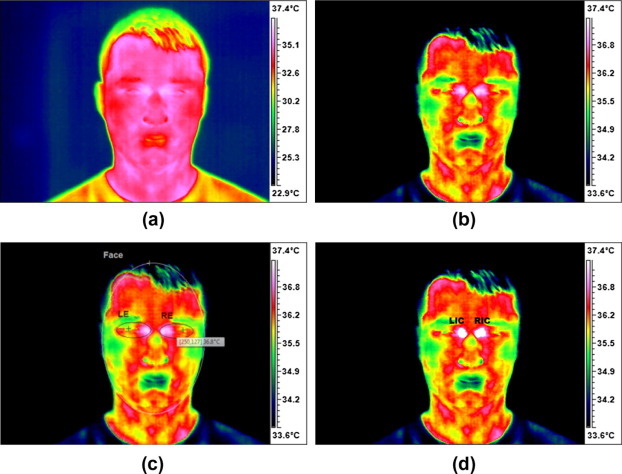
Input thermal image (a), image after normalization (b), image with face and eyes ellipses (c) and image with checked inner canthus areas (d).

In Table 4 the temperature is shown for one of the thermal image samples. The absolute error, calculated as a difference between temperature obtained from the proposed method and measured by the reference sensor, is less than +0.2 °C.

Table 4.

Temperature in the localized regions of interest taken for thermal image shown in Fig. 14, where LE –left eye region, RE – right eye region, LIC – left inner canthus of the eye region, RIC – right inner canthus of the eye region. The axillary temperature in this case was about 36.7 °C.

Region	Average temperature (°C)
Face	35.2
LE	36.1
LIC	36.5
RE	36.0
RIC	36.6

6. Conclusions

In this work a novel, highly accurate and fast algorithm for inner canthus of the eye temperature measurement is presented. Some issues of standardization in medical imaging are also presented, as this is extremely important if one would like to use thermal imaging cameras for temperature measurement in medical applications.

The proposed algorithm uses a combination of the template-matching, knowledge-based and morphological image processing methods. This approach improves the time complexity of the RHT and the inner canthus localization accuracy. The experiments have shown that the developed algorithm can handle automatic temperature measurement which is impossible with traditional methods using the forehead or underarm temperature measurement. The good correlation between the axilla temperature and that measured by the algorithm provides the fundamentals for future experiments.