Abstract
An urgent demand of assessing passengers' exposure risks in airliner cabins was raised as commercial airliners are one of the major media that carrying and transmitting infectious disease worldwide. In this study, simulations were conducted using a Boeing 737 cabin model to study the transport characteristics of airborne droplets and the associated infection risks of passengers. The numerical results of the airflow field were firstly compared against the experimental data in the literature to validate the reliability of the simulations. Airborne droplets were assumed to be released by passengers through coughing and their transport characteristics were modelled using the Lagrangian approach. Numerical results found that the particle travel distance was very sensitive to the release locations, and the impact was more significant along the longitudinal and horizontal directions. Particles released by passengers sitting next to the windows could travel much further than the others. A quantifiable approach was then applied to assess the individual infection risks of passengers. The key particle transport information such as the particle residence time yielded from the Lagrangian tracking process was extracted and integrated into the Wells-Riley equation to estimate the risks of infection. Compared to the Eulerian-based approach, the Lagrangian-based approach presented in this study is more robust as it addresses both the particle concentration and particle residence time in the breathing zone of every individual passenger.
Keywords: CFD, Lagrangian, Infection risks, Airliner cabins, Airborne particles, Wells-riley
Highlights
-
•
Particle travel distance is very sensitive to the release locations.
-
•
Coughing particles released at window seats travel much further than the others.
-
•
A quantifiable and promising approach based on the Wells-Riley equation is proposed.
-
•
It focuses on the risks in breathing zone of each passenger than the overall space.
-
•
An unsteady characteristic of the airflow pattern at the aisle region is noticed.
1. Introduction
After experiencing the fastest growth of passenger numbers in the past decade, there were more than 3.5 billion people traveling by air in 2015 and the number was forecasted to be more than doubled (7.4 billion) in 20 years [1]. Since the average occupancy of commercial flights was very high last year (around 80%) and is still increasing [2], the inflight conditions, such as air quality, thermal comfort and disease transmission risks have been drawing increasing attentions. Among these concerns, the transmission of airborne diseases is now in the spotlight, after the lessons taught from the global outbreaks of Tuberculosis (TB), Severe Acute Respiratory Syndrome (SARS) and Swine Influenza (H1N1) [3].
To study the air quality and disease transmission in airliner cabins, a number of important affecting factors have been identified, such as human thermal plume [4] and passenger movements [5]. Among various types of contaminants found in airliner cabins, the infectious saliva/phlegm droplets released through coughing or sneezing has been emphasised in many epidemiology reports [6], [7]. During the flight, since the passengers are sitting densely in a limited and enclosed space and unable to leave, diseases containing infectious pathogens (such as influenza and tuberculosis) released by index patients through coughing or sneezing would cause direct person-to-person infections [8]. Furthermore, the transmission of airborne diseases in airliner cabins revealed very strong non-linear characteristics in the investigations of several SARS infection cases in 2003 [9], in which the relative locations of the infected passengers to the index patient were found very randomly distributed in the cabins. Therefore, as the perniciousness of the saliva/phlegm droplets has been widely raised, the knowledge of their transport behaviours in the cabin environment is crucial for precise predictions of the infection risks of every individual passenger.
To effectively assess the individual infection risk, epidemiology studies [10] in indoor spaces reported that two essential components are required: the intake dose of the infected person and the probability of infection under the estimated intake dose. A number of infection risk assessment models (e.g. the Von forester model [11] and the competing-risks model [12]) were thereupon developed. Despite the diversity of the mathematical functions, infection risk assessment models can be summarised into two categories: deterministic models and stochastic models [13]. The deterministic models emphasised on the inherent tolerance dose of infectious person and infection only occur when the intake dose of pathogens equivalent to or exceeding the tolerance dose, while the stochastic model mainly estimates the probability of acquiring the infection under the intake dose. Among various models, the Wells-Riley equation developed by Riley et al. [14] based on Wells' concept of “quantum of infection” [15], was widely used as the mathematical models in existing epidemic modeling [8], [16], due to its universal applicability. In the Wells-Riley equation, the required threshold number of infectious airborne particles to cause infection can be defined as a quantum. Escombe et al. [8] employed the Wells-Riley equation to predict the infection risks of tuberculosis under ventilated rooms in eight hospitals. The “quantum” concept was used to describe the “infectious dose” for tuberculosis in their investigation, which directly widen the applicable range of this model. The Wells-Riley infection risk assessment model offers a quick and flexible approach to assess the infection risks of different airborne diseases, which has been employed in a number of indoor space studies on infectious risks [17] and diseases transmission (e.g. tuberculosis transmission [18], [19]). However, although commercial airliners had been determined as the major media carrying and transmitting the SARS worldwide in 2003 [7], very few existing studies were conducted with attempts to predict the inflight infection risks of each passengers, due to the inherent complexity and particularity of the cabin environment.
When assessing the exposure dose related health risks in the cabin environment, existing studies mostly relied on the Eulerian-based concentration distribution of the droplets, to identify the high health hazard regions [20]. It is undoubtedly that the Eulerian-based approach can provide very fast 3D predictions of the contaminants concentration distribution, which is an important parameter when assessing the health risks because passengers sitting inside the high-concentration regions would usually have higher health risks. A most recent study conducted by You et al. [21] employed the aforementioned Wells-Riley equation in conjunction with the Eulerian model to investigate the effect of the gaspers on the passengers' exposure risks in a half-row cabin section. The Wells-Riley method was combined with the two-phase flow model when assessing the exposure risks in the cabin environment. In order to fit the Wells-Riley equation to the Eulerian model, they assumed that the exposure time was the same as the flight duration. However, the actual exposure time could be much less than the flight duration due to the cabin ventilation and is significantly different to every individual passenger, depending on the relative location to the index patient. The exposure time length in the Wells-Riley equation could be a critical parameter affecting the infection risks. Beyond that, the particulate phase is assumed to be a continuum in the Eulerian framework, which directly leads to the loss of some critical information, such as the time of particle residence in a given domain. This shortage makes the Eulerian model physically untrue when assessing the infection risks, since the infectious pathogens are always released in conjunction with the droplets or particles and they are sharing the similar transport characteristics.
Alternatively, the Lagrangian particle tracking model was also utilised in several numerical studies [22], [23] due to its unique advantage in source-to-destination tracing of particle movement. Initial conditions of the released droplets/particles were also carefully in the existing studies. Gupta et al. [23] numerically investigated the distribution of contaminants released through different behaviour (i.e. coughing, breathing and talking). They concluded that contaminants released by coughing of the index patient behaved similar as those from breathing, but the number is much higher. Chao et al. [24] concluded that the geometric mean diameter of contaminants from coughing was 13.5 μm with average release speed of 11.7 m/s. Although studies on initial conditions of the released particles are accumulating in the existing literature, investigations on the other key parameters (i.e. particle traveling distance and particle traveling time) were still inadequate in the cabin environment. Also, when providing detailed 3D characterised trajectories of the released particles, the Lagrangian model requires significantly high computational resources to track them. To save the computational cost, many studies [25], [26] used a reduced size of cabin section (3 rows or less) with unrealistic passenger models to imitate the cabin environment. Thus, the contaminants transport was significantly constrained by the computational domain and thereby the travel distance and time of contaminants could be misleading. Since airborne respiratory pathogens must reach the target infection site of the receptor to commence the infection, accurate predictions of the traveling distance and time of the infectious pathogens are crucial. Thus, it is necessary to apply an extended cabin section with adequate space and realistic passenger models with proper body features when assessing the transmission of airborne diseases. As a good start, Gupta et al. [23] numerically investigated the transport of exhaled droplets in an extended seven-row cabin section. Their study provided detailed investigations on the droplets transport when the droplets were exhaled through coughing, breathing and talking. They found that the evaporation process happens very quickly (less than 0.3 s) and could be even faster with smaller particles. Since their study focused on the single exhalation behaviour of a passenger with evaporation process, the simulation was extremely time consuming even after applying over-simplified manikin models. They also recommended other researchers to focus more on the effect of index passenger location on the expiratory droplet transport in the airliner cabins and to develop a quantifiable approach to assess infection risks. Later on, Gupta et al. [27] further assessed the risk of influenza transport in the seven-row cabin with an index patient on board. They thoroughly introduced two approaches (i.e. the deterministic and probabilistic approaches) to calculate the influenza risk. The aforementioned Wells-Riley equation was employed in the probabilistic approach in their study to estimate the probability of influenza infection, which revealed a promising direction of assessing infection risks in airliner cabins. Their study was conducted under a twin-aisle cabin and they suggested further evaluations in relation to the passenger infection risks under different cabin layout and configuration. Since the focus in Gupta et al.’s [27] study were the exploration and investigation of these two approaches, the diversity and thoroughness of the results that can be yielded by these approaches were unavoidably overlooked. Despite that, their studies have laid a pivotal foundation of assessing infections risks using a combined computational fluid dynamics (CFD) approach and the risk assessment model, although the passenger models were over-simplified as combination of regular blocks due to the extreme high computational cost on simulating contaminants transport in a seven-row cabin.
Therefore, with the awareness of using CFD related infection risks model has been established [8], [27] and the increasing attentions of passenger infection risks in airliner cabins have been drawn [23], this study further and carefully evaluated the infection risks of every individual passenger in a single-aisle airliner cabin section and contributed a systematic approach to analyse the infection risks in cabin environments using a validated CFD model in conjunction with the quantifiable risk assessment model. A seven-row cabin model based on the Boeing 737 was utilised in conjunction with 42 validated manikin models to imitate a more realistic cabin environment. Particulate contaminants were released through coughing by different passengers and tracked using the Lagrangian tracking model. The concentration distribution of contaminants was obtained by converting the particle trajectories using the so called particle source in cell (PSI-C) method [28]. A quantifiable approach based on the Wells-Riley equation [13] in conjunction with the Lagrangian model was applied to assess the infection risks in every passenger's breathing zone. Diverse outcomes including both the transport trajectories and concentration distribution of the released contaminants, and the quantified infection risks of each passenger were yielded from this study and thereby added important information to the current database in the literature in relation to the infection risks in the airliner cabins. Also, important parameters such as threshold number of infectious pathogens and the number of index patients are considered and controllable by this approach, which built an important guidance for further investigations of different diseases not only in the airliner cabins, but other densely occupied environments (e.g. high-speed rail and metro).
2. Method
2.1. Computational models
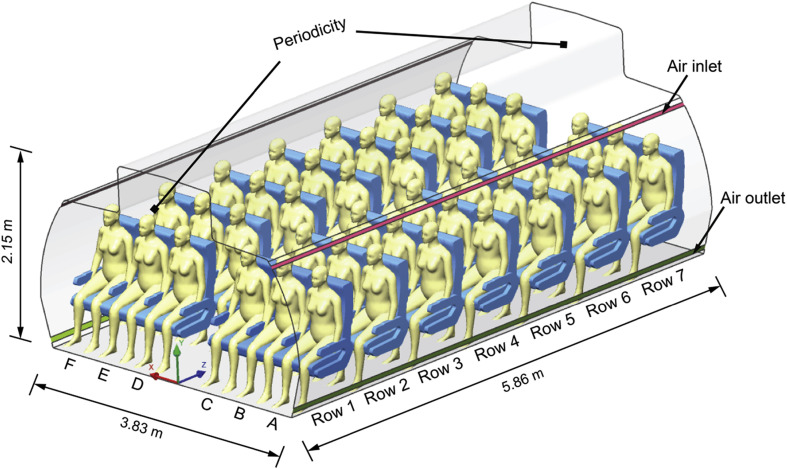
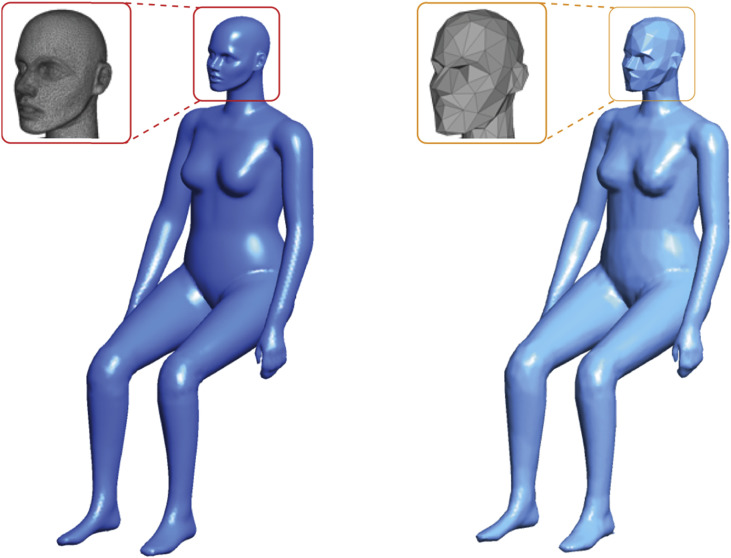
As one of the widely served medium-size commercial aircrafts during the SARS outbreak in 2003 [7], Boeing 737-200 was referred as the prototype aircraft to develop the CFD cabin model and study disease transmission. A seven-row economy cabin section was numerically constructed with dimensions of 3.82 m × 2.15 m × 5.86 m (W × H × L), as illustrated in Fig. 1 , which contains 42 fully occupied passengers with 3-3 seat arrangement. The ventilation inlets and outlets were located at the upper and lower sides of the cabin walls, respectively. In terms of the computational thermal manikin (CTM) models, our previous study reviewed that proper body features of the manikin models are crucial for balancing the computational cost and accuracy [29]. Thus, the simplified and validated CTM from our previous work was employed in this study as the passenger model, as shown in Fig. 2 . The information of the original 3D scanned model is available in the open database (http://www.ie.dtu.dk/manikin). Through contracting the pairs of triangle vertices, the key body features of the simplified manikin models were still retained, while the mesh elements required on the manikin surface were significantly reduced (over 50%) without noticeable computational errors [30].
Fig. 1.
Computational model of cabin section and passengers.
Fig. 2.
Original 3D scanned manikin (left); simplified manikin using mesh-decimating approach (right).
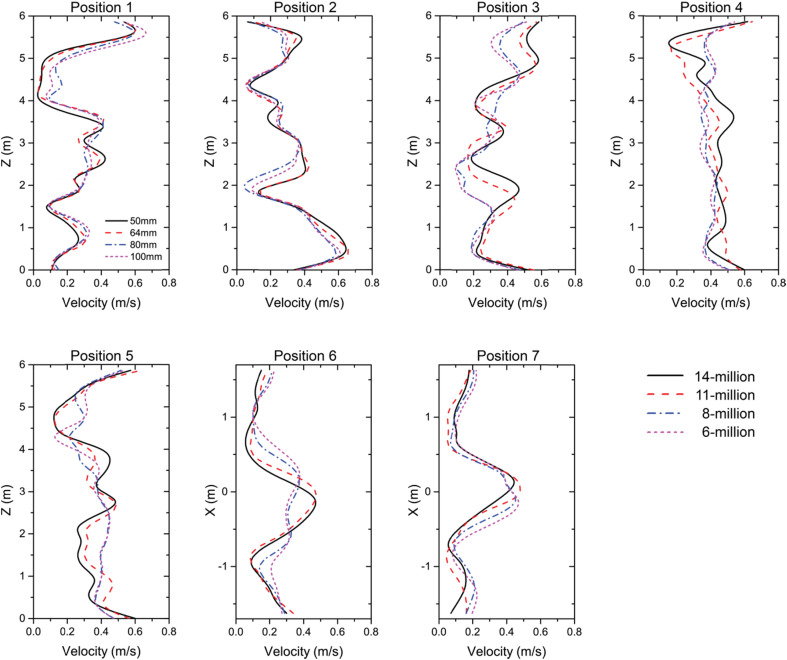
The whole cabin domain including manikins and seats was discretised using unstructured mesh. To achieve accurate prediction of the airflow field in the vicinity of the manikins, grid size was locally refined in passengers' micro-environment and 10 inflation layers with initial height of 1 mm were added on the manikin surfaces to capture the gradient change of velocity, temperature, etc. Four sets of mesh configurations were applied and tested prior to adding the contaminants, which required the total mesh elements of 6 million, 8 million, 11 million and 14 million, respectively. To achieve the mesh independence, all cases were firstly compared in terms of the mesh quality and grid convergence index (GCI) [31]. The results indicated that after reaching 11 million of the mesh elements, further refinement of mesh did not produce significant improvement on the mesh quality and the GCI for finer grid (14 million) solution was less than 3%. The velocity predictions at different positions across the whole cabin domain were compared using the tested mesh configurations, as shown in Fig. 3 . Through the comparison, no considerable deviation on the velocity field was noticed after mesh elements were increased from 11 million to 14 million. Therefore, mesh configuration with 11 million mesh elements was adopted for the subsequent simulations.
Fig. 3.
Mesh independence of velocity field.
2.2. Boundary conditions and numerical setup
The ventilation rate at the inlets was set based on the American Society of Heating, Refrigerating and Air-Condition Engineers (ASHARE) aviation standard [32]. To mimic the worst case scenario, the minimum air supply of 9.4 L/s per person [32] was considered, which was in equivalent to the air mass flow rate of 0.04 kg/s at 20 °C inlet air temperature. Since passengers are the main heat source in the cabin, a convective heat load of 35.6 W was applied at each manikin, which was consistent with the existing literature [33] and our previous study [29]. The front and back planes of the cabin section were assumed as translational periodicity, which added the periodic characteristics to the airflow and particles leaving and re-entering through the set planes. Other solid walls, such as the floor, ceiling and seats were considered as adiabatic.
In terms of the disease transmission, contaminants were assumed to be released as sputum droplets through coughing. Although droplets released by a human cough are distributed in a wide size range (0.5–1000 μm), over 90% of them are fine droplets smaller than 30 μm [24]. The vast majority of the droplets then quickly evaporate and reach their equilibrium diameters less than 0.3 s [23], [34] in indoor spaces. The evaporation process was no considered in this study because the airliner cabin is well-known as a low-humidity environment with relative humidity under 20% [35], the droplets would form to nuclei much quicker than other indoor environments. The equilibrium diameter of a droplet is roughly 26% of its initial size [36]. This means over 90% of the droplet nuclei are smaller than 7.8 μm. For particles with such small sizes (0.1–7.8 μm), their movement and deposition are mechanistically controlled by the air turbulence and do not present any detectable difference. Therefore, this study used a representative average particle diameter of 3.5 μm according to the existing studies by Gupta et al. [23] and Redrow et al. [34].
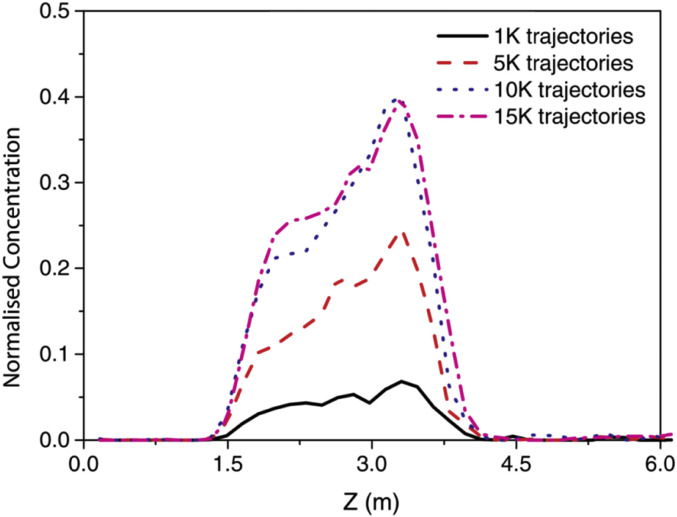
The Lagrangian particle tracking model was employed to continuously trace the particle motions through the cabin domain, while particles were released by coughing to provide sufficient trajectories in the seven-row cabin section. The number of particles was tested prior to the case studies, as shown in Fig. 4 . 10,000 particles were found as the sufficient number to achieve consistent contaminants concentration. To consider the seating locations effects of the index patient, six representative cases were presented, in which every individual passenger (from A to F) sitting at the fourth row was successively assumed as the index patient in each case.
Fig. 4.
Sensitivity test of particle number along the longitudinal direction.
2.3. Mathematical models
The cabin airflow field was solved using the incompressible Navier-Stokes (N-S) equation, while the thermal buoyancy flow induced by the passengers' body heat was considered through the Buossinesq approximation. For micro particle transport in the continuous air, the Lagrangian approach was employed to track the particle movement based on the equation of motion. Significant forces including the drag force , the buoyance force and the virtual mass force were considered and expressed in Eqs. (2), (3), (4).
| (1) |
| (2) |
| (3) |
| (4) |
According to the report from existing literature [37], typical cabin environment has relatively low velocity and high turbulence, which means the main source that leads to the dispersion of the aerosol particles is the fluctuating component of the airflow. Thus, the turbulent dispersion of particle transport in the Lagrangian approach was modelled by adding an eddy fluctuating component onto the mean air velocity in conjunction with the entry of the particles. The local air velocity is redefined in Eq. (5),
| (5) |
where is the mean air velocity and is the fluctuating eddy velocity.
In each eddy, the fluctuating eddy velocity can be varied by the lifetime and the length of the eddy. The impact of the fluctuating eddy velocity on the particles is only valid when the following two conditions are met. Firstly, the interaction time between the entering particle and the eddy is shorter than the eddy lifetime. Secondly, the relative displacement of the particle to the eddy is less than the eddy length. If not, the fluctuating eddy velocity in this eddy is not considered and the particle is assumed to be directly entering into the next eddy with new lifetime, length and thereby the new fluctuating velocity [38].
| (6) |
| (7) |
| (8) |
where is a normal distributed random number which accounts the randomness of turbulence by a mean value. k and ɛ are the local turbulent kinetic energy and dissipation, respectively. is the turbulent constant.
The N-S equations and particle tracking models were solved by CFX 16.2 [39]. Steady computations of airflow and contaminants fields were conducted in conjunction with the RNG k-ɛ model for the air turbulence due to its successful application in modeling indoor airflow and pollutant transport [20], [37]. Particles are assumed to be fully deposited when hitting the floors, seats and cabin walls, due to the factor that the materials applied on these boundaries in real cabins are high absorption materials (wool or nylon carpet, leather upholstery, fabric, etc.).
2.4. Risk assessment
Trajectory tracking of particles using the Lagrangian approach would provide very detailed and visualised transport history of the particles, which could give an idea of the possible deposition locations. However, it is insufficient to understand disease transmission only based on the transport characteristics of the particles. Concentration and distribution of particles are also essentially required to estimate the high risk regions. Since the Lagrangian approach only predicts the particle trajectories, the particle concentration was calculated based on the so-called particle source in cell (PSI-C) method [28] using Mathematica. The cabin domain containing the history of the particle trajectories was firstly discretised again using a number of control volumes (cells) and then the local particle concentration in a control cell was estimated based on the particle residence time, as expressed in Equ. (9),
| (9) |
where is the local particle concentration in the jth cell and is the volume of that cell. M is the mass flow rate represented by a particle trajectory and is the residence time of the ith particle in the jth cell.
The Wells-Riley's equation [13] was utilised in conjunction with the CFD predictions to assess the infection risks of passengers.
| (10) |
where, P I is the probability of infection, I is the number of infectors, which equals to 1 for single index patient case. q is the quanta generation rate. For worst case scenario of infectious disease transmission (e.g. tuberculosis), q = a unity infectivity term × number of quanta/unit time, in which passengers were assumed to be very vulnerable to pathogen. A unity infectivity term delineates that one quantum is equal to one infectious particle/pathogen [13], which makes the model deterministic. p and t are passenger breathing rate and the exposure time interval, respectively.
3. Results and discussion
3.1. Airflow field and model validation
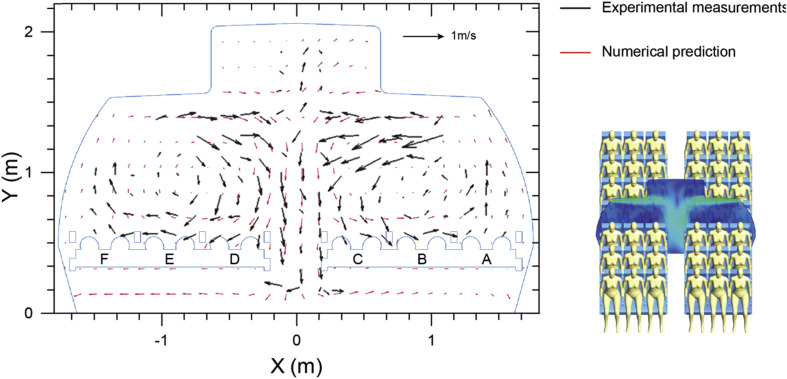
The expiermental data of airflow field by Li et al. [40] was firstly selected for model validation. In their study, a seven-row aircraft cabin mock-up was built inside a thermostatic chamber with seated thermal manikins to mimic the cabin environment of Boeing 737-200. The global airflow distribution and local velocity profiles were measured using large-scale 2D particle image velocimetry (PIV) technic. Their high resolution PIV measurements from both publication and supplementary materials provided very detailed data for validations. The velocity vectors measured at the fourth row of the cabin section (in front of the passengers) was selected and compared between the experimental measurements [40] and our numerical predictions, as illustrated in Fig. 5 . The velocity vectors predicted in this study yielded very similar airflow directions and distributions to the experimental results in most of the regions on this selected plane. It was noticable that the PIV measurements only cover the main region of this plane, while some of the spaces under the seats and between the roof racks were not included due to the limitation of experimental setups. Slight deviations were found at the corresponding edges of the PIV measurements, such as the airflow direction near the ground level. Despite some local deviations, both experimental measurements and numerical predictions captured the same airflow pattern of the compared plane that two main circulations were formed after airflow injecting from the inlets and interacting at the aisle region.
Fig. 5.
Velocity vector comparisons between numerical predictions and experimental measurements [40] at row-4.
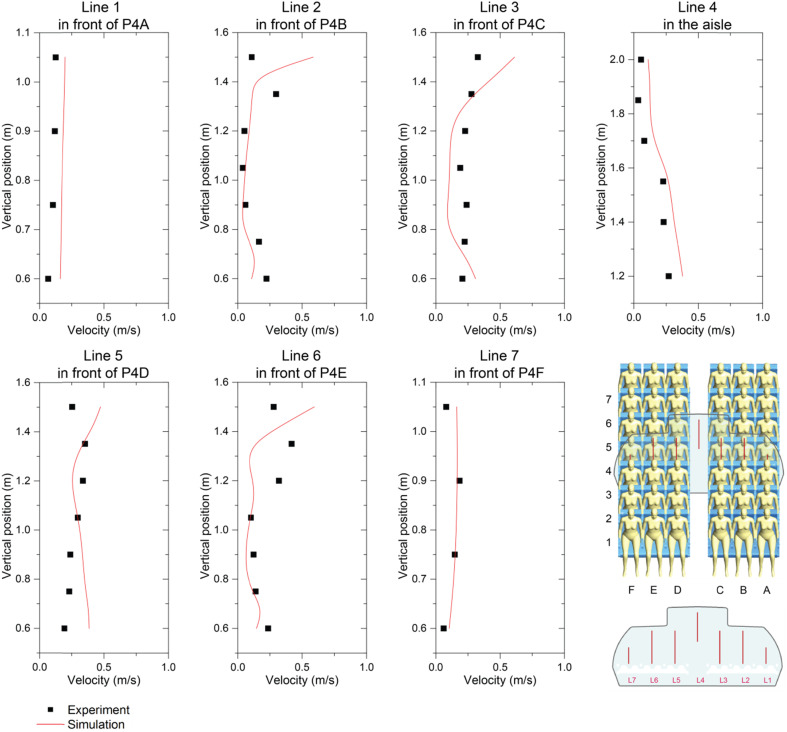
To quantitatively compare the airflow field, the predicted velocity profiles were further compared against the experimental data along 7 vertical lines, as shown in Fig. 6 . All vertical lines were extracted from the same plane given in Fig. 5. The position and length of these lines were remained the same as those in Li et al.’s [40] experimental setup. In their study, arms of all manikin models were removed for the purpose of fitting experimental equipments, whilst the manikin models used in this study contained comprehensive body segments with full body features. The geometric difference of the applied manikin models could affect the predictions on the regions very close to the manikin body. Although deviations were noticable at some local sample points due to the manikin model difference, the overall numerical predictions were very close to the experimental data, especially at the airsle region (Line 4) where the affect of manikins were minimised, the predicted velocity profiles agreed very well with the experimental measurements.
Fig. 6.
Comparison of velocity profiles between numerical predictions and experimental measurements [40] at selected lines.
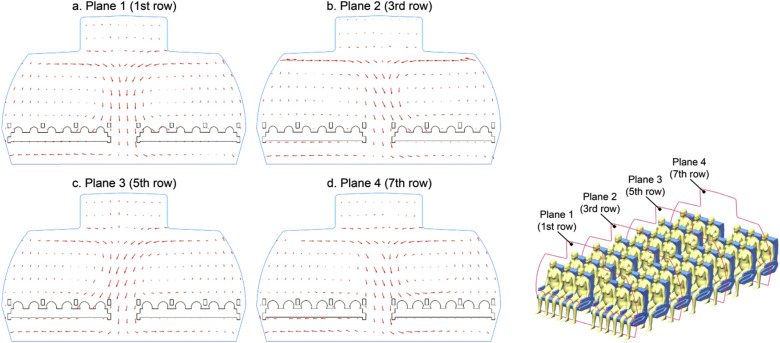
Since the airflow re-circulation exists at the entire cabin domain, it is important to assess whether the airflow patterns are regular at various cabin cross-sections (i.e. at different rows). The predicted airflow distributions were thereby compared along multiple cross-sections across the whole cabin domain. Four representative planes placed in front of passengers sitting at 1st row, 3rd row, 5th row and 7th row, respectively, were selected to demonstrate the results in Fig. 7 . The predicted results revealed that the airflow pattern is not entirely symmetrical along the horizontal direction (left to right), since the downward airflow was fluctuating unsteadily at the aisle regions. Similar asymmetric airflow field was also experimentally observed by Li et al.’s [40] in a cabin mock-up, which was believed to be induced by the random turbulent fluctuations of airflow in the cabin and the impact of the turbulent fluctuations was significantly enlarged with the increase length of cabin domain along the longitudinal direction. Therefore, to accurately investigate the contaminants transport which is mainly dominated by the airflow field, it is necessary to conduct investigations under a considerable large cabin domain.
Fig. 7.
Velocity distribution at four selected planes in front of the passengers; a. Plane 1 (1st row), b. Plane 2 (3rd row), c. Plane 3 (5th row) and d. Plane 4 (7th row).
3.2. Particle transport and case study
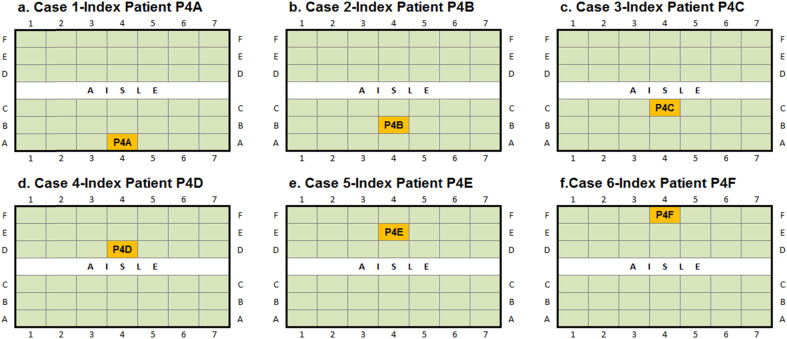
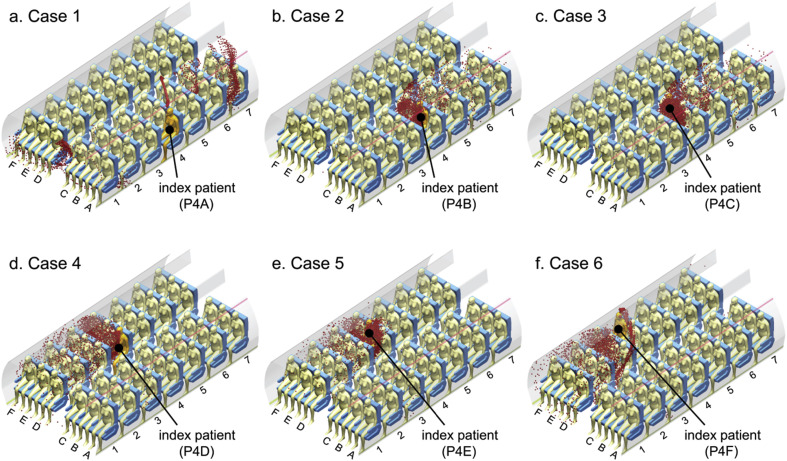
The particulate contaminants were assumed to be released through coughing by passengers to imitate the release of infectious diseases. In this study, a uniform droplet nuclei diameter of 3.5 μm was selected according to the study by Redrow et al. [34]. Since particles with diameter of 3.5 μm would be mainly dominated by the ventilated airflow inside the cabin and the local airflow profiles were found very different in front of different passengers, as can be noticed in Fig. 6, the particle transport was expected to be very sensitive to the release location (the siting location of the index patient). Therefore, in order to include the effect of index patient sitting locations, 42 computational cases were accomplished in this study, in which each passenger was considered as the sole index patient in one case study. Among all the cases, six representative cases were selected and presented to illustrate the particle transport and distribution characteristics. In these six cases, passengers sitting at row-4 were considered as the sole index patient successively, which allows the same longitude droplet travel distance range behind and in front of them, as described in Fig. 8 .
Fig. 8.
Case studies with different index patients.
Fig. 9 illustrated the predicted particle transport after exhalation under different cases, in which particles were released through coughing by one of the passenger sitting at row 4 in each case. Through investigating the particle trajectories, it is noticeable that when the particles were released by passengers sitting at different locations, their transport characteristics were completely different. For passenger A and F, who were sitting just under the inlet air jet and above the outlet, the airflow velocity was relatively low at that region and was mainly dominated by passengers' thermal plume. Since the thermal plume effect was significant in the cabin environment, in which passengers are sitting very close to each other, particles released by passenger A and F were quickly entrained up by the buoyancy driven thermal plume. Once particles were lifted high enough, it joined the main flow stream and then was completely dominated by the inject airflow. Therefore, the contaminants released by passenger A and F would travel much further and faster than the others due to the interaction with the ventilation jet. On the other hand, particulate contaminants released by passengers sitting closer to the aisle (B, C, D and E) travelled much slower and mainly suspended in front of the index patient and the neighbours. Since these passengers were sitting at the centre of the airflow re-circulation regions, the contaminants were mainly driven by the recirculating airflow. As a result, these particles would stay longer in passengers' breathing zone. Contaminants seem to be locked inside the passengers' breathing zone and hardly to be able to escape.
Fig. 9.
Particle transport across the whole cabin domain.
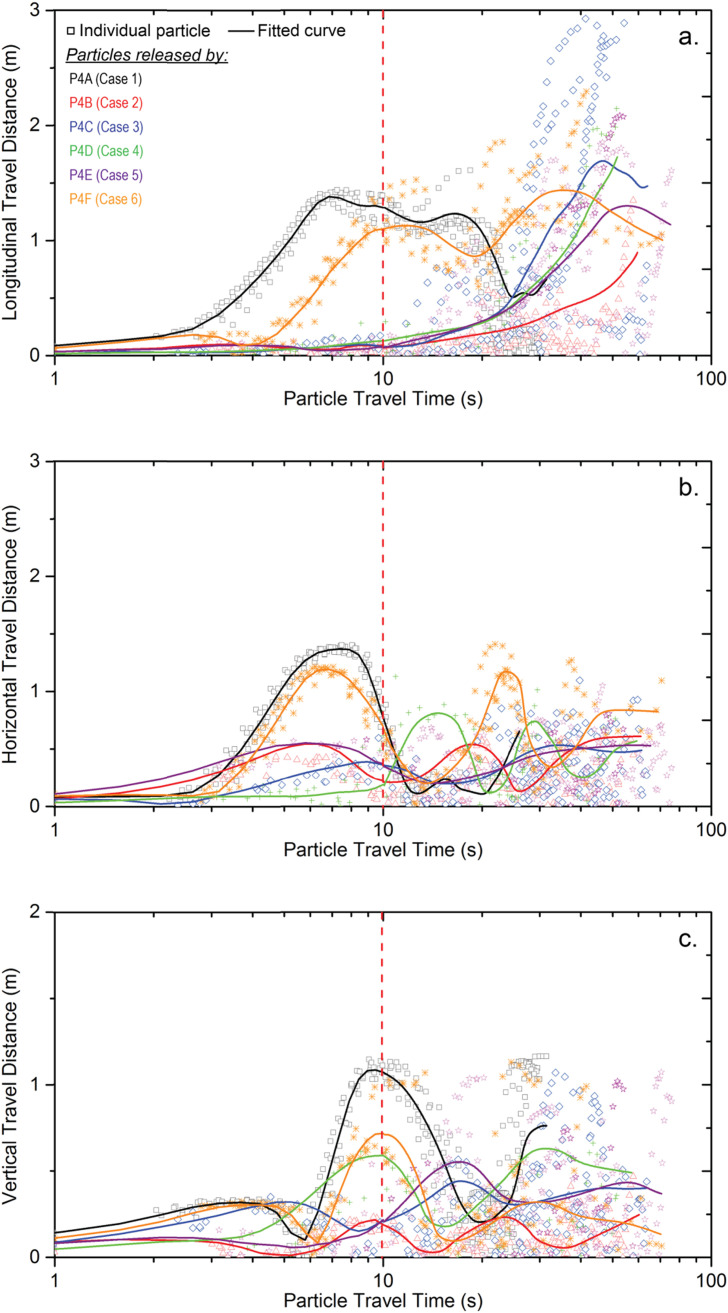
In order to quantify the difference of particle trajectories noticed in Fig. 9, the travel distance of released particles by different passengers were carefully compared along the three coordinate directions (i.e. longitudinal, horizontal and vertical directions) and the results were plotted against the travel time, as illustrated in Fig. 10 . Every symbol plotted in Fig. 10 represents the individual particle trajectory released by the index patient and different case studies were distinguished using different colour and shape of the symbols. The overall particle transport characteristics can be quickly compared using the fitted curves. It can be noticed that contaminants released by passenger A and F travelled much faster than the other cases at the first ten seconds along all directions. Although the travel direction was opposite between particles released by passenger A and F, the particle travel distances were very close between these two cases, which means the particle transport characteristics were similar when passengers sitting at sides of the cabin were coughing. It also can be noticed that when passengers sitting at the aisle seats (Passengers C and D) were coughing, particles experienced the shortest travel distance, especially along the horizontal direction (Fig. 10b). This finding revealed that when aisle seats passengers were releasing harmful contaminants, the contaminants would be locked at themselves' and their adjacent passengers' breathing zones for very long time (more than 20 s in cases 3 and 4) under the particular ventilation scheme. This lock-up phenomenon in passengers' breathing zone could directly increase the exposure risk of passengers. Once harmful contaminants from other sources enter this lock-up region, the contaminants would not be able to leave the breathing zone easily due to the re-circulation and would eventually cause uncomfortableness or even serious health issues.
Fig. 10.
Particle travel distance along (a) longitudinal; (b) horizontal; (c) vertical directions.
3.3. Infection risk assessment
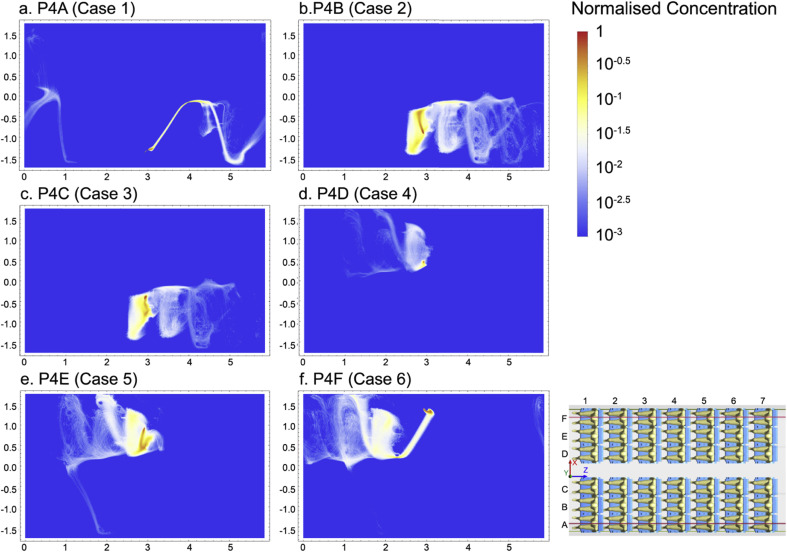
To assess the infection risk of passengers in cabin environment, the concentration of exhaled particles was firstly required to estimate the high-risk regions. The PSI-C method was referred to convert the particle trajectories into the concentration distribution using Mathematica. For each case, particle concentrations were firstly extracted along 30 cut planes (XZ-plane) at various heights inside the breathing zone and integrated into one normalised plane. All the normalised concentration distributions of particles yielded from six cases as aforementioned were demonstrated in Fig. 11 . It can be clearly observed that when different index patients were releasing contaminants, the particles were mostly concentrated at the same side of the cabin without traveling further across the aisle. The reason could be that the couple of large re-circulations (shown in Fig. 7) split the airflow into two main domains (left and right), while passengers were mostly sitting at the centre of the re-circulations where the fresh air was not sufficient. The regions of higher risks can be easily and phenomenologically estimated through the concentration distribution in Fig. 11. For instance, when passengers B and E were releasing contaminants, normalised concentration distribution revealed that particles were highly concentrated around the passengers sitting nearby. However, if the particles after release were quickly brought away by the injected airflow (i.e. case 1) due to the release position, they would travel much quicker and further, while the concentration distribution would be less significant. Under this circumstance, it would be very challenging only relying on the concentration distribution to identify the high infection risk regions. Therefore, it is necessary to seek an alternative approach to quantifiably assess the infection risk for each individual passenger.
Fig. 11.
Normalised concentration of exhaled particles (top view).
To achieve a quantifiable assessment of infection risks of each passenger, analysing the particle transport and distribution in passenger's breathing zone is crucial. According to the Australia Work Safety Standard [41], the breathing zone of each passenger was defined as a hemisphere of 300 mm radius extending in front of the face and the centre of the hemisphere was measured from the midpoint of the joining line between the ears. Detailed particle transport data (particle residence time, travel distance and etc.) in each passenger's breathing zone was firstly extracted and then the infection risks were calculated and assessed based on the Wells-Riley equation (Equ. 10). One index patient was included at various locations for each case. Other passengers were assumed to be very vulnerable to pathogen, which set the quanta generate rate as a unity infectivity term multiply the number of quanta/unit time. Passengers' breathing rate was carefully set based on the ASHARE standard [32], while the average particle residence time in the breathing zone was considered as the exposure time interval.
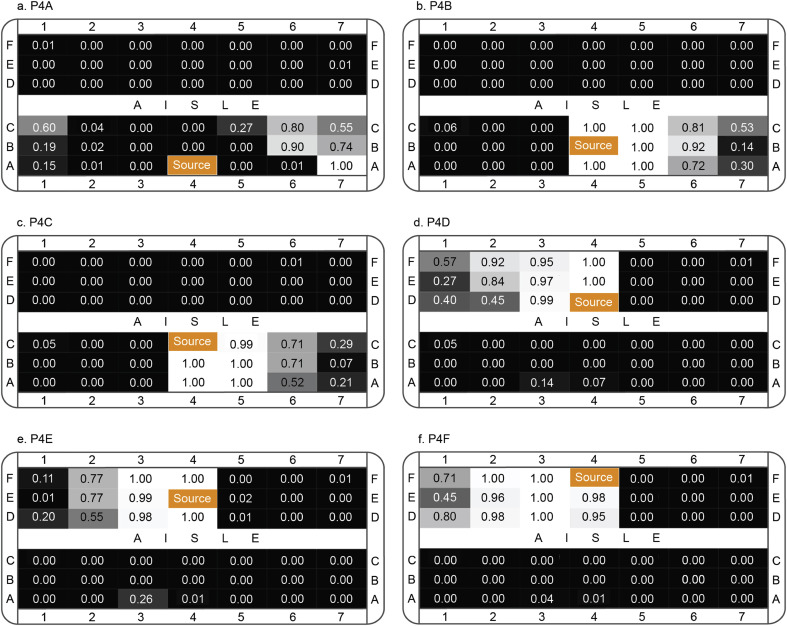
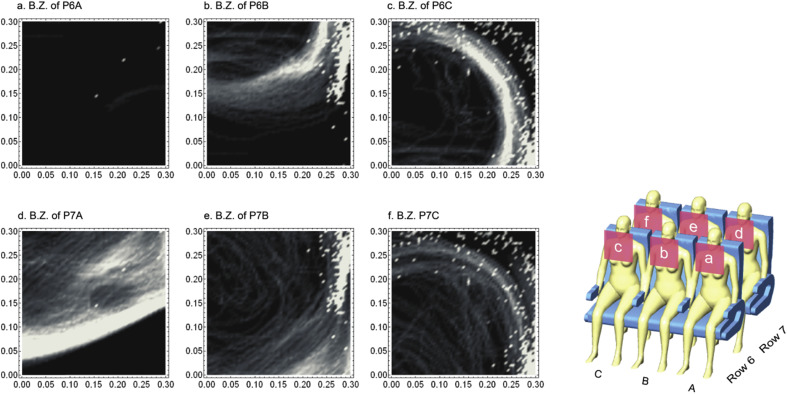
The assessed infection risks in each passenger's breathing zone under different case were illustrated in Fig. 12 , in which the probability of infection was ranged from 0 to 1. The increase of the infection risks in passengers' breathing zones could be directly reflected on the growth of the normalised figure, as well as on the change of colour from dark to light. The results shown in Fig. 12 revealed that passengers sitting within 3–4 rows to the index patient would have very high chance to be infected in most cases. For case 2–5, extremely high infection risks were found in passengers' breathing zones who were sitting adjacent to the index patient (same row and the next row). On the other hand, since the released particles were quickly suppressed and carried by the inject airflow in case 1, high infection risks were found a few rows behind the index patient. This finding indicated that passengers sitting far away from the index patient could also have high infection risks, although the particle concentration outside the breathing zone may not be significant. Once the passengers with high infection risks were identified, further evaluations can be conducted only in these passengers' breathing zones, which would significantly accelerate the analysis and improve the efficiency. For example, in case 1, as passengers sitting at the left side of rows 6 and 7 were found with high infection risks, the particle transport and distribution in their breathing zones can be further investigated in details, as demonstrated in Fig. 13 . The results given in Fig. 13 offered one approach to investigate the particle transport and distribution in the breathing zone by using light colour indicating high concentration of particles. More detailed investigations inside passengers' breathing zone in relation to the particle transport and distribution is required in the future study, since the breathing zone is still a considerable large space when passengers are sitting very close to each other under multi-occupied cabin environment, although it is already significantly smaller comparing to the overall domain of the airliner cabin.
Fig. 12.
Infection risks in passengers' breathing zones.
Fig. 13.
Particle trajectories in highly risked passengers' breathing zones (case 1).
4. Conclusion
This study employed a seven-row cabin model based on Boeing 737 to investigate the airflow and particle transport characteristics in the cabin environments, followed by the assessment of inflight infection risks. 3D characterised particle transport trajectories were provided and discussed in conjunction with the comparison of particle travel distances among six cases. The PSI-C method was used in this study to convert particle trajectories into concentration, while the infection risks of passengers were assessed using a quantifiable approach. The conclusions arising from this study are the follows:
-
(1)
Particle travel distance was found to be very sensitive to the release locations (i.e. released by passengers sitting at various locations), while the impact was more significant along the longitudinal and horizontal directions. Particles released by passengers sitting at the window seats would travel much further than the others. When passengers sitting closer to the aisle were coughing, particles would suspend longer in the index patient's breathing zone, as well as the adjacent passengers.
-
(2)
A quantifiable approach based on the Wells-Riley equation was applied in this study to assess the infection risks of inflight passengers. The approach is robust as it focuses on the exposure risks in the breathing zone of every individual passenger rather than the overall spaces. More importantly, this approach is capable of providing a fast and direct assessment of the infection risks with normalised results. When an index patient is found in the airliner cabin, the probability of infection of the rest passengers will be quickly and accurately assessed using this approach.
Also, an unsteady characteristic of the airflow pattern at the aisle region was noticed from this study, while a long cabin section was found to be necessary to capture this unsteady flow behaviour. This finding indicated that the size of the cabin section also plays an important role on when conducting simulations in cabin environment, whilst this factor was mostly compromised in existing study due to the high computational cost.
Overall, this study provided a systematic approach through not only combining the Wells-Riley equation in conjunction with the Lagrangian model in CFD, but also providing detailed and comprehensive analysis on the infection risks of every passenger. The ultimate intention of this study is to provide a systematic CFD approach in conjunction with the risk assessment model so that qualitative and quantifiable predictions and evaluations of infection risks would be achieved within a reasonable time of period (within a week). This would effectively help preventing further spread of the disease when index patient is determined.
Acknowledgements
The financial supports provided by the Natural Science Foundation of China (Grant No. 91643102), Australian Research Council (Project ID: DP160101953) and Railway Manufacturing CRC of Australia (Project ID: R3.6.1) are gratefully acknowledged.
References
- 1.Tyler T. International Air Transport Association (IATA); Miami: 2015. Annual Review 2015-71st Annual General Meeting. [Google Scholar]
- 2.Gill M. Air Transport Action Group (ATAG); Switzerland: 2016. Aviation: Benefits beyond Borders, Global Summary. [Google Scholar]
- 3.Zhu S., Demokritou P., Spengler J. Experimental and numerical investigation of micro-environmental conditions in public transportation buses. Build. Environ. 2010;45(10):2077–2088. doi: 10.1016/j.buildenv.2010.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yan Y., Li X., Tu J. Effects of passenger thermal plume on the transport and distribution characteristics of airborne particles in an airliner cabin section. Sci. Technol. Built Environ. 2015;22(2):153–163. [Google Scholar]
- 5.Poussou S.B., Mazumdar S., Plesniak M.W., Sojka P.E., Chen Q. Flow and contaminant transport in an airliner cabin induced by a moving body: model experiments and CFD predictions. Atmos. Environ. 2010;44(24):2830–2839. [Google Scholar]
- 6.Kenyon T.A., Valway S.E., Ihle W.W., Onorato I.M., Castro K.G. Transmission of multidrug-resistant mycobacterium tuberculosis during a long airplane flight. N. Engl. J. Med. 1996;334(15):933–938. doi: 10.1056/NEJM199604113341501. [DOI] [PubMed] [Google Scholar]
- 7.Mangili A., Gendreau M.A. Transmission of infectious diseases during commercial air travel. Lancet. 2005;365:989–996. doi: 10.1016/S0140-6736(05)71089-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Escombe A.R., Oeser C.C., Gilman R.H., Navincopa M., Ticona E., Pan W., Martinez C., Chacaltana J., Rodriguez R., Moore D.A., Friedland J.S., Evans C.A. Natural ventilation for the prevention of airborne contagion. PLoS Med. 2007;4(2):e68. doi: 10.1371/journal.pmed.0040068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Olsen S.J., Chang H., Cheung T.Y., Tang A.F., Fisk T.L., Ooi P., Kuo H., Jiang D.D., Chen K., Lando J., Hsu K., Chen T., Dowell S.F. Transmission of the Severe Acute respiratory Syndrome on aircraft. N. Engl. J. Med. 2003;349:2416–2422. doi: 10.1056/NEJMoa031349. [DOI] [PubMed] [Google Scholar]
- 10.Hass C.N., Rose J.B., Gerba C.P. second ed. John Wiley & Sons; New York: 1999. Quantitative Microbial Risk Assessment. [Google Scholar]
- 11.Fraser C., Riley S., Anderson R.M., Ferguson N.M. Factors that make an infectious disease outbreak controllable. Proc. Natl. Acad. Sci. U. S. A. 2004;101(16):6146–6151. doi: 10.1073/pnas.0307506101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Brookmeyer R., Johnson E., B. R Public health vaccination policies for containing an anthrax outbreak. Nature. 2004;432:901–904. doi: 10.1038/nature03087. [DOI] [PubMed] [Google Scholar]
- 13.Sze To G.N., Chao C.Y. Review and comparison between the Wells-Riley and dose-response approaches to risk assessment of infectious respiratory diseases. Indoor air. 2010;20(1):2–16. doi: 10.1111/j.1600-0668.2009.00621.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Riley E.C., Murphy G., Riley R.L. Airborne spread of measles in a suburban elementary school. Am. J. Epidemiol. 1978;107:421–432. doi: 10.1093/oxfordjournals.aje.a112560. [DOI] [PubMed] [Google Scholar]
- 15.Wells W.F. Harvard University Press for The Commonwealth Fund, Mass., U.S.A; Cambridge: 1955. Airborne Contagion and Air Hygiene: an Ecological Study of Droplet Infections. [Google Scholar]
- 16.Noakes C.J., Beggs C.B., Sleigh P.A., Kerr K.G. Modelling the transmission of airborne infections in enclosed spaces. Epidemiol. Infect. 2006;134(5):1082–1091. doi: 10.1017/S0950268806005875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wu Y., Tung T.C.W., Niu J.-l. On-site measurement of tracer gas transmission between horizontal adjacent flats in residential building and cross-infection risk assessment. Build. Environ. 2016;99:13–21. doi: 10.1016/j.buildenv.2016.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Andrews J.R., Morrow C., Wood R. Modeling the role of public transportation in sustaining tuberculosis transmission in South Africa. Am. J. Epidemiol. 2013;177(6):556–561. doi: 10.1093/aje/kws331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nardell E.A. Indoor environmental control of tuberculosis and other airborne infections. Indoor air. 2016;26(1):79–87. doi: 10.1111/ina.12232. [DOI] [PubMed] [Google Scholar]
- 20.Isukapalli S.S., Mazumdar S., George P., Wei B., Jones B., Weisel C.P. Computational fluid dynamics modeling of transport and deposition of pesticides in an aircraft cabin. Atmos. Environ. 2013;68:198–207. doi: 10.1016/j.atmosenv.2012.11.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.You R., Chen J., Lin C.-H., Wei D., Chen Q. Investigating the impact of gaspers on cabin air quality in commercial airliners with a hybrid turbulence model. Build. Environ. 2017;111:110–122. doi: 10.1016/j.buildenv.2016.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zhu S., Kato S., Yang J.-H. Study on transport characteristics of saliva droplets produced by coughing in a calm indoor environment. Build. Environ. 2006;41(12):1691–1702. [Google Scholar]
- 23.Gupta J.K., Lin C.H., Chen Q. Transport of expiratory droplets in an aircraft cabin. Indoor air. 2011;21(1):3–11. doi: 10.1111/j.1600-0668.2010.00676.x. [DOI] [PubMed] [Google Scholar]
- 24.Chao C.Y.H., Wan M.P., Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M., Mengersen K., Corbett S., Li Y., Xie X., Katoshevski D. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. J. Aerosol Sci. 2009;40(2):122–133. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zítek P., Vyhlídal T., Simeunović G., Nováková L., Čížek J. Novel personalized and humidified air supply for airliner passengers. Build. Environ. 2010;45(11):2345–2353. [Google Scholar]
- 26.Rai A.C., Guo B., Lin C.-H., Zhang J., Pei J., Chen Q. Ozone reaction with clothing and its initiated particle generation in an environmental chamber. Atmos. Environ. 2013;77:885–892. [Google Scholar]
- 27.Gupta J.K., Lin C.H., Chen Q. Risk assessment of airborne infectious diseases in aircraft cabins. Indoor air. 2012;22(5):388–395. doi: 10.1111/j.1600-0668.2012.00773.x. [DOI] [PubMed] [Google Scholar]
- 28.Zhang Z., Chen Q. Comparison of the Eulerian and Lagrangian methods for predicting particle transport in enclosed spaces. Atmos. Environ. 2007;41(25):5236–5248. [Google Scholar]
- 29.Yan Y., Li X., Yang L., Tu J. Evaluation of manikin simplification methods for CFD simulations in occupied indoor environments. Energy Build. 2016;127:611–626. [Google Scholar]
- 30.Li X., Yan Y., Tu J. The simplification of computer simulated persons (CSPs) in CFD models of occupied indoor spaces. Build. Environ. 2015;93:155–164. [Google Scholar]
- 31.Roache R.J. Perspective a method for uniform reporting of grid refinement studies. J. Fluids Eng. 1994;116:405–413. [Google Scholar]
- 32.ASHRAE . ASHRAE; Atlanta, GA: 2013. ANSI/ASHRAE Standard 161-2013, Air Quality within Commercial Aircraft. [Google Scholar]
- 33.Topp C., Nielsen P.V., Sorensen D.N. Application of computer simulated persons in indoor environmental modeling. ASHRAE Trans. 2002;108(2):1084–1089. [Google Scholar]
- 34.Redrow J., Mao S., Celik I., Posada J.A., Feng Z.-g. Modeling the evaporation and dispersion of airborne sputum droplets expelled from a human cough. Build. Environ. 2011;46(10):2042–2051. [Google Scholar]
- 35.Cui W., Ouyang Q., Zhu Y. Field study of thermal environment spatial distribution and passenger local thermal comfort in aircraft cabin. Build. Environ. 2014;80:213–220. [Google Scholar]
- 36.Liu L., Wei J., Li Y., Ooi A. Evaporation and dispersion of respiratory droplets from coughing. Indoor air. 2017;27(1):179–190. doi: 10.1111/ina.12297. [DOI] [PubMed] [Google Scholar]
- 37.Liu W., Wen J., Chao J., Yin W., Shen C., Lai D., Lin C.-H., Liu J., Sun H., Chen Q. Accurate and high-resolution boundary conditions and flow fields in the first-class cabin of an MD-82 commercial airliner. Atmos. Environ. 2012;56:33–44. [Google Scholar]
- 38.ANSYS® . 2014. ANSYS CFX-solver Theory guide., Canonsburg, PA 15317: Southpointe. [Google Scholar]
- 39.ANSYS® . ANSYS, Inc.; 2015. Academic Research Release 16.0, Help System, Coupled Field Analysis Guide. [Google Scholar]
- 40.Li J., Cao X., Liu J., Wang C., Zhang Y. Global airflow field distribution in a cabin mock-up measured via large-scale 2D-PIV. Build. Environ. 2015;93:234–244. [Google Scholar]
- 41.Safe Work Australia . 2013. Workplace-exposure-standards-airborne-contaminants, Safe Work Australia, Canbeera. [Google Scholar]