Coupling dynamics of epidemic spreading and information diffusion on complex networks

Highlights

• •Empirical results show the two dynamics significantly influence each other.
• •A nonlinear model is to describe coupling dynamics, results and consist.
• •A multi-outbreak phenomenon emerges both in data and threoretical analysis.

Abstract

The interaction between disease and disease information on complex networks has facilitated an interdisciplinary research area. When a disease begins to spread in the population, the corresponding information would also be transmitted among individuals, which in turn influence the spreading pattern of the disease. In this paper, firstly, we analyze the propagation of two representative diseases (H7N9 and Dengue fever) in the real-world population and their corresponding information on Internet, suggesting the high correlation of the two-type dynamical processes. Secondly, inspired by empirical analyses, we propose a nonlinear model to further interpret the coupling effect based on the SIS (Susceptible-Infected-Susceptible) model. Both simulation results and theoretical analysis show that a high prevalence of epidemic will lead to a slow information decay, consequently resulting in a high infected level, which shall in turn prevent the epidemic spreading. Finally, further theoretical analysis demonstrates that a multi-outbreak phenomenon emerges via the effect of coupling dynamics, which finds good agreement with empirical results. This work may shed light on the in-depth understanding of the interplay between the dynamics of epidemic spreading and information diffusion.

1. Introduction

Recently, understanding how diseases spread among individuals has been an increasing hot research area of nonlinear studies [1]. Generally, epidemic spreading is considered to be a dynamic process in which the disease is transmitted from one individual to another via physical contact in peer-to-peer networks. To date, there is a vast amount of research tries to understand the epidemic spreading phenomenon, which could be mainly categorized into three types: (i) epidemic spreading on various types of networks [2], such as the scale-free network [3], [4], the small-world network [5], [6] and the interdependent network [7], [8]; (ii) propagation mechanisms that describe the dynamic spreading process, such as the Susceptible-Infected-Recovered (SIR) model for influenza [9], [10], the Susceptible-Infected-Susceptible (SIS) model for sexually transmitted disease [11], [12] and the Susceptible-Exposed-Infected-Recovered (SEIR) model for rabies [13], [14]; (iii) data-driven modeling approaches that tackle the epidemic transmission [15] by analyzing the available real datasets, such as the scaling laws in human mobility [16], [17], individual interactions [18], [19], and contact patterns [20], [21].

The majority of the aforementioned studies focused on epidemic spreading independently, ignoring the fact that information diffusion of the diseases themselves may also have significant impact on epidemic outbreaks [22]. For example, the outbreak of a contagious disease may lead to quick spreading of disease information, through either medias or friends. Conversely, the information shall also drive people to take corresponding protective measures, such as staying at home, wearing face masks, and getting vaccinated [23]. Such behavioral responses may further impact epidemic outbreak in large population [24]. Therefore, studies on the coupling effect between epidemic spreading and information diffusion have attracted much attention from various disciplines. Theoretical models have been proposed to explain how both disease and information simultaneously spread in the same population [25], [26], [27], [28], [29]. In particular, the nonlinear influence of coupling parameters on the basic reproductive number (R ₀) is studied to show the interplay between the two spreading processes [26]. Theoretical results indicate that the coupling interaction could decrease epidemic outbreak size in a well-mixed population [25]. In some cases, enough behavioral changes would emerge in response to the diffusion of a great deal of disease information so that the severe epidemic would vanish completely, even the epidemic transmission rate was higher than the classical threshold initially [30], [31], [32], [33], [34]. In addition, the interplay between information diffusion and epidemic spreading is elucidated on multiplex networks, where each type of dynamics diffuses on respective layers (e.g., information diffusion on communication layer versus epidemic spreading on physical layer) [35], [36], [37]. As a consequence, the epidemic threshold, as related to the physical contact layer, can be increased by enhancing the diffusion rate of information on the communication layer. Therefore, the effect of behavioral changes arises in three aspects [27]: (i) disease state of the individuals, e.g., vaccination [38], [39], [40], [41], [42]; (ii) epidemic transmission and recovery rate [35], [43]; (iii) topological structure of contact network, e.g., the adaptive process [44], [45], [46], [47]. Besides researches from physical discipline, scholars from mass communication share similar views on the causal linkages of the two diffusion processes. The outbreak of severe diseases usually attracts heavy media coverage, subsequently resulting in massive responses from the public: (i) cognitive responses, such as the attention to the information and increased awareness of the situation [48]; (ii) affective responses, such as anxiety, fear, or even panic [49]; (iii) behavioral responses, such as the adoption of new practices in order to replace undesirable habits [50]. However, those assumptions are just theoretical hypotheses rather than empirical facts as it is difficult to find relevant data of one-to-one relationship in the spreading process. Even when the data is available, it is also difficult to separate the unique effect of information on the control of epidemics from interference factors, such as variation of virus, seasonal factors and improved medical treatments, etc.

Present studies on the coupling dynamics mainly focus on the suppression effect of epidemic spreading by information diffusion. The occurrence of a disease prompts the sharing of corresponding information, leading to preventive measures that inhibit further epidemic spreading [25], [37]. Researchers have also pointed out that when the epidemic outbreak is under control, people shall not be very vigilant in discussing or sharing relevant information. It will lead to a consequent decrease in protection actions and may result in a recurrence of epidemics in future. For example, the spread of SARS (Severe Acute Respiratory Syndromes) is alleviated in early March 2003, however, a sudden increase appear later that month (as indicated in the evolution curve of the probable cases of SARS, see Fig. 2 in Ref. [24]). In this work, firstly, we demonstrate a similar outbreak pattern using data on the spread of two representative diseases, i.e., avian influenza A (H7N9) [51], [52], [53] and Dengue fever [54], [55], along with the diffusion of respective disease information. Secondly, a nonlinear mathematical model is proposed to describe the coupled spreading dynamics as an SIS spreading model. Results show that information diffusion can significantly inhibit epidemic spreading. Finally, both empirical analysis and the proposed model find good agreements in revealing a multi-outbreak phenomenon in the coupled spreading dynamics.

Fig. 2.

Illustration of the spreading model used to interpret the coupling effect between disease and disease information. The horizontal shows the model of the disease and the longitudinal shows the disease information diffusion process. The symbols of the parameters are detailed described in Table 1.

2. Data and empirical results

To better illustrate this work, we collected data of two representative diseases, H7N9 and Dengue fever. Each disease has two time series datasets: (i) daily number of individuals infected by the corresponding disease in China, which are collected from the Chinese Center for Disease Control and Prevention; (ii) online diffusion messages discussing or forwarding the information of the corresponding disease during the same period of epidemic spreading. The message diffusion data was crawled from the largest micro-blogging system in China [56], Sina Weibo (http://www.weibo.com/). We have essentially obtained one-year data for the disease H7N9 from the year 2013 to 2014, and two-year data for Dengue from the year 2012 to 2014. We assume that individuals who post or retweet messages about the observed diseases are considered to be aware of the disease.

Empirical analysis of H7N9: Fig. 1 (a) shows the spreading processes of both disease and disease information of H7N9. It can be seen that the evolutionary trend of two processes are highly correlated, with Pearson correlation coefficient of 0.49. When the epidemic broke out in Apr. 2013 and Feb. 2014 (Fig. 1(a)), it shows that many people were discussing it online simultaneously. Actually, public responses to H7N9, such as staying at home or wearing face masks, can also affect the spread of the epidemic. The peaks of the disease spreading and the information diffusion shown in Fig. 1(a) suggest that the mutual influence of these two spreading processes could be significant. Interestingly, the size of the first epidemic peak (Apr. 2013) is smaller than the second one (Feb. 2014), which is inversely correlated with the information amount. That is to say, the number of individuals discussing the disease during the first outbreak is much greater than that of the second one. This might imply that the awareness of epidemics and the physical epidemics could influence each other.

Fig. 1.

Evolution of the number of infected cases (blue circles) and informed cases (pink diamonds) for disease: (a) H7N9; (b) Dengue fever. (b1) and (b2) are details of partial enlargement of dengue fever). The figure shows a high correlation between the spread of disease and the disease information diffusion. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Empirical analysis of Dengue fever: Fig. 1(b) describes the spreading processes of both disease and disease information of Dengue. Similar to the analysis of H7N9, the evolution trend of the two processes is also consistent with each other, with even much higher correlation coefficient of 0.89. According to the two largest peaks (in Sept. 2012 and Sept. 2013, respectively) of disease spreading, we find that the first epidemic peak is also smaller than the second one, while the corresponding information peaks show a contrary trend. Considering the two small peaks of information in Fig. 1(b1) and (b2), we can also find the same relationship between the the two dynamic processes as that of two largest peaks, suggesting also the possible coupling effect of the awareness of epidemics and the infected cases of dengue.

3. Model

3.1. Model description

In the aforementioned section, we empirically showed that the spread of disease and disease information has a coupling effect with each other by analyzing the data from two contagious diseases. Inspired by the empirical results, we propose a network based nonlinear model to describe the interaction between epidemic spreading and information diffusion in this section. In this model, we assume there are two states for disease spreading: susceptible (S) and infected (I), and two states of information diffusion: aware (+) and unaware (-). As a consequence, each individual will be at one of the four states during the model evolution:

• • $S_{-}$: The susceptible individual who is unaware of the epidemic;
• • $S_{+}$: The susceptible individual who is aware of the epidemic;
• • $I_{-}$: The infected individual who is unaware of the epidemic;
• • $I_{+}$: The infected individual who is aware of the epidemic.

Fig. 2 illustrates the transformation among those states based on the SIS model. Thus, the model can be described as follows.

• •Initially, one arbitrary individual is randomly picked from the given network as the spreading seed ($I_{+}$ state). The rest individuals are set to be $S_{-}$ state.
• •At each time step, the infected individuals ($I_{+}$ and $I_{-}$ states) will spread epidemics to their susceptible network neighbors ($S_{+}$ and $S_{-}$ states) with given spreading probability. The infected individuals ($I_{+}$ and $I_{-}$ states) could recover to the susceptible state with given recovery probability.
• •At each time step, individuals that are aware of the disease ($I_{+}$ and $S_{+}$ states) will transmit the information to their unaware neighbors ($I_{-}$ and $S_{-}$ states) with probability α. In addition, the informed individuals ($I_{+}$ and $S_{+}$) could become unaware of the disease with the probabilities of λ and δλ, respectively.

Beyond the parameters given in Table 1, we define σ as the probability of individuals taking protective measures. Thus, σ_S < 1 is defined as that a susceptible aware individual ($S_{+}$) will take protective measures to avoid becoming infected, and σ_I < 1 is defined as infected aware individuals ($I_{+}$ state) will reduce contact with their susceptible neighbors or adopt medical treatments. In addition, we assume the infected probabilities for these two different populations are independent with each other, hence ${\sigma }_{SI}={\sigma }_S{\sigma }_I$ is defined as the probability of the $I_{+}$ state individuals infecting the $S_{+}$ state ones. When an $I_{+}$ individual is aware of the epidemic, s/he will take positive measures, leading to an increased recovery rate, which is represented by the factor ε > 1. Furthermore, $I_{+}$ state individuals, which could be assumed to better understand the seriousness of epidemics, would be less likely to neglect relevant information, leading to δ < 1. In this work, since the spreading processes of information and disease are primarily determined by the corresponding transmission probabilities, we fix other parameters and mainly investigate the effects of α and β. In the following analysis, we set ${\sigma }_S=0.3,$ ${\sigma }_I=0.6,$ $\delta =0.8,$ $\varepsilon =1.5,$ $\lambda =0.15$ and $\gamma =0.1$.

Table 1.

Illustration of parameters used in the spreading processes.

β	The probability that $S_{-}$ is infected via the $I_{-}$ neighbor  ($S_{-}{I}_{-}\to I_{-}{I}_{-}$)
σSβ	The probability that $S_{+}$ is infected via the $I_{-}$ neighbor  ($S_{+}{I}_{-}\to I_{+}{I}_{-}$)
σIβ	The probability that $S_{-}$ is infected via the $I_{+}$ neighbor  ($S_{-}{I}_{+}\to I_{-}{I}_{+}$)
σSIβ	The probability that $S_{+}$ is infected via the $I_{+}$ neighbor  ($S_{+}{I}_{+}\to I_{+}{I}_{+}$)
γ	The probability that $I_{-}$ recover to $S_{-}$
εγ	The probability that $I_{+}$ recover to $S_{+}$
α	Information transmission rate
λ	Information fading rate  ($S_{+}\to S_{-}$)
δλ	Information fading rate  ($I_{+}\to I_{-}$)

3.2. Model analysis

Subsequently, the proposed model is performed on an ER network with a total population $N=10,000$ and average degree $〈k〉=15$. To measure the spreading effects, we denote the infected level (I) as the fraction of infected individuals (both $I_{+}$ and $I_{-}$), and the informed level (Info) as the fraction of individuals who are aware of the disease (both $S_{+}$ and $I_{+}$). Fig. 3 shows the simulation results by fixing the infection probability $\beta =0.3$. In this model, the parameter α can be considered as the information diffusion capability, hence larger α indicates that information diffuses much easier, resulting in a monotonically increase in the number of informed individuals (see the inset of Fig. 3). In Fig. 3, it also shows that the increase in α will inversely hamper the speed of epidemic spreading, hence diminish the overall epidemic outbreak size. As a consequence, appropriate publicity might be an effective strategy to inhibit further spreading of epidemics, which is also consistent with the empirical analysis shown in Fig. 1.

Fig. 3.

The change of infected density (I) of disease with time (T) when using different values of α. The main figure shows that the increase of α slows down the epidemic in both the outbreak size and the spreading speed. The inset shows the information level in the stationary state as a function of α. The other parameters are setting as $\beta =0.3,$${\sigma }_S=0.3,$${\sigma }_I=0.6,$$\delta =0.8,$$\varepsilon =1.5,$$\lambda =0.15$ and $\gamma =0.1$.

In Fig. 2, the model also indicates that there is mutual influence between information diffusion and epidemic spreading. A high prevalence of epidemic would lead to a small information fading probability δ, consequently resulting in a high infected level I. It in turn inhibits the epidemic spreading (σ _{I,S,SI} < 1). This coupling effect can be clearly described by the full set of differential equations (see Appendix). In addition, the equations are solved by mean-field and pairwise approaches, respectively. Fig. 4 shows the results of simulation, theoretical analysis of both mean-field and pairwise analysis. We find that the pairwise approach can better fit the model than the mean-field method. Therefore, we use pairwise approach to perform further studies in the following analysis.

Fig. 4.

The change of infected density (I) with time (T) by using different approaches: (a) simulation (pink circle); (b) pairwise analysis (green solid), and (c) mean-field analysis (blue dashed). The corresponding parameters are set as $\alpha =0.6,$$\beta =0.3,$${\sigma }_S=0.3,$${\sigma }_I=0.6,$$\delta =0.8,$$\varepsilon =1.5,$$\lambda =0.15$ and $\gamma =0.1$. Compared with the results of mean-field analysis, the evolution of infected density from the pairwise approach is more consistent with the simulation results. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

In order to investigate the effect of the mutual interaction between α and β on the spreading process, we explore the phase diagram showing the fraction of infected individuals caused by combination of such coupling effects (see Fig. 5 ). The results of the pairwise analysis and the simulation, which are highly consistent with each other, are shown in Fig. 5(a) and (b). The dashed black curve in each subfigure of Fig. 5 represents the critical point in the epidemic spreading process, (β_c, α_c). That is to say, epidemic outbreak will occur if the parameter combination is larger than the critical value, otherwise the epidemic will die out. The results also clearly show that more individuals will be infected with large β and small α, suggesting that the information diffusion can impede the disease spreading. It is noted that the process degenerates to the standard SIS model if $\alpha =0,$ where there is no information diffusion in the system. Thus, the epidemic outbreak threshold is ${\beta }_c={\displaystyle \frac{\gamma }{〈k〉}}=0.0067$ [1], which is also consistent with the results of pairwise analysis and simulation shown in Fig. 5. In addition, Fig. 5(c) shows a detailed view of pairwise analysis for α, β ∈ [0, 0.05] in order to better observe the threshold changes. The threshold value of β is around 0.0067 when α → 0, as the epidemic information cannot spread out in this case according to the inset of Fig. 3. When α > 0, the epidemic threshold can be significantly increased because of the effect of information diffusion.

Fig. 5.

Comparison between pairwise analysis and simulation for the infected density in the stationary state (colors represent the fraction of infected individuals). (a) pairwise analysis; (b) simulation; (c) enlarged view of pairwise analysis for small value of β and α. The black dotted line in each figure shows the threshold point (β_c, α_c) for epidemic spreading. Results show that the infected density of the pairwise analysis in the stationary state is consistent with the simulation results. The other parameters are setting as ${\sigma }_S=0.3,$${\sigma }_I=0.6,$$\delta =0.8,$$\varepsilon =1.5,$$\lambda =0.15$ and $\gamma =0.1$.

On the contrary, Fig. 3 shows that the informed level only slightly ascends when α is large enough (e.g., α > 0.3), which leads to an obscure change in the epidemic threshold. This result additionally indicates that abundant information would not always work for obstructing epidemic spreading. For example, in the case that a disease with a strong infectiveness (corresponds to large β in Fig. 5), enhancing the public awareness alone is insufficient to control the large outbreak of epidemics. In order to obtain better understanding of dynamics of the critical phenomenon, we observe the evolution of infection density for various values of β in Fig. 6 . From the differential equation, ${\displaystyle \frac{dI}{dt}}=-I+\beta 〈k〉I(1-I)$ (where $I=I_{-}+I_{+}$), we can obtain $I\propto t^{-1}$ at the critical point, which shows a power-law decay. In addition, the inset of Fig. 6 also presents a power-law decay of the infection density when β ≈ 0.0444. By contrast, the infection turns to break out as an endemic, namely steady state, for β > 0.0444 ($\beta =0.05$ in Fig. 6), otherwise the epidemic will be eliminated, so-called healthy state for β < 0.0444 ($\beta =0.04$ in Fig. 6). Therefore, it can be inferred that β_c is approximately 0.0444 in this case, which is consistent with the results in Fig. 5, where β_c is around 0.045 for $\alpha =0.6$.

Fig. 6.

Infection density as a function of β with the pairwise analysis. The inset is the infection density as a function of time with the theoretical analysis around the threshold. The other parameters are setting as α=0.6, ${\sigma }_S=0.3,$${\sigma }_I=0.6,$$\delta =0.8,$$\varepsilon =1.5,$$\lambda =0.15$ and $\gamma =0.1$.

Interestingly, the empirical analysis also demonstrates that a multi-outbreak phenomenon emerges for both epidemic spreading [14], [57], [58], [59] and information diffusion [22], in which there are several outbreaks during the dynamic process of epidemic spreading. Generally, there are many complicated factors that might contribute to this phenomenon, including seasonal influence, climate change, and incubation period, etc. In this model, the periodic outbreaks can be interpreted by the influence of information diffusion. As discussed above, there is a mutual interaction as the two dynamics are coupled with each other during the process. On one hand, a larger proportion of infected individuals should result in an increase in preventive behavioral responses [30] due to the increased awareness of the disease, consequently leading to a steady decrease of further infected cases. On the other hand, when the spread of epidemic tends to be under control, people shall become less sensitive to discuss or share relevant messages, which leads to dissemination of information and simultaneously raises the possibility of a second outbreak.

Notably, there are also some cases where the size of the second outbreak is smaller than the first one. For example, the eight Dengue outbreaks in Thailand over 30 years from 1973 to 1999 [60], and there are also some cases that the second outbreak is larger than the previous one, as in the case of SARS in 2003 [24] and dengue in Taiwan in 2001–2002 [59]. In order to better understand the underlying mechanism that drives the multi-outbreak phenomenon of the coupled dynamics, we set two thresholds, I_high and I_low, to represent different infected levels. That is to say, when the fraction of infected individuals is larger than I_high, the information diffusion parameter α will be set as high as $\alpha =0.8$ so that the information will diffuse even more quickly. Accordingly, when it is smaller than I_low, the parameter will directly decay to $\alpha =0.3$ to represent the corresponding response to abatement effect of information. Fig. 7 shows the simulation results. It can be seen that the epidemic spreads very quickly at the beginning as there are very few people aware of it, and soon reaches the threshold I_high and triggers the designed high information transmission probability $\alpha =0.8$. As a consequence, as the information bursts out, the high informed level has a significant impact on inhibiting epidemic spreading (the decay period of the epidemic), which will be completely suppressed if the high informed level remains. However, when the epidemic spreading is notably controlled from the first outbreak (i.e. the infected density is smaller than I_low), people are less likely to consider the epidemic as a threat, hence ignore relevant information and no longer actively engage in taking protective measures, which will in turn lead to a subsequent epidemic outbreak in the future. Two representative outbreak patterns are shown in Fig. 7, where the first outbreak is smaller than the second one (Fig. 7(a)) and vice versa (Fig. 7(b)). Moreover, Fig. 7(a) displays the similar phenomenon to the empirical analysis shown in Fig. 1, where the size of the first epidemic outbreak is smaller than that of the second one, while the informed level shows to the contrary. It should be noted that, due to the difficulty in collecting data of patient-to-fans to precisely quantify the informed level in the empirical analysis, the number of messages that discuss the epidemic is alternatively used in Fig. 1. Different from the trend shown in Fig. 1, a high informed level(Info > 0.5) must be maintained during the period when the infected level decreases shown in Fig. 7. Based on the model analysis, it could be concluded that it is important to raise public awareness of epidemic occurrence, especially during when the epidemic seems to be under control, otherwise, there is a likelihood of subsequent outbreak in the foreseeable future.

Fig. 7.

Multi-outbreak phenomenon of epidemic spreading and information diffusion. (a) Case of the first epidemic outbreak size is smaller than the second one with I_high=0.05, I_low=0.0003; (b) case of the first epidemic outbreak is larger than the second one with I_high=0.1, I_low=0.001. The parameter $\beta =0.18>{\beta }_c=0.0067$. Info represents the density of informed individuals, and I is the density of infected individuals in the network. The other parameters are setting as α=0.6, ${\sigma }_S=0.3,$${\sigma }_I=0.6,$$\delta =0.8,$$\varepsilon =1.5,$$\lambda =0.15$ and $\gamma =0.1$.

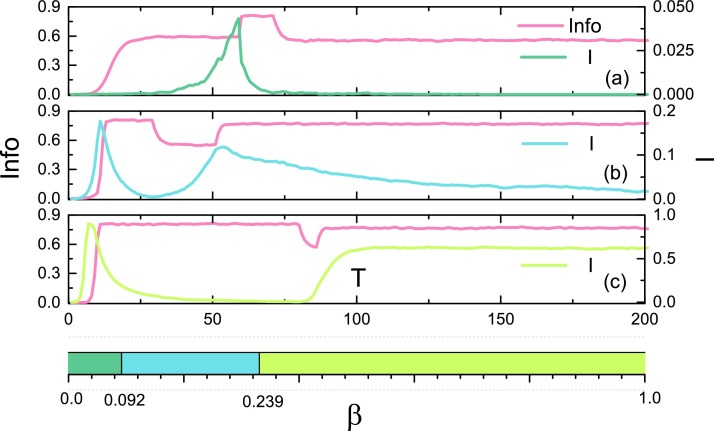
Furthermore, we explore the evolution of the informed and infected density with different values of β in Fig. 8 . In Fig. 8(a), it shows that the infected density firstly achieves a small peak and then rapidly vanishes, resulting in a evolution pattern known as healthy, which means there is approximately no disease. In Fig. 8(b), an oscillatory pattern is revealed for 0.092 < beta ≤ 0.239. Similarly, for large β ∈  (0.239,1], the infected density firstly achieves a large peak (almost close to one), then rapidly decrease to a low level (nearly zero) and gradually raised to a steady state, showing a unimodal pattern [44].

Fig. 8.

Evolution pattern of the density of informed and infected with different values of β: (a) $\beta =0.05$; (b) $\beta =0.2$; (c) $\beta =0.8$. The bottom is an interval indication of β, which corresponds to three phases of informed level: (i) healthy state for 0 ≤ β0.092; (ii) oscillatory state for 0.092 < β ≤ 0.239; (iii) unimodal for 0.239 < β ≤ 1. The result is obtained by 10,000 independent realizations, and we set $\alpha =0.6$ in all the realizations. The other parameters are setting as α=0.6, ${\sigma }_S=0.3,$${\sigma }_I=0.6,$$\delta =0.8,$$\varepsilon =1.5,$$\lambda =0.15$ and $\gamma =0.1$.

4. Conclusions and discussion

In this paper, we have studied the coupling dynamics between epidemic spreading and relevant information diffusion. Empirical analyses from representative diseases (H7N9 and Dengue fever) show that the two kinds of dynamics could significantly influence each other. In addition, we propose a nonlinear model to describe such coupling dynamics based on the SIS (Susceptible-Infected-Susceptible) process. Both simulation results and theoretical analyses show the underlying coupling phenomenon. That is to say, a high prevalence of epidemic will lead to a slow information decay, consequently resulting in a high infected level, which shall in turn prevent the epidemic spreading. Further theoretical analysis demonstrates that a multi-outbreak phenomenon emerges via the effect of coupling dynamics, which finds good agreement with empirical results.

The findings of this work may have various applications of network dynamics. For example, as it has been proved that preventive behaviors introduced by disease information can significantly inhibit the epidemic spreading, and information diffusion can be utilized as a complementary measure to efficiently control epidemics. Therefore, the government should make an effort to maintain the public awareness, especially during the harmonious periods when the epidemic seems to be under control. In addition, in this work, we only consider the general preventive behavioral response of crowd. However, the dynamics of an epidemic may be very different due to the behavioral responses of people, such as adaptive process [44], migration [61], vaccination [39], and immunity [62]. This work just provides a starting point to understand the coupling effect between the two spreading processes, a more comprehensive and in-depth study of personalized preventive behavioral responses shall need further efforts to discover.

Appendix

A.1. Mathematical analysis

In the following, [∗] represents the number of state variables (∗) in the system at time step t. $\left[S_{+}\right],$ $\left[S_{-}\right],$ $\left[I_{+}\right]$ and $\left[I_{-}\right]$ represent the number of aware susceptible, unaware susceptible, aware infected and unaware infected individuals. In the pairwise analysis, [∗] also denotes the number of the corresponding state variable of the edges, for example, $\left[S_{+}{I}_{+}\right]$ represents the number of edges between two individuals at states $S_{+}$ and $I_{+}$.

Mean-field analysis: According to Fig. 2, we adopt mean-field analysis for the spread of epidemic and information in a homogeneous network as follows:

$$\{\begin{array}{c}\frac{d\left[S_{-}\right]}{dt}=-〈k〉\beta \left[I_{-}\right]\frac{\left[S_{-}\right]}{N}-〈k〉{\sigma }_I\beta \left[I_{+}\right]\frac{\left[S_{-}\right]}{N}-〈k〉\alpha (\left[S_{+}\right]+\left[I_{+}\right])\frac{\left[S_{-}\right]}{N}+\lambda \left[S_{+}\right]+\gamma \left[I_{-}\right]\hfill \\ \frac{d\left[S_{+}\right]}{dt}=-〈k〉{\sigma }_S\beta \left[I_{-}\right]\frac{\left[S_{+}\right]}{N}-〈k〉{\sigma }_S{\sigma }_I\beta \left[I_{+}\right]\frac{\left[S_{+}\right]}{N}+〈k〉\alpha (\left[S_{+}\right]+\left[I_{+}\right])\frac{\left[S_{-}\right]}{N}-\lambda \left[S_{+}\right]+\varepsilon \gamma \left[I_{+}\right]\hfill \\ \frac{d\left[I_{-}\right]}{dt}=〈k〉\beta \left[I_{-}\right]\frac{\left[S_{-}\right]}{N}+〈k〉{\sigma }_I\beta \left[I_{+}\right]\frac{\left[S_{-}\right]}{N}-〈k〉\alpha (\left[S_{+}\right]+\left[I_{+}\right])\frac{\left[I_{-}\right]}{N}+\delta \lambda \left[I_{+}\right]-\gamma \left[I_{-}\right]\hfill \\ \frac{d\left[I_{+}\right]}{dt}=〈k〉{\sigma }_S\beta \left[I_{-}\right]\frac{\left[S_{+}\right]}{N}+〈k〉{\sigma }_S{\sigma }_I\beta \left[I_{+}\right]\frac{\left[S_{+}\right]}{N}+〈k〉\alpha (\left[S_{+}\right]+\left[I_{+}\right])\frac{\left[I_{-}\right]}{N}-\delta \lambda \left[I_{+}\right]-\varepsilon \gamma \left[I_{+}\right]\hfill \end{array}$$ (1)

Where N is the number of individuals in the system, ⟨k⟩ is the average degree of the network and the other parameters are illustrated in Table 1.

Pairwise analysis: Pairwise models have recently been widely used to illustrate the dynamic process of epidemics on networks, as those models take into account of the edges of the networks [63], [64], [65]. In this study, we consider a set of evolution equations which are comprised of four types of individuals and 10 types of edges. Using the well-known closure, expressed as $\left[ABC\right]={\displaystyle \frac{\left[AB\right]\left[BC\right]}{\left[B\right]}}$ (assuming the neighbors of each individual obey Poisson distribution) [63], we can get a set of differential equations as follows:

$$\{\begin{array}{c}\frac{d\left[S_{-}\right]}{dt}=-\beta \left[S_{-}{I}_{-}\right]-{\sigma }_I\beta \left[S_{-}{I}_{+}\right]-\alpha (\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])+\lambda \left[S_{+}\right]+\gamma \left[I_{-}\right]\hfill \\ \frac{d\left[S_{+}\right]}{dt}=-{\sigma }_S\beta \left[S_{+}{I}_{-}\right]-{\sigma }_S{\sigma }_I\beta \left[S_{+}{I}_{+}\right]+\alpha (\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])-\lambda \left[S_{+}\right]+\varepsilon \gamma \left[I_{+}\right]\hfill \\ \frac{d\left[I_{-}\right]}{dt}=\beta \left[S_{-}{I}_{-}\right]+{\sigma }_I\beta \left[S_{-}{I}_{+}\right]-\alpha (\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])+\delta \lambda \left[I_{+}\right]-\gamma \left[I_{-}\right]\hfill \\ \frac{d\left[I_{+}\right]}{dt}={\sigma }_S\beta \left[S_{+}{I}_{-}\right]+{\sigma }_S{\sigma }_I\beta \left[S_{+}{I}_{+}\right]+\alpha (\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])-\delta \lambda \left[I_{+}\right]-\varepsilon \gamma \left[I_{+}\right]\hfill \\ \frac{d\left[S_{-}{I}_{-}\right]}{dt}=-\beta \left[S_{-}{I}_{-}\right]+\lambda (\left[S_{+}{I}_{-}\right]+\delta \left[S_{-}{I}_{+}\right])+\beta \frac{\left[S_{-}{I}_{-}\right](\left[S_{-}{S}_{-}\right]-\left[S_{-}{I}_{-}\right])}{\left[S_{-}\right]}+{\sigma }_I\beta \frac{\left[S_{-}{I}_{+}\right](\left[S_{-}{S}_{-}\right]-\left[S_{-}{I}_{-}\right])}{\left[S_{-}\right]}\hfill \\ -\alpha \frac{\left[S_{-}{I}_{-}\right](\left[S_{-}{I}_{+}\right]+\left[S_{-}{S}_{+}\right])}{\left[S_{-}\right]}-\alpha \frac{\left[S_{-}{I}_{-}\right](\left[I_{-}{I}_{+}\right]+\left[S_{+}{I}_{-}\right])}{\left[I_{-}\right]}-\gamma \left[S_{-}{I}_{-}\right]+\gamma \left[I_{-}{I}_{-}\right]\hfill \\ \frac{d\left[S_{-}{I}_{+}\right]}{dt}=-{\sigma }_I\beta \left[S_{-}{I}_{+}\right]+\lambda \left[S_{+}{I}_{+}\right]-\alpha \left[S_{-}{I}_{+}\right]-\delta \lambda \left[S_{-}{I}_{+}\right]-\beta \frac{\left[S_{-}{I}_{-}\right]\left[S_{-}{I}_{+}\right]}{\left[S_{-}\right]}+{\sigma }_S\beta \frac{\left[S_{+}{I}_{-}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{+}\right]}-{\sigma }_I\beta \frac{{\left[S_{-}{I}_{+}\right]}^2}{\left[S_{-}\right]}\hfill \\ +{\sigma }_S{\sigma }_I\beta \frac{\left[S_{+}{I}_{+}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{+}\right]}+\alpha \frac{\left[S_{-}{I}_{-}\right](\left[I_{-}{I}_{+}\right]+\left[S_{+}{I}_{-}\right])}{\left[I_{-}\right]}-\alpha \frac{\left[S_{-}{I}_{+}\right](\left[S_{-}{I}_{+}\right]+\left[S_{-}{S}_{+}\right])}{\left[S_{-}\right]}-\varepsilon \gamma \left[S_{-}{I}_{+}\right]+\gamma \left[I_{-}{I}_{+}\right]\hfill \\ \frac{d\left[S_{+}{I}_{-}\right]}{dt}=-{\sigma }_S\beta \left[S_{+}{I}_{-}\right]+\delta \lambda \left[S_{+}{I}_{+}\right]-\lambda \left[S_{+}{I}_{-}\right]-\alpha \left[S_{+}{I}_{-}\right]-{\sigma }_S\beta \frac{{\left[S_{+}{I}_{-}\right]}^2}{\left[S_{+}\right]}-{\sigma }_S{\sigma }_I\beta \frac{\left[S_{+}{I}_{+}\right]\left[S_{+}{I}_{-}\right]}{\left[S_{+}\right]}+\beta \frac{\left[S_{-}{I}_{-}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{-}\right]}\hfill \\ +{\sigma }_I\beta \frac{\left[S_{-}{I}_{+}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{-}\right]}+\alpha \frac{\left[S_{-}{I}_{-}\right](\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])}{\left[S_{-}\right]}-\alpha \frac{\left[S_{+}{I}_{-}\right](\left[I_{-}{I}_{+}\right]+\left[S_{+}{I}_{-}\right])}{\left[I_{-}\right]}-\gamma \left[S_{+}{I}_{-}\right]+\varepsilon \gamma \left[I_{-}{I}_{+}\right]\hfill \\ \frac{d\left[S_{+}{I}_{+}\right]}{dt}=-{\sigma }_S{\sigma }_I\beta \left[S_{+}{I}_{+}\right]+\alpha \left[S_{-}{I}_{+}\right]+\alpha \left[S_{+}{I}_{-}\right]+{\sigma }_S\beta \frac{\left[S_{+}{I}_{-}\right](\left[S_{+}{S}_{+}\right]-\left[S_{+}{I}_{+}\right])}{\left[S_{+}\right]}+{\sigma }_S{\sigma }_I\beta \frac{\left[S_{+}{I}_{+}\right](\left[S_{+}{S}_{+}\right]-\left[S_{+}{I}_{+}\right])}{\left[S_{+}\right]}\hfill \\ +\alpha \frac{\left[S_{-}{I}_{+}\right](\left[S_{-}{I}_{+}\right]+\left[S_{-}{S}_{+}\right])}{\left[S_{-}\right]}+\alpha \frac{\left[S_{+}{I}_{-}\right](\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])}{\left[I_{-}\right]}-\varepsilon \gamma \left[S_{+}{I}_{+}\right]+\varepsilon \gamma \left[I_{+}{I}_{+}\right]-\lambda \left[S_{+}{I}_{+}\right]-\delta \lambda \left[S_{+}{I}_{+}\right]\hfill \\ \frac{d\left[I_{-}{I}_{-}\right]}{dt}=2\beta \left[S_{-}{I}_{-}\right]+2\delta \lambda \left[I_{-}{I}_{+}\right]]+2\beta \frac{{\left[S_{-}{I}_{-}\right]}^2}{[S-]}+2{\sigma }_I\beta \frac{\left[S_{-}{I}_{+}\right]\left[S_{-}{I}_{-}\right]}{\left[S_{-}\right]}-2\alpha \frac{\left[I_{-}{I}_{-}\right](\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])}{\left[I_{-}\right]}-2\gamma \left[I_{-}{I}_{-}\right]\hfill \\ \frac{d\left[I_{-}{I}_{+}\right]}{dt}={\sigma }_I\beta \left[S_{-}{I}_{+}\right]+{\sigma }_S\beta \left[S_{+}{I}_{-}\right]+\delta \lambda (\left[I_{+}{I}_{+}\right]-\left[I_{-}{I}_{+}\right])-\alpha \left[I_{-}{I}_{+}\right]+\beta \frac{\left[S_{-}{I}_{-}\right]\left[S_{-}{I}_{+}\right]}{\left[S_{-}\right]}+{\sigma }_I\beta \frac{{\left[S_{-}{I}_{+}\right]}^2}{\left[S_{-}\right]}+{\sigma }_S\beta \frac{{\left[S_{+}{I}_{-}\right]}^2}{\left[S_{+}\right]}\hfill \\ +{\sigma }_S{\sigma }_I\beta \frac{\left[S_{+}{I}_{+}\right]\left[S_{+}{I}_{-}\right]}{\left[S_{+}\right]}+\alpha \frac{\left[I_{-}{I}_{-}\right](\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])}{\left[I_{-}\right]}-\alpha \frac{\left[I_{-}{I}_{+}\right](\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])}{\left[I_{-}\right]}-\varepsilon \gamma \left[I_{-}{I}_{+}\right]-\gamma \left[I_{-}{I}_{+}\right]\hfill \\ \frac{d\left[I_{+}{I}_{+}\right]}{dt}=2{\sigma }_S{\sigma }_I\beta \left[S_{+}{I}_{+}\right]+2\alpha \left[I_{-}{I}_{+}\right]-2\delta \lambda \left[I_{+}{I}_{+}\right]+2{\sigma }_S\beta \frac{\left[S_{+}{I}_{-}\right]\left[S_{+}{I}_{+}\right]}{\left[S_{+}\right]}+2{\sigma }_S{\sigma }_I\beta \frac{{\left[S_{+}{I}_{+}\right]}^2}{\left[S_{+}\right]}\hfill \\ +2\alpha \frac{\left[I_{-}{I}_{+}\right](\left[S_{+}{I}_{-}\right]+\left[I_{-}{I}_{+}\right])}{\left[I_{-}\right]}-2\varepsilon \gamma \left[I_{+}{I}_{+}\right]\hfill \\ \frac{d\left[S_{-}{S}_{-}\right]}{dt}=2\lambda \left[S_{-}{S}_{+}\right]-2\beta \frac{\left[S_{-}{I}_{-}\right]\left[S_{-}{S}_{-}\right]}{\left[S_{-}\right]}-2{\sigma }_I\beta \frac{\left[S_{-}{I}_{+}\right]\left[S_{-}{S}_{-}\right]}{\left[S_{-}\right]}-2\alpha \frac{\left[S_{-}{S}_{-}\right](\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])}{\left[S_{-}\right]}+2\gamma \left[S_{-}{I}_{-}\right]\hfill \\ \frac{d\left[S_{-}{S}_{+}\right]}{dt}=\lambda \left[S_{+}{S}_{+}\right]-\lambda \left[S_{-}{S}_{+}\right]-\alpha \left[S_{-}{S}_{+}\right]-{\sigma }_S\beta \frac{\left[S_{+}{I}_{-}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{+}\right]}-{\sigma }_S{\sigma }_I\beta \frac{\left[S_{+}{I}_{+}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{+}\right]}-\beta \frac{\left[S_{-}{I}_{-}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{-}\right]}\hfill \\ -{\sigma }_I\beta \frac{\left[S_{-}{I}_{+}\right]\left[S_{-}{S}_{+}\right]}{\left[S_{-}\right]}+\alpha \frac{\left[S_{-}{S}_{-}\right](\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])}{\left[S_{-}\right]}-\alpha \frac{\left[S_{-}{S}_{+}\right](\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])}{\left[S_{-}\right]}+\varepsilon \gamma \left[S_{-}{I}_{+}\right]+\gamma \left[S_{+}{I}_{-}\right]\hfill \\ \frac{d\left[S_{+}{S}_{+}\right]}{dt}=2\alpha \left[S_{-}{S}_{+}\right]-2\lambda \left[S_{+}{S}_{+}\right]-2{\sigma }_S\beta \frac{\left[S_{+}{I}_{-}\right]\left[S_{+}{S}_{+}\right]}{\left[S_{+}\right]}-2{\sigma }_S{\sigma }_I\beta \frac{\left[S_{+}{I}_{+}\right]\left[S_{+}{S}_{+}\right]}{\left[S_{+}\right]}\hfill \\ +2\alpha \frac{\left[S_{-}{S}_{+}\right](\left[S_{-}{S}_{+}\right]+\left[S_{-}{I}_{+}\right])}{\left[S_{-}\right]}-2\varepsilon \gamma \left[S_{+}{I}_{+}\right].\hfill \end{array}$$ (2)