Privacy-protecting multivariable-adjusted distributed regression analysis for multi-center pediatric study

Abstract

Background

Privacy-protecting analytic approaches without centralized pooling of individual-level data, such as distributed regression, are particularly important for vulnerable populations, such as children, but these methods have not yet been tested in multi-center pediatric studies.

Methods

Using the electronic health data from 34 healthcare institutions in the National Patient-Centered Clinical Research Network (PCORnet), we fit 12 multivariable-adjusted linear regression models to assess the associations of antibiotic use <24 months of age with body mass index z-score at 48 to <72 months of age. We ran these models using pooled individual-level data and conventional multivariable-adjusted regression (reference method), as well as using pooled summary-level intermediate statistics and the more privacy-protecting distributed regression technique. We compared the results from these two methods.

Results

Pooled individual-level and distributed linear regression analyses showed virtually identical parameter estimates and standard errors. Across all 12 models, the maximum difference in any of the parameter estimates or standard errors was 4.4833×10⁻¹⁰.

Conclusions

We demonstrated empirically the feasibility and validity of distributed linear regression analysis using only summary-level information within a large multi-center study of children. This approach could enable expanded opportunities for multi-center pediatric research, especially when sharing of granular individual-level data is challenging.

INTRODUCTION

The use of large clinical data sources for research on children can substantially improve pragmatic evaluations of clinical interventions, enable disease surveillance and rare disease research, and expedite assessments of exposure-disease associations (1). The widespread adoption of electronic health records (EHRs) and the development of multi-center clinical data networks have facilitated these types of investigations on diverse populations using real-world data (2). This new era presents unique challenges, especially for pediatric research (3). Privacy protections for children are more stringent than the general population, because of the classification of children as a vulnerable population in the U.S. Department of Health and Human Services regulations for the protection of human subjects in research (4). New methodologies and approaches are needed to properly protect children and their data.

There are several ways to conduct multi-center or multi-database studies. An intuitive and conventional approach is to pool the entire databases or the derived study-specific individual-level datasets for analysis. However, centralized pooling of detailed individual-level datasets, even when stripped of direct patient identifiers, is not always possible. Healthcare systems and patients are often concerned about patient privacy and confidentiality, unauthorized uses of transferred data, or unintended disclosures of sensitive corporate or institutional information, issues compounded with pediatric research (5–8). Contractual agreements between health plans, delivery systems, and their members or patients may further restrict sharing of individual-level data with other entities for secondary purposes such as research. These challenges can be addressed in part by proper governance, appropriate ethical approval and data use agreements, and applicable updates to laws or regulations that oversee privacy protection in research. However, the considerable amount of time and resources required to obtain layers of formal agreements and approvals may render the project infeasible.

Another promising option is to employ more privacy-protecting analytic methods that require less granular information from participating sites yet provide results equivalent or very similar to those from the conventional pooled individual-level data analysis. In this article, we describe the application of distributed linear regression, a method that allows researchers to use only summary-level information to perform standard multivariable-adjusted linear regression analysis that is traditionally done by pooling individual-level data (9, 10). Distributed regression requires only intermediate summary statistics (e.g., sums of squares and cross product matrix) to be shared but produces statistically equivalent results as if the individual-level datasets were pooled (9, 10). We have previously demonstrated the use of this analytic method by comparing different bariatric surgery procedures in an adult study conducted within a large distributed research network (11). Here we describe the use of this analytic method in a pediatric study conducted within the same network.

METHODS

Pooled de-identified individual-level data analysis in a multi-center study

In a typical multi-center pediatric study, the analysis center, which can also be a data-contributing site, receives data from all participating sites and performs the statistical analysis using the pooled data. The convention in most multi-center studies is to request de-identified individual-level datasets from the participating sites. In pooled-individual-level data analysis, the participating sites send the analysis center an analytic dataset with distinct covariate information from each patient. Each site-specific dataset includes one or more rows (or observations) per patient and one column per covariate (e.g., treatment status, outcome status, confounders). Upon pooling, the combined dataset is essentially a bigger individual-level dataset that allows the analysis center to perform a wide range of statistical analyses. Direct patient identifiers and most protected health information per the U.S. Health Insurance Portability and Accountability Act can often be removed or masked without compromising the validity of the analysis (12).

Distributed linear regression in a multi-center study

Distributed regression is another approach that allows for the execution of standard multivariable-adjusted regression analysis in a multi-center study using only summary-level information from each data-contributing site (9–11). It performs the same numeric algorithm as standard individual-level regression analysis and therefore should theoretically produce the same results. For continuous outcomes, researchers can employ distributed linear regression to generate total sums of squares and cross products (SSCP) matrix for the intercept, the dependent variable (i.e., outcome), and independent variables (i.e., treatment and covariates) at each data-contributing site. Once this summary-level information is provided to the analysis center, it can be used to produce parameter estimates and standard errors (or 95% confidence intervals) (9–11). Some standard statistical software procedures, including PROC REG in SAS (SAS Institute, Cary, North Carolina), can input or output the SSCP matrix, which can then be used to perform the distributed analysis. In practice, distributed linear regression analysis and the pooled-individual-level data analysis follow similar steps but the former requires more data processing (specifically, the creation of SSCP matrix) to occur at the participating sites.

Application of distributed linear regression in a multi-center pediatric study

Setting

The National Patient-Centered Clinical Research Network (PCORnet) is a large distributed data network designed to facilitate multi-center research. During the time of this study, PCORnet included 13 Clinical Research Networks (CRNs), 20 Patient-Powered Research Networks (PPRNs), and 2 Health Plan Research Networks (HPRNs) (13). In Fall 2018, the network condensed to 9 CRNs, all of which were included in this study. The CRNs are each composed of multiple healthcare institutions, which in total contribute EHR or other healthcare data, including some pharmacy dispensing data, from millions of individuals. The PPRNs and HPRNs also can contribute data for patient-centered research projects. PCORnet uses a common data model that includes data across 15 tables and approximately 100 variables (14). Data elements include patient demographics, diagnoses, procedures, vital signs, prescribed or dispensed medications, laboratory test results, and mortality. The PCORnet Antibiotics and Childhood Growth Study was one of two inaugural observational demonstration projects funded to help develop the PCORnet data infrastructure. The other study was the PCORnet Bariatric Study (15, 16), which has previously examined the distributed linear regression technique in an adult cohort (11). For these two studies, we had pooled individual-level data and the capacity to conduct distributed linear regression, allowing for direct comparisons of results from both analytic approaches.

Study cohort

Initiated in 2016, the PCORnet Antibiotics and Childhood Growth Study examined the association of antibiotic use at <24 months of age with body mass index (BMI) z-score and overweight and obesity at age 48 to <72 months. Details of the study are available elsewhere (17, 18). Briefly, the study included data from 2009 to 2016 from 35 healthcare institutions that were organized into 28 “network partners” or distinct databases that served as the basis of the distributed analysis described in this article. Children were eligible for inclusion if they had same-day height and weight measures at 0 to <12 months, 12 to <30 months, and 48 to <72 months of age. Requiring multiple longitudinal measures ensured that children were receiving regular care over time, allowing for better capture of antibiotic prescriptions. During the outcome assessment period of age 48 to <72 months, we used the same-day height and weight measure closest to 60 months to calculate age-sex-specific BMI z-scores, using publicly available macros from the Centers for Disease Control and Prevention (19). The final sample size in the main study was 362,550 children. For the methods study described here, we used data from 27 network partners, including 34 of the 35 healthcare institutions; one network partner was unable to participate because it did not have the necessary SAS software to run the linear regression model.

Statistical analysis

As we did in the main PCORnet Antibiotics and Childhood Growth Study (18), we examined the continuous outcome of BMI z-score using the analyses of the pooled de-identified individual-level data as the benchmark. We fit 12 linear regression models to assess the associations of antibiotic use <24 months of age with BMI z-score at 48 to <72 months of age. The 12 models separately analyzed different categories of antibiotic exposure (all, broad-spectrum, narrow-spectrum), two exposure types (binary [yes/no], categorical [0, 1, 2, 3, ≥4 episodes]), and two strata (patients with and without complex chronic conditions). We used the condition list developed by Feudtner (20) plus hypothyroidism and pituitary disorders to define complex chronic conditions; these conditions were generally considered serious chronic childhood illnesses.

Because multiple antibiotic prescriptions may be written to treat a single illness, we joined together all prescriptions written within 10 days of another prescription to create an antibiotic episode, and we classified the episode as broad- or narrow-spectrum based on the broadest spectrum antibiotic prescribed. Narrow-spectrum antibiotics included mostly amoxicillin but also penicillin and dicloxacillin; broad-spectrum antibiotics were all others. All models adjusted for age in months within the 48 to <72 month outcome assessment window, sex (male/female), race (Asian, Black or African American, White, Other, Unknown), Hispanic ethnicity (yes/no), network partner (26 binary indicator variables), preterm birth status (yes/no), asthma diagnosis (yes/no), and the number of infection episodes (0, 1, 2, 3, ≥4; treated as a continuous variable for the purpose of the analysis), systemic corticosteroid prescription episodes (0, 1, 2, 3, ≥4; treated as a continuous variable for the purposes of the analysis), and healthcare encounters (log transformed; continuous variable) measured before 24 months of age.

We then fit the same 12 models using the distributed regression approach. The SAS package used to extract the individual-level data from the participating sites (for the benchmark analysis) and summary-level information (for the distributed linear regression analysis), as well as the SAS package used to analyze the pooled data in each approach at the analysis center is freely available at https://github.com/pcornet-analytics/antibiotics. We performed all analyses using SAS version 9.4 (SAS Institute, Cary, North Carolina).

RESULTS

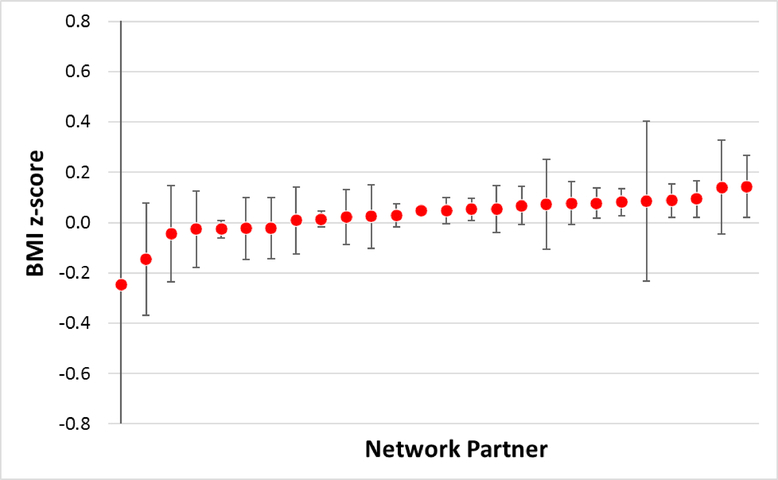
We identified 356,283 patients within 27 network partners (Table 1). The number of patients ranged from 34 to 187,226 across network partners. Figure 1 shows the results from the pooled de-identified individual-level linear regression model that assessed the association of any (vs. no) antibiotic use before 24 months of age with BMI z-score at 48 to <72 months, by network partner, among patients without complex chronic conditions. Table 2 shows the results from the benchmark pooled individual-level models (exposure of any vs. no antibiotics for children without a chronic condition) and the corresponding distributed regression models. The results were virtually identical between the two analytic approaches, with a maximum difference in any of the parameter estimates and standard errors being 2.5886×10⁻¹⁰. The results from the remaining 11 models were also essentially identical between the two analytic approaches (Table 3). Across all 12 models, the maximum difference in any of the values was 4.4833×10⁻¹⁰.

Table 1.

Baseline characteristics of the study population from 34 healthcare organizations, organized into 27 distinct network partners or distinct databases, in the PCORnet Antibiotics and Childhood Growth Study.

Characteristic	Total	No complex chronic condition	With complex chronic condition
	n=356,283	n=304,869	n=51,414
Female, n (%)	170,784 (48)	147,514 (48)	23,270 (45)
Age at outcome (in months), n (%)	57.9 (5.2)	57.9 (5.3)	58.0 (4.8)
Race, n (%)
Asian	14,413 (4)	12,874 (4)	1,539 (3)
Black	96,634 (27)	84,076 (28)	12,558 (24)
Other	27,063 (8)	21,514 (7)	5,549 (11)
Unknown	31,001 (9)	28,122 (9)	2,879 (6)
White	187,172 (53)	158,283 (52)	28,889 (56)
Hispanic ethnicity, n (%)	63,173 (18)	55,439 (18)	7,734 (15)
Preterm birth status, n (%)	25,801 (7)	16,785 (6)	9,016 (18)
Asthma diagnosis, n (%)	47,177 (13)	37,951 (12)	9,226 (18)
No. of infection episodesa
0	45,679 (13)	39,835 (13)	5,844 (11)
1	27,396 (8)	23,770 (8)	3,626 (7)
2	32,296 (9)	28,705 (9)	3,591 (7)
3	34,014 (10)	30,413 (10)	3,601 (7)
4+	216,898 (61)	182,146 (60)	34,752 (68)
No. of corticosteroid prescription episodesa
0	309,206 (87)	266,258 (87)	42,948 (84)
1	31,468 (9)	26,716 (9)	4,752 (9)
2	8,842 (2)	7,095 (2)	1,747 (3)
3	3,471 (1)	2,616 (1)	855 (2)
4+	3,296 (1)	2,184 (1)	1,112 (2)
No. of healthcare encountersa
0	19,836 (6)	19,092 (6)	744 (1)
1	3,252 (1)	2,898 (1)	354 (1)
2	3,020 (1)	2,530 (1)	490 (1)
3	3,951(1)	3,257 (1)	694 (1)
4+	326,224 (92)	277,092 (91)	49,132 (96)
No. systemic antibiotic prescription episodesa
0	151,229 (42)	128,108 (42)	23,121 (45)
1	76,117 (21)	66,177 (22)	9,940 (19)
2	45,443 (13)	39,436 (13)	6,007 (12)
3	28,388 (8)	24,610 (8)	3,778 (7)
4+	55,106 (15)	46,538 (15)	8,568 (17)
BMI z-score 48 to <72 months (SD)	0.40 (1.19)	0.41 (1.17)	0.35 (1.30)

BMI: body mass index; SD: standard deviation

^aMeasured before 24 months of age

Figure 1.

Results from linear regression models that considered antibiotic use as a binary variable (any use vs. no use) and body mass index z-score as the continuous outcome variable among patients without complex chronic conditions, by network partner. The models included all the covariates in Table 2.

Note: The values are parameter estimates for any antibiotic use (vs. no use) and their 95% confidence intervals. One of the 27 network partners was excluded from this figure due to small sample size (n=34) but its data was included in the pooled individual-level data analysis and distributed regression analysis.

Table 2.

Comparison of results from pooled individual-level data analysis and distributed regression analysis based on data from 34 healthcare organizations, organized into 27 distinct network partners (or distinct databases), in the PCORnet Antibiotics and Childhood Growth Study. The results were from a linear regression model that considered antibiotic use as a binary variable (any use vs. no use) and body mass index z-score as the continuous outcome variable among patients without complex chronic conditions. The model included all the covariates in the table plus 26 indicator variables for network partners.

Variable	Parameter estimate		Standard error
	Pooled individual-level data analysis	Distributed regression	Pooled individual-level data analysis	Distributed regression
Any antibiotic use (vs. no use)a	0.03419	0.03419	0.00478	0.00478
Female (yes vs. no)	0.01466	0.01466	0.00418	0.00418
Age at outcome (in months)b	0.00489	0.00489	0.00040	0.00040
Race
Asian	−0.20892	−0.20892	0.01070	0.01070
Black	0.05863	0.05863	0.00522	0.00522
Other	0.03098	0.03098	0.00890	0.00890
Unknown	0.03669	0.03669	0.00794	0.00794
White	REF	REF	REF	REF
Hispanic ethnicity (yes vs. no)	0.33664	0.33664	0.00679	0.00679
Preterm birth status (yes vs. no)	−0.22002	−0.22002	0.00928	0.00928
Asthma diagnosis (yes vs. no)	0.15297	0.15297	0.00694	0.00694
No. of infection episodesa,b,c	0.02184	0.02184	0.00195	0.00195
No. of corticosteroid prescription episodesa,b, c	0.06124	0.06124	0.00394	0.00394
No. of healthcare encountersa,b,d	−0.01568	−0.01568	0.00214	0.00214

^aMeasured before 24 months of age

^bAdjusted for as a continuous variable in the model

^cRe-coded as 0, 1, 2, 3, 4+

^dLog-transformed

Table 3.

Comparison of results from pooled individual-level data analysis and distributed regression analysis based on data from 34 healthcare organizations, organized into 27 distinct network partners (or distinct databases), in the PCORnet Antibiotics and Childhood Growth Study, by antibiotic exposure classification. Each model included all the covariates listed in Table 1 plus 26 indicator variables for network partners.

No Complex Chronic Condition (n=304,868)						With Complex Chronic Condition (n=51,413)
		Pooled Individual-level Data Analysis		Distributed Regression				Pooled Individual-level Data Analysis		Distributed Regression
	Episodes	Parameter Estimate	Standard Error	Parameter Estimate	Standard Error		Episodes	Parameter Estimate	Standard Error	Parameter Estimate	Standard Error
Any antibiotic exposure (Model 1)		0.03419	0.00478	0.03419	0.00478	Any antibiotic exposure (Model 2)		0.05774	0.01302	0.05774	0.01302
Broad spectrum (Model 3)		0.04037	0.00474	0.04037	0.00474	Broad-spectrum (Model 4)		0.06680	0.01290	0.06680	0.01290
Narrow spectrum (Model 5)		0.01978	0.00583	0.01978	0.00583	Narrow-spectrum (Model 6)		0.02435	0.01810	0.02435	0.01810
Systemic antibiotic prescribing episodes (Model 7)	0	REF	REF	REF	REF	Systemic antibiotic prescribing episodes (Model 8)	0	REF	REF	REF	REF
	1	0.01327	0.00574	0.01327	0.00574		1	0.02715	0.01607	0.02715	0.01607
	2	0.03853	0.00701	0.03853	0.00701		2	0.06950	0.01957	0.06950	0.01957
	3	0.04646	0.00843	0.04646	0.00843		3	0.06892	0.02356	0.06892	0.02356
	4+	0.06890	0.00701	0.06890	0.00701		4+	0.09635	0.01853	0.09635	0.01853
Systemic broad-spectrum antibiotic prescribing episodes (Model 9)	0	REF	REF	REF	REF	Systemic broad-spectrum antibiotic prescribing episodes (Model 10)	0	REF	REF	REF	REF
	1	0.03229	0.0058	0.03229	0.0058		1	0.04039	0.01596	0.04039	0.01596
	2	0.04542	0.00837	0.04542	0.00837		2	0.06685	0.02182	0.06685	0.02182
	3	0.03256	0.01116	0.03256	0.01116		3	0.14779	0.02763	0.14779	0.02763
	4+	0.06760	0.00938	0.06760	0.00938		4+	0.08664	0.02207	0.08664	0.02207
Systemic narrow-spectrum antibiotic prescribing episodes (Model 11)	0	REF	REF	REF	REF	Systemic narrow-spectrum antibiotic prescribing episodes (Model 12)	0	REF	REF	REF	REF
	1	0.01341	0.00661	0.01341	0.00661		1	0.01285	0.02104	0.01285	0.02104
	2	0.02940	0.00972	0.02940	0.00972		2	0.07939	0.03227	0.07939	0.03227
	3	0.02605	0.01528	0.02605	0.01528		3	0.02877	0.05172	0.02877	0.05172
	4+	0.05771	0.02098	0.05771	0.02098		4+	−0.06616	0.06041	−0.06616	0.06041

DISCUSSION

Using the association of antibiotics in early life with weight outcomes in later childhood, we demonstrated the validity and feasibility of conducting distributed linear regression analysis in a real-world pediatric study. To our knowledge, this is the first study that employed the more privacy-protecting distributed regression technique in multi-center pediatric studies. The validated distributed analytic approach is particularly valuable for pediatric studies, which face greater scrutiny and require more privacy protections. In the main PCORnet Antibiotics and Childhood Growth study, we required institutions to share de-identified individual-level data, in part because the distributed approach had not been used in PCORnet at the time. Two healthcare institutions that originally signed up for the study could not participate because they were unwilling to share individual-level data for the main analysis of the study. If distributed regression were the sole the analytic approach used, both could have participated. Moving forward, PCORnet, as a large distributed network, could consider using only distributed regression to conduct certain analyses.

Distributed regression can be implemented for other generalized linear methods, including logistic, Poisson, and Cox proportional hazards models (10, 21–26). These modeling approaches require multiple iterative steps, in contrast to the to the single computation step we demonstrated in this study for linear regression. The extra iterative process includes exchanges of intermediate statistics between the analysis center and the participating sites (27). These steps can be labor-intensive; and the lack of ability to execute them automatically in standard statistical software limits the use of the distributed regression. Researchers have been working to develop statistical packages and stand-alone software to facilitate the use of distributed regression in PCORnet and other networks (21, 22, 25–27). However, there are also some modelling procedures that cannot currently be performed with distributed regression, including multi-level modelling and generalized estimating equations. Some model diagnostics cannot readily be computed using summary-level information without making some compromises. For example, residual plots require data points from individual patients. More methodological development is needed to expand the capability of distributed regression methods.

Distributed regression can be more prone to errors because the analysis center does not have access to the individual-level data from all participating sites for data exploration and data quality assessment. This may lead to biased results due to the impact of unappreciated data characteristics that could not be accounted for in developing the analysis. Because of the reliance on quality of the underlying data, distributed analyses may be best suited for mature networks in which multiple cycles of data characterization and quality assurance have been done. PCORnet is now reaching that stage of maturity. As an alternative, researchers doing multi-center research can pursue a hybrid approach whereby they have access to individual-level data for one or a few institutions as a beta-testing environment, allowing for assessment of data quality and testing of analytic programs. A phased process with an initial round of queries to provide descriptive results for key variables could also help identify potential data issues early in the process, before the analytic queries are done.

Distributed regression may also introduce additional time and burden on data-contributing sites. However, this may not be a major concern within research networks like PCORnet that have standardized their information into a common data format. In these networks, the analysis center can develop an analytic program that processes the data into the correct format (e.g., SSCP matrix). Because all sites have their data structured in the same manner, the participating sites can execute the program with minimal modification to the code. In the case of PCORnet distributed queries, sites were asked to execute the queries unaltered except for changing the data library name. As with conventional pooled individual-level data analysis, all statistical code in distributed regression can be shared, allowing for any institution to execute analytic programs on their data in the same manner as the institutions included in the study.

In addition to distributed regression, there are other privacy-protecting analytic methods that can perform sophisticated statistical analysis using only summary-level information in multi-center pediatric studies, including methods that leverage confounder summary scores (e.g., propensity scores) and meta-analysis of site-specific effect estimates (28–31). Some of the analytic options are available across various methods while others are unique to specific techniques. Specifically, it is possible to use only summary-level information to perform confounder summary score-matched or -stratified analysis of binary or categorical exposures and binary or time-to-event outcomes with any of these methods; the results will be identical to those obtained from the corresponding pooled individual-level data analysis (28–31). Meta-analysis of site-specific effect estimates allow researchers to examine the relations between different types of exposures (binary, categorical, and continuous) and outcomes (binary, categorical, continuous, and time-to-event); site-specific confounding adjustment can be achieved via matching, stratification, weighting, or modeling. However, meta-analysis generally produces results that are similar, but not identical, to those obtained from the corresponding pooled individual-level data analysis (28–31).

In conclusion, privacy-protecting methods, such as distributed linear regression, can perform multivariable-adjusted regression analysis without transferring individual-level data in multi-center pediatric studies. The analytic approach enables researchers to analyze data that are otherwise not accessible due to restrictions to sharing individual-level data, including pediatric data, for which this approach may be particularly well-suited.

Appendix 1. PCORnet Antibiotics and Childhood Growth Study Group

Brad Appelhans, PhD, Rush University Medical Center, Chicago, Illinois;

David Arterburn, MD, Washington Permanente Medical Group, Internal Medicine, Kaiser Permanente Washington Health Research Institute, Seattle Washington

Janne Boone-Heinenon, PhD, MPH, Oregon Health & Science University, Portland, Oregon;

Andrew L. Brickman, PhD, Strategic Clinical Initiatives, Health Choice Network, Doral, Florida;

H. Timothy Bunnell, PhD, Nemours Children’s Health System, Wilmington, Delaware;

F. Sessions Cole, III, MD, Edward Mallinckrodt Department of Pediatrics, Washington University School of Medicine/St. Louis Children’s Hospital, St. Louis, Missouri;

Matthew. F. Daley, MD, Institute for Health Research, Kaiser Permanente Colorado, Denver, Colorado;

Amanda Dempsey, MD, PhD, MPH, Department of Pediatrics, University of Colorado School of Medicine, Denver, Colorado;

Jonathan Finkelstein, MD, MPH, Department of Pediatrics, Harvard Medical School, Boston, Massachusetts;

Stephanie L. Fitzpatrick, Kaiser Permanente Center for Health Research, Portland, Oregon;

William Heerman, MD, MPH, Vanderbilt University Medical Center, Nashville, Tennessee;

Michael Horberg, MD, MAS, Kaiser Permanente Mid-Atlantic Permanente Research Institute, Rockville, Maryland;

Carmen R. Isasi, MD, PhD, Department of Epidemiology, Albert Einstein College of Medicine, Bronx, New York;

Melanie Jay, MD, MS, Department of Population Health, New York University School of Medicine, New York, New York;

Elyse Kharbanda, MD, MPH, HealthPartners Institute, Bloomington, Minnesota;

Ritu Khare, PhD, Center for Applied Clinical Research, Children’s Hospital of Philadelphia, Philadelphia, Pennsylvania;

Dominick Lemas, PhD, Department of Health Outcomes and Biomedical Informatics, College of Medicine, University of Florida, Gainesville, Florida;

Simon M. Lin, MD, MBA, The Research Institute, Nationwide Children’s Hospital, Columbus, Ohio;

Mary Jo Messito, MD, Department of Pediatrics, New York University School of Medicine, New York, New York;

Allison O’Neill, MPH, OCHIN Inc, Portland, Oregon;

Holly Landrum Peay, PhD, MS, CGC, RTI International, Research Triangle Park, North Carolina;

Micah Prochaska, MD, MS, Department of Medicine, University of Chicago, Chicago, Illinois;

Daksha Ranade, MPH, MBA, Research Informatics, PEDSnet, Seattle Children’s, Seattle, Washington;

Goutham Rao, MD, Case Western Reserve University and University Hospitals of Cleveland, Cleveland, Ohio;

Maria Rayas, MD, University of Texas Health Science Center at San Antonio, San Antonio, Texas;

Juliane S. Reynolds, MPH, Department of Population Medicine, Harvard Medical School and Harvard Pilgrim Health Care Institute, Boston, Massachusetts;

Marc Rosenman, MD, Ann & Robert H. Lurie Children’s Hospital of Chicago and Northwestern University Feinberg School of Medicine, Chicago, Illinois;

Bradley Taylor, BS, Medical College of Wisconsin, Milwaukee, Wisconsin;

Zachary Willis, MD, MPH, University of North Carolina School of Medicine, Chapel Hill, North Carolina