Abstract
This paper seeks to determine the macro-economic impacts of changes in health care provision. The resource allocation issues have been explored in theory, by applying the Rybczynski theorem, and empirically, using a computable general equilibrium (CGE) model for the UK with a detailed health component. From the theory, changes in non-health outputs are shown to depend on factor-bias and scale effects, the net effects generally being indeterminate. From the applied model, a rise in the National Health Service (NHS) budget is shown to yield overall welfare gains, which fall by two-thirds assuming health care-specific factors. A nominally equivalent migration policy yields even higher welfare gains.
Keywords: Computable general equilibrium, International trade theory, International migration, Health care, Labour markets
1. Introduction
The interactions between health care, health and the remainder of the economy are complex. On one hand, changes in income affect the consumption and/or provision of health care and other goods, and thus the health of populations in terms of illness and mortality. On the other hand, changes in health impact upon the well-being of populations, hence labour market participation, productivity and income.
Developed countries, with high living standards and levels of health, are argued to be in a state where the marginal contribution of health care to health is minimal and other factors, such as diet, lifestyle, environment and education, are more important in explaining variations in health (Folland et al., 2001, Chapter 5). However, many former sceptics of the contribution of health care now accept that, even after allowing for diet and lifestyle, health care does make a difference for specific conditions, such as cardiovascular disease (Wallace, 2004). Moreover, medical care also enhances the quality of life through pain relief and increased mobility.
Nevertheless, it has been argued that the majority of developed country health care systems fail to deliver specific medical services to a “satisfactory” standard, commonly attributing this to limited financial means and inefficient use of resources. In the UK, such pressures result in poor health outcomes for some diseases (such as cancer), poor service quality, including long waiting lists and waiting times for certain treatments, and inequities in access and health outcomes. These impose significant costs on society above those of health provision itself. Health care costs themselves are bound to rise given an ageing population and advances in medical technology.
While the interdependencies between health care, health and the rest of the economy are now widely acknowledged, most of the economic models used to assess these fail to incorporate the main channels through which interactions take place. Most empirical studies employ econometric analysis and usually ignore the general equilibrium effects of changes in health and health care across sectors, factors, and households, and their implications for the government budget.
Econometric models typically focus on multiple linkages between health, health expenditures and economic growth at the aggregate (macro) level (e.g., Baldacci et al., 2004, Bhargava et al., 2001, Bloom and Canning, 2003, Bloom et al., 2004, Crémieux et al., 1999, Ettner, 1996, Hamoudi and Sachs, 1999, Hitiris and Posnett, 1992, Jamison et al., 2003, Knowles and Owen, 1997, Mayer, 2001a, Mayer, 2001b, Pritchett and Summers, 1996, Strauss and Thomas, 1998, Stronks et al., 1997, Thomas and Frankenberg, 2002).
The few computable general equilibrium (CGE) models that exist are diverse in their application area. Those set in a developing country context may be categorised into Basic Needs models (Kouwenaar, 1986, Van der Hoeven, 1987, Van der Hoeven, 1988, Vianen and Waardenburg, 1975), Externality models (Savard and Adjovi, 1997), HIV/AIDS models (Arndt, 2003, Arndt and Lewis, 2000, Arndt and Lewis, 2001, Arndt and Wobst, 2002, Dixon et al., 2004, Kambou et al., 1992) and Millennium Development Goal (MDG) models (e.g., Lofgren and Diaz-Bonilla, 2006, Sundberg and Lofgren, 2006). There are some “Global” models, such as Lee and McKibbin's (2003) model of the economic effects of Severe Acute Respiratory Syndrome (SARS), and most recently Smith et al.’s (2005) UK model of the macro-economic impact of antimicrobial resistance. While each of these strands of CGE literature has its own merits, most do not assess the endogenous impact of changes in health care provision on population health, and on the labour force in particular and its impact on production, income and welfare.1
Empirical studies typically fail to account for the main feature of all nations’ health care systems, namely that they treat and (perhaps partially) cure people, i.e., improve their health, which not only makes them “feel better” but also enlarges the effective size of the population through increased working time for some and reduced death rates for all. At the same time, health care systems use factors of production, which reduces their effective supply in the rest of the economy. It is in addressing this caveat that this paper seeks to make a contribution.
The analysis is novel in two main respects.2 The first contribution is in terms of international trade theory, using the Rybczynski theorem to cast light on some of the resource allocation issues related to the provision of health care. While there is a strong literature on endogenous labour supply models (e.g., Martin, 1976, Martin and Neary, 1980), the analysis has largely focused on direct labour supply responses to higher wages. Here, changes in effective labour supplies come from changes in the size of the health sector.
The second contribution is empirical, the development of a static CGE model for the UK with a detailed health component. The CGE model is calibrated to a purpose-built Social Accounting Matrix (SAM) for the UK for the year 2000 with considerable refinement in terms of sectors (distinguishing health care and its main input suppliers), factors (capital, skilled and unskilled labour) and household types (based on the age and labour market participation of household members). It is the first of its kind in that it has been designed to analyse the macro-economic impacts of changes in health care provision, while recognising the simultaneous effects of changes in health on effective labour supplies and the resource claims made by the health sector. The effects on welfare of higher health provision come through two main channels: (a) the direct gain from increasing the “well-being” of the population, and (b) the indirect effects of an increase in the size of the effective (i.e., “able to work”) endowments of skilled and unskilled labour for use in non-health activities.
Taking as a case study the UK, an archetype of a developed country health care system in which government provision and funding dominates, allows the modelling and analysis of current “rationed” health care policies. Specifically, we contrast three strategies for increasing health care provision through a higher National Health Service (NHS) budget on the assumption that domestic factor endowments are given. First, under the assumption that all factors are fully mobile within the economy and that there is no immigration of foreign skilled workers. Second, by amending this by assuming that some factors are health care-specific factors. Third, that there is immigration of foreign skilled workers at the current wage.
The remainder of the paper is organised as follows. Section 2 presents an application of the Rybczynski theorem where changes in effective labour endowments are modelled via changes in health provision. Section 3 explains the UK CGE model and SAM. Section 4 presents the results of the counterfactual simulations of policies aimed at alleviating rationing. The final section concludes and suggests directions for future research.
2. Effective labour endowments and the health sector: some low-dimension analytics
Consider a small open “Heckscher-Ohlin” economy, endowed with two types of labour, skilled (S) and unskilled (U), both subject to illness at given rates. There are four sectors (“uses” for factors): Goods 1 and 2 are conventional tradables, H is the non-tradable health sector treating the ill (modelled as ‘adding value’ to the ill) and W is an artificial “waiting list sector”. The waiting list records those who are ill and not yet (successfully) treated by the health sector and so are unable to work. We assume that health care is provided by the government and that its expenditure is determined politically (and so is exogenous to this model). The exogenous product prices determine the factor prices and hence skilled–unskilled labour ratios in the three production sectors. These remain constant throughout the analysis.
Within the period concerned, some skilled and unskilled workers become ill and so unable to work. However, the health service successfully treats all but S W and U W respectively of these (the loss of working time for those successfully treated is taken, for simplicity, as negligible). Accounting for factor use (paralleling the full employment conditions for standard trade models) gives:
| (1) |
| (2) |
where S i and U i, i = 1, 2, H, are the numbers working, and S W and U W are the numbers of potential workers that remain unable to work.3
We are interested in the effective labour forces, S E and U E, where
| (3) |
| (4) |
Fig. 1 shows a possible initial equilibrium. It is drawn on the assumptions that the health sector H is the most skill-intensive sector and sector 2 is the least skill-intensive, that the incidence of illness is the same for both groups of workers,4 that the health sector allocates its output of health treatment in proportion to the numbers falling ill, and that treatment is equally effective across labour types.
Fig. 1.
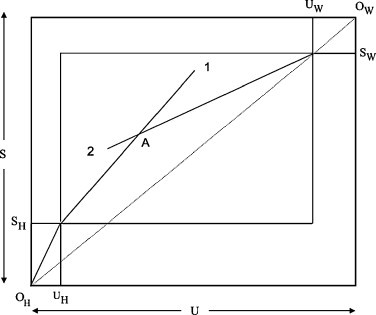
An initial equilibrium.
The maximum possible endowments of skilled and unskilled labour are S and U respectively (in the sense that there is no ill health and hence no need for health provision). Inputs into the health sector are measured from O H, while those unable to work are measured from O W. The government health budget purchases S H and U H of labour inputs at given wages. At that level of health provision the numbers of potential workers remaining on the waiting list are S W and U W (and by virtue of the previous assumptions are in the same proportion as the economy's endowment ratio). The inner box then gives the skilled and unskilled labour available to work in the two tradables sectors. Measuring inputs into sector 2 from the north-east corner of this box and inputs into sector 1 from the south-west corner allows us to determine the equilibrium at point A (where the production isoquants of sector 1 and 2, not drawn for simplicity, are tangential, with a slope equal to the absolute value of the relative wage of unskilled to skilled labour).
Fig. 2 illustrates the consequences of the government increasing the health budget in the case where there is no change in the overall endowments. Inputs of skilled and unskilled labour in the health sector increase to and respectively. The provision of extra health care reduces the numbers on the waiting lists to and . The remaining labour inputs are allocated to sectors 1 and 2 which, given relative wages, yields equilibrium point C.
Fig. 2.
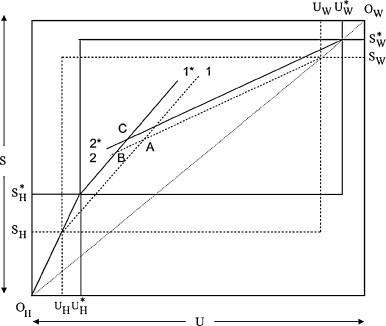
An example of an expanding health sector with unchanged endowments.
The expansion of the health sector and the contraction of the waiting list change both the total and relative amounts of factors available to the two tradables sectors. It is convenient to decompose these into a “scale effect” (increasing the effective endowments of both skilled and unskilled labour due to improved health) and a “factor-bias” effect (changing the effective endowment ratio due to differences in skill-intensities between health and non-health sectors). Splitting the changes into the two components allows us to draw some insights from standard trade theory results that have their origin in the seminal paper by Rybczynski (1955). Since the health sector is, in this example, the most skill-intensive sector, its expansion will lead to a reduction in the skilled-unskilled labour endowment ratio available to the rest of the economy, so that, on the basis of the Rybczynski theorem, the output of the relatively skill-intensive good (sector 1) will fall and the output of the other good (sector 2) will rise. This is the factor-bias effect, depicted in Fig. 2 by the move from A to B. The scale effect, from B to C, shows the effect of reducing the amounts of skilled and unskilled labour on the waiting lists, i.e., increasing effective labour supplies, which in this example increases the production of both goods.5
In the example of Fig. 2 it is evident that the net effect is a contraction of sector 1 and an expansion of sector 2. However, it will also be evident that in general the effects on the tradables sectors depend on the ordering of factor intensities of the three production sectors and the endowment ratio, on the incidence of illness and on the provision and effectiveness of treatments for the two types of labour. For developed countries the available evidence suggests that the elasticity of effective labour supplies with respect to health care is small (and less than one) so that scale effects are small, as in Fig. 2. Hence, if we are willing to assume that health care is relatively skill-intensive and that factor-bias effects dominate, we expect an exogenous increase in health expenditures to benefit the unskilled-intensive sector and harm the skilled-intensive sector.
Whether the health sector is, in fact, more skill-intensive than all other sectors is an empirical question, as is that of whether the incidence of illness and the provision and effectiveness of health care are independent of labour type. In a multi-sectoral model with more than two factors, possibly health care-specific, and other real-life complexities the foregoing predictions are unlikely to be wholly true. Nevertheless, these effects will still operate in the background and thus give a useful guide to the interpretation of the outcomes of such a model.
3. The UK CGE model and SAM
The analysis is based on a comparative static CGE model of the UK.6 The SAM underlying the model has been constructed by augmenting the UK Input–Output Supply and Use Tables for 2000 (Office for National Statistics, 2002), using data from the General Household Survey (GHS) for 2000–2001 (Office for National Statistics, 2001). An outline of the model is given below, with special detail on health and welfare effects.
The CGE model has in most respects a standard structure (e.g., Francois and Reinert, 1997), the novelty coming from the explicit modelling of the health sector, comprising public (NHS) and private health care (PHC), and its interaction with the rest of the economy through its differential impact across sectors, factors and household types (specified in Table 1 ).
Table 1.
The CGE model classifications.
| Factors of production (f) | Sectors (i)/commodities (j) | |
| Skill | Skilled | 1 Primary |
| Unsk | Unskilled | 2 Pharmaceuticals |
| Cap | Capital | 3 Medical instruments |
| 4 Other manufacturing | ||
| Households (h) | 5 Energy | |
| Hse1 | Pensioners | 6 Construction |
| Hse2 | Non-working, children | 7 Distribution and transport |
| Hse3 | Non-working, no children | 8 Finance |
| Hse4 | Working, children | 9 Public administration and defence |
| Hse5 | Working, no children | 10 Health care (NHS, PHC) |
| 11 Other services | ||
All sectors are perfectly competitive and multi-product industries. The production technologies are constant returns to scale, with production a Leontief function of intermediates and value-added, itself a Constant Elasticity of Substitution function of homogeneous factors of production. The accompanying substitution elasticities are displayed in Table 2 . Household preferences are homothetic, with utility a Cobb Douglas (CD) function of consumption and savings.
Table 2.
Elasticity parameters in production.
| Sectors | Elasticity of substitution between factors of production |
|---|---|
| 1 Primary | 0.2 |
| 2 Pharmaceuticals | 1.3 |
| 3 Medical instruments | 1.3 |
| 4 Other manufacturing | 1.3 |
| 5 Energy | 1.3 |
| 6 Construction | 1.4 |
| 7 Distribution and transport | 1.7 |
| 8 Finance | 1.3 |
| 9 Public administration and defence | 1.3 |
| 10 Health care | 1.3 |
| 11 Other services | 1.3 |
Source: GTAP version 7.
Cross-border trade is treated using the assumption that the UK is a small open economy facing exogenous world prices for imports and exports, and accommodates ‘entrepôt’ trade, i.e., the re-exporting (re-importing) of imported (exported) goods, and transport and trade margins. In addition, the Armington assumption (Armington, 1969) is imposed on both production and consumption: goods produced domestically are destined for either the domestic market or for the export market, while consumers differentiate between domestic and imported varieties of the “same” good. The Armington substitution and transformation elasticities are assumed equal to two in this model.7
The government uses its revenue from employment, production and consumption taxes to finance a fixed expenditure on goods (health care, public administration and defence, and other services) and a fixed amount of foreign exchange at the exchange rate to accommodate the trade surplus. The remainder of its budget is spent on income transfers to households (i.e., state benefits) which adjust so as to maintain the government account balance. Households allocate the latter income and earnings from the supply of capital, skilled and unskilled labour to savings and consumption, assuming that only working households save.
All factor and product markets clear through price adjustments. Equilibrium in the capital goods market requires that the value of total savings equals the value of total investments. With the exchange rate as numéraire and the trade balance fixed in terms of foreign exchange, investments are savings-driven so that the model closure is neoclassical.
3.1. Health provision effects
We model the interaction between health care and effective labour supplies by the use of a non-participation rate for each type of labour. Non-participation can be interpreted as “being on the waiting list”, whereas participation implies employment in one of the sectors of the economy. The effective supply of factor endowments f by households h, FE hf, is specified in Eq. (5), and the waiting list for factor f by household h, WL hf, in Eq. (6).
| (5) |
| (6) |
where 0 < η f < 1 for labour types f ∈ l, l = {Skill,Unsk}; otherwise (for capital) η f = 0. The waiting list is a fraction of total given factor endowments of household h (), and is defined positively only for labour (f ∈ l), whereas capital is always fully effective and fully employed.
The fraction of people on the waiting list, i.e., the non-participation rate, is assumed to be identical across all households and is defined as a constant elasticity function of a health composite:
| (7) |
where η 0f∈l is a scale parameter, which measures the effectiveness of a given level of health care in treating and/or curing people and is calibrated so that 0 < η f∈l < 1. HC f∈l is a health composite and ɛ f∈l > 0 is the waiting list elasticity, which measures the effectiveness of a change in health provisioning in treating and/or curing people. The latter is defined as the proportionate change in the size of labour type l's waiting list for household h following a change in the health composite, ɛ f∈l = −(∂WL hf/∂HC f)·(HC f/WL f) > 0.
The health care composite for labour type l is a measure of the ‘healthiness’ or health status of this labour type and is a Cobb Douglas function of its public and private health care consumption:
| (8) |
where 0 ≤ υ l ≤ 1 denotes the share of public health care in the health status of labour type l. G “10” denotes health care (commodity “10” in Table 1) provided via the NHS – as given by real government consumption of health care, G j – and represents the level of private health care provisioning – as given by the sum of household consumptions, C jh, of health care.
Given Eqs. (5), (6), (7), (8), waiting lists (effective labour supplies) are decreasing (increasing) in the health composites, at a decreasing rate. Fig. 3 illustrates (subscripts are ignored for simplicity).
Fig. 3.
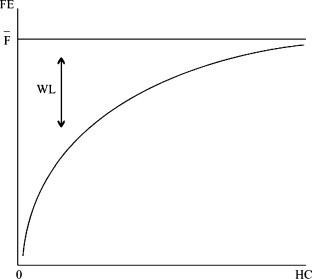
Waiting lists and effective endowments.
The contribution of public health care to the health status of skilled and unskilled labour, as measured by υ, is obtained from Emmerson et al. (2000). Using Family Resource Survey data for the period 1994/1995–1997/1998, they calculate the percentage of adults with private medical insurance by social class. By applying population weights corresponding to each social class from the General Household Survey, the proportions of skilled and unskilled labour having private medical insurance are estimated at 16.6% and 4% respectively, yielding a residual of 83.4% and 96% of skilled and unskilled labour for whom health care is financed via the NHS. The latter serve as proxies for υ.
The scale parameter η 0 is calibrated to the benchmark non-participation rate. Its value is based on the Barmby et al., 2002, Barmby et al., 2004 measure of sickness absence, calculated as the ratio of the number of hours absent due to sickness to the number of hours contracted to work. Using Labour Force Survey data, we find a fairly stable long-run average for the (yearly) sickness absence rate in the UK of around 3.20%. Another finding, corroborated by other studies (Confederation of British Industry, 2001, Barham and Leonard, 2002), is that sickness absence varies by socio-economic characteristics. Typically, the higher the wage and the higher the level of responsibility involved in the job, the lower the absence from work. Illness-related absence from work is approximately 1.5 times higher for manual than that for non-manual workers. Assuming that the non-participation rate in the base year for unskilled workers is 1.5 times that of skilled workers and postulating an overall non-participation rate of 3.20% yields η 0 = 2.89% for skilled and η 0 = 4.34% for unskilled workers.
The waiting list elasticity parameter, ɛ, is set to 2 for both labour types, so that a 10% increase in health status leads to a 20% decrease in waiting lists. A value of 2 seems reasonable since it gives health elasticities for skilled and unskilled labour of around 0.1 (0.06 and 0.09 for skilled and unskilled labour respectively), consistent with the scant empirical evidence that exists in this area.8 The results are tested for sensitivity to alternative values of the waiting list elasticities.
3.2. Welfare effects
The effects on welfare of higher health provision are two-fold: it directly increases the “well-being” of the population and indirectly improves welfare by increasing the size of the effective (i.e., “able to work”) endowments of skilled and unskilled labour for use in non-health activities. Accordingly, changes in household welfare are calculated from private household utility using the standard Hicksian equivalent variation, to which the benefits from changes in NHS provisioning are added. For linear homogeneous preferences, the equivalent variation for household h can be written as:
| (9) |
where U h and Y h denote household utility and income respectively, and superscript 0 and 1 respectively refer to the equilibria before and after a particular shock occurs.
Assuming that each household receives a share α h of the change in NHS provisioning (where ), the overall change in household welfare becomes:
| (10) |
where denotes benchmark government expenditure on health care, i.e., NHS care. α h is calculated from each household's share in the total number of NHS general practitioner consultations. The resulting values are shown in Table 3 , together with the household shares in government transfers.
Table 3.
Household shares in government transfers and NHS care.
| Household type | Share in transfers | Share in NHS care (αh) | |
|---|---|---|---|
| HSE1 | Pensioners | 0.523 | 0.251 |
| HSE2 | Non-working, children | 0.102 | 0.087 |
| HSE3 | Non-working, no children | 0.106 | 0.076 |
| HSE4 | Working, children | 0.234 | 0.306 |
| HSE5 | Working, no children | 0.035 | 0.280 |
Source: Authors, own calculations from GHS 2000–2001.
Adding up all household welfare changes including those related to NHS provisioning gives an overall welfare change for the UK economy of:
| (11) |
4. Policies aimed at alleviating rationing in UK health care
We examine the effects of two types of policies which have identical implications for the nominal government budget on health care (the NHS budget), but differ in terms of their real budgetary impact due to differential price effects.
Experiments 1 and 2 simulate the impact of an increase in government health expenditures assuming mobile and health care-specific factors respectively. The introduction of health care-specific skilled labour and capital in the second experiment provides an alternative specification more suited to the short run. The former type consists of mainly doctors and nurses (approximately 85% of skilled labour employed in health care) and the latter consists of buildings and land (approximately 90% of capital employed in health care), and both earn a health care-specific remuneration.
Using the same model specification as in experiment 2, experiment 3 considers the alternative policy of importing medical services, i.e., health care-specific skilled workers consisting of doctors and nurses, in order to mitigate the shortage of highly skilled workers in UK health care (the effects of which have modelled in experiment 2). On entering the UK, foreign doctors and nurses are assumed to become part of the existing domestic household structure, i.e., they are perfect substitutes for their domestic equivalents. This assumption takes into account that many of them plan to stay and will thus become permanent UK households in the long-term. Health care-specific skilled wages are maintained at pre-immigration levels so that domestic workers are not worse off in nominal terms as a consequence of the policy. This assumption is representative of the UK situation, given that wages of health workers in the UK are essentially fixed in bilateral bargaining rounds between the Department of Health (constrained by the Treasury) and the medical profession (represented by, among others, the British Medical Association).9 The experiment uses three alternative assumptions regarding the share of foreign worker income remitted abroad, adopting illustrative values of 0%, 50% and 100% respectively.10 Varying the share of migrant income remitted will have differential welfare effects since remittances have to be compensated for by a rise in exports and/or a fall in imports so as to maintain the balance of payments.11
For the purpose of comparability, we carry out the experiments so that they will have identical implications for the nominal government budget on health care (i.e., the NHS budget). In experiment 3, it is assumed that an equivalent of 10% of domestic endowments of health care-specific skilled labour takes up the offer to migrate to the UK, so that the government budget on health care has to rise by 11.31% (approximately £6.09 billion) to maintain their wages at pre-immigration levels in the UK health sector. This budget increase is taken as point of departure for experiments 1 and 2.12 Table 4 summarises the key results.
Table 4.
The economic impacts of changes in NHS provision levels on the UK economy.
| Experiment |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 |
|||||||
| A rise in NHS budget by 11.31%; mobile factors | A rise in NHS budget by 11.31%; health care-specific factors | 10% immigration of health-specific skilled workers; the NHS budget rises by 11.31% so as to maintain their wages |
|||||||
| – | – | 0%a | 50%a | 100%a | |||||
| Change in | |||||||||
| Production (%) | 1 Primary | −0.34 | −0.15 | −0.05 | 0.05 | 0.14 | |||
| 2 Pharmaceuticals | 5.93 | 2.44 | 5.53 | 5.79 | 6.05 | ||||
| 3 Medical Instruments | 2.34 | 1.03 | 2.35 | 2.48 | 2.61 | ||||
| 4 Other manufacturing | −0.26 | −0.12 | 0.08 | 0.13 | 0.18 | ||||
| 5 Energy | −0.21 | −0.13 | 0.11 | 0.05 | −0.01 | ||||
| 6 Construction | 0.06 | 0.27 | 0.39 | 0.26 | 0.12 | ||||
| 7 Distribution and transport | −0.15 | −0.09 | 0.18 | 0.15 | 0.13 | ||||
| 8 Finance | −0.13 | −0.02 | 0.20 | 0.19 | 0.17 | ||||
| 9 Public administration and defence | −0.03 | 0.03 | 0.03 | 0.14 | 0.24 | ||||
| 10 Health care | NHS | 11.30 | 5.61 | 10.31 | 10.39 | 10.47 | |||
| PHC | −0.37 | −5.25 | −0.88 | −1.07 | −1.26 | ||||
| 11 Other services | −0.18 | −0.12 | 0.07 | 0.05 | 0.04 | ||||
| Health status and labour market impacts (%) | Health care status | Skill | Skilled labour | 9.27 | 3.72 | 8.37 | 8.40 | 8.43 | |
| Unsk | Unskilled labour | 10.81 | 5.15 | 9.84 | 9.91 | 9.97 | |||
| Waiting list | Skill | Skilled labour | −16.25 | −7.05 | −14.85 | −14.90 | −14.94 | ||
| Unsk | Unskilled labour | −18.55 | −9.56 | −17.12 | −17.21 | −17.31 | |||
| Effective labour supply | Skill | Skilled labour | 0.48 | 0.21 | 0.44 | 0.44 | 0.45 | ||
| Unsk | Unskilled labour | 0.84 | 0.43 | 0.78 | 0.78 | 0.79 | |||
| Factor returns (%) | Mobile factors of production | Skill | Skilled labour | 0.02 | −0.09 | −0.11 | −0.22 | −0.32 | |
| Unsk | Unskilled labour | −0.37 | 0.20 | −0.08 | −0.19 | −0.30 | |||
| Cap | Capital | 0.15 | −0.01 | 0.20 | 0.08 | −0.03 | |||
| Health care-specific factors of production | Skill | Skilled labour | – | 11.84 | 0 | 0 | 0 | ||
| Cap | Capital | – | 12.02 | 7.97 | 7.97 | 7.98 | |||
| Government (%) | Tax revenues | 0.16 | 0.30 | 0.47 | 0.34 | 0.21 | |||
| Transfers to households | −4.92 | −4.55 | −4.11 | −4.45 | −4.80 | ||||
| Private household welfare (EVh) in million pounds (%) | Hse1 | Pensioners | −2770 (−1.56) | −2402 (−1.36) | −1993 (−1.12) | −2150 (−1.21) | −2307 (−1.30) | ||
| Hse2 | Non-working, children | −574 (−4.06) | −523 (−3.71) | −472 (−3.34) | −500 (−3.54) | −528 (−3.74) | |||
| Hse3 | Non-working, no children | −567 (−1.62) | −521 (−1.49) | −417 (−1.19) | −447 (−1.28) | −477 (−1.36) | |||
| Hse4 | Working, children | −540 (−0.23) | −130 (−0.06) | 297 (0.13) | −71 (−0.03) | −441 (−0.19) | |||
| Hse5 | Working, no children | 1115 (0.36) | 1730 (0.56) | 2136 (0.68) | 1594 (0.51) | 1051 (0.34) | |||
| Public welfare from changes in NHS provisioning (million pounds) | Hse1 | Pensioners | 1527 | 758 | 1394 | 1404 | 1414 | ||
| Hse2 | Non-working, children | 529 | 263 | 483 | 487 | 490 | |||
| Hse3 | Non-working, no children | 462 | 229 | 422 | 425 | 428 | |||
| Hse4 | Working, children | 1861 | 924 | 1699 | 1712 | 1724 | |||
| Hse5 | Working, no children | 1703 | 845 | 1555 | 1566 | 1578 | |||
| Overall household welfareb (EVT) in million pounds (%) | Hse1 | Pensioners | −1244 (−0.65) | −1644 (−0.86) | −600 (−0.31) | −746 (−0.39) | −893 (−0.47) | ||
| Hse2 | Non-working, children | −44 (−0.24) | −261 (−1.39) | 11 (0.06) | −13 (−0.07) | −38 (−0.20) | |||
| Hse3 | Non-working, no children | −105 (−0.27) | −292 (−0.75) | 5 (0.01) | −22 (−0.06) | −48 (−0.12) | |||
| Hse4 | Working, children | 1321 (0.54) | 793 (0.32) | 1997 (0.81) | 1640 (0.66) | 1284 (0.52) | |||
| Hse5 | Working, no children | 2819 (0.86) | 2575 (0.79) | 3691 (1.13) | 3160 (0.97) | 2629 (0.80) | |||
| Total private welfare in million pounds (%) | −3336 (−0.43) | −1847 (−0.24) | −449 (−0.06) | −1575 (−0.21) | −2701 (−0.35) | ||||
| Total pubic welfare in million pounds (%) | 6083 (11.30) | 3019 (5.61) | 5553 (10.31) | 5594 (10.39) | 5635 (10.47) | ||||
| Total welfare for the UK (EVUK) in million pounds (%) | 2748 (0.33) | 1172 (0.14) | 5104 (0.62) | 4019 (0.49) | 2934 (0.36) | ||||
Remittance scenario's (% of foreign worker income).
Note: percent change also provides a per-capita measure of welfare changes by household type.
4.1. Experiment 1—a rise in NHS expenditures
The additional NHS resources result in an increase in NHS provision and, via input-output linkages, increase the demand for and domestic production of pharmaceutical products and medical, precision and optical instruments. As a consequence health care, pharmaceuticals and instruments become slightly more expensive, which increases the costs to and hence reduces the size of private health care provision.
Are the sectoral effects consistent with the predictions from the theoretical model of Section 2? From the theory we expect that “on average” the relatively skill-intensive sectors (2, 5, 8 and 9 in Table 1) contract and the relatively unskilled-intensive sectors (1, 3, 4, 6, 7 and 11 in Table 1) and the health sector expand.13 The results reveal that most skill-intensive sectors do contract, albeit mildly, but that the pharmaceuticals sector expands. This suggests that, following a rise in the NHS budget and the consequent expansion of the health sector, the increased demand for intermediate inputs from this sector outweighs the reduced availability of skilled labour relative to unskilled labour. Also, most of the unskilled-intensive sectors contract, apart from construction and the medical instruments sector. The latter's expansion is much more pronounced and, as before, is likely to be due to the intermediate demand effect from the health sector, rather than the increased availability of unskilled relative to skilled labour. The predictions of the theoretical Heckscher-Ohlin model thus do not carry over completely to the applied CGE model, providing a strong argument for the use of the latter.
The increase in public health care boosts the health of unskilled labour, its participation in the labour market, and reduces its waiting list by more relative to skilled labour, as the former is affected primarily by changes in public health care, whereas the latter also responds to changes in private health care provision which is more costly and less available.
The changes in (effective) factor supplies and sectoral factor demands result in a (minor) fall in unskilled wages, whereas skilled wages and capital rents rise slightly. Despite the fall in unskilled wages, the increase in labour market participation ensures that all households’ income from unskilled (and skilled) labour rises.
The fall in government transfers to households, which follows from the assumed balanced government budget, leads to reductions in income for working households with children, but relatively more so for pensioners and non-working households. Only childless working households, who own most of skilled labour endowments and rely least on government transfers, gain slightly.
Adjusting private welfare losses for changes in NHS provisioning reduces welfare losses, with pensioners and non-working households losing, whereas working households gain. Nevertheless, in total welfare increases by £2.748 billion (a gain of 0.33% relative to the original level of welfare).
4.2. Experiment 2—a rise in NHS expenditures in the presence of health care-specific factors
This simulation implements the same policy as in experiment 1, but accounts for the fact that a large part of the labour and capital employed in health sector are, respectively, highly trained or highly specialised and therefore arguably specific to health care and immobile.
Key findings are that, unsurprisingly, the presence of health care-specific skilled labour and capital constrains the production expansion of health care and related sectors. An 11.31% increase in the NHS budget leads to a rise in real levels of NHS provisioning of less than half of that, the remainder of the budget being spent on higher wages of highly skilled doctors and nurses and capital rents, and resulting in higher unit costs (and a contraction in private care).
As a consequence, indirect welfare gains from improved health on effective labour supplies, and direct welfare gains from improvements in well-being, are lower compared to the previous experiment. Non-working households and pensioners lose by more and working households gain by less, cutting the total welfare gain by 57%.
4.3. Experiment 3—importing health care-specific skilled workers at the current wage
This simulation presents the results of a policy of importing health care-specific skilled workers (i.e., doctors and nurses), which addresses the bottleneck of not being able to hire additional workers of this type in the domestic market in the short run.
In the absence of remittances abroad, the specified rise in the NHS budget which is targeted towards the immigration of foreign health care-specific skilled workers, yields a rise in real levels of NHS provisioning of 10.31%. This is less than in the first experiment since the wages of the domestic and foreign workers of aforementioned type are sustained at benchmark levels, thereby increasing the unit costs of health care provisioning (and reducing private sector production). The direction of effects across sectors, factors and households are nevertheless similar to those in experiment 1.
Whereas direct and indirect welfare gains from the rise in NHS provision levels and health improvements are lower, government transfers to households need to fall by less to finance the expansion of the NHS budget due to higher government tax revenues. Thus, in the absence of remittances, working households and, to a lesser extent, non-working households gain, and only pensioners lose.
Remittances abroad reduce welfare gains for some groups and increase welfare losses for the others so that, as in the previous experiments, pensioners and non-working households lose and working households gain.
The total welfare gains however still exceed those of the generic rise in the government budget, certainly if one compares experiments with the same model specification (i.e., experiments 2 and 3). This can be explained by the fact that the immigration of doctors and nurses in the third experiment addresses the bottleneck of the scarcity of this type of labour in the UK, while increasing the NHS budget in the second experiment aggravates it (by putting upward pressure on the wages of doctors and nurses).
Finally, a remark on the sign of the changes in total private welfare versus the changes in overall welfare recorded for all simulations is in place here. The negative sign of the former and the positive sign of the latter suggests that the indirect welfare gains from improved health on effective labour supplies are relatively small for the UK and that most of the overall welfare gain is generated by direct welfare gains from improvements in well-being. This is a direct result of the rather conservative estimates used for the waiting list (and health) elasticities, which we imposed since for the UK as a whole we assume that we are “on the flat of the health production curve”. If we were to model a specific health care problem and alternative health interventions with a higher marginal return, or if we were to take a different country where the health system is still relatively underdeveloped and the marginal impact of an increase in health provisioning is high, waiting list (and health) elasticities may well be higher, increasing the indirect welfare gains from improved health on effective labour supplies so that total private welfare gains may become positive. This is illustrated below in the sensitivity analyses.
4.4. Sensitivity analyses
Sensitivity analyses for the elasticities of substitution and transformation show that the results of the counterfactual simulations are relatively robust: although sign changes do occur for some variables, the impact of changing the respective elasticities upon overall welfare is negligible.
Varying the waiting list elasticities for skilled and unskilled labour, which govern the indirect health effects of improved health on effective labour supplies, does however affect the results considerably: generally, in the presence of increasingly strong skill-neutral health effects, the expansion of NHS care, although representing an immediate cost to society, yields substantial welfare gains in the long-run through increases in effective labour supply and production, and by enhancing the tax revenue of the government, which benefits both working households (in terms of their wage income) and non-working households (in terms of their receipt of state benefits).
Specifically, a waiting list elasticity for both skilled and unskilled labour of at least 4.42 in experiment 1, 4.57 in experiment 2 and 4.11 in experiment 3 (taking the most negative scenario of 100% remittances), i.e., an approximate doubling of the waiting list (and health) elasticity, generates positive total private welfare gains.
Moreover, in experiments 1–3 (scenario of 100% remittances) total UK welfare rises for relatively low values of the waiting list elasticity (lower boundary values of 0.35, 0.48 and 0.10 respectively) so that the main results continue to hold.
These results suggest that if we were to employ the model for a specific health care problem and alternative health interventions, or for a different country, then we could get quite different results, depending on, inter alia, the incidence of illness (which determines the number of people treated by the health sector and so the number of healthy workers that could be ‘produced’) and the ‘efficiency’ of the health sector in producing healthy workers.
5. Conclusions
This paper seeks to determine the macro-economic impacts of changes in health care provision, while recognising the simultaneous effects of consequent changes in health on effective labour supplies and the resource claims made by the health care sector. The resource allocation issues have been explored in theory, by applying the standard Rybczynski theorem in a low-dimension Heckscher-Ohlin framework and, empirically, by developing a CGE model, calibrated to a purpose-built dataset for the UK.
Using the theory, the impact of an expanding health sector on the outputs of non-health sectors was shown to depend on the sign and magnitude of a scale effect of increased effective labour supplies and a factor-bias effect of changes in the ratio of skilled to unskilled labour. The net effects generally are indeterminate. Given that effective labour supplies are relatively inelastic with respect to health care provision in developed countries since they are “on the flat of the health production curve”, factor-bias effects may dominate so that an increase in health care provision, which is relatively skill-intensive, may “on average” result in an expansion of the relatively unskilled-intensive sectors and a contraction of the relatively skill-intensive sectors in the long-term. These predictions were generally not found to hold in the CGE model due to added-real-life complexities, most notably the presence of intermediate inputs. This is a strong argument for the use of an applied model in addition to a theoretical model.
Using an applied CGE model for the UK, which in addition to the labour market effects also incorporates the direct impact of health provision on the “well-being” of the population, we have compared the nominally equivalent policies of increasing the NHS budget under the assumptions of mobile and health care-specific factors and the immigration of foreign skilled workers (doctors and nurses) at the current wage with one another. The main findings are that the increase in the NHS budget, while drawing away resources from its private counterpart and from other non-health related sectors, leads to an overall welfare gain through increased worker incomes and, more importantly, direct increases in population well-being. The presence of health care-specific skilled labour and capital reduces the overall welfare gain by about two thirds, as over half of the specified budget rise is absorbed by higher wages and rents. This suggests the importance of tackling short-term rigidities in the health sector. The shortage of highly skilled workers may in the short-term be addressed via the recruitment of highly skilled foreign doctors and nurses. This policy was found to yield the highest overall welfare gains, even if all foreign worker income is remitted abroad, since government transfers need to fall by less to finance the health care budget increase due to higher government tax revenues. It is, however, unlikely to be a desirable policy given that many migrant workers come from developing countries which need their own educated staff. Consequently, in the long-term increasing the number of medical school places in the UK may be a more suitable policy response.
The sensitivity of the results to the waiting list (and health) elasticity for skilled and unskilled labour suggests that if we were to employ the model for a specific health care problem and alternative health interventions, or for a different country, then we could get quite different results, depending on, inter alia, the incidence of illness and the “efficiency” of the health sector in producing healthy workers. In our model these impacts are relatively small since in the UK we assume that at the aggregative level we are on the “flat of the health production curve”. Interesting applications in this respect are to apply the framework developed in this paper to the perspective of a developing country with a relatively underdeveloped health care system and a high burden of disease (e.g., a country in Sub-Saharan Africa) or to model the impact of an epidemic, such as influenza, and alternative policy options in a developed country context, such as the UK, so as to test the ability of the health system to cope with a disease outbreak.
Our model may be extended in various ways. Firstly, incorporating long-term population processes (births, deaths, transitions from “young” to “working” to “retired”) in a dynamic (overlapping generations) model would link our analysis to the issue of ageing. Secondly, the modelling of health-related gains in “well-being” in the model, which at the moment are estimated rather conservatively at the real value of NHS service provision, may be improved using for example the literature on happiness (Clark and Oswald, 2002). Thirdly, it could be made more realistic by increasing the level of disaggregation in health care in terms of, for example, types of treatments and care so as to assess the allocative efficiency of current spending, and types of health care staff and equipment to allow for differential substitution between them.
Acknowledgements
The authors are grateful to Joe Francois, Adam Blake, Dave Whynes, Rod Falvey, Doug Nelson, Eddy van Doorslaer, Kirsten Rohde and an anonymous reviewer for their helpful comments and suggestions. The paper is based on the first author's Ph.D. Thesis at the University of Nottingham (Rutten, 2004). Preliminary versions of this paper were presented at the 2003 EcoMod International Conference on Policy Modeling in Istanbul, the 2004 Third GEP Postgraduate Conference at the University of Nottingham, the 2005 RES Annual Conference in Nottingham and the 2007 Health Economics Seminar Series at the Erasmus University Rotterdam. The responsibility for any remaining errors or infelicities remains with the authors. This paper presents the opinions of the authors, and is not meant to reflect the opinion or official position of any institution with which they are or have ever been affiliated with.
Footnotes
An exception is the Dixon et al. (2004) model of the impact of the HIV/AIDS pandemic and alternative health interventions on the Botswana economy. However, this model focuses on one particular disease in a developing country setting.
See Rutten (forthcoming) for an analysis from the perspective of migration of skilled medical personnel into the UK, using a different version of the CGE model and including a formal derivation of the theory.
We could equally well work in terms of the numbers of worker-hours lost.
There is evidence that the incidence of illness is higher in the low-income groups, but we ignore this for simplicity of exposition.
For a formal derivation of the factor bias and scale effects see Rutten (forthcoming).
The MPSGE model files necessary to replicate the results are available from http://www.i4ide.org/people/∼rutten/.
Most goods produced in the UK are traded with similar high-income countries and are of the same high quality so that substitution and transformation elasticities are reasonably high. At the multi-commodity level the elasticity values in GTAP version 7 (http://www.gtap.org) are around 2–2.5.
Folland et al. (2001, pp. 108–109). These elasticities measure the proportionate change in the size of effective endowments of skilled and unskilled labour following a change in the health composite, and are calculated as (∂FEhf/∂HCf)·(HCf/FEhf) = ɛf·WLhf/FEhf = ɛf·ηf/(1 − ηf). The elasticity is higher for unskilled labour due to the fact that a relatively higher proportion of the unskilled suffer illness, so that health expenditure's “leverage” is greater for this labour type.
Health care-specific skilled wages are fixed relative to the numéraire. Since the consumer price index changes only marginally (by less than 0.02% in absolute terms), fixing health care-specific skilled wages relative to the consumer price index would not alter our results.
A reliable estimate of the share of foreign worker income remitted abroad cannot be obtained since the evidence on remittances by migrant workers itself is mixed and difficult to establish for three main reasons: (1) a large proportion of remittances is transferred informally and is therefore not recorded in official statistics; (2) remittance behaviour will depend on the characteristics of the migrants in question, for example, the skill type, income level, length of stay and the country of origin and (3) it is unclear how much of the remittance flows can actually be attributed to health workers.
In contrast with the standard neoclassical CGE model closure, in which the current account balance is fixed and assumed equal to the capital balance, the modelling of migration and associated remittances implies that the trade balance has to adjust so as to maintain the balance of payments. Note that our model does not explicitly account for other components of the capital account since it is focused on (the consequences of international trade in services on) the domestic economy.
Note that the government closure is such that transfers to households adjust so as to maintain the government balance ceteris paribus changes in government tax revenues so that households bear the brunt of the adjustments. However, in CGE modelling there are many sources of funds that are fungible and an infinite number of distortionary taxes that may be introduced, which all are politically difficult to implement. The main point in CGE modelling and more generally in modern welfare economics is that, as long as overall welfare gains arise, losers may be compensated by winners so that it is possible to undertake a potential Pareto-improving redistribution (Johansson, 1991).
When there are many sectors in a Heckscher-Ohlin model, the Rybczynski Theorem becomes a “correlation”. As Falvey (1994) states, “There is a tendency for an increase in those outputs using intensively those factors whose endowments have risen and a decline for others.” Further uncertainty about outcomes in induced by the existence of intermediate inputs. The UK health sector is relatively skill-intensive, though its skill-intensity is only just above the endowment ratio, so we would expect the “correlation” to be low.
References
- Armington, P.S., 1969. A Theory of Demand for Products Distinguished by Place of Production. IMF Staff Papers 16, 159–176. International Monetary Fund, Washington, DC.
- Arndt, C., 2003. HIV/AIDS, Human Capital, and Economic Growth Prospects for Mozambique. Africa Region Working Paper Series 48. The World Bank, Washington, DC.
- Arndt C., Lewis J.D. The Macro implications of HIV/AIDS in South Africa: a preliminary assessment. South African Journal of Economics. 2000;68:856–887. [Google Scholar]
- Arndt C., Lewis J.D. The HIV/AIDS pandemic in South Africa: sectoral impacts and unemployment. Journal of International Development. 2001;13:427–449. [Google Scholar]
- Arndt, C., Wobst, P., 2002. HIV/AIDS and labor markets in Tanzania. TMD Discussion Paper 102. International Food Policy Research Institute, Washington, DC.
- Baldacci, E., Clements, B.J., Gupta, S., Cui Q., 2004. Social spending, human capital and growth in developing countries: implications for achieving the MDGs. IMF Working Paper 04/217. International Monetary Fund, Washington, DC.
- Barham C., Leonard J. Trends and sources of data on sickness absence. Labour Market Trends. 2002;110:177–185. [Google Scholar]
- Barmby T., Ercolani M., Treble J.G. Sickness absence: an international comparison. Economic Journal. 2002;112:F315–F331. [Google Scholar]
- Barmby T., Ercolani M., Treble J.G. Sickness absence in the UK: 1984–2002. Swedish Economic Policy Review. 2004;11:65–88. [Google Scholar]
- Bhargava A., Jamison D.T., Lau L.J., Murray C.J.L. Modeling the effects of health on economic growth. Journal of Health Economics. 2001;20:423–440. doi: 10.1016/s0167-6296(01)00073-x. [DOI] [PubMed] [Google Scholar]
- Bloom D.E., Canning D. The health and poverty of nations: from theory to practice. Journal of Human Development. 2003;4:47–71. [Google Scholar]
- Bloom D.E., Canning D., Sevilla J. The effect of health on economic growth: a production function approach. World Development. 2004;32:1–13. [Google Scholar]
- Clark A.E., Oswald A.J. A simple statistical method for measuring how life events affect happiness. International Journal of Epidemiology. 2002;31:1139–1144. doi: 10.1093/ije/31.6.1139. [DOI] [PubMed] [Google Scholar]
- Confederation of British Industry, 2001. Business and healthcare for the 21st century. Healthcare Brief. CBI Publications Sales, Centre Point, 103 New Oxford Street, London WC1A1DU.
- Crémieux P.-Y., Ouellette P., Pilon C. Health care spending as determinants of health outcomes. Health Economics. 1999;8:627–639. doi: 10.1002/(sici)1099-1050(199911)8:7<627::aid-hec474>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
- Dixon, S., McDonald, S., Roberts, J., 2004. AIDS in Botswana: evaluating the general equilibrium implications of healthcare interventions. Paper prepared for the conference Growth, Poverty Reduction and Human Development in Africa, hosted by the Centre for the Study of African Economies, University of Oxford, 21st to 22nd of March 2004. Preliminary Version.
- Emmerson, C., Frayne, C., Goodman, A., 2000. Pressures in UK healthcare: challenges for the NHS. Commentary 81. Institute for Fiscal Studies, London.
- Ettner S.L. New evidence on the relationship between income and health. Journal of Health Economics. 1996;15:67–85. doi: 10.1016/0167-6296(95)00032-1. [DOI] [PubMed] [Google Scholar]
- Falvey R.E. The theory of international trade. In: Greenaway D., Winters L.A., editors. Surveys in International Trade. Basil Blackwell; Oxford: 1994. pp. 9–42. [Google Scholar]
- Folland S., Goodman A.C., Stano M. third edition. Prentice Hall; Upper Saddle River, New Jersey: 2001. The Economics of Health and Health Care. [Google Scholar]
- Francois J.F., Reinert K.A. Cambridge University Press; Cambridge, UK: 1997. Applied Methods for Trade Policy Analysis: A Handbook. [Google Scholar]
- Hamoudi, A.A., Sachs, J.D., 1999. Economic consequences of health status: a review of the evidence. CID Working Paper 30. Center for International Development, Harvard University.
- Hitiris T., Posnett J. The determinants and effects of health expenditure in developed countries. Journal of Health Economics. 1992;11:173–181. doi: 10.1016/0167-6296(92)90033-w. [DOI] [PubMed] [Google Scholar]
- Jamison D.T., Lau L.J., Wang J. Health's contribution to economic growth in an environment of partially endogenous technical progress. In: Lopez-Casasnovas G., Rivera B., Currais L., editors. Health and Economic Growth: Findings and Policy Implications. MIT Press; Cambridge, MA: 2003. pp. 67–91. [Google Scholar]
- Johansson P.-O. Cambridge University Press; Cambridge: 1991. An Introduction to Modern Welfare Economics. [Google Scholar]
- Kambou G., Devarajan S., Over M. The economic impact of AIDS in an African country: simulations with a computable general equilibrium model of Cameroon. Journal of African Economies. 1992;1:109–130. [Google Scholar]
- Knowles S., Owen P.D. Education and health in an effective-labour empirical growth model. Economic Record. 1997;73:314–328. [Google Scholar]
- Kouwenaar, A., 1986. A basic needs policy model: a general equilibrium analysis with special reference to Ecuador. Ph.D. Thesis, Erasmus Universiteit Rotterdam.
- Lee, J.-W., McKibbin, W.J., 2003. Globalization and disease: the case of SARS. Working Papers in Trade and Development 2003/16. Division of Economics, Research School of Pacific and Asian Studies, Australian National University.
- Lofgren, H., Diaz-Bonilla, C., 2006. Economywide simulations of Ethiopian MDG strategies. Paper prepared for presentation at the Ninth Annual Conference on Global Economic Analysis, held in Addis Ababa, Ethiopia in June.
- Martin J.P. Variable factor supplies and the Heckscher-Ohlin-Samuelson model. Economic Journal. 1976;86:820–831. [Google Scholar]
- Martin J.P., Neary J.P. Variable labour supply and the pure theory of international trade: an empirical note. Journal of International Economics. 1980;10:549–559. [Google Scholar]
- Mayer D. The long-term impact of health on economic growth in Latin America. World Development. 2001;29:1025–1033. [Google Scholar]
- Mayer D. The long-term impact of health on economic growth in Mexico, 1950–1995. Journal of International Development. 2001;13:123–126. [Google Scholar]
- Office for National Statistics . The Stationary Office; London: 2001. Living in Britain: Results From the 2000/01 General Household Survey. [Google Scholar]
- Office for National Statistics . The Stationary Office; London: 2002. United Kingdom Input–Output Analyses 2002 Edition. [Google Scholar]
- Pritchett L., Summers L.H. Wealthier is healthier. Journal of Human Resources. 1996;31:841–868. [Google Scholar]
- Rutten, M., 2004. The economic impact of health care provision: a CGE assessment for the UK. Ph.D. Thesis submitted to the University of Nottingham, September 2004.
- Rutten, M. The economic impact of medical migration: a receiving country's perspective. Review of International Economics, forthcoming.
- Rybczynski T.M. Factor endowments and relative commodity prices. Economica. 1955;22:336–341. [Google Scholar]
- Smith R.D., Yago M., Millar M., Coast J. Assessing the macroeconomic impact of a healthcare problem: the application of computable general equilibrium analysis to antimicrobial resistance. Journal of Health Economics. 2005;24:1055–1075. doi: 10.1016/j.jhealeco.2005.02.003. [DOI] [PubMed] [Google Scholar]
- Savard, L., Adjovi, É., 1997. Adjustment, liberalization and welfare, in presence of health and education externalities: a CGE applied to Benin”. Cahier 97-07, CREFA, Laval University.
- Strauss J., Thomas D. Health, nutrition and economic development. Journal of Economic Literature. 1998;36:766–817. [Google Scholar]
- Stronks K., van de Mheen H., van den Bos J., Mackenbach J.P. The interrelationship between income, health and employment status. International Journal of Epidemiology. 1997;26:592–600. doi: 10.1093/ije/26.3.592. [DOI] [PubMed] [Google Scholar]
- Sundberg M., Lofgren H. Absorptive capacity and achieving the MDGs: the case of Ethiopia. In: Isard P., Lipschitz L., Mourmouras A., Yontcheva B., editors. The Macroeconomic Management of Foreign Aid: Opportunities and Pitfalls. International Monetary Fund; Washington, DC: 2006. pp. 141–167. [Google Scholar]
- Thomas D., Frankenberg E. Health, nutrition and prosperity: a microeconomic perspective. Bulletin of the World Health Organization. 2002;80:106–113. [PMC free article] [PubMed] [Google Scholar]
- Van der Hoeven, R., 1987. Planning for basic needs: a basic needs simulation model applied to Kenya. Ph.D. Thesis, Vrije Universiteit Amsterdam. Free University Press, Amsterdam.
- Van der Hoeven R. Gower; Aldershot: 1988. Planning for Basic Needs: A Soft Option or a Solid Policy? A Basic Needs Simulation Model Applied to Kenya. [Google Scholar]
- Vianen, J.G., Waardenburg, J.G., 1975. Integration of health care into a multi-sector model: with a quantification for Tanzania. Discussion Paper 29. Centre for Development Planning, Erasmus University Rotterdam.
- Wallace P. The health of nations: a survey of health-care finance. The Economist. 2004:2004. [Google Scholar]


