Abstract
A cross-classified and multiple membership Cox model was applied to calf mortality data from Western Canada, where 23,409 calves from 174 herds were followed for up to 180 days after calving. The herds were cross-classified by 49 veterinary clinics and 9 ecological regions and in a multiple membership relation to the veterinary clinics, resulting in a 3-level cross-classified and multiple membership data structure. The model was formulated in a mixed-effects Poisson model framework with normally distributed random effects, and was fitted to the data by Bayesian Markov Chain Monte Carlo (MCMC) estimation. Important fixed effects included whether the calf was a twin, calf gender, assistance at calving, cow age, average temperature the first week after calving, the percentage of the herd that had already calved, whether calf shelters were provided, whether cow-calf pairs were moved to a nursery area, and whether any animals were purchased into the herd at or near the time of calving. The analysis demonstrated a greater variation among herds than among both ecological regions and veterinary clinics. Further, a simulation study for a setting similar to the real data gave evidence that the used approach provides valid estimates.
Keywords: Beef calf mortality, Multiple membership models, Frailty Cox model, Cross-classified random effects, MCMC estimation
1. Introduction
Researchers in veterinary epidemiology are often interested in modelling hierarchical data with a time-to-event response variable. Hierarchical time-to-event models, also referred to as hierarchical survival or frailty models, can be used with nested data structures (e.g. animals nested within herds and herds located in different ecological regions) commonly found in veterinary science. One potential limitation of nested frailty models typically used for hierarchical survival data, however, is that they are designed to be used with perfectly hierarchical survival data, but in reality not all data structures found in the veterinary sciences are perfectly hierarchical. If in the previous example (some) herds are serviced by multiple veterinary clinics, an imperfect hierarchical data structure is present where the lower level units (herds) are members of multiple higher level units (clinics) simultaneously. This structure is called a multiple membership data structure (Browne et al., 2001). In addition, different classifications may not be hierarchically nested in each other; in our example, herds serviced by a given clinic could be located in different ecological regions. This would mean that clinics are not hierarchically nested within regions, and the two factors should instead be viewed as (partially) cross-classified. In summary, the structure described corresponds to a 3-level cross-classified and multiple membership data structure (Browne et al., 2001).
Cross-classified and multiple membership (CMM) models have been proposed to account for such data structures (Browne et al., 2001, Fielding and Goldstein, 2006). The CMM model uses weights for multiple membership and takes into account cross-classified factors that might arise in the data. A few studies in veterinary epidemiology have used the CMM model with different response variables. Browne et al. (2001) applied a CMM model with a binary response to Danish poultry salmonella outbreak data. Masaoud et al. (2011) fitted a CMM logistic regression model to a dataset from aquaculture. Goldstein et al. (2002) introduced a linear response example of a multiple membership model for the milk yield of cows.
Many studies have shown that ignoring multiple membership or cross-classified data structure in the analysis can lead to invalid inference about the importance of the relevant data structure on the outcome of interest. For instance, Meyers and Beretvas (2006) and Luo and Kwok (2009) showed that ignoring one of the cross-classified factors in linear models results in biased estimation in the variance components and in the standard error of the regression coefficients. Results from Goldstein et al. (2007) demonstrated that using traditional models that ignore the multiple membership in the analysis when it is present underestimate the variance at the multiple membership level. In addition, models that take into account the multiple membership structure give a better fit than models that ignore such structures. Recently, a simulation study conducted by Chung and Beretvas (2012) showed that ignoring multiple membership structure causes bias in the estimates of the regression coefficients and the variance component at the multiple membership level.
Despite the availability of veterinary data with CMM structure, few researchers have applied CMM models in veterinary medicine, and to our knowledge no studies have used a CMM model when the response variable is time-to-event. This could be due to complex estimation techniques for survival models with random effects (frailty models).
A review of the literature also suggested the need to re-examine the individual cow, herd management, and environmental factors associated with mortality in beef calves using a dataset with both detailed individual animal data and a relatively large number of herds. Many of the existing reports focus on calf loss at birth or in the perinatal period. While there are a number of observational studies published documenting calf loss after the perinatal period, most studies are either longitudinal studies from single research facilities focussing on individual animal attributes (Patterson et al., 1987, Azzam et al., 1993, Wittum et al., 1993), surveys with some data on individual animal attributes but a relatively small number of privately owned herds (Wittum et al., 1994, Ganaba et al., 1995), or herd level surveys with limited or no individual animal data (Schumann et al., 1990; Mathison, 1993, Dutil et al., 1999). Because previous studies have not taken the time to calf loss into account in the analysis, we found no reports that look objectively at when individual risk factors are of greatest risk to calf survival.
The first objective of the study is to explore and demonstrate the use of Poisson generalized linear mixed models (GLMMs) in Bayesian framework for estimating a Cox model with cross-classified and multiple membership frailties, and apply the approach to a large observational dataset on calf mortality. The second objective is to simultaneously examine the individual, herd management, and environmental factors associated with beef calf mortality in Western Canada and, where appropriate, to estimate the age period where calves are most at risk.
2. Materials and methods
2.1. Data
The data originated from the Western Canada beef productivity study (Waldner, 2008) which collected information on calf loss and mortality in beef cattle in Western Canada. We studied mortality in calf beef cattle from January to June 2002 (180 days) which included a total of 24,647 calves and 971 cases of calf mortality from herds with complete local meteorological data. Calves with invalid values or missing information were excluded from the analysis. This eliminated about 5% of observations including 74 cases of mortality. This strategy resulted in 23,409 calves, with 897 of these calves experiencing the event of interest. The event was defined as a case of calf mortality that happened at least 1 h after birth; the event time was defined as the time from calving to death (recorded in days), and for those calves that died on the same day of birth the event time was set at 0.5. Calves that were sold during the follow-up period or survived until the end of the follow-up period were considered right censored observations. Because the observation period ended at the same time for all calves (June 30th), but all calves were born at different times during the calving season, we recognized the need for an analysis technique that accounted for different follow up times across the study population.
The dataset had a special hierarchical structure. In addition to calves being hierarchically nested within 174 herds, herds were cross-classified by 49 veterinary clinics and 9 ecological regions (Waldner, 2008), and about 8% of the herds were registered in two veterinary clinics, resulting in a 3-level cross-classified and multiple membership data structure (Fig. 1 ).
Fig. 1.
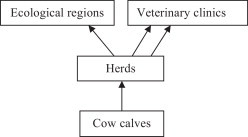
Calf mortality data structure: calves (level 1) nested in herds (level 2), herds in a multiple membership to veterinary clinics and cross-classified by ecological regions and veterinary clinics (level 3).
2.2. Statistical modelling
2.2.1. Frailty models for hierarchical survival data
Consider the example of 3-level hierarchical survival data with N animals from multiple herds and these herds located in different ecological regions. Let T i and C i denote the survival and censoring times, respectively, for animal i. The response time for animal i is Y i = min(T i, C i) and the event indicator δ i takes the value 1 if the event of interest occurs and 0 otherwise. A commonly used model for such data is a Cox proportional hazards model with two nested frailties and acting multiplicatively on the baseline hazard (Rondeau et al., 2006) to take into account unmeasured herd and ecological region factors (the numbers in superscript parentheses represent the hierarchical levels). The conditional hazard function of the nested frailty model can be written as,
| (1) |
where λ 0(·) is the baseline hazard, and are two nested frailties following a particular probability distribution, X i is the covariate vector for the ith animal, and β is the corresponding vector of regression parameters. Model (1) can be rewritten in random effects context as,
| (2) |
where the frailty and random effect terms are linked by: u = exp(b).
One approach to fit model (2) is to utilize the relationship between the Cox model and a suitable Poisson model to translate the nested random effects Cox model into a nested random effects Poisson model (Rabe-Hesketh and Skrondal, 2012, chapter 15). As shown by Ma et al. (2003) and Feng et al. (2005), the likelihood function of Cox models with normal random effects (i.e., lognormal frailties) is proportional to the likelihood function of such random effects Poisson models. In detail, Cox models with normal random effects can be estimated as generalized linear mixed models (GLMMs) with a binary Poisson count response and a specific offset. The approach requires each observation in the data to be split into a multiple records based on the complete set of failure times in the dataset, and the offset equals the logarithm of the length of each time interval. The baseline hazard is modelled as a smooth function of time, in our case a 4th order polynomial as suggested by Rabe-Hesketh and Skrondal (2012).
Using available software for GLMMs, random effects Cox models can be fitted to survival data with several hierarchical levels and more complex data structures.
2.2.2. Cross-classified and multiple membership frailty models
The full structure of the calf mortality data described in Section 2.1 can be taken into account through a CMM random effects Cox modelling approach. The model accounts for the cross-classified factors of veterinary clinics and ecological regions, and uses weights for the multiple membership relation of herds to the veterinary clinics so that each herd will have weights for all the veterinary clinics that the herd is serviced by. The CMM Cox model can be written as,
| (3) |
where is the herd random effect, is the ecological region random effect, and the term involves a set of veterinary clinic random effects and weights assigned to each herd for their veterinary clinic group membership with .
Assuming normal random effects, the CMM Cox model can be estimated in a Poisson modelling framework for a survival time response as described in Section 2.2.1 using Markov Chain Monte Carlo (MCMC) techniques and Bayesian inference.
2.2.3. MCMC estimation and Bayesian inference
MCMC estimation employed three chains for diagnostic purposes, 100,000 estimation samples, and a burn-in of 5,000 samples. The three chains used different initial values, were specified in Stata/MP 12.1 and run one at a time in MLwiN software version 2.25 called from within Stata using the runmlwin utility (Leckie and Charlton, 2013). The vague priors were: a uniform prior p(β) ∝ 1 (flat prior) for the fixed effect parameters and a gamma (10−3, 10−3) for the inverse variances of the normal random effects. The Raftery–Lewis diagnostic (Raftery and Lewis, 1992) provided in MLwiN and the ratio rule of Monte Carlo (MC) error to the standard deviation (Lunn et al., 2013, p. 78) were used to determine the needed number of MCMC samples. The ratios of the MC error to the standard deviations for all model parameters were all less than 5%. Also the Raftery–Lewis diagnostic indicated that 100,000 samples were sufficient for estimation. Other Markov chain diagnostics, including all those given by Gelman and Rubin (1992) and implemented in R software version 2.15.3 (coda package), were carried out and found to be satisfactory.
Significance for single parameter effects in Bayesian inference was assessed using 95% credible intervals (whether or not zero lies in such intervals) or by computing a tail probability of the posterior distribution; such probability is analogous to P-value in frequentist statistics.
2.3. Data analysis
2.3.1. Model building
Descriptive analyses were carried out for explanatory variables listed in the dataset to check distributions and invalid values, as well as to identify collinearity among variables. To facilitate the first stages of the analyses, unconditional (simple) associations between each explanatory variable and the outcome were obtained from a standard Cox regression model with the Breslow method for ties. A liberal p-value of 0.20 was chosen to determine potential important explanatory variables. Using lowess smoothing graphs, functional forms of continuous variables were evaluated by plotting the variable in question against martingale residuals, and if necessary appropriate transformation was performed or a quadratic term was added to the model.
The second step of the model building consisted in a stepwise backward selection for the standard Cox model with p < 0.10 as inclusion criterion since a hierarchical Cox model was impractical and very time consuming. All two-way interactions between predictors retained in the model were evaluated and tested for statistical significance; interactions that turned out significant and biologically meaningful were kept in the model. During the selection process, the non-significant predictors were rechecked for confounding and a change of 20% or more in the parameter estimate was used as a criterion for identifying confounders. The proportional hazards assumption was evaluated for model predictors individually and globally by a statistical test based on the scaled Schoenfeld residuals (Dohoo et al., 2009). To account for non-proportional hazards for some predictors, the dataset was split at events, and an interaction term between the predictor in question and the logarithm of time was added to the model. The assumption of independent censoring was checked by sensitivity analysis comparing the change of positive and negative correlation scenarios between censoring and new mortality events. All descriptive statistics and model building were performed in Stata/MP 12.1.
2.3.2. Accounting for data structure
The CMM structure of the data was accounted for by including random effects for herds, veterinary clinics and ecological regions, as described in Section 2.2.2. The multiple membership weights of veterinary clinics servicing a given herd were computed as proportions of visits of that herd by each clinic, out of the total number of visits to the herd.
3. Results of calf mortality data analysis
3.1. Descriptive statistics
The overall mortality observed in the 174 herds was 3.8% (897/23,409) with a 90% range across herds of (0.5%, 7.5%), and the percentages of calf loss occurred within the first 1 day, 3 days, 7 days, 14 days and 30 days at risk were, respectively, 19% (171/897), 29% (258/897), 40% (362/897), 55% (496/897) and 68% (614/897). The medians of event time (calf death) and censoring time were 12 and 104 days, respectively. The full list of predictor variables included in the analysis is shown in Table 1 (animal-level predictors) and Table 2 (herd-level predictors) with descriptive statistics.
Table 1.
Descriptive statistics for animal-level predictors in the calf mortality dataset (23,409 calves from 174 herds) including the proportion of calves and the probability of calf mortality for each categorical variable, as well as the mean and standard deviation (sd) for continuous variables.
| Predictor | Proportion | Mortality probability |
|---|---|---|
| Calf gender | ||
| Female | 0.48 | 0.035 |
| Male | 0.52 | 0.041 |
| Twin | ||
| Single | 0.96 | 0.037 |
| Twin | 0.04 | 0.069 |
| Cow age at calving | ||
| ≤2 years old | 0.18 | 0.049 |
| 3 years old | 0.17 | 0.046 |
| 4 years old | 0.12 | 0.036 |
| 5–10 years old | 0.45 | 0.032 |
| >10 years old | 0.08 | 0.044 |
| Cow breed type | ||
| British | 0.43 | 0.038 |
| Continental | 0.49 | 0.037 |
| Cross | 0.08 | 0.046 |
| Calving assistance | ||
| Unassisted | 0.91 | 0.037 |
| Easy pull | 0.05 | 0.040 |
| Hard pull | 0.02 | 0.102 |
| Malpresentation | 0.01 | 0.071 |
| Surgery | 0.01 | 0.067 |
| Cow body condition at pregnancy test | ||
| BCS < 5 | 0.09 | 0.046 |
| BCS ≥ 5 | 0.91 | 0.038 |
| Cow pre-calving body condition score | ||
| BCS < 5 | 0.04 | 0.047 |
| BCS ≥ 5 | 0.96 | 0.038 |
| Cow problems following calvinga | ||
| Yes | 0.01 | 0.052 |
| No | 0.99 | 0.038 |
| Predictor | Mean (sd) (Cases) |
Mean (sd) (Non-cases) |
|---|---|---|
| Average temperature (°C) for the first 7 days post calving | −7.353 (8.198) | −6.362 (8.483) |
| Within-herd calving proportion at calvingb | 0.516 (0.291) | 0.514 (0.286) |
Cow problems including retained placentas, uterine prolapses, and metritis.
Computed as a number of new calves at a particular calving day divided by the total number of calves in a herd.
Table 2.
Descriptive statistics for herd-level predictors in the calf mortality dataset (174 herds) including the proportion of herds and mortality probability for each categorical variable.
| Predictor | Proportion | Average of mortalitya | |
|---|---|---|---|
| Cows due to calve and cows that have calved are together | (Yes) | 0.37 | 0.037 |
| (No) | 0.63 | 0.039 | |
| Heifers due to calve before rest of the cow herd | (Yes) | 0.29 | 0.042 |
| (No) | 0.71 | 0.037 | |
| Provide shelters for calves separate from cows and heifers | (Yes) | 0.79 | 0.038 |
| (No) | 0.21 | 0.041 | |
| Move cow-calf pairs to a nursery pasture within 48 h of birth | (Yes) | 0.70 | 0.038 |
| (No) | 0.30 | 0.040 | |
| Buy foster calves (Holstein bull calves) | (Yes) | 0.10 | 0.038 |
| (No) | 0.90 | 0.038 | |
| Were any animals purchased in the month prior to or during calving | (Yes) | 0.76 | 0.039 |
| (No) | 0.24 | 0.035 | |
| Cows vaccinated for E. coli prior to calving | (Yes) | 0.49 | 0.040 |
| (No) | 0.51 | 0.037 | |
| Heifers vaccinated for E. coli prior to calving | (Yes) | 0.53 | 0.038 |
| (No) | 0.47 | 0.038 | |
| Cows vaccinated for rota/corona virus prior to calving | (Yes) | 0.50 | 0.038 |
| (No) | 0.50 | 0.039 | |
| Heifers vaccinated for rota/corona virus prior to calving | (Yes) | 0.53 | 0.037 |
| (No) | 0.47 | 0.040 |
Average of within herd mortality.
Predictors selected for further consideration during the model building process (p < 0.20) were: whether the calf was a twin, calf gender, calving assistance, cow age, cow breed type, cow body condition at pregnancy test, within-herd calving proportion, mean 7-day temperature, shelters provided for calves separate from cows and heifers, cow-calf pairs moved to a nursery pasture within 48 h of birth, and whether any animals were purchased in the month prior to or during calving. The variables of twin, surgical assistance at calving, and the mean 7-day temperature after calving were identified as time-varying effects.
3.2. Multivariable analysis
3.2.1. Model comparisons
In the Poisson modelling approach, the best model fit (i.e. the model with the smallest deviance information criteria (DIC); Spiegelhalter et al., 2002) was obtained using the logarithm of time to model both time-varying predictor effects and the baseline hazard.
To demonstrate the utility of CMM modelling for the calf mortality data, results are shown for three survival models including a standard Cox model neglecting the hierarchical structure present in the data (model 1), a Cox model with random herd effects ignoring the top hierarchical level in the data (model 2), a CMM Cox model taking into account the full hierarchical data structure (model 3). The three models were fitted to the dataset where continuous predictors were centred at the mean and the predictors twin, calving assistance and average of 7-day temperature were modelled with time-varying effects (by adding interactions with log of time). Results from the final models are tabulated in Table 3 .
Table 3.
Parameter estimates for the analysis of calf mortality dataset: the mean, median, and standard deviation (sd) of posterior distribution from a standard Cox model (model 1), a Cox model with random herd effect (model 2), and a CMM Cox model (model 3).
| Predictor/parametera | Model 1 |
Model 2 |
Model 3 |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Median | sd | Mean | Median | sd | Mean | Median | sd | |
| Twin | |||||||||
| Twin vs. single | 0.145 | 0.149 | 0.199 | 0.205 | 0.208 | 0.197 | 0.213 | 0.218 | 0.202 |
| Twin × Tb | −0.338 | −0.338 | 0.077 | −0.331 | −0.331 | 0.075 | −0.331 | −0.330 | 0.077 |
| Calf gender | |||||||||
| Male vs. female | 0.154 | 0.154 | 0.068 | 0.151 | 0.152 | 0.068 | 0.150 | 0.150 | 0.068 |
| Calving assistance | |||||||||
| Easy pull vs. unassisted | −0.105 | −0.103 | 0.150 | −0.050 | −0.048 | 0.151 | −0.049 | −0.046 | 0.150 |
| Hard pull vs. unassisted | 0.872 | 0.877 | 0.169 | 0.921 | 0.924 | 0.173 | 0.917 | 0.920 | 0.174 |
| Malpresentation vs. unassisted | 0.532 | 0.541 | 0.253 | 0.535 | 0.543 | 0.251 | 0.537 | 0.546 | 0.254 |
| Surgery vs. unassisted | −1.304 | −1.202 | 0.980 | −1.243 | −1.131 | 0.976 | −1.198 | −1.090 | 0.960 |
| Surgery × T | −0.737 | −0.720 | 0.300 | −0.743 | −0.725 | 0.298 | −0.739 | −0.721 | 0.294 |
| Cow age | |||||||||
| ≤2 years old vs. 5–10 years old | 0.401 | 0.402 | 0.095 | 0.382 | 0.381 | 0.096 | 0.384 | 0.384 | 0.096 |
| 3 years old vs. 5–10 years old | 0.340 | 0.341 | 0.095 | 0.342 | 0.342 | 0.095 | 0.349 | 0.350 | 0.096 |
| 4 years old vs. 5–10 years old | 0.099 | 0.100 | 0.113 | 0.121 | 0.121 | 0.112 | 0.124 | 0.126 | 0.113 |
| >10 years vs. 5–10 years old | 0.332 | 0.333 | 0.126 | 0.308 | 0.309 | 0.127 | 0.305 | 0.307 | 0.127 |
| Within-herd calving prop. | |||||||||
| Linear | 0.631 | 0.631 | 0.128 | 0.759 | 0.758 | 0.137 | 0.767 | 0.766 | 0.136 |
| Quadratic | 1.041 | 1.040 | 0.467 | 1.233 | 1.232 | 0.473 | 1.243 | 1.243 | 0.474 |
| Mean 7-day temperaturec (°C) | −0.030 | −0.030 | 0.006 | −0.090 | −0.090 | 0.006 | −0.100 | −0.100 | 0.006 |
| Mean 7-day temperaturec × T | 0.100 | 0.100 | 0.003 | 0.110 | 0.110 | 0.003 | 0.110 | 0.110 | 0.003 |
| Provide sheltersd | |||||||||
| Yes vs. no | −0.309 | −0.310 | 0.083 | −0.325 | −0.325 | 0.144 | −0.240 | −0.240 | 0.145 |
| Move calf pairse | |||||||||
| Yes vs. no | −0.306 | −0.307 | 0.074 | −0.244 | −0.245 | 0.125 | −0.237 | −0.237 | 0.126 |
| Animals purchasedf | |||||||||
| Yes vs. no | 0.258 | 0.257 | 0.085 | 0.243 | 0.242 | 0.145 | 0.285 | 0.283 | 0.141 |
| Herd variance | 0.334 | 0.327 | 0.070 | 0.272 | 0.267 | 0.062 | |||
| Veterinary clinic variance | 0.024 | 0.012 | 0.030 | ||||||
| Ecological region variance | 0.099 | 0.073 | 0.100 | ||||||
| DIC | 14724.2 | 14566.1 | 14558.5 | ||||||
Coefficients for the 4th order polynomial of log(time) represents the baseline hazard not shown.
T is a standardized log time (log time-mean/sd) or T = [log(time in days) − 3.604]/1.062.
Coefficients × 10.
Provide shelters for calves separate from cows and heifers.
Move cow–calf pairs to a nursery pasture within 48 h of birth.
Animal purchased in the month prior to or during calving.
In model 2, the random herd variance parameter was estimated at 0.334 (posterior mean), with 95% credible interval (95% CI) of [0.215, 0.484]. When accounting for the full hierarchical data structure (model 3), the random herd variance estimate decreased by 19% to 0.272 [95% CI; 0.168, 0.409]. The variance for ecological regions was estimated to be about four times greater than the variance for veterinary clinics with corresponding posterior standard deviations as large as the point estimates.
Model 3 explained a greater portion of the survival outcome variation than model 2 due to handling the third hierarchical level in the dataset (the veterinary clinics and the ecological regions). The DIC was the smallest for model 3 among the three models indicating a better model fit.
The standard Cox model (model 1) estimated with a Bayesian approach as a Poisson model gave similar estimates to those from a Cox model using a frequentist (classical) approach (results not shown). Some differences in estimates were seen compared with the random effects models (models 2 and 3). Further, the standard errors of regression coefficients from the simple Cox model ignoring the data structure were smaller than those from the CMM Cox model, especially (and as expected) for the herd-level predictors.
3.2.2. Interpretations of effects from model 3
In model 3, the effect of twin birth on the hazard of calf mortality depended on time and remained statistically significant until day 22 from calving. The hazard ratio (HR) for twin-birth calves relative to single-birth calves of age 1 day was estimated to be 3.80 with 95% credible interval (95% CI) of [2.70, 5.25]. Similarly, the HRs of twin-birth calves compared with single-birth calves of age 7, 22 and 60 days were estimated at 2.07 [95% CI; 1.58, 2.68], 1.45 [95% CI; 1.02, 2.01] and 1.06 [95% CI; 0.66, 1.63], respectively, suggesting that the hazard of mortality at any given time before 60 days of age was highest for twin-birth calves, and such that hazard ratios declined over time until vanishing after about two months of age. The HR for male (vs. female) calves was 1.16, 16% higher hazard in males than in females at any point in time.
For calving assistance, the HR of calves that were born with a hard pull or malpresentation relative to calves born without calving assistance were 2.50 and 1.71, respectively, and thus associated with substantially higher hazard of mortality. The effect of Caesarean section surgery vs. unassisted varied with time: days 1, 2, 3 and day 7 had estimated HRs of 3.70 [95% CI; 1.44, 7.98], 2.29 [95% CI; 0.93, 4.82], 1.72 [95% CI; 0.65, 3.78], and 0.96 [95% CI; 0.26, 2.52], respectively, indicating that the hazard of mortality for calves with surgical assistance at calving was higher immediately after calving and statistically significant on day 1 and then dropped down quickly.
After accounting for the other risk factors in the final model, the HRs for calves from cows aged 2, 3, 4 and greater than 10 years at calving relative to those from mature cows (5–10 years old) were estimated, respectively, to be 1.47, 1.42, 1.13 and 1.36. These results suggest that the hazard of death at any given time was greatest for calves from young (2–3 years old) and old (>10 years old) cows, but that there was little difference in the hazard for calves of cows aged 4 years compared with calves from mature cows.
In addition, the hazard of calf mortality increased as the calving season progressed with an increasing number of calves in the herd. For instance, when the proportion of cows calving in a herd reached 0.11 and 0.91 (10% and 90% percentiles, respectively), the HRs for mortality were estimated, respectively, to be 0.90 and 1.64 compared with a proportion of 0.51 (50% percentile) indicating that the hazard of mortality increased with increasing number of births in the herd.
Modelling temperature as the mean of first 7 days post calving gave a better DIC than the temperature on day of calving. Very cold weather was associated with a high hazard of calf mortality and such hazard decreased over time. For example, when the averages of 7-day temperature post calving was 20, 10 and 5 °C below the mean (−6.42 °C), the HR of mortality relative to the mean would be, respectively, 2.53 [95% CI; 1.86, 3.36], 1.57 [95% CI; 1.36, 1.83] and 1.24 [95% CI; 1.17, 1.35] for calves of age 24 h; and 1.70 [95% CI; 1.39, 2.08], 1.30 [95% CI; 1.18, 1.44] and 1.13 [95% CI; 1.08, 1.20] for calves of 7 days of age; and 1.27 [95% CI; 1.01, 1.61], 1.12 [95% CI; 1.00, 1.27] and 1.06 [95% CI; 1.00, 1.13] for calves of 30 days of age, suggesting that the hazard of calf mortality was greatest if calving took place in a very cold weather. After about month of age, the time varying effect of temperature was statistically non-significant.
Three herd-level predictors related to biosecurity practices were also important predictors of calf mortality. The estimated HR was lower (HR = 0.79 with a probability analogous to P-value of 0.048) for calves from herds where the owner provided shelters for calves separate from cows and heifers as well as for calves from herds where cow-calf pairs were moved to a nursery pasture within 48 h of birth (HR = 0.79 with probability of 0.031). Calves from herds where any animals were purchased in the month prior to or during calving were at higher risk of death (HR = 1.33 with probability parallel to P-value of 0.020).
3.2.3. Non-significant effects
The variables cow breed type and cow body condition at pregnancy test had no effect on the hazard of calf mortality (i.e., these predictors did not contribute substantially to the model DIC) and were not included in the multivariable model. The HRs for continental and cross breeds relative to British types of breed after accounting for other risk factors were estimated, respectively, to be 1.03 [95% CI; 0.85, 1.25] and 1.13 [95% CI; 0.81, 1.58], whereas the HRs for cow body condition score at pregnancy test and pre-calving (<5 vs. ≥5) were 1.05 [95% CI; 0.82, 1.33] and 0.99 [95% CI; 0.72, 1.36], respectively.
4. Simulation studies
Two simulation studies were conducted to evaluate the performance of the cross-classified and multiple membership Cox modelling approach discussed above. In simulation study I, the data structure and the magnitudes of variation at different levels were similar to the calf mortality dataset. In simulation study II, a more pronounced multiple membership data structure and larger variations at different levels were considered. Both simulation studies used 200 simulated datasets.
In order to reduce the computing time of the simulations, the simulation structures were based on a subset of the real data after eliminating randomly 75% of non-cases. This reduction increased the prevalence of calf mortality to 14%. The reduced dataset had 6,519 observations and the same hierarchical structure as the full data. Analysis of the reduced data showed only minor changes in model estimates compared with the results of the full data (results not shown).
4.1. Data structure and model parameters
Similar to the reduced real dataset, a total of 6,519 animals from 174 different herds (from 3 to 111 animals per herd) were considered. In simulation study I, the data structure and multiple membership weights were the same as in the real data. In simulation study II, herds were considered to be registered in 1, 2 and 3 veterinary clinics with proportions of 52%, 25% and 23%, respectively. One dichotomous animal-level predictor was used in the two simulation models. The true values of model parameters and other features for each simulation study are presented in Table 4 .
Table 4.
Model parameters and proportions of herds in a multiple membership with veterinary clinics used for simulation studies I and II based on the structure of calf mortality dataset.
| Feature | Simulation study I | Simulation study II |
|---|---|---|
| Fixed effect (β) | 0.150 | 1.000 |
| Herd variance () | 0.300 | 0.500 |
| Veterinary clinic variance () | 0.025 | 0.500 |
| Ecological region variance () | 0.100 | 0.500 |
| Baseline hazard parametersa (p, λ0) | (0.4, 0.019) | (0.4, 0.008) |
| Herds in a multiple membership | 8% | 52% |
Weibull distribution: p = shape, λ0 = scale.
4.2. Simulating data
Using the technique of Bender et al. (2005), 200 simulated datasets for each simulation study were generated from model (3) using R software version 2.15.3. In each dataset, the random herds, random veterinary clinics, and random ecological regions were generated independently from a normal distribution with mean of zero and variances , , and , respectively. The weights in simulation study II were assigned as follows: if a herd was registered in 3 veterinary clinics, weights for the first two clinics were randomly generated from a uniform distribution U(0, 1)/2 and the complement of the sum of these weights was assigned as weight for the third clinic; if a herd was serviced by 2 clinics the weight of the first clinic was randomly generated from U(0, 1) and the complement of that weight was the weight for the second clinic and 0 otherwise; and for herds that visited by one clinic a weight of 1 was assigned to that clinic and 0 otherwise. The fixed effect predictor was generated in each simulation from a Bernoulli distribution with a probability of 0.5.
The mortality time T i for animal i was randomly generated from a Weibull distribution with shape parameter P = 0.4 and scale parameter equal to the intensity λ i(t|.) defined in (3). The time at risk C i was randomly generated from a normal distribution with mean μ = 105 and standard deviation σ = 32, censored to the interval (0.5, 180). Censoring occurred when the mortality time T i was longer than the time at risk C i, i.e. Y i = min(T i, C i) and δ i = I(T i, C i). These simulation settings led to approximately 86% censoring animals which was equivalent to the censoring rate in the reduced version of the calf mortality data.
Finally, to reduce the computing time in the simulations, the MCMC sampler was run for 55,000 iterations in each simulated model of which the initial 5,000 iterations were discarded as burn-in. The same MCMC diagnostics as described in Section 2.2.3 were carried out for selected simulated datasets and all were satisfactory.
4.3. Calculating summary statistics
The posterior mean, median, standard deviation, and 95% CI end points for each simulated dataset were extracted, and averages and empirical standard deviations were computed across the simulated datasets. Absolute relative bias was computed as the absolute value of the difference between the averaged estimate and the true value divided by the true value, and the mean squared error (MSE) was computed as the average of the squared differences between the estimated values and the true value over the simulated datasets.
4.4. Simulation results
The results of the two simulation studies are presented in Table 5 . In simulation study I, the fixed effect β and the variance of random herd effect were estimated well with relative biases not exceeding 2%. Further, the “model-based standard errors” (posterior sd) of β was on average very close to its empirical standard deviation, and the probability converges of β and were somewhat over the nominal. For , and , the average posterior medians were very close to the true values, but the average posterior means were larger than the true values, with substantial relative biases of 48% and 35%, respectively. The estimate showed strongly CI over-coverage, whereas the estimate of had CI under-coverage. The mean squared errors were similar to the posterior-mean and posterior-median estimates of the β and , and smaller mean squared error for the posterior-median estimates of the and than for the posterior-mean estimates.
Table 5.
Results of simulation studies I and II based on the calf mortality dataset: average of the estimates (posterior mean and posterior median) with empirical standard deviations (Esd), 95% end point confidence intervals (95% CI), and of posterior standard deviation (sd) over 200 simulated data sets, as well as probability coverage, absolute relative bias and mean squared error (MSE) for posterior mean-based and median-based estimates.
| Parameter | True value | Estimate |
95% CI end points | Prob. cover | Abs. relative bias |
MSE (×1000) |
||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean (Esd) | Median (Esd) | sd | Mean | Median | Mean | Median | ||||
| Simulation study I | ||||||||||
| β | 0.150 | .153 (.061) | .153 (.061) | .067 | (.022, .284) | 97% | .020 | .020 | 0.370 | 0.371 |
| 0.300 | .299 (.064) | .294 (.063) | .066 | (.187, .443) | 97% | .003 | .020 | 0.407 | 0.403 | |
| 0.025 | .037 (.032) | .027 (.031) | .036 | (.002, .131) | 99% | .480 | .080 | 0.115 | 0.094 | |
| 0.100 | .135 (.099) | .100 (.080) | .127 | (.021, .454) | 92% | .350 | .000 | 1.088 | 0.641 | |
| Simulation study II | ||||||||||
| β | 1.000 | .990 (.074) | .989 (.074) | .075 | (.844, 1.137) | 95% | .010 | .011 | 0.562 | 0.561 |
| 0.500 | .517 (.120) | .504 (.118) | .121 | (.317, .489) | 95% | .034 | .008 | 1.453 | 1.381 | |
| 0.500 | .509 (.216) | .480 (.210) | .205 | (.194, .989) | 91% | .018 | .040 | 4.669 | 4.411 | |
| 0.500 | .645 (.362) | .510 (.295) | .516 | (.169, 1.930) | 95% | .290 | .020 | 15.17 | 8.656 | |
In simulation study II, the β, and were estimated very well based on both the posterior means and posterior medians with relative biases of at most 1.1%, 3.4% and 4%. For , estimation based on the posterior medians performed better than for posterior means. The CI converges of all model estimates were good except for where CI under-coverage was observed.
5. Discussion
5.1. Calf mortality data
The calf mortality rate reported for these herds is slightly higher than in most previous Canadian studies with exception of one from Quebec (McDermott et al., 1991, Dutil et al., 1999, Waldner, 2001). However, our analysis included all losses from 1 h after birth, rather than from 24 h of age. When the calf losses after 24 h were summarized for the present study, the average risk of mortality was 3.1%. In an on-farm study of 7 Alberta herds over a 12-year period, Waldner (2001) and Waldner et al. (2001) reported median risks of calf mortality between 24 h of age and weaning of 3.3% and 3.5%, similar to earlier reports from Ontario of 3.3% for first-calf heifers and 2.6% for mature cows (McDermott et al., 1991). The age distribution of calf deaths was also similar to what was expected based on other reports. The 1986–1987 survey by Alberta Agriculture found that 52% of deaths of calves occurred in the first 14 days compared to 55% in the current study (Mathison, 1993). The mortality rates for calves that died between 1 h and 3 days of age (1.1%) and in the first 30 days (2.6%) were slightly higher than the 0.7% and 1.6% reported from a 2010 mail survey of 303 herds from western Canada (Waldner et al., 2013).
The large observational data set and time-to-event analyses provided us with a unique opportunity for an intensive assessment of risk factors for calf mortality reported in previous papers, as well as an opportunity to explore new environmental and herd management variables. For example, an association between twin birth and average calf mortality from 12 h to 45 days was reported in a previous study of 10 herds in Colorado (Wittum et al., 1994). Gregory et al. (1996) also reported higher survival rates for singles as compared to twins from one research herd at 72 h and 150 days when there was no requirement for assistance. Our study found that while the death rate is highest for twins in the perinatal period, there is a significant increased risk of loss in privately owned commercial calves up to 22 days of age after accounting for other risk factors.
The increased risk of mortality for male calves remained constant throughout the observation period similar to what was observed using unconditional analysis by Patterson et al. (1987). Azzam et al. (1993) also reported an increase in mortality for bull calves after accounting for dystocia and the relative calf size. The paper is different in that the authors used data from a research centre and included all calves that were alive at the start of calving.
The higher mortality rate for calves classified as having a hard pull or malpresentation at birth did not decrease during the study period. In contrast, the increased death rate for calves born by Caesarean section was only significant for day 1 and was only elevated for the first week. While other studies have identified dystocia as a risk factor for perinatal calf mortality (Wittum et al., 1994, Ganaba et al., 1995), only one study in a single research herd specifically explored the longer term effects on calf survival using individual data (Gregory et al., 1996). Dutil et al. (1999) reported a weak association between herd dystocia rates and preweaning mortality in 148 Quebec herds, but did not account for confounding by individual factors such as parity.
After accounting for all other risk factors, the only important cow attribute was age. Previous studies have identified increased postnatal calf loss from heifers in addition to the well-established increased risk of loss in heifers’ calves that died at or very near birth (Wittum et al., 1994). Our study is unique in that higher risks of postnatal calf mortality were also identified for cows having their second calf and cows ≥10 years old. The increased risk of postnatal calf mortality for each cow age group was consistent throughout the follow up period. Others looking at cow age either had a smaller sample size and did not see a difference (Wittum et al., 1994) or looked at all mature cows together and did not differentiate older cows (Azzam et al., 1993).
After accounting for cow age and assistance at calving there was no difference in calf survival across the range of observed body condition scores. While others have documented an association between poor nutrition in the last trimester and calf mortality due to scours (Corah et al., 1975), <5% of cows in this cohort were thin at calving, thus providing very little power to examine this hypothesis.
While a number of authors have suggested that as the calving grounds become more contaminated the risks of calf morbidity and mortality increase, there have been no previously studies that test this hypothesis across a large number of herds. Schumann et al. (1990) reported that as the proportion of the nursing area that was poorly drained, wet and muddy increased the odds of mortality from diarrhoea also increased. In this study, we looked at the contextual effect of when the calf was born in relation to the other calves in the herd. The idea was simply that calves that are born later in their cohort are potentially exposed to a greater build-up of pathogens. In this study, there was a substantial increase in the mortality rate for calves born after the half-way point in each herd. Clement et al. (1995) had previously documented increased odds of developing diarrhoea in calves born after the median calving date. They hypothesized that the numbers of diarrhoea-causing pathogens increased during the calving season.
While some previous studies have used postmortem findings (Bellows et al., 1987) and owner reported cause of loss to document the importance of calf deaths due to cold weather (Wittum et al., 1993), only one other study has actually looked at meteorological conditions (Azzam et al., 1993). This study like ours found an increased calf mortality rate for calves born under cold conditions. Because the other study was limited to a single research herd, they also had access to local precipitation data which were not consistently available in the present analysis. Azzam et al. (1993) used logistic regression to examine effect of temperature on the day of birth on total risk of calf loss from birth to weaning. However, this study did not account for repeated measures in the analysis or consider whether the effect of meteorological conditions at birth changed with calf age. We used the average temperature for the first week after birth and demonstrated that for calves born in very cold weather (<−10 °C), the associated hazard extended through the first month of life.
Because of the relatively large number of herds compared to previous studies we were also able to evaluate a number of common management and biosecurity practices. In our study, herd owners that moved calves out of the calving area and to a nursery pasture within 48 h had lower calf losses. This practice removes cow-calf pairs from the contaminated environment and prevents crowding in the calving area by dispersing newborn calves soon after birth (Radostits and Acres, 1980). The use of calf shelters which are not accessible to cows and heifers (Radostits and Acres, 1980, Olson, 1986) was also associated with decreased calf mortality. Schumann et al. (1990) reported that increasing the nursery shelter area helped to protect against calf diarrhoea, but did not differentiate between shelters accessible to both cows and calves and shelters accessible to just calves.
Finally, herds where any cattle were purchased in the month before or during calving had higher calf mortality rates than those that did not. Schumann et al. (1990) reported a similar unconditional association between replacing dead calves with purchased calves less than one month of age and higher odds of calf mortality. We did not see an increased rate of loss specifically associated with the purchase of foster calves; however, this practice was uncommon in the current study.
The analysis of calf mortality data demonstrated a larger variation between herds than between both veterinary clinics and ecological regions, and a clear improvement in model fit after accounting for the variation between veterinary clinics and ecological regions.
5.2. Simulations
In the setting similar to the real data (study I), the results indicated that the proposed model performed well in estimating most of the model parameters if posterior medians were used for the inference and overestimated the between-clinic and between-ecoregion variances when the inference was based on posterior means. The simulation study therefore supported our findings of relatively small variance components for veterinary clinics and regions in the real data. In addition, simulation study II showed that the estimation of between-clinic variance was improved in a more pronounced multiple membership structure and with larger variance components. Both simulation studies demonstrated difficulties with estimation of the between-ecoregion variance and its standard error, and this can probably attributed to the small number of ecologic regions.
We finally note that the performance of the proposed model and estimation can depend on many parameters, for instance, the censoring rate, the shape of baseline hazard, the number of clusters, the cluster size, and the magnitude of heterogeneity. A detailed exploration of how such parameters might affect performance is beyond the scope of the present study, but could be a topic for future investigation.
Conflict of interest
None.
Acknowledgements
This study is part of a research project funded and supported by the Libyan Ministry of Higher Education and Scientific Research (MOHESR). The data in this paper were collected as part of the field research activities for the Western Canada Study of the Animal Health Effects Associated with Exposure to Emissions from Oil and Natural Gas Field Facilities. Funding support was provided through the Western Interprovincial Scientific Studies Association (WISSA). The authors appreciate the dedication of all of the veterinarians and producers who contributed to this project.
References
- Azzam S.M., Kinder J.E., Nielsen M.K., Werth L.A., Gregory K., Cundiff E., Koch L.V.R.M. Environmental effects on neonatal mortality of beef calves. J. Anim. Sci. 1993;71:282–290. doi: 10.2527/1993.712282x. [DOI] [PubMed] [Google Scholar]
- Bellows R.A., Patterson D.J., Burfening P.J., Phelps D.A. Occurrence of neonatal and postnatal mortality in range beef cattle. I. Factors contributing to calf death. Theriogenology. 1987;28:573–586. doi: 10.1016/0093-691x(87)90274-3. [DOI] [PubMed] [Google Scholar]
- Bender R., Augustin T., Blettner M. Generating survival times to simulate Cox proportional hazards models. Stat. Med. 2005;24:1712–1723. doi: 10.1002/sim.2059. [DOI] [PubMed] [Google Scholar]
- Browne W., Goldstein H., Rasbash H. Multiple membership multiple classification (MMMC) models. Stat. Model. 2001;1:103–124. [Google Scholar]
- Chung H., Beretvas N. The impact of ignoring multiple membership data structures in multilevel models. Br. Math. Stat. Psychol. 2012;65:185–200. doi: 10.1111/j.2044-8317.2011.02023.x. [DOI] [PubMed] [Google Scholar]
- Clement J.C., King M.E., Salmon M.D., Wittum T.E., Casper H.H., Odde K.G. Use of epidemiologic principles to identify risk factors associated with the development of diarrhea in calves in five beef herds. J. Am. Vet. Med. Assoc. 1995;207:1334–1338. [PubMed] [Google Scholar]
- Corah L.R., Dunn T.G., Kaltenback C.C. Influence of prepartum nutrition on the reproductive performance of beef females and the performance of their progeny. J. Anim. Sci. 1975;41:819–824. doi: 10.2527/jas1975.413819x. [DOI] [PubMed] [Google Scholar]
- Dohoo I., Martin W., Stryhn H. 2nd ed. VER-Inc.; Charlottetown: 2009. Veterinary Epidemiologic Research. [Google Scholar]
- Dutil L., Fecteau G., Bouchard E., Dutremblay D., Pare J. A questionnaire on the health, management, and performance of cow–calf herds in Quebec. Can. Vet. J. 1999;40:649–656. [PMC free article] [PubMed] [Google Scholar]
- Feng S., Wolfe R., Port F. Frailty survival model analysis of the national deceased donor kidney transplant dataset using Poisson variance structures. J. Am. Stat. Assoc. 2005;100:728–735. [Google Scholar]
- Fielding A., Goldstein H. University of Birmingham, Department of Education and Skills; Birmingham, UK: 2006. Cross-classified and multiple membership structures in multilevel models: an introduction and review (Research Report Number 791) [Google Scholar]
- Ganaba R., Bigra-Poulin M., Belanger D., Couture Y. Description of cow-calf productivity in Northwestern Quebec and path models for calf mortality and growth. Prev. Vet. Med. 1995;24:31–42. [Google Scholar]
- Gelman A., Rubin D. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992;4:457–511. [Google Scholar]
- Goldstein H., Browne W., Rasbash J. Tutorial in biostatistics: multilevel modelling of medical data. Stat. Med. 2002;21:3291–3315. doi: 10.1002/sim.1264. [DOI] [PubMed] [Google Scholar]
- Goldstein H., Burgess S., McConnell B. Modelling the effect of pupil mobility on school differences in educational achievement. J. R. Stat. Soc. Ser. A. 2007;170:941–954. [Google Scholar]
- Gregory K.E., Echternkamp S.E., Cundiff L.V. Effects of twinning on dystocia, calf survival, calf growth, carcass traits, and cow productivity. J. Anim. Sci. 1996;74:1223–1233. doi: 10.2527/1996.7461223x. [DOI] [PubMed] [Google Scholar]
- Leckie G., Charlton C. runmlwin: a program to run the MLwiN multilevel modelling software from within Stata. J. Softw. Stat. 2013;52(11) [Google Scholar]
- Lunn D., Jackson C., Best N., Thomas A., Spiegelhalter D. Taylor & Francis Group, LLC; Boca Raton: 2013. The BUGS Book: A Practical Introduction to Bayesian Analysis. [Google Scholar]
- Luo W., Kwok O. The impacts of ignoring a crossed factor in analyzing cross-classified data. Multivar. Behav. Res. 2009;44:182–212. doi: 10.1080/00273170902794214. [DOI] [PubMed] [Google Scholar]
- Ma R., Krewski D., Burnett R. Random effects Cox models: a Poisson modelling approach. Biometrika. 2003;90:157–169. [Google Scholar]
- Masaoud E., Stryhn H., Whyte S., Browne W. Statistical modelling of neighbour treatment effects in aquaculture clinical trials. J. Agric. Biol. Environ. Sci. 2011;16:202–220. [Google Scholar]
- Mathison G.W. The beef industry. In: Martin J., Hudson R.I., Young B.A.E., editors. Animal Production in Canada. University of Alberta; Edmonton, Alberta: 1993. pp. 35–74. [Google Scholar]
- McDermott J.J., Alves D.M., Anderson N.G., Martin S.W. Measures of herd health and productivity in Ontario cow–calf herds. Can. Vet. J. 1991;32:413–420. [PMC free article] [PubMed] [Google Scholar]
- Meyers J., Beretvas N. The impact of inappropriate modelling of cross-classified data structures. Multivar. Behav. Res. 2006;41:473–497. doi: 10.1207/s15327906mbr4104_3. [DOI] [PubMed] [Google Scholar]
- Patterson D.J., Bellows R.A., Burfening P.J., Carr J.B. Occurrence of neonatal and postnatal mortality in range beef cattle. I. Calf loss incidence from birth to weaning, backward and breech presentations and effects of calf loss on subsequent pregnancy rate of dams. Theriogenology. 1987;28:557–571. doi: 10.1016/0093-691x(87)90273-1. [DOI] [PubMed] [Google Scholar]
- Olson D.P. Field studies of protective shelters for beef calves. Bovine Pract. 1986;21:19–22. [Google Scholar]
- Rabe-Hesketh S., Skrondal A. 3rd ed. Stata Press; 2012. Multilevel and Longitudinal Modeling using Stata. Volume II: Categorical Responses Counts, and Survival. [Google Scholar]
- Radostits O.M., Acres S.D. The prevention and control of epidemics of acute undifferentiated diarrhea of beef calves in western Canada. Can. Vet. J. 1980;21:243–249. [PMC free article] [PubMed] [Google Scholar]
- Raftery A., Lewis S. How many iterations in the Gibbs Sampler? In: Bernardo J., Berger J., Dawid A., Smith A., editors. Bayesian Statistics 4. Oxford University Press; 1992. pp. 763–773. [Google Scholar]
- Rondeau V., Filleul L., Joly P. Nested frailty models using maximum penalized likelihood estimation. Stat. Med. 2006;25:4036–4052. doi: 10.1002/sim.2510. [DOI] [PubMed] [Google Scholar]
- Schumann F.J., Townsend H.G., Naylor J.M. Risk factors for mortality from diarrhoea in beef calves in Alberta. Can. J. Vet. Res. 1990;54:366–372. [PMC free article] [PubMed] [Google Scholar]
- Spiegelhalter D., Best N., Carlin B., van der Linde A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B. 2002;64:583–640. [Google Scholar]
- Waldner C.L. Monitoring beef cattle productivity as a measure of environmental health. Environ. Res. Sect. A. 2001;86:94–106. doi: 10.1006/enrs.2001.4239. [DOI] [PubMed] [Google Scholar]
- Waldner C.L. Western Canada study of animal health effects associated with exposure to emissions from oil and natural gas field facilities. Study design and data collection I. Herd performance records and management. Arch. Environ. Occup. Health No. 4. 2008;63:167–184. doi: 10.3200/AEOH.63.4.167-184. [DOI] [PubMed] [Google Scholar]
- Waldner C.L., Ribble C.S., Janzen E.D., Campbell J.R. Associations between total sulphation, hydrogen sulphide deposition, and beef cattle breeding outcomes in Western Canada. Prev. Vet. Med. 2001;50:19–33. doi: 10.1016/s0167-5877(01)00213-6. [DOI] [PubMed] [Google Scholar]
- Waldner C.L., Jelinski M.D., McIntyre-Zimmer K. Survey of western Canadian beef producers regarding calf-hood diseases, management practices, and veterinary service usage. Can. Vet. J. 2013;65:420–559. [PMC free article] [PubMed] [Google Scholar]
- Wittum T.E., Salman M.D., Odde K.G., Mortimer R.G., King M.E. Causes and costs of calf mortality in Colorado beef herds participating in the National Animal Health Monitoring System. J. Am. Vet. Med. Assoc. 1993;203:232–236. [PubMed] [Google Scholar]
- Wittum T.E., Salman M.D., King M.E., Mortimer R.G., Odde K.G., Morris D.L. Individual animal and maternal risk factors for morbidity and mortality of neonatal beef calves in Colorado, USA. Prev. Vet. Med. 1994;19:1–13. [Google Scholar]


