Abstract
Usually, whether to take vaccination or not is a voluntary decision, which is determined by many factors, from societal factors (such as religious belief and human rights) to individual preferences (including psychology and altruism). Facing the outbreaks of infectious diseases, different people often have different estimations on the risk of infectious diseases. So, some persons are willing to vaccinate, but other persons are willing to take risks. In this paper, we establish two different risk assessment systems using the technique of dynamic programming, and then compare the effects of the two different systems on the prevention of diseases on complex networks. One is that the perceived probability of being infected for each individual is the same (uniform case). The other is that the perceived probability of being infected is positively correlated to individual degrees (preferential case). We show that these two risk assessment systems can yield completely different results, such as, the effectiveness of controlling diseases, the time evolution of the number of infections, and so on.
Keywords: Infectious diseases, Voluntary vaccination, Risk estimation, Dynamic programming, Complex networks
Research highlights
► On an outbreak of an infectious disease, individual decisions on vaccination depend on whether they can accurately estimate the risk of the disease. ► So, in this work, we establish two different risk assessment systems using the technique of dynamic programming. By comparing the two different risk assessment systems, we find that how individuals estimate the risk of infection determines the effectiveness of control strategy. ► Furthermore, many other interesting results are enclosed in this work.
1. Introduction
Recently, the outbreaks of Severe Acute Respiratory Syndrome (SARS) [1], [2], Avian influenza [3], [4], and Swine influenza (H1N1) [5], [6] have posed great threats to the human population. Modeling the spread of epidemics is an important topic in understanding the impact of diseases and designing effective control strategies, and has therefore become a task of utmost importance and attracted a revival of interest from the scientific community. Classical mathematical approaches make simplifying assumptions about the patterns of disease-causing interactions among hosts. In particular, homogeneous-mixing models assume that all hosts have identical rates of disease-causing contacts [7]. However, many infectious diseases are diffused from individual to individual following a heterogeneous contact pattern between them. So the transmission of diseases in the human population can be conveniently abstracted as diseases propagate on complex networks with different structures. Examples include the web of human sexual contacts [8], the distribution of avian influenza [4], and so on. Therefore, the dynamics of epidemics on complex networks [9], [10], [11], [12], [13], [14], [15], [16], [17], [18] and a wide variety of immunization or vaccination strategies, including targeted immunization [19], acquaintance immunization [20], ring immunization [21], etc., are investigated under the framework of complex networks.
Though the above immunization strategies have proven to be efficient in controlling the diseases under certain conditions, an often neglected factor is that many vaccinations are voluntary rather than mandatory (for example influenza vaccination [22] and smallpox in some countries [23]). Under a voluntary vaccination mechanism, individuals typically aim at increasing their own interests, so they will balance the cost of vaccination against the risks of infection to decide whether to vaccinate or not in the presence of infection. However, the decision on vaccination is highly dependent on the individuals’ perceived risk of the diseases, which is in turn determined by many factors, such as the prevalence of diseases, the transmission rate of diseases, the duration of diseases, and so on [22], [23], [24], [25], [26], [27], [28], [29]. Thus, in this paper, the dynamics of infectious diseases on complex networks under the voluntary vaccination mechanism is investigated. Meanwhile, the effects of these factors on the perceived risk of diseases are established by a dynamic programming method in this paper.
Furthermore, to compare the effects of risk estimation systems on controlling the spread of epidemics on complex networks, we study two different cases: for the first case, we assume that the perceived risk of being infected for each susceptible individual on network is the same (uniform case), that is, each susceptible individual estimates the perceived risk of infection only depending on the prevalence of infection, not on its own degree/immediate neighbors at each time step. In the second case, we assume individuals are more rational, so the more links/neighbors they have, the higher the probability of being infected. As a result, the perceived risk of infection is not only proportional to the prevalence of the disease but also on the individual’s degree/immediate neighbors (preferential case). Interestingly, even though there is only a small discrepancy between the two cases, completely different results are observed. For example, for the uniform case, the effect of voluntary vaccination on a scale-free network is worse than on random network. For the preferential case, however, the opposite occurs.
2. Model
In this paper we adopt the SIS epidemiological model to investigate the role of voluntary vaccination. In the SIS model, at each time step, each susceptible () node is infected with transmission rate if it is connected to an infected () node. Meanwhile, the infected node recovers and returns to the susceptible state again with probability .
When facing an impending infectious disease, each susceptible individual has to decide whether to vaccinate or not by weighing the perceived risk of infection against the cost of vaccination. We assume that the perceived risk function for susceptible individuals comes from several aspects: the perceived prevalence of the disease estimated by individuals themselves, the transmission rate , and the duration time of the disease . Furthermore, we assume that individuals are forward-looking, and they discount future wealth by a discount factor . The discount factor represents how much weight an individual places on the future when deciding what action to take [30]. (The concept of such a discount is common in economic and accounting fields when computing the net present value of an asset. In general, the idea is that value at some distant time in the future has less utility than an equivalent value now, i.e., a present value becomes after time periods.)
Suppose that each individual has the same initial wealth , and if the individual is infected then his/her wealth is , here indicates the cost of infection. We assume that each individual estimates the prevalence of disease in a uniform way
| (1) |
where is uniform distribution in [0, 1], describing the imperfect information about the disease and the diversity of individuals, and is the proportion/density of infection among the total population.
Denote () and () as the perceived risk function and cost of vaccination for the uniform case (preferential case), respectively. To reflect the optimal behavior of susceptible individuals, in this work we use the technique of dynamic programming [31] (see a brief introduction in the Appendix) to deduce the perceived risk functions for the uniform case and for the preferential case.
Let and be the value functions of individual evaluated in the susceptible state and the infected state, respectively. So for the uniform case, satisfies the following Bellman equation [30], [32]
| (2) |
The first term and second term in the brackets of Eq. (2) are the individual ’s benefit from vaccination and from non-vaccination, respectively. Moreover, is the benefit of escaping from infection though it takes risky behavior, and is the benefit of being infected because of the risky behavior. The value function of evaluated in infected state is given as
| (3) |
To obtain the maximum value of , we first establish the following two equations from Eqs. (2), (3)
| (4) |
Solving Eq. (4)(a) and (b), one has
| (5) |
Without loss of generality, by setting and taking the maximum value of in Eq. (5)(a) and (b), we have
| (6) |
From Eq. (6), we know that if
| (7) |
then vaccination is the preferred choice; otherwise, if , non-vaccination is a better choice.
Remark 1
To facilitate the analysis, we assume that the efficiency of vaccination is 100% during the period of the vaccine’s validity.
For the preferential case, we assume that individuals are more rational than the uniform case, i.e., susceptible individuals know that the more neighbors they have the greater their probabilities of being infected. As a result, the degree of each susceptible individual is considered in the preferential case. In this case, individual ’s value function satisfies
| (8) |
here is the degree of node , other parameters are the same as the uniform case.
Similar to the uniform case, for the preferential case, if
| (9) |
susceptible individuals are willing to be vaccinated; otherwise, susceptible individuals prefer to take risks.
3. Main results
In this section, we use two different risk functions—Eq. (7) for the uniform case and Eq. (9) for the preferential case—to study their different effects on the dynamics of epidemics. Our main results are based on the scale-free BA network proposed by Barabási and Albert (BA) in 1999 [33]. We also use the random network [34] here as a comparison, when the effects of structure on the dynamics of epidemic are considered. Both of them have the same size and average degree and our results obtained here are averaged over 50 realizations.
Now, we investigate how different factors affect the dynamics of an epidemic on complex networks. First we study the effects of discount factor on the spread of epidemics in general. From the definition of , we know that for both the uniform case and the preferential case, the smaller is, the less loss from infection. So a lower level of vaccination causes a higher level of infection. The analysis is verified by Fig. 1 .
Fig. 1.
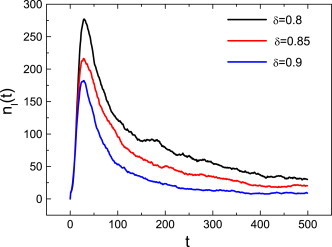
The effect of on the number of infections for the preferential case with , and . We also take other values for these parameters and make simulations for the uniform case, and the results are similar. Furthermore, in the following figures, and denote the number of infections and vaccinations at time , respectively.
It is well known that the structure of networks have a strong influence on the spread of an epidemic. For example, because of the existence of hub nodes, the spread of an epidemic on scale-free networks is much easier than other types of networks, such as random networks and small-world networks [9], [10], [19]. However, in our previous work [35], we showed that diseases can be more effectively controlled on scale-free networks than on random networks when voluntary vaccination mechanisms are considered (see Fig. 2 in Ref. [35]). Though the result is encouraging, we have assumed one ideal situation: each node knows the number of infectious neighbors. In practice, individuals can hardly know how many neighbors are infected. Take sexually transmitted diseases as an example, even when infected, individuals may not want others to know their illnesses for some reasons. As a result, their sexual partners do not know whether he/she is infected.
In the present work, we relax the severe condition and study the effects of two more realistic cases—the uniform case and the preferential case on controlling the spread of diseases, neither of these cases requires detailed information on how many neighbors are infected. It is then natural to ask: what will occur in these two cases? We first compare the effects of the uniform case on the BA network and on an ER network. From Fig. 2 (a), one can find that the number of infections on the BA network is larger than on the ER network. Namely, under the voluntary vaccination mechanism, the uniform case is invalid for the BA network. This is a frustrating result as many social contact patterns can be viewed as scale-free networks. A natural question is: whether such worsening will happen in the preferential case too? Luckily, as shown in Fig. 2(b), even the small improvement in the perceived risk function in the preferential case, an exciting result emerges: the number of infections on the BA network is less than that of the ER networks. It is encouraging to see that there is even less restriction for the preferential case, it also has a positive result.
Fig. 2.
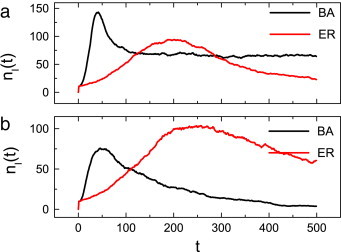
The impacts of two different cases on the BA network and the ER networks. (a): uniform case; (b): preferential case. Here and for the uniform case and the preferential case, respectively. Other parameters are set as and .
To explain such a substantial change, we study the inclination for these two different cases in more detail. We define vaccination inclination for nodes with different as:
| (10) |
where is the number of nodes with degree , and is the number of vaccination with degree over the whole time range . Fig. 3 plots the vaccination inclination for individuals with different for the uniform case and the preferential case, respectively.
Fig. 3.
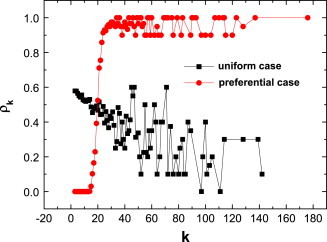
(Color online) The inclination of vaccination as a function of degree for the uniform case and the preferential case. The parameters are same as Fig. 2.
For the preferential case, at first, the nodes with small degree (e.g., ) have no inclination for vaccination (i.e., ). Such a result can be explained as: from the red line in Fig. 2(b), one can find that the number of infections is always lower than 100, namely, . Under this condition and , the risk function in Eq. (9)is always smaller than the cost function , so their inclinations for vaccination are always zero. Then, the inclination increases with degree , and this leads to the high inclination of hub nodes. This means that these hub nodes tend to take vaccination voluntarily, and the diseases can be effectively controlled on the BA networks.
However, for the uniform case, we find that “larger” nodes have lower than “smaller” nodes. The phenomenon is somewhat against our intuition— should be same regardless of different . We should state that such a counterintuitive phenomenon comes from the case that “larger” nodes have few opportunities to stay in a susceptible state because of the higher probability of being infected. So the lower inclination comes from the lower chance of choice, but not from the lower willingness of vaccination. To verify our analysis, in Fig. 4 we plot the total time in the infected state for individuals with different degrees over the whole time range . As one can see, the hub nodes have a higher chance to be infected, so they have fewer opportunities to decide whether to take vaccination or not.
Fig. 4.
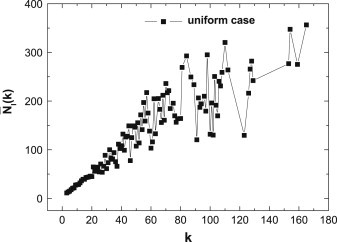
(Color online) For the uniform case, the total time in infected state versus different degrees . Here , and .
As one can predict: diseases can much more easily spread on networks with an increase of the average degree. However, under the voluntary vaccination mechanism, a higher level of disease leads to more vaccinated persons, so the discussed phenomenon above may change. In Fig. 5 we study the final number of infections versus average degree of networks for the two cases. As one can see from Fig. 5(a), for the uniform case, the final number of infections increases with the average degree of network. However, for the preferential case, the final number of infections increases with average degree at first, and then the less favorable situation is controlled when the average degree is large (see Fig. 5(b)). What causes such a distinct result? To answer this question, we reexamine Eqs. (7), (9). From Eq. (7) we can find that the perceived risk function of the uniform case is not related to the degree. As a result, even though the high prevalence of disease for large average degree can provoke more individuals to take vaccination, such an endeavor is not large enough to offset the serious result from the larger average degree, which offers greater conveniences for the spread of the epidemic on networks. For the preferential case, since each individual’s perceived risk function is positively correlated to its degree, when the average degree is so large that everyone’s perceived risk function is larger than the cost of vaccination , then everyone is willing to take vaccination and then the diseases can be eradicated completely.
Fig. 5.
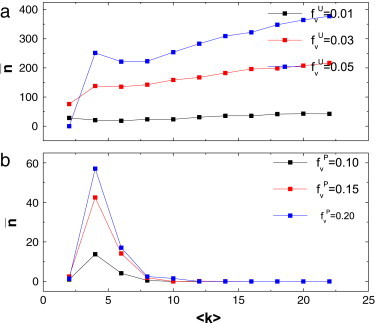
(Color online) The effects of average degree of network on the final number of infections for the uniform case (a) and for the preferential case (b) are studied. The parameters are given as .
Moreover, if no measures are taken, the final number of infections increases with the transmission rate . However, under the voluntary vaccination mechanism, either for the uniform case or for the preferential case, the final number of infections increases with and then decreases to some lower level. The phenomena can be explained as: at first, the final number of infections increases with , then the proportion/density of infection is not large enough to cause alarm. As a result, the final number of infections increases with initially. However, with the further increase transmission rate , the risk functions for both cases are sufficiently high so that more and more susceptible individuals will take vaccination voluntarily. Thus, the infectious diseases are inhibited successfully. The analysis is verified by Fig. 6 . Moreover, an obvious result is also verified by Fig. 5, Fig. 6: the lower the cost of vaccination or is, the more persons participate in the campaign of self-vaccination, and the better the consequences for disease prevention.
Fig. 6.
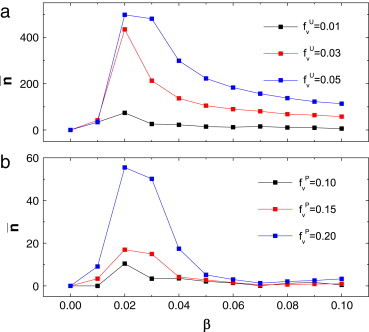
(Color online) The final number of infections versus the transmission rate for the uniform case (a) and the preferential case (b). Here .
Usually, whether the vaccines are permanent or not can change individuals’ attitude towards vaccination. For example, due to the short validity of the influenza vaccine and not so serious consequences of regular human influenza, many individuals are reluctant to take vaccinations. However, for hepatitis B, even with the short validity of its vaccine, many people are still willing to take vaccination iteratively because of the high risk of hepatitis B. So, in the following we will investigate the effects of the validity of the vaccine on the spread of epidemics for the uniform case and the preferential case, respectively. To describe the variation of vaccine effectiveness among individuals, we assume that the vaccine validity period for each individual satisfies a normal distribution . Namely, the mean value is 50 and the standard deviation is 1.0 (We also take in other forms, generally, the longer the period of validity is, the lower the level of infection is.)
By comparing the uniform case with the preferential case, one can find that the number of infections and the number of vaccinations form more significant oscillations in the uniform case (see Fig. 7 ). Such a phenomenon is obvious: once the disease is prevalent, because of the imprecise information on the disease, most individuals choose to take vaccination en masse, the outbreak of the disease is controlled to a very low level, and individuals then relax their vigilance. However, the disease will break out again once the vaccine loses its effect on protecting individuals. Again, most individuals will take vaccination. In this way we observe strong oscillations with time (see Fig. 7(a)). For the preferential case, because “larger nodes” are more diligent in taking vaccination, both the number of infections and the number of vaccinations show damped periodic oscillations and then reach a relative steady state, as shown in Fig. 7(b).
Fig. 7.
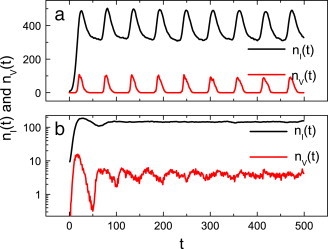
(Color online) The effects of the period of a vaccine’s validity on the spread of epidemic for the uniform case (a) and the preferential case (b), respectively. Here for the uniform case and for the preferential case respectively, other parameters are set as and .
Remark 2
The above oscillations do not always appear. For example, when the cost of vaccination is so cheap that everyone is willing to take vaccination, then the disease is eradicated at the initial time steps, whereas when the cost of vaccination is so expensive that no one takes vaccination, then the disease is always prevalent.
4. Conclusions and discussions
Due to self-interest, individuals balance the cost of vaccination and the risk of diseases to decide whether to take risky behavior or self-protection. This suggests perceived risk functions taken by individuals which determine an individual’s decision, and consequently the success or failure of the eradication of infectious diseases. So, in this work, by using the technique of dynamic programming, the perceived risk functions of the uniform case and the preferential case are first established, and then, under the assumption of a voluntary vaccination mechanism, the effects of two different risk assessment systems on the spread of epidemics on complex networks are investigated. We find that there are some similarities and differences between the two cases. For example, for both cases, a smaller discount factor causes a higher proportion/density of infection, and a non-monotonic phenomenon occurs for the number of infections versus transmission rate . However, there are significantly different results between two cases. First, due to the high vaccination inclination of “large nodes” in the preferential case, the effect of controlling the spread of diseases on scale-free networks is much better than the uniform case. Second, for the uniform case, the number of infections increases with the average degree of the networks, yet, for the preferential case, owing to the perceived risk of infection being positively correlated to degree, the number of infections increases first and then decreases to a low level. Furthermore, when the finite period of a vaccine’s validity is considered, perhaps due to the irrationality of individuals in the uniform case, either the number of infections or the number of vaccinations oscillates significantly with time. In this case, individuals’ decisions on whether to take vaccination or not could become collective, which can cause turmoil and nervousness in society when the vaccines are limited. Nevertheless, for the preferential case, because of increased rationality of individuals, both the number of infections and the number of vaccinations may show damped periodic oscillations and then reach a relative steady state.
In reality, when facing the outbreak of a new kind of infectious disease, many external factors (such as the imperfection of information, the delay of information, rumors, the mistrust of authorities, the diversity of individuals, and so on) can cause people to make an inaccurate estimation on the risk of infection. According to our analysis, these incorrect decisions may determine the success or failure of the campaign to control diseases. So, government should take measures, such as releasing timely and perfect information about diseases, stopping rumors, etc., to guide the public in reaching the correct decisions. Furthermore, we can find that it is difficult to completely eradicate diseases under voluntary vaccination due to the self-interests of individuals. Thus, in order to completely eradicate the prevalence of diseases, government should take mandatory measures on vaccination or increase subsidies to the public to reduce the cost of vaccination.
Acknowledgements
This work is supported from Hong Kong University Grants Council General Research Fund B-Q14G, the National Natural Science Foundation of China (Grant Nos. 11005001, 61004101, 91024026, 10975126, 10635040) and the 211 Project of Anhui University (2009QN003A, KJTD002B).
Communicated by A. Mikhailov
Appendix. Dynamic programming
In terms of mathematical optimization, dynamic programming usually refers a simplification of a decision by breaking it down into a sequence of decision steps over time. This is done by defining a sequence of value functions , with an argument representing the state of the system at times from 1 to . The definition of is the value obtained in state at the last time . The values at earlier times can be found by working backwards, using a recursive relationship called the Bellman equation. For , at any state is calculated from by maximizing a simple function (usually the sum) of the gain from decision and the function at the new state of the system if this decision is made. Since has already been calculated for the needed states, the above operation yields for those states. Finally, at the initial state of the system is the value of the optimal solution. The optimal values of the decision variables can be recovered, one by one, by tracking back the calculations already performed [31].
References
- 1.Molecular evolution of the SARS coronavirus during the course of the SARS epidemic in China. Science. 2004;303:1666. doi: 10.1126/science.1092002. The Chinese SARS Molecular Epidemiology Consortium. [DOI] [PubMed] [Google Scholar]
- 2.Fouchier RAM. Aetiology: Koch’s postulates fulfilled for SARS virus. Nature. 2003;423:240. doi: 10.1038/423240a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.John H.B. Avian influenza A (H5N1) infection in humans. N ENGL MED. 2007;353:1374. doi: 10.1056/NEJMra052211. [DOI] [PubMed] [Google Scholar]
- 4.Small M., Walker D.M., Tse C.K. Scale-free distribution of avian influenza outbreaks. Phys. Rev. Lett. 2007;99:188702. doi: 10.1103/PhysRevLett.99.188702. [DOI] [PubMed] [Google Scholar]
- 5.Fraser C. Pandemic potential of a strain of influenza A (H1N1): early findings. Science. 2009;324:1557. doi: 10.1126/science.1176062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Coburn B.J., Wagner B.G., Blower S. Modeling influenza epidemics and pandemics: insights into the future of swine flu (H1N1) BMC Med. 2009;7:30. doi: 10.1186/1741-7015-7-30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bansal S., Grenfell B.T., Meyers L.A. When individual behaviour matters: homogeneous and network models in epidemiology. J. R. Soc. Interface. 2007;4(16):879. doi: 10.1098/rsif.2007.1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liljeros F., Edling C.R., Amaral L.A.N., Stanley H.E., Åberg Y. The web of human sexual contacts. Nature (London) 2001;411:907. doi: 10.1038/35082140. [DOI] [PubMed] [Google Scholar]
- 9.Pastor-Satorras R., Vespignani A. Epidemic dynamics and endemic states in complex networks. Phys. Rev. E. 2001;63:066117. doi: 10.1103/PhysRevE.63.066117. [DOI] [PubMed] [Google Scholar]
- 10.Pastor-Satorras R., Vespignani A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2001;86:3200. doi: 10.1103/PhysRevLett.86.3200. [DOI] [PubMed] [Google Scholar]
- 11.Zanette D.H. Critical behavior of propagation on small-world networks. Phys. Rev. E. 2001;64:050901(R). doi: 10.1103/PhysRevE.64.050901. [DOI] [PubMed] [Google Scholar]
- 12.Gross T., D’ Lima C.J.D., Blasius B. Epidemic dynamics on an adaptive network. Phys. Rev. Lett. 2006;96:208701. doi: 10.1103/PhysRevLett.96.208701. [DOI] [PubMed] [Google Scholar]
- 13.Miramontes O., Luque B. Dynamical small-world behavior in an epidemical model of mobile individuals. Physica D. 2002;168:379. [Google Scholar]
- 14.Zhang H.F., Fu X.C. Spreading of epidemics on scale-free networks with nonlinear infectivity. Nonlinear Anal.: TMA. 2009;70:3273. [Google Scholar]
- 15.Meloni S., Arenas A., Moreno Y. Traffic-driven epidemic spreading in finite-size scale-free networks. Proc. Natl. Acad. Sci. USA. 2009;106:16897. doi: 10.1073/pnas.0907121106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhou T., Liu J.G., Bai W.J., Chen G.R., Wang B.H. Behaviors of susceptible-infected epidemics on scale-free networks with identical infectivity. Phys. Rev. E. 2006;74:056109. doi: 10.1103/PhysRevE.74.056109. [DOI] [PubMed] [Google Scholar]
- 17.Liu Z.H., Hu B.B. Epidemic spreading in community networks. Europhys. Lett. 2005;72:315. [Google Scholar]
- 18.Small M., Tse C.K., Walker D.M. Super-spreaders and the rate of transmission of the SARS virus. Physica D. 2006;215:146. doi: 10.1016/j.physd.2006.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pastor-Satorras R., Vespignani A. Immunization of complex networks. Phys. Rev. E. 2002;65:036104. doi: 10.1103/PhysRevE.65.036104. [DOI] [PubMed] [Google Scholar]
- 20.Cohen R., Havlin S., ben-Avraham D. Efficient immunization strategies for computer networks and populations. Phys. Rev. Lett. 2003;91:247901. doi: 10.1103/PhysRevLett.91.247901. [DOI] [PubMed] [Google Scholar]
- 21.Müller J., Schönfisch B., Kirkilionis M. Ring vaccination. J. Math. Biol. 2000;41:143. doi: 10.1007/s002850070003. [DOI] [PubMed] [Google Scholar]
- 22.van Boven M., Klinkenberg D., Pen I., Weissing F.J., Heesterbeek H. Self-interest versus group-interest in antiviral control. PLoS ONE. 2008;3(2):e1558. doi: 10.1371/journal.pone.0001558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bauch C.T., Galvani A.P., Earn D.J.D. Group interest versus self-interest in smallpox vaccination policy. Proc. Natl. Acad. Sci. USA. 2003;100:10564. doi: 10.1073/pnas.1731324100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.G. Heal, H. Kunreuther, Center for Risk Management and Decision Process Working Paper No. 05-10-HK, February.
- 25.Coelho F.C., Codeço C.T. Dynamic modeling of vaccinating behavior as a function of individual beliefs. PLoS Comput. Biol. 2009;5(7):e1000425. doi: 10.1371/journal.pcbi.1000425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fu F., Rosenbloom D.I., Wang L., Nowak M.A. Imitation dynamics of vaccination behavior on social networks. Proc. R. Soc. B. 2011;278:42. doi: 10.1098/rspb.2010.1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vardavas R., Breban R., Blower S. Can influence epidemics be prevented by voluntary vaccination? PloS Comput. Biol. 2007;3(5):e85. doi: 10.1371/journal.pcbi.0030085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Perisic A., Bauch C.T. Social contact networks and disease eradicability under voluntary vaccination. PLoS. Comput. Biol. 2009;5(2):e1000280. doi: 10.1371/journal.pcbi.1000280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bagnoli F., Liò P., Sguanci L. Risk perception in epidemic modeling. Phys. Rev. E. 2007;76:061904. doi: 10.1103/PhysRevE.76.061904. [DOI] [PubMed] [Google Scholar]
- 30.Chen F.H. Modeling the effect of information quality on risk behavior change and the transmission of infectious diseases. Math. Biosci. 2009;217:125. doi: 10.1016/j.mbs.2008.11.005. [DOI] [PubMed] [Google Scholar]
- 31.http://en.wikipedia.org/wiki/Dynamic_programming
- 32.T. Philipson, Economic epidemiology and infectious diseases, in: Handbook of Health Economics, 2000.
- 33.Barabási A.L., Albert R. Emergence of scaling in random networks. Science. 1999;286:509. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- 34.Erdös P., Rényi A. On random graphs. I. Publ. Math. 1959;6:290. [Google Scholar]
- 35.Zhang H.F., Zhang J., Zhou C.S., Small M., Wang B.H. Hub nodes inhibit the outbreak of epidemic under voluntary vaccination. New J. Phys. 2010;12:023015. [Google Scholar]


