Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Mar 17;5(12):6545–6555. doi: 10.1021/acsomega.9b04228

The Effect of Clay Content on the Spin–Spin NMR Relaxation Time Measured in Porous Media

Mahmoud Elsayed †, Guenther Glatz †, Ammar El-Husseiny ‡,*, Abdullah Alqubalee §, Abdulrauf Adebayo §, Karem Al-Garadi †, Mohamed Mahmoud †
PMCID: PMC7114610  PMID: 32258890

Abstract

graphic file with name ao9b04228_0002.jpg

Clays, hydrous aluminous phyllosilicates, have a significant impact on the interpretation of physical measurements and properties of porous media. In particular, the presence of paramagnetic and/or ferromagnetic ions like iron, nickel, and magnesium in clays can complicate the analysis of nuclear magnetic resonance (NMR) data for porous media characterization. This is due to the internal magnetic field gradient induced by the clay minerals. In this study, we aim to investigate the impact of clay content on spin–spin relaxation time (T2), which is strongly influenced by the pore surface chemistry. Seven rock core plugs, characterized with variable clay content, were used for this purpose. The clay mineralogy and volume were determined by means of quantitative evaluation of minerals by scanning electron microscopy (QEMSCAN). The T2 relaxation time was measured using a Carr–Purcell–Meiboom–Gill (CPMG) sequence with variable echo spacing (TE). The maximum percentage difference in dominant T2 values (MRDT2) between shortest and longest echo spacing was subsequently correlated with clay content obtained from QEMSCAN. Our results show that the reduction in T2 distribution with increasing echo time TE is more significant in samples characterized by higher clay contents. The MRDT2 was found to be strongly correlated with clay content. An analytical equation is presented expressing MRDT2 as a function of clay content providing a quick and non-destructive approach for clay content estimation. Moreover, the MRDT2–clay content relationship showed a nonlinear behavior: MRDT2 increases drastically as the clay content increases up to 15%, beyond which the rate of MRDT2 change with clay content diminishes. This behavior could be attributed to the clay distribution. At higher clay contents (above 15%), it is more likely for clay to form clusters (structural clays), which will not significantly increase the clay surface in contact with the pore fluid. Further, experimental data suggests that ignoring the impact of clay on internal magnetic gradients and T2 signal may result in considerable underestimation of the actual pore size distribution.

Introduction

Identification and quantification of authigenic clay minerals, a group of hydrous aluminous phyllosilicates, are important components of sandstone reservoir characterization due to their significant impact on petrophysical and hydraulic properties like pore size distribution, acoustic velocity, permeability, capillary pressure, wettability, and water saturation.1

Pore-filling clays like non-swelling kaolinite, Al2Si2O5(OH)4, or illite, (K,H3O)(Al,Mg,Fe)2(Si,Al)4O10[(OH)2,(H2O)], and swelling type clays like smectites (e.g., montmorillonite, (Na,Ca)0.33(Al,Mg)2(Si4O10)(OH2)·nH2O, or willemseite, Ni3Si4O10(OH)2·4H2O), are known to reduce both porosity and permeability.2−4 It is worth mentioning that the previous chemical compositions of the clays are not standard, and clays can exist in different forms.5

Conversely, chlorite, (Mg,Fe)3(Si,Al)4O10(OH)2·(Mg,Fe)2(OH)2, coating of siliciclastic grains can serve as a physical barrier retarding the quartz overgrowth allowing for anomalous porosity preservation in deeply buried sandstones.2

Clays, or any particle of clay-like size1 for that matter, aggravate capillary retention effectively exacerbating residual water saturation.3,4 For sandstone reservoir logging, in particular, accurate determination of the total clay content for tool response correction and, hence, improved interpretation of, e.g., gamma-ray logs is crucial given the significant concentration of naturally occurring radioactive elements, like potassium, thorium, and uranium in shales.4 Neutron porosity logs, sensitive to the amount of hydrogen present, tend to overestimate porosity by reason of clays, major constituents of shales, being able to store substantial amounts of surface bound water.6,7 With respect to both P-wave or compressional and shear wave velocity, several studies attributed a reduction in wave travel times to the presence of clay.8−11

The chemical composition of clay minerals can have a significant impact on the nuclear magnetic resonance (NMR) signal response.12−14 NMR-based technologies exploit the spin angular momentum associated with a proton to determine the time required for spins to return to equilibrium or “relax” after being perturbed by an oscillating magnetic field.15,16 The relaxation processes occur through bulk fluid diffusion and interaction with the surrounding solids comprising the pore-scale environment.17−20 Thus, NMR measurements, either in the well bore or in the laboratory, can provide a useful insight into pore size, pore network complexity, and capillary bound water in porous media.21−27 NMR relaxation parameters commonly exploited for investigations pertaining porous media are T1, the spin–lattice relaxation, or longitudinal time, and T2, referred to as the spin–spin or transverse relaxation time.28

Understanding factors that control T1 and T2 relaxation time respectively is critical for meaningful interpretation of the NMR signal. NMR measurements are sensitive to the magnetic susceptibility difference between pore fluids and the solid along the pore surface that gives rise to inhomogeneity in the magnetic field, commonly referred to as the internal magnetic gradient.6 As evidenced in the literature,7,29 the internal field can be influenced by paramagnetic and/or ferromagnetic ions like iron, nickel, and magnesium, common constituents of clay minerals.29,30

The presence of strong internal gradients adds to the complexity of NMR data interpretation. For example, clay coating of the pore space can induce internal field gradients leading to reduced T2 relaxation rates. The reduction in T2 time can, erroneously, be interpreted as a result of smaller pore sizes,17,31−33 thus leading to an underestimation of NMR derived porosity.34,35

With increasing amounts of clay, the impact of the internal gradient on T2 time readings is expected to escalate, fostering further reduction in NMR relaxation rates. Nevertheless, the exact relationship between reduced NMR relaxation time and clay content is yet to be elucidated. Specifically, it is not clear yet whether the correlation between NMR relaxation time reduction and clay volume follows a linear trend or needs to be described by a more complicated model.

Shifts in NMR relaxation times due to strong internal gradients can be monitored in a lab setting by varying the time interval between oscillating magnetic pulses (i.e., echo time).36 We hypothesize that a variation in clay minerals, giving rise to variations in internal gradient strength, might be captured through NMR measurements. Thus, a correlation between clay content and reduction of NMR relaxation times, once calibrated, may potentially provide a quick and non-destructive approach for the estimation of clay content percentage in porous media compared to traditional laboratory techniques, like XRD, that are both destructive (requires a powdered sample) and time-consuming.

The objective of this study is to investigate the relationship between clay content and reduction of NMR relaxation times based on seven rock samples with varying amounts and types of clay. The clay mineralogy and volume were determined by means of scanning electron microscopy (QEMSCAN). The T2 relaxation time was measured using a Carr–Purcell–Meiboom–Gill (CPMG) sequence with variable echo spacing. The percentage change in dominant T2 time values at shortest and longest echo spacing was subsequently correlated with clay content obtained from QEMSCAN. The conclusions of this study are of particular importance for interpretation of NMR signals derived from clay bearing porous media.

Background

The resonance, precession, or Larmor frequency f (MHz), as a result of an externally applied magnetic field B0 (Tesla), is described by Larmor’s equation:

graphic file with name ao9b04228_m001.jpg 1

where γ is the gyromagnetic or magnetogyric ratio. This ratio is an atomic species-dependent value relating the molecule’s magnetic moment to its angular momentum. Hydrogen, for example, has a ratio of 42.58 MHz/Tesla.37

A radio frequency field applied at the Larmor frequency results in the transverse magnetization, Mx, y, to decay exponentially with respect to time as follows:

graphic file with name ao9b04228_m002.jpg 2

In eq 2, T2 is the transverse relaxation decay constant time, commonly given in seconds. For fluids in a porous medium, T2 is a function of the molecular nature of the fluid and its interactions with the pore network structure.38 The observable T2 time is effectively reduced by molecular diffusion through inhomogeneous magnetic fields if the diffusion length is long and/or the magnetic field gradients are large.39 Combining fluid properties, surface effects, and diffusion relaxation, the effective T2 time observed for fluid in a porous media is described by40

graphic file with name ao9b04228_m003.jpg 3

In eq 3, the three right-hand side (RHS) terms relate to bulk fluid relaxation characteristics, relaxation enhancement through pore-surface interactions, and relaxation through diffusion through the effect of an internal magnetic field, respectively. In the first RHS term, T2, bulk refers to the characteristics of the bulk fluid where the decay of magnetization is governed by spin–spin interactions.41 The middle term combines the surface relaxivity ρ2, describing the T2 relaxation enhancement when spins interact with a particular surface, with S/V, the average surface-to-volume ratio of the pores. The last RHS term is the product of the diffusion coefficient D of the fluid, the gyromagnetic ratio γ of the nuclear spin (MHz/T), the internal magnetic field gradient strength g, and TE, the time between so-called Carr–Purcell–Meiboom–Gill (CPMG) refocusing pulses, a special sequence of radio frequency pulses applied to measure T2.16

In practice, a CPMG sequence starts by subjecting the specimen under investigation to a constant magnetic field to develop initial magnetization in the z axis. Subsequently, a 90° focusing pulse (radio frequency field) is applied to the specimen to shift its molecules (spins) to the transverse plane (x,y). Next, a train of 180° refocusing pulses are applied.42 Upon repeating the 180° pulse, the height of the various echoes is successively reduced due to of the dephasing process of the T2 time.16

It is evident from eq 3 that increasing TE amplifies the impact of the internal magnetic field gradient strength g on T2. For a given gradient strength, T2 decreases as TE increases. A long echo time coupled with a high internal field gradient is known to significantly decrease the T2 distribution.43 Conversely, increasing TE will not significantly reduce T2 if the internal gradient field is very low (low clay content) for the specimen under investigation.

For porous media, the internal gradient field is often attributed to the presence of paramagnetic and/or ferromagnetic ions, like iron, nickel, and magnesium, commonly found in clays.41,44−46 Therefore, the percentage decrease in T2 (due to TE increase) is expected to increase as the clay content increases. Hence, in this study, we test the hypothesis that any clay present in a porous medium is correlated with shifts in T2 time. Clearly, a correlation would be convenient to estimate the clay content in a quick and non-destructive manner.

Notably, an increase in TE value is, in general, accompanied by a decline of D.36 This effect is particularly noticeable in the presence of micropores.26 Ultimately, however, the impact of the internal gradient on T2 is more dominant compared to the effect of D in the presence of clay as evident from eq 3 where the term g has an exponent of 2 compared with an exponent of 1 for D.

Given that the applied magnetic field strength is proportional to the internal magnetic field gradient, rocks are primarily studied at low magnetic field strengths in the range of 0.05–0.5 Tesla. From an experimental point of view, substantial efforts are made to minimize the internal gradient effect.19−21

Though there is evidence that the internal gradient for carbonate rocks is lower than the tool gradient and thus can be neglected due to the absence of paramagnetic materials, sandstone rocks potentially yield internal gradients greater than tool gradients due to the presence of clays.37 According to eq 3, T2 decreases as g increases even for the same pore size that is the same S/V. Consequently, neglecting the impact of clays on the T2 measurement can lead to underestimation of pore size and permeability of sandstone, or any rock, that contains clay.

There is another NMR measurement, T1 relaxation time, that is less sensitive to g and therefore can be used to obtain a more comprehensive understanding about the pore size distribution.47T1 relaxation represents the time needed for the net magnetization vector to return to its equilibrium position along the z axis is characterized by the spin lattice relaxation time.48 Thus, the T1 relaxation time reflects the time required for the longitudinal magnetization, Mz, and equilibrium magnetization, M0, to be reduced by a factor of e as indicated in eq 4.48 Generally, in order to acquire the T1 relaxation time, an inversion recovery (IR) pulse sequence is used.48 The free induction decay (FID) is repeatedly measured at defined increasing time intervals between 180° and 90° of the radio frequency pulses.37 Subsequently, T1 is calculated by fitting the measured data to the following eq 4:

graphic file with name ao9b04228_m004.jpg 4

Several studies provided evidence that the T1 relaxation time is not affected by the internal gradient through diffusion.16,17 Hence, the T1 relaxation time is exploited when T2 relaxation time experiments become inordinately affected by the presence of an internal gradient potentially resulting in an incorrect interpretation of porosity and saturation values. As shown in eq 5, the T1 relaxation is inversely proportional to the bulk fluid density ρ1 and surface to volume ratio relaxations S/V:49

graphic file with name ao9b04228_m005.jpg 5

Materials and Experiments

Rock Core Sample Selection and Preparation

In this study, a total of three sandstone and one limestone rock samples with 4 inch length and 1.5 inch diameter were investigated. For each sandstone type, two sister plugs, labeled as 1 and 2, were used. A summary of the particular sandstone types and petrophysical parameters is provided in Table 1. Samples were cut into two core plugs, each with approximately 2.5 inches in length, and cleaned using the Soxhlet extraction method for a 24 h period to ensure complete removal of fluids residing inside the core samples. Subsequently, the plugs were dried at 70 °C in a vacuum oven. Porosity and permeability measurements were performed using an automated permeameter–porosimeter (AP-608). Pore volumes were calculated based on Boyle’s law, and Klinkenberg-corrected permeability was derived based on the pressure decay concept.50 A summary of the porosity and permeability measurements is provided in Table 1.

Table 1. Petrophysical Parameters for the Rock Core Samples.

sample name ϕ (%) k (mD)
Kentucky 1 13.77 0.67
Kentucky 2 17.07 1.66
Bandera Brown 1 23.05 27.05
Bandera Brown 2 27.62 32.52
Berea 1 20.98 147.68
Berea 2 22.74 192.16
Indiana limestone 17.43 216.89
Open in a new tab

Scanning Electron Microscopy (SEM)

For each sample, thin sections were analyzed using scanning electron microscopy (QEMSCAN), preceded by carbon coating using a Q150T Quorum EMS 150R ES, to provide a quantitative estimate of the minerals present. An operating X-ray beam voltage of 15 kV, with a beam current of 10 nA (±0.05 nA), was used to improve quantification of the mineralogical compositions of the samples. In particular, measurements were taken with a 5 μm point spacing in field picture scan mode on a region of 1 cm2. During the data processing stage, several frequently used preprocessors and filters, such as field stitch, granulator, and boundary phase processor, were applied.51 Finally, a mass percentage for each mineral and every sample was calculated.

NMR Relaxation Experiments

Using an Oxford Instruments Core Analyzer Geospec2, operating at a 1H Larmor frequency of 2 MHz (0.05 T), CPMG measurements were performed on cores saturated with a 10 wt % KCl brine solution. For each sample, a series of five CPMG pulse sequences with TE echo times of 0.1, 0.4, 0.8, 1.2, and 2 ms were conducted to measure the T2 distribution at each TE. The core samples were wrapped with an NMR-silent material to prevent loss of saturation during the test. All measurements were conducted at room temperature.

T1 data sets were acquired based on 32 inversion recovery times with logarithmic spacing from 1 × 10–4 to 10 s, a 10 s recycle delay, and eight repeat scans for signal averaging. Each experiment lasted about 58 min. Tikhonov regularization was employed to mitigate issues of multicollinearity, often encountered as a result from experimental noise during determination of distributions for T1 and T2, respectively.19 The choice of an optimal regularization smoothing parameter, efficiently balancing response fidelity with non-physical alternatives, was achieved by means of the generalized cross-validation (GCV) method.52

T2 and T1 measurements were completed for all seven samples. Subsequently, the percentage change in the dominant T2 value due to increasing TE times from 0.1 to 2 ms is plotted against the clay content of the sample. The difference between T2 and T1 for each sample is further used to investigate the influence of clay amount and internal gradient on the interpretation of pore size distribution. Note that both T2 and T1 relaxation experiments were done with the same acquisition parameters in order to have a comparable results.

Internal Magnetic Field Determination

For an infinite medium with a uniform gradient the 1/T2, peak dependence on TE is considered linear.40 As noted above, the presence of molecular diffusion gives rise to an accelerated decay of the sequence of echo amplitudes yielding an inhomogeneous static magnetic field. The time constant of this additional, diffusion induced decay in a porous medium is, however, non-linear due to the restriction experienced by the molecules effectively reducing the diffusion coefficient of the fluid. For confined systems, like sedimentary rocks, the maximum displacement of the diffusing molecules is determined by the matrix’s length scale rather than the time allowed for the molecules to propagate. This phenomenon, known as “anomalous diffusion”, is a function of the diffusion time of the experiment and distinguishable by a lower diffusion coefficient compared to the coefficient of the bulk pore fluid.53 From the slope of the line fitted to the first few points on a 1/T2, peak versus TE2 plot, the magnitude of the internal field gradient can be calculated.45 Notably, the first couple of points fit well to a straight line, while points at greater TE time deviate from it, indicative of restricted diffusion effects.36

Results and Discussion

Pore Scale Mineralogy

The Indiana limestone sample was found to be composed of 100% calcite. SEM analyses of the sandstone samples corroborated the presence of illite, smectite, kaolinite, and chlorite clay minerals. QEMSCAN mineral analysis confirmed quartz to be the main constituent for all sandstones ranging from a low of 47.9% for Bandera Brown to high of 84.8% in the case of Berea. In general, Kentucky and Bandera samples were found to have the highest total amount of clay constituents with chlorite and illite dominating the mix. Lesser amounts of clay were detected for the Berea specimen with illite and kaolinite being the most abundant minerals. A summary of the respective constituents of the sandstone samples is provided in Table 2.

Table 2. Mineral Composition of Sandstone Samples from QEMSCAN Analysis (Clays Are Indicated in Bold Type).

  Kentucky
 Bandera Brown
 Berea
1 2 1 2 1 2
mineral name mass % mass % mass % mass % mass % mass %
quartz 61.4 59.2 47.9 56.2 84.8 83.6
K-feldspar 0.9 0.7 0 0 2.7 3.2
plagioclase 15.2 14.5 10.3 11.1 1.5 1.7
siderite 0 0 0.1 0 0.5 0.6
mica 9.8 11.1 10.4 8.2 2.5 2.5
illite 5.4 9 7 6.7 2 2.5
smectite 0.5 0.3 0.3 0.3 0.1 0.1
kaolinite 0.3 0.4 2.9 3.8 2.6 3.8
chlorite 2.4 1.6 16.6 10.3 0.5 0.4
others 4.1 3.2 4.4 3.5 2.7 1.7
total clay 8.6 11.3 26.8 21.1 5.2 6.8
Open in a new tab

Figures 1 and 2 show the mineral distribution field maps as determined by QEMSCAN for Berea 2 and Kentucky 2, respectively. Heavy minerals are identified as minerals with densities greater than 2.9 g/cm3.

Figure 1.

Figure 1

Open in a new tab

QEMSCAN field map of minerals in the Berea sample.

Figure 2.

Figure 2

Open in a new tab

QEMSCAN field map of minerals in the Kentucky sample.

Figure 3 provides exemplary SEM images of Berea and Bandera sandstones, respectively. Both SEM scans give visual evidence of clays that present distinctive differences with respect to the quartz grain size, ≈100–200 μm for Berea and ≈50–100 μm for Bandera, as well as the amount and spatial distribution of the clay minerals are observed. Importantly, the SEM image on the left (Figure 3a) qualitatively substantiates the QEMSCAN results for the Berea samples, which were found to have the lowest overall clay content of all samples. In the case of Berea, clays predominantly line the pore walls, whereas for the Bandera sample, clays tend to aggregate, in addition, in the center of the pores forming clusters.

Figure 3.

Figure 3

Open in a new tab

SEM images of (a) Berea highlighting dispersed clays (red arrows) partially filling the interparticle pore space and (b) Bandera highlighting clusters (red outlines) of clays (structural clays).

Impact of Internal Gradient on T2 Distribution

The CPMG sequences collected for different TE values formed the basis to calculate T2 distributions for each sample. The data points were fitted to 128 linearly spaced T2 values between 0.1 ms and 1 s applying the aforementioned Tikhonov regularization method.52 The representative T2 relaxation time, used for correlation with TE and internal gradient, was estimated from the dominant peak or mode of the T2 distribution.36

Figure 4 provides an overview of the T2 distribution values obtained at 0.1, 0.4, 0.8, 1.2, and 2 ms echo times for all samples. For sandstone samples, T2 shifts toward shorter time values when increasing TE is observed. This shift correlates with an increasing amount of clays present.

Figure 4.

Figure 4

Open in a new tab

Effect of increasing echo time TE values on T2 distributions. With increasing clay content and constant TE times, T2 times shift toward smaller values.

Table 3 summarizes the T2, peak values for all samples at minimum and maximum echo times used in this study. The maximum relative percentage difference in T2, peak, MRDT2 for short, was calculated based on eq 6. As mentioned above, we observe a greater shift in T2 distribution, which is a larger maximum relative difference, for samples characterized by higher clay contents (see Figure 4 and Table 3) toward smaller time values.

graphic file with name ao9b04228_m006.jpg 6

Table 3. T2, peak Values for TE = 0.1 and 2 ms, Relative Differences in Percentage, NMR Porosity Values Calculated at TE = 0.1 and 2 ms along Accompanied by the Percentage Difference, and the Average Internal Gradient Values.

sample Kentucky 1 Kentucky 1 Bandera Brown 1 Bandera Brown 2 Berea 1 Berea 2 Indiana limest.
T2, peak@TE = 0.1ms (ms) 29.94 34.65 46.42 31.05 193.07 215.44 537.23
T2, peak@TE = 2ms (ms) 10.37 8.03 2.99 4.48 86.4 124.52 464.16
max. relative diff. (%) 65.35 76.82 93.55 85.59 55.25 42.2 13.6
ϕNMR@TE = 0.1ms (%) 13.02 17.83 22.81 28.21 21.07 22.43 17.81
ϕNMR@TE = 2ms (%) 10.54 13.83 15.22 19.79 19.27 19.72 17.21
relative error (%) 19.05 22.43 33.27 29.85 8.54 12.08 3.37
avg. int. grad. (G/cm) 283 313 478 460 60 82 N/A
Open in a new tab

With respect to eq 3, an increase in clay content is expected to give rise to a greater internal gradient, g, consequently furthering reduction in T2 as TE values increase. This is especially true for clays rich in iron, nickel, and magnesium, like chlorite and illite.

In order to evaluate the average internal gradient of each sample, a straight line is fitted to the ostensibly linear part of the 1/T2, peak versus TE2 plot.45 A linear relation between 1/T2, peak and TE is evidence of free diffusion allowing to estimate g.54 The calculated values of g for the respective samples, ranging from 60 to 478 G/cm, are listed in Table 3. Values obtained are well in range with results reported for similar sandstones.45 The calculated relative error values in Table 3 clearly show that the error in porosity increases as the induced internal gradient increases. When comparing the porosity calculated using the data at TE = 2 ms with that from TE = 0.1 ms, the error in porosity calculation can reach up to 33% in Bandera Brown 1 (high clay content sample). Average internal gradient values are higher for rock samples with higher clay contents as expected. In fact, these values are greater than the applied gradient of the NMR logging tool, which causes distortion for the magnetic field.

Figure 5 summarizes 1/T2, peak versus TE2 plots for all specimens. The brine diffusion coefficient value used in the calculations, 2.37 × 10–5 cm2/s, is obtained by means of pulsed magnetic field gradient (PFG) NMR.55 It is observed that the slope of the fitted line, and thus g, is greater for Bandera Brown than Berea and Indiana limestone, indicating a higher internal gradient. Note that, in respect of eq 3, other factors like the saturating fluid, echo time, and gyromagnetic ratio are the same for all experiments.

Figure 5.

Figure 5

Open in a new tab

Plots of 1/T2, peak versus TE2. Orange circles are indicative of the free diffusion system that can be utilized to delineate the average internal gradient g. Black circles represent the restricted diffusion regime in which molecules interact with the pore walls. Indiana limestone T2 times did not change due to the absence of clay content.

A greater internal gradient implies a bigger susceptibility difference between the rock matrix and the saturating fluid. We propose that the variation in the slope and, consequently, the internal gradient value results from varying the clay content in the matrix; an increased slope value indicates the presence of higher amounts of clay in agreement with clay content values obtained by QEMSCAN analysis and is summarized in Table 2.

Plotting the total clay content against the maximum relative difference in T2 (MRDT2) for echo times ranging from 0.1 to 2 ms, a strong correlation is observed as apparent in Figure 6. Initially, an increase in the amount of clay yields an increase in MRDT2. Once the amount of clay present starts to exceed 15%, the associated response in MRDT2 starts to become less significant, suggesting the existence of an upper limit for MRDT2.

Figure 6.

Figure 6

Open in a new tab

Maximum relative difference in T2, peak as a function of total clay content. The regression model used is detailed in eq 7.

We hypothesize that this observation may be explained by the spatial localization of the clays within the pore space. At low concentrations, clays are found dispersed throughout the pore space lining the pore walls, as evident from the SEM image shown in Figure 3a, allowing for strong contact with the pore fluid. With increasing amounts of clay, aggregates in the form of structural clays, occupying not only the pore surface but also the entire matrix, appear as seen in Figure 3b, thus limiting the effective contact of clay with the pore fluid. Given that the pore space is finite, an upper limit for clay volume and thus MRDT2 must exist.

The relationship between clay amount and MRDT2 appears sigmoidal in nature. Hence, the logistic function is a pragmatic choice to model their dependency:

graphic file with name ao9b04228_m007.jpg 7

In eq 7, the coefficient a reflects the curves asymptotic maximum value, b relates to the growth rate, and c influences near which asymptote maximum growth occurs. The coefficient of determination, R2, is calculated to be 0.989.

Notably, our experimental results are in agreement with numerical studies46 on 3D imaged rocks, which showed that structural clays have a weaker impact on the T2 distributions. It is worth mentioning that the impact of dispersed clay on other important geophysical properties, like porosity and permeability, is more significant compared to that of the structural clays.56

Although the Indiana limestone sample is free from clay, the small MRDT2 value could be attributed to the increase in TE. Even for a very low g, there will be some decrease in T2 due to increasing TE (as per eq 3) This decrease in T2 can be explained by the impact of micropores through which diffusion will be restricted if sufficient TE was used.57 That is, the echo time is long enough so that diffusion and relaxation will be impacted by the interaction with the pore surface, which will reduce T2 slightly (Figure 3a). Based on Figure 4a, it is very clear that diffusion in the Indiana limestone sample was free only in the first TE. As TE increases, D becomes restricted (especially due to the impact of micropores), and T2 stabilizes. It is worth mentioning that the impact of internal gradient variation of T2 due to TE increase is more significant than the impact of diffusion or micropores.

In eq 7 above, the y intercept (MRDT2 at zero clay content) can be explained by the impact of restricted diffusion (due to micropores) as mentioned earlier. Equation 7 was produced based on data for different rock types, and the correlation coefficient is very high (0.986) as shown in Figure 6. Therefore, eq 7 might potentially provide an approach to estimate the clay content using NMR measurement. Such an approach is quick and non-destructive compared to traditional laboratory techniques, such as XRD, that are destructive (requires powdered sample) and time-consuming. It is important to note however that the NMR approach proposed here can be only useful for the estimation of clay content percentage in porous media, and it does not provide information about the specific mineralogy.

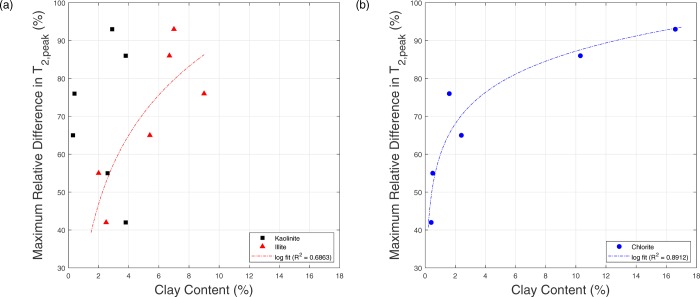
In order to better understand the contribution of different clay minerals to the changes in MRDT2, the data shown in Figure 6 was replotted as a function of individual clay minerals (chlorite, illite, and kaolinite) instead of total clay content. Figure 7a shows the correlation between MRDT2 and both the Kaolinite and Illite content, while Figure 7b displays the MRDT2–chlorite content relationship. Smectite was not included in this analysis due to its scarce occurrence in all samples (<0.5%). The good correlation (R2 = 0.89) between MRDT2 and chlorite content suggests that chlorite has the highest impact on internal NMR gradient and T2 relaxation compared to the other clay minerals. This could be explained by the high content of ferromagnetic ions such as iron in chlorite. Illite comes second in terms of ferromagnetic ion content, and thus it shows a relatively good correlation (but lower than chlorite) with MRDT2, as shown in Figure 7. On the other hand, kaolinite shows no correlation with MRDT2, suggesting a very minimal impact on T2 relaxation. Such observation might be explained by the low ferromagnetic content in kaolinite and/or by the kaolinite distribution being more structural. The cross plots in Figure 7 can also be used to infer information about which clay type is covering the pore space more (i.e., dispersed distribution) and is in contact with the fluid. The strong correlation between chlorite and MRDT2 as well as the drastic increase in MRDT2 due to a small increase in chlorite content (especially at a low clay content; see Figure 3b) suggest that chlorite is the dominant dispersed clay mineral covering the pore space in the studied samples. The results presented here show that clay content percentage may not be sufficient to understand the impact on the NMR signal. Knowledge about clay mineralogy and type (dispersed or structural) can be also crucial for accurate NMR interpretation. Therefore, clay mineralogy quantification in sandstone should be considered during the interpretation of NMR data.

Figure 7.

Figure 7

Open in a new tab

Maximum relative difference in T2, peak (MRDT2) as a function of (a) kaolinite and illite content and (b) chlorite content.

Comparing T1 and T2 Relaxation Times

Due to the fact that T1 relaxation is independent of internal gradient through diffusion, T1 and T2 distributions for the same sample were plotted to investigate the effect of internal gradient in the interpretation of pore size distribution. The T2 distribution here is taken with an echo time equals 0.1 ms (least internal gradient impact).

It is clear from Figure 8 that the Bandera sample experienced a higher difference between T1 and T2 compared to the other samples. Such comparison gives an indication about the influence of the internal gradient in the interpretation of T2 distribution for pore sizes. Higher clay contents lead to higher internal gradients and thus more significant discrepancy between T1 and T2. The impact of clays in this case is to reduce the T2 in comparison with T1 due to the impact of clay-induced internal gradient that affects T2 but not T1. The T1 distribution can be seen as more representative of the pore size distribution, while T2 can provide comparable results (similar T2 peak values) only when the clay content and internal gradient are very low (Figure 8a). When clays are present, the T2 distribution will show lower values compared to T1 distribution (Figure 8c,d). This can lead to underestimation of pores sizes when T2 measurements are used in clay-rich sandstone. Our results then suggest the need to account the effect of clay content and internal gradient when interpreting T2 distribution for pore sizes. Shortening TE can reduce the impact clay-induced internal gradient but not in iron-rich clays. Therefore, it is recommended to use T1 (which is not sensitive to induced internal gradients) to show how the relaxation distribution, reflecting the actual pore size, should look like.

Figure 8.

Figure 8

Open in a new tab

T1 and T2 relaxation distribution. T1 (red) and T2 (blue) distributions for four different samples.

Conclusions

In this study, we investigated the impact of clay content on the spin–spin (T2) relaxation time. Seven core plugs, characterized with variable clay content, were used for this purpose. The T2 distribution was measured for each sample at variable echo time TE, and the observed shift in T2 distribution was correlated with clay content. Our results show that the reduction in T2 distribution with increasing TE is more significant in samples characterized by higher clay contents. The maximum relative difference in peak T2 (MRDT2) was found to be strongly correlated with clay content. An empirical relation is presented expressing the change percentage in MRDT2 as a function of clay content. Such an equation might provide a quick non-destructive approach for clay content evaluation. The MRDT2–clay content relationship showed nonlinear behavior: MRDT2 increases drastically as the clay content increases up to 15%, beyond which the rate of MRDT2 changes when the clay content is decreased. Such a behavior could be attributed to the clay distribution. At higher clay contents (above 15%), it is more likely that clay forms clusters (i.e., structural clays), which will not significantly impact the clay surface contact with the fluid. Moreover, the outcomes of this study suggest the importance of clay mineralogy quantification for accurate NMR interpretation. Due to its high ferromagnetic ion content, chlorite was found to have the highest impact on internal NMR gradient and T2 relaxation compared to the other clay minerals such as kaolinite. Our analysis also showed that accounting for clay induced internal gradient is essential to perform accurate pore size distribution. A comparison with spin–lattice (T1)relaxation time showed that the discrepancy between T1 and T2 (acquired at sufficiently low TE) is significant for samples characterized by high clay contents. In such a case, using the T2 distribution would result in underestimation of actual pore sizes, which could be better represented by the measurements of T1 relaxation distribution.

Acknowledgments

The authors thank the College of Petroleum Engineering and Geosciences in King Fahd University of Petroleum and Minerals for supporting this work. This work was supported by the Research Startup Grant no. SF19007 awarded to A.E.-H. by the College of Petroleum Engineering and Geosciences, KFUPM.

The authors declare no competing financial interest.

Footnotes

1

Grain size at or below 1/256 mm.

References

  1. Lai J.; Wang G.; Cai C.; Fan Z.; Wang S.; Chen J.; Luo G. Diagenesis and reservoir quality in tight gas sandstones: the fourth member of the Upper Triassic Xujiahe Formation, Central Sichuan Basin, Southwest China. Geol. J. 2018, 53, 629–646. 10.1002/gj.2917. [DOI] [Google Scholar]
  2. Jácomo M. H.; Trindade R. I.; de Oliveira E. L.; Leite C. D. M.; Montrazi E. T.; Andreeta M.; Bonagamba T. J. Nuclear Magnetic Resonance and Pore Coupling in Clay-Coated Sandstones With Anomalous Porosity Preservation, Água Grande Formation, Recôncavo Basin, Brazil. Petrophysics 2018, 59, 136–152. [Google Scholar]
  3. Wentworth C. K. A scale of grade and class terms for clastic sediments. The journal of geology 1922, 30, 377–392. 10.1086/622910. [DOI] [Google Scholar]
  4. Worthington P. F. The Petrophysics of problematic reservoirs. J. Pet. Technol. 2011, 63, 88–97. 10.2118/144688-JPT. [DOI] [Google Scholar]
  5. López-Galindo A.; Viseras C.; Cerezo P. Compositional, technical and safety specifications of clays to be used as pharmaceutical and cosmetic products. Appl. Clay Sci. 2007, 36, 51–63. 10.1016/j.clay.2006.06.016. [DOI] [Google Scholar]
  6. Tan M.; Mao K.; Song X.; Yang X.; Xu J. NMR petrophysical interpretation method of gas shale based on core NMR experiment. J. Pet. Sci. Eng. 2015, 136, 100–111. 10.1016/j.petrol.2015.11.007. [DOI] [Google Scholar]
  7. Gao Y.; Wang Z.; She Y.; Lin S.; Lin M.; Zhang C. Mineral characteristic of rocks and its impact on the reservoir quality of He 8 tight sandstone of Tianhuan area, Ordos Basin, China. J. Nat. Gas Geosci. 2019, 4, 205–214. 10.1016/j.jnggs.2019.07.001. [DOI] [Google Scholar]
  8. Wawrzyniak-Guz K. Rock physics modelling for determination of effective elastic properties of the lower Paleozoic shale formation, North Poland. Acta Geophys. 2019, 67, 1967–1989. 10.1007/s11600-019-00355-6. [DOI] [Google Scholar]
  9. Eberhart-Phillips D.; Han D.-H.; Zoback M. D. Empirical relationships among seismic velocity, effective pressure, porosity, and clay content in sandstone. Geophysics 1989, 54, 82–89. 10.1190/1.1442580. [DOI] [Google Scholar]
  10. Boutrid A.; Bensihamdi S.; Chettibi M.; Talhi K. Strength hardness rock testing. J. Min. Sci. 2015, 51, 95–110. 10.1134/S1062739115010135. [DOI] [Google Scholar]
  11. Olowofela J. A.; Kamiyole I. C.; Adegoke J. A. Effects of clay content and porosity on wave velocities in unconsolidated media using empirical relations. J. Geophys. Eng. 2004, 1, 234–239. 10.1088/1742-2132/1/3/009. [DOI] [Google Scholar]
  12. Sposito G.; Prost R. Structure of water adsorbed on smectites. Chem. Rev. 1982, 82, 553–573. 10.1021/cr00052a001. [DOI] [Google Scholar]
  13. Luca V.; Cardile C. M.; Meinhold R. H. High-resolution multinuclear NMR study of cation migration in montmorillonite. Clay Miner. 1989, 24, 115–119. 10.1180/claymin.1989.024.1.10. [DOI] [Google Scholar]
  14. Wu T. H. A nuclear magnetic resonance study of water in clay. J. Geophys. Res. 1964, 69, 1083–1091. 10.1029/JZ069i006p01083. [DOI] [Google Scholar]
  15. Carravetta M.; Levitt M. H. Long-lived nuclear spin states in high-field solution NMR. J. Am. Chem. Soc. 2004, 126, 6228–6229. 10.1021/ja0490931. [DOI] [PubMed] [Google Scholar]
  16. Pourmodheji H.; Ghafar-Zadeh E.; Magierowski S. A multidisciplinary approach to high throughput nuclear magnetic resonance spectroscopy. Sensors 2016, 16, 850–868. 10.3390/s16060850. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Stejskal E. O.; Tanner J. E. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J. Chem. Phys. 1965, 42, 288–292. 10.1063/1.1695690. [DOI] [Google Scholar]
  18. Brown R. J. S. Proton relaxation in crude oils. Nature 1961, 189, 387–388. 10.1038/189387a0. [DOI] [Google Scholar]
  19. Whitaker S. Diffusion and dispersion in porous media. AIChE J. 1967, 13, 420–427. 10.1002/aic.690130308. [DOI] [Google Scholar]
  20. Mendelson K. S. Nuclear magnetic relaxation in porous media. J. Electrochem. Soc. 1986, 133, 631–633. 10.1149/1.2108633. [DOI] [Google Scholar]
  21. Watson A. T.; Chang C. T. P. Characterizing porous media with NMR methods. Prog. Nucl. Magn. Reson. Spectrosc. 1997, 31, 343–386. 10.1016/S0079-6565(97)00053-8. [DOI] [Google Scholar]
  22. Mitchell J.; Howe A. M.; Clarke A. Real-time oil-saturation monitoring in rock cores with low-field NMR. J. Magn. Reson 2015, 256, 34–42. 10.1016/j.jmr.2015.04.011. [DOI] [PubMed] [Google Scholar]
  23. Timur A. Pulsed nuclear magnetic resonance studies of porosity, movable fluid, and permeability of sandstones. J. Pet. Technol. 1969, 21, 775–786. 10.2118/2045-PA. [DOI] [Google Scholar]
  24. Song Y.-Q. Using internal magnetic fields to obtain pore size distributions of porous media. Concepts Magn. Reson., Part A 2003, 18A, 97–110. 10.1002/cmr.a.10072. [DOI] [Google Scholar]
  25. Zhang Y.; Xiao L.; Liao G.; Song Y.-Q. Direct correlation of diffusion and pore size distributions with low field NMR. J. Magn. Reson. 2016, 269, 196–202. 10.1016/j.jmr.2016.06.013. [DOI] [PubMed] [Google Scholar]
  26. El-Husseiny A.; Knight R. A laboratory study of the link between NMR relaxation data and pore size in carbonate skeletal grains and micrite. Petrophysics 2017, 58, 116–125. [Google Scholar]
  27. Yang K.; Li M.; Ling N. N. A.; May E. F.; Connolly P. R. J.; Esteban L.; Clennell M. B.; Mahmoud M.; El-Husseiny A.; Adebayo A. R.; Elsayed M. M.; Johns M. L. Quantitative Tortuosity Measurements of Carbonate Rocks Using Pulsed Field Gradient NMR. Transp. Porous Media 2019, 130, 847–865. 10.1007/s11242-019-01341-8. [DOI] [Google Scholar]
  28. Bloch F. Nuclear induction. Phys. Rev. 1946, 70, 460–474. 10.1103/PhysRev.70.460. [DOI] [Google Scholar]
  29. Anderson R. L.; Ratcliffe I.; Greenwell H. C.; Williams P. A.; Cliffe S.; Coveney P. V. Clay swelling—a challenge in the oilfield. Earth-Sci. Rev. 2010, 98, 201–216. 10.1016/j.earscirev.2009.11.003. [DOI] [Google Scholar]
  30. De Paiva L. B.; Morales A. R.; Díaz F. R. V. Organoclays: properties, preparation and applications. Appl. Clay Sci. 2008, 42, 8–24. 10.1016/j.clay.2008.02.006. [DOI] [Google Scholar]
  31. Capuani S.; Alesiani M.; Alessandri F. M.; Maraviglia B. Characterization of porous media structure by non linear NMR methods. Magn. Reson. Imaging 2001, 19, 319–323. 10.1016/S0730-725X(01)00243-0. [DOI] [PubMed] [Google Scholar]
  32. McCutcheon A. L.; Kannangara G. K.; Wilson M. A.; Ben-Nissan B. Preliminary analysis of pore distributions using NMR in natural coral and hydrothermally prepared hydroxyapatite. J. Mater. Sci. 2004, 39, 5711–5717. 10.1023/B:JMSC.0000040080.98372.04. [DOI] [Google Scholar]
  33. Costabel S.; Yaramanci U. Estimation of water retention parameters from nuclear magnetic resonance relaxation time distributions. Water Resour. Res. 2013, 49, 2068–2079. 10.1002/wrcr.20207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Josh M.; Esteban L.; Delle Piane C.; Sarout J.; Dewhurst D. N.; Clennell M. B. Laboratory characterisation of shale properties. J. Pet. Sci. Eng. 2012, 88-89, 107–124. 10.1016/j.petrol.2012.01.023. [DOI] [Google Scholar]
  35. Brooks R. A.; Moiny F.; Gillis P. On T2-shortening by weakly magnetized particles: the chemical exchange model. Magn. Reson. Med. 2001, 45, 1014–1020. 10.1002/mrm.1135. [DOI] [PubMed] [Google Scholar]
  36. Kleinberg R. L.; Kenyon W. E.; Mitra P. P. Mechanism of NMR relaxation of fluids in rock. J. Magn. Reson 1994, 108, 206–206. 10.1006/jmra.1994.1112. [DOI] [Google Scholar]
  37. Daigle H.; Dugan B. Extending NMR data for permeability estimation in fine-grained sediments. Mar. Pet. Geol. 2009, 26, 1419–1427. 10.1016/j.marpetgeo.2009.02.008. [DOI] [Google Scholar]
  38. Brownstein K. R.; Tarr C. E. Importance of classical diffusion in NMR studies of water in biological cells. Phys. Rev. A 1979, 19, 2446. 10.1103/PhysRevA.19.2446. [DOI] [Google Scholar]
  39. Torrey H. C. Bloch equations with diffusion terms. Phys. Rev. 1956, 104, 563–565. 10.1103/PhysRev.104.563. [DOI] [Google Scholar]
  40. Kenyon W. E. Petrophysical principles of applications of NMR logging. Log Anal. 1997, 38, 21–43. [Google Scholar]
  41. Connolly P. R. J.; Yan W.; Zhang D.; Mahmoud M.; Verrall M.; Lebedev M.; Iglauer S.; Metaxas P. J.; May E. F.; Johns M. L. Simulation and experimental measurements of internal magnetic field gradients and NMR transverse relaxation times (T2) in sandstone rocks. J. Pet. Sci. Eng. 2019, 175, 985–997. 10.1016/j.petrol.2019.01.036. [DOI] [Google Scholar]
  42. Carr H. Y.; Purcell E. M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 1954, 94, 630–638. 10.1103/PhysRev.94.630. [DOI] [Google Scholar]
  43. Hürlimann M. D. Effective gradients in porous media due to susceptibility differences. J. Magn. Reson. 1998, 131, 232–240. 10.1006/jmre.1998.1364. [DOI] [PubMed] [Google Scholar]
  44. Anand V.; Hirasaki G. J. Paramagnetic relaxation in sandstones: Distinguishing T1 and T2 dependence on surface relaxation, internal gradients and dependence on echo spacing. J. Magn. Reson. 2008, 190, 68–85. 10.1016/j.jmr.2007.09.019. [DOI] [PubMed] [Google Scholar]
  45. Zhang G. Q.; Hirasaki G. J.; House W. V. Internal field gradients in porous media. Petrophysics 2003, 44, 422–434. [Google Scholar]
  46. Cho H. J.; Sigmund E. E.; Song Y. Magnetic resonance characterization of porous media using diffusion through internal magnetic fields. Mater. 2012, 5, 590–616. 10.3390/ma5040590. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Mitchell J.; Fordham E. J. Contributed review: Nuclear magnetic resonance core analysis at 0.3 T. Rev. Sci. Instrum. 2014, 85, 111502. [DOI] [PubMed] [Google Scholar]
  48. Wang H.; Zhao M.; Ackerman J. L.; Song Y. Saturation-inversion-recovery: A method for T1 measurement. J. Magn. Reson. 2017, 274, 137–143. 10.1016/j.jmr.2016.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Mohnke O.; Jorand R.; Nordlund C.; Klitzsch N. Understanding NMR relaxometry of partially water-saturated rocks. Hydrol. Earth Syst. Sci. 2015, 19, 2763–2773. 10.5194/hess-19-2763-2015. [DOI] [Google Scholar]
  50. Wu Y.-S.; Pruess K. Gas flow in porous media with Klinkenberg effects. Transp. Porous Media 1998, 32, 117–137. 10.1023/A:1006535211684. [DOI] [Google Scholar]
  51. Honeyands T.; Manuel J.; Matthews L.; O’Dea D.; Pinson D.; Leedham J.; Zhang G.; Li H.; Monaghan B.; Liu X. Comparison of the mineralogy of iron ore sinters using a range of techniques. Miner. 2019, 9, 333–350. 10.3390/min9060333. [DOI] [Google Scholar]
  52. Hollingsworth K.; Johns M. Measurement of emulsion droplet sizes using PFG NMR and regularization methods. J. Colloid Interface Sci. 2003, 258, 383–389. 10.1016/S0021-9797(02)00131-5. [DOI] [PubMed] [Google Scholar]
  53. Elwinger F.; Pourmand P.; Furo I. Diffusive transport in pores. tortuosity and molecular interaction with the pore wall. J. Phys. Chem. B 2017, 121, 13757–13764. [Google Scholar]
  54. Fay E. L.; Knight R. J.; Song Y.-Q. Investigating internal magnetic field gradients in aquifer sedimentsInternal gradients in aquifer sediments. Geophys. 2015, 80, D281–D294. 10.1190/geo2014-0445.1. [DOI] [Google Scholar]
  55. Price W. S. Pulsed-field gradient nuclear magnetic resonance as a tool for studying translational diffusion: Part 1. Basic theory. Concepts Magn. Reson., Part A 1997, 9, 299–336. [Google Scholar]
  56. Mkinga O. J.; Skogen E.; Kleppe J. Petrophysical interpretation in shaly sand formation of a gas field in Tanzania. J. Pet. Explor. Prod. Technol. 2019, 1–13. [Google Scholar]
  57. Grunewald E.; Knight R. A laboratory study of NMR relaxation times and pore coupling in heterogeneous media. Geophys. 2009, 74, E215–E221. 10.1190/1.3223712. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES