Abstract
Carbonaceous or oxy-carbon species are intermediates formed during CxHy combustion on a Ptn/Al2O3 catalyst, which contain carbon, hydrogen, and oxygen atoms. The accumulation of the carbonaceous species, arguably, leads to catalytic deactivation; therefore, their removal is of importance. As the diffusion process is occasionally the rate-determining step in the growth of carbonaceous species, the present study aims to reveal the diffusion mechanisms. The free energy barriers of acetate, formate, and methoxy diffusion on the (100)-γ-Al2O3 surface were evaluated through extensive metadynamics simulations at the density-functional tight-binding level. The present work deduces that each adopted carbonaceous species exhibits different diffusion mechanisms and supports experimental evidence that the acetate species exhibits the slowest diffusivity among the adopted carbonaceous species.
1. Introduction
The three-way catalyst (TWC) technology is among the innovative catalyst technologies for eliminating the generated hazardous exhaust gases, that is, carbon monoxide (CO), nitrogen oxides (NOx), and unburnt hydrocarbons (CxHy) from vehicles.1−3 The catalysts are composed of, and not limited to, noble metals (Pt, Pd, or Rh) and metal oxides. The commonly used metal oxides that support TWC are alumina (Al2O3),4−7 zirconia (ZrO2),8−12 and ceria (CeO2).13−17 Experimental18−20 and theoretical21−24 studies were performed extensively for exploring the catalytic activity and elucidating the reaction mechanism.22,23 During the removal process, CO and CxHy are oxidized into CO2, whereas NOx is reduced to N2.25 In such reactions, the CxHy oxidation leads to the formation of intermediates reported in ref (26), namely, oxygenated carbonaceous (oxy-carbon) species. The oxy-carbon intermediates are mainly accumulated on the Al2O3 surface.26 The role of the oxy-carbon species is questionable. However, it has been presumed that the oxy-carbons only act as inert spectators during the oxidation reaction.26 An experimental study was performed to investigate oxy-carbon growth on a metal oxide surface.26
The growth of the oxy-carbon species was observed by diffuse reflectance infrared Fourier-transform spectroscopy coupled with Fourier-transform infrared spectroscopy.26 The same technique has been used extensively for investigating oxidation over various catalysts, namely, Pd/CeO2/Al2O3,27 Pt/Al2O3,28−30 Pt/WOx/Al2O3,28 MgCr2O4,31,32 Co3O4,32 CuO,32 and Pt/CeO2–ZrO2.33 The oxy-carbon species observed on the support materials include acetate (CH3COO–),28,31,32 formate (HCOO–),27,28,31,32 alkoxy (RO–),32 carbonate (CO32–),27−29,33 bicarbonate (HCO3–),33 acetone,31,32 and unidentified species.30 The unidentified species was detected when the experiment was conducted in the presence of the SO2 gas. Temperature-programmed oxidation (TPO) successfully elucidated the composition, location, reactivity, and the role of the oxy-carbon species in hydrocarbon oxidation.34 The catalytic activity of the supported nanoparticles was also influenced by the kinetics of the TPO process, where the activity increased as the diffusion barrier decreased.34
Based on the previous experimental study in ref (26), the reactions represented in eqs 1–8 are plausible elementary reactions for the formation of the oxy-carbon species, where * denotes the active site of the surface. No observation was made to elaborate where the reactions were occurring. Assuming that all the processes occur on the metal nanocluster surface, the oxy-carbon species would spill over on the γ-Al2O3 surface.
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
The previous experimental study showed that it is more difficult to oxidize acetate species than the alkoxy and ketone derivatives.26,34 It was further confirmed that the diffusion of oxy-carbon species plays an important role in the removal process, as diffusion is the rate-determining step of oxy-carbon oxidation.34 Motivated by the aforementioned experimental facts, in the present theoretical study, the diffusion process of oxy-carbon species was elucidated via molecular dynamics simulations at the density-functional tight-binding (DFTB) level.35−38 Molecular details on the diffusion mechanism and the surface driving force γ-Al2O3 were investigated.
2. Computational Details
All DFTB calculations were performed using an in-house code DC-DFTBMD program,39,40 whereas the reference calculations were performed at the density-functional theory (DFT) level using the Vienna ab Initio Simulation Package (VASP).41,42 The DFTB calculation was performed using the third-order variant (DFTB3) with the modified parameter set made using the automatized DFTB parameterization toolkit,99 hereafter called the Al2O3 parameter. As a reference, the calculations were also performed at the DFT level using the generalized-gradient approximation functional, Perdew–Burke–Ernzerhof, revised for solids (PBEsol).43 To describe the dispersion interaction between the oxy-carbon and the γ-Al2O3 surface, the DFT-D3 dispersion correction with Becke–Johnson damping was employed in both DFTB and DFT calculations.44 The initial structure of the bulk γ-Al2O3 was reconstructed based on the information obtained from refs (45) and (46). The chosen initial structure is a nonspinel type that has been extensively studied in some previous works.24,47−52
First, the initial geometry of the bulk Al2O3 was optimized at the DFT and DFTB levels. The lattice parameters and the optimized geometries were considered for generating the slab structures. The (100)-γ-Al2O3 slabs were generated by cutting the atoms along the (100) plane. Two slab models with different sizes that consist of 160 and 960 atoms, respectively, are shown in Figure 1. To overcome the computational cost for a large system, the divide-and-conquer (DC) option in the DCDFTBMD program was enabled.39,40,53,54 The subsystems were created automatically using the cubic grid with dimensions of 3 × 3 × 3 Å3. A buffer radius of 6 Å was used to adjust the accuracy to the same level as the conventional DFTB method.
Figure 1.
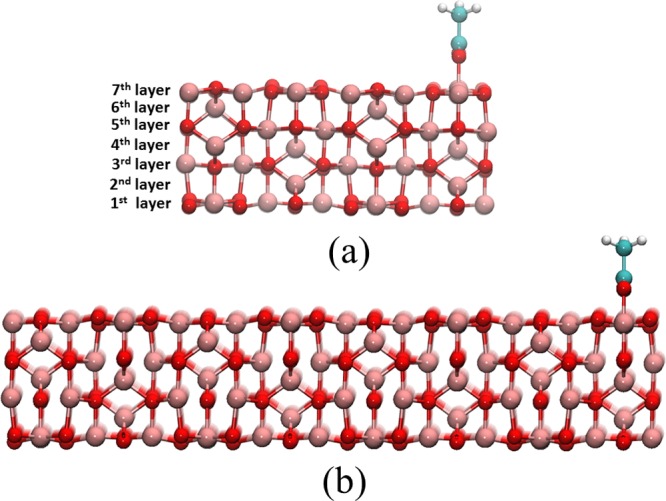
Representative (a) small and (b) large-size slab models adopted in the present work.
During the geometry optimization, three-bottom layers of the slab were fixed, while other atoms were relaxed. The oxy-carbon intermediates, namely, methoxy (CH3O–), bicarbonate (HCO3–), formate (HCOO–), acetate (CH3COO–), and propionate (CH3CH2COO–) were attached on the slab surface. In each prepared structure, oxygen atoms of the oxy-carbon are bound to aluminum atoms, such that they form an octahedral geometry centered at the aluminum atom. The adsorption energies between the oxy-carbon and (100)-γ-Al2O3 slab were calculated at the DFT and DFTB levels with the following formula
| 9 |
Eads, Eslab, and Ecarb represent the total energies of the adsorbed system, slab, and oxy-carbon species, respectively.
The adsorption energies calculated at the DFTB level were compared to the reference calculations at the DFT level. After confirming the parameter accuracy in describing the binding energy, the optimized adsorbed structures were used for MD simulations. At first, the equilibrations were performed under the canonical (NVT) ensemble at the DFTB3-D3(BJ) level for 20 ps with a time step of 1.0 fs to integrate the equation of motion. The equilibrated structures with the details summarized in Table 1 were adopted for further production runs via the metadynamics sampling scheme.55−58 The surface coverages listed in Table 1 are calculated based on eq 10.
| 10 |
Table 1. Slab Size, Adsorbate, Surface Coverage, Number of Adsorbed Oxy-Carbon Species, and Total Number of Atoms of the Adopted Systems.
| slab size | adsorbate | surface coverage [%] | Noxy-carbon | Natoms |
|---|---|---|---|---|
| small | CH3COO– | 5.00 | 1 | 167 |
| small | HCOO– | 5.00 | 1 | 164 |
| small | CH3O– | 2.50 | 1 | 165 |
| large | CH3COO– | 0.83 | 1 | 967 |
| large | CH3COO– | 1.67 | 2 | 974 |
| large | CH3COO– | 9.17 | 11 | 1037 |
Under the metadynamics scheme, the Al–O coordination number, as formulated in eq 11, was chosen as the collective variable.
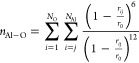 |
11 |
rij and r0 denote the Al–O distance and cutoff radius, respectively. The value r0 = 1.9 Å was specified to smoothly define Al–O bond breaking and formation during the metadynamics simulations. The Gaussian bias potential with a height of 1.88 kcal/mol and a width of 0.1 (dimensionless, as the coordination number was chosen as the collective variable) was added every 40 fs. The simulations were performed until the estimated free energy barriers converged. The free energy barriers converged after performing 9 metadynamics trajectories with a simulation length of 60 ps. The free energy surfaces were reconstructed by estimating the unbiased probability density function via the weighted histogram analysis method.59
3. Results and Discussion
3.1. Structural Property of Bulk γ-Al2O3
The cell parameters of the optimized bulk structure are listed in Table 2. All DFT functionals fairly reproduce the experimental cell volumes. The PBEPBE functional shows the largest deviation of 6.94% with a volume of 49.61 Å3, while the experimental cell volume is 46.39 Å3. Other functionals, such as PBEsol, M11-L, MN12-L, and PW91, exhibit smaller volume deviations of −3.54, −1.60, 1.42, and 2.18%, respectively. The DFTB variants also show smaller volume deviations, namely, –0.13 and −1.74%, for the DFTB3 and DFTB3-D3(BJ) methods, respectively. Despite the volume deviation, the dispersion correction is important for describing weak interactions between oxy-carbon moieties.
Table 2. Comparison of Cell Parameters, Optimized at Different DFT Functionals, and the DFTB Method.
| method | PBEsol | PBEPBEa | M11-La | MN12-La | PW91b | DFTB3 | DFTB3-D3(BJ) |
|---|---|---|---|---|---|---|---|
| a [Å] | 5.466 | 5.648 | 5.491 | 5.559 | 5.587 | 5.570 | 5.533 |
| b [Å] | 8.245 | 8.528 | 8.285 | 8.364 | 8.413 | 8.427 | 8.378 |
| c [Å] | 7.956 | 8.241 | 8.029 | 8.097 | 8.068 | 7.897 | 7.865 |
| β [deg] | 90.76 | 91.00 | 91.24 | 91.28 | 90.59 | 89.46 | 90.66 |
| volume [Å3/Al2O3] | 44.75 | 49.61 | 45.65 | 47.05 | 47.40 | 46.33 | 45.58 |
| volume deviation [%]c | –3.54 | 6.94 | –1.60 | 1.42 | 2.18 | –0.13 | –1.75 |
3.2. Adsorption of Oxy-Carbon Species on the (100) Surface of γ-Al2O3
The oxy-carbon species or carbonaceous species was deposited on the (100)-γ-Al2O3 surface, which was formed after the spillover process. The optimized geometries of the oxy-carbon species adsorbed on the (100)-γ-Al2O3 surface, namely, methoxy (#1–#2), ethoxy (#3–#5), formate (#6–#9), acetate (#10–#13), propionate (#14–#17), and bicarbonate (#18–#20) are shown in Figure 2.
Figure 2.
Adsorbed methoxy (#1–#2), ethoxy (#3–#5), formate (#6–#9), acetate (#10–#13), propionate (#14–#17), and bicarbonate (#18–#20) species on (100)-γ-Al2O3 obtained from geometry optimizations at the DFTB3-D3(BJ) level.
The calculated adsorption energies (ΔEads) for the acetate, formate, and methoxy species on (100)-γ-Al2O3 are shown in Table 3. The DFTB method predicts shorter O–Al bond lengths with a mean average deviation (MAD) of 0.06 Å, relative to the bond lengths obtained at the PBEsol level. Despite such short bond distances, the calculated ΔEads at the DFTB level are smaller than those calculated at the DFT level. The adsorption energies are also well reproduced with a MAD of 0.09 eV (2.08 kcal/mol). Such a deviation is under the level of accuracy of the DFTB method as reported in previous works.62−66 Inclusion of the dispersion correction to both DFT and DFTB calculations also leads to the same MAD as shown in Table 4.
Table 3. Calculated Adsorption Energies and O–Al Bond Distances for Acetate, Formate, and Methoxy on the (100)-γ-Al2O3 Surfacea without Dispersion Correction.
|
rO–Al [Å] |
Eads[eV] |
||||
|---|---|---|---|---|---|
| entry | oxy-carbon | PBEsol | DFTB3b | PBEsol | DFTB3b |
| #1 | methoxy | 1.84 | 1.79 (−0.05) | –1.36 | –1.40 (−0.04) |
| #2 | methoxy | 1.89 | 1.81 (−0.08) | –0.96 | –0.94 (+0.02) |
| #3 | ethoxy | 1.84 | 1.77 (−0.07) | –1.22 | –1.38 (−0.16) |
| #4 | ethoxy | 1.90 | 1.82 (−0.08) | –0.94 | –0.91 (+0.04) |
| #5 | ethoxy | 1.90 | 1.82 (−0.08) | –1.09 | –1.17 (−0.08) |
| #6 | formate | 1.91 | 1.81 (−0.10) | –0.98 | –0.90 (+0.09) |
| #7 | formate | 1.89 | 1.86 (−0.04) | –1.23 | –1.07 (+0.16) |
| #8 | formate | 1.90 | 1.86 (−0.04) | –0.98 | –0.79 (+0.19) |
| #9 | formate | 1.93 | 1.85 (−0.08) | –0.84 | –0.74 (+0.10) |
| #10 | acetate | 1.90 | 1.81 (−0.09) | –0.96 | –0.98 (−0.02) |
| #11 | acetate | 1.88 | 1.86 (−0.02) | –1.21 | –1.15 (+0.07) |
| #12 | acetate | 1.88 | 1.86 (−0.02) | –0.95 | –0.87 (+0.09) |
| #13 | acetate | 1.92 | 1.85 (−0.07) | –0.80 | –0.81 (−0.01) |
| #14 | propionate | 1.90 | 1.81 (−0.09) | –0.99 | –0.91 (+0.08) |
| #15 | propionate | 1.88 | 1.85 (−0.03) | –1.24 | –1.08 (+0.16) |
| #16 | propionate | 1.88 | 1.85 (−0.03) | –0.99 | –0.80 (+0.19) |
| #17 | propionate | 1.92 | 1.84 (−0.08) | –0.83 | –0.75 (+0.08) |
| #18 | bicarbonate | 1.90 | 1.81 (−0.09) | –1.01 | –1.18 (−0.17) |
| #19 | bicarbonate | 1.88 | 1.86 (−0.02) | –1.26 | –1.34 (−0.08) |
| #20 | bicarbonate | 1.89 | 1.86 (−0.03) | –1.01 | –1.07 (−0.06) |
| MAD | 0.06 | 0.09 | |||
Herein, the O atom refers to the one that belongs to the oxy-carbon species. The calculations were performed without dispersion correction.
Differences from the PBEsol method are shown in parentheses.
Table 4. Calculated Adsorption Energies and O–Al and the Acetate, Formate, and Methoxy Bond Distances on the (100)-γ-Al2O3 Surfacea with Dispersion Correction.
|
rO–Al [Å] |
Eads[eV] |
||||
|---|---|---|---|---|---|
| entry | oxy-carbon | PBEsol-D3(BJ) | DFTB3-D3(BJ)b | PBEsol-D3(BJ) | DFTB3-D3(BJ)b |
| #1 | methoxy | 1.84 | 1.80 (−0.05) | –1.57 | –1.62 (−0.05) |
| #2 | methoxy | 1.90 | 1.83 (−0.07) | –1.15 | –1.20 (−0.05) |
| #3 | ethoxy | 1.84 | 1.78 (−0.06) | –1.52 | –1.69 (−0.17) |
| #4 | ethoxy | 1.89 | 1.82 (−0.07) | –1.16 | –1.20 (−0.04) |
| #5 | ethoxy | 1.91 | 1.82 (−0.09) | –1.08 | –1.03 (+0.06) |
| #6 | formate | 1.89 | 1.86 (−0.03) | –1.32 | –1.20 (+0.12) |
| #7 | formate | 1.90 | 1.86 (−0.04) | –1.08 | –0.93 (+0.14) |
| #8 | formate | 1.93 | 1.86 (−0.08) | –0.93 | –0.85 (+0.08) |
| #9 | formate | 1.90 | 1.82 (−0.08) | –1.33 | –1.28 (+0.05) |
| #10 | acetate | 1.88 | 1.85 (−0.03) | –1.08 | –1.10 (−0.03) |
| #11 | acetate | 1.88 | 1.85 (−0.03) | –1.08 | –1.00 (+0.08) |
| #12 | acetate | 1.92 | 1.85 (−0.07) | –0.92 | –0.93 (−0.01) |
| #13 | acetate | 1.90 | 1.81 (−0.09) | –1.13 | –1.05 (+0.08) |
| #14 | propionate | 1.88 | 1.85 (−0.03) | –1.38 | –1.22 (+0.15) |
| #15 | propionate | 1.88 | 1.85 (−0.03) | –1.13 | –0.95 (+0.18) |
| #16 | propionate | 1.91 | 1.85 (−0.07) | –0.97 | –0.87 (+0.10) |
| #17 | propionate | 1.91 | 1.81 (−0.10) | –1.12 | –1.30 (−0.18) |
| #18 | bicarbonate | 1.88 | 1.85 (−0.03) | –1.36 | –1.46 (−0.10) |
| #19 | bicarbonate | 1.89 | 1.85 (−0.04) | –1.12 | –1.20 (−0.08) |
| #20 | bicarbonate | 1.92 | 1.85 (−0.07) | –0.96 | –1.12 (−0.16) |
| MAD | 0.06 | 0.09 | |||
Herein, the O atom refers to the one that belongs to the oxy-carbon species. All calculations were performed with the DFT-D3(BJ) dispersion correction.
Differences from the PBEsol method are shown in parentheses.
Based on Table 4, the calculated Eads values strongly depend on the location where the oxy-carbon is adsorbed on the surface. According to the estimated Eads values at the DFTB level, the tendency of the oxy-carbon adsorbed on the surface of (100)-γ-Al2O3 is ethoxy ≈ methoxy > bicarbonate > propionate ≈ formate > acetate. Such an order suggests that removing the acetate species from the surface is energetically easier than that of the formate and methoxy species. However, despite this the acetate species exhibits the smallest adsorption energy, it does not mean that it is easier to be removed from the surface. Because one acetate molecule is adsorbed to the surface via two O–Al bonds, a complete acetate removal requires dissociation of those bonds. Therefore, a more thorough analysis on the free energy of diffusion in the next subsection is of importance to further determine which oxy-carbon species is easier to be removed from the surface.
3.3. Diffusion of Acetate, Formate, and Methoxy Species on the (100) Surface of γ-Al2O3
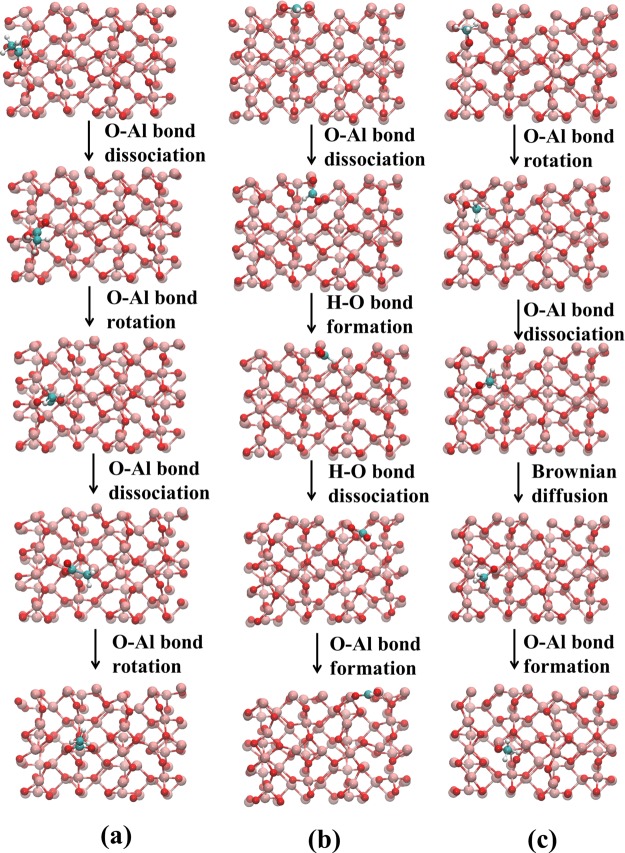
Snapshots of acetate, formate, and methoxy diffusion are shown in Figure 3. Initially, the oxygen from the acetate, formate, and methoxy was attached on the aluminum atom of the (100)-γ-Al2O3 surface. For the case of acetate and formate, the O–Al bond dissociation retains another O–Al bond on the surface. As a result, the remaining O–Al bond becomes flexible and thus it performs a rotation that enables the oxygen atom of the carbonyl group to interact with another empty orbital of the aluminum atom. As the rotation that took place occurred right after the bond dissociation, the process is analogous to ballet.
Figure 3.
Representative metadynamics snapshots of (a) acetate, (b) formate, and (c) methoxy diffusion on (100)-γ-Al2O3 surface.
Similar to the case of the acetate diffusion mechanism, in the beginning, O–Al, the bond between formate and the (100)-γ-Al2O3, was dissociated. Unlike the case of acetate, where oxygen is the only atom that can interact with the surface, herein, the hydrogen atom has a tendency to interact with the surface oxygen atoms. Such an interaction is slightly weaker with a bond length of 1.82 Å, whereas the O–Al bond length between formate and the surface is 1.75 Å. Once the H–O interaction is complete, the formate moiety is destabilized, leading to the dissociation of the second O–Al. Therefore, generally, formate diffusion is facilitated by a ballet jumping motion that originates from the formation of the H–O bond.
In contrast with the acetate and formate cases, the methoxy radical has only one O–Al bond with the (100)-γ-Al2O3 surface. As shown in Figure 3c, at first, the radical rotates until it finds a good conformation to promote O–Al bond dissociation. Once it is detached from the surface, it performs a random vehicular diffusion67,68 until a proper orientation is identified for it to be re-adsorbed on to the surface. The random motion on the surface increases the degree of freedom, in particular, for reorienting and forming the O–Al bond.
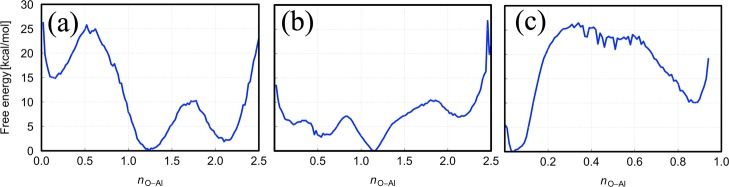
To further investigate these three mechanisms, the free energy diffusion surfaces were re-constructed and are shown in Figure 4. The free energy barriers, ΔF‡, are summarized in Table 5. As shown in Figure 4a, there are two activated complexes formed during acetate diffusion, with diffusion barriers of 8.01 and 25.31 kcal/mol, respectively. These transition states refer to the dissociation of the O–Al bonds, indicating that each O–Al bond has a different strength, with a ratio ΔFf2‡/ΔFf1 of 3.16. A lower ΔFf2‡/ΔFf1 ratio represents faster diffusivity as the second bond dissociation O–Al is the rate-determining step of the overall diffusion process. On the other hand, owing to the dissociations facilitated by the H–O surface interaction, the formate diffusion exhibits a lower ΔFf2‡/ΔFf1 of 1.90, leading to faster diffusivity than the acetate radical. The third step of formate diffusion involves the dissociation of a relatively weak H–O bond, which is represented by a low free energy barrier of 5.73 kcal/mol.
Figure 4.
Reconstructed free energy surfaces of (a) acetate, (b) formate, and (c) methoxy diffusion.
Table 5. Estimated Free Energy Barriers of Acetate, Formate, and Methoxy Diffusion on the (100)-γ-Al2O3 Surface in kcal/mol.
| species | ΔFf1‡ | ΔFf2‡ | ΔFf3‡ | ΔFf2‡/ΔFf1 | ΔFb1‡ | ΔFb2‡ | ΔFb3‡ |
|---|---|---|---|---|---|---|---|
| acetate | 8.01 | 25.31 | 3.16 | 9.59 | 10.97 | ||
| formate | 6.82 | 12.95 | 5.73 | 1.90 | 19.28 | 7.42 | 1.58 |
| methoxy | 15.46 | 25.45 |
As described above for the case of methoxy diffusion, only one O–Al bond was dissociated with a moderately high free energy barrier of 15.46 kcal/mol. The ΔFf1‡ of methoxy diffusion is higher than that of formate diffusion, but still lower than that of acetate. As the methoxy radical performs Brownian diffusion before it is re-adsorbed to the surface, the transition state becomes broader with a few noises as the marks of the small vehicular diffusion barrier. The Brownian diffusion is rather random; therefore, the free energy barrier for methoxy diffusion hardly converges, that is, with a standard deviation of 2.5 kcal/mol.
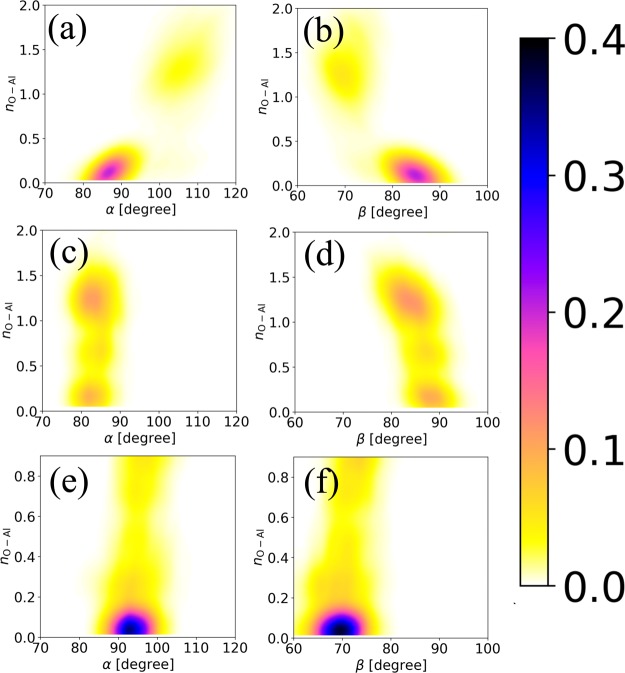
Note that the ΔF‡ values listed in Table 5 are in the range of experimental values, namely, 5.74–26.05 kcal/mol.34,69−71 Moreover, in agreement with the TPO experiment, removing acetate radicals is more difficult compared to removing enolate, aliphatic ester, and acetone.34 Based on the MD simulation at the DFTB level, for the case of the acetate radical, the surface atom configuration, in particular, surface O–Al–O angles where the oxy-carbon was adsorbed (α and β), is primarily responsible for the O–Al bond dissociation. As shown in Figure 5a,b, when the O–Al bond dissociates, namely, when nO–Al reaches zero, α decreases from 105 to 85°, while β increases from 70 to 85°. On the other hand, for the case of formate as shown in Figure 5c,d, the α and β angles do not change significantly, in particular, α is relatively stable at 82°, while β slightly increases from 84 to 88°. In this case, the surface atoms provided a lower driving force for facilitating formate diffusion. As explained previously, formate diffusion is partly facilitated by the interaction between the hydrogen atom of the formate and the oxygen atom on the surface; hence, the diffusion takes place with less efforts from the surface. In stark contrast, as shown in Figure 5e,f, both, the α and β angles, do not change significantly during methoxy diffusion. Although methoxy diffusion is not the fastest among the adopted oxy-carbon species, the surface atoms have a low contribution to the overall diffusion process.
Figure 5.
Probability density distribution of the correlation between α and β angles and the coordination number of oxygen atom, nO–Al of acetate (a,b), formate (c,d), and methoxy species (e,f).
3.4. Coverage Dependence on the Barriers to Acetate Diffusion
The surface coverage affects the estimated barriers of acetate diffusion as summarized in Table 6. At a low surface coverage, namely, 0.83%, the free energy barriers for the dissociations of the second and first O–Al bonds are 11.23 and 20.92 kcal/mol, respectively. The first intermediate state, where one O–Al bond remains adsorbed on the surface, is more stable than the initial state, as implied by the backward free energy barrier of 17.79 kcal/mol. The first intermediate state is even more stable than the final state where the remaining O–Al bond is dissociated. Conversely, despite the high free-energy dissociation of the second O–Al bond, the backward reaction requires a lower energy of 5.28 kcal/mol. Hence, the second O–Al bond dissociation is an endergonic process with ΔFf2 > 0, which indicates that a larger thermal energy is required to induce spontaneity.
Table 6. Estimated Free Energy Barriers (ΔF‡) and Free Energy Differences (ΔF) of Acetate Diffusion at Different Surface Coverage Levels.
| surface coverage [%] | ΔFf1‡ [kcal/mol] | ΔFf2‡ [kcal/mol] | ΔFb1‡ [kcal/mol] | ΔFb2‡ [kcal/mol] | ΔFf1 [kcal/mol] | ΔFf2 [kcal/mol] |
|---|---|---|---|---|---|---|
| 0.83 | 11.23 | 20.92 | 17.79 | 5.28 | –6.56 | 15.64 |
| 1.67 | 4.39 | 14.41 | 7.61 | 3.77 | –3.22 | 10.64 |
| 9.17 | 4.61 | 15.29 | 1.80 | 5.92 | 2.80 | 9.37 |
As the surface coverage increases to 1.67%, both ΔFf1‡ and ΔFf2 decrease to 4.39 and 14.41 kcal/mol, respectively. Similarly, the barriers for backward processes also decrease to 7.61 and 3.77 kcal/mol. Overall, such changes lead to an increase in the free energy difference for the first dissociation process, namely, −3.22 kcal/mol. This indicates that the dissociation of the first O–Al bond becomes more energy demanding. On the other hand, the dissociation of the second bond requires a lower energy than the one at the coverage of 0.83%, with a free energy difference of 10.64 kcal/mol. Overall, at a surface coverage of 1.67%, a lower temperature will be sufficient to promote the entire diffusion process as the total free energy difference, ΔFf1 + ΔFf2 of 7.42 kcal/mol, is smaller than the one at 0.83% surface coverage, namely, 9.08 kcal/mol. The decrement in ΔFf2 helps mitigate the increment in ΔFf1. It is speculated that such decrement stems from the surface deformation when an additional acetate molecule is adsorbed on the surface.
When the surface coverage is further increased to 9.17%, the dissociation barriers of the first and second O–Al bonds slightly increase to 4.61 and 15.29 kcal/mol, respectively. These increments are, however, insignificant, at 0.22 and 0.88 kcal/mol, respectively. Such values are still within the statistical error of metadynamics sampling and re-weighting. In contrast, the backward process for the first dissociation step is reduced significantly from 7.61 to 1.80 kcal/mol. As the backward process is easier, the first dissociation process becomes thermodynamically unfavorable with a free energy difference of 2.80 kcal/mol. The difficulty with dissociating the first O–Al bond may arise from the steric hindrance between the acetate moieties. On the other hand, the second dissociation process is slightly easier than that with a surface coverage of 1.67%, with a free energy difference of 9.37 kcal/mol. As acetate diffusion is difficult at 9.17% surface coverage, one needs to control and minimize the growth of the acetate radical on the Al2O3 surface.
4. Conclusions
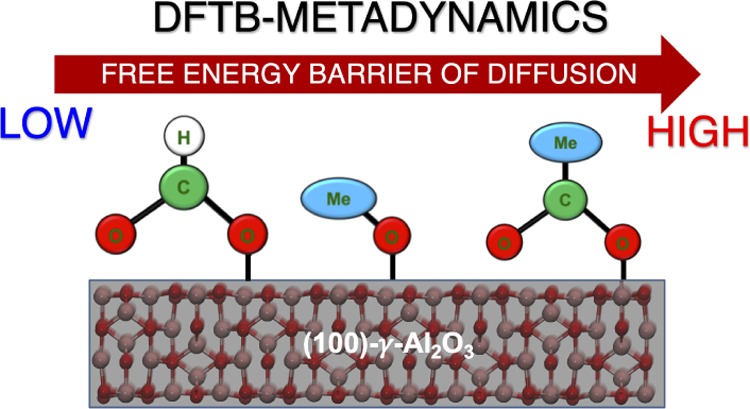
In conclusion, metadynamics simulations at the DFTB level successfully revealed molecular mechanisms of acetate, formate, and methoxy diffusion on a (100)-γ-Al2O3 surface. The present study has examined three diffusion mechanisms that depend on unique interactions between the oxy-carbon radical with the surface. Although acetate and formate have the same functional group, namely, carboxylate (−COO•), they exhibit different diffusion mechanisms. For these carboxylic species, the oxygen atoms were attached asymmetrically, where the O–Al bonds had nonequivalent strength. The acetate diffusion uniquely mimics a ballerina dancer, namely, one O–Al bond rotation occurs immediately after another O–Al bond dissociates. The acetate radical displays the slowest diffusivity among the other oxy-carbon species adopted in the present work. Further investigation shows that the spontaneity of the O–Al bond dissociation is affected by the surface coverage. Increasing the surface coverage to 9.17% leads to nonspontaneous O–Al bond dissociation. Although further investigation to elucidate this phenomenon has not been carried out, it is speculated that the steric hindrance between acetate residues is at play in suppressing the acetate diffusion. The present work suggests that removing the acetate species from the surface is easier at an early stage of its growth, that is, when the surface coverage less than 9%.
On the other hand, the formate radical exhibits the fastest diffusion by forming the O–H bond between the hydrogen atom of the formate radical with the surface oxygen atom. The nature of its fast diffusion, however, is experimentally unobservable, as the diffusion of the formate radical is indistinguishable among the other oxy-carbon species.26 The present work suggests that it is easier to remove the formate radical from the (100)-γ-Al2O3 surface than the acetate or methoxy species. In contrast to the acetate and formate cases, the methoxy radical performs Brownian diffusion. As only one O–Al bond dissociates, Brownian diffusion occurs right after dissociation. Despite the dissociation of only one O–Al bond, the process is slower than formate diffusion due to the lack of surface deformation during methoxy diffusion. Overall, the order of diffusivity among the adopted oxy-carbon species is acetate < methoxy < formate. While the order was not experimentally confirmed, it was reported that the acetate radical exhibits the slowest diffusion.34
Acknowledgments
Some of the presented calculations were performed at the Research Center for Computational Science (RCCS), Okazaki Research Facilities, Institutes of Natural Sciences (NINS). This work was supported in part by a Grant-in-Aid for Scientific Research (S) “KAKENHI Grant Number JP18H05264” from the Japan Society for the Promotion of Science (JSPS). This work was also supported by Element Strategy Initiative “JPMXP0112101003” from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan.
Glossary
Abbreviations
- MTD
metadynamics
- MD
molecular dynamics
- DFTB
density-functional tight-binding
- DC-DFTB
divide-and-conquer-density-functional tight-binding
The authors declare no competing financial interest.
References
- Rainer D. R.; Koranne M.; Vesecky S. M.; Goodman D. W. CO + O2 and CO + NO Reactions over Pd/Al2O3 Catalysts. J. Phys. Chem. B 1997, 101, 10769–10774. 10.1021/jp971262z. [DOI] [Google Scholar]
- Taylor K. C. Nitric Oxide Catalysis in Automotive Exhaust Systems. Catal. Rev. 1993, 35, 457–481. 10.1080/01614949308013915. [DOI] [Google Scholar]
- Shelef M.; Otto K. Appearance of N2O in the catalytic reduction of NO by CO. J. Catal. 1968, 10, 408–412. 10.1016/0021-9517(68)90157-7. [DOI] [Google Scholar]
- Montini T.; Melchionna M.; Monai M.; Fornasiero P. Fundamentals and Catalytic Applications of CeO2-Based Materialsr. Chem. Rev. 2016, 116, 5987–6041. 10.1021/acs.chemrev.5b00603. [DOI] [PubMed] [Google Scholar]
- Koleva I. Z.; Aleksandrov H. A.; Vayssilov G. N. Decomposition behavior of platinum clusters supported on ceria and γ-alumina in the presence of carbon monoxide. Catal. Sci. Technol. 2017, 7, 734–742. 10.1039/c6cy02586b. [DOI] [Google Scholar]
- Trueba M.; Trasatti S. P. γ-Alumina as a Support for Catalysts: A Review of Fundamental Aspects. Eur. J. Inorg. Chem. 2005, 2005, 3393–3403. 10.1002/ejic.200500348. [DOI] [Google Scholar]
- Kim Y. E.; Lee W.; Youn M. H.; Jeong S. K.; Kim H. J.; Park J. C.; Park K. T. Leaching-resistant SnO2/γ-Al2O3 nanocatalyst for stable electrochemical CO2 reduction into formate. J. Ind. Eng. Chem. 2019, 78, 73–78. 10.1016/j.jiec.2019.05.042. [DOI] [Google Scholar]
- Zakaria M. B.; Malgras V.; Nagata T.; Kim J.; Bando Y.; Fatehmulla A.; Aldhafiri A. M.; Farooq W. A.; Jikihara Y.; Nakayama T.; Yamauchi Y.; Lin J. Gold nanoparticles anchored on mesoporous zirconia thin films for efficient catalytic oxidation of carbon monoxide at low temperatures. Microporous Mesoporous Mater. 2019, 288, 109530. 10.1016/j.micromeso.2019.05.055. [DOI] [Google Scholar]
- Wang J.; Wen J.; Shen M. Effect of Interaction between Ce0.7Zr0.3O2 and Al2O3 on Structural Characteristics, Thermal Stability, and Oxygen Storage Capacity. J. Phys. Chem. C 2008, 112, 5113–5122. 10.1021/jp711331g. [DOI] [Google Scholar]
- Lin S.; Yang L.; Yang X.; Zhou R. Redox properties and metal–support interaction of Pd/Ce0.67Zr0.33O2– Al2O3 catalyst for CO, HC and NOx elimination. Appl. Surf. Sci. 2014, 305, 642–649. 10.1016/j.apsusc.2014.03.153. [DOI] [Google Scholar]
- Lin S.; Yang X.; Yang L.; Zhou R. Three-way catalytic performance of Pd/Ce0.67Zr0.33O2– Al2O3 catalysts: Role of the different Pd precursors. Appl. Surf. Sci. 2015, 327, 335–343. 10.1016/j.apsusc.2014.11.176. [DOI] [Google Scholar]
- Morikawa A.; Suzuki T.; Kanazawa T.; Kikuta K.; Suda A.; Shinjo H. A new concept in high performance ceria–zirconia oxygen storage capacity material with Al2O3 as a diffusion barrier. Appl. Catal. B Environ. 2008, 78, 210–221. 10.1016/j.apcatb.2007.09.013. [DOI] [Google Scholar]
- Koga H.; Hayashi A.; Ato Y.; Tada K.; Hosokawa S.; Tanaka T.; Okumura M. Effect of ceria and zirconia supports on NO reduction over platinum-group metal catalysts: A DFT study with comparative experiments. Catal. Today 2019, 332, 236–244. 10.1016/j.cattod.2018.07.023. [DOI] [Google Scholar]
- Lan L.; Wang J.; Chen S.; Li D.; Li H.; Liu D.; Wang W.; Chen Y. Enhanced activity and hydrothermal stability of Rh-based three-way catalyst for emission control from motorcycles with the assistance of monoethanolamine. J. Ind. Eng. Chem. 2019, 71, 127–136. 10.1016/j.jiec.2018.11.014. [DOI] [Google Scholar]
- Li P.; Chen X.; Li Y.; Schwank J. W. A review on oxygen storage capacity of CeO2-based materials: Influence factors, measurement techniques, and applications in reactions related to catalytic automotive emissions control. Catal. Today 2019, 327, 90–115. 10.1016/j.cattod.2018.05.059. [DOI] [Google Scholar]
- Kim J.-R.; Myeong W.-J.; Ihm S.-K. Characteristics of CeO2– ZrO2 mixed oxide prepared by continuous hydrothermal synthesis in supercritical water as support of Rh catalyst for catalytic reduction of NO by CO. J. Catal. 2009, 263, 123–133. 10.1016/j.jcat.2009.02.001. [DOI] [Google Scholar]
- Lambrou P. S.; Efstathiou A. M. The effects of Fe on the oxygen storage and release properties of model Pd– Rh/CeO2– Al2O3 three-way catalyst. J. Catal. 2006, 240, 182–193. 10.1016/j.jcat.2006.03.014. [DOI] [Google Scholar]
- Djéga-Mariadassou G.; Berger M.; Gorce O.; Park J. W.; Pernot H.; Potvin C.; Thomas C.; Da Costa P.. Studies in Surface Science and Catalysis. In Past and Present in DeNO Catalysis; Granger P., Pârvulescu V. I., Eds.; Elsevier, 2007; Vol. 171; pp 145–173. [Google Scholar]
- Rogemond E.; Essayem N.; Fréty R.; Perrichon V.; Primet M.; Chevrier M.; Gauthier C.; Mathis F. Characterization of Model Three-Way Catalysts: III. Infrared Study of the Surface Composition of Platinum-Rhodium Ceria Alumina Catalysts. J. Catal. 1999, 186, 414–422. 10.1006/jcat.1999.2585. [DOI] [Google Scholar]
- Chuang S. S. C.; Tan C.-D. Combined infrared and mass spectrometric study of reactions of adsorbed NO and CO on 0.5 wt% Rh/SiO2 catalyst. Catal. Today 1997, 35, 369–377. 10.1016/s0920-5861(96)00216-7. [DOI] [Google Scholar]
- Ishimoto R.; Jung C.; Tsuboi H.; Koyama M.; Endou A.; Kubo M.; Del Carpio C. A.; Miyamoto A. Periodic density functional and tight-binding quantum chemical molecular dynamics study of catalytic properties on γ-Al2O3 supported Pt catalysts. Appl. Catal., A 2006, 305, 64–69. 10.1016/j.apcata.2006.02.049. [DOI] [Google Scholar]
- Yang J.; Wang H.; Zhao X.; Li Y. L.; Fan W. L. Correlating the surface structure and hydration of a γ-Al2O3 support with the Run (n = 1 – 4) cluster adsorption behavior: a density functional theory study. RSC Adv. 2016, 6, 40459–40473. 10.1039/c5ra28173c. [DOI] [Google Scholar]
- Yang T.; Ehara M. Probing the electronic structures of Con (n = 1 – 5) clusters on γ-Al2O3 surfaces using first-principles calculations. Phys. Chem. Chem. Phys. 2017, 19, 3679–3687. 10.1039/c6cp06785a. [DOI] [PubMed] [Google Scholar]
- Yang T.; Fukuda R.; Hosokawa S.; Tanaka T.; Sakaki S.; Ehara M. A Theoretical Investigation on CO Oxidation by Single-Atom Catalysts M1/γ-Al2O3 (M=Pd, Fe, Co, and Ni). ChemCatChem 2017, 9, 1222–1229. 10.1002/cctc.201601713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deushi F.; Ishikawa A.; Nakai H. Density Functional Theory Analysis of Elementary Reactions in NOx Reduction on Rh Surfaces and Rh Clusters. J. Phys. Chem. C 2017, 121, 15272–15281. 10.1021/acs.jpcc.7b04526. [DOI] [Google Scholar]
- O’Brien C. P.; Lee I. C. A detailed spectroscopic analysis of the growth of oxy-carbon species on the surface of Pt/Al2O3 during propane oxidation. J. Catal. 2017, 347, 1–8. [Google Scholar]
- Faria W. L. S.; Perez C. A. C.; César D. V.; Dieguez L. C.; Schmal M. In situ characterizations of Pd/Al2O3 and Pd/CeO2/Al2O3 catalysts for oxidative steam reforming of propane. Appl. Catal., B 2009, 92, 217–224. 10.1016/j.apcatb.2009.07.001. [DOI] [Google Scholar]
- Wu X.; Zhang L.; Weng D.; Liu S.; Si Z.; Fan J. Total oxidation of propane on Pt/WOx/Al2O3 catalysts by formation of metastable Ptδ+ species interacted with WOx clusters. J. Hazard. Mater. 2012, 225–226, 146–154. 10.1016/j.jhazmat.2012.05.011. [DOI] [PubMed] [Google Scholar]
- Carlsson P.-A.; Mollner S.; Arnby K.; Skoglundh M. Effect of periodic operation on the low-temperature activity for propane oxidation over Pt/Al2O3 catalysts. Chem. Eng. Sci. 2004, 59, 4313–4323. 10.1016/j.ces.2004.06.024. [DOI] [Google Scholar]
- Hinz A.; Skoglundh M.; Fridell E.; Andersson A. An Investigation of the Reaction Mechanism for the Promotion of Propane Oxidation over Pt/Al2O3 by SO2. J. Catal. 2001, 201, 247–257. 10.1006/jcat.2001.3248. [DOI] [Google Scholar]
- Finocchio E.; Busca G.; Lorenzelli V.; Willey R. J. The Activation of Hydrocarbon CH Bonds over Transition Metal Oxide Catalysts: A FTIR Study of Hydrocarbon Catalytic Combustion over MgCr2O4. J. Catal. 1995, 151, 204–215. 10.1006/jcat.1995.1022. [DOI] [Google Scholar]
- Finocchio E.; Willey R. J.; Busca G.; Lorenzelli V. FTIR studies on the selective oxidation and combustion of light hydrocarbons at metal oxide surfaces. J. Chem. Soc., Faraday Trans. 1997, 93, 175–180. 10.1039/a605341f. [DOI] [Google Scholar]
- Wang B.; Wu X.; Ran R.; Si Z.; Weng D. IR characterization of propane oxidation on Pt/CeO2– ZrO2: The reaction mechanism and the role of Pt. J. Mol. Catal. A: Chem. 2012, 356, 100–105. 10.1016/j.molcata.2011.12.030. [DOI] [Google Scholar]
- O’Brien C. P.; Lee I. C. Kinetic Modeling of Spillover and Temperature-Programmed Oxidation of Oxy-Carbon Surface Species on Pt/Al2O3. J. Phys. Chem. C 2017, 121, 12329–12336. 10.1021/acs.jpcc.7b03858. [DOI] [Google Scholar]
- Porezag D.; Frauenheim T.; Köhler T.; Seifert G.; Kaschner R. Construction of tight-binding-like potentials on the basis of density-functional theory: Application to carbon. Phys. Rev. B: Condens. Matter Mater. Phys. 1995, 51, 12947–12957. 10.1103/physrevb.51.12947. [DOI] [PubMed] [Google Scholar]
- Elstner M.; Porezag D.; Jungnickel G.; Elsner J.; Haugk M.; Frauenheim T.; Suhai S.; Seifert G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B: Condens. Matter Mater. Phys. 1998, 58, 7260–7268. 10.1103/physrevb.58.7260. [DOI] [Google Scholar]
- Seifert G.; Porezag D.; Frauenheim T. Calculations of molecules, clusters, and solids with a simplified LCAO-DFT-LDA scheme. Int. J. Quantum Chem. 1996, 58, 185–192. . [DOI] [Google Scholar]
- Gaus M.; Cui Q.; Elstner M. DFTB3: Extension of the Self-Consistent-Charge Density-Functional Tight-Binding Method (SCC-DFTB). J. Chem. Theory Comput. 2011, 7, 931–948. 10.1021/ct100684s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishizawa H.; Nishimura Y.; Kobayashi M.; Irle S.; Nakai H. Three pillars for achieving quantum mechanical molecular dynamics simulations of huge systems: Divide-and-conquer, density-functional tight-binding, and massively parallel computation. J. Comput. Chem. 2016, 37, 1983–1992. 10.1002/jcc.24419. [DOI] [PubMed] [Google Scholar]
- Nishimura Y.; Nakai H. Dcdftbmd: Divide-and-Conquer Density Functional Tight-Binding Program for Huge-System Quantum Mechanical Molecular Dynamics Simulations. J. Comput. Chem. 2019, 40, 1538–1549. 10.1002/jcc.25804. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
- Chou C.-P.; Nishimura Y.; Fan C. C.; Mazur G.; Irle S.; Witek H. A. Automatized Parameterization of DFTB Using Particle Swarm Optimization. J. Chem. Theory Comput. 2016, 12 (1), 53–64. 10.1021/acs.jctc.5b00673. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. 10.1103/physrevlett.100.136406. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Digne M.; Sautet P.; Raybaud P.; Euzen P.; Toulhoat H. Hydroxyl Groups on γ-Alumina Surfaces: A DFT Study. J. Catal. 2002, 211, 1–5. 10.1006/jcat.2002.3741. [DOI] [Google Scholar]
- Digne M.; Sautet P.; Raybaud P.; Euzen P.; Toulhoat H. Use of DFT to achieve a rational understanding of acid–basic properties of γ-alumina surfaces. J. Catal. 2004, 226, 54–68. 10.1016/j.jcat.2004.04.020. [DOI] [Google Scholar]
- Valero M. C.; Raybaud P.; Sautet P. Nucelation of Pdn (n = 1 – 5) clusters and wetting of Pd particles on γ Al2O3 surfaces: A density functional theory study. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 75, 045427. 10.1103/physrevb.75.045427. [DOI] [Google Scholar]
- Shi X.-R.; Sholl D. S. Nucleation of Rhn (n = 1 – 5) Clusters on γ-Al2O3 Surfaces: A Density Functional Theory Study. J. Phys. Chem. C 2012, 116, 10623–10631. 10.1021/jp301114n. [DOI] [Google Scholar]
- Wang Y.; Su Y.; Kang L. Stability and nucleation of Irn (n = 1 – 5) clusters on different γ-Al2O3 surfaces: A density functional theory study. Phys. Lett. A 2016, 380, 718–725. 10.1016/j.physleta.2015.12.009. [DOI] [Google Scholar]
- Liu Z.; Wang Y.; Li J.; Zhang R. The effect of γ-Al2O3 surface hydroxylation on the stability and nucleation of Ni in Ni/γ-Al2O3 catalyst: a theoretical study. RSC Adv. 2014, 4, 13280–13292. 10.1039/c3ra46352d. [DOI] [Google Scholar]
- Liu Y.; Cen W.; Feng G.; Chu Y.; Kong D.; Yin H. First principles study on the adsorption of Ptn (n = 1 – 4) on γ-Al2O3(110) surface. Appl. Surf. Sci. 2014, 313, 424–431. 10.1016/j.apsusc.2014.05.226. [DOI] [Google Scholar]
- Li J.; Zhang R.; Wang B. Influence of the hydroxylation of γ-Al2O3 surfaces on the stability and growth of Cu for Cu/γ-Al2O3 catalyst: A DFT study. Appl. Surf. Sci. 2013, 270, 728–736. 10.1016/j.apsusc.2013.01.139. [DOI] [Google Scholar]
- Kobayashi M.; Nakai H. How does it become possible to treat delocalized and/or open-shell systems in fragmentation-based linear-scaling electronic structure calculations? The case of the divide-and-conquer method. Phys. Chem. Chem. Phys. 2012, 14, 7629–7639. 10.1039/c2cp40153c. [DOI] [PubMed] [Google Scholar]
- Nishimura Y.; Nakai H. Parallel implementation of efficient charge-charge interaction evaluation scheme in periodic divide-and-conquer density-functional tight-binding calculations. J. Comput. Chem. 2018, 39, 105–116. 10.1002/jcc.25086. [DOI] [PubMed] [Google Scholar]
- Laio A.; Rodriguez-Fortea A.; Gervasio F. L.; Ceccarelli M.; Parrinello M. Assessing the Accuracy of Metadynamics. J. Phys. Chem. B 2005, 109, 6714–6721. 10.1021/jp045424k. [DOI] [PubMed] [Google Scholar]
- Iannuzzi M.; Laio A.; Parrinello M. Efficient Exploration of Reactive Potential Energy Surfaces Using Car-Parrinello Molecular Dynamics. Phys. Rev. Lett. 2003, 90, 238302. 10.1103/physrevlett.90.238302. [DOI] [PubMed] [Google Scholar]
- Laio A.; Gervasio F. L. Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep. Prog. Phys. 2008, 71, 126601. 10.1088/0034-4885/71/12/126601. [DOI] [Google Scholar]
- Laio A.; Parrinello M. Escaping free-energy minima. Proc. Natl. Acad. Sci. U.S.A. 2002, 99, 12562–12566. 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chodera J. D.; Swope W. C.; Pitera J. W.; Seok C.; Dill K. A. Use of the Weighted Histogram Analysis Method for the Analysis of Simulated and Parallel Tempering Simulations. J. Chem. Theory Comput. 2007, 3, 26–41. 10.1021/ct0502864. [DOI] [PubMed] [Google Scholar]
- Gu J.; Wang J.; Leszczynski J. Structure and Energetics of (111) Surface of γ-Al2O3: Insights from DFT Including Periodic Boundary Approach. ACS Omega 2018, 3, 1881–1888. 10.1021/acsomega.7b01921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson S. J. The dehydration of boehmite, γ-AlOOH, to γ-Al2O3. J. Solid State Chem. 1979, 30, 247–255. 10.1016/0022-4596(79)90106-3. [DOI] [Google Scholar]
- Addicoat M. A.; Stefanovic R.; Webber G. B.; Atkin R.; Page A. J. Assessment of the Density Functional Tight Binding Method for Protic Ionic Liquids. J. Chem. Theory Comput. 2014, 10, 4633–4643. 10.1021/ct500394t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang R.; Swanson J. M. J.; Voth G. A. Benchmark Study of the SCC-DFTB Approach for a Biomolecular Proton Channel. J. Chem. Theory Comput. 2014, 10, 451–462. 10.1021/ct400832r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Settergren N. M.; Bühlmann P.; Amin E. A. Assessment of Density Functionals, Semiempirical Methods, and SCC-DFTB for Protonated Creatinine Geometries. Theochem 2008, 861, 68–73. 10.1016/j.theochem.2008.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliveira A. F.; Seifert G.; Heine T.; Duarte H. A. Density-functional based tight-binding: an approximate DFT method. J. Braz. Chem. Soc. 2009, 20, 1193–1205. 10.1590/s0103-50532009000700002. [DOI] [Google Scholar]
- Zheng G.; Irle S.; Morokuma K. Performance of the DFTB method in comparison to DFT and semiempirical methods for geometries and energies of C20–C86 fullerene isomers. Chem. Phys. Lett. 2005, 412, 210–216. 10.1016/j.cplett.2005.06.105. [DOI] [Google Scholar]
- Toro-Mendoza J.; Rodriguez-Lopez G.; Paredes-Altuve O. Brownian diffusion of a particle at an air/liquid interface: the elastic (not viscous) response of the surface. Phys. Chem. Chem. Phys. 2017, 19, 9092–9095. 10.1039/c6cp07442a. [DOI] [PubMed] [Google Scholar]
- Bai Z.-W.; Ding L.-P. Surface diffusion of a Brownian particle subjected to an external harmonic noise. Int. J. Mod. Phys. B 2017, 31, 1750082. 10.1142/s0217979217500825. [DOI] [Google Scholar]
- Zhu N.; Liu Y.-y.; Wang Y.; Chen F.-Q.; Zhan X.-l. Kinetic Models for the Coke Combustion on Deactivated ZSM-5/MOR Derived from n-Heptane Cracking. Ind. Eng. Chem. Res. 2010, 49, 89–93. 10.1021/ie900855y. [DOI] [Google Scholar]
- Mahamulkar S.; Yin K.; Agrawal P. K.; Davis R. J.; Jones C. W.; Malek A.; Shibata H. Formation and Oxidation/Gasification of Carbonaceous Deposits: A Review. Ind. Eng. Chem. Res. 2016, 55, 9760–9818. 10.1021/acs.iecr.6b02220. [DOI] [Google Scholar]
- Li C.; Minh C. L.; Brown T. C. Kinetics of CO and CO2 Evolution During the Temperature-Programmed Oxidation of Coke Deposited on Cracking Catalysts. J. Catal. 1998, 178, 275–283. 10.1006/jcat.1998.2135. [DOI] [Google Scholar]