Jump point detection using empirical mode decomposition

Highlights

• •A robust signal decomposition method, EMD for removing noise from the real world time series is present.
• •A third-order derivative based detector is proposed to capture the jump points of the time series.
• •The housing price indices and stock price index are evaluated.
• •The proposed method can detect more jump points that correspond to the announcement of some international/regional regulation and policies.
• •The proposed method does not have any sensitive parameter.

Abstract

Real estate is an important form of investment in Hong Kong. Recent researches on the analysis of real estate market have revealed that jump points in the housing price time series play an essential role in the Hong Kong economy. Detecting such jump points thus becomes important as they represent vital findings that enable policy-makers and investors to look forward. In this paper, we propose a jump point detection methodology, which makes use of the empirical mode decomposition algorithm and a derivative-based detector, to detect jump points in the time series of some housing price indices in Hong Kong. Experimental results reveal that our proposed method has a superior performance and outperforms the current state-of-the-art wavelet approach.

1. Introduction

Real estate is one of the most important forms of investment and plays an essential role in the economy of Hong Kong. It is believed that changes in housing prices would influence consumer price inflation and have substantial impact on the economy, which subsequently may also affect the competitiveness of Hong Kong. As Hong Kong has adopted a free market economic system and its economy is governed under positive non-interventionism, the level of government interventions in the economy is comparatively low in the world. Resulted from high degree of economic freedom, the real estate market in Hong Kong is basically market-driven and dependent on demand and supply. Nevertheless, the Hong Kong government is the only supplier of new developable land, it has far more ability to influence the housing prices than aggregate demand. The short of land and housing would lead to the rise in housing prices and rents. Thus, land supply is one of the major factors affecting the housing prices. For instance, the Hong Kong government introduced detailed measures to improve the flexibility of land use and land supply in March 1994, which made the property prices drop by 20%–30% in 1994–1995. In addition to some other factors affecting the market downturns, we believe that the government’s land use policies also have had impact on the real estate market. More recently, the Hong Kong government has gradually been introducing various “cooling” measures to cool the overheating real estate market and stamp out short-term speculation. For instance, stamp duty was raised to 4.25% for properties worth more than HK$20 million since February 2010; My Home Purchase Plan was introduced and Special Stamp Duty (SSD) was imposed in November 2010; the Buyer’s Stamp Duty (BSD) for non-permanent residents and foreign companies was introduced in October 2012; and the Double Stamp Duty (DSD), which doubles the stamp duty rate for property transactions, was announced in February 2013. These measures appeared to have temporarily cooled down the real estate market to some extent.

Many studies in the literature indicated that housing prices in Hong Kong are subject to international and regional economic events. For instance, due to the Asian financial crisis began in early 1997, Hong Kong suffered an economic recession and the real estate market was badly hit with property prices dropped by more than 40% between the last quarter of 1997 and the last quarter of 1998. Given the importance of real estate in Hong Kong economy, it is essential to study what drives the changes in Hong Kong’s housing prices and how real estate market is influenced by international and regional economic events.

In the studies on real estate market, it is well known that housing prices are influenced by many key factors such as interest rate (mortgage rate), land supply and inflation rate (see, for example, Tian and Ma, 2009, Tsatsaronis and Zhu, 2004). Thus many researchers proposed various statistical methodologies for modeling housing price measurements and assessing the importance of these factors. However, we remark that jump points may occur in financial and housing price measurements that will affect the overall analysis of the time series. Jump points, sharp or abrupt changes are typically related to some regional or international events which are possibly driven by government policies and economic events, and thus, detecting and identifying these sharp changes are vital since they reveal important findings that enable policy-makers and investors to look forward. Since such sharp changes may be caused by a mixture of information and noise, it is difficult to observe them directly in the time series. Hence the detection of these sharp changes has drawn much attention from researchers and practitioners.

Motivated by the recent researches on jump point detection, the aim of this paper is to propose an effective approach for identifying and detecting jump points in the time series of Hong Kong housing price indices. In the proposed method, we apply the empirical mode decomposition (EMD) (Rilling et al., 2003, Rilling et al., 2007, Huang and Shen, 2005) to decompose a given signal1 into a set of sub-signals. A series of reconstructed signals are then obtained by sub-signals concatenation. Finally, the jump points are detected based on the rate of change in each of the reconstructed signals. The merits of our approach are threefold. First, adaptive basis functions are used in the decomposition process that leads to an effective reconstruction of the original signal, which can enhance the detection of jump points. Second, a high-level derivative detector is proposed that can improve the detection performance for a highly nonlinear and fluctuated signal. Third, our method does not introduce any sensitive parameter. Comparative experimental results show that our method outperforms the wavelet approach in Hui et al. (2010).

This paper is organized as follows: we are providing a literature review in the next section, presenting the proposed jump point detection methodology in Section 3, reporting experimental results in Section 4, which is followed by the conclusion in Section 5.

2. Literature review

2.1. Applications of jump point detection

The detection of jump points, sharp or abrupt changes (for simplicity, we shall refer all sharp or abrupt changes to as jump points hereafter) has been applied successfully in various fields such as quality control, economics and finance, signal and image processing, and engineering. In Willsky and Jones (1976), the authors demonstrated that jump point detection is useful in the design of failure detection and compensation systems. Basseville and Nikiforov (1993) discussed the theory and applications of jump point detection in quality control, navigation system monitoring, seismic data processing, segmentation of signals and vibration monitoring of mechanical systems. Some studies discuss the applications to stock data, exchange and interest rate series. For instance, Ip et al. (2004) proposed a computing algorithm to detect jump points of the daily exchange rate of US Dollar against Deutsche Mark. Hillebrand and Schnabl (2006) and Ito (2003) identified jump points in the exchange rate series to study the impact of Japanese foreign exchange intervention. Lavielle and Teyssière (2006) detected jump points in the multivariate series of daily stock indices returns while Strikholm (2006) applied a sequential method to investigate and determine the number of breaks in the US ex-post real interest rate series. More examples on the applications of jump point detection in stock exchange data can be found in Wang (1995) and Arago-Manzana and Fernandez-Izquierdo (2007). The jump point detection is also applicable to the study of crude oil markets (see, for example, Kang et al., 2011). More recently, Hui et al. (2010) detected jump points in the time series of private domestic price indices in Hong Kong. They further investigated the effects of various economic events on four Asian office markets (Hui et al., 2013) (including Beijing, Shanghai, Hong Kong and Singapore) by detecting the jump points.

2.2. Methodologies of jump point detection

Various approaches for the detection of jump points have been extensively studied in the literature. Muller (1992) adopted a nonparametric regression approach to obtain weakly consistent estimators for the locations of jump points and the corresponding jump sizes. Yin (1988) proposed a detection method for the number, location and magnitudes of jumps of a regression function in the presence of noise. While the aforementioned methods work well, satisfactory results are obtained by manually selecting an appropriate regression kernel. We remark that a small kernel will lead to spurious jump point locations whereas a large kernel may not detect jump points with relatively small jump sizes. Based on the sequence of parameter constancy tests in the smooth transition regression framework, a sequential method was used in Strikholm (2006) for determining the number of breaks in a piecewise linear structural break model, which breaks the time series into a number of polynomial functions. In addition, Yang and Song (2014) proposed a polynomial spline approach for jump point detection and the estimation of the discontinuities of regression functions. Although these methods provide a sound mathematical theory that underpins the validity of the framework, we note that their methods may miss the jump points with small jump sizes. Moreover, some of the detection methods perform well only for a data set with moderate size.

In addition to the approaches mentioned above, a time-frequency transformation method is also popular in the literature. Lombard (1988) applied Fourier transform to extract details from the signal. With the use of Fourier analysis, jump points could be detected but their locations (i.e. time) cannot be identified. In addition, some jump points may be missed due to the smoothness of the Fourier basis function. To remedy the shortcoming of Fourier transform, Hui et al. (2010) presented a wavelet method with non-smooth Haar wavelet for detecting jump points in the time series of the private domestic price indices and stock price index. They found that jump points detected by the wavelet approach reflect the announcement of regulations/policies or some regional/international events. With reference to the wavelet approaches in Ip et al. (2004) and Donoho and Johnstone (1994), Hui et al. (2013) employed an improved nonparametric wavelet model to detect jump points in the Asian office markets. Although wavelet approaches usually achieve promising results, the major drawback is that it adopts a fixed basis function which may not approximate signals very well.

3. Jump point detection

One of the main characteristics of a jump point in a time series is its sharp changes (ascent or descent) in a consecutive time period, which can be detected by measuring its rate of change. A larger rate of change implies a sharper change and vice versa. Our strategy to detect a jump point from the complicated real-world time series involves the following two stages. We first employ the EMD algorithm to obtain a set of the smoothed versions of original signal. Then we detect jump points by measuring the rate of change in each of the smoothed signals.

3.1. Empirical mode decomposition

Empirical mode decomposition (EMD) aims to decompose a given signal $x(t)$ into n elementary sub-signals (Rilling et al., 2003, Huang and Shen, 2005) as follows:

$$x(t)=c_1(t)+c_1(t)+\cdot \cdot \cdot +c_n(t)+r(t)$$

where $c_1(t)$, $c_2(t)$, …, $c_n(t)$ are the Intrinsic Mode Functions (IMF) and $r(t)$ is the residual. The EMD has been widely used in time-frequency analysis applications including audio engineering (Klügel, 2012), climate analysis (Barnhart and Eichinger, 2011), various flux, respiratory and neuromuscular signals found in medicine and biology (Assous et al., 2005, Andrade et al., 2006, Liu et al., 2008, Mostafanezhad et al., 2009), etc. Generally speaking, the EMD algorithm recursively detects local extrema in the signal followed by estimating the lower/upper envelopes based on the interpolation of these extrema. The average of the envelopes, which is a low-pass centerline, is then removed from the signal and the high-frequency oscillations (i.e. IMF), which capture the oscillatory patterns of the original signal, are extracted.

Fig. 1 summarizes the EMD algorithm. The algorithm starts by identifying all extrema from the input signal based on the first derivative test (i.e., Step 2(a)), which is used to check whether a function “switches” from increasing to decreasing (maxima) or decreasing to increasing (minima). All the local minima/maxima are then interpolated using the cubic spline so as to form the lower and upper envelopes (i.e., Step 2(b)). In Steps 2(c)–(d), the mean envelope is obtained by taking the average of lower and upper envelopes and the residual is obtained by subtracting the mean envelope from the input signal. There are two stopping criteria in the algorithm. The first one is the validity check for the IMFs as shown in Step 2(e) and the second one is the termination of the algorithm in Step 3 (Rilling et al., 2007). In Step 2(e), the residual is regarded as an IMF if $(({\displaystyle \underset{t}{\mathrm{\Sigma }}}{\left(r_{k-1}(t)-r_k(t)\right)}^2)/({\displaystyle \underset{t}{\mathrm{\Sigma }}}{\left(r_{k-1}(t)\right)}^2))\le 0.5$. Briefly speaking, this stopping criterion measures the relative difference between two residuals. Note that when $r_k(t)=r_{k-1}(t)-m_k(t)$, the stopping criterion becomes $(({{\displaystyle \underset{t}{\mathrm{\Sigma }}}\left(m_k(t)\right)}^2)/{\displaystyle \underset{t}{\mathrm{\Sigma }}}{\left(r_{k-1}(t)\right)}^2)\le 0.5$. In other words, the IMF is obtained when the mean envelope $m_k\left(t\right)$ can only capture weak oscillatory patterns of the original signal. In Step 3, the algorithm ends when the number of extrema of $r_k(t)$ is less than three or the number of extrema and the number of zero-crossings differ at most by 1 (Rilling et al., 2007).

Fig. 1.

Empirical model decomposition algorithm.

Fig. 2 shows an example of applying the EMD algorithm to the time series. Fig. 2(a) is the original time series $x(t)$ and Fig. 2(b)–(g) display the reconstructed signal $D_m(t)={\displaystyle \sum _{k=1}^m}{c}_{n-k+1}(t)+r(t)$, where $m=1,\mathrm{2,...},n$, with $D_0(t)=r(t)$. Note that when m is small, $D_m\left(t\right)$ represents the general trend of $x(t)$. When m becomes larger, $D_m\left(t\right)$ looks more similar to $x(t)$. In case $m=n$, $D_m(t)=x(t)$, i.e., the time series is completely reconstructed by the IMFs.

Fig. 2.

Signal reconstruction using the EMD algorithm: (a) Original time series; (b)–(g) $D_0(t)$–$D_5(t)$.

3.2. Derivative-based detector

In this section, we introduce the derivative-based jump point detection based on the reconstructed signals obtained from the EMD algorithm discussed in the previous section. As explained before, the jump point has a very sharp change (ascent or descent) in a consecutive time period and the degree of sharpness can be captured by measuring the rate of change of the time series. If the rate of change has a very large positive (negative) value at a time period, then there is a steepest “ascent” (“descent”) at that particular time. To identify the steepest ascent/descent of the rate of change, we employ the second order derivative of the rate of change, which is exactly equivalent to the third order derivative of the time series. Our strategy to find jump points is to apply the third order derivative to each of the reconstructed signals $D_m\left(t\right)$, where $m=1,\mathrm{2,...},n$, and then computes the average of the third order derivatives of all $D_m(t)$, i.e.,

$$M(t)=\frac{1}{n}{\displaystyle \sum _{m=1}^n}\frac{d^3}{d{t}^3}{D}_m(t)$$

The merit of this average value is that the steepest “ascent” and “descent” are counted repeatedly in all $D_m\left(t\right)$, and therefore, the jump points would correspond to the larger average values in $M\left(t\right)$. In our case, all data points that are z standard deviation away from the mean of $M\left(t\right)$ are regarded as jump points. Hence, a given signal at time t is said to be a jump point if,

$$M(t)>\mu +z\sigma \text{or}M(t)<\mu -\mathrm{z}\sigma$$

where μ and $\sigma$ are the mean and standard deviation of $M(t)$, respectively. We have tried different values of z in all the following experiments2 and the results show that $\text{z}=1.5$ gives the best results, and thus, we shall simply use $\text{z}=1.5$ in this paper.

4. Experiments

4.1. Data source

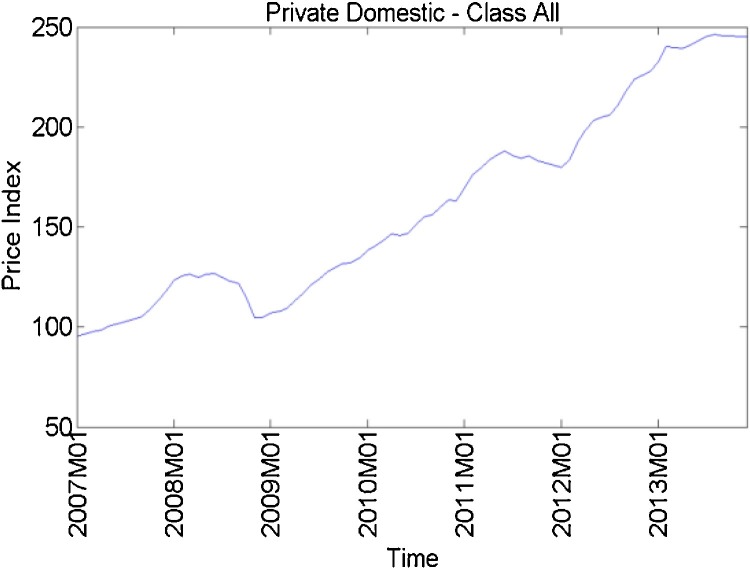
We examine the Hong Kong residential housing price indices as shown in Fig. 3 . The private domestic price indices are monthly price indices from January 2007 (2007M01) to December 2013 (2013M12) obtained from the Rating and Valuation Department (RVD) of Hong Kong Special Administrative Region (HKSAR).

Fig. 3.

Private domestic price index of all classes.

According to the RVD, the private domestic comprises independent domestic units with an exclusive cooking area, bathroom and toilet, but does not include village houses, quarters held by the people’s Liberation Army, quarters attached to premises of utility companies, dormitories (student dormitories), quarters held by the Hospital Authority, hotels and hostels. In addition, private domestic units are subdivided into Classes A, B, C, D and E by reference to floor area as shown in Table 1 .

Table 1.

Classification of private domestic units.

Private Domestic Unit	Saleable Area
Class A	Less than 40 m2
Class B	40 m2 to 69.9 m2
Class C	70 m2 to 99.9 m2
Class D	100 m2 to 159.9 m2
Class E	160 m2 or above

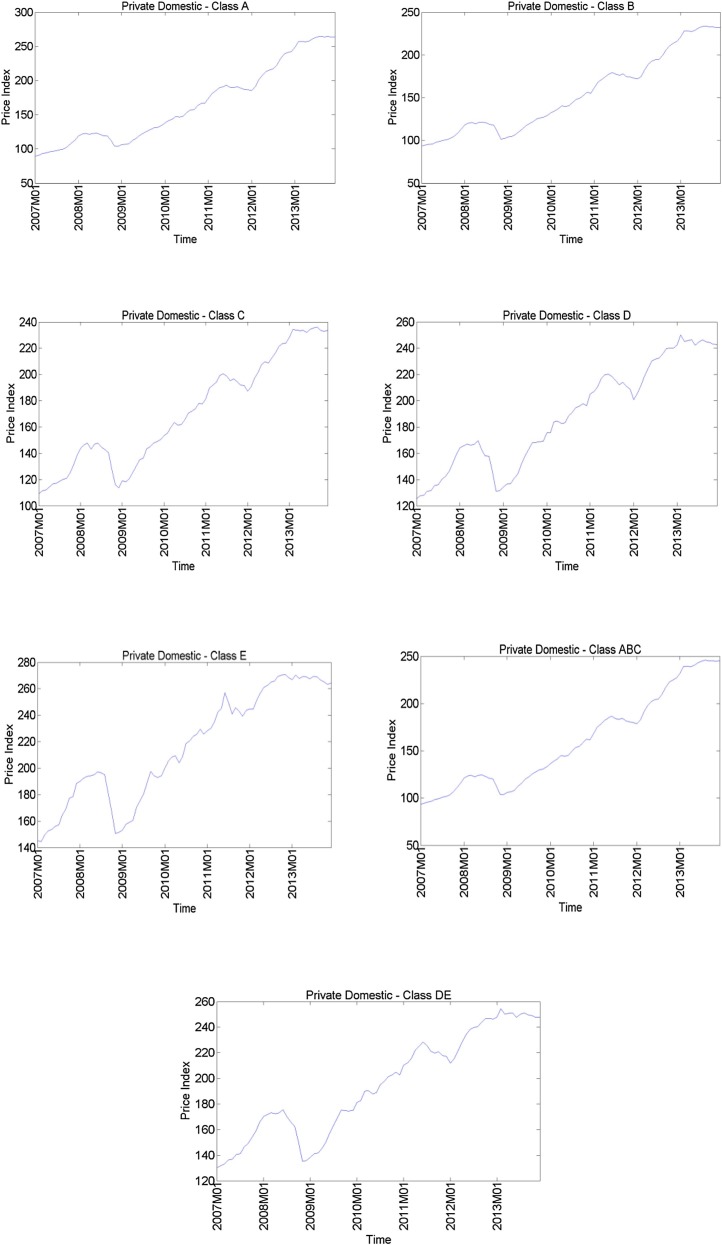
On the basis of the classification shown in Table 1, the private domestic units can also be divided into two subsectors, namely, small/medium units and large/luxury units. The former comprises units with saleable area of less than 100 m² (i.e. Classes A, B and C) whereas the latter represents units with saleable area of 100 m² or above (i.e., Classes D and E). For simplicity, we shall refer small/medium units to as ‘ABC’ and large/luxury units to as ‘DE’. Fig. 4 shows the private domestic price indices for different classes.

Fig. 4.

Private domestic price indices by class.

4.2. Results and discussion

We apply the proposed method to the Hong Kong residential housing price indices. The results are summarized in Table 2 where “✓” represents that a jump point is detected for a housing price index in that period of time. The discussions on the jump points are as follows.

• (a)The Global Financial Crisis 2007–2009 was triggered by the bursting of the United States (U.S.) housing bubble in July 2007, leading to the steep fall in the values of securities tied to U.S. real estate pricing, impact on global stock markets and bankruptcy of some financial institutions. The Hong Kong residential property market was vigorous in 2007. The residential housing prices in the secondary market recorded a notable growth in the fourth quarter of 2007. Meanwhile, the residential property transactions, especially of properties with valued between HK$1 million and HK$2 million, rose. This is probably due to the fact that the interest rates fell, household incomes increased, and the rate of stamp duty on transaction of properties in this price bracket decreased. Jump points in the domestic price indices of Classes B, D and ABC are detected in 2007M11–M12 and 2008M3. In addition, jump points in all the domestic price indices are detected in 2008M9–M10, reflecting the impact of the Global Financial Crisis.
• (b)The Hong Kong economy came out of recession in 2009. The GDP grew and unemployment rate slid alongside the economic recovery. The market demand was stimulated by the inflow capital and low interest rate, leading to an increase in residential housing prices. In particular, the prices of luxury domestic units were fuelled by the inflow capital. To temper the surge of luxury domestic units, the Hong Kong Monetary Authority (HKMA) issued guidelines to banks in October 2009 capping the mortgage loan of properties priced HK$20 million or above to 60% and limiting the maximum loan amount at HK$12 million for properties priced below HK$20 million. It seems that the effect of the move was mild and no jump points are detected around that period. The residential property market continued to grow in 2010. To discourage short-term sales of residential properties, the HKSAR government proposed to increase the stamp duty for properties priced over HK$20 million in February 2010. In addition, the SSD was imposed in November 2010 on properties resold within 24 months. Transactions and flipping trade fell notably after the introduction of SSD in late 2010. The HKSAR government continued to introduce measures in 2011 to curb property speculation, prevent excessive expansion in mortgage lending and ensure transparency in the property market, and hence ensure the healthy and stable development of the residential property market. Residential property prices experienced a market correction in the second half of 2011. Jump points in most of the domestic price indices are detected in 2010M5, 2010M11–2011M1 and 2011M7–M8. After a respite in late 2011, the property prices resumed rising and trading activities grew again in 2012. Domestic price units recorded an average increase of 25.2%. It is observed that jump points are detected for most of the domestic price indices in 2012M2–M3.
• (c)To suppress speculation on residential properties, the HKSAR government announced two new measures in October 2012. The first one was the BSD for non-permanent residents and foreign companies and the second one was to adjust the rates and extend the SSD for another 3 years. In February 2013, the HKSAR government announced new stamp duty measures, DSD, to double the rates of stamp duty on property transactions, applicable to all persons, except Hong Kong permanent residents buying residential properties but who do not own any residential property in Hong Kong at the date of agreement. After the HKMA further tightened the prudential measures, the property market experienced a period of consolidation in 2013. Residential property price inflation was softened and speculative transactions almost vanished. Jump points in most of the domestic price indices are detected to reflect the policies issued during the period 2013M1–M3.

Table 2.

Jump points detected by the proposed method (2007–2013).

Time	Class
	A	B	C	D	E	ABC	DE	All
2007M11–M12		✓		✓		✓		✓
2008M3		✓				✓		✓
2008M9–M10	✓	✓	✓	✓	✓	✓	✓	✓
2010M5		✓	✓			✓	✓	✓
2010M11–2011M1	✓	✓	✓		✓	✓	✓	✓
2011M7–M8	✓		✓		✓	✓	✓
2012M2–M3	✓	✓	✓	✓		✓	✓	✓
2013M1–M3	✓	✓	✓	✓		✓	✓	✓

4.3. Comparative results

We shall compare our proposed method with the wavelet approach in Hui et al. (2010). Briefing speaking, this approach applied discrete wavelet transform with Haar wavelet to the time series of housing price indices and the jump points were detected by the hard threshold on the wavelet coefficients. Since the dataset used in Hui et al. (2010) is monthly price indices from January 1993 (1993M01) to December 2006 (2006M12), we shall apply our proposed method to the same dataset and the results are shown in Table 3 . The discussions on the jump points for our approach are as follows.

• (a)The U.S. experienced an interest rate hike cycle in 1993–1994 which in turn significantly affected the Hong Kong real estate market and stock market. In our analysis, jump points are detected for the domestic price index of all classes in the period 1993M9–1993M11.
• (b)In February 1994, the HKMA made two prudential recommendations to the banks to maintain their ration of property lending to loans. The recommendations were (i) to introduce a 40% benchmark for property lending by financial institutions and (ii) to propose a benchmark on the growth of property lending at 15% per annum, in line with the growth of nominal GDP.3 At the same time, the HKSAR government maintained a tight fiscal policy. In March 1994, the HKSAR government introduced detailed measures to improve the flexibility of land use and land supply, and to curb speculation in properties. These caused the market downturns in 1994–1995 and property prices fell by 20%–30%. Changes in the prices of almost all private domestic units are detected in 1994M4–M6 by our method. Moreover, jump points in the domestic price indices of Classes A, D and DE are detected in 1995M1. Note that there are no jump points detected in the domestic price index of Class E in this time period. This is probably due to the fact that property speculation usually occurred in small/medium units. Class E comprises luxury units of largest size and the curb on property speculation has less influence on such luxury units.
• (c)Jump points in most of the domestic price indices are detected in 1996M12–1997M1. This reflects the political worries about the handover of Hong Kong to China. After the handover of Hong Kong sovereignty to China on 01 July 1997, the Asian financial crisis started with attacks on currencies in the region. Hong Kong was involved in the crisis and the Hang Seng Index fell by 22.8% between 20 and 23 October 1997. At least up till early 1999, the crisis had not yet been over and the general atmosphere in the economy remained pessimistic. The financial sector was the first to suffer from this economic turmoil while Hong Kong was mired in an economic recession throughout 1998. In the subsequent correction in the wake of the Asian financial crisis, real property prices dropped by more than 40% between the last quarter of 1997 and the last quarter of 1998, returning to their levels in the early 1990s. As the Asian financial crisis has a disastrous effect on the real estate, changes in prices of private domestic units are detected in 1997M11–1998M1.
• (d)In his maiden Policy Speech on 08 October 1997, the Chief Executive of the HKSAR set out three main targets: to build at least 85,000 flats a year in the public (55,000) and private (30,000) sectors; to raise home ownership rate from 50% to 70% in ten years; and to reduce the average waiting time for public rental housing from seven to three years. In June 1998, the HKSAR government announced a nine-month moratorium on land sale and thereby disrupted the adjustment mechanism of the property market. The policy was another main factor that caused the real estate bubble burst. Hence, jump points in domestic price indices for most classes are detected in 1998M6, 1998M10 and 1998M12–1999M2.
• (e)The Hang Seng Index recovered from the Asian financial crisis in 1999 with a year high of 16,962 in November 1999. The residential property market was reacting slowly to the event in 2000 and the residential property prices fell by about 10% during the first quarter of 2000. Jump point in the domestic price index of Class A is detected in 1999M11–2000M1. We believe that small private domestic units are more volatile than large private domestic units, and thus, the jump points are only detected for small units.
• (f)Due to the Severe Acute Respiratory Syndrome (SARS) outbreak in the second quarter of 2003, Hong Kong experienced very difficult economic conditions in the first half of 2003. When SARS was brought under control, the market started to improve in May. The property market was also affected by SARS but a couple of factors (i.e. the economic recovery, new supply restraint measures introduced in November 2002, an associated rise in consumer optimism and low funding costs) led to a revival of the market in the last few months of 2003. The property market continued to recover from SARS in 2004. Residential property prices increased by 27.4% during the year of 2004. The recovery of property market was continued in the first quarter of 2005. However, the increases in interest rate since March had an impact on the property market and led to a decline in the prices in late 2005. Despite the decline, private residential property prices increased moderately by 6.7% in 2005. In our analysis, changes in prices of private domestic units in Classes D, DE and ABC occurred successively in 2004M9 and 2005M4.

Table 3.

Jump points detected by the proposed method (1993–2006).

Time	Class
	A	B	C	D	E	ABC	DE	All
1993M9–M11								✓
1994M4–M6	✓	✓	✓	✓		✓	✓	✓
1995M1	✓			✓			✓
1996M12–1997M1	✓		✓	✓	✓	✓		✓
1997M11–1998M1		✓	✓	✓	✓	✓	✓	✓
1998M6	✓	✓	✓	✓	✓	✓	✓	✓
1998M10	✓	✓				✓	✓	✓
1998M12–1999M2			✓	✓	✓
1999M11–2000M1	✓
2004M9				✓			✓
2005M4						✓	✓

The jump point detection results (1993M01–2006M12) using the wavelet approach are summarized in Table 4 . We observe that almost all jump points detected in Hui et al. (2010) can be detected by our method. In addition, we can also detect some jump points which are not otherwise detectable by the wavelet approach. This implies that our proposed method outperforms the wavelet approach, which is mainly due to the following reasons:

• •The greatest difference between wavelet and EMD is the basis function. Wavelet transform adopts a fixed basis whereas the EMD approach adopts an adaptive basis. The Haar wavelet used in Hui et al. (2010) is a square-shaped basis, which does not approximate signals very well. For the adaptive basis used in the EMD approach, the basis functions have different shapes. These basis functions are specifically designed so that a series of reconstructed time series can be obtained according to the trend of the original time series (see Fig. 2 for example). Intuitively, the general trend can reveal the jump points more effectively, and therefore, the EMD approach is better than the wavelet approach in Hui et al. (2010).
• •The approach in Hui et al. (2010) applied two-level wavelet decomposition with square-shaped Haar wavelet to the time series of housing price indices, and thus the wavelet approach adopted a low-level derivative detector to detect jump points. The EMD approach uses an adaptive basis and a third order derivative to detect jump points and thus a high-level derivative detector is used in the proposed method. Since the time series is highly nonlinear and fluctuated, it is expected that a high-level derivative detector will outperform a low-level derivative detector.
• •The results of wavelet approach highly depend on the threshold value on the wavelet coefficients. This means a slight change in threshold value will lead to a large detection error (Hui et al., 2010). On the other hand, our proposed method is not sensitive to any parameters in the EMD algorithm and derivative-based detector.

Table 4.

Jump points detected by the wavelet approach (1993–2006).

Month	Class
	A	B	C	D	E	ABC	DE	All
1993M9–M11
1994M4–M6
1995M1					✓		✓
1996M12–1997M1	✓	✓	✓			✓		✓
1997M11–1998M1			✓	✓			✓
1998M6	✓	✓	✓	✓		✓	✓	✓
1998M10
1998M12–1999M2
1999M11–2000M1
2004M9
2005M4						✓

5. Conclusion and future work

Empirical mode decomposition plays an important role in signal processing and has been widely used in many applications. However, to the best of our knowledge, the use of EMD for jump point detection has not been studied in the literature. To fill the gap, we have employed the EMD and an effective derivative-based detector to detect jump points in the time series of the Hong Kong housing price indices. Comparative experiments have revealed that our proposed method generally performs better than the wavelet approach.

Our experimental results have shown that jump points detected by the proposed method correspond to the announcement of some international/regional regulation and policies. As real estate is an important form of investment, it is essential to understand the characteristics of the housing prices for investment success from the investor’s point of view. Jump points can also be viewed as an upward/downward signal to investors for them to take appropriate action afterwards. Our study reveals that some government policies/measures related to real estate have inferences to housing prices to some extent, which in turn impact the economy of Hong Kong and result in affecting the competitiveness of Hong Kong. For instance, the application of DSD is to stem the possibility of speculative capital being redirected away from residential to non-residential properties. However, this has indirectly penalized corporate owner-occupiers and long-term investors and hence has an adverse impact on business sectors. Thus the government should take into consideration “side-effects” which would likely affect the economy before launching its policies or measures on real estate.

While our proposed method provides promising jump point detection results, we shall study the following aspects in future work.

• •We are applying the jump point detection approach to the Hong Kong residential housing price indices only. More analyses of the proposed method to different market indices and indices of other countries should be done in the future.
• •It is believed that Hang Seng Index and Real Estate Index may have lead-lag effect. Investigating the relationship between these two indices is important and useful for investors to make decision in the market.

Biographies

Dr. Lam received both B.Sc. and M.Phil. in Mathematical Science from the Department of Mathematics at the Hong Kong Baptist University. Then, he went to City University of Hong Kong to peruse his Ph.D. degree. Upon his completion of Ph.D. degree, he joined Griffith University (Brisbane, Australia) as a researcher for two years.

Dr. Yu received her B.Sc. in Mathematics with FINANCE from the University of Hull. She obtained her M.Phil. and Ph.D. degree from the Hong Kong Polytechnic University. Her major research interests include asset management, risk management, financial optimization and option pricing.

Dr Choy received his B.Sc. in Mathematical Science, M.Sc. in Scientific Computing (Graduated with Distinction), and Ph.D. in Mathematics, all from the Department of Mathematics at the Hong Kong Baptist University. Before joining HSMC, he was a Research Fellow in the Centre for Biotechnology and Informatics, The Methodist Hospital Research Institute, Weill Medical College of Cornell University in USA, and a Research Assistant and Postdoctoral Research Fellow at the Hong Kong Baptist University.

Dr Leung is an Assistant Professor in the Department of Mathematics and Statistics at Hang Seng Management College. He obtained his B.Sc. and Ph.D. at the Hong Kong Baptist University. Before joining HSMC, he was a Postdoctoral Scholar at Hong Kong Baptist University.