Characteristics of air pollutant dispersion around a high-rise building

Abstract

A numerical wind tunnel model was proposed. The computed results of the pollutant diffusion around a typical Hong Kong high-rise building model (at a linear scale of 1:30), were found to show a similar trend to the outcomes of self-conducted experimental measurements that the pathways of pollutant migration for windward and leeward pollutant emission are different. For the case with windward pollutant emission at the 3rd floor within a re-entry, the pollutant migrated downwards due to the downwash created by the wind. In contrast, for the case with leeward pollution emission, dispersion is dominated by intense turbulent mixing in the near wake and characterized by the upward migration of the pollutant in the leeward re-entry. The simulated results of haze-fog (HF) studies confirm that the pathway of pollutant migration is dominated by wind–structure interaction and buoyancy effect only plays a minor role in the dispersion process.

Graphical abstract

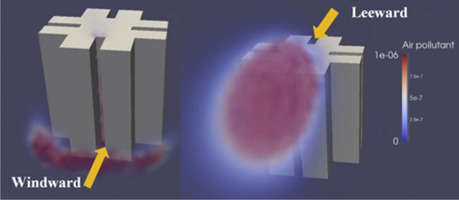
Highlights

• •A self-developed numerical wind tunnel model was proposed.
• •Characteristics of air pollutant dispersion with windward/leeward emission were discussed.
• •Wind–structure interaction controls the air pollutant dispersion around the building.

The different characteristics of air pollutant dispersion around a high-rise building, for both cases of a dispersion source in either the windward face or leeward face, are dominated by wind–structure interaction, with buoyancy effect playing only a minor role.

1. Introduction

1.1. Motivations

The degradation of air quality in an urban environment becomes one of the most serious life quality and public health issues nowadays. Poor quality air promotes the spread of respiratory and other communicable diseases (Portney and Mullahy, 1990), and even results in serious cardiovascular diseases (Brook et al., 2004), particularly for the very young and very old, and people with chronic diseases and those with immune deficiency. The alarming progressive degradation of air quality worldwide is attributable to the growth of manufacturing and resource industry in East and South Asia to meet the burgeoning demand for goods and services by a growing affluent population, a lack of control of air pollution caused by fossil fuel combustion to meet the demand for energy and the inadequacy of air ventilation in urban area where a large proportion of the world population reside (Alejo et al., 2010, Lu et al., 2012). Evidently, building arrays and street canyons have an undesirable impact on the ground level wind flow, air ventilation within the urban fabric, as well as the dispersion of air pollution; however wind–structure interaction which governs the effects of buildings on atmospheric flow is often not properly considered when making urban development and urban planning decisions (Abd Razak et al., 2013).

Although dispersion of air pollutant and air ventilation in urban environment attracts great research interest, there remains a lack of understanding of the mechanism as it includes complicated phenomenon, for example pollutant transport in high turbulent flow, buoyancy flows, flow separation and reattachment around buildings, and vortex-induced flow around buildings. Among these elements, which one drives the spread of pollutant/respiratory ailment the most is still a controversial issue. For instance, after the outbreak of Severe Acute Respiratory Syndrome (SARS) in Hong Kong in 2002, many researches have been reported to address the mechanisms of disease spreading. Nevertheless, it remains unclear whether buoyancy effect or wind flow plays the more significant role (Niu and Tung, 2008, Yip et al., 2007, Zhou and Jiang, 2004, Li et al., 2005). Hence a reliable method is urgently needed for the assessment of air ventilation and air quality in urban environments.

1.2. Background

One of the most common approaches adopted for the study of air pollution and air ventilation is a wind tunnel model test, in which the measurements of airflow and pollutant transport around building models are performed in a physical wind tunnel. An alternative approach is a numerical wind tunnel method, which builds a computational model and performs computational fluid dynamics (CFD) to predict the air flow and distribution of pollutant concentrations. The advantages and disadvantages of both methods are outlined hereunder.

Physical wind tunnel test is a widely accepted method and considered the main source of information for wind flow and pollutant dispersion around buildings and in street canyons (Pavageau and Schatzmann, 1999, Meroney et al., 1996, Hajra et al., 2013, Liu et al., 2010). One of the advantages of wind tunnel test is that model testing in a wind tunnel produces a set of physical data. The physical data are reliable provided that the test processes and measurements are undertaken in accordance to established experimental methods. However, there are also obvious limitations of physical wind tunnel test: the building models must be scaled down to fit in the wind tunnel, which creates low resolution of the measurements; and the boundary effect of the wind tunnel cannot be fully eliminated from the test. Although the physical measurements obtained in a wind tunnel model test are reliable, a scaled model is not a true reproduction of the real world. The need to satisfy the governing scaling and similitude requirements, such as Reynolds Number and Froude Number scaling, remains a formidable challenge.

An alternative approach is using computational technology to build a numerical wind tunnel. According to previous attempts (Li et al., 2006, Moonen et al., 2006, Endalew et al., 2009, Chavez et al., 2011, Blocken et al., 2012), a numerical wind tunnel approach has a number of advantages. The calculation domain of a numerical wind tunnel is adjustable and different boundary conditions can be applied so that the boundary effects on the simulations are minimized. If the computational power is large enough to accommodate a proper calculation domain, a numerical wind tunnel can test life-size objects, so that the scale effect can be minimized. However, there are limitations for existing numerical wind tunnels. Most notably the adopted numerical method affects the simulated results, i.e. different numerical scheme, different grid arrangement may make significantly different predictions.

It is noteworthy that the uncertainties of the simulation results are the main drawback of existing numerical wind tunnels. There are a number of studies using two-equation RANS models, including $k-\epsilon$, RNG-$k-\epsilon$, realizable $k-\epsilon$ (Kim and Baik, 1999, Tsai and Chen, 2004, Jicha et al., 2002). However, those predictions were not fully reliable; in some circumstances, the predictions contradict the physical data, which suggests that either the general turbulent models adopted have common deficiencies, or the whole calculation process was not properly controlled, in terms of the convergency, time step and mathematical accuracy. Therefore, in Li's paper (Li et al., 2006), it was clearly indicated that a standardized quality assurance procedure is required. Furthermore, Blocken et al. (Bert Blocken, 2004) concluded that when using CFD, the best that one can do for the validation is to conduct the wind tunnel experiments oneself for the particular configuration.

1.3. Research objectives

The objectives of this research were to develop a numerical wind tunnel model with a self-developed solver on an open source CFD platform, to validate the model by self-conducted experimental measurement, and to discuss the air pollutant dispersion around high-rise buildings. The emphasis of this research was to investigate the different pathways of air pollutant dispersion around a high-rise building where the emission source is located at certain building heights in the windward, and leeward face of the building.

2. Numerical wind tunnel

Commercial software, such as Ansys-Fluent, Ansys-CFX (ANSYS Inc., Canonsburg, PA, USA), is widely used to create a numerical wind tunnel (Mo et al., 2013, Zheng et al., 2012, Huang et al., 2014). User-friendliness and robustness are the advantages of commercial software, but commercial software functions as a closed “black box” which does not allow the users to freely control the calculation process and hence is not convenient for the development of mathematical and physical models. Therefore, in-house/open-source CFD code is preferred for reliable and flexible simulations.

In our research, the numerical wind tunnel was built on an open-source CFD platform, OpenFOAM (www.openfoam.org), which was tested and validated in previous publications (Mack and Spruijt, 2013, Nagaosa, 2014). A self-developed solver was compiled for the simulation of air pollutant distribution. In this solver, PISO (Pressure-Implicit Splitting Operator (Seif et al., 2010)) algorithm, one of the extended versions of the SIMPLE (Semi-Implicit Method for Pressure-Linked Equations (Barton, 1998)) algorithm was applied to solve the governing equations of momentum and air pollutant concentration. The general form of conservation equation is listed as below.

$$\frac{\partial }{\partial t}\left(\rho \phi \right)+\frac{\partial }{\partial x_j}\left(\rho v_j\phi \right)=\frac{\partial }{\partial x_j}\left({\Gamma }_{\phi }\frac{\partial \phi }{\partial x_j}\right)+S_{\phi }$$ (1)

where φ is the generalized independent variables, and S_φ is the source item. ${\Gamma }_{\phi }$ is the diffusion coefficient of φ in turbulent flow. For fluid motion, ${\Gamma }_{\phi }$ is the dynamic viscosity of turbulence (${\mu }_e$). S_φ = $-\frac{\partial p}{\partial x_i}+\Delta \rho g_i+\frac{\partial }{\partial x_i}\left[{\mu }_e\frac{\partial u_j}{\partial x_i}\right]$. For pollutant dispersion, ${\Gamma }_{\phi }=\frac{{\mu }_e}{\sigma }$, $\sigma \approx 1$ and $S_{\phi }=0$.

The application of general turbulent models in the simulation of air pollutant dispersion have been compared extensively (Yuan et al., 2014). It is well known that LES and K−ω−SST models can give better predictions than others, but this is mostly meaningful in flow simulation. It has shown that the widely-used eddy-viscosity models in LES are not able to correctly predict time scales of turbulent mixing (He et al., 2002) and dispersions (Jin et al., 2010, Yang et al., 2008), which presents a new challenge for adopting LES in the study of pollutant dispersion. Often the improvement offered by these time-consuming models is not significant enough to justify the additional computational time. Furthermore, the measurements taken using conventional chemical probe are not accurate enough to necessitate model predictions of transient flow well in excess of the accuracy associated with physical measurements. Hence a standard $k-\epsilon$ model was employed in the current numerical wind tunnel simulation. The model used in this paper is not dissimilar to that in commercial software, thus providing further advantages in using an in-house code with the self-developed eddy-viscosity models that are convenient to embed in the proposed numerical wind tunnel for this study and for future work.

Four millions tetrahedron/hexahedron computational cells were placed in the computational domain, with more than half of them were applied in the region close to the building model to bolster the spatial resolution around the building. Unsteady state calculations were performed. Auto-adapted time step was applied, which allows the variation of time step (10⁻⁵s to 10⁻⁴s) at iterations to ensure that the maximum Courant number during the calculation is less than 0.5, as per required by unsteady state solver (Patankar, 1980). The residuals of both momentum and mass conservation equations were setup as 10⁻⁶, allowing sufficient numerical solution to capture the air pollutant with low concentration. The CFD results were time-averaged after the calculation reached a “stable state”, which is typically used to compare unsteady state simulation with steady state measurement (Zhang et al., 2011).

3. Result and discussion

3.1. Experimental validation

The experimental study was carried on in a turbulent boundary layer wind tunnel at the CLP Power Wind/Wave Tunnel Facility at Hong Kong University of Science and Technology (HKUST). The working section is 41 m in length, 4 m in height and 5 m in width. Detail parameters of the wind tunnel can be found in reference (Liu et al., 2010).

The velocity profile of the atmospheric boundary layer generated in the wind tunnel test assumes the following power law equation (Liu et al., 2010):

$$\frac{U\left(Z\right)}{U_{ref}}={\left(\frac{Z}{Z_{ref}}\right)}^{\alpha }$$ (2)

where Uref is mean velocity at the reference height, Zref is the reference height, which is equal to the building model height in this study, and α is the power law exponent, which was 0.2 for this case. The turbulence intensity profile in the approaching flow was simulated in accordance with Terrain Category 2 stipulated in Australian/New Zealand Standard (Australian Standard, 1989), with a turbulence intensity of 15% at the building model height. The atmospheric boundary layer flow in the wind tunnel was generated by a combination of turbulence generating spires, a barrier at the entrance of the wind tunnel, and roughness elements along the wind tunnel floor upstream of the model. The reliability of the physical wind tunnel modeling has been validated in previous work (Tse et al., 2012, Liu et al., 2013).

A 1:30 scale model was constructed to represent a 10 stories high-rise building of 30 m height in prototype, which has a crucifix shape typical of residential buildings in Hong Kong, as shown in Fig. 1 (a). Each building wing has a “re-entry” to comply with building regulation that requires all rooms to be fitted with a window/opening. This cul-de-sac design mostly accommodates kitchens, bathrooms and/or toilets fitted with exhaust fans through which odorous and other contaminated/spent gas/air and steam are emitted into the generally poorly ventilated space bounded by the cul-de-sac. Experiments were conducted to study the pollutant dispersion around this complex building structure. The tracer gas used was air with a 10% propane concentration. The tracer gas was released through a flow-meter at a constant flow rate of 58.5 ml/s, and this flow rate was low enough to ensure that source momentum effects were not significant. The tracer gas was emitted at the same position within the re-entry at 3rd floor, with the emission at either windward or leeward relative to the incident wind direction. Measurement of tracer gas concentration at each floor in the re-entry area was carried out after the wind flow stabilised. Details of the experimental work can be found in one of our previous publications (Liu et al., 2010).

Fig. 1.

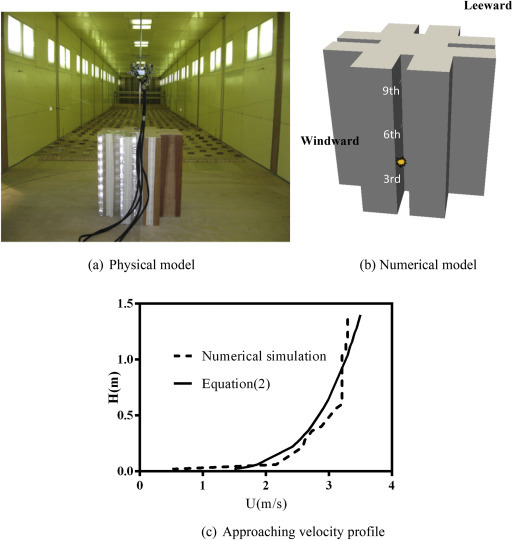
Turbulent boundary layer wind tunnel and 1:30 scaled model of typical Hong Kong high-rise building.

The computational model is shown in Fig. 1(b). The geometric parameters of the digital model were setup identical to that of the physical model tested in the wind tunnel. 3rd, 6th and 9th floor are marked in Fig. 1(b) to represent low, middle, and high floors of the building. By adjusting the inlet condition (inlet velocity profile), the desired approaching velocity profile can be accomplished before reaching the building model. The numerical wind tunnel generated a turbulent boundary layer flow approaching the building model with a mean wind velocity profile with a power law exponent of approximately 0.23 and a global turbulence intensity of approximately 0.15 at the building model height. The comparison of targeting velocity profile and the approaching velocity profile is presented in Fig. 1 (c) which shows a good agreement, with the approaching wind speed at the building height (1 m) = 3.27 m/s, closely matching the experimental condition. Based on the approaching velocity and the model building width, the model test Reynolds number was around 2.2 × 10⁵, suggesting the flow is a fully developed turbulent flow. 10% propane with a 58.5 ml/s volume flow rate was numerically emitted from within the re-entry at 3rd floor, as shown in Fig. 1(c). Two cases were simulated to represent a windward or leeward pollutant emission position relative to incident wind direction, as shown in Table 1 .

Table 1.

Experimental and computational cases.

Case	Emission position of pollutant/tracer gas	Pollutant/tracer gas concentration (%)	Emission position relative to incident wind direction
A	3rd floor	10% propane	Windward
B	3rd floor	10% propane	Leeward

The comparison of CFD simulation and experimental results is shown in Fig. 2 . The simulated air pollutant concentration was expressed in a non-dimensional format (Kc) using the following equation (Liu et al., 2010).

$$Kc=\frac{C{U}_H{H}^2}{Q}$$ (3)

where C is the measurement mean concentration, $U_H$ is the mean wind speed at building model height ($H$), and $Q$ is the volumetric flow rate of the tracer gas.

Fig. 2.

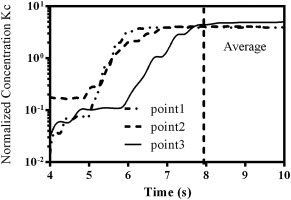
The averaged Kc of unsteady state results.

Fig. 2 shows the fluctuation of K_C with time at 3 points, randomly picked up on 4th floor in Case A. It should be noted that 10 points at each level were selected and averaged to minimize the positional errors, Fig. 2(a) shows 3 of them. It can be seen that after 8 s, K_C reaches a stable value and the averaged K_C from 8 to 10 s was used to compare with experimental measurement. (R1,Q6).

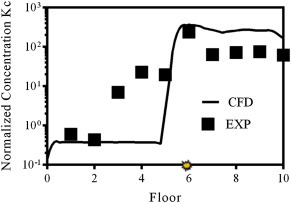
The computed and experimental results of the dispersion of air pollution emitted from the 3rd floor re-entry exhibit a similar trend of the pollutant distribution within the re-entry along the height of the test building, as shown in Fig. 3 . Consequently the pollutant dispersion pathway for the emission at the 3rd floor re-entry, which is well below the stagnation, is primarily downward where high pollutant concentrations are found within the re-entry of the lower floor. Migration of pollutant from the 3rd floor towards the higher floors was largely curtailed by the strong downwash, with the pollutant concentration dropping sharply to be close to zero beyond 5th floor.

Fig. 3.

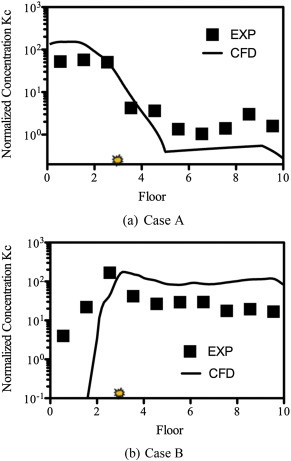
Comparison of CFD simulation and experimental results for case A and B.

In contrast, for Case B with a leeward pollution emission, although turbulent mixing enhance the dilution and dispersion processes, the air pollutant is entrapped within the highly turbulent recirculation zone in the near wake. Hence the pollutant concentration is generally of a higher concentration and more uniformly distributed along the re-entry of the higher floor above the 3rd floor emission position, as shown in Fig. 3(b). Interestingly, both the measured and particularly the computed results show a rapid decline in pollutant concentration below 3rd floor, suggesting a predominantly upward migration of pollutant. This is believed to be the characteristics of the overall pressure field and resultant flow regime representative of leeward flow driven by wind–structure interaction.

To affirm that the upward migration is not a consequence of the specific discharge position (3rd floor), we further tested a case with the leeward emission located at 6th floor. The comparison of simulation and experimental measurement is shown in Fig. 4 , and the results reinforced the finding that air pollutant dispersion for a leeward emission is primarily going upwards.

Fig. 4.

With leeward discharge at 6th floor (to test the effect of discharge position).

The velocity field around the building in a windward View A and leeward View B is shown in Fig. 5 . For windward View A, wind generally rushed past the building, with no obvious separation and vortex induced flow in windward view. However, by zooming in the area close to the emission point, the downwash flow within the re-entry is highlighted. In comparison, velocity field around a regular rectangular bluff body is shown on the right side of the frame. A similar flow pattern is found here, but since there is no re-entry the downwash in windward view of such a rectangle is obvious even without local zooming, which is needed to highlight the downwash flow within the re-entry.

Fig. 5.

Velocity fields around building model.

For leeward View B, intense mixing within the highly turbulent and re-circulating flow in the near wake and the upward airflow adjacent to the re-entry are clearly evident. These distinctive flow patterns lend support to the different pathways of pollutant dispersion described earlier for a windward and leeward pollution emission position at 3rd floor.

The leeward view of a plain rectangular building (without re-entry) is likewise depicted in this figure. The upward airflow can be observed, but the intensity of the flow is relatively weak in comparison with the case with re-entry. Evidently building shape significant affects the flow regime and correspondingly the pollution dispersion around the building. The current study focused primarily on a crucifix-form building with re-entry, and on a plain rectangular building for comparison purposes only. The flow regime around such prismatic bluff bodies with well-defined separation points is dominated by separated flow and the interaction of the separated shear layers with the building afterbody, particularly for the crucifix-form building with re-entry with its more complex afterbody shape. Correspondingly, the pollution dispersion is primarly driven by the wind–structure interaction which in turn is characterised by the building shape.

The pollutant dispersion process can be visualized at different phases, as shown in Fig. 6 . At an early post-emission Phase 1, mixing and dilution of the pollutant remains primarily inside the re-entry area. At an intermediate mixing Phase 2, the pollutant migrates out of the re-entry area where intense mixing takes place. At a quasi-steady dispersion Phase 3, the pollutant leaves the re-entry area and spreads into the surrounding. For Case A with a windward pollution emission at 3rd floor, the pollutant is driven downwards by the downwash, spreads horizontally at ground level to form the horseshoe vortex, and disperses downstream. For Case B with a leeward pollution emission at 3rd floor, the pollutant is driven upwards, discharges onto the roof and becomes entrained into the near wake. This upwards migration of pollutant in the leeward re-entry is consistent with near wake flow regime driven by wind–structure interaction described earlier.

Fig. 6.

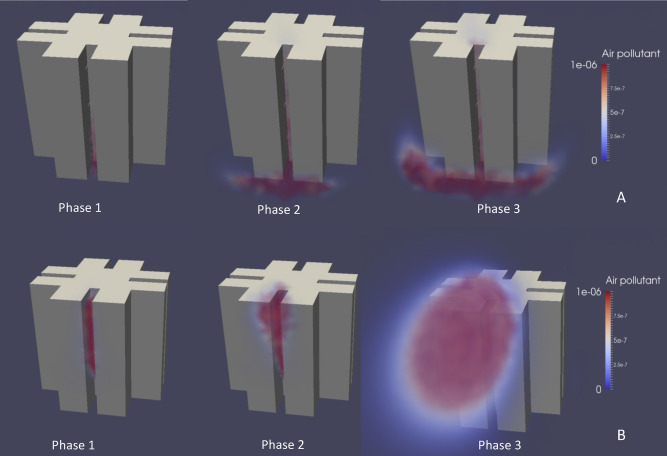
Air pollutant dispersion in different phases.

3.2. Further discussion-haze-fog dispersion

Since wind–structure interaction is believed to dominate the air pollutant dispersion around a building, the effects of emission position and pollutant specific weight on the pollutant distribution need to be further discussed. In order to assess the contribution of those effects compared with wind–structure interaction, a haze-fog (HF) study was undertaken and the results presented in this section. The advantage of using HF as an air pollutant is that the issue of emission position can be fully discarded as HF was “patched” in a field. Furthermore, HF is not a pollutant with specific components; the density of HF is adjustable. This feature allows further test on the effect of buoyancy force of air pollutant by increasing or decreasing the HF density.

HF has attracted increasing interest during the past decade for its impact on global climate change (Kang et al., 2013, Ding and Liu, 2014, Yu et al., 2011). Haze is defined as the unexpected atmospheric phenomenon that leads to weak atmospheric visibility due to the moisture, dust, smoke, and vapor in the atmosphere, while fog is composed of fine liquid droplets suspended in the air near the ground. The formation of HF is a result of long-term air pollution and mostly happens in major cities in the world, thus affects public health of city dwellers. The characteristics of HF are that the source point of the pollutant is generally unspecified (the pollutant could be produced in the city or transferred from other places) and the components are uncertain (the aerosol includes both particular matters (PM) and gas-phase precursors such as nitrogen oxides (NOx) and sulfur dioxides (SOx)).

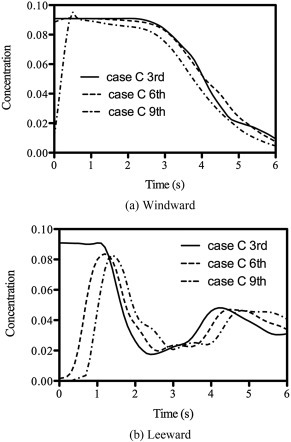
As the uncertain components of the HF, three cases with different HF density were calculated and compared (Table 2 ). For case C, the molecular weight of the fog-haze is assumed to be 44, which is about 150% the molecular weight of air. For case D, the fog-haze has the same density of air. For case E, the fog-haze is 50% lighter than air. Initially, 10% of HF fully occupied the lower half of the tunnel, as depicted in Fig. 7 (a). It should be mentioned that in this simulation no additional pollutant resources were included. The uniformly distributed HF will be discharged out of the tunnel by wind. This guarantees that the computed results are free of the position effect of air pollutant sources.

Table 2.

Haze fog cases.

Case	Molecular weight of haze-fog
C	44 (heavier than air)
D	28 (equal to air)
E	14 (lighter than air)

Fig. 7.

HF dispersion around building in windward and leeward regions for Case C.

In terms of CFD setting, the calculation domain, approaching wind velocity and the model geometry were kept the same as those for effluent cases A and B. HF contains fine particles (particulate matter), as the diameters of those specks are on micrometer level, the particles can be assumed to be fully suspended in the gaseous motion. This implies there is no difference in motion velocity between gas and particles, therefore HF was treated as a constituent of the gas in the current study.

The HF dispersion process is shown in Fig. 7, focusing on HF-building interaction adjacent to both the windward and leeward faces of the test building. The screen shots at 2nd, 4th and 6th second show the pathway of the HF dispersion around the test building. Six seconds after the wind-assisted dispersion commenced, the HF has been completely removed from the windward region of the building. In contrast, it took twice as long, over a period of 12 s, for HF to be evacuated for the leeward near wake region. Evidently, at time 2nd, 4th and 6th second, HF remained within the re-entry area at the leeward face of the building before eventually migrated upward and dispersed, as shown by the indicating arrows.

Fig. 8 presents the quantitative HF concentration as a function of time at 3rd, 6th and 9th floor re-entry in both windward and leeward faces of the building. Evidently, HF concentration at 3rd, 6th and 9th floor re-entry on the windward face decreases with time. At 6th second, HF concentrations were reduced to less than 0.5% at all locations. Within the leeward re-entry, HF concentrations fluctuate; within the first 3 s, concentration firstly decreases and then increases. Indeed, at 6th second, HF remains at about 3% at different stories. The variation in HF concentration suggests that turbulent mixing and recirculation within the near wake spread the diluted HF throughout the near wake and also keep the diluted HF entrapped within the near wake for a sustained period, prolonging the exposure of the leeward face of the building, including the re-entry, to potentially harmful HF exposure.

Fig. 8.

Variation of HF concentrations with time within windward and leeward re-entries at different levels for Case C.

HF of different specific weights, designated Cases C, D and E in Table 2, were simulated and the dispersion pathways compared to assess the effects of wind–structure interaction and buoyancy, focusing on the near wake at the lee of the building where HF of relatively high concentrations have been shown earlier to linger for an extended period of time after the wind-assisted dispersion commenced. As shown in Fig. 9 , the HF concentration at 3rd, 6th and 9th floor fluctuate with respect to time with a same trend, regardless of the specific weight of HF: heavier than air (Case A), same as air (Case B), or lighter than air (Case C). HF concentration at 6th and 9th floors increased for all three cases shortly after the wind-assisted dispersion commenced. At 6th second there is still about 3% of residual HF at different floors. The results reinforced our finding that HF dispersion in the near wake is dominated by wind–structure interaction, with buoyancy effect associated with HF specific weight, within the range tested, playing only a minor role.

Fig. 9.

Variation of HF concentrations with time at different floors within leeward re-entry for Cases C, D and E.

4. Conclusion

This study performed numerical calculations on a self-developed numerical wind tunnel model. The comparison with self-conducted experimental measurement in a turbulent boundary layer wind tunnel showed that the numerical wind tunnel model gives reasonable predictions, in terms of air pollutant migration and dispersion around a typical Hong Kong high-rise building model, particularly within the re-entry of the building.

In the case with emission at a windward location, due to the downwash of wind in the re-entry area, pollutant migrated predominantly downwards and spread horizontally after reaching the ground. For the leeward emission, air pollutant migrated upwards within the re-entry before discharging downstream. Evidently the air pollutant dispersion is dominated by wind–structure interactions.

The effects of emission position and pollutant specific weight on the pollutant concentration distribution around a building were studied using haze-fog (HF) simulation in which the simulated results is independent of position effect of the emission. Evidently, the pathways of HF dispersion in the windward and leeward regions are significantly different. In the leeward region, the evacuation of HF in the re-entry took twice as long as that in the windward region as the ambient HF was trapped and lingered within the leeward re-entry before migrating upward and eventually discharging from the top of the re-entry. This dispersion pathway is similar to that of the leeward emission case.

Furthermore, additional HF studies, where the pollutant density was adjusted to be heavier (+50%), same and lighter than air(−50%), show that the pathway of HF migration for both windward and leeward discharge remain unchanged. Evidently air pollutant dispersion around the building model is dominated by wind–structure interaction and buoyancy effect associated with the pollutant specific weight within the range tested only plays a minor role in the dispersion process.

Appendix A. Supplementary data

The following are the supplementary data related to this article:

Video 1

The pollutant dispersion with a windward emission at the 3rd floor within re-entry.

Video 2

The pollutant dispersion with a leeward emission at the 3rd floor within re-entry.