A human behavior integrated hierarchical model of airborne disease transmission in a large city

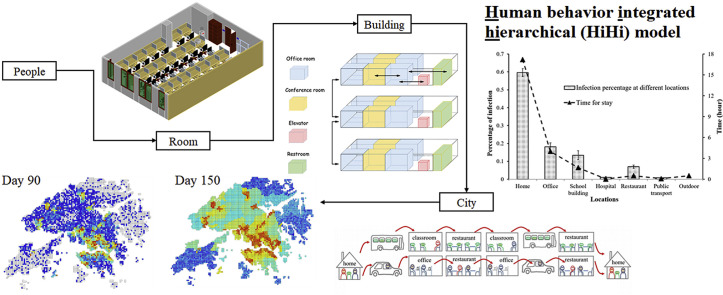
Abstract

Epidemics of infectious diseases such as SARS, H1N1, and MERS threaten public health, particularly in large cities such as Hong Kong. We constructed a human behavior integrated hierarchical (HiHi) model based on the SIR (Susceptible, Infectious, and Recovered) model, the Wells-Riley equation, and population movement considering both spatial and temporal dimensions. The model considers more than 7 million people, 3 million indoor environments, and 2566 public transport routes in Hong Kong. Smallpox, which could be spread through airborne routes, is studied as an example. The simulation is based on people's daily commutes and indoor human behaviors, which were summarized by mathematical patterns. We found that 59.6%, 18.1%, and 13.4% of patients become infected in their homes, offices, and schools, respectively. If both work stoppage and school closure measures are taken when the number of infected people is greater than 1000, an infectious disease will be effectively controlled after 2 months. The peak number of infected people will be reduced by 25% compared to taking no action, and the time of peak infections will be delayed by about 40 days if 90% of the infected people go to hospital during the infectious period. When ventilation rates in indoor environments increase to five times their default settings, smallpox will be naturally controlled. Residents of Kowloon and the north part of Hong Kong Island have a high risk of infection from airborne infectious diseases. Our HiHi model reduces the calculation time for infection rates to an acceptable level while preserving accuracy.

Graphical abstract

Highlights

• •Home and office are the top two risky locations in an infectious disease outbreak.
• •Work stoppage is more efficient to control infectious disease than school closure.
• •Infected patients had better go to hospital rather than rest at homes.
• •Kowloon and north part of Hong Kong Island have high infection risk.
• •Infection would be spontaneously controlled when ventilation increases to 500%.

1. Introduction

Infectious diseases are a severe threat to public health. The severe acute respiratory syndrome (SARS) epidemic affected about 30 countries and resulted in 8422 cases and 916 deaths globally between November 1, 2002, and August 7, 2003 [1]. According to the data provided by the Centers for Disease Control and Prevention (CDC), from April 12, 2009, to April 10, 2010, approximately 60.8 million H1N1 cases and 12,469 deaths occurred in the United States [2]. The Middle East respiratory syndrome coronavirus (MERS-CoV) also causes severe respiratory illness with a high case-fatality rate in humans [3]. As of July 21, 2017, it had attacked 27 countries and induced 2040 cases, including at least 712 deaths [4]. Viral or bacterial respiratory infections are the cause of more than 10% of the 6 million global annual deaths [5]. Hong Kong has a high population density and has been badly affected by SARS [6], H1N1 [7], and H7N9 [8]. For example, from November 1, 2002, to August 7, 2003, approximately 20.8% of the global SARS cases and 32.8% of the SARS deaths occurred in Hong Kong [9]. Therefore, a study of airborne infectious disease transmission at the city level in Hong Kong can provide information that the local government needs to plan for, and deal with, emergencies.

There are two types of models of infectious disease transmission: mathematical and behavior models. Simulation of infectious disease transmission based on mathematical models such as SIR [10], SEIS [11], SIRS [12], SEIR [13], and complex networks [14] is generally very fast, but these models do not reflect micro-patterns such as personal contact, which are essential for studying the effects of intervention at the personal and building levels. Models based on human behavior use simulated human activity at hourly intervals to calculate infection probabilities [15], [16], but are significantly limited by computational power. Most studies of human behavior and infectious disease transmission have focused on a single space, such as a hospital [17], a cruise ship [18], or an office [19]. The total population considered in these studies is usually no more than 50,000; when the total population in a study is several million, it is very computationally complex to simulate all human behavior that occurs in many different indoor environments. For a large city such as Hong Kong, the computer storage requirement alone can be formidably large if detailed behaviors are to be simulated [20]. However, if we combine these two types of models, most of their disadvantages can be solved and simulations can be accurately conducted within an acceptable amount of time.

Many precautions can be taken to reduce risk of infection, such as increasing ventilation [21], wearing a mask, washing hands, and isolation. Models that could simulate human behavior in detail for every room and building and consider many environmental factors would help governments to make more effective intervention plans. This study builds such a model using smallpox as a typical airborne infectious disease. We constructed a human behavior integrated hierarchical (HiHi) model to simulate airborne infectious disease transmission in Hong Kong, which has more than 7 million people, 2.5 million homes, 700,000 offices, 30,000 classrooms, 30,000 restaurants, 54 hospitals, and 2566 public transportation routes. For indoor environments, the simulation accounts for human behaviors and considers transmission patterns in a typical home, office, school, restaurant, hospital, and on public transportation. To reduce computer storage requirements, we determined mathematical patterns for indoor infectious disease transmission in each different type of indoor environment. Airborne infectious disease transmission at a city level was then simulated by combining mathematical equations for locations at a more granular scale (building and room) with daily human behavior.

2. Methods

2.1. Study area, data resources, and setting

The Hong Kong Census [22] shows that Hong Kong occupies an area of 1105.7 km² and hosts 7.1 million people [23], giving a population density of roughly 6395 people/km². There are four primary districts (Hong Kong Island, Kowloon, New Territory, and Outlying Islands) and 18 secondary districts (Central and Western, Eastern, Southern, Wan Chai, Kowloon City, Kwun Tong, Sham Shui Po, Wong Tai Sin, Yau Tsim Mong, Island, Kwai Tsing, North, Sai Kung, Sha Tin, Tai Po, Tsuen Wan, Tuen Mun, and Yuen Long) covering 412 blocks. In this study, we divided Hong Kong into a grid of 4649 squares that are 500 × 500 m in size.

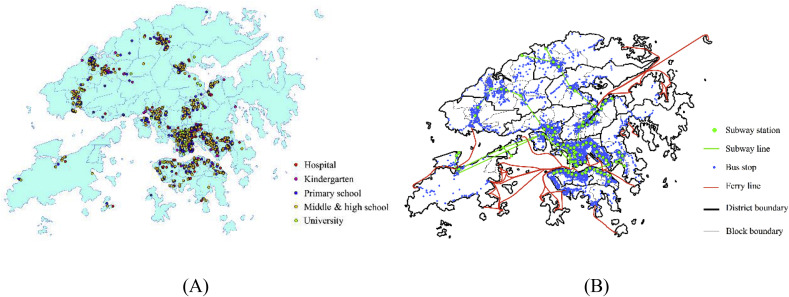
Hong Kong has 2.5 million homes, 700,000 offices, 30,000 classrooms, 30,000 restaurants, 54 hospitals, and 2566 public transportation routes. For this study, Hong Kong residents are divided into four types: worker (office), student (kindergarten, primary/middle/high school, university), patient (hospital), and unemployed, which includes children under 4 years of age and people over 60 years of age (home). The Hong Kong Census provides data on residents' age, gender, household size, employment rate, and percentage attending a kindergarten, primary/middle/high school, or university (KSU) for the 412 blocks [22]. Fig. 1 (A) shows the distribution map of hospitals and KSUs. The statistics collected by the Hong Kong government [24] and the Baidu map were used to obtain the coordinates of all 54 private and public hospitals and institutions, 196 kindergartens, 302 primary schools, 370 middle and high schools, and 25 universities.

Fig. 1.

Hong Kong: (A) Distribution of hospitals and KSUs; (B) Distribution of public transportation stops and routes.

Public transportation, which plays a critical role in infectious disease transmission, connects most people's homes with their work or place of study. Hong Kong has 2566 public transportation lines with 4760 stops, including buses, subways, trams, and ferries [25]. Fig. 1(B) shows the distribution of public transportation.

All of Hong Kong's residents were assigned to the 4649 grids based on the population distribution given in the Hong Kong Census [22]. The census also indicates the probability of a person living in a certain block going to a certain office location or KSU (i.e., a person living in a particular block has a greater probability of going to a nearby block to work or study.) Therefore, office distribution was also obtained from this dataset.

Our simulation of airborne infectious disease transmission was based on the dynamic population flow of 7 million Hong Kong residents among the six functional areas (home, office, school, restaurant, hospital, and public transportation/private car). We only considered weekdays in this study; weekends were not modeled.

2.2. Airborne infectious disease transmission model

In this study, we regarded the outdoors as an infinite space and assumed that people cannot be infected outdoors; thus, all airborne infectious disease transmission events occur in indoor environments. We used the Wells-Riley [26] equation (Eq. (1)) to simulate airborne infectious disease transmission in indoor environments:

$$P=1-\text{exp}\left(-\frac{pQ\tau }{q}\right)$$ (1)

where P is the infection probability per person per hour; Q is the average number of infectious quanta generated by an infector with Q set to 2 quanta/h (20); p is the pulmonary ventilation rate, set at 0.38 m³/h [27]; τ is the duration of exposure to infection (h); and q is the ventilation rate of the location (m³/h).

According to the known progression of smallpox infection, the latent period is the initial 11.6 days and the infectious period lasts from day 11.6 to day 32.39, including the first 2.49 days of the symptomatic period [28]. Infected people usually show symptoms during the infectious period, at which point the majority either go to hospital or stay home until they have recovered. We assumed that 50% of infected patients go to hospital, 45% stay at home, and the rest make no changes in their behavior [20].

This study extrapolates common human behavior in rooms and buildings in a city. If a simulation included all human behavior in every indoor environment, the calculation time would be unacceptably large. Because most human behavior that occurs in a room, a building, or even a city is fairly regular, infection in an indoor environment can be well represented by a mathematical pattern.

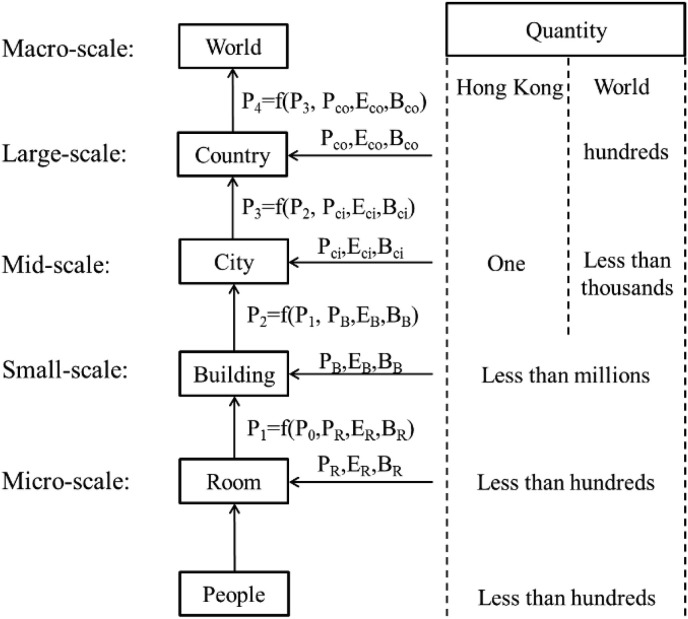
Fig. 2 shows how a mathematical model and behavioral model are combined in this study. At each scale, personal attributes, indoor environment variables, human behavior, and infection probability at the lower scale of a room or a building are simulated as input values, and the output value “Infection Probability (P)” is then summarized as a mathematical pattern that can be imported into the higher scale. In this study, the infection probability is defined as the probability of a person being infected in 1 h. In Fig. 2, using buildings as an example, P₂, which is the infection probability in the building, is calculated from four primary indices: infection probability at the lower scale (room) (P′), personal attributes (P _R), indoor environment variable (E _R), and human behavior in a room (B _R). Personal attributes include resistance (age and gender); indoor environment variables include total population and population density in a building, ventilation, hygiene, temperature, humidity, and building size (number of floors, offices/classes, public rooms including conference rooms and toilets); and human behavior includes the frequency of visits to public rooms, visits to other offices/classes, wearing of a mask, and hand washing. Based on these secondary indices, we can simulate airborne infectious disease transmission in a particular indoor environment, and an infection probability can be obtained. For example, there are millions of buildings in Hong Kong. Each building has fewer than hundreds of rooms, and each room has fewer than hundreds of people. Based on this method, the calculation time can be drastically reduced if the simulation can be hierarchically classified.

Fig. 2.

A HiHi model.

2.3. Personal attributes and daily behavior of Hong Kong residents

According to previous research [16], resistance to airborne infectious disease is related to age (A) and gender (G). In this study, we consider this personal resistance; 46.71% of Hong Kong residents are male, with an age distribution following a reversed parabola [22]. The detailed influence of age and gender on personal resistance is given in Eq. (2).

$$R_b=f\left(A,G\right)=\{\begin{array}{cc}1.014\times \left(0.906+0.0084A-0.00014A^2\right)& male\\ 0.906+0.0084A-0.00014A^2& female\end{array}$$ (2)

We assumed that Hong Kong residents are distributed among the 412 blocks as described in the population census, which records real age and gender distributions. The value used for household size is also based on actual census data. As shown in Table 1 , the Hong Kong Census gives the probability of a connection between the locations of homes, offices, and KSUs for the four primary districts: Hong Kong Island (HK.I), Kowloon, New Territory (N.T.), and Outlying Islands (O.I.). The “same block” percentage for the Home and School category (the probability that a person has a home address and a school address in the same block) is much higher than that for the Home and Office category. In other words, students are more likely to go to school in the block in which they live than adults are to work in the block in which they live. In addition, Hong Kong Island and Kowloon have a higher concentration of offices and schools than the Outlying Islands. Hong Kong residents are assigned to one of the 4649 grids according to the following law: “probability is inversely proportional to 1.55 power of the distance between a home and an office/school” [29].

Table 1.

Relationship between the locations of homes, offices, and KSUs of Hong Kong residents.

Home	Office
	Same block (%)	HK.I (%)	Kowloon (%)	N.T. (%)	O.I. (%)
HK Island	31.78	39.25	19.28	7.47	2.23
Kowloon	21.98	26.07	32.37	16.22	3.36
New Territory	17.46	19.97	31.20	25.85	5.52
Outlying Islands	21.15	31.92	18.87	11.98	16.08
Home	KSU
	Same block (%)	HK.I (%)	Kowloon (%)	N.T. (%)	O.I. (%)
HK Island	56.29	29.32	8.85	4.61	0.93
Kowloon	57.00	6.17	26.69	9.34	0.80
New Territory	56.27	4.42	16.72	20.74	1.85
Outlying Islands	63.54	13.84	8.52	11.24	2.85

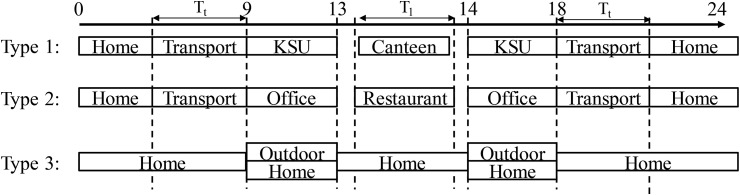
Using the results of previous studies, the daily lives of people in Hong Kong can be simplified as shown in Fig. 3 . The population is divided into three groups: type 1 includes people 4–22 years of age who are studying in KSUs; type 2 includes people 23–60 years of age who work; and type 3 includes people who are less than 3 years of age, retired (over 60 years of age), unemployed, and not studying. In this study, we assumed that all children go to kindergarten from 4 to 6 years of age, that those from 7 to 12 years of age go to primary school, and that 71.7% of people 13–18 years of age go to middle and high school [30]. Furthermore, we assumed that 50% of people 19–22 years of age go to university; that 82.8% of people 23–60 years of age work in an office; and that the unemployed, young children (less than 4 years of age), and retirees (over 60 years of age) will stay at home or walk outside. Time spent at an office or a school is from 9:00 to 13:00 and 14:00 to 18:00, with lunchtime from 13:00 to 14:00. People will travel to and from their homes on foot or by bicycle, private car, or public transportation based on the distance between, and the location of, their homes, offices, and KSUs (the detailed selective mode is introduced below). At 13:00, the people who work in offices and study in KSUs will have lunch in a nearby restaurant or canteen. After 18:00, everyone is assumed to go home.

Fig. 3.

Daily movement of three groups of people in Hong Kong city. Type 1 includes people 4–22 years of age who are studying in KSUs; type 2 includes people 23–60 years of age who work; and type 3 includes children less than 3 years of age, retired adults (over 60 years of age), the unemployed, and those who are not studying. (T_t is commuting time from home to office or office to home; T_l is lunch; transport in this figure includes public transportation, private car, bicycle, and foot.)

2.4. Human behavior in different indoor environments

2.4.1. Home

Home is the most important location in a person's daily life. In Hong Kong, the average living area is 33 m² [31]. According to the census [22], 17.0%, 25.2%, 24.3%, 21.2%, 9.0%, and 3.3% of homes contain 1, 2, 3, 4, 5, or more than 5 residents, respectively, making the per capita living area about 11.4 m²/person. Previous studies have shown that the baseline air change rate in homes is 0.7 ACH [20], [32], and the ventilation rate per person is 21.6 m³/(h·person) (11.4 m² × 2.7 m × 0.7 ACH). To simplify our simulation, we made the following assumptions:

• •In China, people spend about 90% of their time indoors [33]. We thus calculated that 60% of the residents who do not go to offices or KSUs spend, on average, 4 h outdoors per day.

Based on the aforementioned assumptions, the infection probability (P _h) of a person in a home can be calculated using Eq. (3):

$$P_h=1-\text{exp}\left(-0.03519\tau \times \frac{n_{ill,h}}{N_h}\right)$$ (3)

where τ is the continuous number of hours a person spends at home, n _ill,h is the number of infected people, and N _h is the total household number.

2.4.2. Office

In Hong Kong, the average employment rate is 82.8%. Office hours are from 9:00 to 18:00 with a 1-h lunch break between 13:00 and 14:00. The baseline ventilation rate of offices is set to 1 ACH [20]. We made the following assumptions about office buildings:

• •The population of an office building is never more than 1000. Each floor has no more than 20 rooms and each room contains five people.
• •There are a toilet and two meeting rooms on each floor, and each meeting room can accommodate 20 people.
• •The population density in an office room is set at 4.6 m²/person [34]. Therefore, the ventilation rate of a five-person room is 62.1 m³/h (4.6 m²/person × 5 people × 2.7 m × 1 ACH), and is 248.4 m³/h for a meeting room.
• •The average time interval between toilet visits is 3 h [18], and each meeting room is used every 4 h.
• •The area of restrooms in an office building is set to 20 m² with an air change rate of 1 ACH.
• •People visit other rooms once every 2 h.

Based on these assumptions, the infection probability (P _o) of an office was simulated and the results were fitted into Eq. (4):

$$P_o=1-{\left(1-0.1634\times n_{ill,o}^{0.9139}\times N_o^{-0.9043}\right)}^{\frac{\text{τ}}{4}}$$ (4)

where τ is the continuous number of hours a person remains in an office building, n _ill,o is the number of infected people, and N _o is the total number of people in each office building.

2.4.3. Restaurant

A restaurant is an area with high population density during dining hours. The standard population density in a restaurant is 1.25 m²/person [34], which is roughly one third of the area a person occupies in an office. The ventilation rate of the average restaurant is set to 1 ACH. Therefore, the ventilation rate per person in a restaurant is 3.38 m³/(h·person) (1.25 m²/person × 2.7 m × 1 ACH). We made the following assumptions about restaurants in our simulation:

• •People will randomly choose a restaurant within 500 m of their office.
• •All restaurants are the same size and can accommodate 100 people.
• •The time taken to eat lunch is uniformly set at 30–40 min [18].

Based on these assumptions, the infection probability (P _r) of a person in a restaurant can be calculated using Eq. (5):

$$P_r=1-\text{exp}\left(-0.2252\tau \times \frac{n_{ill,r}}{N_r}\right)$$ (5)

where τ is the continuous number of hours a person stays in a restaurant, n _ill,r is the number of infected people, and N _r is the total population in a restaurant.

2.4.4. School building

The NFPA standard states that the population density in a school building should be around 1.9 m²/person [34]. Recognizing that corridors dilute the population density, we assume that population density in a classroom is 1.5 m²/person. Studies have found the ventilation rate in classrooms to be around 2 ACH [20], [35]. We used the following assumptions about school buildings in our simulation of smallpox transmission:

• •Each school building has no more than 2000 students.
• •Each floor has 10 classes and each class has 40 students occupying an area of 60 m². The room height is set to 2.7 m [36], and the volume of each room is therefore 162 m³. The ventilation rate is 324 m³/h (162 m³ × 2 ACH).
• •There is a toilet on each floor. All students stay in the classroom during breaks except those who visit the toilet.
• •The average time interval between toilet visits is 3 h [18].
• •The area of a toilet is 40 m² with an air change rate of 1 ACH.
• •The duration of each class and the break between classes are 50 and 10 min, respectively.
• •Teachers change between classes randomly, whereas all students remain in one room.
• •People spend the same amount of time in KSUs as offices: the 9 h from 9:00 to 18:00.

Based on the preceding assumptions, the infection probability (P _s) of a person in a school building was simulated, and the results fitted into Eq. (6):

$$P_s=\{\begin{array}{cc}\begin{array}{c}1-{\left(1-0.5954\times N_s^{-0.9765}\times n_{ill,s}^{0.9799}\right)}^{\frac{\tau }{4}}\\ 1-{\left(1-0.5544\times N_s^{-0.9438}\times n_{ill,s}^{0.9430}\right)}^{\frac{\tau }{4}}\end{array}& \begin{array}{c}\frac{n_{ill,s}}{N_s}\le 0.05\\ 0.05<\frac{n_{ill,s}}{N_s}\le 0.15\end{array}\\ \begin{array}{c}1-{\left(1-0.4600\times N_s^{-0.8352}\times n_{ill,s}^{0.8347}\right)}^{\frac{\tau }{4}}\\ 1-{\left(1-0.5544\times N_s^{-0.6834}\times n_{ill,s}^{0.6840}\right)}^{\frac{\tau }{4}}\end{array}& \begin{array}{c}0.15<\frac{n_{ill,s}}{N_s}\le 0.50\\ 0.50<\frac{n_{ill,s}}{N_s}\le 1\end{array}\end{array}$$ (6)

where τ is the continuous number of hours a person stays in a school building, n _ill,t is the number of infected people, and N _t is the total population in a school building.

2.4.5. Public transportation

Public transportation is the bridge that connects homes, offices, and KSUs. In Hong Kong, public transportation includes double-decker buses, minibuses, subways, trams, and ferries. There are 2566 lines including 20 tram lines, 30 subway lines, 30 ferry lines, and 2486 bus lines (when counted in both directions). Our simulation of public transportation is based on real data from Hong Kong. Therefore, the population flow during the commute times closely reflects reality. The following eight assumptions were used for the simulation:

• •The ventilation rate of a bus is usually between 2.6 and 4.55 ACH [37]. Because most buses in Hong Kong are double-decker buses, the ventilation rate is assumed to be 4 ACH [20].
• •The volume of a bus is set to 100 m³, and the ventilation rate is 400 m³/h.
• •A carriage of a subway train and a cabin in a ferry are considered a bus.
• •The maximum bus or tram load is 150 people. If a bus is full, people will wait for the next bus.
• •People will choose the public transportation route with the shortest transfer times and the fewest stops. There should be no more than three transfers. If people cannot reach their destination with fewer than four transfers, they will drive their private cars. We calculate that 93% of commuters can reach their destinations using fewer than four transfers.
• •The time between two stops is set as 2 min.
• •If a person's home and office/KSU are in the same or adjacent grids, people will not use public transportation or private cars.
• •Of those people who do not walk or ride a bicycle to the office, 85% will choose public transportation and the remaining 15% (including the 7% of commuters who cannot reach their destinations using fewer than four transfers) will drive private cars.

Based on the preceding assumptions, the infection probability (P _tr) of a person using public transportation can be calculated using Eq. (7):

$$P_{tr}=1-\text{exp}\left(-0.0019\tau \times n_{ill,tr}\right)$$ (7)

where $\tau$ is the continuous number of hours a person spends on public transportation and n _ill,tr is the number of infected people in a public transportation unit.

2.4.6. Hospital

In many outbreaks of infectious diseases, hospitals have the highest risk of infection due to the high density of infected patients [38], [39]. The infection probability in a hospital is directly related to the number of infected patients, the severity of the virus, the hygiene level, isolation, and other relevant factors. The Hong Kong government states that there are 54 private hospitals in Hong Kong [24], and there were 27,895 hospital beds at the end of 2015 [40]. In 2016, Hong Kong had 7.37 million people. We assume that all of the hospital beds are in these 54 hospitals, and thus every hospital has 517 hospital beds.

The Prince of Wales Hospital is frequently chosen as a focal hospital for studies [20], [41]. In this hospital, every ward has four small areas, and each area has ten hospital beds. Therefore, each hospital is assumed to have 13 (≈517/40) large wards, and 52 nurses to serve the patients in each ward (each small area has a nurse). The infectious disease transmission can be simulated based on the following assumptions:

• •A nurse will inspect each small area every hour.
• •The admission rate of hospitals in Hong Kong in 2011 was 4% [42]. Therefore, more than 280,000 people are hospitalized every year. The average hospital stay is 8.31 days [43]; thus, the total number of days that hospital beds are in use is about 2.33 (8.31 × 0.28) million days. The probability of a hospital bed being occupied is 22.75% (2.33 million hospital days/365 days/28,080 hospital beds).
• •Using data from the Prince of Wales Hospital as an example, the ventilation rate is 8085.6 m³/h in a ward and 6195.6 m³/h in a toilet [44]. If the hospital follows a regimen of disinfecting areas every 2 h, the probability of infection is one quarter of that if no disinfection regimen is followed [18].
• •Isolation is not considered in the hospital.

Based on the preceding assumptions, the infection probability (P _hp) of a person in a hospital can be calculated using Eq. (8):

$$P_{hp}=5.068\times {10}^{-5}-2.047\times {10}^{-7}{N}_{hp}+1.098\times {10}^{-5}{n}_{ill,hp}(n_{ill,hp}>0;N_{hp}\le 520)$$ (8)

where $\tau$ is the continuous number of hours a person stays in a hospital, n _ill,hp is the number of infected people in a hospital, and N _hp is the total population in a hospital.

3. Results

3.1. Infection probability in different locations

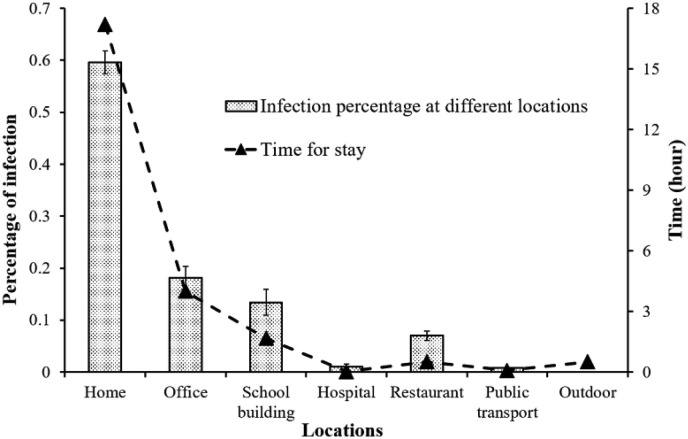
Here, we define infection probability as the probability of one person being infected per hour. Fig. 4 shows the time of stay and infection percentage in homes, offices, school buildings, hospitals, restaurants, and public transportation. Based on the assumptions previously outlined, the average time per capita spent in different locations is as follows: homes (17.19 h), offices (4.01 h), school buildings (1.68 h), hospitals (0.02 h), restaurants (0.50 h), public transportation (0.09 h), and outdoors (0.51 h).

Fig. 4.

Infection probability at different locations.

Home is the riskiest place for infection, and 59.6% of patients are infected in homes. The population density in homes is the lowest, but people spend most of their time in their homes. About 50% of Hong Kong residents work in an office. Although the infection probability per person per hour in an office is lower than in a school, the infection percentage in offices still ranks second at 18.1%. School buildings have a high population density, and 13.4% of patients are infected at school. Restaurants, hospitals, and public transportation represent 7.0%, 1.0%, and 0.9% of infection rates, respectively. Without isolation, the infection probability in hospital is the highest because most infected people are in hospital wards, even though the environment in a hospital is more hygienic than those at other locations.

3.2. Airborne infectious disease transmission during work stoppage and school closure

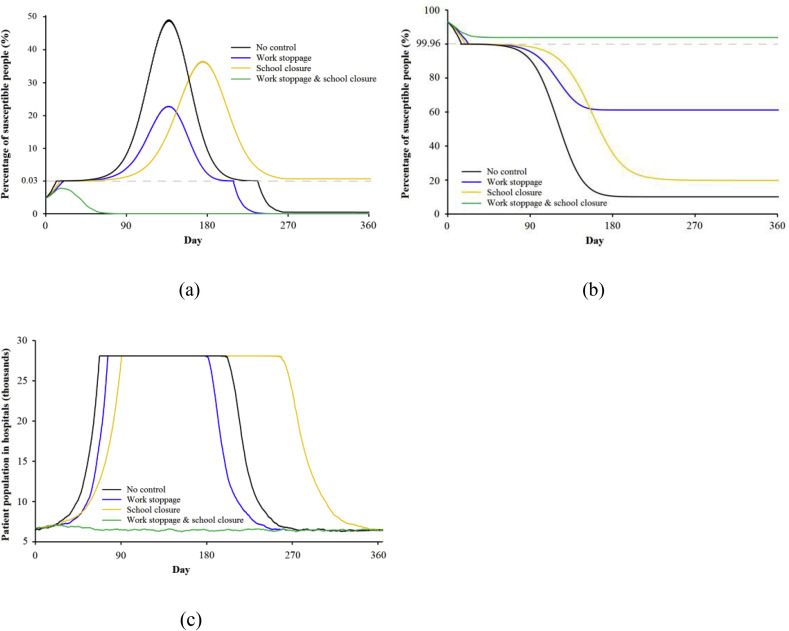
Offices and KSUs play critical roles in the transmission of airborne infectious diseases. In Hong Kong, about half of the population works during office hours, and nearly one fifth attend KSUs every day. It is necessary to consider the role of school closures and work stoppages during an airborne infectious disease outbreak. Fig. 5 shows smallpox transmission in four scenarios: no control (black line), work stoppage (blue line), school closure (orange line), and both work stoppage and school closure (green line). The total patient population in hospitals includes infected and uninfected patients.

Fig. 5.

Number of population in smallpox transmission under four conditions: no control (baseline), work stoppage, school closure, and both work stoppage and school closure. (a) infected; (b) susceptible; (c) hospital patients.

Focusing on no control (black line), after 140 days of uncontrolled transmission, about 48% of the population is infected, and all of the hospital beds remain occupied between days 70 and 210. In this scenario, the hospital runs out of beds if there is no plan to control the spread of the disease. In the work stoppage and school closure scenarios, the peak number of infected population is about 1.6 million or 2.6 million, respectively, and transmission is partially controlled. Work stoppage is a more efficient control of infectious disease transmission than school closure. If necessary, both work stoppages and school closures can be put in place, as shown by the green line in Fig. 5. In this case, the transmission is controlled naturally and the peak number of infected people is never more than 1800. Therefore, combining work stoppages with school closures is a very efficient strategy for protecting residents from airborne infectious disease. However, this is an ideal scenario. In a real situation, people do not stay at home all the time, and governments must make other plans to help halt the transmission of infectious diseases.

3.3. Airborne infectious disease transmission resulting from different personal decisions

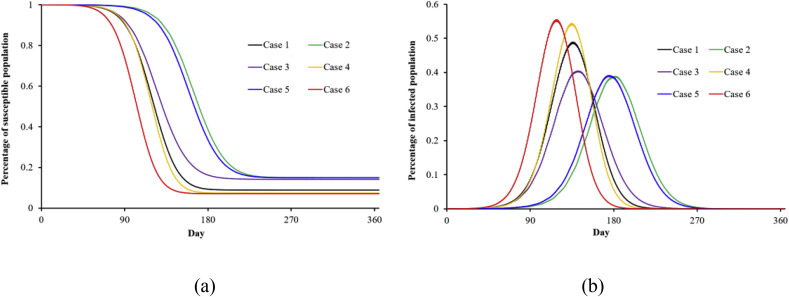
During the infectious period, people with symptoms can choose to go to the hospital, stay at home, or take no action. The proportion of people who adopt these different paths affects how the disease is transmitted. Education and publicity by governments, and people's personal characteristics will influence an infected person's decisions. Fig. 6 shows the effects of different personal decisions on infectious disease transmission. The green line shows the results of the hospital group, and the purple line shows the results when all of the infected people stay home. (We assumed that infected people make a random decision during the infectious period.) The number of infected people is much lower in the scenario where most of the infected people decide to go to hospital. In the case of all infected people staying home (purple line), the infection spreads very quickly because many people have already spread the disease before they decide to stay home. In other words, the efficiency of transmission prevention is low if infected patients stay home, and no other measures such as work stoppages and school closures are taken during the early stage of the outbreak. The red line (case 6) shows the results when 90% of the infected patients stay home and the other 10% take no measures. The percentage of infected people increases to 57% of the population after 115 days if there are no other controls. Comparing the black and purple lines, we can see that staying home is more helpful in controlling disease transmission than taking no measures. If all infected people go to hospital, the hospitals will run out of beds. Therefore, governments should attempt to strengthen hospital loads during the key periods of an infectious disease outbreak.

Fig. 6.

Scenarios of smallpox transmission with different proportions of the population hospitalized/staying at home/taking no measures (initial number of patients: 1000) (Case 1 is a control group with the standard coefficient: 0.5/0.45/0.05; Case 2 is the hospital group, in which all infected people will go to hospital if the hospital is not full: 1/0/0; Case 3 is the home group, in which all infected people will stay at home: 0/1/0; Case 4: 0.9/0/0.1; Case 5: 0.9/0.1/0; Case 6: 0/0.9/0.1).

(a) susceptible; (b) infected.

3.4. Airborne infectious disease transmission under different ventilation rates

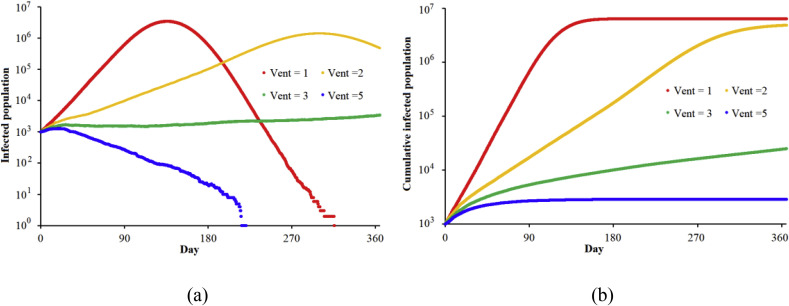
Ventilation is a very important measure for decreasing the probability of infection. In this study, the default settings of ventilation in each indoor room are 0.7 ACH, 1.0 ACH, 1.0 ACH, 2 ACH, 400 m³/h, and 8086 m³/h in a home, an office, a restaurant, a school building, public transportation, and a hospital ward, respectively. We investigate how ventilation rates effect airborne infectious disease transmission. Fig. 7 shows smallpox transmission with different ventilation rates. Fig. 7(a) and (b) show the infected population and cumulative infected population within 365 days. The red line is the baseline with the default settings (Vent = 1). Vent is the ventilation rate in each indoor environment compared with the default settings. When Vent = 2, the peak infectious population is delayed from day 130 to day 300, and the cumulative infected population after 1 year is three quarters of the cumulative infected population under Vent = 1 conditions. When Vent increases to 5, the smallpox will be generally controlled without any additional measures, and the cumulative infected population is less than 3000 after 1 year. However, a high ventilation rate signifies a serious waste of energy, especially in Hong Kong. Therefore, balancing ventilation and energy consumption is very important. In an airborne infectious disease outbreak, governments and residents should control the ventilation rates in public and private indoor environments and take other measures such as wearing masks, hand washing, and vaccination.

Fig. 7.

Smallpox transmission with different ventilation (start patients: 1000) (Vent = 1, 2, 3, and 5 means that the ventilation rate in each indoor environment is 1, 2, 3, and 5 times the default values in this study.) (a) Infected population; (b) Cumulative infected population.

In the two aforementioned cases, the hospitals are not overloaded. Therefore, increasing ventilation to double the standard value and encouraging people to wear masks, wash their hands, and get vaccinated will lower the infection probability to less than 25% and efficiently limit smallpox transmission, especially during outbreaks. Energy-saving measures inhibit increasing indoor ventilation rates; therefore, other measures should also be taken, such as improving the monitoring of social networks to identify and therefore reduce the number of infected people.

3.5. Distribution of infected people in Hong Kong

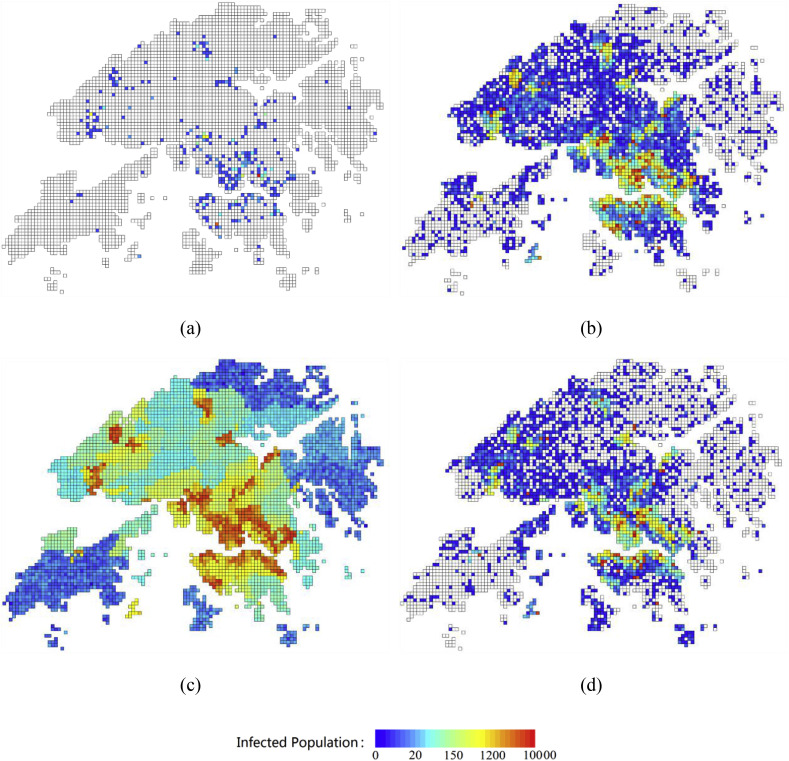
Fig. 8 shows the likely distribution of infected people over time under uncontrolled conditions. The number of infected people at the start of the simulation is set to 100. As shown in Fig. 8(a), there will be more than 700 infected people after 30 days. The disease propagates along the complicated daily population flow. After 90 days, almost 63,000 people will become infected, most of them in Kowloon or Hong Kong Island. Without any controls, the smallpox outbreak will peak around day 150. More than one third of the population will become infected. We also found that the number of infected people increases slowly during the first several weeks and then sharply increases between days 60 and 150. This means that it is very important to control the transmission of smallpox during the early stages of the outbreak.

Fig. 8.

Distribution of infected people in Hong Kong at various times (initial number of people infected: 100): (a) 30 days; (b) 90 days; (c) 150 days; and (d) 240 days.

The risk in coastal areas is much greater than in other areas because of their high population density. Because more of the infected population will concentrate in hospitals, most of the red grids in Fig. 8(d), which indicate a high infection risk, have one or more hospitals. At the peak on day 150, the highest-risk grid has more than 10,000 infected people. Based on the projected distribution of infected people, governments could more efficiently reduce losses by monitoring the most vulnerable areas and improving their resilience. In addition, they could evaluate the number of people infected based on the number of new cases during a defined period.

4. Discussion

Here we compare our results to those of previous studies. About 43% of the population would be infected during the peak period of a smallpox outbreak in Hong Kong [20]. Our simulation also shows that at its peak, three out of every seven people would be infected. Focusing on the infection risks of different places, we determined that the number of people infected during their daily routines (at work or school) is twice the number of those infected at home [45]. This value is 1.4 because we assumed that people stay at home instead of going outside. Based on smallpox data collected in London from 1950 to 1965, the peak number of infected people occurs about 20–22 weeks after the beginning of an outbreak [46]. Due to the higher population density in Hong Kong, this peak will occur at about 19.75 weeks, which is when the most people will become infected by smallpox on 1 day. A smallpox outbreak will be naturally controlled after 150–200 days if no steps are taken to control it. If 50% of the population is vaccinated, the infection risk decreases to 29% [47]. We found that under a no-control scenario, a smallpox outbreak tends to stabilize after day 200. In the case of 50% vaccination, the infection risk becomes 27% if no other control measures are taken. Research has also indicated that the increasing trend agrees with Eq. (9) (R₀ is the basic reproduction number; T _G is the generation time). Smallpox is less infectious (R₀ = 4–10) and has a much longer incubation period (T _G ≈ 21) [48].

$$N_{inf}=\exp \left(\frac{\left(R_0-1\right)t}{T_G}\right)$$ (9)

Under some scenarios, such as going to hospital, the increase in the number of people who become infected is slightly lower than it would be if no measures were taken. The above comparisons with existing studies reveal that our new model can provide a reasonable prediction of the major features of an epidemic by accounting for both environmental parameters such as building ventilation and human travel behavior.

However, there are some limitations to this study. It simulates smallpox transmission under the condition of commonly observed human behavior. We assume that most human behavior is predictable, but there are always people whose behavior does not conform to assumptions about normal behavior. Most of the data we used are actual data from the Hong Kong Census and Hong Kong government, and most assumptions were based on this real data. However, human behavior and indoor environments may change under the threat of an infectious disease. For example, during airborne infectious disease outbreaks, more people wash their hands, wear masks, get vaccinated, and more frequently open the windows in their homes. These types of behavior are not considered in this study.

It is known that climate and seasons have impacts on airborne infectious disease transmission [49]. Air conditioning is widely used in Hong Kong, and the impacts of climate and seasons are not considered in this study. Ventilation methods are a critical factor in an airborne infectious disease transmission. In the study, we used different ventilation rates to characterize the impacts of ventilation design. The effects of very high air exchange rates due to window opening are not considered as a high ventilation rate is known to minimize the airborne spread of diseases and most windows in commercial buildings are not operable in Hong Kong. Moreover, we have ignored exposure in transient spaces such as elevators due to relatively short exposure period. However, these spaces can be important for infectious disease transmission due to other routes such as close contact and fomite transmission. All limitations mentioned above will bring little errors of simulation results.

Similar models could be built to examine contact-borne, food/water-borne, and vector-borne diseases. In addition, the limitations on this study should be addressed in future research to improve the accuracy and reliability of the simulation.

5. Conclusions

This study developed an HiHi model to simulate airborne infectious disease transmission in a large city. Compared with other existing models, the HiHi model, which fully considers spatial and temporal dimensions, efficiently reduces the computation requirements and increases the accuracy and reliability of the results. We modeled a hypothetical smallpox transmission in Hong Kong over a 1-year period, taking into consideration dynamic population flow and daily human behavior in different indoor environments including homes, offices, KSUs, restaurants, hospitals, and public transportation. We conducted the simulation using actual sociodemographic data (gender, age, household size, distribution of KSUs), personal commuting behaviors, and information about public transportation, together with some reasonable assumptions.

The model shows that homes are the riskiest locations in term of infection risk, although they may have the best hygiene measures. Offices and school buildings rank second and third for infection risk, due to their higher population densities, complex people movement, and poorer ventilation. Work stoppages and school closures are shown to be effective at protecting residents from airborne infectious diseases. If both work stoppage and school closure measures are taken when the number of infected people is greater than 1,000, an infectious disease can be effectively controlled after 2 months. Having infected people stay at home also reduces the number of infected patients, but the efficiency of this approach is low if no other measures are taken. If 90% of infected people go to hospital during the infectious period, the peak number of infected people decreases by 25% compared with the do-nothing scenario, and the peak infection period is delayed by about 40 days. In an ideal situation, the spread of smallpox would be halted within a short period if infected people went to hospital during the symptomatic period rather than during the infectious period. If ventilation could be increased to five times the default setting, the smallpox outbreak would be gradually controlled. The HiHi model used in this paper greatly reduces the time needed to calculate the spread of infection.

If models of travel by air, sea and land between cities and countries are included, our method could be used to simulate the transmission of airborne infectious diseases on a larger scale, such as a country or even the entire world. The model may be useful to provide information to health authorities for the formulation of emergency plans.