Predictions and measurements of the stack effect on indoor airborne virus transmission in a high-rise hospital building

Abstract

As the viral diseases such as Severe Acute Respiratory Syndrome (SARS) and Influenza A (H1N1) occur in many countries recently, the epidemic of those influenza viruses causes many human casualties. Moreover, the second infection from infected patients particularly within general hospitals frequently takes places due to improperly hospitalized and/or quarantined patients. Accordingly, it becomes a great concern to accommodate safer ventilation system in general hospital wards against such airborne transmitted viruses. It is also a recent trend that many urban general hospitals are designed and constructed as high-rises. If a virus is transmitted through uncontrolled air movement within a hospital and then infected other patients or healthy visitors, it might be impossible to control the spread of the disease. Thus research has been preceded scrutinizing stack effect on the indoor airborne virus transmission in large hospitals by conducting both the field measurement and numerical analysis according to the outdoor temperature and the releasing vertical points of the tracer gas assumed as a viral contaminant. In the field measurement of a high-rise hospital, the indoor airflow was affected by the stack effect of vertical chute of the building. The numerical simulation was verified by comparing its prediction results and the field measurement data. In result, very high possibility has witnessed that the airborne contaminant emitted from the infected patients in the lower floors could be transported to the higher floors through the airflow driven by the stack effect.

Nomenclature

P

zone pressure (Pa)

P_s

stack pressure (Pa)

P_w

wall surface pressure relative to outdoor static pressure in undisturbed flow (Pa)

C_p

wind surface pressure coefficient

g

gravitational constant (9.8 m/s²)

h

height above reference plane (m)

T

zone temperature (K)

U

wind speed (m/s)

s

shelter factor for particular wind direction

Q

stack effect draft/draught flow rate (m³/s)

A

flow area (m²)

V

zone volume (m³)

R

gas constant for air (J/kg K)

Greek letters

ρ

air density (kg/m³)

α

discharge coefficient

Subscripts

i

indoor

o

outdoor

NPL

neutral pressure level

h

upwind wall height

1. Introduction

The spread of diseases from infected patients within hospitals causes many human casualties. If a virus were to be transmitted through uncontrolled air movement within a hospital and were then to infect other patients or healthy visitors, it would be impossible to contain the spread of the disease [1]. A pressure difference occurs in buildings due to different densities of outside and inside air that arise from temperature variation. Because the exterior of a building is cold and building interiors are warm during wintertime, the pressure above the ground surface is lower inside the building and airflows into the lower section of the building due to such pressure difference. The inflow air travels up the vertical shafts such as elevators to move to the higher section of the building and then flows outside. Until now, research on the stack effect has mainly focused on high-rise apartments that were built from around the year 2000. Many of the relevant studies have made significant progress, and solutions to various problems are steadily being published [2], even studies on concrete construction methods for strengthening the air-tightness of building interiors, such as using revolving doors and windbreak rooms. Although research on the stack effect has been generally limited to high-rise apartments, there is a high probability that such research will also be carried out on high-rise hospital buildings. Unlike in high-rise apartments, however, the changes in airflows due to the stack effect could cause serious problems in high-rise hospitals by allowing airborne viruses to spread. Because the traffic volume of residents in high-rise apartments is small, the stack effect can be reduced by installing features such as windbreak rooms or revolving doors. However, in hospitals where numerous outpatients and hospitalized patients, their families, doctors, nurses and students are constantly moving in and out, such measures do not render any significant results. In this environment, there is a high possibility that infectious airborne viruses could spread out to the entire hospital via vertical routes of elevators or staircases through the stack effect. Currently, however, only studies on the possibility of the stack effect in high-rise hospitals have been published and there have been no detailed reports based on field measurements. Only a few analyses of the impact of the stack effect on the spread of airborne infectious disease have been conducted. Major studies that have been carried out so far dealing with the stack effect are as follows. Jo et al. [2] measured the distribution of pressure differences between floors or spaces in high-rise apartments during winter using a network airflow model, which was also used to analyze the stack effect in various architectural alternatives. To prevent the stack effect, Tamblyn [3], [4] introduced a mechanical ventilation system, and to separate the spaces (between apartment unit doors and elevator halls) where stack pressure significantly occurs due to the increased air-tightness, Jacques [5] and Jo et al. [2] each proposed vestibules and air-lock doors. However, Lovatt and Wilson [6] published research results that demonstrated that it is not desirable to use a mechanical ventilation system because it could produce unexpected problems in the building, and if improvement in the level of air-tightness does not occur throughout the building, it could instead strengthen the stack effect.

Major studies analyzing how airborne viruses spread have also been carried out (Rice et al. [7]; Bjorn and Nielsen [8]; Huang and Tsao [9]; Qian et al. [10]; Rui et al. [11]), mostly on smaller spaces such as surgery rooms or isolation rooms, rather than on the entire hospital, focusing on the diffusion analysis of viral pathogens. In around 2003, when SARS, with its threat of causing the corona virus, broke out in locations such as Hong Kong and North America, several studies were published that dealt with infection route analysis (Li et al. [12]; Yu et al. [13]; Lim et al. [1], [14]). By analyzing actual cases where pathogens spread quickly, these studies derived the conclusion that pathogens can spread through the air. Studies on the spread of viral pathogens and contaminants generally assume that the breathed air exhaled from patients is the source of contaminants or pathogens and their diffusion is therefore analyzed. Considering the breathed air, Hayashi et al. [15] reported that the breathing volume of an adult under normal conditions was 6 L/min based on 0.7 met of activity during sleep (convective heat transfer 33.3 W/person), and the volume of exhaled air under normal conditions was 14.4 L/min. Bjorn and Nielsen [8] proposed a human body model for breathing, in which adults breathed about ten times a minute and produced 6 L/min of breathed air. They also reported that the convective heat transfer of the human body was 76 W. Haselton and Sperandio [16] carried out a study on heat exchange from convection between nose and air. It was shown that, in the case of an adult, the openings for nose and mouth were on average about 0.012 m in diameter, and during breathing, the temperature of exhaled air was 32 °C for the nose and 34 °C for the mouth. Using these research results, Qian et al. [10] prepared actual mannequins and assumed the average speed of exhaled air to be 0.89 m/s at 32 °C. They then carried out tests on pathogen diffusion and CFD analysis. However, because the virus included in the exhaled air is eventually mixed together with sprays, they could not calculate the number of pathogens discharged from the exhaled air of individual patients. Because of this, in the case of studies that examined the spread of airborne pathogens as a network model, the number of pathogens included in the exhaled air were analyzed by assuming the number as a specific value (CFU/m³), whereas studies that used the CFD modeling assumed tracer gases such as CO₂, SF₆ or N₂O as the pathogen and comparatively analyzed the infection route and its likelihood. Lim et al. [14] also suggested that analysis of airborne pathogens was possible using tracer gas. Since viruses are heavier than gas but are very small compared to solid particles, they are more likely to float on air, similarly to gas, than germs with larger and heavier particles. Because of these characteristics, Li et al. [12] and Yu et al. [13] used N₂O, which is slightly heavier than air, to simulate viruses in their studies and analyzed its diffusion route. It is judged, therefore, that if a method of differentiating danger levels according to the concentration of tracer gas was additionally presented, it could somewhat supplement the ambiguities in analyzing diffusion using tracer gas.

The purpose of this paper is to analyze the diffusion path of contaminated air from patients infected with an airborne virus in high-rise hospitals, focusing on the stack effect, and to provide some engineering controls and architectural design plans for minimizing the vertical diffusion of pathogens into the entire hospital space. By comparing between field measurements and network mathematical model, this study tries to predict the stack effect on indoor airborne virus transmission. The study process is described below:

• 1.A sample high-rise hospital was selected, and pressure difference measurements related to the stack effect were carried out for the entire building in order to examine general airflow patterns.
• 2.By comparing the field measurements and the simulation prediction values, the reliability of the simulation program was compared.
• 3.The infection path was analyzed following the location of patients in each floor and the stack effect was proven to be one of the main factors causing the spread of viruses.

Because the field measurements were taken from an actual hospital in operation, there were many limitations. Because we carried out measurements during early morning hours, we had complete control over public areas, such as elevator halls and hallways, but for measuring rooms that required privacy, we carried out measurements only in those rooms where we obtained the consent of both the patients residing in those rooms and their doctors. The field measurement of tracer gas was not carried out because we did not get permission from the hospital administrators, and hence we carried out simulations instead. In future follow-up studies, we plan to build a miniature model and conduct mock-up tests using tracer gas.

Several multicompartment flow models have been developed, i.e. CONTAMW [17] and COMIS [18] that can estimate inter-zonal flow rates. The commonly used network model has been found to be appropriate for this study, where calculation process is reasonable. CONTANW was employed to simulate both airflow and concentration. The results will be very useful for exposure assessment and control strategy planning. The evaluation of how infectious pollutants spread due to changes in indoor airflow will focus purely on stack effect, and any effect from wind will accordingly be excluded from consideration. For health risk assessment, after obtaining the concentration profile, detailed exposure modeling can be advanced, if necessary. It would be more meaningful to estimate a long-term exposure because there are some external factors which vary significantly with time.

2. Factors influencing indoor airflow

There are three main factors that affect indoor airflow in high-rise buildings during cold winter season: stack effect, wind speed/direction and air balance of HVAC system (supply and return air volumes).

2.1. Stack effect

The stack effect occurs when the air inside the building is either more or less dense than the outside air because of the temperature difference. If the air inside the building, which has a high opening in one and low opening in another, is warmer than the outside air like winter, this warmer air will float out the top opening, being replaced with cooler air from outside. The pressure distribution for inside and outside the building arising from stack effect can be shown as in Fig. 1. Here, a section exists where the air pressures outside and inside the building become the same, which is called a neutral pressure level (NPL). Accordingly during winter season, infiltration occurs in sections below the NPL while exfiltration occurs in sections above it. In such situation, the pressure difference ΔP _s is the difference between outside pressure P _s(o) and inside pressure P _s(i) for any random height h. Stack effect can be calculated from the following relation [19]:

$$\Delta P_{\text{s}}=P_{\text{s}\left(\text{o}\right)}-P_{\text{s}\left(\text{i}\right)}=\left({\rho }_{\text{o}}-{\rho }_{\text{i}}\right)g\left(h_{\text{NPL}}-h\right)={\rho }_{\text{o}}\left[\frac{T_{\text{i}}-T_{\text{o}}}{T_{\text{i}}}\right]g\left(h_{\text{NPL}}-h\right)$$ (1)

Fig. 1.

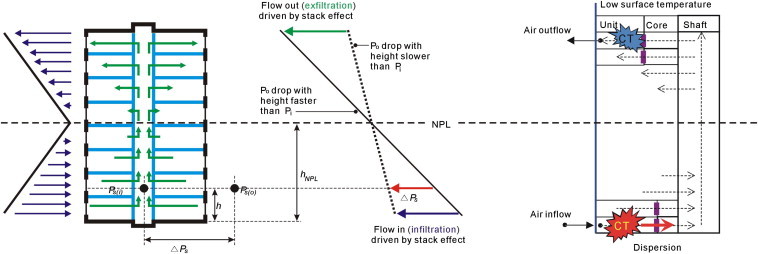
Stack effect: indoor airflows in tall buildings.

The pressure difference ΔP _s arising from stack effect can thus be shown as a function of vertical distance from the NPL and difference between the outside and inside average air densities of a building, or a function of distance from the NPL, outside air density, and absolute temperature of inside and outside air. It can be seen that greater inside and outside temperature difference and greater building height correlate with greater pressure difference due to stack effect. It can also be seen that pressure difference at the NPL is zero, and during wintertime, pressure difference below the NPL has a positive (+) value while pressure difference above the NPL has a negative (−) value.

$$Q=\alpha A\sqrt{\frac{2g}{\rho }\Delta P}=\alpha A\sqrt{2gh\frac{T_{\text{i}}-T_{\text{o}}}{T_{\text{i}}}}$$ (2)

The rate at which air flows depends on several factors, the inside and outside air temperatures, the area of the openings, and the height difference between the top and bottom openings, the draft or draught flow rate induced by the stack effect can be calculated with equation (2) [20].

2.2. Wind

The wind pressure created in a building can be shown as a function of variables such as air density, the direction and wind speed. Equation (3) [20] shows how the wind pressure is calculated.

$$P_{\text{w}}=C_{\text{p}}{\rho }_{\text{o}}\frac{U^2}{2}=s^2{C}_{\text{p}}{\rho }_{\text{o}}\frac{U_{\text{h}}^2}{2}$$ (3)

Because wind pressure at the side of building can differ according to the side receiving the wind, the direction of the wind can distort the pressure difference profile on traditional stack effect shown in Fig. 2 . In other words, when wind blows on a building with stack effect, the wind pressure applies not evenly to all sides of the building but differently according to where the building side is located in relation to the wind direction, and thus the pressure difference between inside and outside the building differs for each side of the building. For example, in Fig. 1 when there is no wind, the pressure distribution between floors has a fixed pressure difference profile between floors arising from stack effect, with the NPL being at the center point. When there is wind, however, as shown is Fig. 2, the side of the building receiving the wind has high pressure while the opposite side has low pressure, and thus many pressure areas form in the building. Accordingly, in the low floors, if the wind pressure is high, it aggravates the pressure difference from stack effect and increases infiltration through openings. At the opposite side of the building, however, while infiltration could still occur through stack effect, the low pressure caused by the wind could also cancel the pressure difference, thus eliminating infiltration, or reverse the pressure difference, thus causing airflow to go out from the building. In contrast, while inside building pressure is normally higher than outside pressure in high floors due to stack effect and airflow that go out of the building through openings, wind could apply enough pressure to cancel out the pressure difference, thus canceling airflow, or even reverse such pressure difference and cause infiltration. In conclusion, while wind pressure could enhance stack effect, it could also cancel out of reverse the effect, and thus has the potential to cause indoor airflow to change patterns and move in various directions.

Fig. 2.

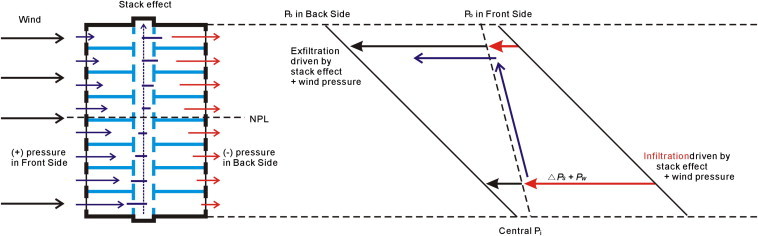
Stack effect and wind pressure: indoor airflows in tall buildings.

2.3. Indoor air balance of HVAC system

Indoor air balance can show various patterns according to the difference between the supply and return air volumes of HVAC or mechanical ventilation systems. In general, supply air volume is more than return air volume because of individual exhaust. Spaces with greater supply air volume have higher pressure in comparison to other spaces, and in order to find a pressure equilibrium point, the surplus air is made to go out through the openings or find low pressure spaces to flow to. Thus having greater supply of air volume is positive in that it can not only supply fresh air and dilute pollutants, thus lowering their exposure concentration, but it can also make controlling indoor airflow difficult, and in the worst scenario, the airflow to low pressure spaces could further aggravate the spread of pollutants.

In this paper, because the main focus is on the observation of pathogen transmission within the hospital due to factors related to stack effect only, we eliminated factors for wind speed/direction and indoor air balance of HVAC system. We assumed there was no wind and set the boundary condition for indoor air balance based on the HVAC operating and design data of the subject hospital.

3. Field measurements of pressure distribution

3.1. Outline of measurements

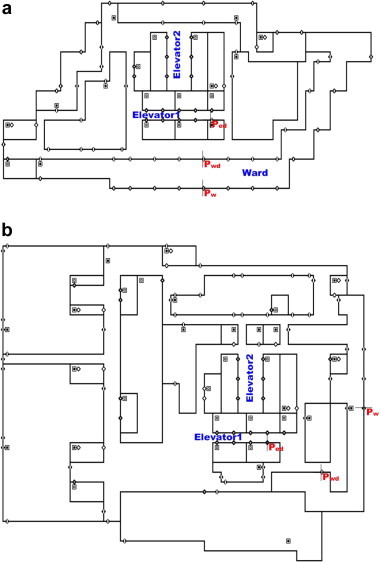
Field measurements were conducted on two buildings during the cold season to obtain the actual pressure distribution profiles and to verify the problems caused by stack effect. In order to identify the existence and degree of the stack effect in high-rise hospitals, S-Hospital, one of the recently constructed high-rise hospitals, was selected as the study subject. Fig. 3 shows the test hospital’s current state in detail, and the measurement locations for its wards are marked. The measurement details and instruments are shown in Table 1 . To prepare for the field measurements of the hospital building, the building’s airflow paths were examined through a previous on-site survey. To ensure the accuracy of experiment, the first round of measurements was carried out on March 15, and the second round was carried out on April 15. The measurements were carried out between 3 and 5 am, when the elevator operation could be controlled and the outside temperature was low. As shown in Fig. 3, for the test hospital, for each building, there is a central core with two elevator halls, ward units surrounding the core, and the connecting corridor. In the typical floor plan, each floor is separated by exterior walls, ward unit boundaries including entrance doors, and vertical shaft walls including elevator doors. The pressure differences across these building components are measured to obtain the pressure distribution profiles. Absolute pressures of the essential zones were measured. The absolute pressure was measured at the floor surface of the zones on each floor simultaneously by using absolute pressure barometers going down from the top floor to the basement floor of the building. In measuring the pressure in the elevator hall, the measurements were taken with the elevator doors closed by using distal micro nanometer. Air flow through large openings is usually bi-directional. Since the elevator doors and ward doors are closed, the opening is not large. During the initial measurement, the bi-directional flow of the door was checked. There was no occurrence of bi-directional flow phenomena. Furthermore, to measure the airflow and direction when the elevator doors were open, only one elevator was used to conduct the experiment for each floor, and airflow was measured from the center using an anemometer after the elevator door opened. Field measurements were carried out at dawn in cold weather and stable conditions to minimize other influences such as wind, elevator use by residents, and opening of doors. Of the two, the first elevator hall was selected, which was used frequently by visitors, and the pressure difference at its elevator doors was measured. The first elevator hall had eight elevators, but because not all elevators could be measured, only one representative elevator was chosen. To do this, the pressure difference at each elevator door needed to stay the same. Fig. 4 shows the pressure difference measurements of elevator doors up to the 20th floor while all eight elevators were stationed at the third basement floor. The pressure difference at the elevator doors ranged from 21.8 Pa (minimum) to 22.5 Pa (maximum), showing a difference of less than 1 Pa between the doors. Accordingly, the eighth elevator door was selected and the pressure difference at the door was measured for all floors. Pressure difference was also measured at the doors and windows of selected wardrooms, and the elevator shaft and hall temperatures were also measured. In addition, after measuring the pressure difference and temperatures, one elevator from among the eight stationed in the third basement floor was brought up to the floor being measured, and the air flow direction and wind speed from the elevator were measured when its door opened. This measurement process was repeated ten times. However, as the pressure difference at the ward doors and windows could affect the condition of hospitalized patients, measurements of select wardrooms on the first, third, sixth, ninth, 12th, 16th, and 19th floors were carried out twice with the consent from the hospital’s personnel.

Fig. 3.

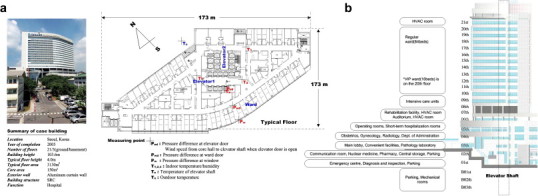
Sample hospital’s selection and basic information. (a) Hospital overview and ward sections’ floor plan and measurement points; and (b) Hospital sections’ vertical locations.

Table 1.

Measurement details and instruments used for field measurements.

Fuel type	Model	Range	Error	Measurement points
Absolute pressure	PTB-220TS digital barometer	50 – 1100 hPa	±0.1 hPa	Each floor
Pressure difference	TSI Inc. DP-C and Micro manometer model 8705-M-GB	−1245–+3735 Pa	1% of reading 1 Pa, ±0.01	Elevator door Ward room door Ward room window
Temperature	Grant 1250	-200 °C–+200 °C	±0.1 °C	Elevator shaft/Core
Wind speed	TSI Inc. VelociCalc Plus model 8360-M-GB	0.15 m/s–50 m/s	3% of reading 0.02 m/s	Elevator door

Fig. 4.

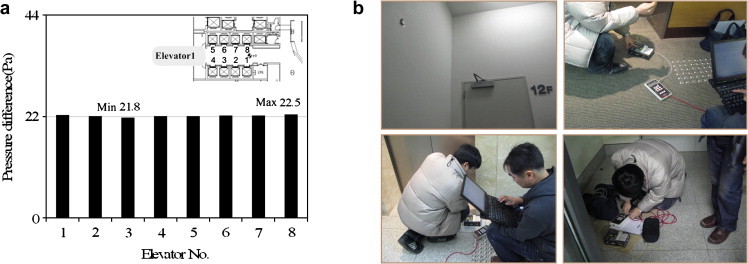
Field measurement. (a) Pressure difference at each elevator door; and (b) Measurement methods and instrumentation.

3.2. Measurement results

The temperature measurement results are shown in Fig. 5 , which lists the average inside and outside temperatures and the highest and lowest temperatures for each floor. Because the measurements were performed early in the morning, temperature measurements were stable without any noticeable deviations between measurements. The average outside temperature was 4.0 °C, with the temperature distribution ranging from the lowest temperature of 3.31 °C and the highest temperature of 5.4 °C. The temperature inside the elevator shaft differed for each floor: 17 °C in the first basement floor, and 23 °C in the 19th floor. Although there were slight variations according to whether or not the floor had a door connected to the outside, the temperature generally increased with the increase in floor height of the building. The temperature inside the core (elevator hall) was 18 °C in the second basement floor, rising to an average of 0.2 °C with the increase in floor height of each floor and was 22 °C in the 19th floor. In particular, when the temperature curves in the elevator shaft were compared with those of the core, there was no significant difference in the lower section of the building, but the core temperature was higher, and in the upper section of the building, the elevator shaft temperature was higher.

Fig. 5.

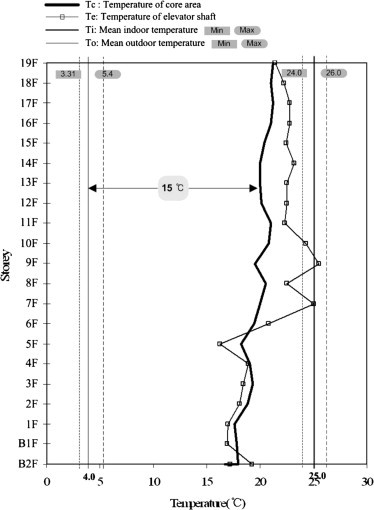
Inside temperature distribution for each floor corresponding to outside air temperatures.

Fig. 6 (a) shows the measurements of pressure difference at the elevator doors and ward doors and windows connected to the outside air for each floor, and Fig. 6(b) shows the air flow direction and wind speed entering and exiting the elevator and the core when the elevator door opens on each floor. Fig. 6(a) actually shows a typical pressure difference profile due to the stack effect. The NPL without any pressure difference forms in the central part of the building between the eighth and 11th floors. Regarding pressure difference at the elevator doors (elevator shaft pressure – hall pressure), the difference was shown to be minimal at less than 1 Pa in the first basement floor and second floor because there were no doors connecting these floors to the outside. On the first floor where there was an entrance, the average pressure difference was −13.88 Pa. From the first floor to the fifth floor, the pressure difference between the floors was fairly even at −13 Pa, and in the 20th floor, the average pressure difference was high at 22.81 Pa. In particular, the pressure difference between the first floor and the fifth floor was low compared to that in the 20th floor and the difference was not large between the floors. This is because, in the first floor, the inflow of outside air was comparatively higher than in other floors due to its wide surface area and windows connecting to the outside, while in the fifth floor, the pressure did not significantly differ from that in the first floor due to the effect of an atrium that was vertically connected from the first floor to the fourth floor. Unlike the pressure difference at the elevator doors, there was no significant pressure difference at the divided doors and windows in locations such as consulting rooms and wardrooms. This was because the pressure difference due to the stack effect was dispersed by many rooms surrounding the outer walls, and that dispersed pressure was collecting in the elevator area at the center of the building. In addition, because the floor surface and outer surface areas were wide from the first to the fifth floors, the pressure difference at each door and window in those floors became very small. Due to these reasons, the pressure differences at the doors and windows in the first floor were −2.80 Pa and −0.87 Pa, respectively. In contrast, in wards on the sixth floor or higher, because the floor surface and outer surface area became comparatively smaller with smaller wardrooms divided with interior walls into rooms for five people or two people, the pressure difference at the ward doors and windows was greater than in the lower section of the building. Thus, in the 19th floor, the pressure differences at ward doors and windows were 5.98 Pa and 0.85 Pa, respectively. In particular, the values significantly differed for the doors and the windows because the pressure difference for the windows was smaller due to the smaller wardrooms, while the pressure difference for the doors was greater due to the fact that the pressure concentrated in the elevator halls from the stack effect was distributed to each of the wardrooms. Fig. 6(b) shows the airflow direction and wind speed when the elevator doors are opened. Negative values show airflow from the core to the elevator shaft while positive values show it moving from the elevator shaft to the core. The airflow direction and wind speed for each floor were shown to be determined according to the pressure difference in relation to the NPL. When the elevator door was opened in the first floor of the building, the inside air flow was shown to flow into the elevator at a wind speed of 0.53 m/s. Once in the upper section of the building, however, above the NPL, the wind speed was shown to steadily increase and, in the 20th floor, the airflow was measured flowing out of the elevator at a wind speed of 3.02 m/s. Even though the time of measurement was in April when the inside and outside temperature difference was comparatively smaller than in December, in the upper section of the building, an air flow with unpleasantly high wind speed was flowing out from the elevator shaft when the elevator doors were opened. As shown in Fig. 6(b), the airflow direction and wind speed profiles for when the elevators in each floor were opened support the argument that the stack effect does occur at the hospital being measured.

Fig. 6.

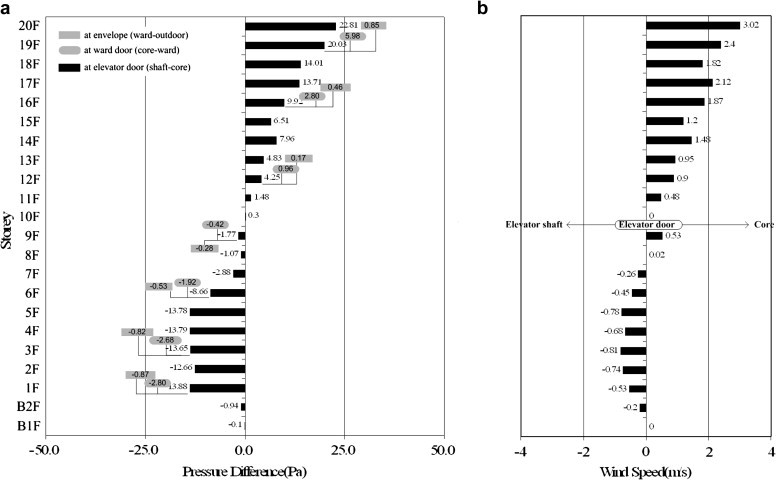
Field measurement results for each floor and section. (a) Pressure difference between spaces for each floor; and (b) Air flow direction and wind speed when elevator doors are opened in each floor.

4. Multi-zone airflow simulation

4.1. Network mathematical model

In multi-zone buildings, especially in high-rise buildings, airflows through exterior walls, openings and adjacent spaces are affected by the resistance of leakage areas depending on the part of building, opening area, etc. Therefore, a network model method is suitable for predicting the pressure distribution to analyze the impact of stack effect in high-rise buildings. In this study, CONTAMW is used. The airflow calculations in CONTAMW are based on Equations (4), (5), (6) [17].

The air flow rate from zone x to zone y, Q _x,y is some function of the pressure drop along the flow path, P _x –P _y:

$$Q_{\text{x},\text{y}}=f\left(P_{\text{x}}-P_{\text{y}}\right)$$ (4)

The mass of air, m _x, in zone x is given by the ideal gas law:

$$m_{\text{x}}={\rho }_{\text{x}}{V}_{\text{x}}=\frac{P_{\text{x}}{V}_{\text{x}}}{R{T}_{\text{x}}}$$ (5)

For a transient solution the principle of conservation of mass states is shown in Equation (6)

$$\frac{\partial m_{\text{x}}}{\partial t}={\rho }_{\text{x}}\frac{\partial V_{\text{x}}}{\partial t}+V_{\text{x}}\frac{\partial {\rho }_{\text{x}}}{\partial t}=\sum _j{Q}_{\text{y},\text{x}}+Q_{\text{x}}$$ (6)

The reliability of a multi-zone airflow simulation program for evaluating the vertical spread of airborne pathogens was simulated. In order to interpret the air movements measured in the test hospital, the task of simplifying complex interior spaces by dividing them into zones is necessary. Fig. 7 shows simplified computer modeling of the complex floors or surface areas for CONTAMW simulation. In the case of the building’s lower section, the areas used for consulting and administrative duties were set as a large zone, and in the case of the ward section, the areas used as patients’ rooms were set as another large zone. The elevator halls and the hallways, the washrooms, and vertical shafts (stairways and elevators) were set as separate zones, and the vertical shafts of different floors, which affect the air flow between floors, were then connected. To obtain a stable state interpretation, the calculation conditions were, as much as possible, set at the same values as the real measurements. Accordingly, the outside temperature was set at the average temperature of field measurements at 4.0 °C, and the inside temperature was also set at the average temperature of field measurements at 25 °C (average of inside temperatures that were actually measured). Numerous input data must be supplied in the CONTAMW to define a building. Air leakage is one of the influential factors of pressure distribution. Therefore, the air leakages of essential components on major airflow paths were measured for airflow simulations. For components whose air leakages were not measured, published data [2] were used as input for the simulation model. The basic input values on infiltration are as shown in Table 2 , and the supply air and return air volumes for each floor are as shown in Table 3 . The examination of data from the building management showed that the supply and return air volumes at night were being operated at 20% of their maximum levels, and the supply air volume was about 20% greater than the return air volume. At night, with the exception of the emergency room on the first floor, the consulting rooms and office rooms were located from the first floor to the fifth floor, and only a minimum ventilation system was operating in order to maintain the inside temperature. From the results of field measurements, it is judged that the supply and return air volumes did not exert any noticeable influence on the pressure difference profiles due to the stack effect that occurs in the test hospital.

Fig. 7.

The test hospital’s CONTAMW modeling. (a) Typical floors (ward zones); and (b) Public zones (lower section).

Table 2.

Infiltration (air leakage) data [2].

	Building component	Air leakage data
Exterior wall	Lobby	Average: EqLA75 2.1 cm2/m2
	Typical floors	EqLA10 1.51 cm2/m2
Door	Ward entrance door	EqLA10 70 cm2/item
	Elevator door	EqLA10 325 cm2/item
	Stairwell door	EqLA10 120 cm2/item
	Swing door located on lobby floor	430 CMH at 50 Pa
	Revolving door located on lobby floor	73 CMH at 50 Pa
Etc	Top of elevator shaft	Equivalent orifice area of 1.0 m2

EqLA₇₅: Equivalent leakage area at 75 Pa; EqLA₁₀: Equivalent leakage area at 10 Pa.

Table 3.

Supply and return air volumes data.

	Area (m2)	Height (m)	Supply air rate (m3/h)	Return air rate (m3/h)
Public area (lower section)	11,000	6.0	58,372	43,959
Nursing department (typical floors)	3200	4.0	12,527	10,365
Ward unit (single)	48.5	4.0	1200	1020
Ward unit (double)	28.8	4.0	750	510
Ward unit (5 persons)	23.8	4.0	720	609

4.2. Simulation results

The assumed input data were checked through numerous simulations to obtain agreement between the simulated and the measured pressure distributions. Since stack effect problems on typical floors occur mostly around the core area, input data were checked by matching the pressure differences mainly across the elevator doors and ward entrance doors. The initial simulations results did not match the measurement results well. It is assumed that the simulated values deviated from the measured values because the air leakage data of exterior walls of test building was not being estimated accurately and lobbies and basement floors had numerous doorways connected to the outdoor air. Therefore, the air leakage data were modified for the exterior walls, entrance doors located on lobbies and basement floors, and orifice area on the top of the elevator shafts, which is connected to the elevator machine room. The leakage data for the elevator, stairwell, and residential entrance doors, however, were not adjusted because they were based on tested values. When the elevator doors are operating under normal conditions, the initial simulation estimates that were used to analyze the air movements in the test hospital showed that the pressure differences in the first and second basement floors were about 8 Pa greater than the actual pressure difference measurements. Because of these differences between the simulation estimates and the field measurements of the pressure differences in the first and second basement floors, in the 20th floor, the simulation estimate was about 10 Pa higher than the field measurement. This shows that the input data in the connecting area, such as between the basement parking lot and the elevators, is probably incorrect. Accordingly, the input data for other floors were fixed and those for the basement were revised. The revision was carried out in the process of changing the air-tightness of the surface area and the infiltration volume data for the doors at the basement parking lot. Also, with the revision, the pressure difference in the first and second basement floors was compared with the field measurements and was reduced to less than 1 Pa. As the basement floors were revised, the gap between simulation and actual values for the 20th floor also naturally decreased. The differences between field measurements and estimates for elevator doors and ward entrance doors in all floors were less than 4 Pa and 1.5 Pa, respectively, which showed the reliability of the simulation. Fig. 8 compares the pressure differences across elevator doors and ward entrance doors, obtained by measurement and simulation. This figure shows that, in general, the simulation results match the measurement results well, except for a few floors. Based on the test hospital’s CONTAMW input variables that were confirmed to be reliable, various proposals for analyzing the infectious airborne virus were made and applied, thus enabling diverse simulation tests.

Fig. 8.

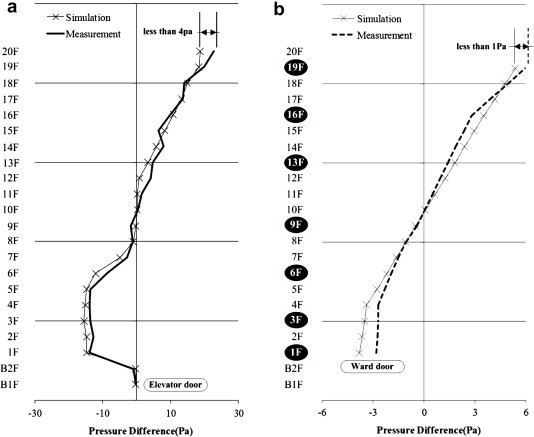
Comparison of field measurements and simulation results. (a) Pressure difference at elevator doors; and (b) Pressure difference at the ward entrance doors.

5. Prediction of airborne virus spread

The airflow pattern changes due to outside air temperature in various spaces were identified for each floor, and the influence of the stack effect on the vertical spread of airborne viruses was analyzed. The calculation conditions were the same as the simulation verification conditions discussed above except for the outside temperature. For the basic outside air temperature, −10 °C was selected based on the Seoul region’s TAC 2.5%, and the temperature was then changed sequentially to −5 °C, 0 °C, 5 °C, and 10 °C, and analyzed as stable states. Also, in order to analyze only the consequence of the stack effect, it was assumed that there was no wind outside the building. The spread of the airborne virus was calculated and interpreted by assuming the volume of air breathed by infected patients. N₂O was chosen as the tracer gas for tracing the spread of the airborne virus that originated from breathed air emitted from infected patients and released from the breathing area of a sitting human to simulate the coughing or sneezing of a sick patient. It is present in the atmosphere with variable background levels fluctuating around 0.32 ppm. However, the fluctuations are slow and the test results can be background corrected [21]. And we assumed that the tracer gas originated at second floor, fourth floor and seventh floor. Fig. 9 shows the indoor airborne virus transmission path.

Fig. 9.

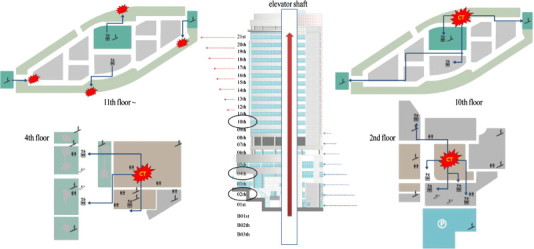
The indoor airborne virus (tracer gas) transmission path.

5.1. The effect of pressure difference caused by outside air temperature

Fig. 10 shows the changes in pressure difference due to outside air temperature for each floor. Examining the pressure difference at the elevator doors when the outside temperature was −10 °C (because first and second basement floors did not have outside walls), the pressure difference was less than −1 Pa, but for the first floor with entrance doors, it was −27.59 Pa due to the high pressure in the elevator halls. For the second, third, and fourth floors, the pressure difference did not change significantly from that of the first floor because the floors were vertically connected to the first floor through the void. From the fifth floor onwards, the pressure difference increased from 5 Pa to 10 Pa for each floor, and it was 34.92 Pa in the 21st floor. Examining the pressure difference at the doors of various rooms and wardrooms, it was −7.2 Pa for the first floor and steadily increased with the increase in the height of the floors, reaching 6.5 Pa for the 15th floor. The pressure difference at the windows showed the same pattern, and the fluctuations stayed within ±2 Pa. It was also shown that a lower outside temperature led to a wider pressure difference profile than that of the stack effect because of the increase in the temperature gap with the inside temperature. This means that the stack effect became more pronounced and increased the air inflow and outflow volumes between spaces. When the rate of change in pressure difference was compared to the rate of change in outside temperature, an increase in the outside temperature from −10 °C to −5 °C showed about 15% decrease in the pressure difference due to the stack effect, an increase from −10 °C to 0 °C showed a 31.4%, an increase from −10 °C to 5 °C showed a 46.5% decrease, and an increase from −10 °C to 0 °C showed a 60.6% decrease.

Fig. 10.

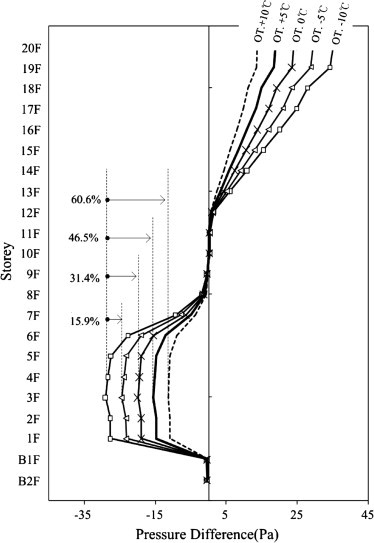
Pressure difference changes caused by outside air temperature.

5.2. Tracer gas simulation

5.2.1. Infection risk according to tracer gas concentration

The investigation is focused on the passive tracer gas concentration field and infection risks. Some of the results are compared with the earlier on-site measurements [22]. Considering that the sizes of human-generated aerosols typically range from 5 to 100 μm, using a tracer gas to represent their aerodynamic behaviors by neglecting the gravity effect on the aerosols can reasonably give meaningful results, especially for those fine droplets. The aerosols’ movement modeling, which can more accurately capture the dispersion characteristics of sneezed/coughed virus-containing droplets, will be studied and reported in a separate paper [23]. Based on the knowledge of infection dose (the number of organisms required to cause infection), the risk of airborne infection and ventilation rate per person can be correlated by Wells–Riley equation [24].

$$P=\frac{C}{S}=\left(1-e^{-\frac{Iqpt}{Q}}\right)$$ (7)

The quantum, q, represents the generation rate of infectious doses. Exposure to one quantum gives an average infection probability of (1 − e ⁻¹). The Wells–Riley equation is set up on the assumption of a well-mixed and steady-state condition. We can get the concentration of infectious particles at a certain point, which allows derivation of spatial distribution of infection risk. It does not require the assumption of well-mixed conditions. The spatial variance of infection probability is similar to the distribution of mass fraction of the tracer gas and a high concentration denotes a high risk [23].

5.2.2. Tracer gas concentration distribution for each floor

Fig. 11 shows the tracer gas concentration for each floor according to the outside temperature and the floors where the tracer gas originated (second floor, fourth floor, seventh floor). The overall concentration range was weak at less than 1.5E-05, but because this concentration represents the average concentration for the entire space, a comparative analysis is needed. The tracer gas, which represents the spread of airborne viruses, rose through the elevator halls and was detected in the upper section of the building, but it was not detected in the lower section of the building below the NPL. Within the upper section, the concentration increased as floor heights increased. Examining the concentration according to where the tracer gas originated from, when the outside temperature was −10 °C, the second floor showed about 95% higher concentration than that of the fourth and seventh floors. This was because the air inflow was much greater in the first and second floors, whereby the inflowing air was rising to the upper parts through the elevator shafts. The tracer gas originating from the fourth and seventh floors was also detected in the upper floors, but investigating the pressure difference profile due to the stack effect, because the volume of air moving up to the upper floors through the fourth and seventh floors is rather small, only a small amount of gas is detected. In the upper floors above the NPL, when the tracer gas is released it does not spread toward the elevator halls but rather moves toward the windows facing outside air, thus limiting the gas from being detected throughout the floor. Looking at these results, it is judged that controlling the outside air flowing in through openings and entrances on the first and second floors will play an important role in blocking the spread of infectious viruses due to the stack effect. Fig. 11 shows the tracer gas concentration profile over the height of the hospital building, when the gas is released from the second floor and the outside temperature is set at −10 °C, 0 °C, and 10 °C. In the figure, looking at the concentration distribution for each floor when the temperature was −10 °C, the concentration detected in the upper floors was about 44% higher than when the temperature was +10 °C. This was in-line with the above assumption that the outside temperature affected the concentration of tracer gas detected in the upper floors.

Fig. 11.

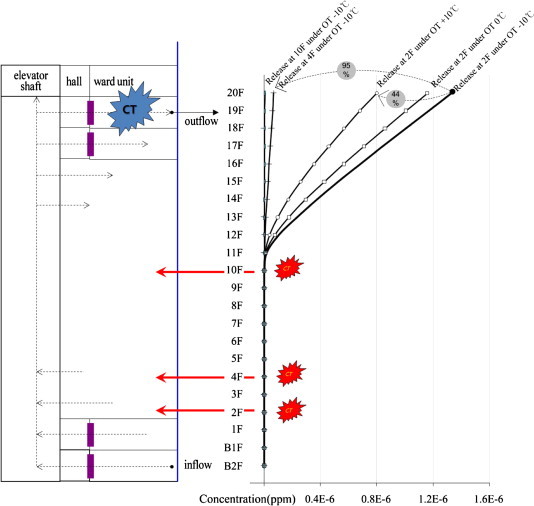
Tracer gas concentration profile over the height of the hospital building.

6. Conclusions

At a time when epidemics such as H1N1 are spreading throughout the world, the general hospital is a place of battle with biological pathogens and, in certain cases, can become the most dangerous place from where infectious disease can spread. This paper has used previous studies as a basis and proved through on-site measurements and multi-zone airflow simulations the possibility of infectious airborne viruses spreading through the stack effect in large, high-rise hospitals. Also, by analyzing the influence of the stack effect regarding vertical spread of gas to the entire hospital space, the paper presented basic data for ventilation planning for high-rise hospitals. The results of this research are as follows:

• (1)The pressure difference pattern for each floor of the test hospital shows a typical stack effect, and in the process of comparing field measurements with the CONTAMW estimates, the estimate values were checked based on the actual values in order to obtain reliability. Investigating the air inflow pattern due to pressure difference and using the NPL as the standard, in the lower section of the building the outside air flowed in through openings and cracks, such as entrances and windows, and moved to the core, where it rose to the upper floors through elevator shafts and staircases, and then flowed out again through the upper floor openings and cracks, such as ward room windows.
• (2)The elevator shaft and core temperatures rose as floor heights increased, and when the elevator doors opened, the air flow direction flowed into the elevator shafts in the lower floors whereas it flowed out from the core in the upper floors. The wind speed when the elevator doors opened was about 3 m/s on the 20th floor, causing an unpleasant experience for the people using the elevator halls. Examining the changes in the pressure difference profile in each of the spaces due to changes in the outside temperature, when the outside temperature decreased, the overall pattern did not change, but the pressure difference changed dramatically. Each 5 °C decrease in outside temperature caused about 15% increase in pressure difference. Also, when tracer gas representing infectious airborne viruses was released from designated floors, the current movement pattern due to the stack effect caused the gas to be detected in the upper floors but not in the lower floors. As the floor where the tracer gas was released reduced in height, or as the outside temperature reduced, the concentration detected in the upper floors increased, and this concentration level increased in the higher floors.

When all the results of the study are considered together, in order to minimize the spread of air flow movement due to the stack effect, the existing construction method should continue to be used but an additional plan for the frequently used entrances of the hospital to be made more airtight is required. Moreover, a zoning plan could be considered where the wardrooms for patients with a possible infectious disease are placed in the upper floors above the NPL.